Color Point Cloud Registration Algorithm Based on Hue
Abstract
:1. Introduction
2. Color Theory Analysis
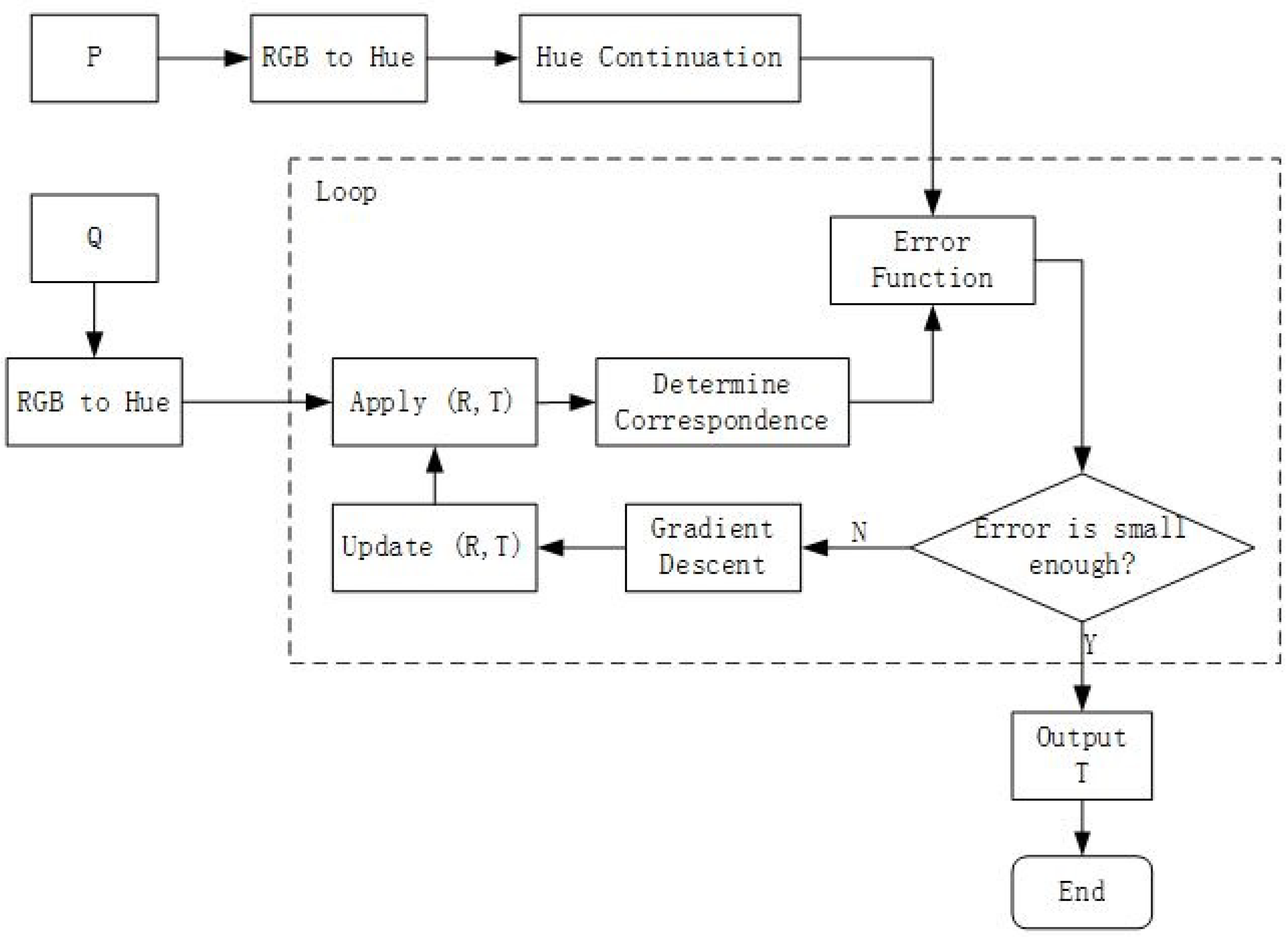
3. Algorithm Implementation
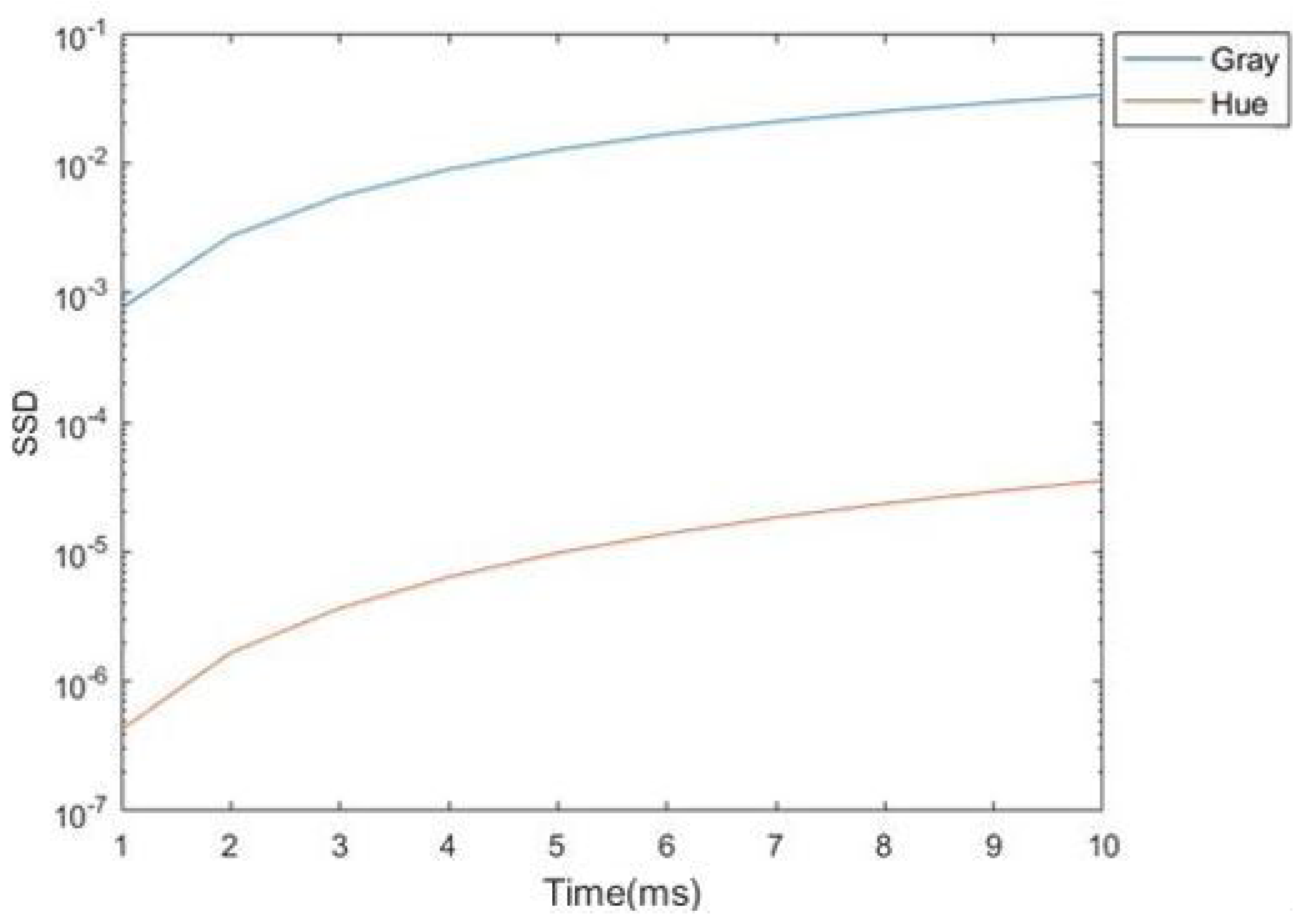
3.1. Continuation of Hue Distribution
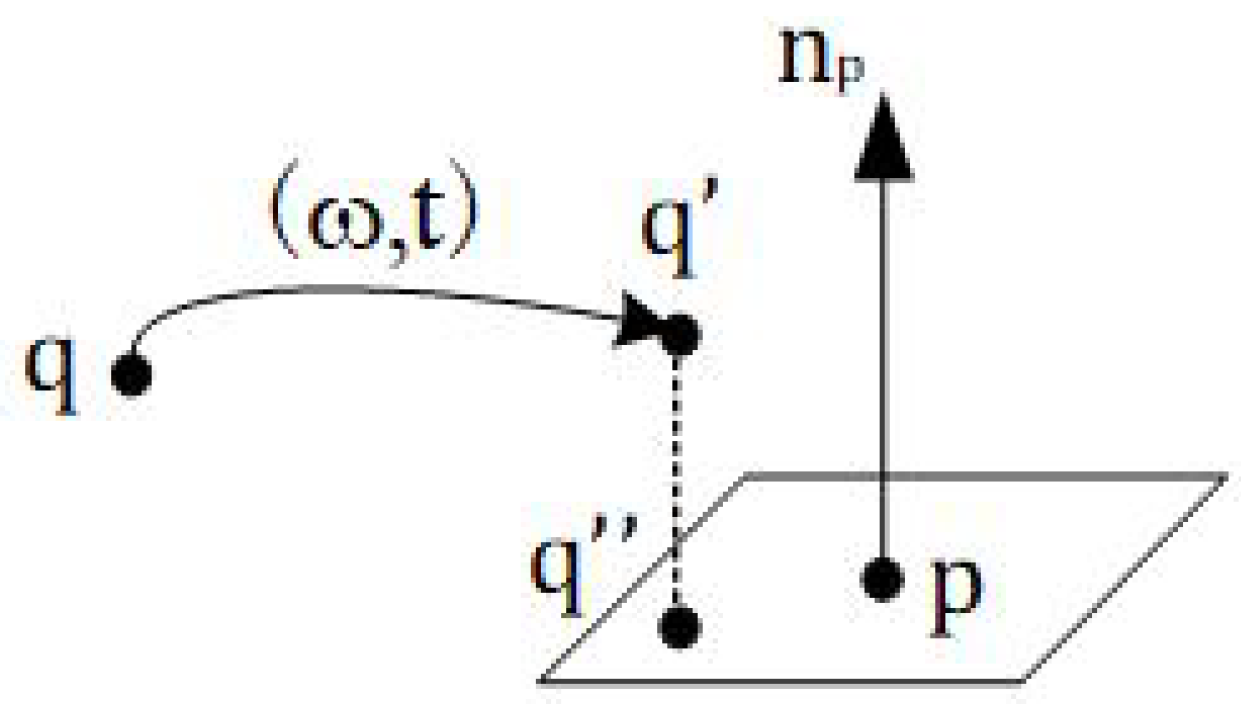
3.2. Error Function
3.3. Optimization Method
4. Experiment
4.1. Point Cloud Registration
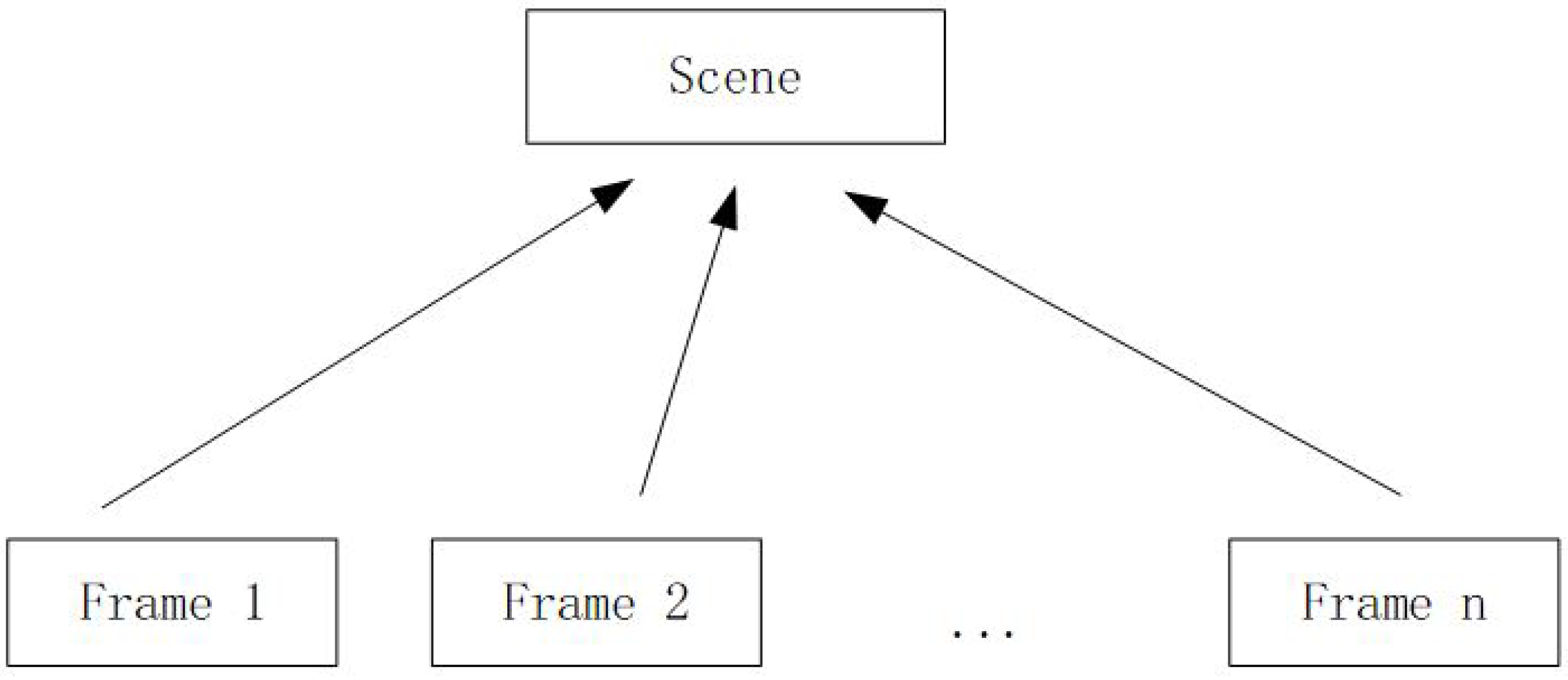
4.2. Scene Reconstruction
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Conflicts of Interest
References
- Besl, P.J.; Mckay, H.D. A method for registration of 3-D shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Zhou, Q.Y.; Koltun, V. Depth camera tracking with contour cues. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Kang, S.B.; Johnson, A.E. Registration and integration of textured 3D data 1. Image Vis. Comput. 1999, 17, 135–147. [Google Scholar]
- Yang, C.; Medioni, G. Object modeling by registration of multiple range images. Image Vis. Comput. 2002, 10, 145–155. [Google Scholar]
- Rusinkiewicz, S.; Levoy, M. Efficient Variants of the ICP Algorithm. In Proceedings of the Third International Conference on 3-D Digital Imaging and Modeling, Quebec City, QC, Canada, 28 May–1 June 2001; pp. 145–152. [Google Scholar]
- Gelfand, N.; Ikemoto, L.; Rusinkiewicz, S.; Levoy, M. Geometrically Stable Sampling for the ICP Algorithm. In Proceedings of the Fourth International Conference on 3-D Digital Imaging and Modeling, Banff, AB, Canada, 6–10 October 2003; pp. 260–267. [Google Scholar]
- Chetverikov, D.; Svirko, D.; Stepanov, D.; Krsek, P. The Trimmed Iterative Closest Point Algorithm. In Proceedings of the International Conference on Pattern Recognition, Quebec City, QC, Canada, 11–15 August 2002. [Google Scholar]
- Lu, W.; Wan, G.; Zhou, Y.; Fu, X.; Song, S. DeepICP: An End-to-End Deep Neural Network for 3D Point Cloud Registration. arXiv 2019, arXiv:1905.04153. [Google Scholar]
- Wang, Y.; Solomon, J. Deep Closest Point: Learning Representations for Point Cloud Registration. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 20–26 October 2019; pp. 3523–3532. [Google Scholar]
- Ji, H.J.; An, K.H.; Kang, J.W.; Chung, M.J.; Yu, W. 3D environment reconstruction using modified color ICP algorithm by fusion of a camera and a 3D laser range finder. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots & Systems, St. Louis, MO, USA, 10–15 October 2009. [Google Scholar]
- Korn, M.; Holzkothen, M.; Pauli, J. Color supported generalized-ICP. In Proceedings of the International Conference on Computer Vision Theory & Applications, Lisbon, Portugal, 5–8 January 2015. [Google Scholar]
- Men, H.; Gebre, B.; Pochiraju, K. Color point cloud registration with 4D ICP algorithm. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011. [Google Scholar]
- Lai, K.; Bo, L.; Fox, D. Unsupervised feature learning for 3D scene labeling. In Proceedings of the IEEE International Conference on Robotics & Automation, Hong Kong, China, 31 May–7 June 2014. [Google Scholar]
- Park, J.; Zhou, Q.Y.; Koltun, V. Colored Point Cloud Registration Revisited. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 143–152. [Google Scholar]
- Smith, A.R. Color gamut transform pairs. ACM Siggraph Comput. Graph. 1978, 12, 12–19. [Google Scholar] [CrossRef]
- Ganesan, P.; Rajini, V.; Sathish, B.S.; Shaik, K.B. HSV color space based segmentation of region of interest in satellite images. In Proceedings of the International Conference on Control, Kanyakumari, India, 10–11 July 2014. [Google Scholar]
- Zhang, X.N.; Jiang, J.; Liang, Z.H.; Liu, C.L. Skin color enhancement based on favorite skin color in HSV color space. IEEE Trans. Consum. Electron. 2010, 56, 1789–1793. [Google Scholar] [CrossRef]
- Liu, J.; Zhong, X. An object tracking method based on Mean Shift algorithm with HSV color space and texture features. Clust. Comput. 2018, 22, 6079–6090. [Google Scholar] [CrossRef]
- Rusu, R.B.; Cousins, S. 3D is here: Point Cloud Library (PCL). In Proceedings of the IEEE International Conference on Robotics & Automation, Shanghai, China, 9–13 May 2011. [Google Scholar]
- Rusu, R.B.; Blodow, N.; Beetz, M. Fast Point Feature Histograms (FPFH) for 3D registration. In Proceedings of the IEEE International Conference on Robotics & Automation, Kobe, Japan, 12–17 May 2009. [Google Scholar]



| Scene | ICP(Point-to-Plane) | Colored ICP | DeepICP | DCP | Ours |
|---|---|---|---|---|---|
| Scene 01 | 0.30169 | 0.2565 | 0.22677 | 0.25655 | 0.31243 |
| Scene 02 | 0.46729 | 0.49933 | 0.39056 | 0.45560 | 0.57276 |
| Scene 03 | 0.40828 | 0.43826 | 0.43055 | 0.39081 | 0.43183 |
| Scene 04 | 0.72208 | 0.64827 | 0.59185 | 0.57669 | 0.69705 |
| Scene 05 | 0.39475 | 0.44788 | 0.46891 | 0.48991 | 0.47814 |
| Average | 0.45882 | 0.458047 | 0.42173 | 0.43391 | 0.498444 |
| Scene | ICP(Point-to-Plane) | Colored ICP | DeepICP | DCP | Ours |
|---|---|---|---|---|---|
| Scene 01 | 0.011659 | 0.010644 | 0.011566 | 0.0133556 | 0.0083734 |
| Scene 02 | 0.009786 | 0.008685 | 0.010001 | 0.012001 | 0.0078229 |
| Scene 03 | 0.010901 | 0.009949 | 0.013001 | 0.009551 | 0.0090334 |
| Scene 04 | 0.009115 | 0.009015 | 0.009511 | 0.010331 | 0.0072203 |
| Scene 05 | 0.013106 | 0.011067 | 0.015600 | 0.011331 | 0.009821 |
| Average | 0.011198 | 0.009872 | 0.011936 | 0.013140 | 0.008454 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, S.; Chen, X.; Cai, H.; Wang, Y.; Liang, H.; Li, H. Color Point Cloud Registration Algorithm Based on Hue. Appl. Sci. 2021, 11, 5431. https://doi.org/10.3390/app11125431
Ren S, Chen X, Cai H, Wang Y, Liang H, Li H. Color Point Cloud Registration Algorithm Based on Hue. Applied Sciences. 2021; 11(12):5431. https://doi.org/10.3390/app11125431
Chicago/Turabian StyleRen, Siyu, Xiaodong Chen, Huaiyu Cai, Yi Wang, Haitao Liang, and Haotian Li. 2021. "Color Point Cloud Registration Algorithm Based on Hue" Applied Sciences 11, no. 12: 5431. https://doi.org/10.3390/app11125431
APA StyleRen, S., Chen, X., Cai, H., Wang, Y., Liang, H., & Li, H. (2021). Color Point Cloud Registration Algorithm Based on Hue. Applied Sciences, 11(12), 5431. https://doi.org/10.3390/app11125431






