Code Calibration of the Eurocodes

Featured Application

The article proposes a new model for the Eurocodes.

Abstract

This article addresses the process to optimally select safety factors and characteristic values for the Eurocodes. Five amendments to the present codes are proposed: (1) The load factors are fixed, γ_G = γ_Q, by making the characteristic load of the variable load changeable, it simplifies the codes and lessens the calculation work. (2) Currently, the characteristic load of the variable load is the same for all variable loads. It creates excess safety and material waste for the variable loads with low variation. This deficiency can be avoided by applying the same amendment as above. (3) Various materials fit with different accuracy in the reliability model. This article explains two options to reduce this difficulty. (4) A method to avoid rounding errors in the safety factors is explained. (5) The current safety factors are usually set by minimizing the reliability indexes regarding the target when the obtained codes include considerable safe and unsafe design cases with the variability ratio (high reliability/low) of about 1.4. The proposed three code models match the target β₅₀ = 3.2 with high accuracy, no unsafe design cases and insignificant safe design cases with the variability ratio 1.07, 1.03 and 1.04.

1. Introduction

This article explores the code calibration of the Eurocodes [1,2,3,4], i.e., the process to select the safety factors and the characteristic values to optimally fit with the probabilistic mathematical action-resistance model and to obtain simple and accurate codes that require little calculation work.

The article starts by explaining some deficiencies of the current Eurocodes. The two main objects, simplicity and accuracy, are described. The basic assumptions and equations are disclosed. The material safety factors for the Eurocodes are given with the current characteristic values and changeable characteristic values. Two methods are explained to improve the reliability accuracy by setting the material safety factors as alternating. A method to avoid rounding errors is disclosed. Approximate comparison of the proposed codes and the current ones is given. The steel safety factor is an issue in the current Eurocodes that are discussed. Economic and environmental aspects are briefly addressed.

1.1. Limitations

The focus of the article is to disclose amended Eurocodes with changeable characteristic values. Many selections are made that need optimization, further work and discussion among researchers and code writers, such as:

• Selection of the load factor, γ_L = 1.2, is selected here.
• Selection of the primary material, timber, V_M = 0.2, is selected here.
• A method to set the material factors, no unsafe design cases are allowed, and the load cases including less than 20% permanent load or variable load is omitted.

Only the basic design cases with the three main materials, steel, timber and concrete, loaded by one permanent load and one variable load, are addressed. Thus, the codes proposed here can be characterized as the first draft that can be improved.

1.2. Review

The structural codes and articles regarding codes are divided into three accuracy levels: I, II and III [1,2,3,4,5,6,7,8,9,10,11,12].

The Eurocodes were previously based on level I, i.e., on deterministic, historic and empiric methods, where the code calibration was also deterministic, historic and empiric.

The safety factors of the current Eurocodes are based on level II, i.e., on the first-order reliability method. The primary assumption of this method is the independent load combination where a load reduction occurs. It is implemented by sensitivity factors α_E and α_R, which decrease the target reliability and cause a load reduction, as in this load combination, it is improbable that the highest permanent load and the highest variable load occur simultaneously. The load reduction is implemented by calculating the variable load reliability for 5-year loads [1,2,3,4,5,6,7,8,9,10,11,12] and should be calculated for 50-year loads [13].

The accuracy level III is a full probabilistic method. Such a method has not been implemented in any structural codes yet but was allowed for in [1]. The codes presented in this article are based on the full probabilistic model.

The current safety factors are normally [14,15,16,17] set by minimizing the sums of second powers of reliability index differences of the actual ones regarding to the target. In other words, the safety factors γ_G, γ_Q and γ_M are set by minimizing the expression (1) in all feasible design cases, i.e., in all materials and in permanent-variable load proportions.

$${\displaystyle \sum }_{\mathrm{i}}{\mathrm{w}}_{\mathrm{i}}{\left({\mathsf{\beta }}_{\mathrm{i}}-{\mathsf{\beta }}_{\mathrm{t}}\right)}^2$$

(1)

where ${\mathrm{w}}_{\mathrm{i}}$ denotes the weight factor of the design case i, ${\mathsf{\beta }}_{\mathrm{i}}$ is the reliability index in the design case i and ${\mathsf{\beta }}_{\mathrm{t}}$ is the target reliability index. In this calculation, the overall outcome is correct for its mean reliability index only. There is roughly an equal number of unsafe and safe design cases, and the codes may include substantial safe and unsafe design cases. Further, Equation (1) is biased as explained in [18].

This article proposes a code calibration process without using the reliability index, and the proposed codes have high accuracy in terms of the target reliability.

In the current codes, the characteristic values are constant. This article proposes that the characteristic values are changeable.

1.3. Weaknesses

The current Eurocodes include some disadvantages:

• The load factors are dissimilar, γ_G ≠ γ_Q, i.e., the permanent load safety factor is different from the variable load safety factor, which increases the required calculation work, complicates the codes, and makes the codes prone to design errors. The basic assumptions in the partial safety factor approach are that the characteristic value of the permanent load is the mean, and the characteristic value of the variable load is the 0.98-fractile of the one-year load. These assumptions result in dissimilar load factors, γ_G ≠ γ_Q. As these assumptions have not been questioned earlier, partial safety factor codes with the same load factors have not been proposed previously.
• The characteristic load of the variable load is the same for all variable loads, which is the 0.98-fractile of the one-year distribution, regardless of the load variation, and the variable load safety factor (γ_Q = 1.5) is the same for all variable loads in the design of normal structures. This creates excess safety and material waste for the variable loads with low variation. The article explains that this deficiency is mainly overcome by setting the characteristic load of the variable load changeable and the function on the alterability of the variable load. It means that each variable load has its own characteristic load. As the variable load characteristic values are changeable, this feature is used to obtain another positive result, i.e., the load factors are fixed as the same.
• In the current Eurocodes, various materials fit differently with the reliability model. The design of some materials is more accurate regarding the target reliability than others. The proposed procedure allows the formulation of codes where one material can be selected to have an almost ideal fit with the target reliability and with virtually no reliability error. The timber, V_M = 0.2, is selected here to be the ideal material. Other materials have higher reliability variations. This article presents two options in which the material safety factors are functions of the load proportions when all materials fit well with the reliability model.
• The current Eurocodes may include wide reliability variation regarding the target, about −20% to 20%, i.e., a variability ratio (high safety factor or reliability index regarding the low value) of about 1.4 [14,19]. The high-reliability variability is due to the fixed characteristic load of the variable load, the independent load combination and the indirect safety factor setting procedure using the reliability index as a reference. In this article, the safety factors are calculated directly without using the reliability index as a calculation aid, and the variability ratio is about 1.03–1.07.
• Current codes include several safety factors with rounding errors. This article explains a method to eliminate the rounding errors in the safety factors.
• This article proposes partial safety factor codes with the same load factors, γ_G = γ_Q. Thus, the proposed codes can be used as the design value format, i.e., as allowable stress codes, by removing the load factors and by multiplying the characteristic resistance values with the load factors.

1.4. Two Major Objectives

The Eurocodes, as well as several other codes, have two major deficiencies: complexity and inaccuracy regarding the target reliability. This proposal particularly addresses these two issues.

Most current codes are partial safety factor codes with dissimilar load factors, γ_G ≠ γ_Q, in the Eurocodes, γ_G = 1.35 and γ_Q = 1.5. This is a major reason for the complexity of the codes. The design value codes γ_G = γ_Q = 1 are the simplest, but it has not been proposed here, as the partial safety factor concept is widely implemented. This proposal is based on partial safety factor codes with equal load factors, γ_G = γ_Q. It simplifies the codes and decreases the calculation work. The load tables of such codes are the same as the design value codes, and the codes with equal load factors, γ_L = γ_G = γ_Q, can easily be converted into the design value codes, γ_G = γ_Q = 1, by altering the material safety factors (γ_M^.) as

$${\mathsf{\gamma }}_{\mathrm{M}}{}^{,}={\mathsf{\gamma }}_{\mathrm{L}}{\mathsf{\gamma }}_{\mathsf{M}}$$

(2)

where ${\mathsf{\gamma }}_{\mathrm{M}}{}^{,}$ is the new material safety factor for the design value codes, i.e., it is the allowable stress and that ${\mathsf{\gamma }}_{\mathrm{L}}$ is the load factor.

In the Eurocodes, the load factors can be set as the same using the reasoning below:

The basic design equation of the current Eurocodes [1] is

$$1.35\mathrm{G}+1.5\mathrm{Q}\le \frac{\mathrm{M}}{{\mathsf{\gamma }}_{\mathrm{M}}}$$

(3)

The variable load safety factor is multiplied and divided by 1.35.

$$1.35\mathrm{G}+1.35\frac{1.5}{1.35}\mathrm{Q}\le \frac{\mathrm{M}}{{\mathsf{\gamma }}_{\mathrm{M}}}$$

(4)

A new variable load ${\mathrm{Q}}_{\mathrm{u}}$

$${\mathrm{Q}}_{\mathrm{u}}=\frac{1.5}{1.35}\mathrm{Q}$$

(5)

is defined, i.e., it is 11% higher than the present one. Assuming Gumbel distribution and the coefficient of the variation V_Q = 0.4, the characteristic load of ${\mathrm{Q}}_{\mathrm{u}}$ is the 103-year return load, while $\mathrm{Q}$ has a characteristic load of the 50-year return load.

Thus, the new design equation with γ_G = γ_Q is obtained by replacing $\mathrm{Q}$ with ${\mathrm{Q}}_{\mathrm{u}}$.

$$1.35\mathrm{G}+1.35{\mathrm{Q}}_{\mathrm{u}}\le \frac{\mathrm{M}}{{\mathsf{\gamma }}_{\mathrm{M}}}$$

(6)

This equation always presents the same outcome as Equation (3) and can be simplified further by dividing by 1.35, with the same outcome as Equation (3) in most cases

$$\mathrm{G}+{\mathrm{Q}}_{\mathrm{u}}\le \frac{\mathrm{M}}{1.35{\mathsf{\gamma }}_{\mathrm{M}}},$$

(7)

when the design value equation is obtained. The reliability calculation of Equations (3), (6) and (7) are different. Thus, this subject is tackled in detail here.

The codes proposed here are based on the partial safety factors. However, as the load factors are the same γ_G = γ_Q, the codes can easily be changed to allowable stress codes.

The Eurocodes may include considerable safe and unsafe design cases [14,19] with a variability ratio of about 1.4. The inaccuracy arises mainly from four reasons.

• The characteristic load of the variable load is fixed; it is the 0.98-fractile of the one-year distribution, which induces excess safety for loads with low variation.
• The loads are combined independently, which demands considerably different material safety factors in various permanent-variable load ratios.
• The current safety factor setting procedure induces large variability, as constraints for big errors are missing.
• The current safety factors are calculated indirectly using the reliability index as a reference, which induces extra error [18].

The authors of [13] have explained that the loads should be combined dependently, which is applied here. The dependent load combination is safe regarding the independent combination as it results in about 10% higher safety factors.

In this proposal, the characteristic load of the variable load is set as adaptable. It reduces the inaccuracy considerably, especially the excess safety and the material waste generated is reduced. This amendment does not increase the design work nor complicate the codes. The code writer only must do a little extra work in setting each variable load with its own characteristic load.

2. Materials and Methods

The notation of the Eurocodes applies [1].

2.1. Assumptions

Assumptions of the current structural probability theory and the Eurocodes apply, except for the independent load combination [1,5,6,7,8,9,10,11,12] and the target reliability.

As previously explained [13], the independent load combination is unsafe. The Eurocodes include three load combination rules, (8.12), (8.13a,b) and (8.14a,b). The first one is dependent and, in the author’s opinion, correct, and it has been applied here. The others are independent and not applied here. In the current Eurocodes, the material safety factors are always calculated in all load combination options independently. The material safety factors are calculated here dependently.

The target reliability index of the current Eurocodes is β₁ = 4.7, however, β₁ = 4.2 is assumed here.

In the reliability calculation, the design point is needed where the characteristic loads of all distributions, the permanent load, the variable load and the material property are fixed. The design point can be selected arbitrarily, as all distributions may be multiplied by an arbitrary number, i.e., the load distributions need not be the actual ones. The design point is set here at unity in the distribution-setting phase, i.e., in the serviceability limit state (SLS) and in the ultimate limit state (ULS). In the ULS-reliability calculation, safety factors are applied, which shift the distributions further away from the design point. It is arbitrary whether they are shifted left (down to lower loads) or right (up to higher loads), given that the load and the resistance distributions are moved further away from each other. Here, the loads are shifted down and the material properties up in the ULS. Thus, the load distributions in the ULS are obtained by dividing the SLS distributions through safety factors, and the ULS material property distributions are obtained by multiplying the SLS distributions by the material safety factors.

Three materials [2,3,4], steel, timber and concrete, are examined here, and it is assumed that the coefficients of the variations are V_M = 0.1, 0.2 and 0.3, respectively.

2.2. The Target Reliability

The target one-year reliability index is set here as β₁ = 4.2. Thus, the 50-year reliability index is β₅₀ = 3.2, i.e., the 50-year failure probability is P_f50 = 1/1499. This target reliability index is recommended in [7], and preliminary studies by the author indicate that the current safety factors of the Eurocodes approximately correspond to this reliability; in other words, it is less than intended, β₅₀ = 3.8 when the loads are combined dependently.

2.3. Permanent Load

The permanent load distribution is normal, the cumulative distribution is ${\mathrm{F}}_{\mathrm{G}}\left({\mathrm{x}; \mathsf{\mu }}_{\mathrm{G}}{, \mathsf{\sigma }}_{\mathrm{G}}\right)$ and the density distribution is ${\mathrm{f}}_{\mathrm{G}}\left({\mathrm{x}; \mathsf{\mu }}_{\mathrm{G}}{, \mathsf{\sigma }}_{\mathrm{G}}\right)$. The characteristic load is the mean. The current Eurocodes have the permanent load safety factor of γ_G = 1.35 and the target reliability index of β₅₀ = 3.8, suggesting that the coefficient of variation is V_G = 0.091. Here, the V_G = 0.1 is assumed to include uncertainty, which suggests γ_G = 1.32 for β₅₀ = 3.2.

The permanent load distribution, as well as the variable load distribution and the material resistance distributions, are illustrated in [18].

The basic design of Equation (3) discloses that any one of the safety factors γ_G, γ_Q and γ_M can be selected arbitrarily, e.g., the load safety factor γ_G can be selected as lower than the ideal value when the material safety factor (γ_M) is accordingly increased. Thus, γ_G = 1.2 is selected here, as that results in the material safety factors (γ_M), which are about the same as the existing safety factors of the Eurocodes.

2.4. Variable Load

The variable load distribution is assumed here, as normally in the structural probability theory, to be the Gumbel distribution. This distribution is used to model the maximum values. The maximum values of the variable loads are critical in the structural design.

The cumulative distribution is ${\mathrm{F}}_{\mathrm{Q}}\left({\mathrm{x}; \mathsf{\mu }}_{\mathrm{Q}}{, \mathsf{\sigma }}_{\mathrm{Q}}\right)$ and the density distribution is ${\mathrm{f}}_{\mathrm{Q}}\left({\mathrm{x}; \mathsf{\mu }}_{\mathrm{Q}}{, \mathsf{\sigma }}_{\mathrm{Q}}\right)$ fixed with the 0.98-fractile of the one-year distribution at the design point—the characteristic load. This variable load setting corresponds with the actual load measurements and the parameter settings of the Eurocodes. As explained above, the variable load safety factor is set the same as the permanent one, i.e., γ_Q = γ_G = 1.2.

In the reliability calculation, the one-year and the service time mode must be distinguished.

The variable load safety factor of the current Eurocodes is γ_Q = 1.5. It is based on the independent load combination and 5-year loads, which is due to the load reduction ${\mathsf{\alpha }}_{\mathrm{E}}{\mathsf{\beta }}_{50}$, ${\mathsf{\alpha }}_{\mathrm{E}}$ = −0.7 [1].

In the dependent load combination, no reliability reduction is applied [13]. The variable load distribution is in the 50-year mode of the reliability calculation, i.e., the distribution is in the distribution setting stage ${\mathrm{F}}_{\mathrm{Q}}\left({\mathrm{x}; \mathsf{\mu }}_{\mathrm{Q}}{, \mathsf{\sigma }}_{\mathrm{Q}}\right),{ \mathrm{in} \mathrm{the} \mathrm{SLS} \mathrm{design} \mathrm{F}}_{\mathrm{Q}}{\left({\mathrm{x}; \mathsf{\mu }}_{\mathrm{Q}}{, \mathsf{\sigma }}_{\mathrm{Q}}\right)}^{50}$ and in the ULS design ${\mathrm{F}}_{\mathrm{Q}}{\left(\mathrm{x}; \frac{{\mathsf{\mu }}_{\mathrm{Q}}}{{\mathsf{\gamma }}_{\mathrm{Q}}},\frac{{ \mathsf{\sigma }}_{\mathrm{Q}}}{{\mathsf{\gamma }}_{\mathrm{Q}}}\right)}^{50}$.

As explained above, the timber V_M = 0.2 is selected to be the primary material to fit the reliability model ideally. The material safety factor for this material is the same for the permanent load and for the variable load. As explained later, this is obtained when the characteristic load of the variable load is 1.32 times higher than the current one. Thus, the current load tables for the load V_Q = 0.4 must be increased by 32%, and for the load V_Q = 0.2, these must be increased by 15%.

2.5. Materials

The material resistance distribution is assumed to be the log-normal distribution, the cumulative distribution is ${\mathrm{F}}_{\mathrm{M}}\left({\mathrm{x}; \mathsf{\mu }}_{\mathrm{M}}{, \mathsf{\sigma }}_{\mathrm{M}}\right)$ and the density distribution is ${\mathrm{f}}_{\mathrm{M}}\left({\mathrm{x}; \mathsf{\mu }}_{\mathrm{M}}{, \mathsf{\sigma }}_{\mathrm{M}}\right)$, fixed with the 0.05-fractile at the design point—the characteristic load. The distribution parameters of the three materials are given in

Table 1. The three examined materials steel, timber and concrete with parameters: V_M = coefficient of variation; μ_M = mean; σ_M = deviation; γ_M = material safety factor.

Material	VM	μM	σM	γM
Steel	0.1	1.1841	0.1184	1.0
Timber	0.2	1.4125	0.2825	1.3
Concrete	0.3	1.6921	0.5076	1.5

[2,3,4].

2.6. Uncertainty

The uncertainty is omitted here as the actual uncertainty parameters are missing, and the method to combine the uncertainty with other effects is undetermined. Thus, the target reliability β₅₀ = 3.2 applies the reliability without the uncertainty. Alternatively, it may be assumed that the load and the resistance parameters include the uncertainty. As explained later, the current steel safety factor of the Eurocodes is questionably low. If the uncertainty is considered, this controversy is even more severe.

2.7. The Basic Equations

The author has revealed the safety factor calculation procedure in detail earlier [13,18,19,20], and thus, it is explained only concisely here. Two equations are needed in the reliability calculation.

When one load (L) with the cumulative distribution ${\mathrm{F}}_{\mathrm{L}}\left({\mathrm{x}; \mathsf{\mu }}_{\mathrm{L}}{, \mathsf{\sigma }}_{\mathrm{L}}\right)$ and the safety factor ${\mathsf{\gamma }}_{\mathrm{L}}$ strikes a material with the resistance ${\mathrm{f}}_{\mathrm{M}}\left({\mathrm{x}; \mathsf{\mu }}_{\mathrm{M}}{, \mathsf{\sigma }}_{\mathrm{M}}\right)$, the equation to calculate the safety factors (γ_L or γ_M) or the failure probability (P_f) is [13,18,19,20]

$${{\displaystyle \int }}_0^{\infty }{\mathrm{F}}_{\mathrm{L}}\left(\mathrm{x}; \frac{{\mathsf{\mu }}_{\mathrm{L}}}{{\mathsf{\gamma }}_{\mathrm{L}}},\frac{{\mathsf{\sigma }}_{\mathrm{L}}}{{\mathsf{\gamma }}_{\mathrm{L}}}\right){\mathrm{f}}_{\mathrm{M}}\left({\mathrm{x}; \mathsf{\mu }}_{\mathrm{M}}{\mathsf{\gamma }}_{\mathrm{M}}{, \mathsf{\sigma }}_{\mathrm{M}}{\mathsf{\gamma }}_{\mathrm{M}}\right){\mathrm{dx}=1-\mathrm{P}}_{\mathrm{f}}$$

(8)

Both distributions are set in the design point with equal characteristic values.

When the load comprises the permanent load and the variable load, and the variable load proportion is α, in relation to the total load, α = ${\mathsf{\mu }}_{\mathrm{Q}}/{\mathsf{\mu }}_{\mathrm{G}}+{\mathsf{\mu }}_{\mathrm{Q}}$, the cumulative distribution can be obtained from adding up the partial distributions by fractiles. Monte Carlo simulation with one seed number is one calculation option, i.e., a random seed number is selected, the permanent load and the variable load is computed from the distributions and the obtained values are added up; this denotes the combination load value. The combination distribution crosses the crossing point of the partial distributions, and this fact can be used for the combination distribution calculation [19]. These methods are impractical, and the next recursive equation is a simple method to calculate the dependent combination distribution (${\mathrm{F}}_{\mathrm{d}}$) in load proportion (α) [13]

$${\mathrm{F}}_{\mathrm{d}}\left(\mathrm{x},\mathsf{\alpha }\right)=\left|\begin{array}{c}\mathrm{y}\leftarrow \mathrm{root}\left[{\mathrm{F}}_{\mathrm{G}}\left[\mathrm{x}-\mathrm{r}; \frac{{\mathsf{\mu }}_{\mathrm{G}}\left(1-\mathsf{\alpha }\right)}{{\mathsf{\gamma }}_{\mathrm{G}}},\frac{{\mathsf{\sigma }}_{\mathrm{G}}\left(1-\mathsf{\alpha }\right)}{{\mathsf{\gamma }}_{\mathrm{G}}}\right]-{\mathrm{F}}_{\mathrm{Q}}\left[\mathrm{r}; \frac{{\mathsf{\mu }}_{\mathrm{Q}} \mathsf{\alpha }}{{\mathsf{\gamma }}_{\mathrm{Q}}},\frac{{\mathsf{\sigma }}_{\mathrm{Q}} \mathsf{\alpha }}{{\mathsf{\gamma }}_{\mathrm{Q}}}\right],\mathrm{r}\right]\\ {\mathrm{F}}_{\mathrm{d}}\leftarrow {\mathrm{F}}_{\mathrm{Q}}\left[\mathrm{y}; \frac{{\mathsf{\mu }}_{\mathrm{Q}} \mathsf{\alpha }}{{\mathsf{\gamma }}_{\mathrm{Q}}},\frac{{\mathsf{\sigma }}_{\mathrm{Q}} \mathsf{\alpha }}{{\mathsf{\gamma }}_{\mathrm{Q}}}\right]\end{array}\right.$$

(9)

The safety factors γ_G, γ_Q, γ_M or the failure probability P_f are calculated using Equation (8) when the load distribution ${ \mathrm{F}}_{\mathrm{L}}$ is replaced by ${\mathrm{F}}_{\mathrm{d}}$.

3. Results

A method to select the safety factors and the characteristic values is explained next.

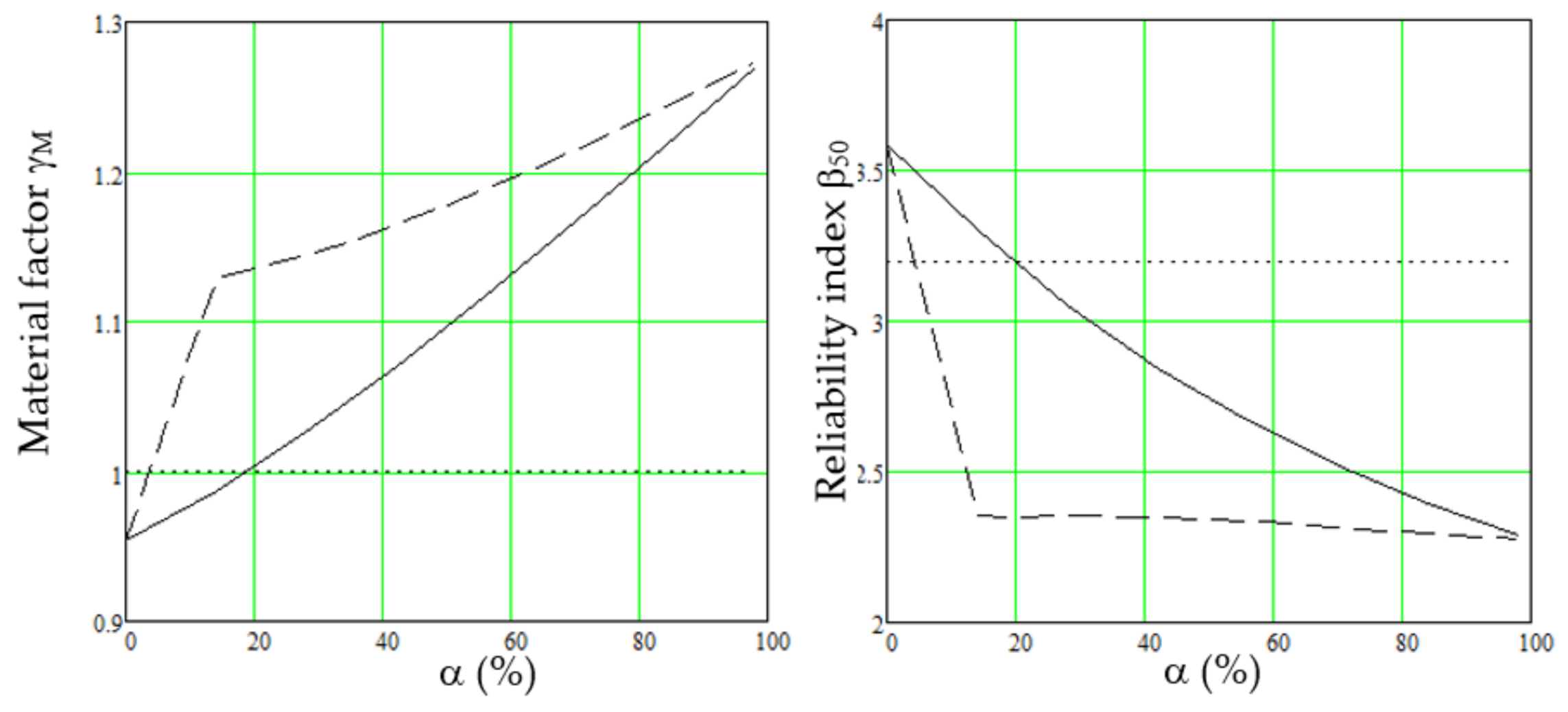
3.1. The Material Factors with the Current Characteristic Values

As per the material safety factors based on the Equations (8) and (9) and the assumptions explained above—β₅₀ = 3.2, γ_L = γ_G = γ_Q = 1.2—the characteristic variable load is the same as the current load table value, i.e., the 50-year return load. This is illustrated in Figure 1, right. The solid line denotes steel, V_M = 0.1, V_Q = 0.4; the dashed line denotes timber, V_M = 0.2, V_Q = 0.4; and the dash-dotted line denotes concrete, V_M = 0.3, V_Q = 0.4. The dotted lines imply V_Q = 0.2. Figure 1, left applies to an analogous calculation with γ_G = 1.35, γ_Q = 1.5.

We see that the lines are inclined upwards, and the assumptions mentioned above denote a poor outcome for the safety factors of the codes. As in the codes, the material safety factors are constant for each load proportion; thus, these curves should be horizontal or close to horizontal. The variable load safety factor γ_Q should be 20%–40% higher than assumed for loads V_M = 0.4 and 10%–20% higher for loads V_Q = 0.2. This deficiency is overcome by setting the characteristic load of the variable load as alternating in the manner explained in the next section.

3.2. Alternating Characteristic Load of the Variable Load

As explained above, timber (V_M = 0.2) is selected here to be the primary material, which ideally matches with the reliability model, i.e., the material safety factor (γ_M) is the same for the permanent load and for the variable load, and this applies to both V_Q = 0.2 and V_Q = 0.4 loads.

The material safety factor for the permanent load calculated from Equation (8) is γ_M = 1.21, which is obtained by solving the equation

$${{\displaystyle \int }}_0^{\infty }{\mathrm{F}}_{\mathrm{G}}\left(\mathrm{x}; \frac{1}{1.2},\frac{0.1}{1.2}\right){\mathrm{f}}_{\mathrm{M}}\left(\mathrm{x}; 1.412{\mathsf{\gamma }}_{\mathrm{M}},0.282{\mathsf{\gamma }}_{\mathrm{M}}\right)\mathrm{dx}=1-1/1499$$

(10)

This safety factor is the same for the variable load, which is obtained when the characteristic load for V_Q = 0.4 loads is increased by the factor ${\mathsf{\Delta }}_{0.4}$ = 1.32, obtained by solving the equation

$${{\displaystyle \int }}_0^{\infty }{\mathrm{F}}_{\mathrm{Q}}{\left(\mathrm{x}; \frac{0.491}{{1.2\mathsf{\Delta }}_{0.4}},\frac{0.196}{{1.2\mathsf{\Delta }}_{0.4}}\right)}^{50}{\mathrm{f}}_{\mathrm{M}}\left(\mathrm{x}; 1.21*1.412,1.21*0.282\right)\mathrm{dx}=1-1/1499$$

(11)

Analogous equation for loads V_Q = 0.2 results in the factor ${\mathsf{\Delta }}_{0.2}$ = 1.15.

The material safety factors based on these assumptions are presented in Figure 2. The solid line denotes V_M = 0.1, steel, V_Q = 0.4; dashed line implies V_M = 0.2, timber, V_Q = 0.4; and dash-dotted line means V_M = 0.3, concrete, V_Q = 0.4. The adjacent dotted lines apply to V_Q = 0.2.

Assuming that the safety factors are set with no unsafe design at the load ratios α = 20%–80%, the material safety factor for steel is γ_M = 1.18, which is applicable to V_Q = 0.4 and α = 80%, whereas other load cases include excess safety of up to 7%. The safety factor for timber is γ_M = 1.21, which includes excess safety of up to 2%. The safety factor for concrete is denoted as γ_M = 1.37, which applies to V_Q = 0.2 and α = 20%, whereas other load cases include excess safety of up to 5%. This code calibration is called the “constant concept”, as the material safety factors are constant in each material as they are constant in the current Eurocodes.

We see in Figure 2 that considerable savings are obtained when the characteristic load of the variable load is set to changeable. The total safety factor for loads V_Q = 0.2 is 13% lower than for loads V_Q = 0.4, which means about 7% material savings in all materials for loads V_Q = 0.2. However, there is an insignificant disadvantage. In concrete, the loads V_Q = 0.2 become critical and the material factor of concrete is γ_M = 1.37 instead of γ_M = 1.35.

The accuracy and the overall feasibility of this code calibration are good, but it can be enhanced further, as explained in the next section.

3.3. Alternating Material Safety Factors

Figure 2 illustrates that the accuracy for steel and concrete can be improved when the material safety factors are functions of the load proportion (α). There are two feasible options to achieve this: linear interpolation or the “linear concept”, and different safety factors for permanent load and variable load’s dominant loads, also known as the “variable concept”.

3.3.1. Linear Concept

When the material safety factor for steel is turned into a linear interpolation between α = 20%, γ_M = 1.10 and α = 80%, γ_M = 1.18, the reliability for loads V_Q = 0.4 almost fully match with that of the target, but the loads V_Q = 0.2 present up to 3% excess safety. Correspondingly, the safety factor for concrete is transformed through a linear interpolation between α = 20%, γ_M = 1.37 and α = 80%, γ_M = 1.34, and the reliability for loads V_Q = 0.2 match with that of the target almost ideally, but the loads V_Q = 0.4 present up to 3% excess safety. This safety factor setting results in a good overall reliability accuracy but harmful excess calculation work, as the material safety factors must be calculated for steel and concrete for each load case, and therefore, this concept is questionable in general codes. However, the code writer may allow this alternative as it is feasible in the computerized design.

3.3.2. Variable Concept

Steel structures are mainly loaded by variable loads, i.e., the load proportion is higher than 50%. On the other hand, in the concrete structures, the permanent load α ≤ 50% is normally dominant. Thus, we may set the primary material safety factors for the dominant cases and secondary factors for rare cases.

In this safety factor setting, the safety factor for steel in normal cases α > 50% is γ_M = 1.18, which presents excess safety of up to 5%. In rare cases, α ≤ 50% is γ_M = 1.13, which includes excess safety of up to 3%.

The safety factor for timber is always γ_M = 1.21, α = 20%–80%, which presents excess safety of up to 2%.

The safety factor for concrete in normal cases α ≤ 50% is γ_M = 1.37, which presents excess safety of up to 4%. In rare cases, α > 50% is γ_M = 1.35, which presents excess safety of up to 4%.

One option is that the steel load cases for α < 50% and concrete load cases for α > 50% are omitted as rare when this concept is simple in the actual design, i.e., the material safety factors for steel, timber and concrete are γ_M = 1.18, 1.21 and 1.37, respectively, which presents no unsafe reliability in load cases 20% < α < 80% and excess reliability error of 3%, 1% and 4%, respectively, assuming that steel load cases α ≤ 50% and concrete load case α > 50% are disregarded.

This option is worked out further in this article.

3.4. Rounding Errors

As explained above, it is feasible that the characteristic load of the variable load is set to changeable. The same applies to the material property.

The load factors are set above as γ_G = γ_Q = 1.2, i.e., they do not have rounding errors. If the codes are defined to include material safety factors, they include rounding errors.

In the current codes, the safety factors are normally rounded numbers with two decimals, and the last decimal is either 0 or 5. When the characteristic value of the material property is the 0.05 fractile, γ_G = γ_Q = 1.2 and the material safety factors for steel, timber and concrete are γ_M = 1.18, 1.21 and 1.37, respectively, the same outcome is obtained when the material safety factors are in unity, γ_M = 1, and the characteristic values are in fractiles 0.000476, 0.00456 and 0.00329, respectively. Such a setting simplifies the codes, lessens the design work and avoids the rounding errors in the material safety factors of about 2%. We may denote the fractiles using quantile indexes: β_q, quantile = Φ(-β_q), where Φ is the cumulative distribution function of the standardized normal distribution function, β_q = 3.30, 2.61 and 2.72. If γ_G = γ_Q = 1, β_q = 5.13, 3.53 and 3.34.

Though the safety factors are applied in the loads, it is feasible to remove the material safety factor as this way, the rounding errors are avoided.

4. Discussion

The proposed codes make an improvement regarding the current one in five points:

• The codes are simpler as the load factors are the same, γ_G = γ_Q = 1.2, and therefore there are less design errors.
• The codes result in less calculation work, less design output, and less design checking as the load factors are the same, and therefore, one structural analysis often is sufficient instead of the current two analyses in the SLS and in the ULS.
• The codes can be equally used in the partial factor design approach and in the design value approach, and the proposal enables the use of the simplest design codes, i.e., the allowable stress design method.
• The proposed codes result in material saving due to better reliability accuracy and due to less excess safety and less material in the cases of variable loads with low variation.
• The unsafe design cases are less, and therefore, failures are less.

A comparison is made approximately based on the mean cases, i.e., the load proportion α = 0.5 and the coefficient of variation of the variable load V_Q = 0.3. The proposed load factors are γ_G = γ_Q = 1.2, and the material safety factors for steel, timber and concrete are γ_M = 1.18, 1.21 and 1.37, respectively. The mean characteristic load, i.e., load V_Q = 0.3 is 23.5%, (15% + 32%)/2 higher than the current 50-year return load. Consequently, the safety factor for the variable load compared with the current one is γ_Q = 1.48 (1.2 ∗ 1.235), and the mean load factor, i.e., the load factor for 50% load proportion, is 1.34 (1.2 + 1.48)/2. Thus, the total mean safety factors for the basic materials are 1.58, 1.62 and 1.84, respectively.

The analogous mean load factor in the current Eurocodes, in the load combination (8.12), is 1.43 (1.35 + 1.5)/2 and the total mean total safety factors of the basic materials are 1.43, 1.86 and 2.15, respectively.

The proposed total safety factor for steel is 10% higher than in the current Eurocodes, which suggests that the safety factor for steel γ_M = 1.0 is not enough for β₅₀ = 3.2 and should be increased by about 20% for this reliability. The questionable steel reliability was concluded by the author earlier [20]. In the calculation above, the uncertainty is omitted. If this factor is considered, the safety factor of steel should be increased even more.

4.1. Discussion on the Steel Reliability

The current safety factors of the Eurocodes are based on the independent load combination where a load reduction is applied. It is realized by calculating the variable load reliability for the 5-year load. The author explained earlier [13] that the variable load reliability should be calculated for the service time load, i.e., for the 50-year load, as this load strikes every structure. The current calculation is correct for the permanent loads, but the safety factors are too low for the variable loads. If the safety factors of the Eurocodes are calculated for the current target reliability index, β₅₀ = 3.8, all safety factors should be increased, however, the increase in the steel safety factor is especially big.

The current material safety factors of steel, timber and concrete are γ_M = 1.0, 1.3 and 1.5, respectively. These factors should be in the variable load for β₅₀ = 3.8 and γ_Q = 1.5, γ_M = 1.51, 1.55 and 1.72, respectively, i.e., 51%, 19% and 15% higher than the current values, respectively. In this article, the target reliability is set, β₅₀ = 3.2, when the safety factors in the variable load γ_Q = 1.5 should be γ_M = 1.27, 1.28 and 1.37, respectively, i.e., the current safety factors for timber and concrete are enough for β₅₀ = 3.2, but the safety factor of steel should be increased by 27%. If the safety factors are calculated independently, i.e., for the 5-year load and β₅₀ = 3.8, the safety factors for the variable load should be γ_M = 1.28, 1.29 and 1.38, respectively, i.e., the current safety of steel should be increased by 28%.

The safety factor and the reliability index of steel is illustrated in Figure 3, β₅₀ = 3.2, γ_G = 1.15, 1.35, γ_Q = 1.5, as a function of load proportion (α).

The solid line in Figure 3 left denotes the material safety factor of steel calculated using the dependent combination rule (8.12) [1] (this line is the same as the solid line in left Figure 1), and the dashed line means the corresponding safety factor calculated using the independent combination rule (8.14,a,b) [1]. We also find in this calculation that the current safety factor for steel γ_M = 1.0 should be increased by about 20% when the variable load is dominating. The dotted line shows the current safety factor of steel, γ_M = 1.0.

The solid line in Figure 3 right denotes the reliability index calculated using the combination rule (8.12) [1], and the dashed line shows the corresponding reliability index calculated using the independent combination rule (8.14,a,b) [1]. The dotted line means the target reliability index β₅₀ = 3.2. We see that the reliability index in the load combination (8.14,a,b) is about β₅₀ = 2.3, α > 0.15, i.e., the failure probability is only P_f50 ≈ 1/100, and should be 15 times less for β₅₀ = 3.2.

The apparent reason for the low material safety factor of steel γ_M = 1.0 is the current safety factor calculation, i.e., Equation (1), which wrongly estimates the safety factors that are seen in Figure 3. The dependent safety factors and reliability indexes at α = 0.15, 0.85 are γ_M.d = 0.99, 1.22; β_50,d = 3.30, 2.40, i.e., a 23% increase in γ_M,d creates a 27% decrease in β_50,d. The corresponding independent values are γ_M,i = 1.13, 1.24; β_50,i = 2.36, 2.30, i.e., a 10% increase in γ_M,i creates a 3% decrease in β_50,i. However, the same equation (Equation (1)) and the same scale are used for the dependent and the independent cases. Further, there are no limits for excessive deviation from the target.

The unsafe error of about 20% is big, and one may wonder why failures, for this reason, have not been reported in reality. There are at least two causes that mitigate the controversy:

• In the calculation above, the variable load distribution is assumed to be Gumbel. This distribution has a robust upper tail that makes the distribution excessively safe [21], which especially applies to steel.
• Steel failures normally are ductile, which allows the redistribution of stresses with decreased stress peaks.

4.2. Economic Evaluation

The proposed total safety factors for timber and concrete are 13% and 14% smaller, respectively, than in the current Eurocodes meaning savings in these materials.

The overall structural material used in Europe and set by the Eurocodes accounts for about EUR 150 billion (thousand million) (estimated by Forecon Oy, www.forecon.fi, accessed on 6 April 2020) and about EUR 100 billion is defined by the safety factors and the characteristic values. We assume here that this volume is equally divided into steel, timber and concrete. We may estimate further that when the safety factor decreases by 1%, structural material decreases by 0.5%. Thus, the decreased safety factors of concrete and timber 13% and 14%, respectively, result in the annual material savings of about EUR 4 billion in Europe.

As the load factors are the same, the structural analysis in the SLS and in the ULS often are the same, i.e., there is less calculation work, less design output and less checking. As the codes are simpler, there are fewer design errors. The proposed codes have negligible unsafe design cases regarding the target, and therefore, the structural failures are apparently less. Further, removing the rounding errors results in a theoretical saving of about EUR 1 billion.

Overall, we may estimate an annual saving of about EUR 5 billion in Europe.

The proposed codes make only one essential change to the present Eurocodes. The load tables of the variable loads should be changed. The safety factors should also be changed. Such changes are minor tasks in the amendment of the codes.

4.3. Environmental Impact

This study indicates that the volume of timber and concrete used in the construction work can be reduced by about 6% and 7%, respectively. On the other hand, the volume of steel should be increased. However, the reliability calculation of steel structures needs further studies. The overall economic impact obviously is positive. For example, 7% reduced use of concrete makes about 0.5% decrease in world CO2 emissions (https://en.wikipedia.org/wiki/Environmental_impact_of_concrete, accessed on 26 May 2021).

4.4. Unique Characteristics

The codes presented here have unique features. The primary characteristics are variable characteristic values and the partial safety factor codes which can be used in the allowable stress approach, too. Secondary features are variable material safety factors and avoiding the rounding errors. The author sets name on such codes “Poutanen’s model”.

5. Conclusions

• The target reliability index is set at β₅₀ = 3.2 [7].
• The load factors are set as γ_G = γ_Q = 1.2.
• The characteristic values for the variable loads V_Q = 0.4 are 1.32 times higher than the current ones, and for loads V_Q = 0.2, they are 1.15 times higher. The current variable load table values should be multiplied by 1.15–1.32.
• The material safety factors are the same for all materials, γ_M = 1, and the characteristic values of the basic materials, steel, timber and concrete, are in quantiles β_q = 3.30, 2.61 and 2.72, respectively, which means that the fictitious material safety factors are γ_M = 1.18, 1.21 and 1.37, respectively, and γ_G = γ_Q = 1.2.
• As the characteristic values are higher than the current ones, the fictitious load factors compared with the current Eurocodes are γ_Q = 1.38 for loads V_Q = 0.2 and γ_Q = 1.58 for loads V_Q = 0.4.
• According to this study, the current Eurocodes are about 13% and 14% over safe in timber and concrete designs for β₅₀ = 3.2, respectively, and steel designs are about 10% unsafe.
• The proposed codes have the same load tables as the corresponding design value codes and can be used as the design value codes by setting the load factors at unity γ_G = γ_Q = 1 and by multiplying the material factors by 1.2.
• The proposed codes result in savings in structural material, especially in timber and concrete and savings in design work. The codes are simpler and result in fewer design errors, less design output and less design checking, the reliability accuracy is better, the unsafe design cases are negligible, and the environmental impact is improved.