Abstract
This research is concerned with the use of double walls filled with foam aluminum for an open wagon to decrease loading during operational modes. The research presents the strength calculation for the frame of a wagon with a consideration of the engineering solutions proposed. It was found that the maximum equivalent stresses appeared in the bottom section of the center sill behind the back support; they amounted to about 290 MPa and did not exceed the allowable values. The maximum displacements were in the middle parts of the main longitudinal beams of a section, and they amounted to 8.8 mm. The research also presents the strength calculation for a weld joint in the maximum loaded zones of the frame of a wagon and reports the results of the modal analysis of the frame of the improved wagon. It was found that the oscillation frequencies did not exceed the allowable values. The results of the research may be useful for those who are concerned about designing innovative rolling stock units and improving the operational efficiency of railway transport.
1. Introduction
Higher efficiency of rail transportation within the international transportation network can be ensured by the introduction of innovative wagon structures. As is known, one of the most popular wagon types for international transportation is the flat wagon, particularly the articulated flat wagon. A special feature of such wagons is their two-section carrying structure that rests on three bogies.
In operation, such wagons bear considerable longitudinal loads, which harm both the strength of the carrying structure and traffic safety.
Therefore, a decrease in the dynamic loads on articulated flat wagons is of primary importance; it can be achieved by implementing innovative engineering solutions. These will provide the fatigue strength of the carrying structure, decrease repair and maintenance costs, ensure higher security of the transported freight (e.g., by tank containers), security of detachable bodies, traffic safety, etc.
The issue of how freight displacements impact the motion characteristics of a flat wagon is studied in [1]. The authors obtained dependencies of the basic dynamic characteristics of traffic speed.
Study [2] presents research into the loading and strength of a long-base car. The research confirmed the efficiency of engineering solutions implemented in car design.
It should be noted that the design of the carrying structure of the car did not include any measures aimed at decreasing dynamic loads due to cyclic stresses.
The carrying structure of a flat wagon is analyzed in [3]. The carrying structure of a car intended for intermodal transportation is analyzed in [4]. A special feature of the carrying structure of such a car is a loading/unloading rotating platform.
However, the authors did not consider the longitudinal dynamic loads on the carrying structure of the car under operational modes.
The dynamic loads on the carrying structure of a car are determined in [5]. The authors studied the application of different types of bogies for railcars and analyzed how the technical characteristics impact the dynamic characteristics of the car.
Theoretical and experimental research into the loads on the carrying structure of a freight wagon is demonstrated in [6]. The technique proposed by the authors proved to be efficient, thus confirming that the authors followed the right line in their research.
Nevertheless, they did not consider any measures to decrease the dynamic loads on the carrying structure of railcars.
Studies [7,8] propose and describe the realization of a technique aimed at decreasing loads on a railcar under operational modes. However, the authors did not study how to decrease the dynamic loads on the carrying structure of a long-base railcar.
The analysis of the impact strength of vehicles is considered in publication [9]. The author formed a mathematical model that allows one to calculate the acceleration of a vehicle on impact. At the same time, no solutions have been proposed that are aimed at ensuring the strength of the vehicle in operation.
The unified concept of the impact strength of a railcar body is presented in publication [10]. In the simulation, the assumption was made that the body is absolutely rigid. At the same time, the work did not address the issues of improving the railcar body to ensure its safety.
An experimental study on the dynamics of rolling stock is carried out in publication [11]. The authors proposed solutions, the implementation of which will improve the safety of rolling stock.
Article [12] defines the main indicators of the dynamics and strength of a platform car in operation. The features of the experimental tests to which the car was subjected are highlighted.
It is important to say that the authors of these works have not proposed solutions aimed at reducing the load on the rolling stock in operation.
Analysis of the literature [1,2,3,4,5,6,7,8,9,10,11,12] demonstrates that the issue of determination of the loads on the carrying structure of a flat wagon of circular pipes loaded with tank containers has not been studied yet. Therefore, it requires appropriate research in the field.
The purpose of this study was to investigate the loading of a flat wagon of circular pipes loaded with tank containers using mathematical modeling. To achieve the objective, the following tasks were set:
- -
- To build a design diagram of a flat wagon for determination of the longitudinal loads on the carrying structure;
- -
- To simulate the dynamic loads on the carrying structure of a flat wagon with a standard automatic coupler;
- -
- To simulate the dynamic loads on the carrying structure of a flat wagon with a draft gear construct;
- -
- To determine the basic strength characteristics of the carrying structure of a flat wagon.
2. Presentation of the Basic Material of the Article
The authors proposed the application of circular pipes in the frame of a flat wagon to reduce material consumption [13]. To determine the optimal parameters of the pipes, a strength calculation of the supporting structure of the prototype railcar flat-car model 13-401 was carried out. This type of railcar was chosen as the base railcar because it had several upgrades to improve the efficiency of its operation. For example, it had setting folding or stationary fitting stops on the main longitudinal beams of the frame to be able to transport containers, including in international traffic.
Based on the performed calculations and obtained values of the maximum equivalent stresses, the strength reserves of the components of the supporting structure of the flat car were determined. Taking this into account, according to the range of pipes, the most optimal ones from the viewpoint of the minimum material consumption of pipes were determined. The proposed solutions were confirmed by complex calculations of dynamics, strength, and fatigue strength, as well as a modal analysis of the load-bearing structure of the platform car under operational loads [14].
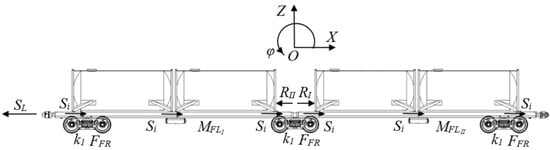
Figure 1 demonstrates an articulated flat wagon built according to the design proposed [14].
The dynamic loads on the frame of the flat wagon loaded with tank containers under operational modes (tensile jerk) were determined using mathematical modeling based on the mathematical model designed by Prof. G.I. Bogomazov [15]. The design diagram of the flat wagon is given in Figure 2.
The research included a load of 2.5 MN on the front stops of an automatic coupler [16,17]. A 1CC tank container was taken as the prototype.
The tank containers were taken as masses attached to the flat wagon frames. All tank containers on the flat wagon had an equal amount of liquid freight.
The motion equations are
is the mass of the i-th carrying structure of a flat wagon. is the inertia moment of the i-th flat wagon relative to the longitudinal axle. is the longitudinal impact force to a coupler. is the amplitude value of the dry friction force. is the bogie mass. is the inertia moment of a wheelset. is the radius of a wheel with moderate wear. is the number of bogie axles. is the half-base of the i-th section of a flat wagon. is the absolute value of the dry friction force in a spring group. are the rigidities of springs of a spring suspension of bogies of a flat wagon. is the number of oscillation modes of the liquid freight. is the mass of a body equivalent to the i-th tank container with part of a liquid freight, which does not move relative to the tank. is the mass of the j-th pendulum in the i-th tank container. is the height of the center of weight of a tank container. is the distance between the plane and the fixation point of the j-th pendulum in i-th tank container. is the length of the j-th pendulum. is the reduced inertia moment of the i-th tank container and the liquid freight, which does not move relative to the tank. is the inertia moment of a pendulum. are the coordinates corresponding to the longitudinal, angular (about the longitudinal axle), and vertical displacements of a flat wagon, respectively. are the coordinates corresponding to the longitudinal and angular displacements about the longitudinal axle of a tank container. is the vertical deviation of the j-th pendulum.
The motion of the liquid freight was described using mathematical pendulums [15].
The hydrodynamic characteristics of the liquid freight were determined by the technique presented in [18]. A boundary value problem was made, which is equivalent to the problem of finding the minimum of a functional. The Ritz method was used as a calculation method. The authors used petrol as the liquid freight. Based on the calculations conducted for the case of the maximum possible loading of the tank shell according to [19], the authors obtained the following values: and . The calculation included that the tank was filled to 95%.
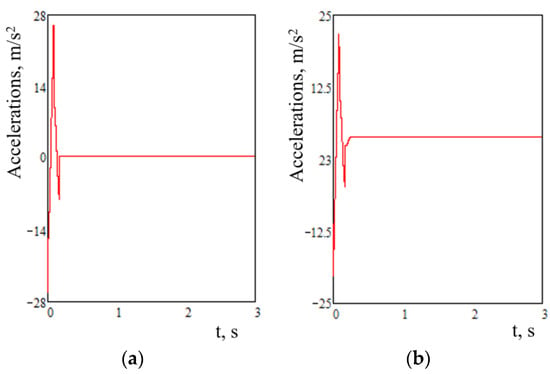
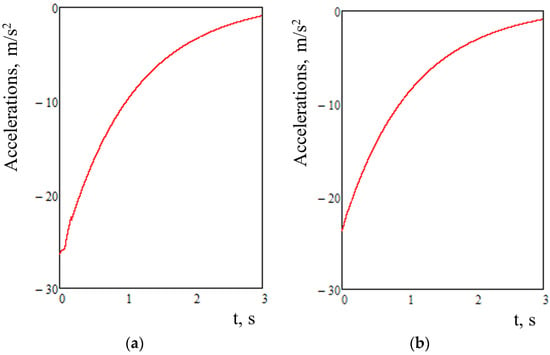
The equations were solved with the Runge–Kutta method in MathCad software [20,21,22,23]. The starting conditions were made equal to zero [24,25,26,27,28]. The results of the research showed that acceleration to the first section of the flat wagon from force application was 27.7 m/s², and it was 24.4 m/s2 to the second section (Figure 3).
Figure 3.
The accelerations to the carrying structure of the flat wagon: (a) First section from force application. (b) second section from force application.
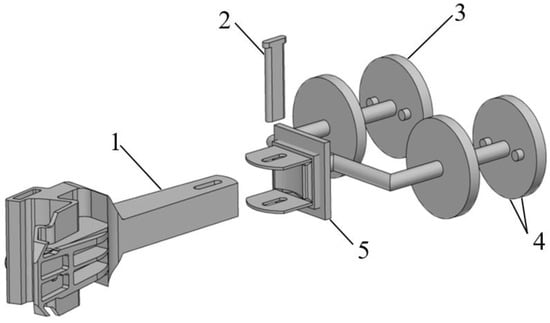
The study also addressed the use of a draft gear construct as an alternative to a standard automatic coupler to decrease the dynamic loads on the frame of the flat wagon (Figure 4) [13]. The concept design includes a typical CA-3 automatic coupler body (1), which interacts with the retainer bar (5) through the connecting wedge (2). The retainer bar has a spherical surface for interaction with the shank of the automatic coupler and the possibility of carrying out movements of the body in the horizontal plane when the car enters the curved sections of the track. The design also includes pistons (3), in which throttle valves (4) are located. This concept can be applied to wagons with a center beam consisting of two pipes. It is also possible to use this concept on wagons, the center beam of which is represented by a single tube. In this case, the concept uses one piston.
Figure 4.
The draft gear construct of an automatic coupler: 1, body; 2, wedge; 3, piston; 4, throttle valves; 5, retainer bar.
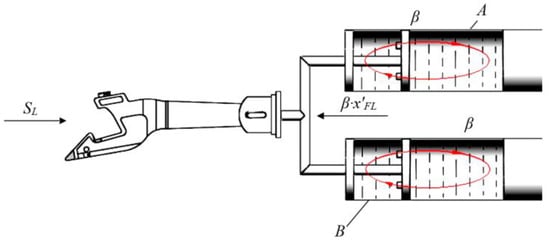
The end parts of the center sill of the flat wagon were filled with damping material with the viscous resistance coefficient β. The draft gear construct was equipped with a piston with two throttle valves (input and output) to transform the kinetic impact energy Sa to the dissipation energy. The longitudinal loading was transferred from the automatic coupler body to the double-disk pistons of the draft gear construct through the retainer bar using a fork. When the pistons moved toward the center plate of the wagon (cavity A), the input valves were open while the output valves were closed. During the backward direction of the pistons (jerk, compression), the output valves were open and the input valves were closed. The viscous solution flew to cavity B from the coupler body. The operation diagram of the draft gear construct is given in Figure 5. The viscous resistance coefficient formed by the draft gear construct was over 70 kNs/m. The optimal value of the viscous resistance coefficient was determined using mathematical modeling of the dynamic loading of the car’s load-bearing structure under operational loads.
It is important to say that the use of the proposed concept contributes to the anti-corrosion properties of the railcar cantilever parts. This concept of a harness device also allows one to reduce the cost of manufacturing the railcar by eliminating the need to use harness devices with absorbing devices.
The motion equations of the design model have the form
where viscous resistance coefficient is formed by the draft gear construct.
The results of the calculation are given in Figure 6.
Figure 6.
The accelerations to the carrying structure of the flat wagon: (a) First section from force application. (b) second section from force application.
The results of the research demonstrate that acceleration to the first section of the flat wagon from force application was about 25.0 m/s² and about 22.0 m/s2 to the second section.
The proposed solution will decrease the loading of the frame of a wagon by 10% in comparison to that for a standard automatic coupler.
The basic strength characteristics of the carrying structure of an articulated flat wagon with a draft gear construct were determined through the strength calculation using the FEM in SolidWorks Simulation (CosmosWorks) software.
Isoparametric tetrahedrons were used as finite elements. The number of elements in the mesh was 1,311,530, and the number of nodes was 418,692. The maximum element size was 20 mm, the minimum element size was 4 mm, and the maximum element side ratio was 2117.6. The percentage of elements with a side ratio of less than three or more than ten was 74.9 and 0.719, respectively.
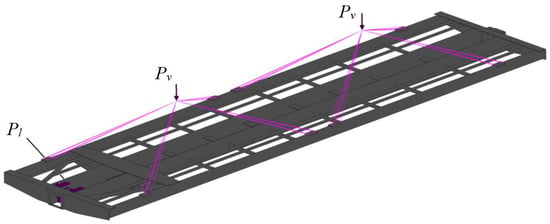
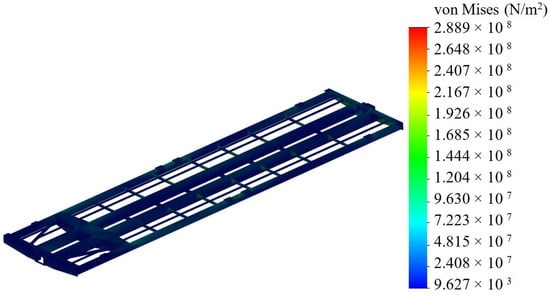
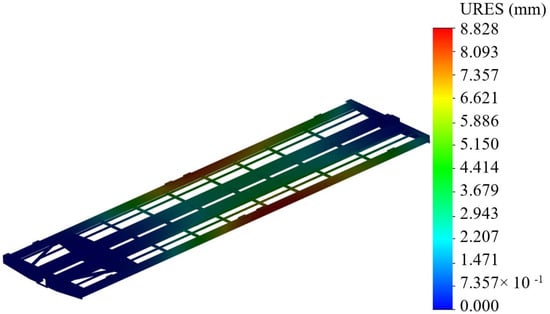
The design diagram of the carrying structure of the flat wagon section included the action of the vertical static loading , conditioned by the gross weight of the tank containers and the longitudinal loading to the front stops of the coupler, which amounts to 2.5 MN (Figure 7). That is, the calculation was carried out for the case of such an operating mode as “jerk.” The vertical loading was applied to the carrying structure as remote loading, which included the height of the weight center of the tank container. The stress state of the supporting structure of the flat car, as well as the displacements in it, are presented in Figure 8 and Figure 9, respectively.
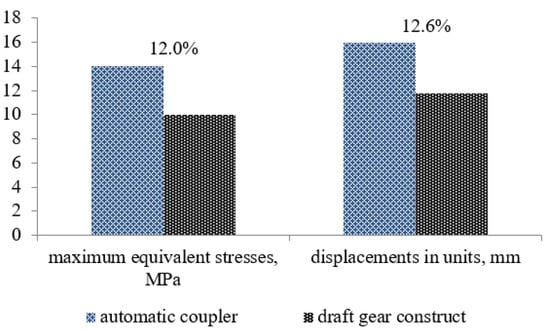
The maximum equivalent stresses were in the interaction area between the center sill and body bolster, and they amounted to about 290 MPa. Thus, they did not exceed the allowable values [16,17]. The maximum displacements were in the middle parts of the main longitudinal section beams, and they amounted to 8.8 mm. The use of the draft gear construct will decrease the maximum equivalent stresses by 12% in the carrying structure of the articulated flat wagon, and by 12.6% in the displacements in comparison to those values in the case of a typical automatic coupler (Figure 10).
3. Discussion of the Results Obtained
The authors determined the dynamic loads on an articulated flat wagon of circular pipes loaded with tank containers. We also determined the accelerations to the carrying structure of the flat wagon with a typical automatic coupler (Figure 3).
The dynamic loads on the carrying structure of a flat wagon can be decreased by the application of a draft gear construct (Figure 4). This will decrease the loads on the frame of a flat wagon by 10% and the maximum equivalent loads by 12% (Figure 8) in comparison to the loads when applying a standard automatic coupler (Figure 6).
It should be noted that the mathematical modeling did not include angular displacements of the coupling unit. Moreover, the strength modeling of one section of the frame of the flat wagon took into account that a section rigidly interacted with the bogies, i.e., the gaps between the center plate and plate bowl were disregarded. These restrictions will be included in the authors’ further research in the field. In addition, the loading on the carrying structure of an articulated flat wagon requires experimental tests.
4. Conclusions
- This study addressed the building of a design diagram of a flat wagon for the determination of longitudinal loads on a carrying structure loaded with four 1CC tank containers. The research was performed in the plane coordinates. The loading of the supporting structure during the “jerk” was taken into account.
- The calculation included a force of 2.5 MN to the front stops of an automatic coupler.
- 2.
- The authors simulated the dynamic loads on the carrying structure of a flat wagon with a standard automatic coupler. The research included the fact that 95% of the tank was filled with liquid freight. The differential equations were solved in MathCad software. The results of the research showed that accelerations to the first section of the flat wagon from force application were 27.7 m/s², and they were 24.4 m/s2 to the second section.
- 3.
- The study investigated the modeling of the dynamic loads on the carrying structure of a flat wagon with a draft gear construct. It was found that acceleration to the first section of the flat wagon from force application was 25.0 m/s² and about 22.0 m/s2 to the second section.
- The solution proposed can decrease the dynamic loads on the carrying structure of a flat wagon by 10% in comparison to those generated by the use of a standard automatic coupler.
- 4.
- The authors determined the basic strength characteristics of the carrying structure of a flat wagon with the finite element method. It was found that the maximum equivalent stresses were in the interaction area between the center sill and body bolster, and they amounted to about 290 MPa. The maximum displacements were in the middle parts of the main longitudinal beams of a section, and they amounted to 8.8 mm.
- It was found that the use of the draft gear construct decreased the maximum equivalent stresses by 12% in the carrying structure of a flat wagon, and by 12.6% in the displacements in comparison to those generated by the use of a standard automatic coupler.
Author Contributions
Conceptualization, O.F. and A.L.; methodology, O.F. and A.L.; software, A.L.; validation, A.L. and J.G.; investigation, O.F., A.L. and K.K.; resources, O.F., A.L. and K.K.; writing—original draft preparation, O.F., A.L. and K.K.; writing—review and editing J.G.; visualization, O.F., A.L. and K.K.; supervision, J.G. All authors have read and agreed to the published version of the manuscript.
Funding
This publication was issued thanks to support from the Cultural and Educational Grant Agency of the Ministry of Education of the Slovak Republic in the project, “Implementation of modern methods of computer and experimental analysis of properties of vehicle components in the education of future vehicle designers” (Project No. KEGA 036ŽU-4/2021). The authors also gratefully acknowledge funding from specific research into “Innovative principles for creating resource-saving structures of railroad cars based on the refined dynamic loads and functionally adaptive flash-concepts,” which is funded from the state budget of Ukraine in 2020.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shatunov, O.V.; Shvets, A.O. Study of dynamic indicators of flat wagon with load centre shift. Science and Transport Progress. Bull. Dnipropetr. Natl. Univ. Railw. Transp. 2019, 2, 127–143. [Google Scholar] [CrossRef]
- WBN. Waggonbau Niesky GmbH: Developing a flexible platform of freight wagons. Internet Ed. 2016, 1, 46. [Google Scholar]
- Nandan, S.; Trivedi, R.; Kant, S.; Ahmad, J.; Maniraj, M. Design, analysis and prototype development of railway wagons on different loading conditions. Int. J. Eng. Appl. Sci. Technol. 2020, 20, 122–129. [Google Scholar] [CrossRef]
- Šťastniak, P.; Kurčík, P.; Pavlík, A. Design of a new railway wagon for intermodal transport with the adaptable loading platform. MATEC Web Conf. 2018, 235, 00030. [Google Scholar] [CrossRef][Green Version]
- Myamlin, S.; Leonas, P.L.; Dailydka, S.; Vaičiūnas, G.; Bogdevičius, M.; Bureika, G. Determination of the dynamic characteristics of freight wagons with various bogie. Transport 2015, 30, 88–92. [Google Scholar] [CrossRef]
- Neduzha, L.O.; Shvets, A.O. Theoretical and experimental research of strength properties of spine beam of freight cars. Science and Transport Progress. Bull. Dnipropetr. Natl. Univ. Railw. Transp. 2018, 1, 131–147. [Google Scholar] [CrossRef]
- Fomin, O.; Lovska, A. Improvements in passenger car body for higher stability of train ferry. Eng. Sci. Technol. Int. J. 2020, 23, 1455–1465. [Google Scholar] [CrossRef]
- Fomin, O.; Lovska, A.; Radkevych, V.; Horban, A.; Skliarenko, I.; Gurenkova, O. The dynamic loading analysis of containers placed on a flat wagon during shunting collisions. ARPN J. Eng. Appl. Sci. 2019, 14, 3747–3752. [Google Scholar]
- Zamecnik, J.; Jagelcak, J. Evaluation of wagon impact tests by various measuring equipment and influence of impacts on cargo stability. Communications 2015, 4, 21–27. [Google Scholar]
- Mrzyglod, M.; Kuczek, T. Uniform crashworthiness optimization of car body for high-speed trains. Struct. Multidiscip. Optim. 2014, 49, 327–336. [Google Scholar] [CrossRef]
- Ermolenko, I.Y.; Zheleznyak, V.N. Study on dynamics of rolling stock using an experimental laboratory car when driving on difficult sections of the road. Mod. Technol. Syst. Anal. Modeling 2016, 4, 199–203. [Google Scholar]
- Chepurnoy, A.D.; Litvinenko, A.V.; Sheychenko, R.I.; Graborov, R.V.; Chuban, M.A. Running strength and dynamic tests of a flat car. Bull. Natl. Tech. Univ. Ser. Eng. CAD 2015, 31, 111–128. [Google Scholar]
- Lovska, A.; Fomin, O.; Kučera, P.; Václav, P. Calculation of loads on carrying structures of articulated circular-tube wagons equipped with new draft gear concepts. Appl. Sci. 2020, 10, 7441. [Google Scholar] [CrossRef]
- Fomin, O.V.; Lovska, A.O. Strength determination of load-bearing structure of articulated flatcar of round pipes. Sci. Transp. Prog. Bull. Dnipropetr. Natl. Univ. Railw. Transp. 2020, 2, 92–102. [Google Scholar]
- Bogomaz, G.I.; Mekhov, D.D.; Pilipchenko, O.P.; Chernomashenceva, Y.G. Loading of tank containers located on a railway platform when hitting an auto-coupling. In Dynamics and Motion Control of Mechanical Systems; Institute of Technical Mechanics under NAS: Kiev, Ukraine, 1992; pp. 87–95. [Google Scholar]
- DSTU 7598:2014. Freight Wagons. General Requirements for Calculations and Design of New and Modernized Wagons of 1520 mm Track (Non-Self-Propelled); UkrNDNTS: Kiev, Ukraine, 2015; 162p. [Google Scholar]
- GOST 33211-2014. Freight Wagons. Requirements for Strength and Dynamic Properties; FGUP “STANDARTINFORM”: Moskow, Russia, 2016; 54p. [Google Scholar]
- Krivovyazyuk, Y.P. Evaluation of the Equivalent Loading of Four-Axle Rail Tank Cars with a Liquid Cargo of Various Densities during Longitudinal Impacts. Ph.D. Thesis, Institute of Technical Mechanics NASU and SSAU, Dniepropetrovsk, Ukraine, 1986. [Google Scholar]
- Rules for the carriage of dangerous goods. In Towards an Agreement on International Rail Freight Traffic: Part 3—Organization for Cooperation between Railways; Transport: Moskow, Russia, 2011; p. 531.
- Dižo, J.; Steišunas, S.; Blatnický, M. Simulation analysis of the effects of a rail vehicle running with wheel flat. Manuf. Technol. 2016, 16, 889–896. [Google Scholar] [CrossRef]
- Vatulia, G.L.; Lobiak, O.V.; Deryzemlia, S.V.; Verevicheva, M.A.; Orel, Y.F. Rationalization of cross-sections of the composite reinforced concrete span structure of bridges with a monolithic reinforced concrete roadway slab. IOP Conf. Ser. Mater. Sci. Eng. 2019, 664, 012014. [Google Scholar] [CrossRef]
- Vatulia, G.; Komagorova, S.; Pavliuchenkov, M. Optimization of the truss beam. Verification of the calculation results. MATEC Web Conf. 2018, 230, 02037. [Google Scholar] [CrossRef]
- Kondratiev, A.V.; Gaidachuk, V.E.; Kharchenko, M.E. Relationships between the ultimate strengths of polymer composites in static bending, compression, and tension. Mech. Compos. Mater. 2019, 52, 259–266. [Google Scholar] [CrossRef]
- Plakhtii, O.; Nerubatskyi, V.; Mashura, A.; Hordiienko, D.; Khoruzhevskyi, H. Improving energy indicators of the charging station for electric vehicles based on a three-level active rectifier. East. Eur. J. Enterp. Technol. 2020, 3, 46–55. [Google Scholar] [CrossRef]
- Plakhtii, O.; Nerubatskyi, V.; Mashura, A.; Hordiienko, D. The analysis of mathematical models of charge-discharge characteristics in lithiumion batteries. In Proceedings of the 40th IEEE International Conference on Electronics and Nanotechnology, Kyiv, Ukraine, 22–24 April 2020; Institute of Electrical and Electronics Engineers Inc.: Kyiv, Ukraine, 2020; pp. 635–640. [Google Scholar]
- Fomin, O.; Lovska, A. Establishing patterns in determining the dynamics and strength of a covered freight car, which exhausted its resource. East. Eur. J. Enterp. Technol. 2020, 6, 21–29. [Google Scholar]
- Lovska, A. Simulation of loads on the carrying structure of an articulated flat car in combined transportation. Int. J. Eng. Technol. 2018, 7, 140–146. [Google Scholar] [CrossRef]
- Fomin, O. Improvement of upper bundling of side wall of gondola cars of 12-9745 model. Metall. Min. Ind. 2015, 1, 45–48. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).