Investigation of Controllable Modes in Active Vibration Cancellation Induced by Piezoelectric Patches
Abstract
:1. Introduction
2. Dynamic Modeling
2.1. Dynamic Equation
2.2. State-Space Model
2.3. AVC System for the Smart Plate
3. Controllable and Uncontrollable Modes for AVC
3.1. Description of Controllable and Uncontrollable Modes
3.2. Theoretical Analysis
4. Simulation and Analysis
5. Experimental Verification
5.1. Experiment Setup
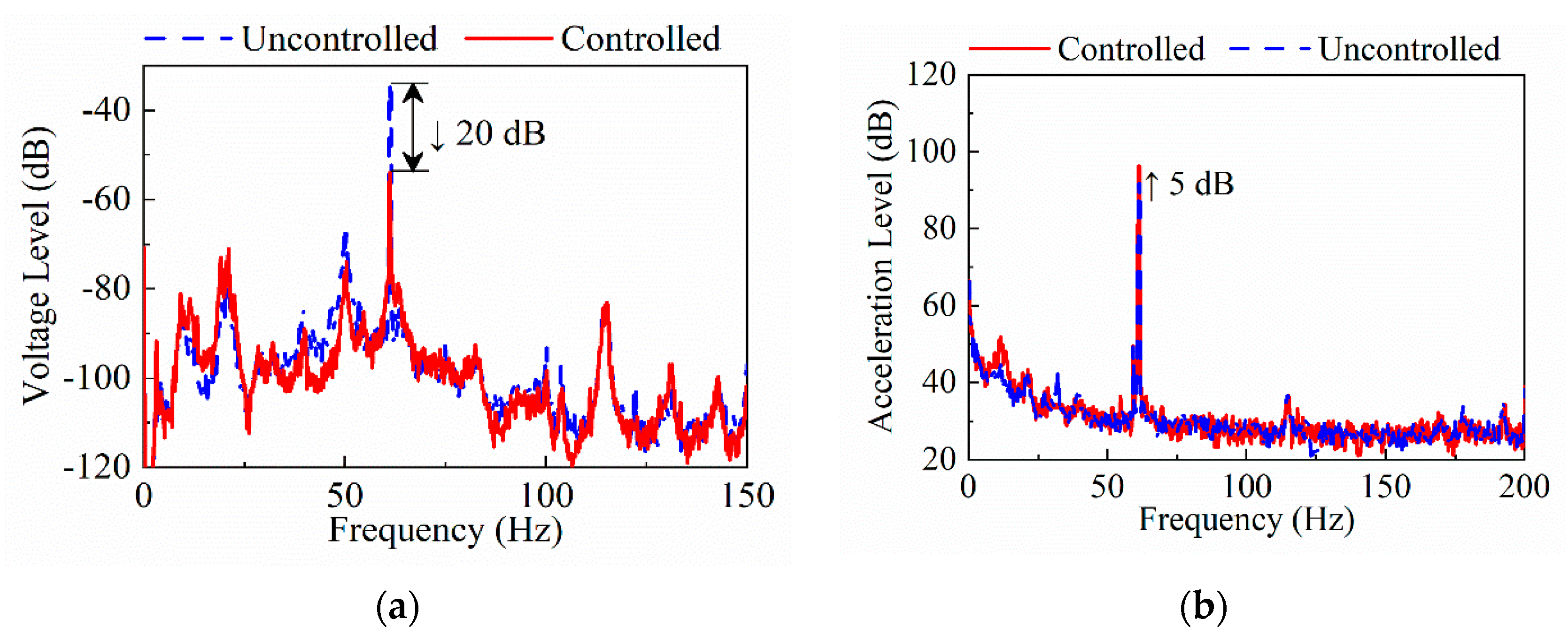
5.2. Uncontrollable Mode: AVC at (3,3) Modal Frequency
5.3. Controllable Mode: AVC at (1,4) Modal Frequency
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sivakumar, A.; Chandrasekaran, G.; Cáceres, C.A. Modeling and Active Vibration Suppression of Dynamical Systems: A Survey. J. Sci. Eng. 2016, 7, 50–71. [Google Scholar]
- Roberto, C.; Luigi, F. Advances in Vibroacoustics and Aeroacustics of Aerospace and Automotive Systems. Appl. Sci. 2018, 8, 366–370. [Google Scholar]
- Yuli, Z.; Xu, W. A Review of Low-Frequency Active Vibration Control of Seat Suspension Systems. Appl. Sci. 2019, 9, 26–33. [Google Scholar]
- Zhang, S.-Q.; Zhao, G.-Z.; Rao, M.N.; Schmidt, R.; Yu, Y.-J. A review on modeling techniques of piezoelectric integrated plates and shells. J. Intell. Mater. Syst. Struct. 2019, 30, 1133–1147. [Google Scholar] [CrossRef]
- Shivashankar, P.; Gopalakrishnan, S. Review on the use of piezoelectric materials for active vibration, noise, and flow control. SMAS 2020, 29, 053001. [Google Scholar] [CrossRef]
- Akira, S.; Kouji, H.; Nobuo, T. Active control of sound transmission through a rectangular panel using point-force actuators and piezoelectric film sensors. JASA 2015, 137, 458–469. [Google Scholar]
- Presas, A.; Luo, Y.; Wang, Z.; Valentin, D.; Egusquiza, M. A Review of PZT Patches Applications in Submerged Systems. Sensors 2018, 18, 2251. [Google Scholar] [CrossRef] [Green Version]
- Moussa, R.E.; Grossard, M.; Boukallel, M.; Hubert, A.; Chaillet, N. Modeling and control of a piezoelectric microactuator with proprioceptive sensing capabilities. Mechatronics 2014, 24, 590–604. [Google Scholar] [CrossRef] [Green Version]
- Abreu, G.L.C.M.; Ribeiro, J.F.; Valder, S.J. Experiments on Optimal Vibration Control of a Flexible Beam Containing Piezoelectric Sensors and Actuators. Shock. Vib. 2003, 10, 283–300. [Google Scholar] [CrossRef]
- Shevtsov, S.; Tsahalis, D.; Flek, M.; Samochenko, I. Comparison of active and passive modes of piezoelectric patch actuators for scaled helicopter rotor blade vibration suppression. In Proceedings of the International Conference on Noise & Vibration Engineering, Leuven, Belgium, 20–22 September 2010. [Google Scholar]
- Mojtaba, B.; Reza, M.H. Integrated and Consistent Active Control Formulation and Piezotransducer Position Optimization of Plate Structures considering Spillover Effects. Shock. Vib. 2014, 2014, 1–14. [Google Scholar]
- Vasques, C.M.A. Improved passive shunt vibration control of smart piezo-elastic beams using modal piezoelectric transducers with shaped electrodes. SMAS 2012, 21, 125003. [Google Scholar] [CrossRef]
- Singhal, N.; Sharma, M.; Mangal, S.K. Optimal placement of piezoelectric patches over a smart structure. Integr. Ferroelectr. 2017, 183, 60–90. [Google Scholar] [CrossRef]
- Tehrani, M.G.; Mottershead, J.E. An overview of the receptance method in active vibration control. IFAC Proc. Vol. 2012, 45, 1174–1178. [Google Scholar] [CrossRef] [Green Version]
- Morris, K.; Yang, S. Comparison of actuator placement criteria for control of structures. JSV 2015, 353, 1–18. [Google Scholar] [CrossRef]
- Xue, K.; Igarashi, A.; Kachi, T. Optimal sensor placement for active control of floor vibration considering spillover effect associated with modal filtering. Eng. Struct. 2018, 165, 198–209. [Google Scholar] [CrossRef]
- Khan, A.; Kim, H. Active Vibration Control of a Piezo-Bonded Laminated Composite in the Presence of Sensor Partial Debonding and Structural Delaminations. Sensors 2019, 19, 540. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sharma, P. Vibration Analysis of Functionally Graded Piezoelectric Actuators; Springer: New York, NY, USA, 2019. [Google Scholar]
- Li, W.L. Vibration analysis of rectangular plates with general elastic boundary supports. J. Sound Vib. 2004, 273, 619–635. [Google Scholar] [CrossRef]
- Moheimani, S.R.; Fleming, A.J. Piezoelectric Transducers for Vibration Control and Damping; Springer Science & Business Media: London, UK, 2006. [Google Scholar]
- Giurgiutiu, V.; Zagrai, A.N. Characterization of Piezoelectric Wafer Active Sensors. J. Intell. Mater. Syst. Struct. 2000, 11, 959–976. [Google Scholar] [CrossRef]
- Preumont, A. Vibration Control of Active Structures An Introduction, 4th ed.; Springer International Publishing: Dordrecht, The Netherlands, 2018. [Google Scholar]
- Georges, D. The use of observability and controllability gramians or functions for optimal sensor and actuator location in finite-dimensional systems. In Proceedings of the 1995 34th IEEE Conference on Decision and Control, New Orleans, LA, USA, 13–15 December 1995; pp. 3319–3324. [Google Scholar]
- Huang, B.; Xiao, Y.; Sun, J.; Wei, G. A variable step-sze FXLMS algorithm for narrowband active noise control. IEEE-ACM T AUDIO SPE 2013, 21, 301–312. [Google Scholar] [CrossRef]
- Spaggiari, A.; Castagnetti, D.; Golinelli, N.; Dragoni, E.; Mammano, G.S. Smart materials: Properties, design and mechatronic applications. J. Mater. Design Appl. 2019, 233, 734–762. [Google Scholar] [CrossRef]
- Guan, Y.H.; Shepard, W.S.; Lim, T.C.; Li, M. Experimental analysis of an active vibration control system for gearboxes. SMAS 2004, 13, 12–30. [Google Scholar] [CrossRef]
- Mao, Q.; Pietrzko, S. Control of Noise and Structural Vibration; Springer: London, UK, 2013. [Google Scholar]
- Hać, A.; Liu, L. Sensor and actuator location in motion control of flexible structures. JSV 1993, 167, 239–261. [Google Scholar] [CrossRef]
- Bayard, D.S.; Hadaegh, F.Y.; Meldrum, D.R. Optimal experiment design for identification of large space structures. Automatica 1988, 24, 357–364. [Google Scholar] [CrossRef]
- Sharma, S.; Vig, R.; Kumar, N. Active vibration control: Considering effect of electric field on coefficients of PZT patches. SMAS 2015, 16, 1091–1105. [Google Scholar] [CrossRef]











| Thickness (m) | Piezoelectric Constant (pC/N) | Young’s Modulus (GPa) | Density (kg/m3) | Poisson’s Ratio | Surface Area (m2) | ||
|---|---|---|---|---|---|---|---|
| d31 | d32 | d33 | |||||
| 0.001 | 124 | 124 | 280 | 79 | 7500 | 0.3 | 0.04 × 0.04 |
| Thickness (m) | Young’s Modulus (GPa) | Density (kg/m3) | Poisson’s Ratio | Surface Area (m2) |
|---|---|---|---|---|
| 0.001 | 216 | 7800 | 0.28 | 0.5 × 0.6 |
| Order | Uncontrolled Vibration of the Plate | Controlled Vibration of the Plate | |
|---|---|---|---|
| (2,2) | 7.2 × 10−4 |  |  |
| (1,3) | 3.4 × 10−4 |  |  |
| (3,1) | 1.3 × 10−7 |  |  |
| (2,3) | 2.6 |  |  |
| (3,2) | 2.9 × 10−5 |  |  |
| (1,4) | 4.0 × 10−7 |  |  |
| (3,3) | 1.1 |  |  |
| (4,1) | 1.3 × 10−7 |  |  |
| (4,2) | 9.7 × 10−4 |  |  |
| (3,4) | 1.4 |  |  |
| (2,4) | 7.6 × 10−3 |  |  |
| (4,4) | 1.9 × 10−3 |  |  |
| (5,2) | 1.9 × 10−5 |  |  |
| (3,6) | 1.3 |  |  |
| (5,4) | 4.5 × 10−4 |  |  |
| (6,1) | 4.8 × 10−8 |  |  |
| Order | |||
|---|---|---|---|
| (2,3) | 2.6 | 4.8 | 3.3 |
| (3,3) | 1.1 | 1.8 | 1.8 |
| (3,4) | 1.4 | 3.7 | 1.5 |
| (3,6) | 1.3 | 5.9 | 1.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Y.; Sheng, M.; Fu, X. Investigation of Controllable Modes in Active Vibration Cancellation Induced by Piezoelectric Patches. Appl. Sci. 2021, 11, 5542. https://doi.org/10.3390/app11125542
Han Y, Sheng M, Fu X. Investigation of Controllable Modes in Active Vibration Cancellation Induced by Piezoelectric Patches. Applied Sciences. 2021; 11(12):5542. https://doi.org/10.3390/app11125542
Chicago/Turabian StyleHan, Yuying, Meiping Sheng, and Xiaohan Fu. 2021. "Investigation of Controllable Modes in Active Vibration Cancellation Induced by Piezoelectric Patches" Applied Sciences 11, no. 12: 5542. https://doi.org/10.3390/app11125542





