Quality Evaluation of Epoxy Pore Casts Using Silicon Micromodels: Application to Confocal Imaging of Carbonate Samples
Abstract
:1. Introduction
1.1. Resin Impregnation
1.2. Confocal Imaging
1.3. X-ray Computed Tomography (XCT)
2. Methods
2.1. Silicon Micromodels
2.1.1. Lithography
2.1.2. Deep Reactive Ion Etching (DRIE)
2.2. Sintered Glass Beads
2.3. Materials
2.3.1. Resin and Chemicals
2.3.2. Viscosity Measurement
2.3.3. Rock Samples
2.3.4. Pore Throat Size Measurement
2.4. Vacuum Impregnation and Degassing
2.5. High-Pressure Impregnation
2.6. Sample Preparation
Etching
2.7. Imaging
2.7.1. CLSM Imaging
2.7.2. Micro-CT
3. Results & Discussion
3.1. Assessment of Impregnation Parameters
- Resin should fill the pore space completely by spontaneous imbibition owing to its wetting behavior. However, this typically never happens in practice because of limited impregnation times.
- The application of high pressure helps resin impregnation, especially at the significant pressures that can be generated in a laboratory. The drastic effect of pressure on the impregnation penetration distance is exemplified in Figure 5, where high-pressure-assisted impregnation is an order of magnitude longer than the other cases.
3.2. Factors Controlling Pore Cast Quality
3.2.1. Vacuum Level
3.2.2. Impregnation Pressure
3.2.3. Viscosity Modifiers
3.2.4. Optimum Impregnation Parameters
- Pressure-assisted impregnation is essential to ensure complete pore invasion. Pressures of up to 65 bars were experimentally verified to have no adverse effects on both sample integrity (i.e., no cracks) and resin curing.
- A degassing step prior to pressurized-impregnation is needed to remove any fluid traces and avoid bubble formation.
- The benefits of adding viscosity modifiers to the epoxy system do not outweigh the risks, and hence a selection of epoxies that have adequate viscosity (i.e., below 0.5 Pas) leads to a higher pore cast quality.
3.3. Imaging Etched Carbonates Pore Casts
3.3.1. Pore Cast Quality
3.3.2. Etching Quality
3.3.3. Confocal Microscopy
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CLSM | Confocal Laser Scanning Microscopy |
| NA | Numerical Aperture |
| DRIE | Deep Reactive Ion Etching |
| SCCM | Standard Cubic Cm per Minute |
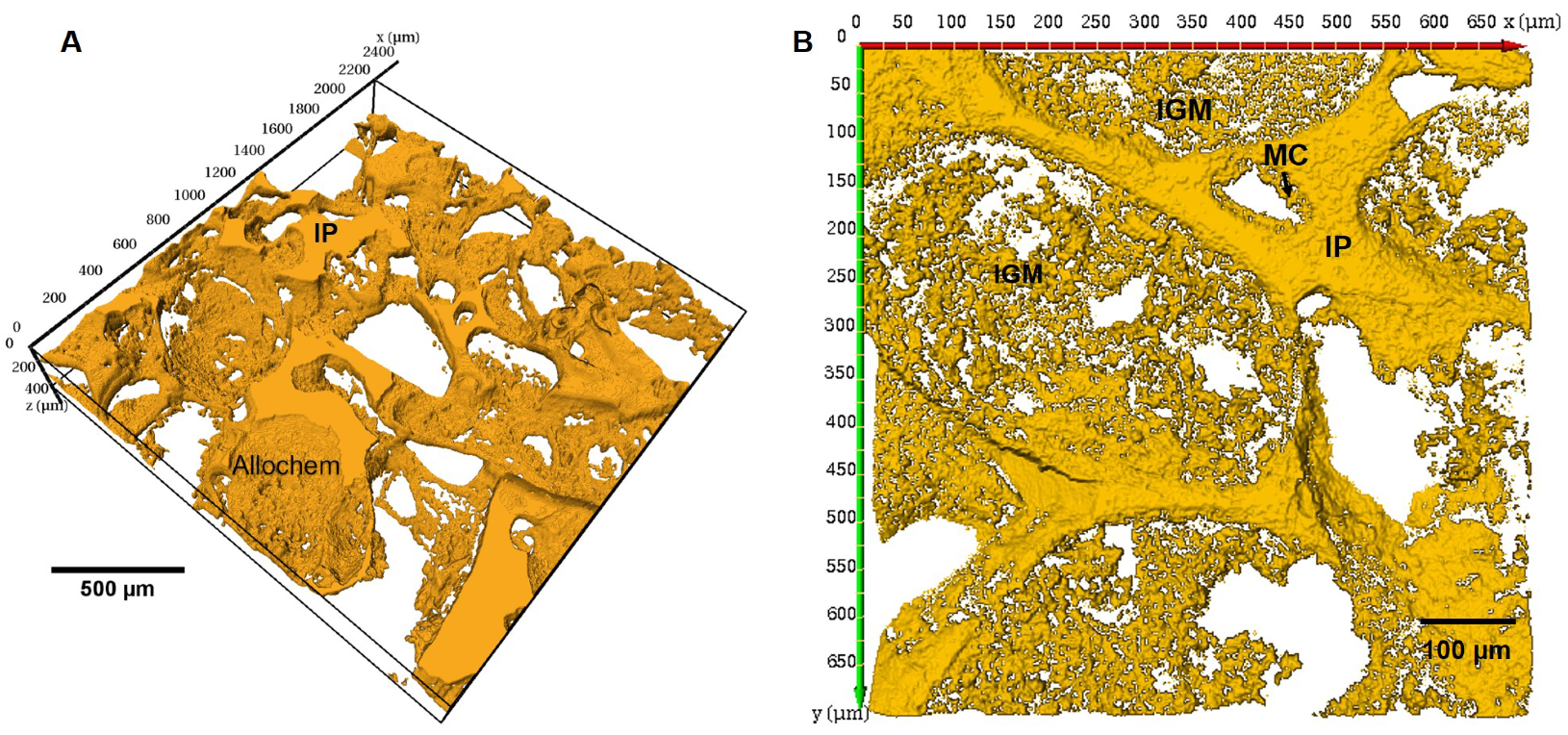
| MC | Micritic Cement |
| MIP | Mercury Intrusion Porosimetry |
| IGM | Intragranular Microporosity |
| Micro-CT | Micro-Computed Tomography |
| IP | Interparticle Porosity |
References
- Waters, B.T.; Savage, D.E. Making duplicates of small vertebrate fossils for teaching and for re-search collections. Curator 1971, 14, 123–132. [Google Scholar] [CrossRef]
- Purnell, M.A. Casting, replication, and anaglyph stereo imaging of microscopic detail in fossils, with examples from conodonts and other jawless vertebrates. Palaeontol. Electron. 2003, 6, 1–11. [Google Scholar]
- Mihlbachler, M.C.; Foy, M.; Beatty, B.L. Surface replication, fidelity and data loss in traditional dental microwear and dental microwear texture analysis. Sci. Rep. 2019, 9, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Jernvall, J.; Selänne, L. Laser confocal microscopy and geographic information systems in the study of dental morphology. Palaeontol. Electron. 1999, 2, 18. [Google Scholar] [CrossRef]
- Macdonald, D.A.; Harman, R.; Evans, A.A. Replicating surface texture: Preliminary testing of molding compound accuracy for surface measurements. J. Archaeol. Sci. Rep. 2018, 18, 839–846. [Google Scholar] [CrossRef]
- Waldo, A.W.; Yuster, S.T. Method of impregnating porous materials to facilitate pore studies. AAPG Bull. 1937, 21, 259–267. [Google Scholar]
- Pittman, E.D.; Duschatko, R.W. Use of pore casts and scanning electron microscope to study pore geometry. J. Sediment. Res. 1970, 40, 1153–1157. [Google Scholar]
- Wardlaw, N. Pore geometry of carbonate rocks as revealed by pore casts and capillary pressure. AAPG Bull. 1976, 60, 245–257. [Google Scholar]
- Yanguas, J.; Paxton, S.T. A new technique for preparation of petrographic thin sections using ultraviolet-curing adhesive. J. Sediment. Res. 1986, 56, 539–540. [Google Scholar] [CrossRef]
- Klaver, J.; Hemes, S.; Houben, M.; Desbois, G.; Radi, Z.; Urai, J. The connectivity of pore space in mudstones: Insights from high-pressure Wood’s metal injection, BIB-SEM imaging, and mercury intrusion porosimetry. Geofluids 2015, 15, 577–591. [Google Scholar] [CrossRef]
- Jobe, T.; Geiger, S.; Jiang, Z.; Agar, S. Micropore network modelling from 2D confocal imagery: Impact on reservoir quality and hydrocarbon recovery. Pet. Geosci. 2018, 24, 323–334. [Google Scholar] [CrossRef]
- Cantrell, D.L.; Hagerty, R.M. Microporosity in arab formation carbonates, Saudi Arabia. GeoArabia 1999, 4, 129–154. [Google Scholar]
- Morrow, N.R.; Buckley, J. Wettability and Oil Recovery by Imbibition and Viscous Displacement from Fractured and Heterogeneous Carbonates; Chemical & Petroleum Engineering, University of Wyoming: Laramie, WY, USA, 2006. [Google Scholar]
- Fullmer, S.M.; Guidry, S.A.; Gournay, J.; Bowlin, E.; Ottinger, G.; Al Neyadi, A.; Gupta, G.; Gao, B.; Edwards, E. Microporosity: Characterization, distribution, and influence on oil recovery. In Proceedings of the IPTC 2014: International Petroleum Technology Conference, Doha, Qatar, 19–22 January 2014. [Google Scholar]
- Minoura, N.; Conley, C. Technique for impregnating porous rock samples with low-viscosity epoxy resin. J. Sediment. Res. 1971, 41, 858–861. [Google Scholar] [CrossRef]
- John, D.S. The use of large-area thin sectioning in the petrographic examination of concrete. In Petrography Applied to Concrete and Concrete Aggregates; ASTM International: West Conshohocken, PA, USA, 1990. [Google Scholar]
- Smith, S.J.; Anderson, R.S. A method for impregnating soft sediment cores for thin-section microscopy. J. Sediment. Res. 1995, 65, 576–577. [Google Scholar] [CrossRef]
- Hurst, A.; Nadeau, P.H. Clay microporosity in reservoir sandstones: An application of quantitative electron microscopy in petrophysical evaluation. AAPG Bull. 1995, 79, 563–573. [Google Scholar]
- Chen, J.; Zampini, D.; Walliser, A. High-pressure epoxy-impregnated cementitious materials for microstructure characterization. Cem. Concr. Res. 2002, 32, 1–7. [Google Scholar] [CrossRef]
- Beckett, D.; Sellwood, B. A simple method for producing high-quality porecasts of carbonate rocks. Sediment. Geol. 1991, 71, 1–4. [Google Scholar] [CrossRef]
- Camuti, K.S.; McGuire, P.T. Preparation of polished thin sections from poorly consolidated regolith and sediment materials. Sediment. Geol. 1999, 128, 171–178. [Google Scholar] [CrossRef]
- Boës, X.; Fagel, N. Impregnation method for detecting annual laminations in sediment cores: An overview. Sediment. Geol. 2005, 179, 185–194. [Google Scholar] [CrossRef]
- Kjellsen, K.; Monsøy, A.; Isachsen, K.; Detwiler, R. Preparation of flat-polished specimens for SEM-backscattered electron imaging and X-ray microanalysis importance of epoxy impregnation. Cem. Concr. Res. 2003, 33, 611–616. [Google Scholar] [CrossRef]
- Soeder, D.J. Applications of Fluorescence Microscopy to Study of Pores in Tight Rocks. AAPG Bull. 1990, 74, 30–40. [Google Scholar]
- Spurr, A.R. A low-viscosity epoxy resin embedding medium for electron microscopy. J. Ultrastruct. Res. 1969, 26, 31–43. [Google Scholar] [CrossRef]
- Head, M.; Buenfeld, N. Confocal imaging of porosity in hardened concrete. Cem. Concr. Res. 2006, 36, 896–911. [Google Scholar] [CrossRef]
- Shah, S.; Crawshaw, J.; Boek, E. Preparation of microporous rock samples for confocal laser scanning microscopy. Pet. Geosci. 2014, 20, 369–374. [Google Scholar] [CrossRef]
- Jim, C. Impregnation of moist and dry unconsolidated clay samples using Spurr resin for microstructural studies. J. Sediment. Res. 1985, 55, 597–599. [Google Scholar] [CrossRef]
- Yadav, G.; Dullien, F.; Chatzis, I.; Macdonald, I. Microscopic distribution of wetting and nonwetting phases in sandstones during immiscible displacements. SPE Reserv. Eng. 1987, 2, 137–147. [Google Scholar] [CrossRef]
- Rothwell, R.G.; Rack, F.R. New techniques in sediment core analysis: An introduction. Geol. Soc. Lond. Spec. Publ. 2006, 267, 1–29. [Google Scholar] [CrossRef] [Green Version]
- Muller, M. Introduction to Confocal Fluorescence Microscopy; SPIE Press: Bellingham, WA, USA, 2006; Volume 69. [Google Scholar]
- Pawley, J. Handbook of Biological Confocal Microscopy; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Fredrich, J.; Menendez, B.; Wong, T.F. Imaging the pore structure of geomaterials. Science 1995, 268, 276–279. [Google Scholar] [CrossRef]
- Petford, N.; Davidson, G.; Miller, J. Investigation of the petrophysical properties of a porous sandstone sample using confocal scanning laser microscopy. Pet. Geosci. 2001, 7, 99–105. [Google Scholar] [CrossRef]
- Fredrich, J. 3D imaging of porous media using laser scanning confocal microscopy with application to microscale transport processes. Phys. Chem. Earth Part A Solid Earth Geod. 1999, 24, 551–561. [Google Scholar] [CrossRef] [Green Version]
- Hsieh, J. Computed Tomography: Principles, Design, Artifacts, and Recent Advances, 3rd ed.; SPIE: Bellingham, WA, USA, 2015. [Google Scholar]
- Withers, P.J.; Bouman, C.; Carmignato, S.; Cnudde, V.; Grimaldi, D.; Hagen, C.K.; Maire, E.; Manley, M.; Du Plessis, A.; Stock, S.R. X-ray computed tomography. Nat. Rev. Methods Prim. 2021, 1, 1–21. [Google Scholar]
- Sánchez, S.; Narciso, J.; Rodríguez-Reinoso, F.; Bernard, D.; Watson, I.; Lee, P.; Dashwood, R. Characterization of Lightweight Graphite Based Composites Using X-Ray Microtomography. Adv. Eng. Mater. 2006, 8, 491–495. [Google Scholar] [CrossRef]
- Salvo, L.; Suéry, M.; Marmottant, A.; Limodin, N.; Bernard, D. 3D imaging in material science: Application of X-ray tomography. C. R. Phys. 2010, 11, 641–649. [Google Scholar] [CrossRef]
- Lärmer, F.; Schilp, A. Verfahren zum anisotropen Ätzen von Silizium. Dtsch. Pat. DE 1994, 42, 045. [Google Scholar]
- Cañamero-Martínez, P.; Fernández-García, M.; De la Fuente, J.L. Rheological cure characterization of a polyfunctional epoxy acrylic resin. React. Funct. Polym. 2010, 70, 761–766. [Google Scholar] [CrossRef]
- Patton, J.B.; Carr, D.D. The Salem Limestone in the Indiana Building-Stone District; Technical Report; Indiana Geological Survey: Indianapolis, IN, USA, 1982. [Google Scholar]
- Churcher, P.; French, P.; Shaw, J.; Schramm, L. Rock properties of Berea sandstone, Baker dolomite, and Indiana limestone. In Proceedings of the SPE International Symposium on Oilfield Chemistry, Anaheim, CA, USA, 20–22 February 1991. [Google Scholar]
- Vajdova, V.; Baud, P.; Wu, L.; Wong, T.f. Micromechanics of inelastic compaction in two allochemical limestones. J. Struct. Geol. 2012, 43, 100–117. [Google Scholar] [CrossRef]
- Caccia, M.; Camarano, A.; Sergi, D.; Ortona, A.; Narciso, J. Wetting and Navier-Stokes equation—The manufacture of composite materials. Wetting Wettability 2015, 2015, 105–137. [Google Scholar]
- Shah, S.M.K. Multi-Scale Imaging of Porous Media and Flow Simulation at the Pore Scale. Ph.D. Thesis, Imperial College London, London, UK, 2014. [Google Scholar]
- Szekely, J.; Neumann, A.; Chuang, Y. The rate of capillary penetration and the applicability of the Washburn equation. J. Colloid Interface Sci. 1971, 35, 273–278. [Google Scholar] [CrossRef]
- Maija Leskinen, A. Layer structure in model coatings. Tappi J. 1987, 70, 101–106. [Google Scholar]
- Marmur, A. Penetration and displacement in capillary systems of limited size. Adv. Colloid Interface Sci. 1992, 39, 13–33. [Google Scholar] [CrossRef]
- Pesse, A.V.; Warrier, G.R.; Dhir, V.K. Experimental study of the gas entrapment process in closed-end microchannels. ASME Int. Mech. Eng. Congr. Expo. 2004, 4711, 119–128. [Google Scholar]
- Hamraoui, A.; Nylander, T. Analytical approach for the Lucas—Washburn equation. J. Colloid Interface Sci. 2002, 250, 415–421. [Google Scholar] [CrossRef]
- Dudgeon, A. Penetration of Surfactant Solutions into Capillaries. Ph.D. Thesis, Durham University, Durham, UK, 2011. [Google Scholar]
- Ramos, J.; Pagani, N.; Riccardi, C.; Borrajo, J.; Goyanes, S.; Mondragon, I. Cure kinetics and shrinkage model for epoxy-amine systems. Polymer 2005, 46, 3323–3328. [Google Scholar] [CrossRef]
- Plepys, A.; Farris, R. Evolution of residual stresses in three-dimensionally constrained epoxy resins. Polymer 1990, 31, 1932–1936. [Google Scholar] [CrossRef]
- Eom, Y.; Boogh, L.; Michaud, V.; Sunderland, P.; Månson, J.A. Stress-initiated void formation during cure of a three-dimensionally constrained thermoset resin. Polym. Eng. Sci. 2001, 41, 492–503. [Google Scholar] [CrossRef]
- Thomas, S.; Bongiovanni, C.; Nutt, S. In situ estimation of through-thickness resin flow using ultrasound. Compos. Sci. Technol. 2008, 68, 3093–3098. [Google Scholar] [CrossRef]
- Potter, K. Resin Transfer Moulding; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Gündüz, G.; Yeter, B.; Tuğlu, P.; Ahmed, I. Styrene-acrylonitrile co-polymer impregnated mortar. J. Mater. Sci. 1981, 16, 221–225. [Google Scholar] [CrossRef]
- Gündüz, G.; Yalçin, N. Strength of steel-fibre-reinforced polymer concrete: Effect of impregnation technique. Compos. Sci. Technol. 1987, 30, 127–135. [Google Scholar] [CrossRef]
- Langmuir, D. Stability of calcite based on aqueous solubility measurements. Geochim. Cosmochim. Acta 1968, 32, 835–851. [Google Scholar] [CrossRef]
- Lund, K.; Fogler, H.S.; McCune, C.; Ault, J. Acidization–II. The dissolution of calcite in hydrochloric acid. Chem. Eng. Sci. 1975, 30, 825–835. [Google Scholar] [CrossRef] [Green Version]
- Hassan, A.; Chandra, V.; Yutkin, M.P.; Patzek, T.W.; Espinoza, D. Imaging and Characterization of Microporous Carbonates Using Confocal and Electron Microscopy of Epoxy Pore Casts. SPE J. 2019, 24, 1–220. [Google Scholar] [CrossRef]














| Parameter | Passivation | Etching |
|---|---|---|
| ICP Power | 1300 Watts | |
| Pressure | 30 mTorr | |
| Temperature | ||
| C4F8 flow rate | 100 SCCM * | 5 SCCM |
| SF6 flow rate | 5 SCCM | 100 SCCM |
| Epoxy Resin | |
|---|---|
| Density | 1118 kg/m |
| Viscosity | 0.468 Pas |
| Surface tension | 0.039 N/m |
| Contact-angle on silica | 31 |
| Curing agent | Primary amine |
| Curing time * | 24–36 h * |
| Curing temperature | 25 |
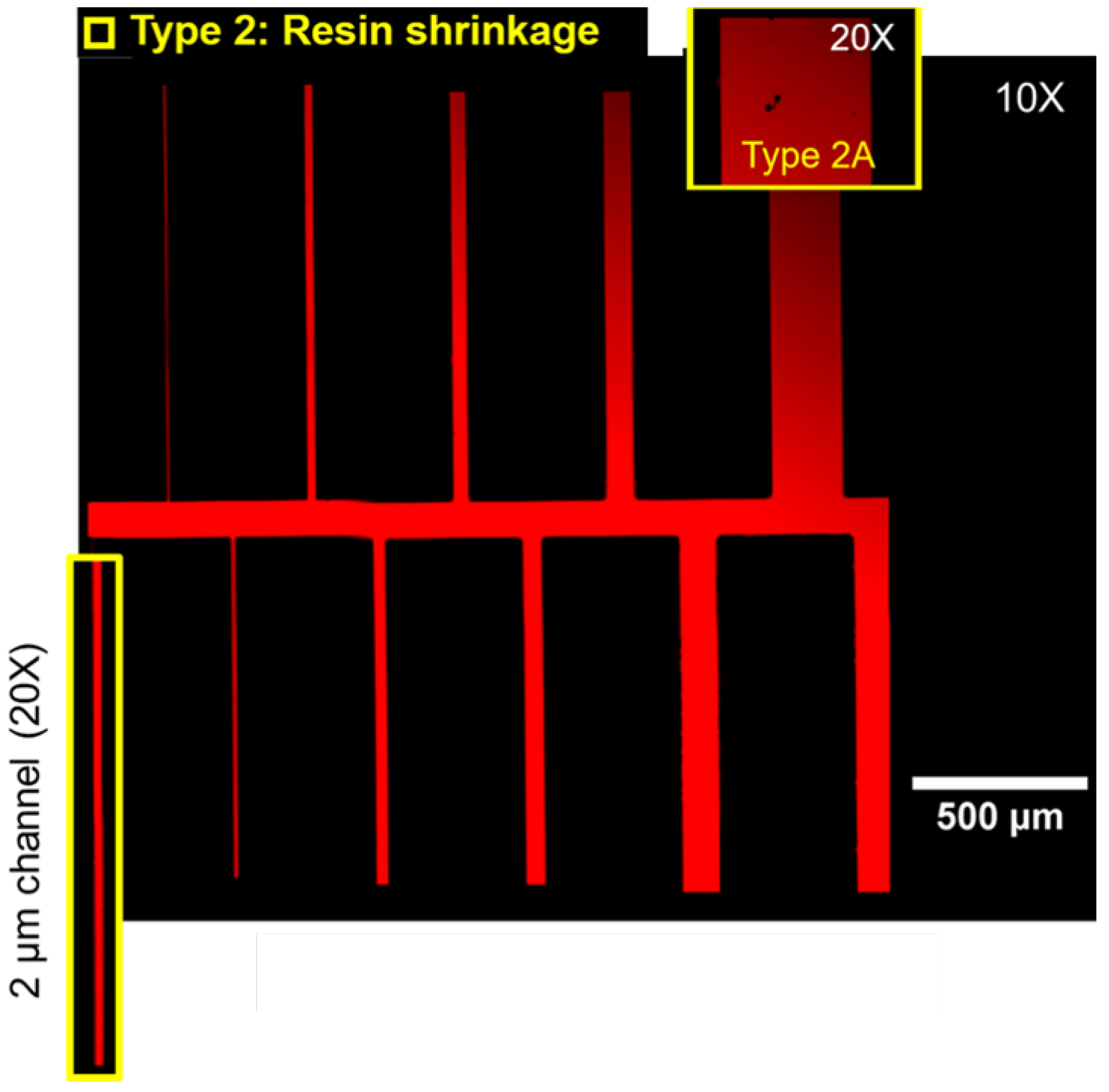
| Defect Type | Description |
|---|---|
| Type 1 | Trapped gases |
| Type 2 | Shrinkage defects |
| Type 2A | Voids with corrugated boundaries and irregular shapes |
| Type 2B | Rough cracks |
| Impregnation Parameters | |
|---|---|
| Degassing | 80 mbar |
| Degassing time | 30 min |
| Impregnation pressure | 65 bar |
| Curing time | 30 h |
| Resin viscosity | 0.468 Pas |
| Temperature | 25 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hassan, A.; Yutkin, M.; Chandra, V.; Patzek, T. Quality Evaluation of Epoxy Pore Casts Using Silicon Micromodels: Application to Confocal Imaging of Carbonate Samples. Appl. Sci. 2021, 11, 5557. https://doi.org/10.3390/app11125557
Hassan A, Yutkin M, Chandra V, Patzek T. Quality Evaluation of Epoxy Pore Casts Using Silicon Micromodels: Application to Confocal Imaging of Carbonate Samples. Applied Sciences. 2021; 11(12):5557. https://doi.org/10.3390/app11125557
Chicago/Turabian StyleHassan, Ahmed, Maxim Yutkin, Viswasanthi Chandra, and Tadeusz Patzek. 2021. "Quality Evaluation of Epoxy Pore Casts Using Silicon Micromodels: Application to Confocal Imaging of Carbonate Samples" Applied Sciences 11, no. 12: 5557. https://doi.org/10.3390/app11125557
APA StyleHassan, A., Yutkin, M., Chandra, V., & Patzek, T. (2021). Quality Evaluation of Epoxy Pore Casts Using Silicon Micromodels: Application to Confocal Imaging of Carbonate Samples. Applied Sciences, 11(12), 5557. https://doi.org/10.3390/app11125557






