A Multiple and Multi-Level Substructure Method for the Dynamics of Complex Structures
Abstract
1. Introduction
2. Component Mode Synthesis of Fixed Interface
- The part that is not connected with other substructures (internal degrees of freedom), denoted as {uo}.
- The part connected with other substructures (external degree of freedom or boundary degree of freedom) is denoted as {ua}.
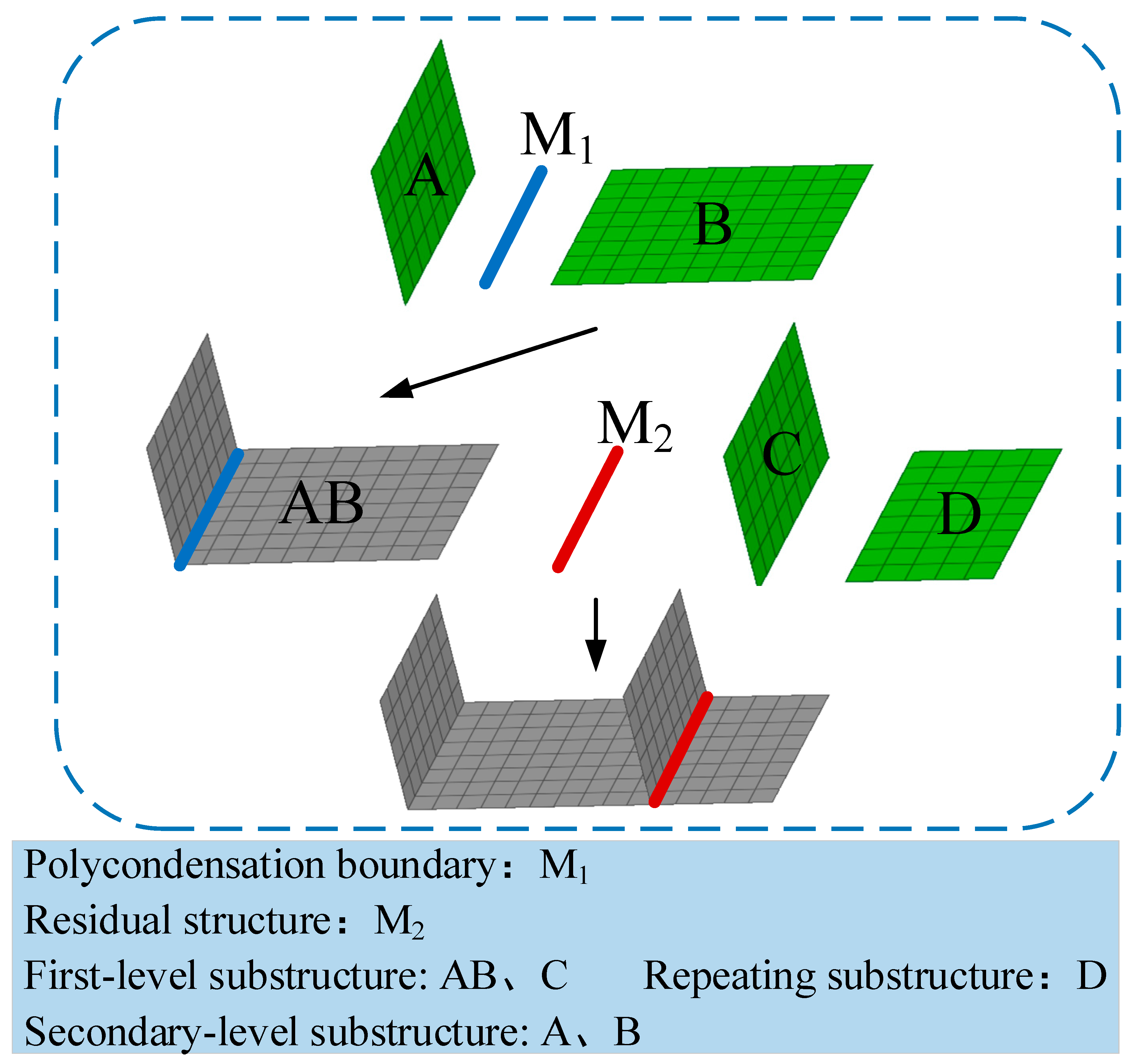
3. Multiple and Multi-Level Substructure Method
4. Analysis of Dynamic Characteristics Based on Substructure
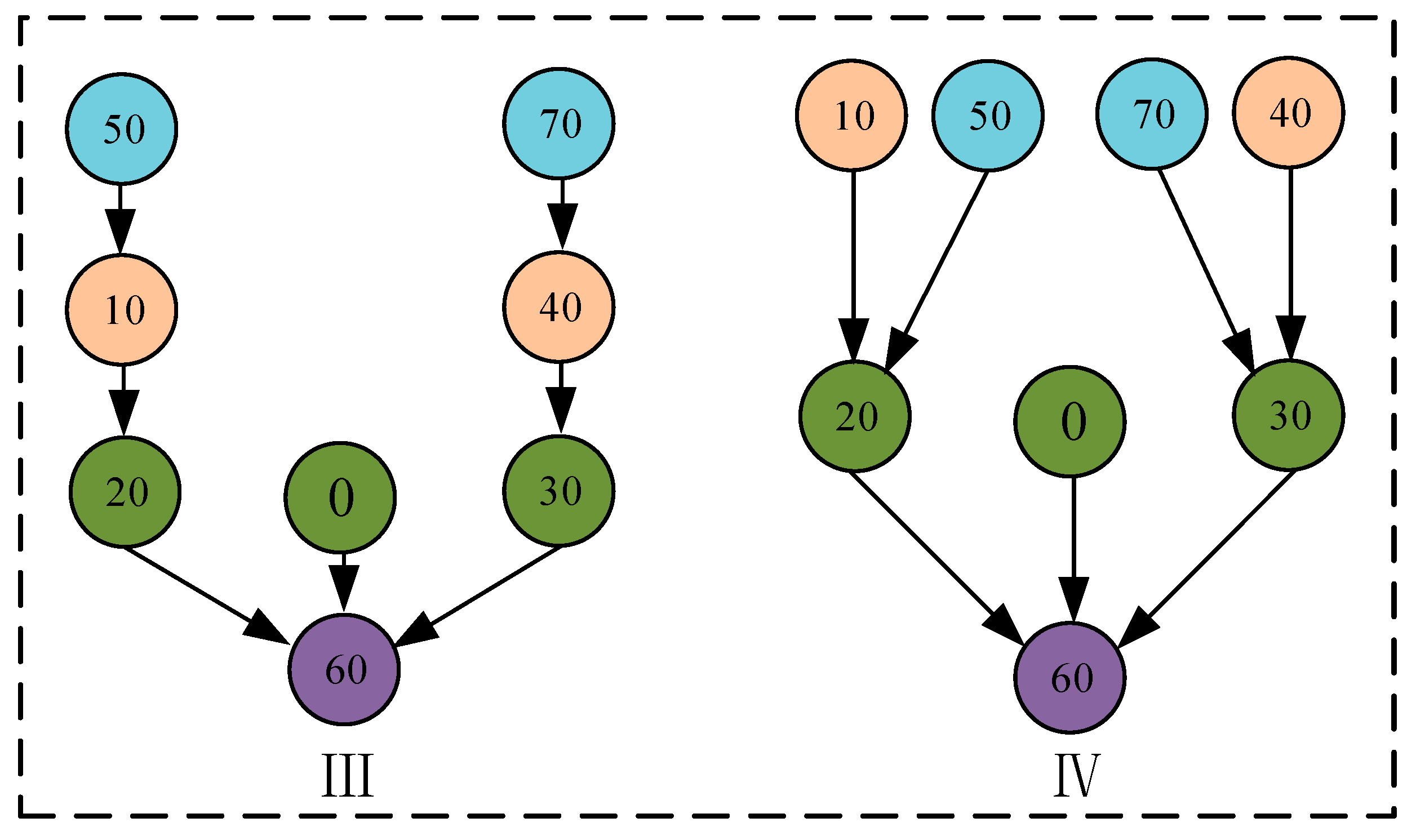
4.1. Assembly Structure with Three Panels
4.2. Gear Box
4.3. Modal Experiment of Combustion Rotor and Verification of Substructure Method
4.3.1. Object of the Experiment
4.3.2. Experiment System
4.3.3. Data Acquisition
4.3.4. Identification of a Modal Parameter
4.3.5. Verification of Substructure Method
5. Conclusions
- In the substructure calculation and analysis of actual engineering structures, the selection of residual structures is not unique;
- For the same residual structure, the calculation accuracy of the substructure will not be affected by different substructure division methods, and the high-precision dynamic characteristic analysis can be realized;
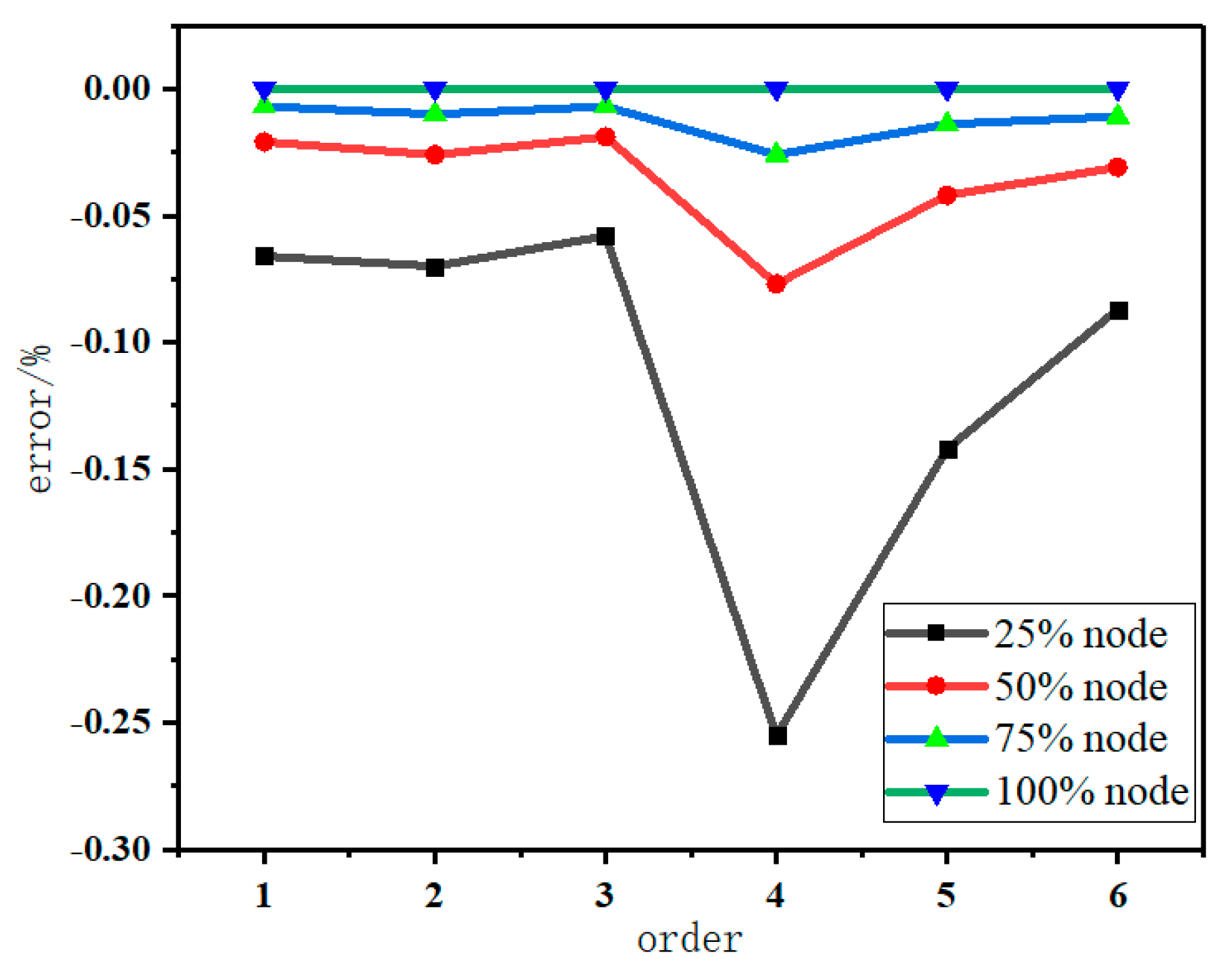
- The modal frequency accuracy of the substructure model is related to the number of selected external nodes of the substructure. On the premise of ensuring accuracy, the selection of 50% external nodes can further improve the computational efficiency.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Weng, S.; Xia, Y.; Xu, Y.-L.; Zhou, X.-Q.; Zhu, H.-P. Improved substructuring method for eigensolutions of large-scale structures. J. Sound Vib. 2009, 323, 718–736. [Google Scholar] [CrossRef]
- Liu, J.; Fei, Q.; Jiang, D.; Zhang, D.; Wu, S. Experimental and numerical investigation on static and dynamic characteristics for curvilinearly stiffened plates using DST–BK model. Int. J. Mech. Sci. 2020, 169, 105286. [Google Scholar] [CrossRef]
- Gu, Y. Mode-dependent phonon transmission in a T-shaped three-terminal graphene nanojunction. Carbon 2020, 158, 818–826. [Google Scholar] [CrossRef]
- Zhou, J.; Xu, L.; Liu, G.; Xuan, Y.; Zhou, H.; Jiang, H. Frequency Response Curves and Dynamic Characteristics of a Ginkgo Tree in Different Growth Periods. Trans. ASABE 2020, 63, 1673–1684. [Google Scholar] [CrossRef]
- Torabi, J.; Ansari, R. A higher-order isoparametric superelement for free vibration analysis of functionally graded shells of revolution. Thin-Walled Struct. 2018, 133, 169–179. [Google Scholar] [CrossRef]
- Zhang, D.; Fei, Q.; Liu, J.; Jiang, D.; Li, Y. Crushing of vertex-based hierarchical honeycombs with triangular substructures. Thin-Walled Struct. 2020, 146, 106436. [Google Scholar] [CrossRef]
- Bai, B.; Bai, G.-C. Dynamic probabilistic analysis of stress and deformation for bladed disk assemblies of aeroengine. J. Central South Univ. 2014, 21, 3722–3735. [Google Scholar] [CrossRef]
- Bai, B.; Bai, G.C.; Li, C. Application of multi-stage multi-objective multi-disciplinary agent model based on dynamic substructural method in Mistuned Blisk. Aerosp. Sci. Technol. 2015, 46, 104–115. [Google Scholar] [CrossRef]
- Bai, B.; Li, H.; Zhang, W.; Cui, Y. Application of extremum response surface method-based improved substructure component mode synthesis in mistuned turbine bladed disk. J. Sound Vib. 2020, 472, 115210. [Google Scholar] [CrossRef]
- Gu Y, F. An efficient Laplace transform-wave packet method hybrid with substructure technique. Comput. Mater. Sci. 2015, 110, 345–352. [Google Scholar] [CrossRef]
- Duan, Y.; Zang, C.; Petrov, E.P. Forced Response Analysis of High-Mode Vibrations for Mistuned Bladed Disks With Effective Reduced-Order Models. J. Eng. Gas Turbines Power 2016, 138, 112502. [Google Scholar] [CrossRef]
- Jung, C.; Saito, A.; Epureanu, B.I. Detection of Cracks in Mistimed Bladed Disks Using Reduced-Order Models and Vibration Data. J. Vib. Acoust. 2012, 134, 061010. [Google Scholar] [CrossRef]
- Zhu, H.; Li, J.; Tian, W.; Weng, S.; Peng, Y.; Zhang, Z.; Chen, Z. An enhanced substructure-based response sensitivity method for finite element model updating of large-scale structures. Mech. Syst. Signal Process. 2021, 154, 107359. [Google Scholar] [CrossRef]
- Tian, W.; Weng, S.; Xia, Y.; Zhu, H.; Gao, F.; Sun, Y.; Li, J. An iterative reduced-order substructuring approach to the calculation of eigensolutions and eigensensitivities. Mech. Syst. Signal Process. 2019, 130, 361–377. [Google Scholar] [CrossRef]
- Weng, S.; Xia, Y.; Xu, Y.L.; Zhu, H. An iterative substructuring approach to the calculation of eigensolution and eigensensitivity. J. Sound Vib. 2011, 330, 3368–3380. [Google Scholar] [CrossRef]
- Weng, S.; Zhu, H.-P.; Xia, Y.; Zhou, X.-Q.; Mao, L. Substructuring approach to the calculation of higher-order eigensensitivity. Comput. Struct. 2013, 117, 23–33. [Google Scholar] [CrossRef]
- Weng, S.; Xia, Y.; Xu, Y.-L.; Zhu, H.-P. Substructure based approach to finite element model updating. Comput. Struct. 2011, 89, 772–782. [Google Scholar] [CrossRef]
- Jiang, D.; Zhang, P.; Fei, Q.; Wu, S. Comparative study of model updating methods using frequency response function data. J. Vibroeng. 2014, 16, 2305–2318. [Google Scholar]
- Shamloofard, M.; Hosseinzadeh, A.; Movahhedy, M.R. Development of a shell superelement for large deformation and free vibration analysis of composite spherical shells. Eng. Comput. 2020, 1–17. [Google Scholar] [CrossRef]
- Fatan, A.; Ahmadian, M. Vibration analysis of FGM rings using a newly designed cylindrical superelement. Sci. Iran. 2017, 25, 1179–1188. [Google Scholar] [CrossRef]
- Plaza, J.; Abasolo, M.; Coria, I.; Aguirrebeitia, J.; De Bustos, I.F. A new finite element approach for the analysis of slewing bearings in wind turbine generators using superelement techniques. Meccanica 2015, 50, 1623–1633. [Google Scholar] [CrossRef]
- Tuysuz, O.; Altintas, Y. Frequency Domain Updating of Thin-Walled Workpiece Dynamics Using Reduced Order Substructuring Method in Machining. J. Manuf. Sci. Eng. 2017, 139, 071013. [Google Scholar] [CrossRef]
- Tuysuz, O.; Altintas, Y. Time-Domain Modeling of Varying Dynamic Characteristics in Thin-Wall Machining Using Perturbation and Reduced-Order Substructuring Methods. J. Manuf. Sci. Eng. 2017, 140, 011015. [Google Scholar] [CrossRef]
- Cao, Z.F.; Fei, Q.G.; Jiang, D.; Wu, S. Substructure-based model updating using residual flexibility mixed-boundary method. J. Mech. Sci. Technol. 2017, 31, 759–769. [Google Scholar] [CrossRef]
- Hang, X.; Su, W.; Fei, Q.; Jiang, D. Analytical sensitivity analysis of flexible aircraft with the unsteady vortex-lattice aerodynamic theory. Aerosp. Sci. Technol. 2020, 99, 105612. [Google Scholar] [CrossRef]
- Zhu, R.; Fei, Q.; Jiang, N.; Cao, Z. Maintaining Specific Natural Frequency of Damped System despite Mass Modification. Int. J. Aerosp. Eng. 2019, 2019, 1–11. [Google Scholar] [CrossRef]
- Géradin, M.; Rixen, D. A ‘nodeless’ dual superelement formulation for structural and multibody dynamics application to reduction of contact problems. Int. J. Numer. Methods Eng. 2015, 106, 773–798. [Google Scholar] [CrossRef]
- Voormeeren, S.N.; Van Der Valk, P.L.C.; Nortier, B.P.; Molenaar, D.-P.; Rixen, D. Accurate and efficient modeling of complex offshore wind turbine support structures using augmented superelements. Wind. Energy 2014, 17, 1035–1054. [Google Scholar] [CrossRef]
- Cui, J.; Guan, X.; Zheng, G. A simultaneous iterative procedure for the Kron’s component modal synthesis approach. Int. J. Numer. Methods Eng. 2015, 105, 990–1013. [Google Scholar] [CrossRef]
- Cui, J.; Wang, X.; Xing, J.; Zheng, G. An eigenvector-based iterative procedure for the free-interface component modal synthesis method. Int. J. Numer. Methods Eng. 2018, 116, 723–740. [Google Scholar] [CrossRef]
- Wu, Y.; Zhu, R.; Cao, Z.; Liu, Y.; Jiang, D. Model Updating Using Frequency Response Functions Based on Sherman–Morrison Formula. Appl. Sci. 2020, 10, 4985. [Google Scholar] [CrossRef]
- Zhu, R.; Fei, Q.-G.; Jiang, D.; Cao, Z.-F. Removing mass loading effects of multi-transducers using Sherman-Morrison-Woodbury formula in modal test. Aerosp. Sci. Technol. 2019, 93, 105241. [Google Scholar] [CrossRef]
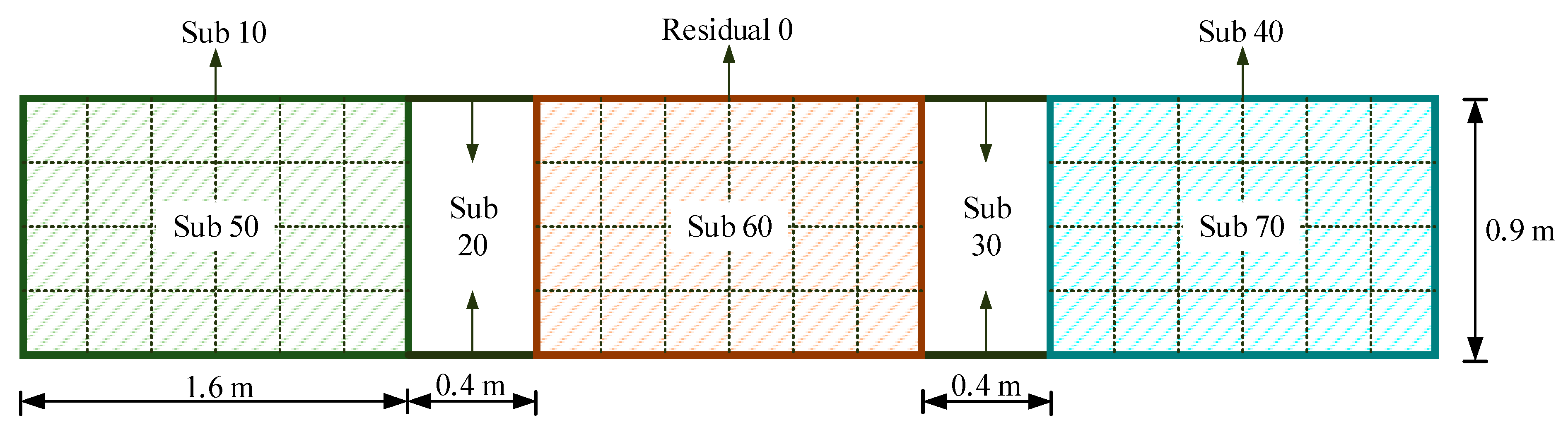


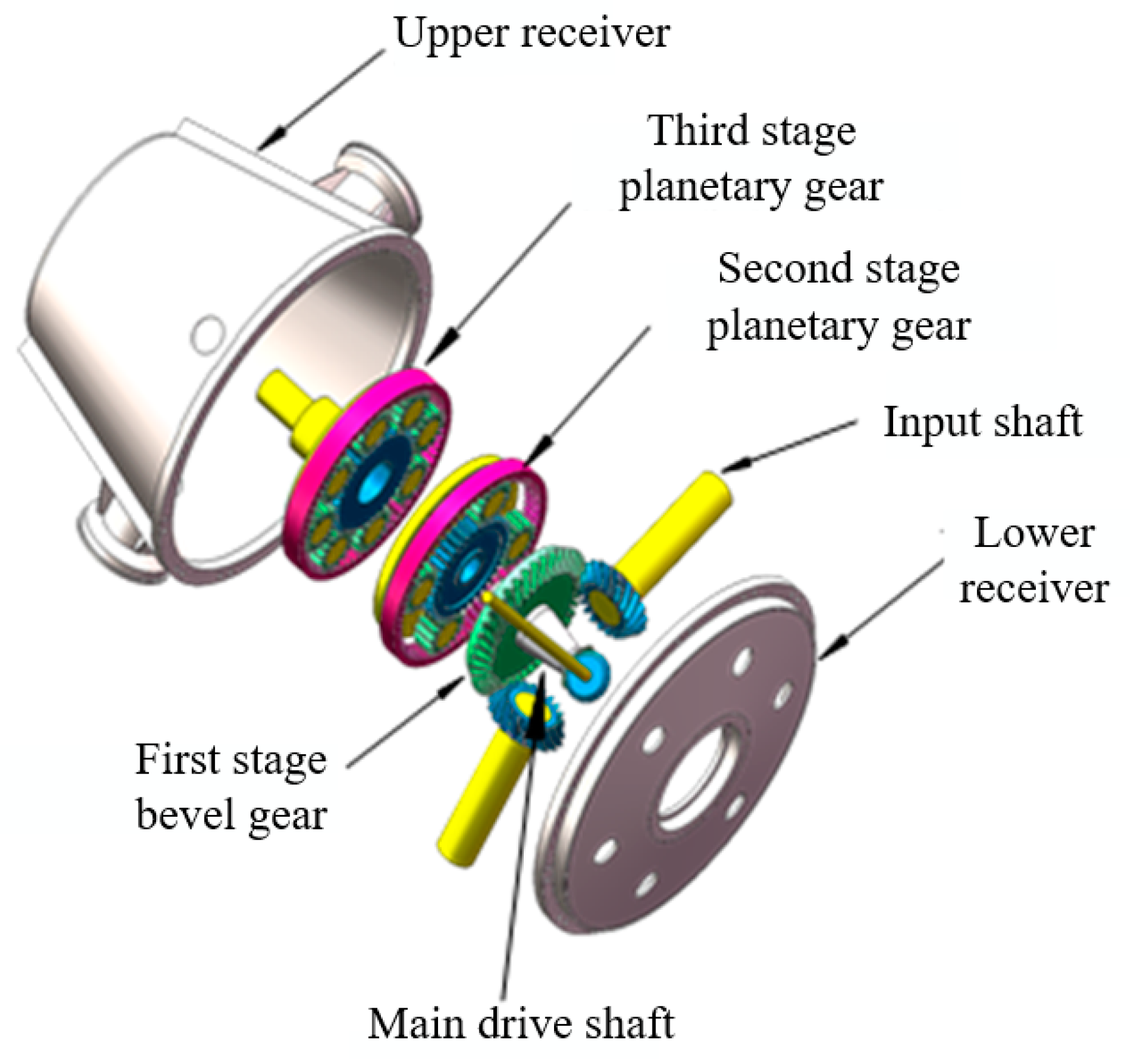
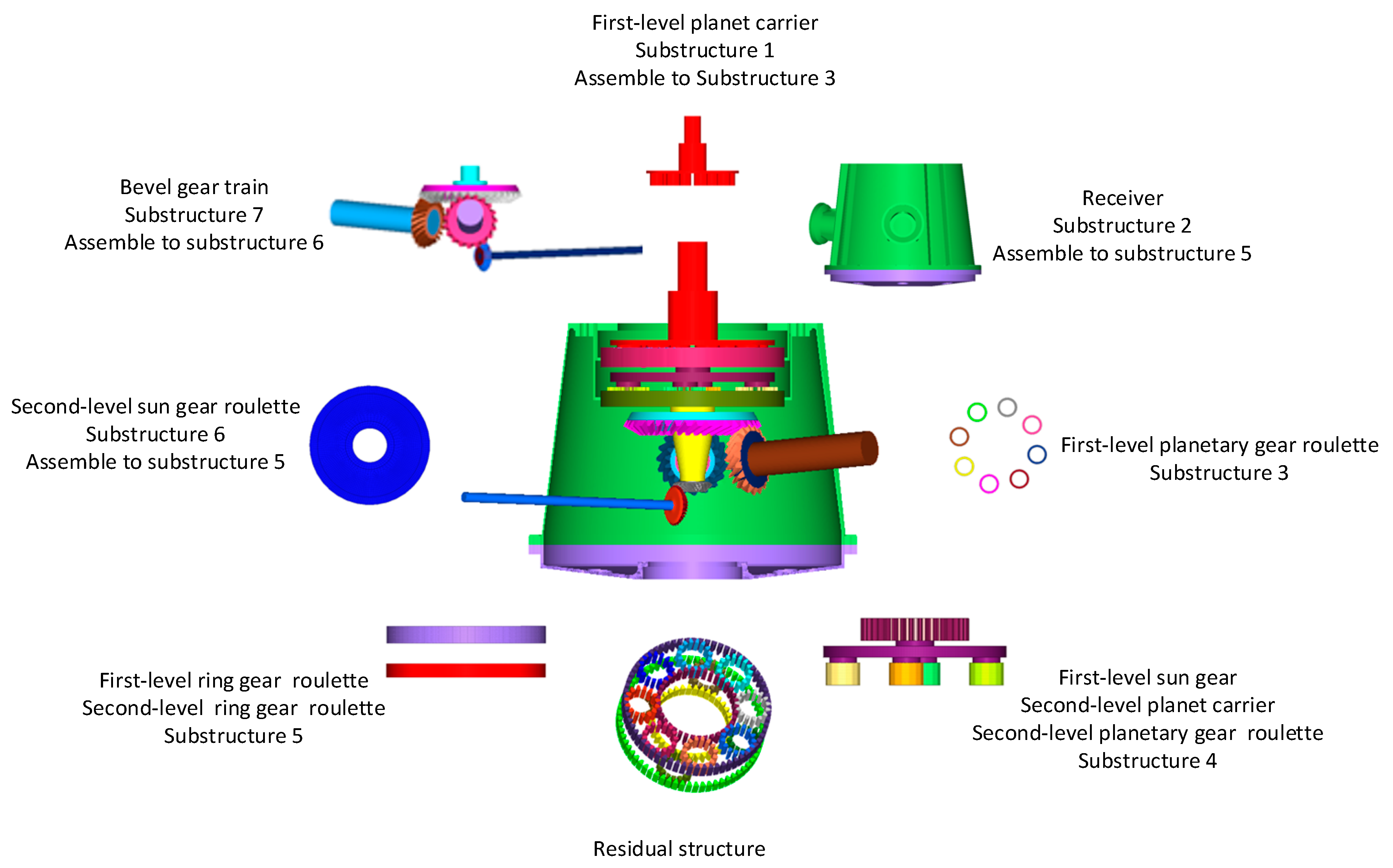
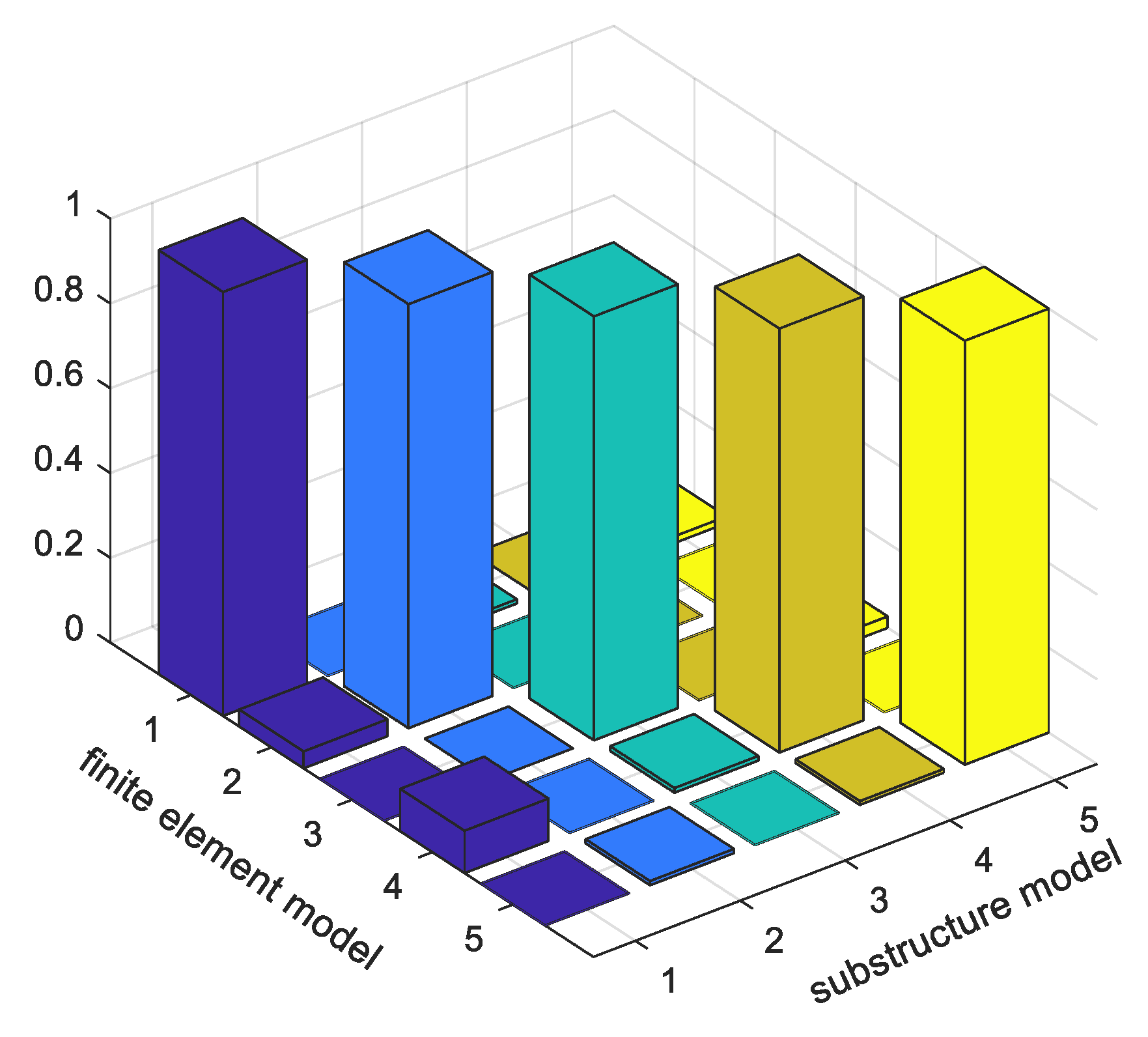
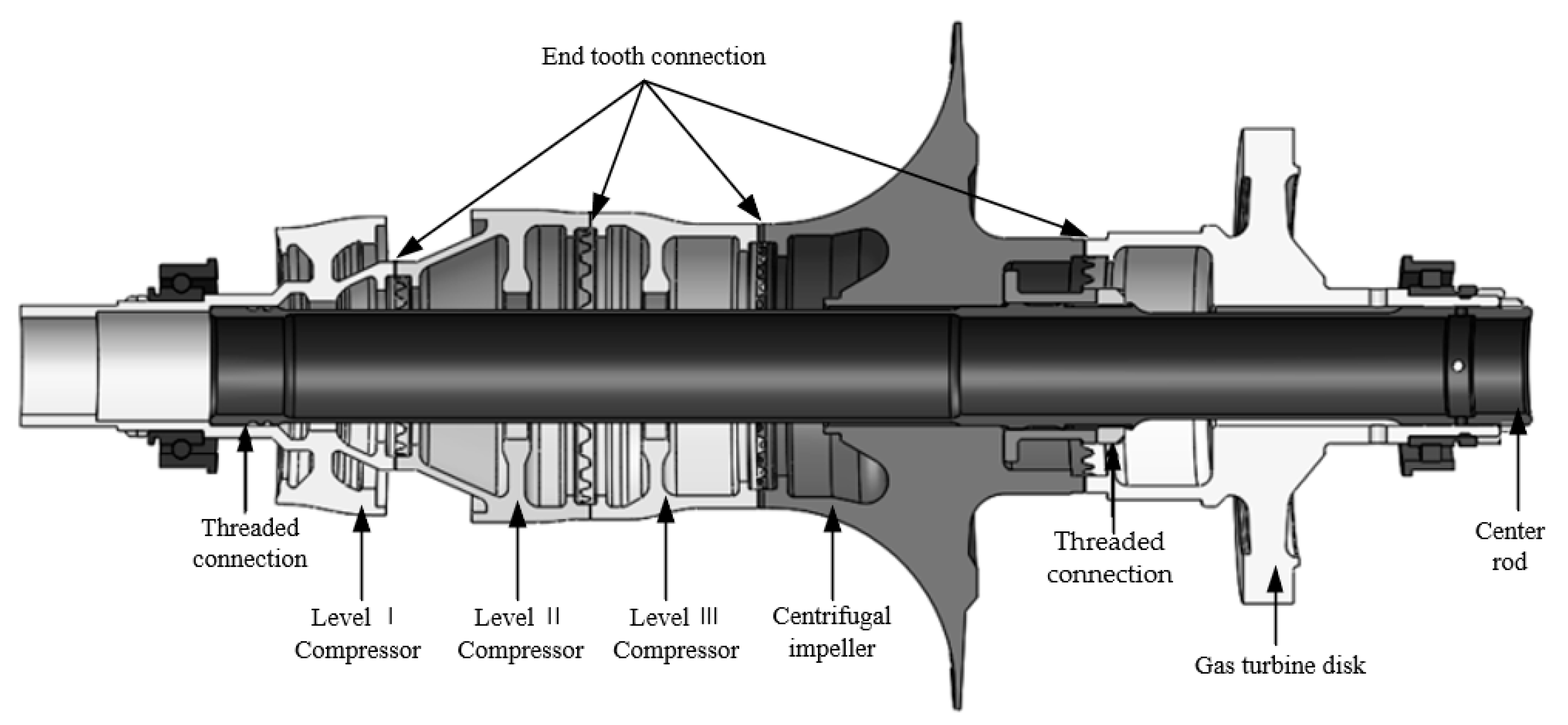






| Type of Element | Material | Elastic Modulus/GPa | Density/g·cm−3 | Poisson’s Ratio |
|---|---|---|---|---|
| Shell element “50” | aluminum | 70 | 2.7 | 0.34 |
| Shell element “60” | aluminum | 70 | 2.7 | 0.34 |
| Shell element “70” | aluminum | 70 | 2.7 | 0.34 |
| Beam element | steel | 200 | 7.85 | 0.32 |
| Order | Natural Frequency/Hz | Error/% | |||
|---|---|---|---|---|---|
| Full Model | Substructure III | Substructure IV | Comparison of Full Model and Substructure III | Comparison of Full Model and Substructure IV | |
| 1 | 1.89100 | 1.89096 | 1.89101 | 0.00212 | 0.00053 |
| 2 | 4.53726 | 4.53703 | 4.53727 | 0.00507 | 0.00022 |
| 3 | 5.16572 | 5.16559 | 5.16574 | 0.00252 | 0.00039 |
| 4 | 9.28268 | 9.28217 | 9.28273 | 0.00549 | 0.00054 |
| 5 | 10.18671 | 10.18639 | 10.18682 | 0.00314 | 0.00108 |
| 6 | 14.15608 | 14.15563 | 14.15698 | 0.00318 | 0.00636 |
| 7 | 16.41321 | 16.40970 | 16.41343 | 0.02138 | 0.00134 |
| 8 | 20.95025 | 20.94964 | 20.95272 | 0.00291 | 0.01180 |
| 9 | 23.28714 | 23.27322 | 23.28847 | 0.05978 | 0.00571 |
| 10 | 28.77556 | 28.78435 | 28.77634 | 0.03055 | 0.00271 |
| 11 | 29.34067 | 29.30249 | 29.34342 | 0.13013 | 0.00937 |
| 12 | 32.17115 | 32.15329 | 32.17310 | 0.05552 | 0.00606 |
| 13 | 33.11550 | 33.07276 | 33.11612 | 0.12906 | 0.00187 |
| 14 | 33.87447 | 33.83622 | 33.87468 | 0.11292 | 0.00062 |
| 15 | 38.41049 | 38.45056 | 38.42395 | 0.10432 | 0.03504 |
| 16 | 39.01908 | 38.95087 | 39.02331 | 0.17481 | 0.01084 |
| 17 | 41.12772 | 41.05179 | 41.13019 | 0.18462 | 0.00601 |
| 18 | 42.52401 | 42.51023 | 42.71097 | 0.03241 | 0.43966 |
| 19 | 47.04580 | 46.98833 | 47.05776 | 0.12216 | 0.02542 |
| 20 | 49.23641 | 49.18840 | 49.24422 | 0.09751 | 0.01586 |
| 25% Nodes | 50% Nodes | 75% Nodes | 100% Nodes | |
|---|---|---|---|---|
| Analysis time/s | 21.871 | 27.919 | 35.598 | 48.427 |
| Order | Natural Frequency/Hz | Error/% | |||
|---|---|---|---|---|---|
| Full Model | Substructure I | Substructure II | Comparison of Full Model and Substructure I | Comparison of Full Model and Substructure II | |
| 1 | 1.89100 | 1.89105 | 1.89093 | 0.00264 | 0.00370 |
| 2 | 4.53726 | 4.53723 | 4.53851 | 0.00066 | 0.02755 |
| 3 | 5.16572 | 5.16579 | 5.17013 | 0.00135 | 0.08537 |
| 4 | 9.28268 | 9.28284 | 9.28297 | 0.00172 | 0.00312 |
| 5 | 10.18671 | 10.18677 | 10.18726 | 0.00059 | 0.00540 |
| 6 | 14.15608 | 14.16634 | 14.14894 | 0.07248 | 0.05044 |
| 7 | 16.41321 | 16.41983 | 16.41348 | 0.04016 | 0.00165 |
| 8 | 20.95025 | 20.95247 | 20.95397 | 0.01060 | 0.01776 |
| 9 | 23.28714 | 23.28816 | 23.28967 | 0.00438 | 0.01086 |
| 10 | 28.77556 | 28.77670 | 28.77638 | 0.00396 | 0.00285 |
| 11 | 29.34067 | 29.30272 | 29.34351 | 0.12934 | 0.00968 |
| 12 | 32.17115 | 32.15182 | 32.16689 | 0.06008 | 0.01324 |
| 13 | 33.11550 | 33.08684 | 33.11634 | 0.08655 | 0.00254 |
| 14 | 33.87447 | 33.81954 | 33.87451 | 0.16215 | 0.00012 |
| 15 | 38.41049 | 38.15891 | 38.42406 | 0.65498 | 0.03533 |
| 16 | 39.01908 | 39.00173 | 39.02286 | 0.04447 | 0.00969 |
| 17 | 41.12772 | 41.05358 | 41.13100 | 0.18028 | 0.00796 |
| 18 | 42.52401 | 42.52094 | 42.71124 | 0.00722 | 0.44029 |
| 19 | 47.04580 | 47.00132 | 47.04365 | 0.09455 | 0.36974 |
| 20 | 49.23641 | 49.16967 | 49.24467 | 0.13555 | 0.01678 |
| Order | Mode 1 | Mode 2 | Mode 3 | Mode 4 | Mode 5 |
|---|---|---|---|---|---|
| Mode shape of FEM |  | 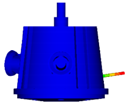 | 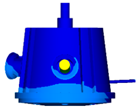 |  | 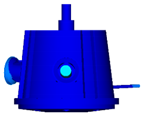 |
| Order | Natural Frequency/Hz | Error/% | |
|---|---|---|---|
| Finite Element Model | Substructure Model | ||
| 1 | 47.23 | 47.60 | 0.7686 |
| 2 | 48.75 | 48.80 | 0.1075 |
| 3 | 94.05 | 92.70 | 1.4333 |
| 4 | 102.59 | 101.99 | 0.5843 |
| 5 | 121.35 | 120.23 | 0.9231 |
| Time-Consuming of Finite Element Model/s | Time-Consuming of Substructure Model/s | Δt/s | The Ratio of Reduction/% |
|---|---|---|---|
| 15062 | 5364 | 9698 | 64.39 |
| Order | Modal Shape | Modal Frequency/Hz | Damping Ratio/% |
|---|---|---|---|
| 1 | 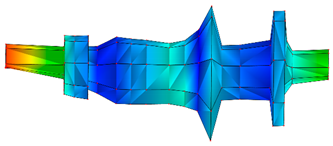 | 1254.9 Hz | 0.166 |
| 2 | 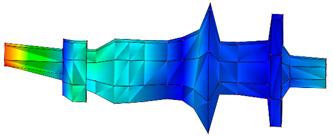 | 2525.2 Hz | 0.216 |
| 3 | 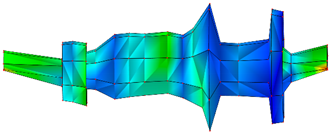 | 3584.7 Hz | 0.067 |
| Material | Elastic Modulus/GPa | Density/g·cm−3 | Poisson’s Ratio |
|---|---|---|---|
| Steel | 196 | 7.8 | 0.3 |
| Titanium alloy | 121 | 4.48 | 0.3 |
| Nickel base alloy | 204 | 8.24 | 0.3 |
| Nickel base alloy | 214 | 8.3 | 0.3 |
| Order | Natural Frequency/Hz | Error/% | |
|---|---|---|---|
| Experimental Model | Sub | Experimental Model and Sub | |
| 1 | 1254.9 | 1335.7 | 6.4 |
| 2 | 2525.2 | 2396.3 | −5.1 |
| 3 | 3584.7 | 3816.4 | 6.5 |
| Finite Element Model | Substructure Model | Δt | The Ratio of Reduction/% | |
|---|---|---|---|---|
| Time-consuming/s | 47.15 | 22.78 | 24.37 | 51.69 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Liu, J.; Cao, Z.; Zhang, D.; Jiang, D. A Multiple and Multi-Level Substructure Method for the Dynamics of Complex Structures. Appl. Sci. 2021, 11, 5570. https://doi.org/10.3390/app11125570
Wang B, Liu J, Cao Z, Zhang D, Jiang D. A Multiple and Multi-Level Substructure Method for the Dynamics of Complex Structures. Applied Sciences. 2021; 11(12):5570. https://doi.org/10.3390/app11125570
Chicago/Turabian StyleWang, Binbin, Jingze Liu, Zhifu Cao, Dahai Zhang, and Dong Jiang. 2021. "A Multiple and Multi-Level Substructure Method for the Dynamics of Complex Structures" Applied Sciences 11, no. 12: 5570. https://doi.org/10.3390/app11125570
APA StyleWang, B., Liu, J., Cao, Z., Zhang, D., & Jiang, D. (2021). A Multiple and Multi-Level Substructure Method for the Dynamics of Complex Structures. Applied Sciences, 11(12), 5570. https://doi.org/10.3390/app11125570






