Effect of Blade Leading and Trailing Edge Configurations on the Performance of a Micro Tubular Propeller Turbine Using Response Surface Methodology
Abstract
:1. Introduction
2. Numerical Analysis
2.1. Model Description
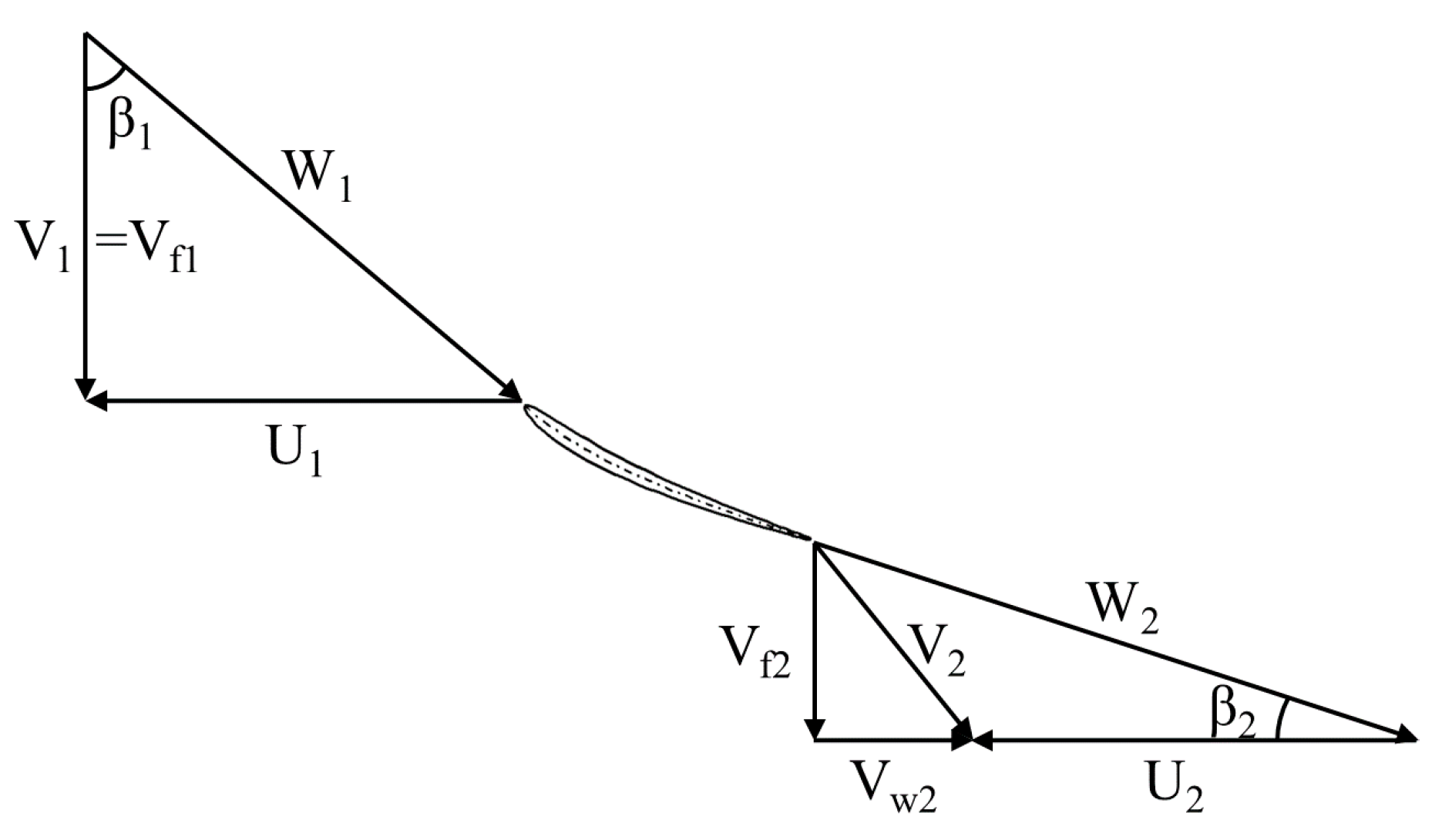
2.2. Evaluation Indicator
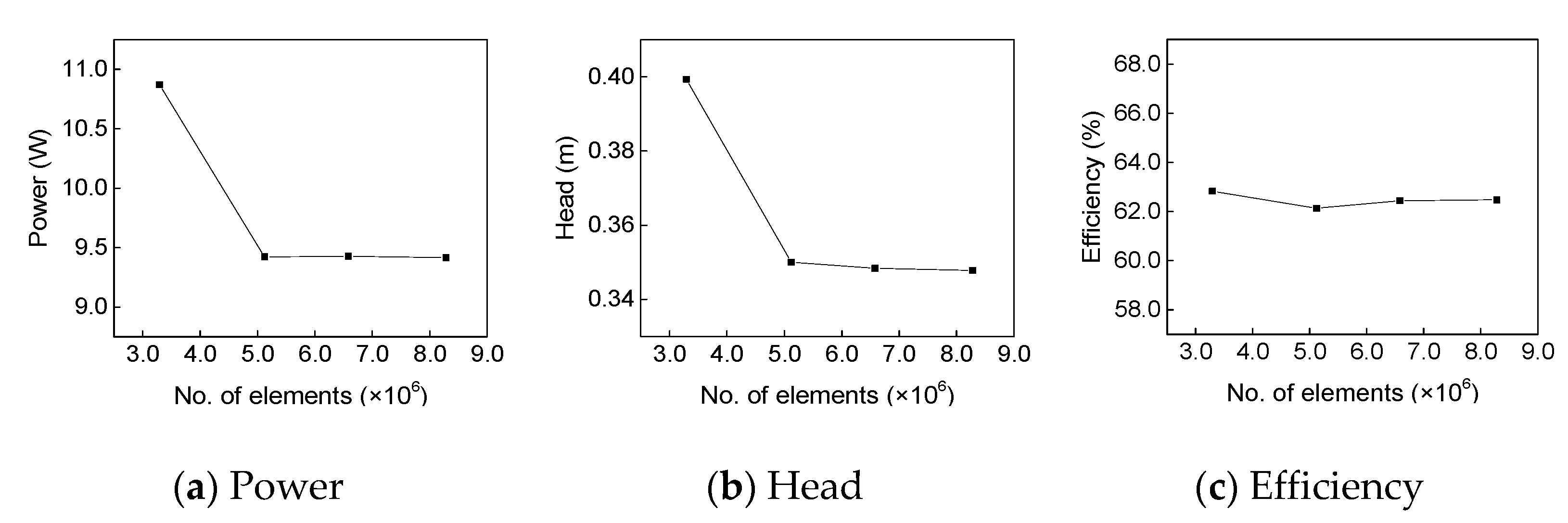
2.3. Grid Generation
2.4. Boundary Conditions
2.5. Governing Equations
2.6. Validation
3. Sensitivity Analysis Method
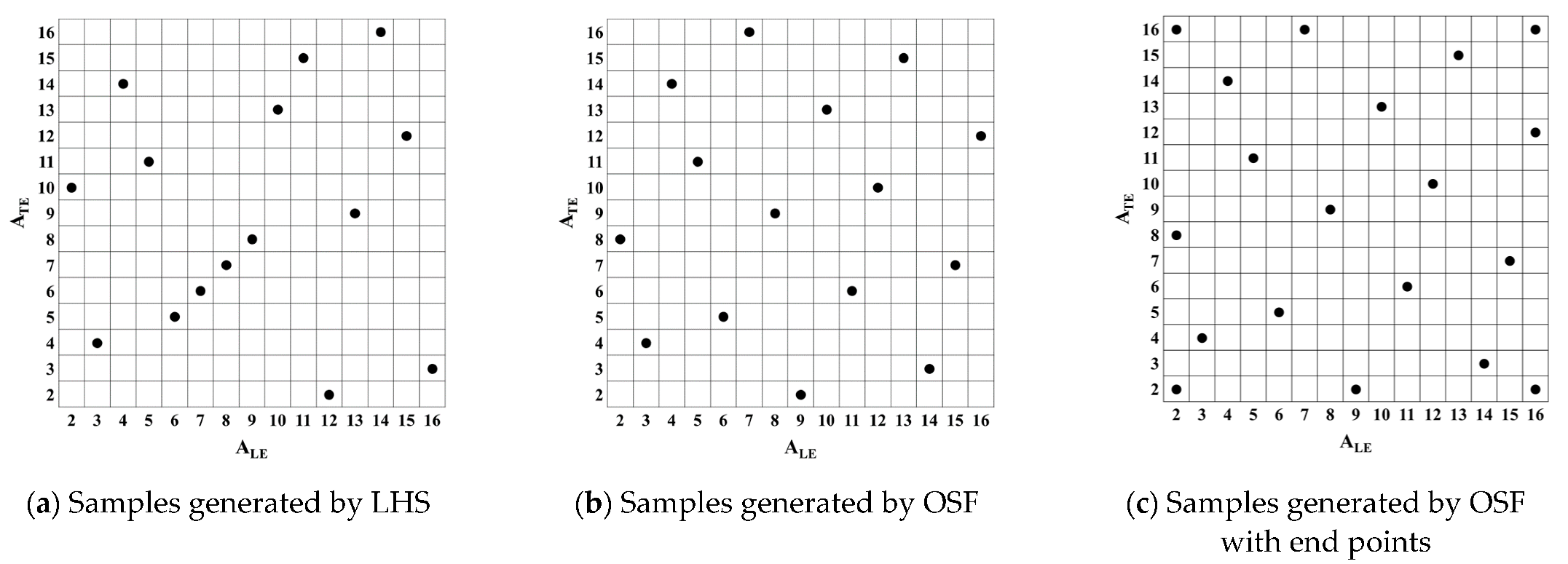
3.1. Design of Experiments
3.2. Response Surface
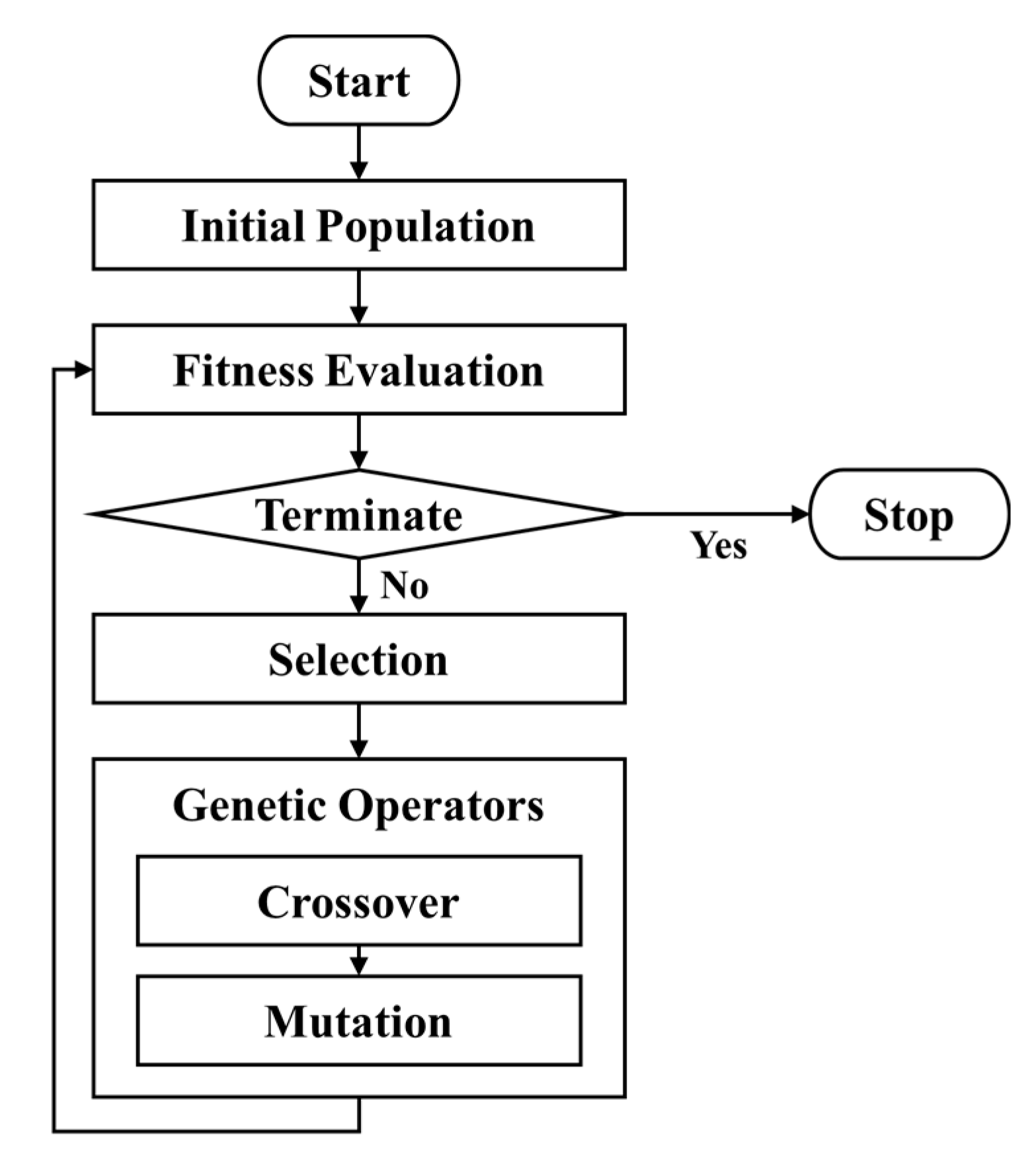
3.3. Optimization
4. Results and Discussion
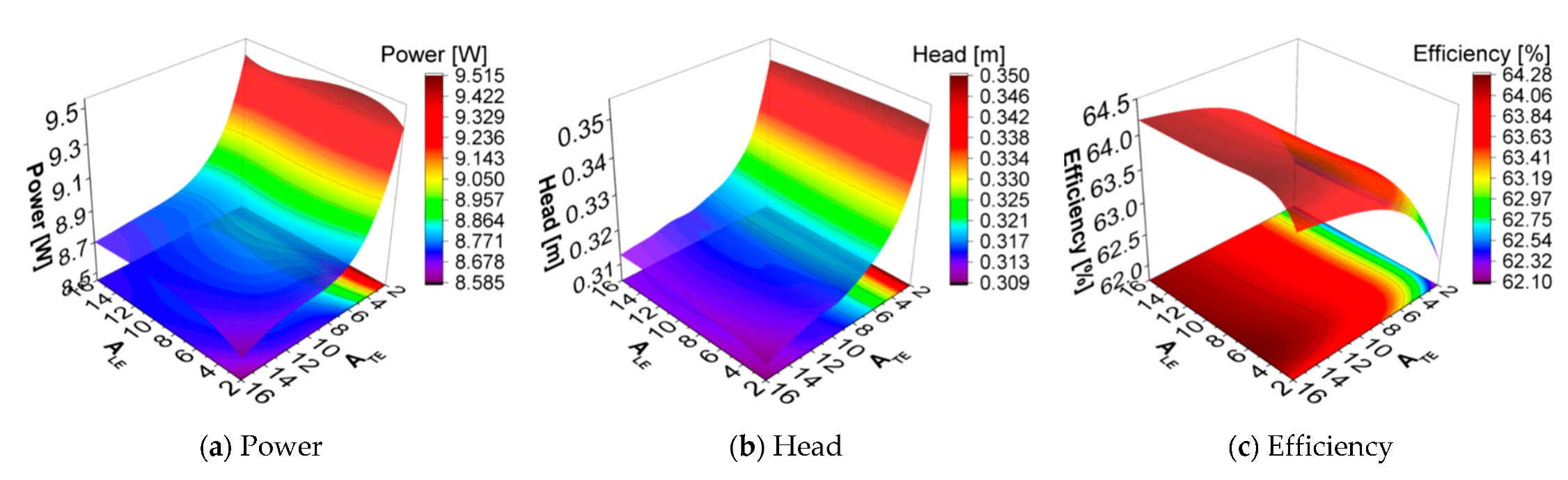
4.1. Sensitivity Analysis
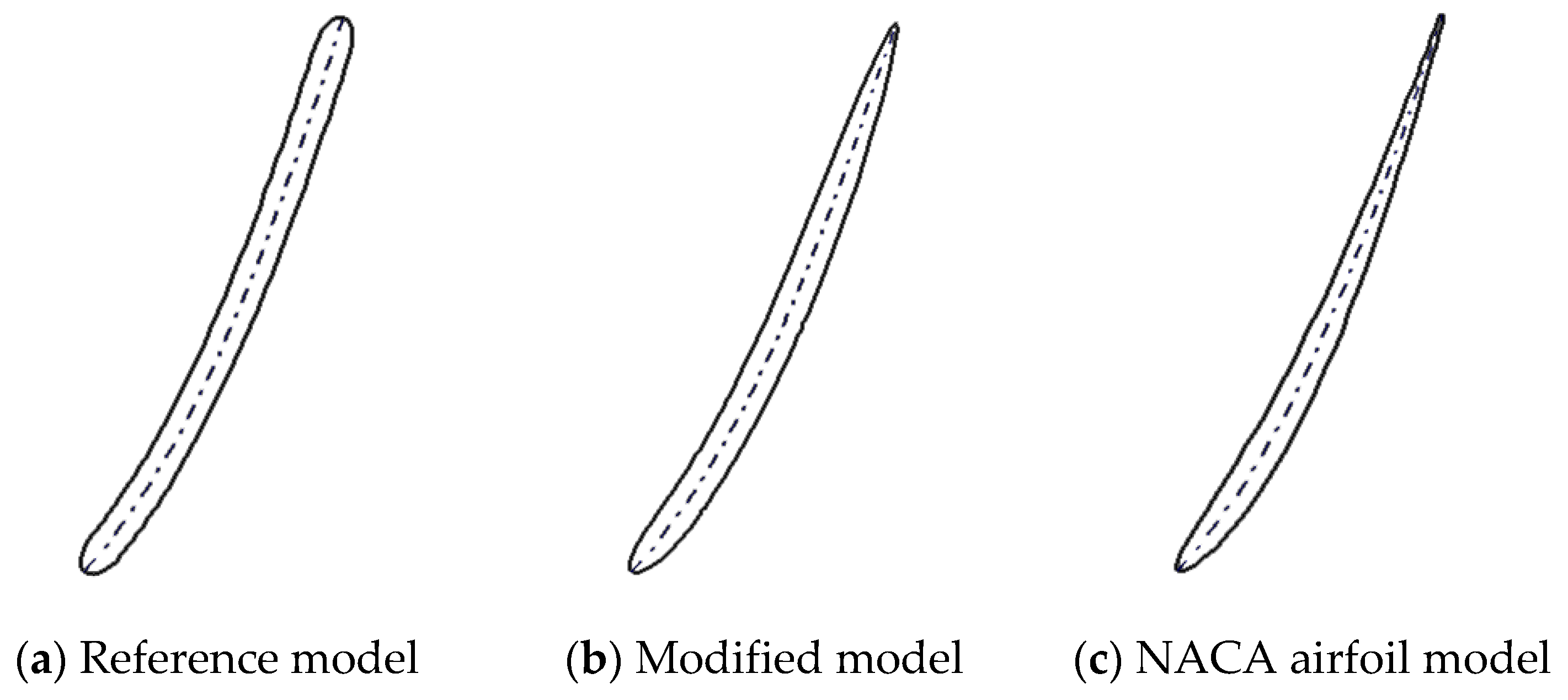
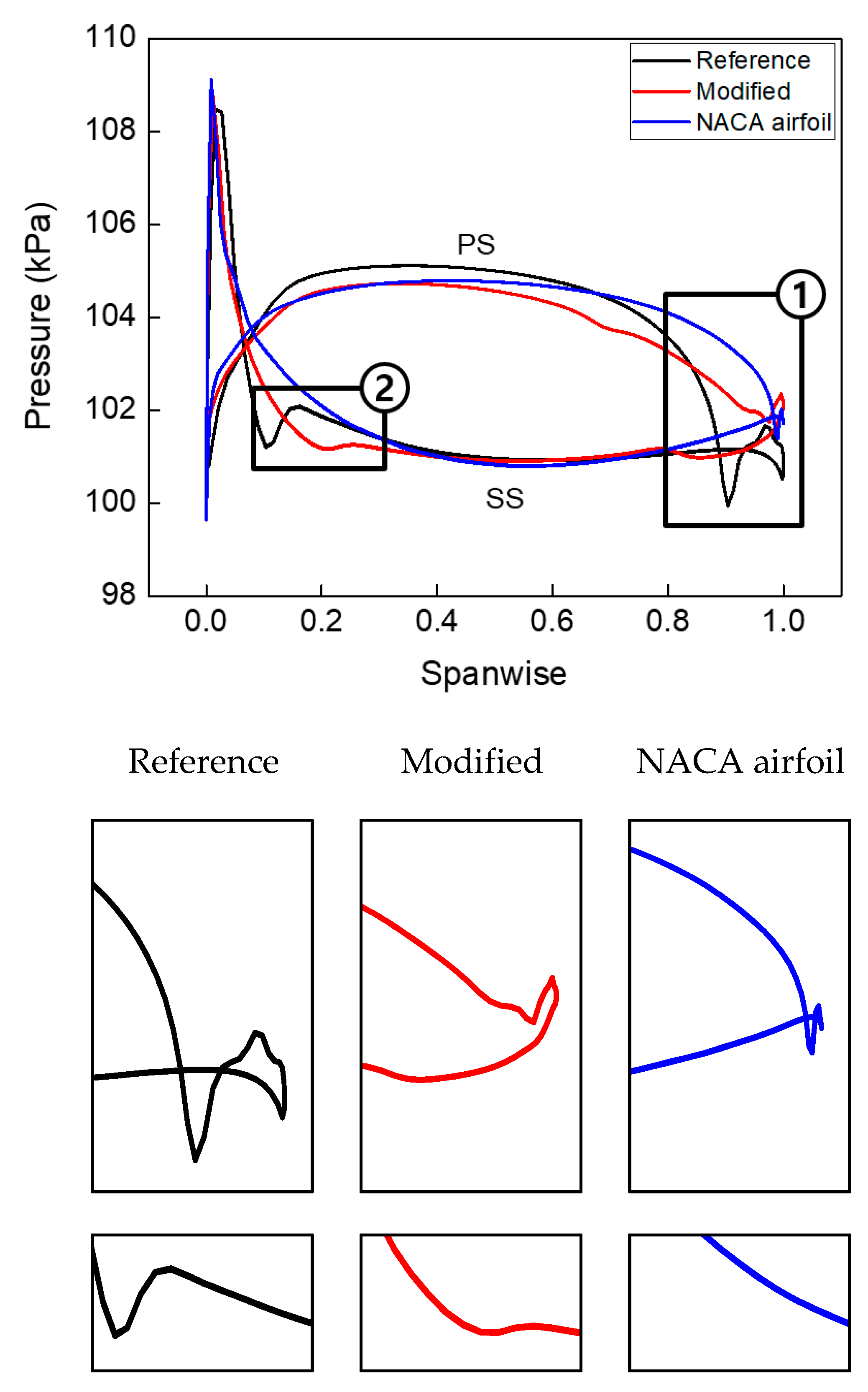
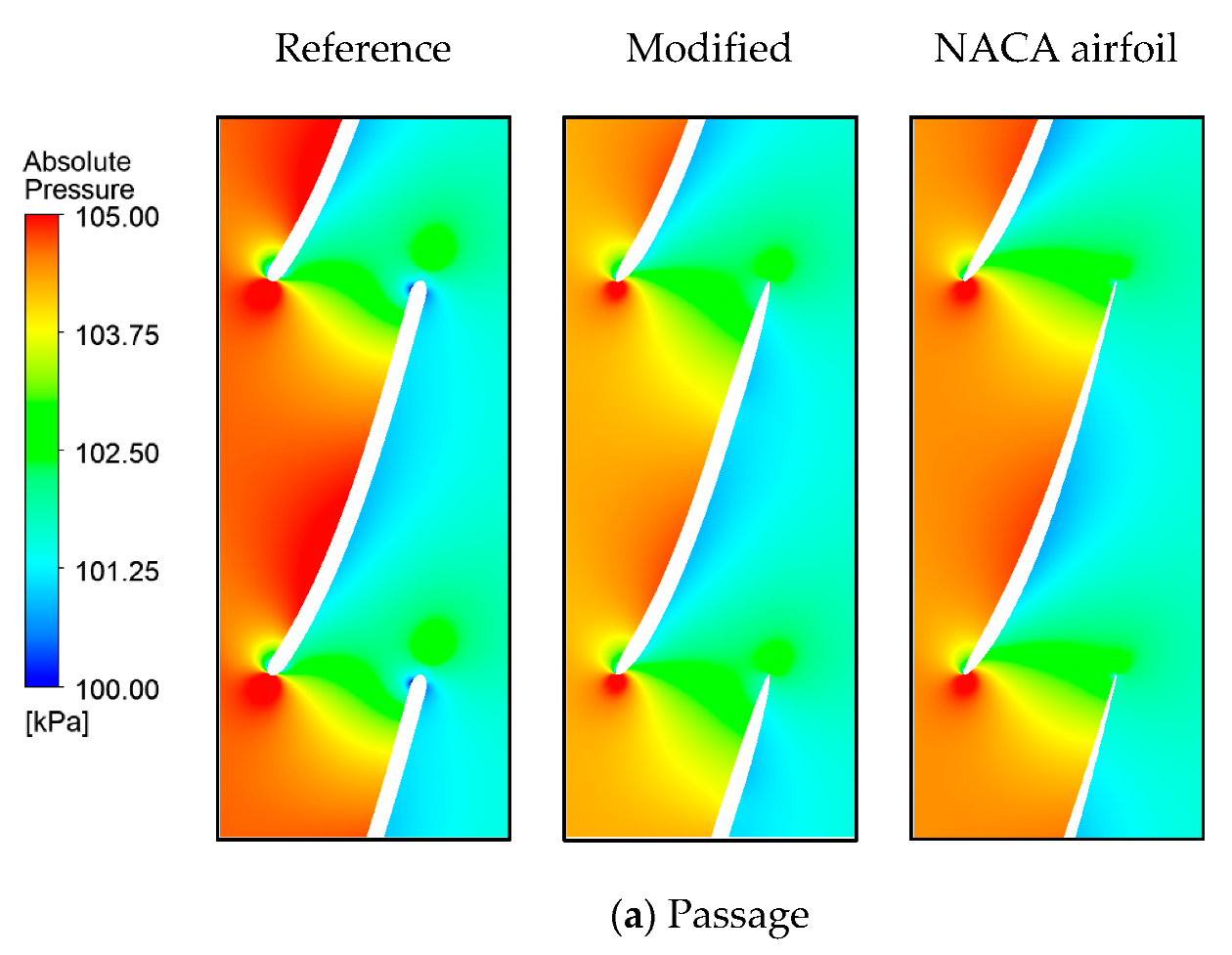
4.2. Results of the Modified Model
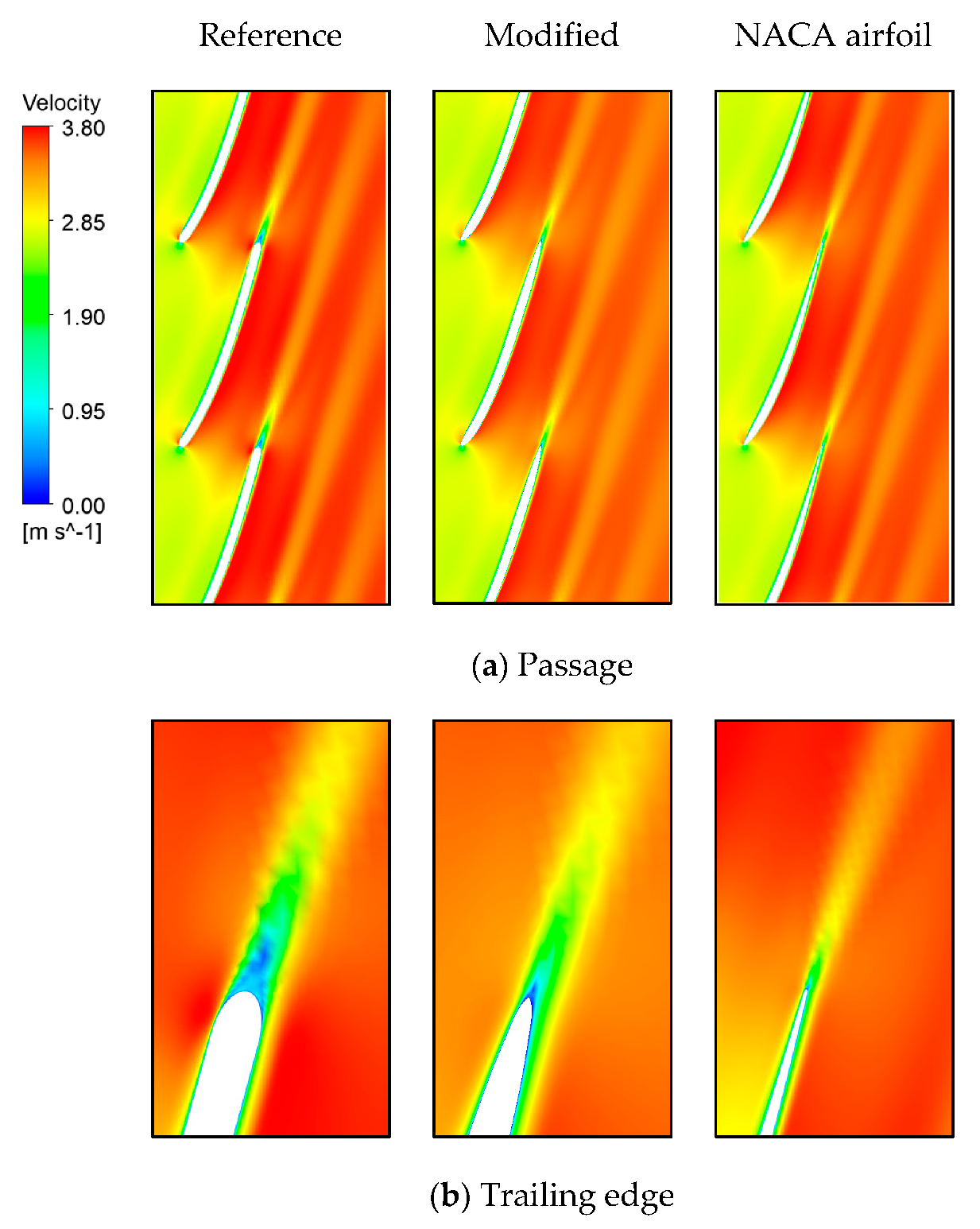
4.3. Application of the NACA Airfoil
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Dp | Pipe diameter [mm] |
| Db | Blade diameter [mm] |
| Dh | Hub diameter [mm] |
| Lh | Front hub length [mm] |
| Lb | Blade length [mm] |
| tb | Blade thickness [mm] |
| tc | Tip clearance [mm] |
| β1 | Hub leading edge angle [°] |
| β2 | Hub trailing edge angle [°] |
| β3 | Tip leading edge angle [°] |
| β4 | Tip trailing edge angle [°] |
| T | Torque [N·m] |
| N | Rotational speed [rad/s] |
| Power [W] | |
| Pressure difference between runner inlet and outlet [Pa] | |
| Head [m] | |
| Working fluid density [kg/m3] | |
| Gravitational acceleration [m/s2] | |
| Flow rate [m3/s] | |
| Hydraulic efficiency [%] | |
| Dynamic viscosity [Pa·s] | |
| Wall shear velocity [m/s] | |
| Wall shear stress [Pa] | |
| Wall distance [m] | |
| Y-plus | |
| Velocity [m/s] (in 2.5 Governing Equations) | |
| Stress tensor [Pa] | |
| Reynolds stresses [Pa] | |
| Kronecker delta | |
| Turbulent dynamic viscosity [Pa·s] | |
| Turbulence kinetic energy [m2/s2] | |
| r1 | Blade leading and trailing edge semi-minor axis length [mm] |
| r2 | Blade leading and trailing edge semi-major axis length [mm] |
| ALE | Elliptic aspect ratio at leading edge |
| ATE | Elliptic aspect ratio at trailing edge |
| Prediction of the ensemble | |
| Number of metamodels used | |
| Weight factor for i-th metamodel | |
| Prediction of i-th metamodel | |
| V | Absolute velocity in velocity triangle [m/s] |
| Vf | Flow velocity in velocity triangle (Vertical component of absolute velocity) [m/s] |
| Vr | Whirl velocity in velocity triangle (Horizontal component of absolute velocity) [m/s] |
| U | Blade velocity in velocity triangle [m/s] |
| W | Relative velocity in velocity triangle [m/s] |
References
- UNFCCC. The Paris Agreement. Available online: https://unfccc.int/process-and-meetings/the-paris-agreement/the-paris-agreement (accessed on 2 February 2021).
- Center for Climate and Energy Solutions. Global Emissions. Available online: https://www.c2es.org/content/international-emissions/ (accessed on 3 February 2021).
- Climatewatch. Historical GHG Emissions. Available online: https://www.climatewatchdata.org/ghg-emissions?breakBy=sector&chartType=percentage&end_year=2017&gases=all-ghg&start_year=1990 (accessed on 3 February 2021).
- Our World in Data. Sector by Sector: Where Do Global Greenhouse Gas Emissions Come from? Available online: https://ourworldindata.org/ghg-emissions-by-sector (accessed on 3 February 2021).
- REN21. Renewables 2020 Global Status Report; REN21 Secretariat: Paris, France, 2020; p. 48. Available online: https://www.ren21.net/wp-content/uploads/2019/05/gsr_2020_full_report_en.pdf (accessed on 21 April 2021).
- Panwar, N.L.; Kaushik, S.C.; Kothari, S. Role of renewable energy sources in environmental protection: A review. Renew. Sustain. Energy Rev. 2011, 15, 1513–1524. [Google Scholar] [CrossRef]
- Okot, D.K. Review of small hydropower technology. Renew. Sustain. Energy Rev. 2013, 26, 515–520. [Google Scholar] [CrossRef]
- IRENA. Renewable Energy Statistics 2020; The International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2020; pp. 1–15. [Google Scholar]
- Hoes, O.A.; Meijer, L.J.; Van Der Ent, R.J.; Van De Giesen, N.C. Systematic high-resolution assessment of global hydropower potential. PLoS ONE 2017, 12, e0171844. [Google Scholar] [CrossRef]
- Nasir, B.A. Design considerations of micro-hydro-electric power plant. Energy Procedia 2014, 50, 19–29. [Google Scholar] [CrossRef]
- Jawahar, C.P.; Michael, P.A. A review on turbines for micro hydro power plant. Renew. Sustain. Energy Rev. 2017, 72, 882–889. [Google Scholar] [CrossRef]
- Elbatran, A.H.; Yaakob, O.B.; Ahmed, Y.M.; Shabara, H.M. Operation, performance and economic analysis of low head micro-hydropower turbines for rural and remote areas: A review. Renew. Sustain. Energy Rev. 2015, 43, 40–50. [Google Scholar] [CrossRef]
- Davis, S. Microhydro: Clean Power from Water; New Society Publishers: Gabriola Island, BC, Canada, 2003; pp. 8–9. [Google Scholar]
- Casini, M. Harvesting energy from in-pipe hydro systems at urban and building scale. Int. J. Smart Grid Clean Energy 2015, 4, 316–327. [Google Scholar] [CrossRef] [Green Version]
- Krzemianowski, Z.; Steller, J. High specific speed francis turbine for small hydro purposes-design methodology based on solving the inverse problem in fluid mechanics and the cavitation test experience. Renew. Energy 2021, 169, 1210–1228. [Google Scholar] [CrossRef]
- Gohil, P.P.; Saini, R. Effect of temperature, suction head and flow velocity on cavitation in a Francis turbine of small hydro power plant. Energy 2015, 93, 613–624. [Google Scholar] [CrossRef]
- Daniels, S.; Rahat, A.; Tabor, G.; Fieldsend, J.; Everson, R. Shape optimisation of the sharp-heeled Kaplan draft tube: Performance evaluation using computational fluid dynamics. Renew. Energy 2020, 160, 112–126. [Google Scholar] [CrossRef]
- Chen, H.; Zhou, D.; Zheng, Y.; Jiang, S.; Yu, A.; Guo, Y. Load rejection transient process simulation of a Kaplan turbine model by co-adjusting guide vanes and runner blades. Energies 2018, 11, 3354. [Google Scholar] [CrossRef] [Green Version]
- Lugauer, F.J.; Kainz, J.; Gaderer, M. Techno-economic efficiency analysis of various operating strategies for micro-hydro storage using a pump as a turbine. Energies 2021, 14, 425. [Google Scholar] [CrossRef]
- Morabito, A.; e Silva, G.D.O.; Hendrick, P. Deriaz pump-turbine for pumped hydro energy storage and micro applications. J. Energy Storage 2019, 24, 100788. [Google Scholar] [CrossRef]
- Lin, T.; Zhu, Z.; Li, X.; Li, J.; Lin, Y. Theoretical, experimental, and numerical methods to predict the best efficiency point of centrifugal pump as turbine. Renew. Energy 2021, 168, 31–44. [Google Scholar] [CrossRef]
- Chen, J.; Yang, H.X.; Liu, C.P.; Lau, C.H.; Lo, M. A novel vertical axis water turbine for power generation from water pipelines. Energy 2013, 54, 184–193. [Google Scholar] [CrossRef]
- Payambarpour, S.A.; Najafi, A.F.; Magagnato, F. Investigation of deflector geometry and turbine aspect ratio effect on 3D modified in-pipe hydro Savonius turbine: Parametric study. Renew. Energy 2020, 148, 44–59. [Google Scholar] [CrossRef]
- Team, Purdue ECT. LUCIDPIPETM power system. ECT Fact Sheets 2016, 224. Available online: https://docs.lib.purdue.edu/ectfs/224/ (accessed on 15 June 2021).
- Yeo, H.; Seok, W.; Shin, S.; Huh, Y.C.; Jung, B.C.; Myung, C.-S.; Rhee, S.H. Computational analysis of the performance of a vertical axis turbine in a water pipe. Energies 2019, 12, 3998. [Google Scholar] [CrossRef] [Green Version]
- Hydrocoil Power, Inc. Available online: http://www.hydrocoil.com (accessed on 8 February 2021).
- Sinagra, M.; Aricò, C.; Tucciarelli, T.; Morreale, G. Experimental and numerical analysis of a backpressure Banki inline turbine for pressure regulation and energy production. Renew. Energy 2020, 149, 980–986. [Google Scholar] [CrossRef]
- Nan, D.; Shigemitsu, T.; Zhao, S.; Ikebuchi, T.; Takeshima, Y. Study on performance of contra-rotating small hydro-turbine with thinner blade and longer front hub. Renew. Energy 2018, 117, 184–192. [Google Scholar] [CrossRef]
- Vagnoni, E.; Andolfatto, L.; Richard, S.; Münch-Alligné, C.; Avellan, F. Hydraulic performance evaluation of a micro-turbine with counter rotating runners by experimental investigation and numerical simulation. Renew. Energy 2018, 126, 943–953. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.W. Handbook of Hydraulic Turbines and Pump Turbines; Auris Reference Ltd.: London, UK, 2014; p. 525. [Google Scholar]
- Duquesne, P.; Maciel, Y.; Deschênes, C. Investigation of flow separation in a diffuser of a bulb turbine. J. Fluids Eng. 2016, 138, 011102. [Google Scholar] [CrossRef]
- Li, Y.; Song, G.; Yan, Y. Transient hydrodynamic analysis of the transition process of bulb hydraulic turbine. Adv. Eng. Softw. 2015, 90, 152–158. [Google Scholar] [CrossRef]
- Chen, H.; Zhou, D.; Kan, K.; Xu, H.; Zheng, Y.; Binama, M.; Xu, Z.; Feng, J. Experimental investigation of a model bulb turbine under steady state and load rejection process. Renew. Energy 2021, 169, 254–265. [Google Scholar] [CrossRef]
- Shandilya, S.; Shelar, S.P.; Das, S.P.; Chatterjee, D.; Saini, R. Performance evaluation of a bulb turbine designed for ultra-low head applications. J. Phys. Conf. Ser. 2019, 1276, 012024. [Google Scholar] [CrossRef]
- Samora, I.; Hasmatuchi, V.; Münch-Alligné, C.; Franca, M.J.; Schleiss, A.J.; Ramos, H.M. Experimental characterization of a five blade tubular propeller turbine for pipe inline installation. Renew. Energy 2016, 95, 356–366. [Google Scholar] [CrossRef]
- Dixon, S.L.; Hall, C.A. Fluid Mechanics and Thermodynamics of Turbomachinery, 7th ed.; Butterworth-Heinemann: Oxford, UK, 2014; pp. 22–25. [Google Scholar]
- Adanta, D.; Budiarso, B.; Siswantara, A.I. Assessment of turbulence modelling for numerical simulations into pico hydro turbine. J. Adv. Res. Fluid Mech. Therm. Sci. 2018, 46, 21–31. [Google Scholar]
- Warjito, W.; Nasution, S.B.; Syahputra, M.F.; Budiarso, B.; Adanta, D. Study of turbulence model for performance and flow field prediction of pico hydro types propeller turbine. CFD Lett. 2020, 12, 26–34. [Google Scholar] [CrossRef]
- ANSYS. ANSYS CFX-Solver Theory Guide; ANSYS Inc.: Canonsburg, PA, USA, 2020; p. 80. [Google Scholar]
- Moukalled, F.; Mangani, L.; Darwish, M. The Finite Volume Method in Computational Fluid Dynamics; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Garud, S.S.; Karimi, I.A.; Kraft, M. Design of computer experiments: A review. Comput. Chem. Eng. 2017, 106, 71–95. [Google Scholar] [CrossRef]
- Viana, F.A. A tutorial on Latin hypercube design of experiments. Qual. Reliab. Eng. Int. 2016, 32, 1975–1985. [Google Scholar] [CrossRef]
- Joseph, V.R. Space-filling designs for computer experiments: A review. Qual. Eng. 2016, 28, 28–35. [Google Scholar] [CrossRef]
- Ben Salem, M.; Roustant, O.; Gamboa, F.; Tomaso, L. Universal prediction distribution for surrogate models. SIAM/ASA J. Uncertain. Quantif. 2017, 5, 1086–1109. [Google Scholar] [CrossRef] [Green Version]
- Mirjalili, S. Genetic Algorithm. In Evolutionary Algorithms and Neural Networks; Springer: Cham, Switzerland, 2019; pp. 43–55. [Google Scholar]
- Sultanian, B. Logan’s Turbomachinery: Flowpath Design and Performance Fundamentals, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2019; pp. 22–23. [Google Scholar]
- Zhang, X.; Li, W.; Liu, H. Numerical simulation of the effect of relative thickness on aerodynamic performance improvement of asymmetrical blunt trailing-edge modification. Renew. Energy 2015, 80, 489–497. [Google Scholar] [CrossRef]
- Gao, B.; Zhang, N.; Li, Z.; Ni, D.; Yang, M. Influence of the blade trailing edge profile on the performance and unsteady pressure pulsations in a low specific speed centrifugal pump. J. Fluids Eng. 2016, 138, 051106. [Google Scholar] [CrossRef]
- NASA. NACA Airfoils. Available online: https://www.nasa.gov/image-feature/langley/100/naca-airfoils (accessed on 11 June 2021).
- Bramantya, M.A.; Ginting, R.R.R. Study of the effect of 4-digit NACA variation on airfoil performance using computation fluid dynamics. AIP Conf. Proc. 2020, 2248, 020002. [Google Scholar]
- Thapa, B.S.; Dahlhaug, O.G.; Thapa, B. Flow measurements around guide vanes of francis turbine: A piv approach. Renew. Energy 2018, 126, 177–188. [Google Scholar] [CrossRef]
- Chitrakar, S.; Thapa, B.S.; Dahlhaug, O.G.; Neopane, H.P. Numerical and experimental study of the leakage flow in guide vanes with different hydrofoils. J. Comput. Des. Eng. 2017, 4, 218–230. [Google Scholar] [CrossRef]
- Jeon, J.-H.; Byeon, S.-S.; Kim, Y.-J. Numerical study on the flow characteristics of the Francis turbine with various blade profiles. In Proceedings of the ASME 2013 Fluids Engineering Division Summer Meeting, Incline Village, NV, USA, 7–11 July 2013. [Google Scholar]
- Goundar, J.N.; Ahmed, M.R. Design of a horizontal axis tidal current turbine. Appl. Energy 2013, 111, 161–174. [Google Scholar] [CrossRef]
- Mohammadi, S.; Hassanalian, M.; Arionfard, H.; Bakhtiyarov, S. Optimal design of hydrokinetic turbine for low-speed water flow in golden gate strait. Renew. Energy 2020, 150, 147–155. [Google Scholar] [CrossRef]



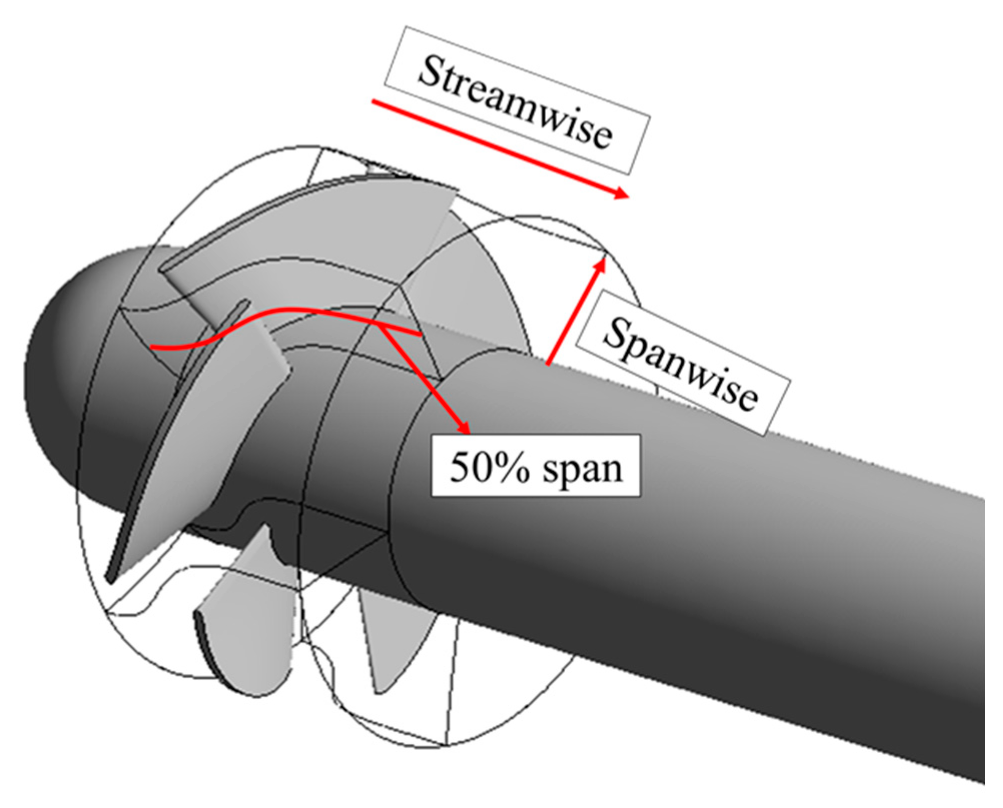
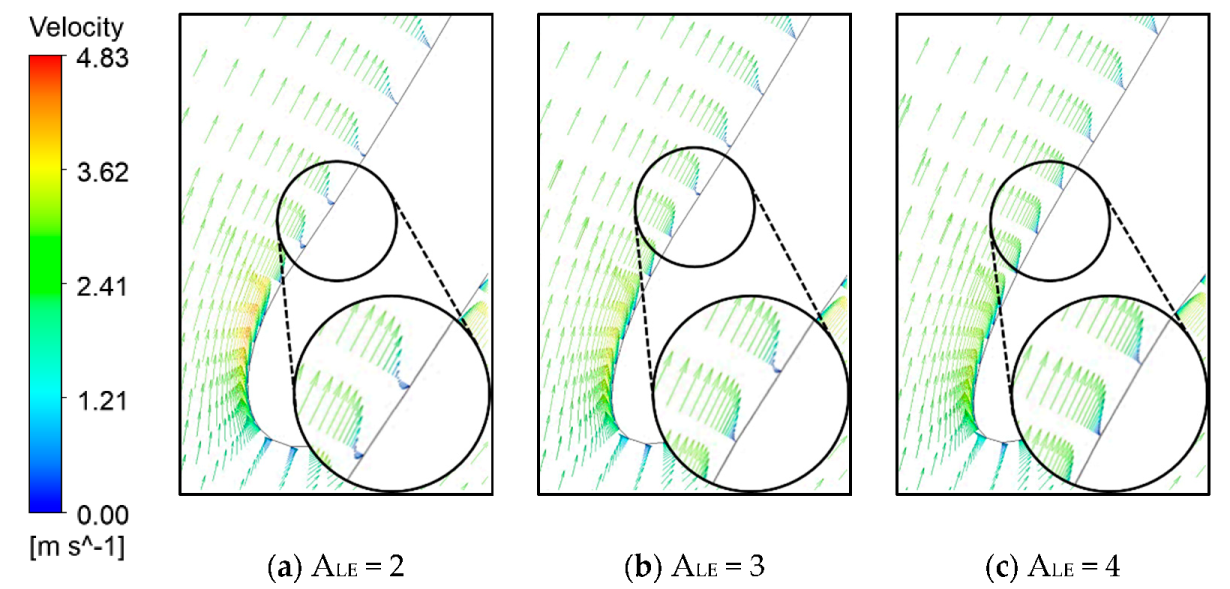
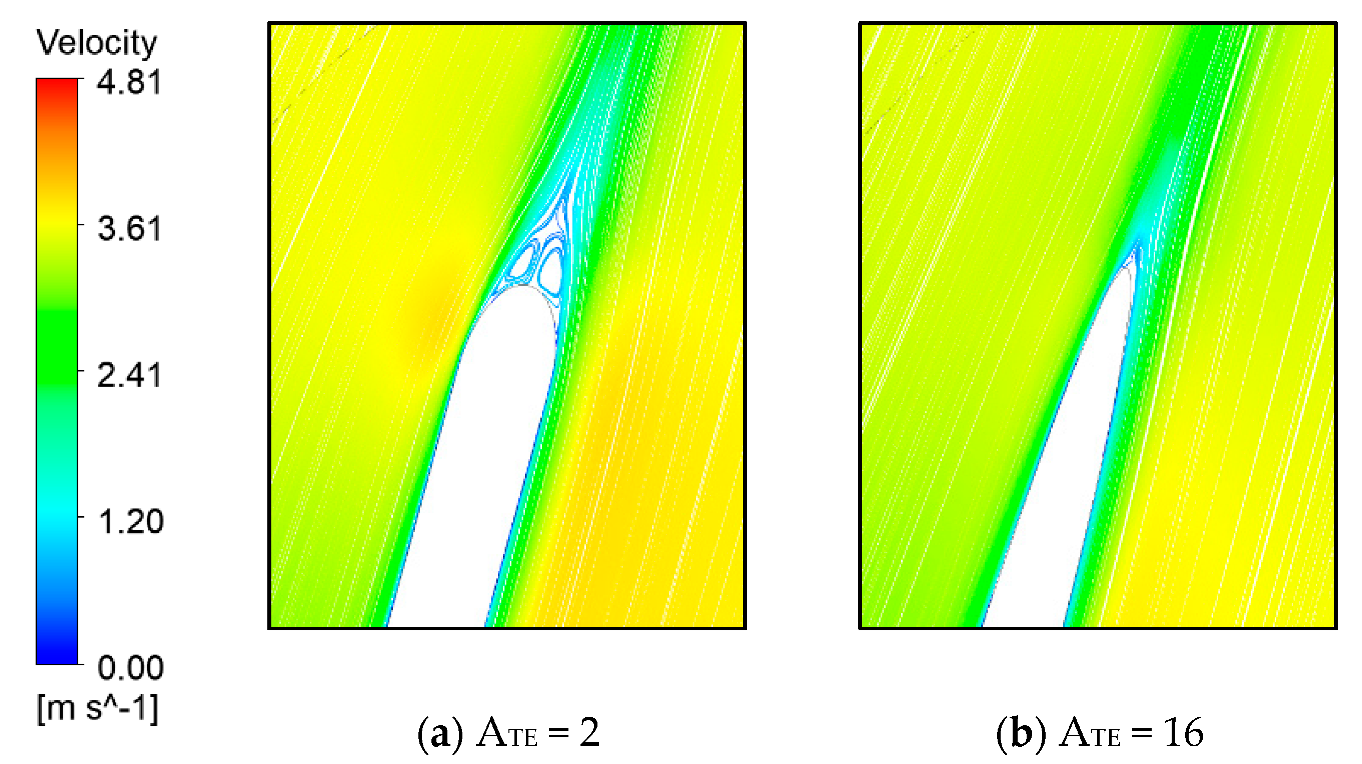
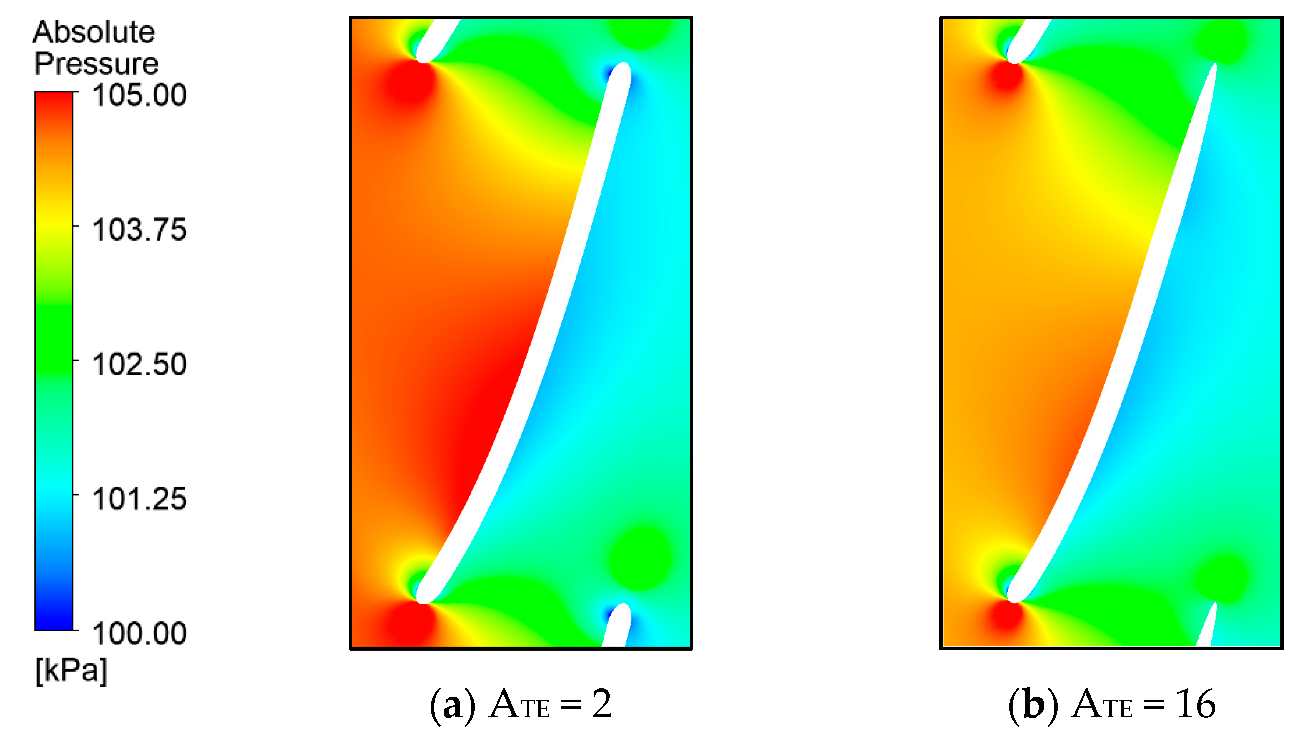




| Classification | Value |
|---|---|
| Pipe diameter, Dp [mm] | 85 |
| Blade diameter, Db [mm] | 84.8 |
| Hub diameter, Dh [mm] | 42.5 |
| Front hub length, Lh [mm] | 23.5 |
| Blade length, Lb [mm] | 18.5 |
| Blade thickness, tb [mm] | 1.7 |
| Tip clearance, tc [mm] | 0.1 |
| Hub leading edge angle, β1 [°] | 42.5 |
| Hub trailing edge angle, β2 [°] | 18 |
| Tip leading edge angle, β3 [°] | 34.5 |
| Tip trailing edge angle, β4 [°] | 13.5 |
| Number of blades [-] | 5 |
| Classification | Value |
|---|---|
| Analysis state | Steady state |
| Interface model | Frozen rotor |
| Turbulence model | SST |
| Working fluid | Water at 25 °C |
| Inlet condition | Flow rate (15.95 m3/h) |
| Outlet condition | Static pressure (1 atm) |
| Rotational speed | 750 rpm |
| Power [W] | Head [m] | Efficiency [%] | |
|---|---|---|---|
| Steady | 9.423 | 0.350 | 62.13 |
| Unsteady | 9.346 | 0.348 | 61.95 |
| Reference | 9.393 | 0.34 | 63.75 |
| ALE | ATE | Power [W] | Head [m] | Efficiency [%] | |
|---|---|---|---|---|---|
| Prediction | 5.5 | 16 | 8.702 | 0.313 | 64.29 |
| Verification | 8.662 | 0.311 | 64.27 | ||
| Error [%] | - | - | 0.46 | 0.55 | 0.03 |
| Power [W] | Head [m] | Efficiency [%] | |
|---|---|---|---|
| Reference model | 9.423 | 0.350 | 62.13 |
| Modified model | 8.662 | 0.311 | 64.27 |
| NACA airfoil model | 9.193 | 0.329 | 64.57 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jang, S.; Je, Y.-W.; Kim, Y.-J. Effect of Blade Leading and Trailing Edge Configurations on the Performance of a Micro Tubular Propeller Turbine Using Response Surface Methodology. Appl. Sci. 2021, 11, 5596. https://doi.org/10.3390/app11125596
Jang S, Je Y-W, Kim Y-J. Effect of Blade Leading and Trailing Edge Configurations on the Performance of a Micro Tubular Propeller Turbine Using Response Surface Methodology. Applied Sciences. 2021; 11(12):5596. https://doi.org/10.3390/app11125596
Chicago/Turabian StyleJang, Seungsoo, Yeong-Wan Je, and Youn-Jea Kim. 2021. "Effect of Blade Leading and Trailing Edge Configurations on the Performance of a Micro Tubular Propeller Turbine Using Response Surface Methodology" Applied Sciences 11, no. 12: 5596. https://doi.org/10.3390/app11125596






