Instantaneous Beam Prediction Scheme against Link Blockage in mmWave Communications
Abstract
:1. Introduction
Motivations and Contributions
2. Related Work
2.1. Beam Recovery Schemes Based on Beamforming Solutions
2.2. Beam Recovery Schemes Based on Deep Learning Networks
2.3. Beam Recovery Schemes Using Out-of-Band Information
2.4. Beam Recovery Schemes in Indoor mmWave Networks
2.5. Beam Recovery Schemes Based on Network Infrastructure
2.6. Beam Recovery Schemes Based on User Mobility
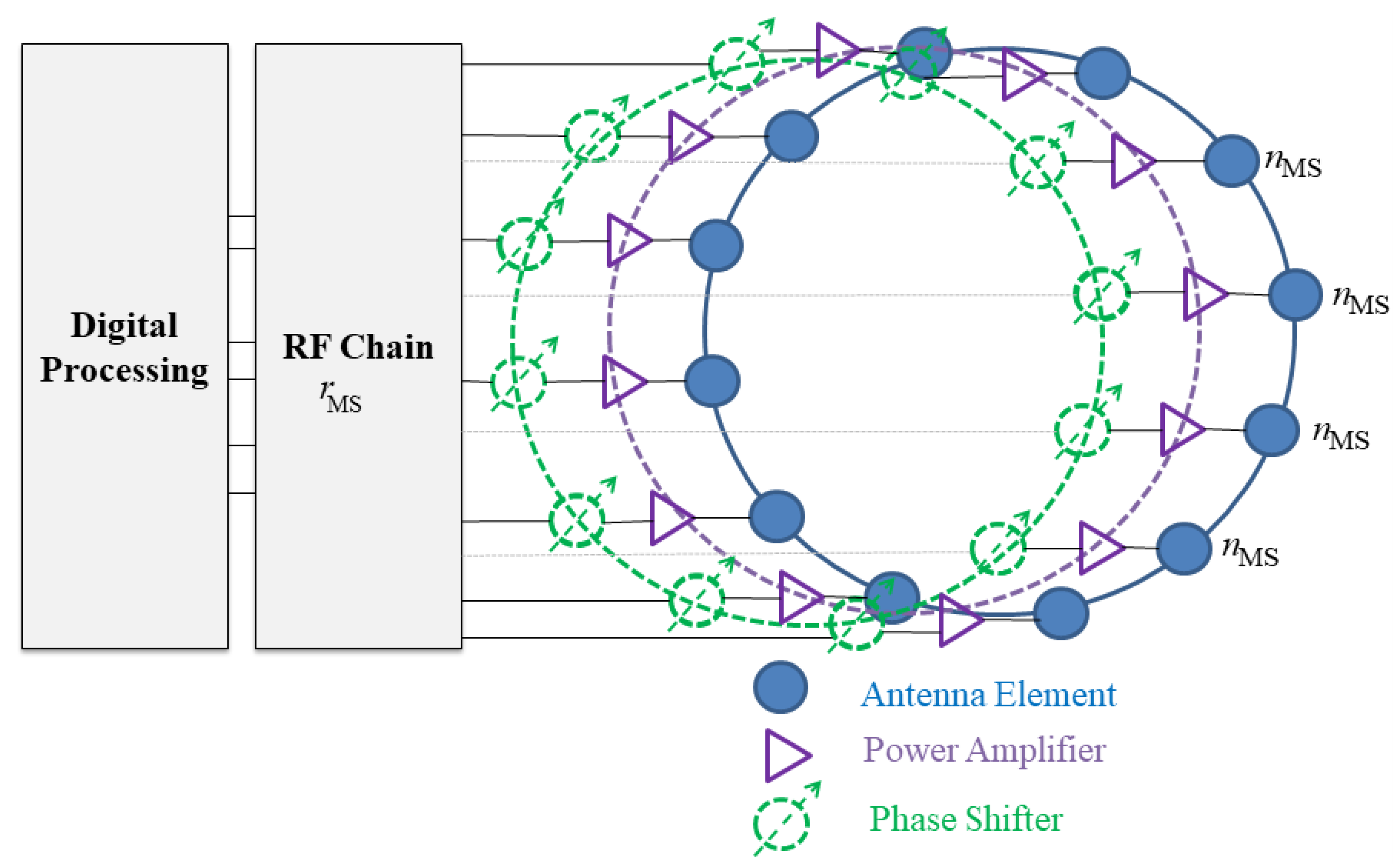
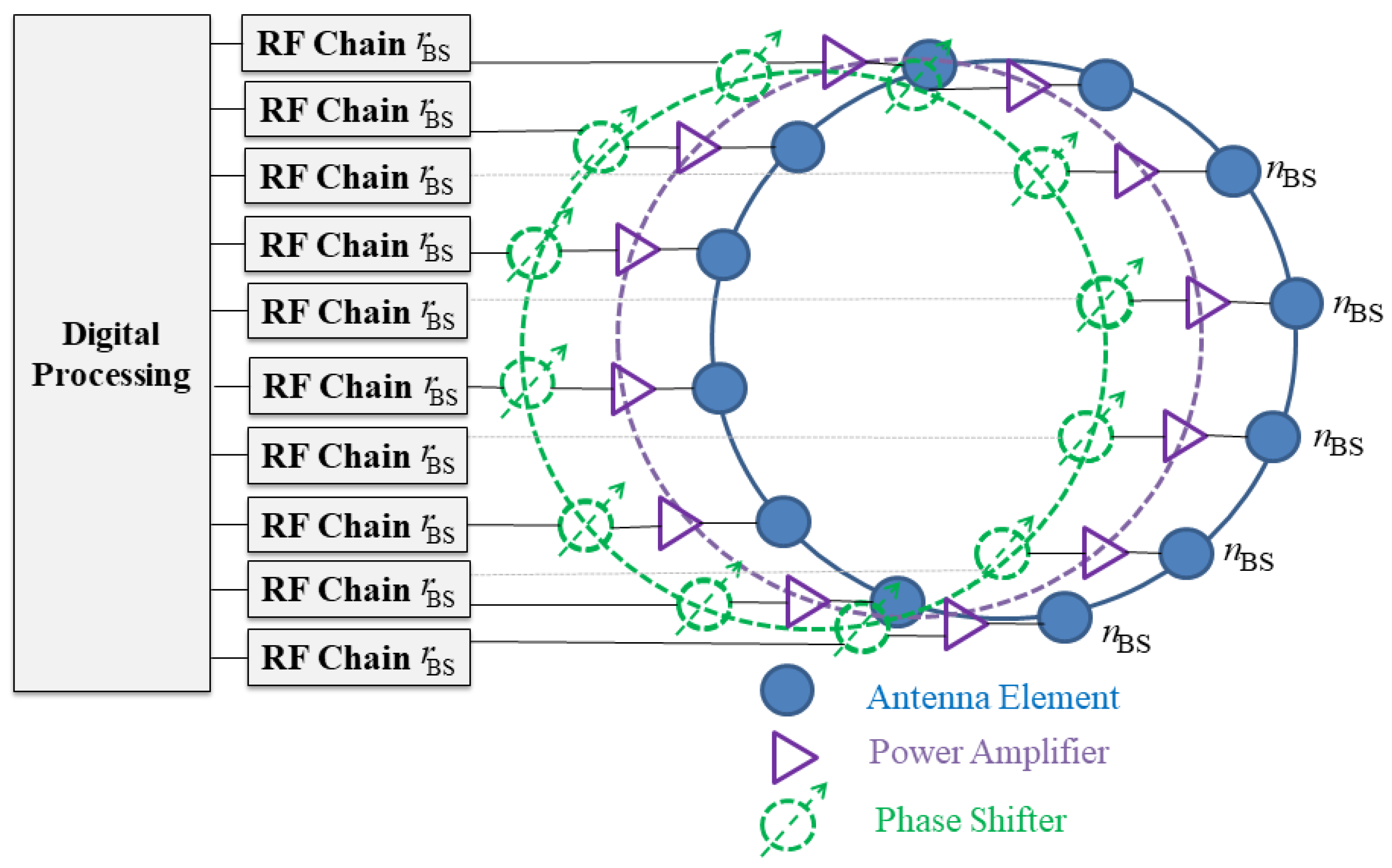
3. System Model
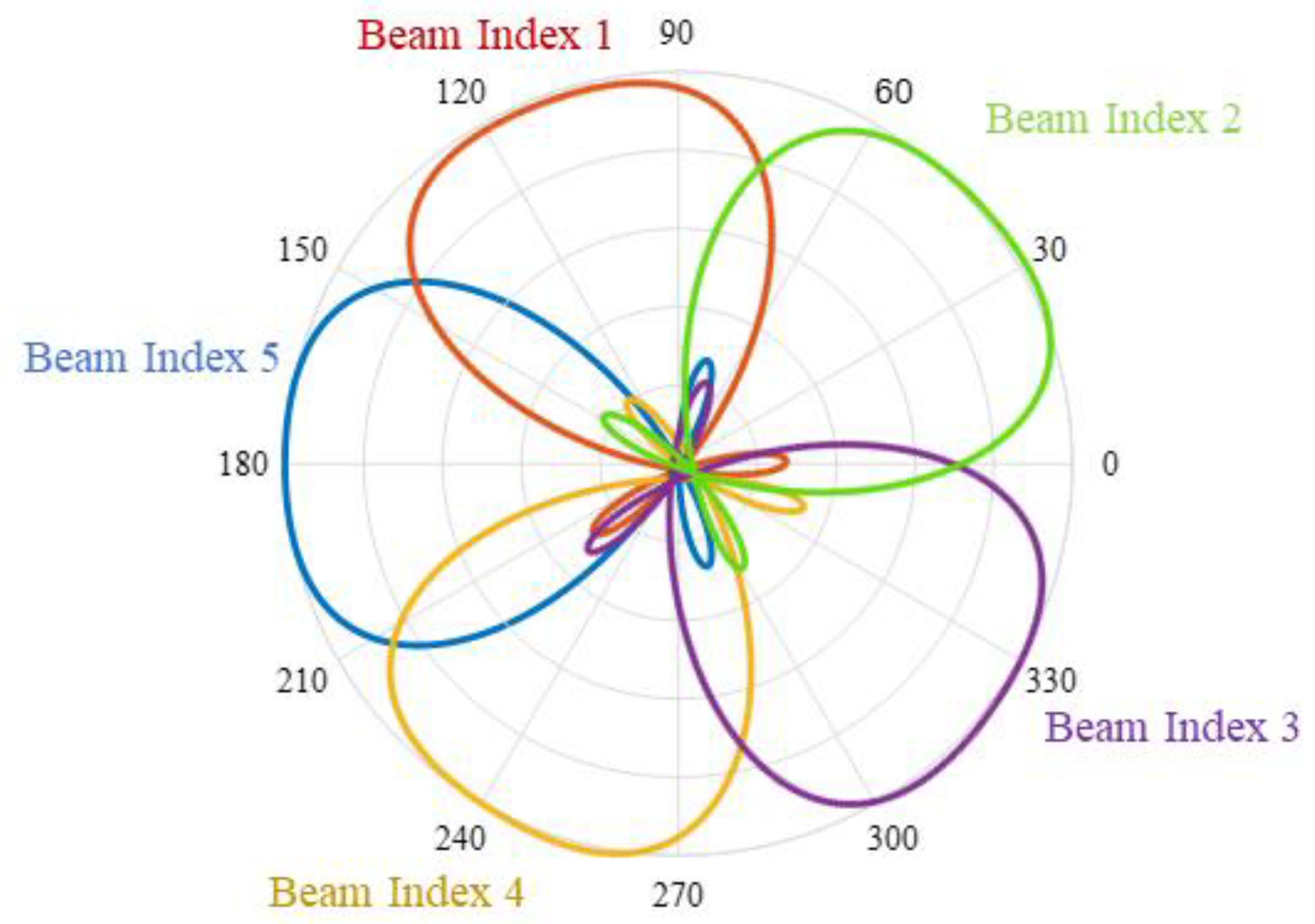
3.1. Beamforming Models
3.2. Signal and Channel Models
3.3. Blockage Model
4. Proposed LSTM-Based Recovery Scheme
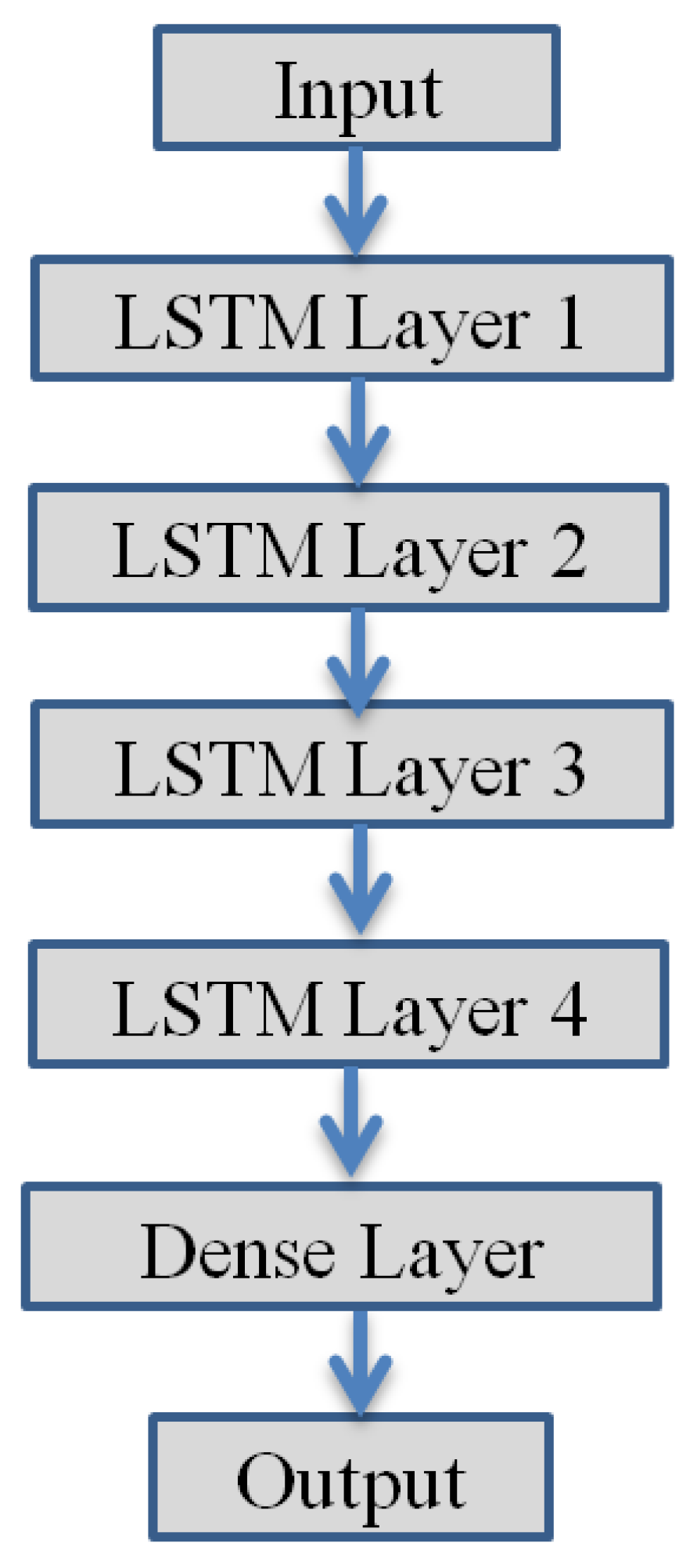
4.1. Network Architecture
4.2. Operating Modes
| Algorithm 1 LSTM-Based Beam Prediction Algorithm against Link Blockage |
| Input:, , Mode I//Use conventional recovery schemes at (t)th time step, Collect Observations for Dataset < s.t. //signal drops below threshold value max(, ): ∈ && ∈, //Select the best pair at (t)th time step that return maximum signal. Output: Dataset that include multiple pairs of at different (t)th time steps. Mode II: // Training mode (trained network), use input dataset for LSTM-based recovery < s.t. //signal drops below threshold value Predict the next beam at (t + 1)th time step using LSTM network as per Figure 5. //Select the best pair at subsequent (t + 1)th time step that return maximum signal. |
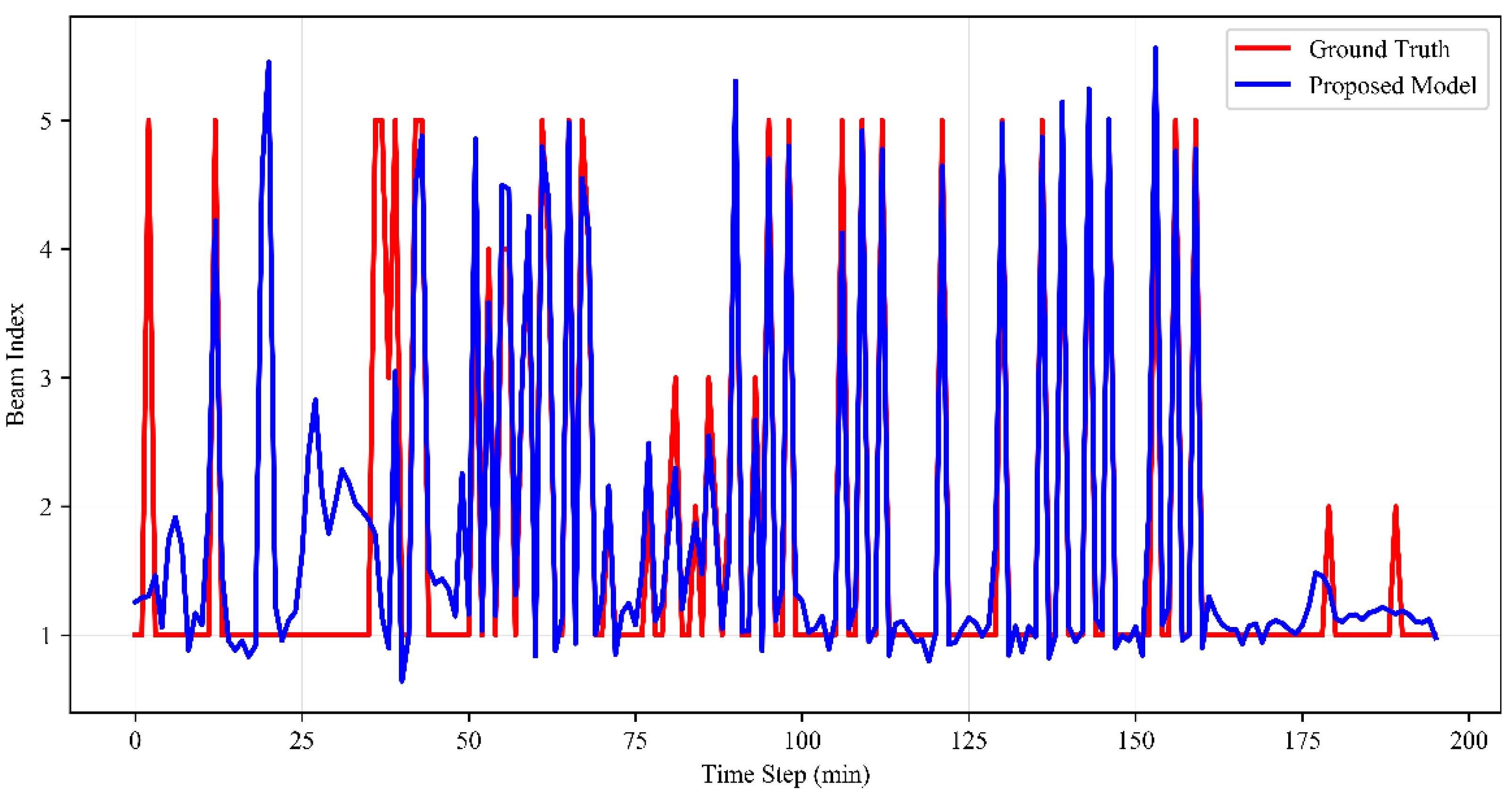
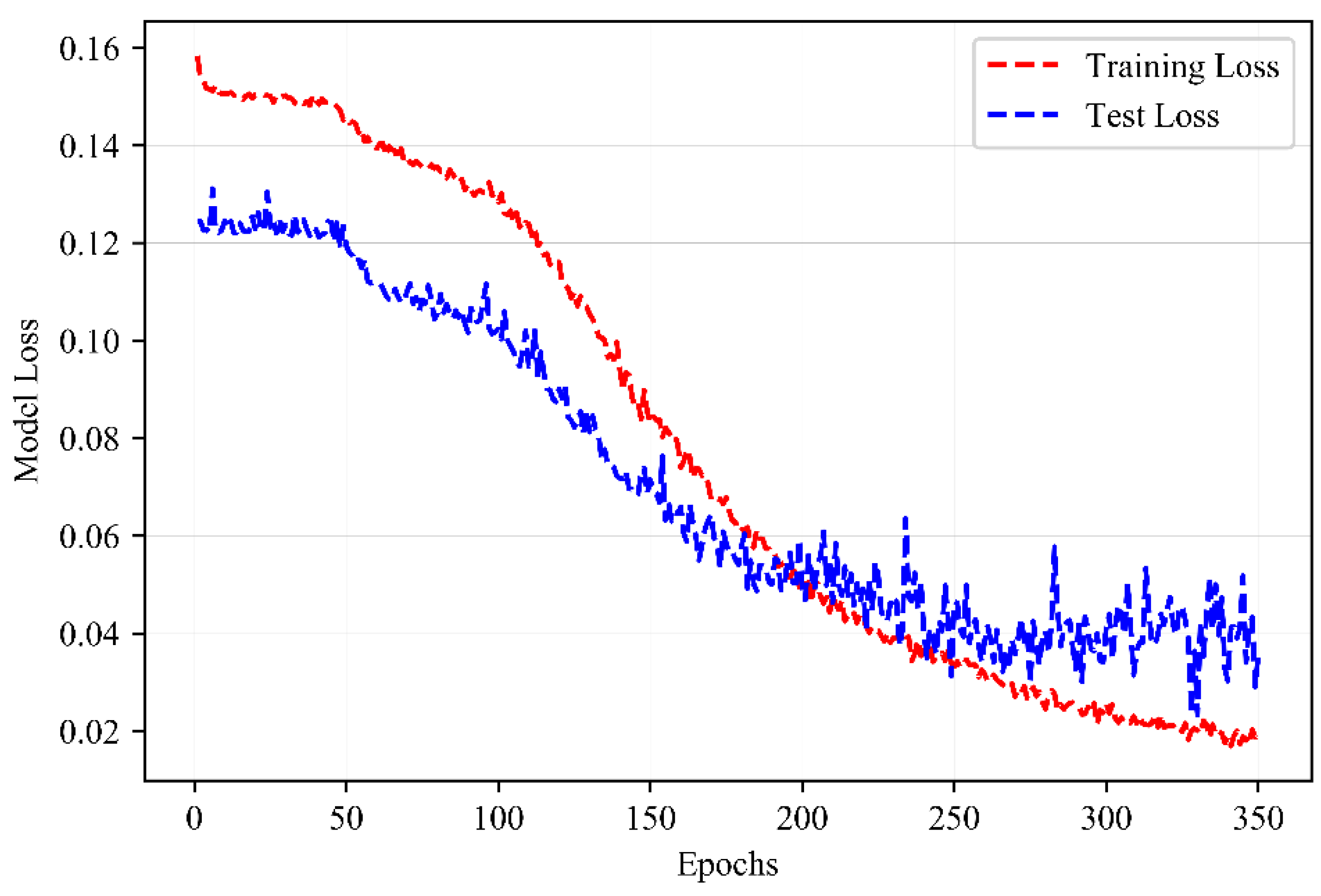
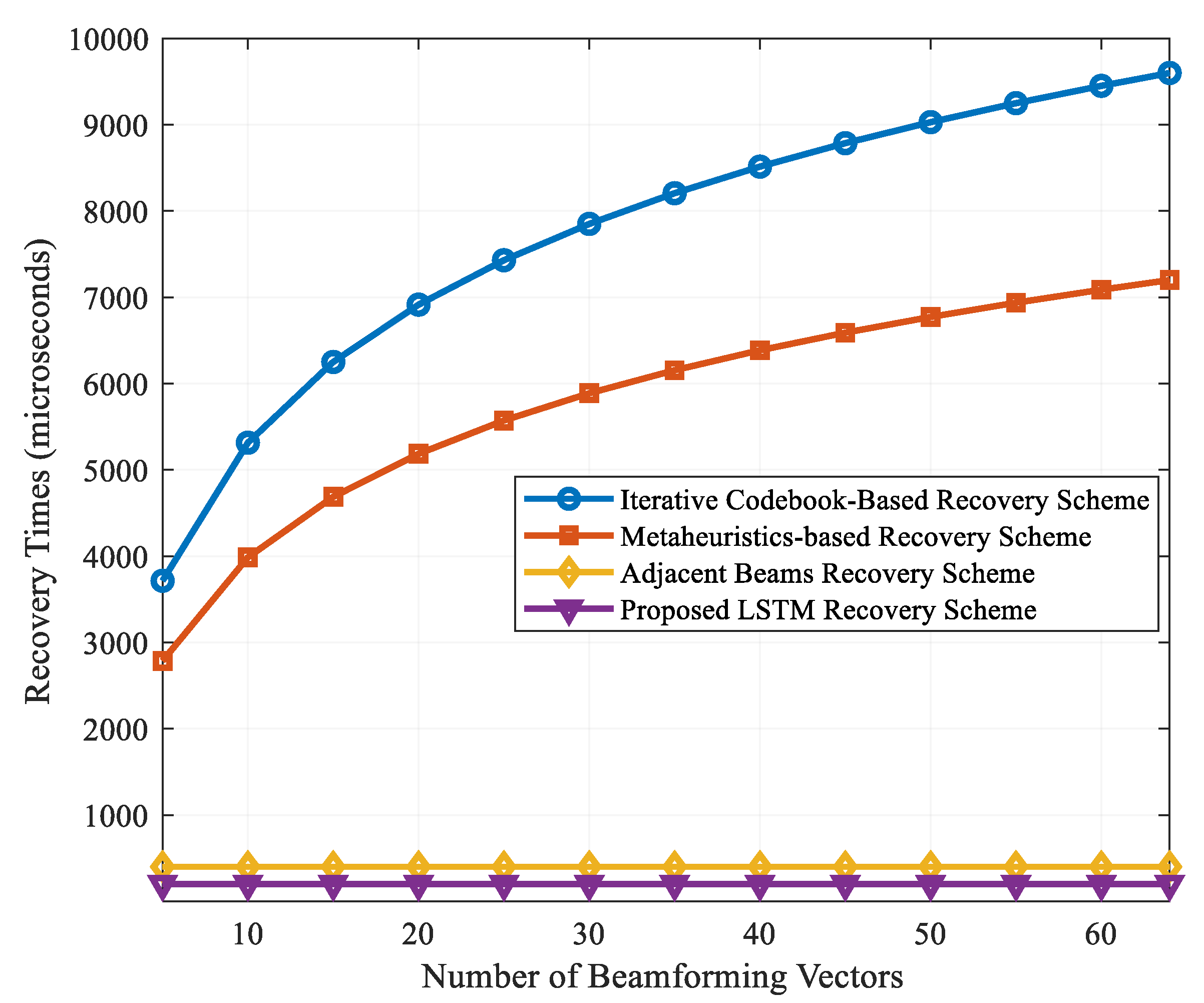
5. Simulation Results and Performance Evaluation
5.1. Recovery Times
5.2. Energy Consumption
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- International Mobile Telecommunications. Minimum Requirements Related to Technical Performance for IMT-2020 Radio Interface; ITU-R Study Group 5: Geneva, Switzerland, 2017; pp. 6–7. [Google Scholar]
- Alkhateeb, A.; El Ayach, O.; Leus, G.; Heath, R.W. Channel estimation and hybrid precoding for millimeter Wave cellular systems. IEEE J. Sel. Top. Signal Process. 2014, 8, 831–846. [Google Scholar] [CrossRef] [Green Version]
- Jasim, M.; Ghani, N. Generalized pattern search for beam discovery in millimeter Wave systems. In Proceedings of the IEEE 86th Vehicular Technology Conference (VTC-Fall), Toronto, ON, Canada, 24–27 September 2017. [Google Scholar]
- Jasim, M.; Aldalbahi, A.; Khreishah, A.; Ghani, N. Hooke Jeeves search method for initial beam access in 5G mmWave cellular networks. In Proceedings of the IEEE 28th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), Montreal, QC, Canada, 8–13 October 2017. [Google Scholar]
- Jasim, M.; Aldalbahi, A.; Shakhatreh, H. Beam aggregation for instantaneous link recovery in millimeter Wave communications. In Proceedings of the IEEE International Conference on Wireless and Mobile Computing, Networking and Communications (WIMOB), Limassol, Cyprus, 15–17 October 2018. [Google Scholar]
- Jasim, M.; Ababneh, M.; Siasi, N.; Ghani, N. Hybrid beamforming for link recovery in millimeter Wave communications. In Proceedings of the IEEE Wireless and MicroWave Technology Conference (WAMICON), Clearwater, FL, USA, 9–10 April 2018. [Google Scholar]
- Jasim, M.; Ababneh, M.; Siasi, N.; Ghani, N. Soft self-handover scheme for mm Wave communications. In Proceedings of the IEEE Southeast Conference, Huntsville, AL, USA, 11–14 April 2019. [Google Scholar]
- Jasim, M.; Aldalbahi, A. Diversity coding for instantaneous link recovery in millimeter Wave communications. In Proceedings of the IEEE International Symposium on Signal Processing and Information Technology (ISSPIT), Louisville, KY, USA, 6–8 December 2018. [Google Scholar]
- Gao, B.; Xiao, Z.; Zhang, C.; Su, L.; Jin, D.; Zeng, L. Double-link beam tracking against human blockage and device mobility for 60-GHz WLAN. In Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC), Istanbul, Turkey, 6–9 April 2014. [Google Scholar]
- Kim, W.; Song, J.; Baek, S. Relay-assisted handover to overcome blockage in millimeter-Wave networks. In Proceedings of the IEEE 28th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), Montreal, QC, Canada, 8–13 October 2017. [Google Scholar]
- Giordani, M.; Mezzavilla, M.; Rangan, S.; Zorzi, M. An efficient uplink multi-connectivity scheme for 5G millimeter-Wave control plane applications. IEEE Trans. Wirel. Com. 2018, 17, 6806–6821. [Google Scholar] [CrossRef] [Green Version]
- Alkhateeb, A.; Beltagy, I.; Alex, S. Machine learning for reliable mm Wave systems: Blockage prediction and proactive handoff. In Proceedings of the IEEE Global Conference on Signal and Information Processing (GlobalSIP), Anaheim, CA, USA, 26–29 November 2018. [Google Scholar]
- Wang, Y.; Narasimha, M.; Heath, R.W. Mm Wave beam prediction with situational awareness: A machine learning approach. In Proceedings of the 2018 IEEE 19th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Kalamata, Greece, 25–28 June 2018. [Google Scholar]
- Anton-Haro, C.; Mestre, X. Learning and data-driven beam selection for mmWave communications: An angle of arrival-based approach. IEEE Access. 2019, 7, 20404–20415. [Google Scholar] [CrossRef]
- Wenyan, M.; Qi, C.; Li, G.Y. Machine learning for beam alignment in millimeter Wave massive MIMO. IEEE Wirel. Comm. Lett. 2020, 9, 875–878. [Google Scholar]
- Xu, C.; Liu, S.; Zhang, C.; Huang, Y.; Yang, L. Joint user scheduling and beam selection in mmWave networks based on multi-agent reinforcement learning. In Proceedings of the IEEE 11th Sensing Array Multichannel Signal Processing Workshop (SAM), Hangzhou, China, 8–11 June 2020. [Google Scholar]
- Alrabeiah, M.; Alkhateeb, A. Deep learning for mmWave beam and blockage prediction using sub-6 GHz channels. IEEE Trans. Com. 2020, 68, 5504–5518. [Google Scholar] [CrossRef]
- Göttsch, F.; Megumi, K. Deep learning-based beamforming and blockage prediction for sub-6GHz/mmWave mobile networks. In Proceedings of the 2020 IEEE Global Communications Conference (GLOBECOM), Madrid, Spain, 7–11 December 2020. [Google Scholar]
- Yang, W.H.; Kuang-Hao, L. Blockage effect and beam cooperation in indoor hotspot based on 3GPP NR blockage model. In Proceedings of the 2019 IEEE International Conference on Communications (ICC), Shanghai, China, 20–24 May 2019. [Google Scholar]
- Bhattacharjee, A.; Ratnajit, B.; Sanjay, K.B. DC-DLLR: A MAC layer approach for reliable and blockage tolerant mmWave indoor networks. In Proceedings of the 2021 International Conference on Communication Systems & Networks (COMSNETS), Bangalore, India, 5–9 January 2021. [Google Scholar]
- Arijit, B.; Ratnajit, B. An approach for mitigation of beam blockage in mmWave based indoor networks. IEEE Internet Things J. 2021, 1–6. [Google Scholar] [CrossRef]
- Gu, T.; Zhicheng, Y.; Prasant, M. BeamSniff: Enabling seamless communication under mobility and blockage in 60 GHz networks. In Proceedings of the 2019 IFIP Networking Conference (IFIP Networking), Warsaw, Poland, 20–22 May 2019. [Google Scholar]
- Alrabeiah, M.; Hredzak, A.; Alkhateeb, A. Millimeter Wave base stations with cameras: Vision-aided beam and blockage prediction. In Proceedings of the 2020 IEEE 91st Vehicular Technology Conference (VTC2020-Spring), Online, 25–28 May 2020. [Google Scholar]
- Jia, C.; Hui, G.; Na, C.; Yuan, H. Machine learning empowered beam management for intelligent reflecting surface assisted MmWave networks. China Commun. 2020, 17, 100–114. [Google Scholar] [CrossRef]
- Gerasimenko, M.; Dmitri, M.; Margarita, G.; Sergey, A.; Yevgeni, K. Capacity of multi-connectivity MmWave systems with dynamic blockage and directional antennas. IEEE Trans. Veh. Tech. 2019, 68, 3534–3549. [Google Scholar] [CrossRef]
- You, L.; Chen, X.; Song, X.; Jiang, F.; Wang, W.; Gao, X.; Fettweis, G. Network massive MIMO transmission over millimeter-Wave and terahertz bands: Mobility enhancement and blockage mitigation. IEEE J. Sel. Areas Commun. 2020, 38, 2946–2960. [Google Scholar] [CrossRef]
- Zheng, C.; Liu, S.; Huang, Y.; Yang, L. MEC-enabled wireless VR video service: A learning-based mixed strategy for energy-latency tradeoff. In Proceedings of the 2020 IEEE Wireless Communications and Networking Conference (WCNC), Seoul, South Korea, 25–28 May 2020. [Google Scholar]
- Rahman, A.U.; Gourab, G. A beam-switching scheme for resilient mmWave communications with dynamic link blockages. In Proceedings of the 2019 International Symposium on Modeling and Optimization in Mobile, Ad Hoc, and Wireless Net-works (WiOPT), Avignon, France, 27–31 May 2019. [Google Scholar]
- Balanis, C. Antenna Theory: Analysis and Design, 3rd ed.; Wiley & Sons: Hoboken, NJ, USA, 2005; pp. 290–304. [Google Scholar]
- Stutzman, W.; Thiele, G. Antenna Theory and Design, 3rd ed.; Wiley & Sons: Hoboken, NJ, USA, 2012; pp. 626–629. [Google Scholar]
- Bai, T.; Desai, V.; Heath, R.W. Millimeter Wave cellular channel models for system evaluation. In Proceedings of the International Conference on Computing, Networking and Communications (ICNC), Honolulu, HI, USA, 3–6 February 2014. [Google Scholar]
- Sun, S.; Rappaport, T.R.; Rangan, S.; Thomas, T.A.; Ghosh, A.; Kovacs, I.Z. Propagation path loss models for 5G urban micro- and macro-cellular scenarios. In Proceedings of the IEEE 83rd Vehicular Technology Conference (VTC2016-Spring), Nanjing, China, 15–18 May 2016. [Google Scholar]
- Akdeniz, M.R.; Liu, Y.; Samimi, M.K.; Sun, S.; Rangan, S.; Rappaport, T.S.; Erkip, E. Millimeter Wave channel modeling and cellular capacity evaluation. IEEE JSAC 2014, 32, 1164–1179. [Google Scholar] [CrossRef]
- Sepp, H.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar]
- Italia, T. Telecommunications–SMS, Call, Internet–MI. Hardvard Dataverse 2015. [Google Scholar] [CrossRef]
- Abbas, W.D.; Zorzi, M. Context information based initial cell search for millimeter Wave 5G cellular networks. In Proceedings of the European Conference on Networks and Communications (EuCNC), Athens, Greece, 27–30 June 2016. [Google Scholar]
- Méndez-Rial, R.; Rusu, C.; Alkhateeb, A.; González-Prelcic, N.; Heath, R.W. Channel estimation and hybrid combining for MmWave: Phase shifters or switches? In Proceedings of the Information Theory and Applications (ITA) Workshop, San Diego, CA, USA, 1–6 February 2015. [Google Scholar]


| Reference | Algorithm | Advantages | Limitations |
|---|---|---|---|
| [2] | Iterative codebook-based approaches. | Reduced complexity versus exhaustive beam reset scanning. | Poor directivity at initial codebook stages, prolonged recovery times (reset scanning). |
| [3,4] | Metaheuristic search schemes. | Reduced complexity versus conventional codebook schemes. | approximate solutions deficiency in estimating optimal beam directions. |
| [5,6] | Dual-beam methods that combine signal from adjacent directions. | Aggregates signal from other directions associated with the defected beam. | High power needs for continuous measurements at other beam directions. |
| [7] | Redundant beams. | Instantaneous beam recovery without scan resetting. | High power levels due to continuous scanning for prolonged time periods. |
| [8] | Self-handover scheme using secondary beam scanning. | Instantaneous recovery without the need for retransmissions. | Contingent upon availability of multiple BSs in MS proximity. Requires redundancy for transmitting back-up packets. |
| [9] | Signal measurements at proximity beams of the failed main beam. | Shorter recovery times as compared to codebook and metaheuristic approaches. | albeit at the prolonged test times that extent the recovery process and yield in session drops. |
| [10] | Data forwarding algorithm. | Reactive method for instantaneous recovery. | Requires intermediate nodes, prolonged times due to relaying, infrastructure cost. |
| [11] | Backup beam for link recovery. | Reactive method for instantaneous recovery. | High power consumption, limited to NSA standard, as backup beam direction is retrieved using microwave bands. |
| [12] | Machine learning for reliable mmWave systems. | Proactive approach enables fast beam switching times between BSs. | limited blockage parameters, marginal link improvements. |
| [13,14] | Situational awareness [13] and data-driven [14] prediction approaches. | Consideration for power at the beam index, high prediction precision. | Location awareness of MS to train the network, accuracy challenges. |
| Reference | Algorithm | Advantages | Limitations |
|---|---|---|---|
| [12] | Machine learning for reliable mmWave systems. | Proactive approach enables fast beam switching times between BSs. | Limited blockage parameters, marginal link improvements. |
| [13,14] | Situational awareness [13] and data-driven [14] prediction approaches. | Consideration for power at the beam index, high prediction precision. | Location awareness of MS to train the network, accuracy challenges. |
| [15] | Alignment method for multi-user mmWave massive MIMO system. | Eliminates the need for MS location (reducing overhead). | Lacks modeling the beam access/recovery times and power consumption levels. |
| [16] | inter-band beam switching scheme between mmWave BSs using multi-armed bandits (MAB) model. | Resiliency through dynamic temporal setting and blockage probabilities. | Location awareness, multi-connectivity, magnified power consumption. |
| [17] | Out-of-band beam prediction leverages transfer learning. | Reduce the learning time overhead. | High complexity due to functions mapping, dependence on sub-6 GHz bands. |
| [18] | Deep neural network for scheduling prediction at BS. | Improved prediction accuracy, reduced complexity, user mobility. | Based on sub-6 GHz channel knowledge, limited to downlink transmission. |
| [19,20,21,22] | Beam cooperation and delegation schemes between UE and APs in indoor mmWave networks. | Mobility-aware, better node visibility and QoS, sustaining communication sessions. | Multi-connectivity (redundancy) requires high power levels, lack of delay models. |
| [23] | Vision-assisted scheme for beam blockage problem. | Robust and accurate recovery scheme. | Dependence on sub-6 GHz channels, large number of installed cameras in dense network deployment. |
| [24] | Intelligent reflecting surface (IRS)-based machine learning method for beam recovery. | Mobility awareness, reduced system overhead, high handover success rate. | High computational complexity, lack of power model, requires massive infrastructure scalability. |
| [25] | Ergodic capacity in beam blockage in urban mmWave networks. | Consideration for AP, blockage density, and degree of multi-connectivity. | Blockage due to pedestrians only (low mobility), dual connectivity adds redundancy and power demands. |
| [26] | Optimization method for mobility and blockage problems in mmWave and THz downlink transmission. | Considerations for mobility, high sum rate, mitigated Doppler and delay dispersion effects. | Limited to downlink transmission, THz bands features different propagation characteristics and transceivers. |
| Notation | Variable |
|---|---|
| A single antenna unit at MS | |
| Number of antennas at MS | |
| a | Radius of the UCA |
| A single RF chain at MS | |
| Total number of RF chains at MS | |
| Combining vector at MS at index I at (t) th time step | |
| i | Index i representing one direction at MS |
| I | The number of pointing directions at MS |
| A single antenna element at BS | |
| Total number of antennas at BS | |
| A single RF chain at BS | |
| Total number of RF chains at BS | |
| j | Index j representing one direction at MS |
| J | Total number of directions at BS |
| Beamforming vectors | |
| MS combining matrix | |
| Beamforming vectors | |
| BS beamforming matrix | |
| AF here for MS | |
| n-th antenna amplitude at MS | |
| v | Wave-number |
| λ | Wavelength |
| Speed of light | |
| Carrier frequency | |
| The n-th antenna angular position | |
| Principal radiation at MS affiliated with vector at (t) th time step | |
| Array gains at the MS | |
| Array gains at the BS | |
| Gain for one antenna |
| Notation | Variable |
|---|---|
| Transmitted power level | |
| H | mmWave channel block |
| z | Control or data signal |
| w | Additive white Gaussian noise |
| Noise variance | |
| Blockage path loss | |
| Channel gain from path l | |
| L | Total paths (rays) |
| K | Clusters |
| Power ratio between first arriving LoS ray and subsequent rays | |
| Azimuth angle at MS | |
| Elevational MS | |
| Indicator function | |
| LoS path loss parameter | |
| NLoS path loss parameter | |
| d | Separation distance between the BS and MS |
| Reference distance | |
| Path loss exponent for LoS link status | |
| Path loss exponent for NLoS link status | |
| LoS probability at distance d | |
| NLoS probability at distance d | |
| Blockage parameter for objects of varying dimensions | |
| Beam index at MS that yields highest signal at (t)th time step | |
| Beam index at BS that yields highest signal at (t)th time step | |
| Highest signal at (t)th time step | |
| Ω | Loss factor |
| Maximum spectral efficiency | |
| Ψ | Boltzmann constant |
| Operating temperature | |
| Bandwidth |
| Notation | Variable |
|---|---|
| Input gate | |
| Input modulation | |
| Forget gate | |
| Output gate | |
| Training period | |
| Bias vectors for the input gate | |
| Bias vectors for the cell state | |
| Bias vectors for the output gate | |
| Bias vectors for the forget gate | |
| hidden state layer | |
| W | Weight matrices |
| Output units | |
| Number of the memory cells | |
| Input units | |
| O(W) | Computational complexity for LSTM per weight in a single time step |
| Actual ground truth | |
| Prediction vector | |
| U | Number of predictions points |
| Class | Parameter | Value |
|---|---|---|
| LSTM layers | No. of cells in LSTM layers | 4: [50,50,50,50] |
| Dense layers | Activation Function | ReLU |
| Hyper-parameters | Batch size | 16 |
| Epochs | 350 | |
| Dropout rate | 0.2 |
| Category | Parameter | Value |
|---|---|---|
| System | (GHz), (MHz), (dBm), d (m) | 28, 800, 30, 250 |
| Channel | ∂ (dB), (dB) , | 0, 1, 3, 0–1 |
| Path loss | (m), , | 5, 2.6, 4 |
| Spectral efficiency | Ω, | 2, 10 |
| Power consumption (mW) | 5.4, 78, 20, 20, 20, 19, 5, 14, 5 |
| Notation | Variable |
|---|---|
| Energy consumption measured at MS | |
| power consumption level in the analog beamformer at MS | |
| The link recovery (restoration) time at MS | |
| The link recovery (restoration) time at BS | |
| Power consumption for a single microstrip antenna | |
| Power consumption for a single-phase shifter | |
| Power consumption for a single low noise amplifier | |
| Power consumption for a single RF chain | |
| Power consumption for a single analog-to-digital converter | |
| Power consumption for a single baseband combiner | |
| Power consumption for a single mixer | |
| Power consumption for a single local oscillator | |
| Power consumption for a single low pass filter | |
| Power consumption for a single baseband amplifier | |
| Energy consumption per conversion in ADC | |
| Sampling rate | |
| Number of bits |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aldalbahi, A.; Shahabi, F.; Jasim, M. Instantaneous Beam Prediction Scheme against Link Blockage in mmWave Communications. Appl. Sci. 2021, 11, 5601. https://doi.org/10.3390/app11125601
Aldalbahi A, Shahabi F, Jasim M. Instantaneous Beam Prediction Scheme against Link Blockage in mmWave Communications. Applied Sciences. 2021; 11(12):5601. https://doi.org/10.3390/app11125601
Chicago/Turabian StyleAldalbahi, Adel, Farzad Shahabi, and Mohammed Jasim. 2021. "Instantaneous Beam Prediction Scheme against Link Blockage in mmWave Communications" Applied Sciences 11, no. 12: 5601. https://doi.org/10.3390/app11125601
APA StyleAldalbahi, A., Shahabi, F., & Jasim, M. (2021). Instantaneous Beam Prediction Scheme against Link Blockage in mmWave Communications. Applied Sciences, 11(12), 5601. https://doi.org/10.3390/app11125601






