Experimental and Numerical Investigation of 3D Dam-Break Wave Propagation in an Enclosed Domain with Dry and Wet Bottom
Abstract
1. Introduction
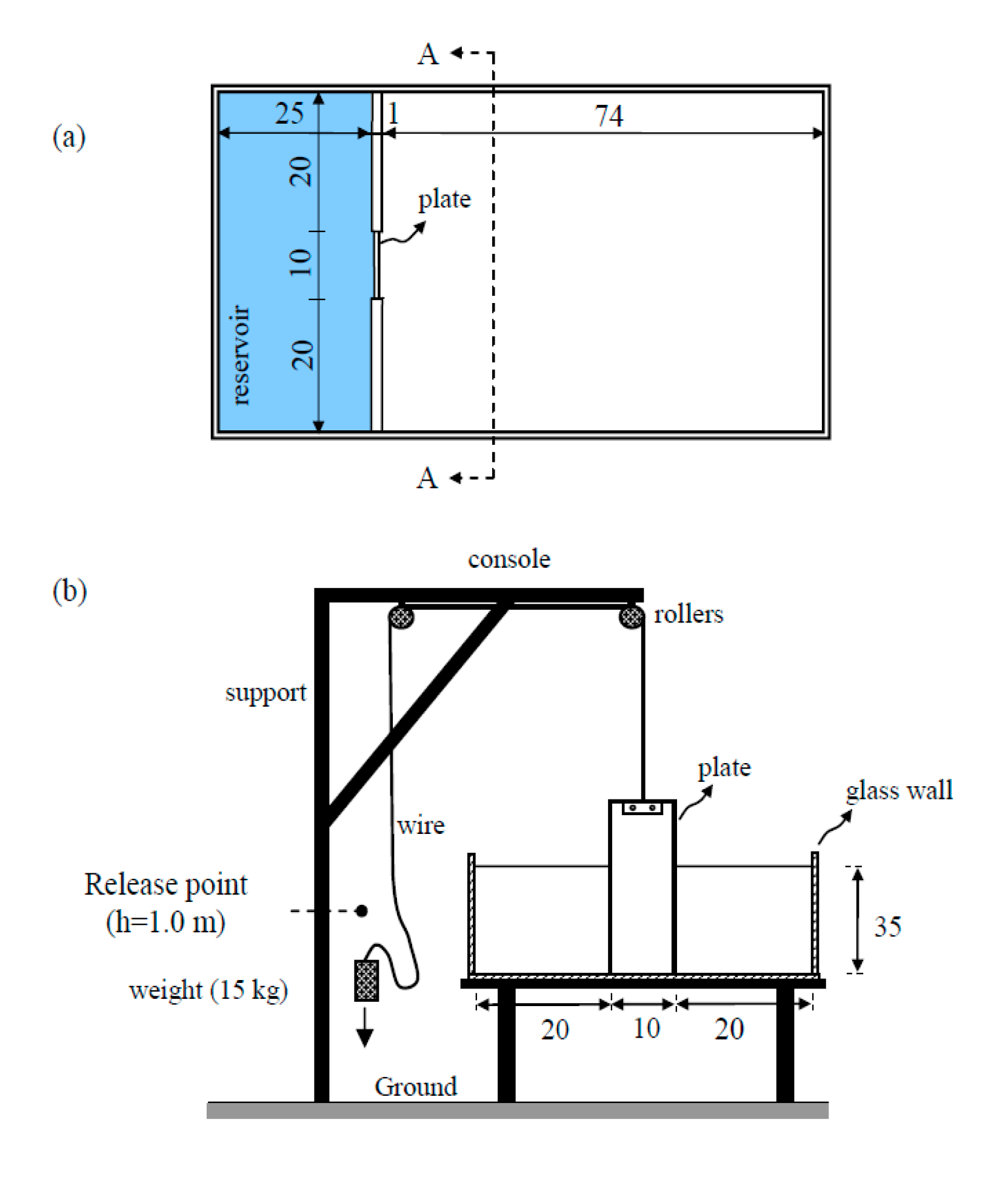
2. Laboratory Experiments
2.1. Experimental Setup
2.2. Performed Tests
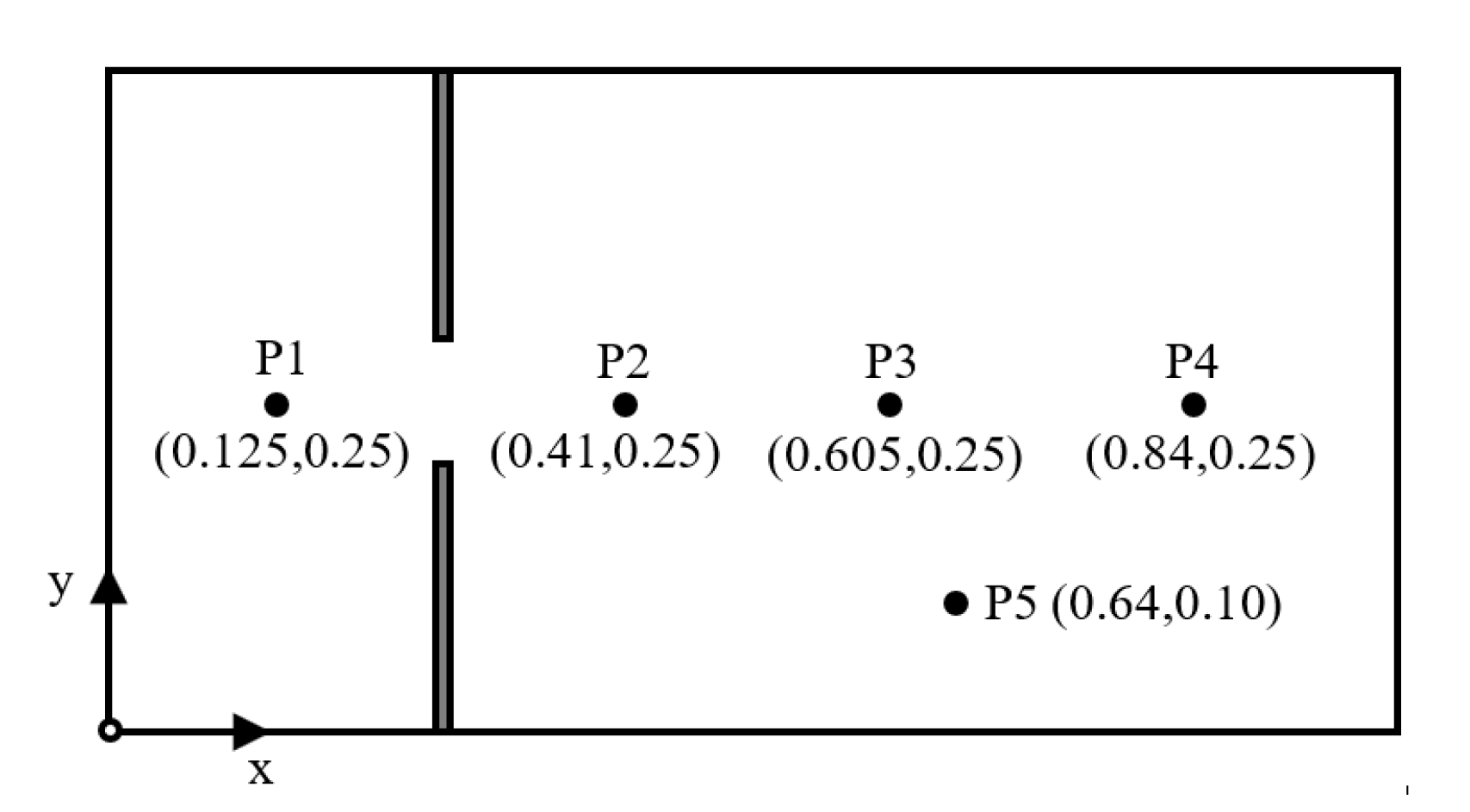
2.3. Measurement Technique
3. Numerical Model
3.1. RANS Equations with k-ε Turbulent Model
3.2. The Shallow Water Equations
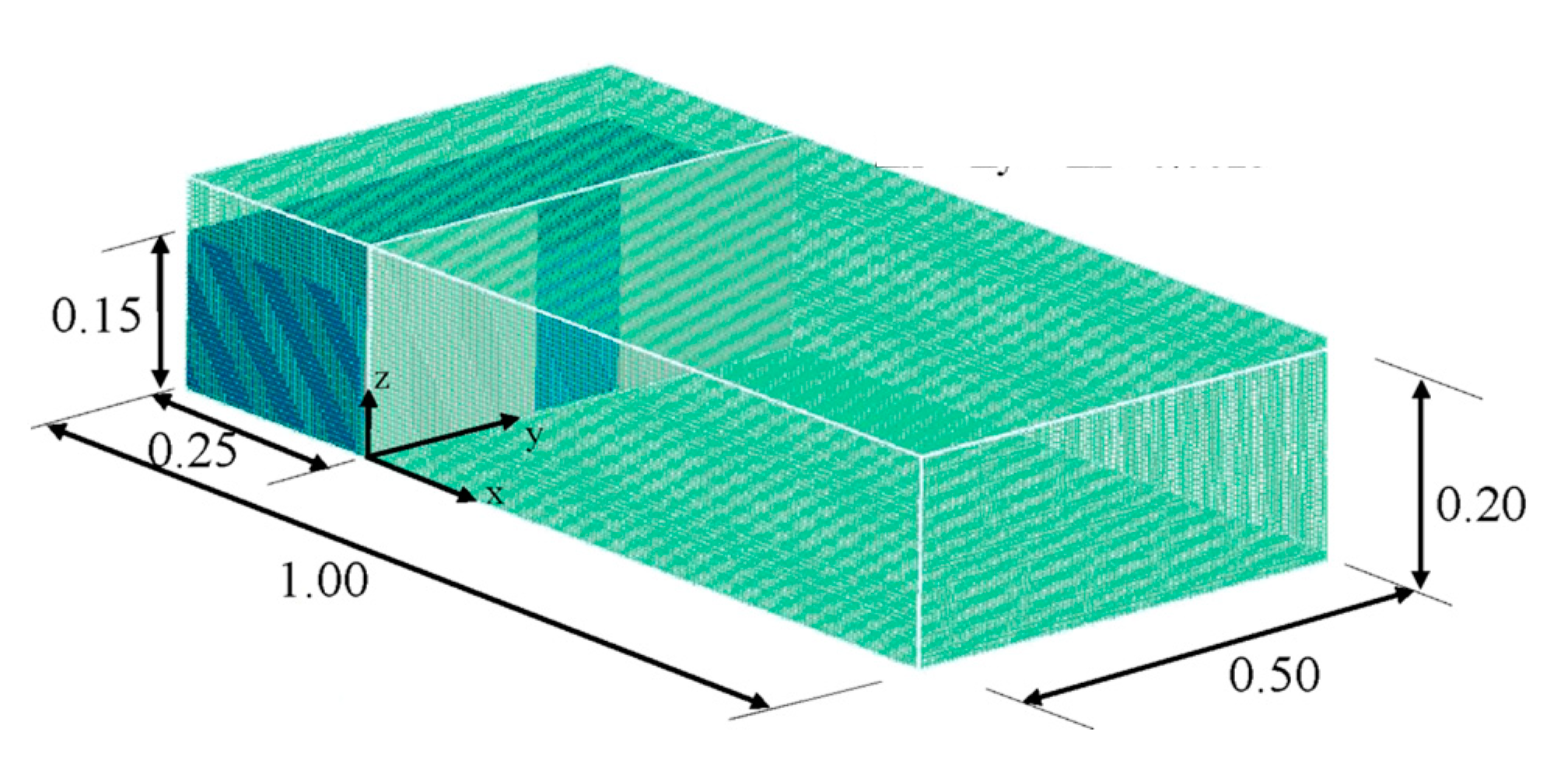
3.3. Solution Domain, Boundary and Initial Conditions
4. Results
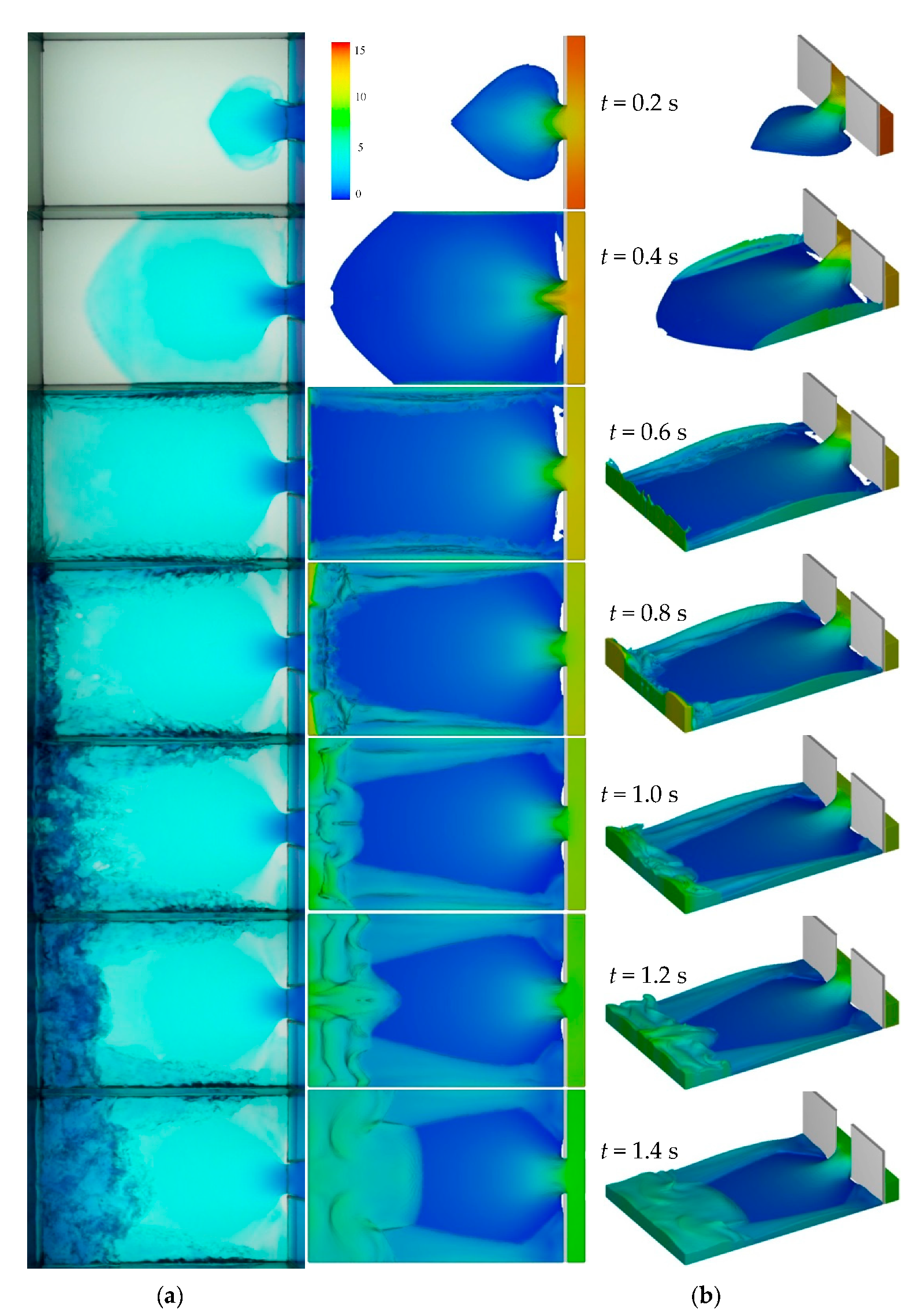
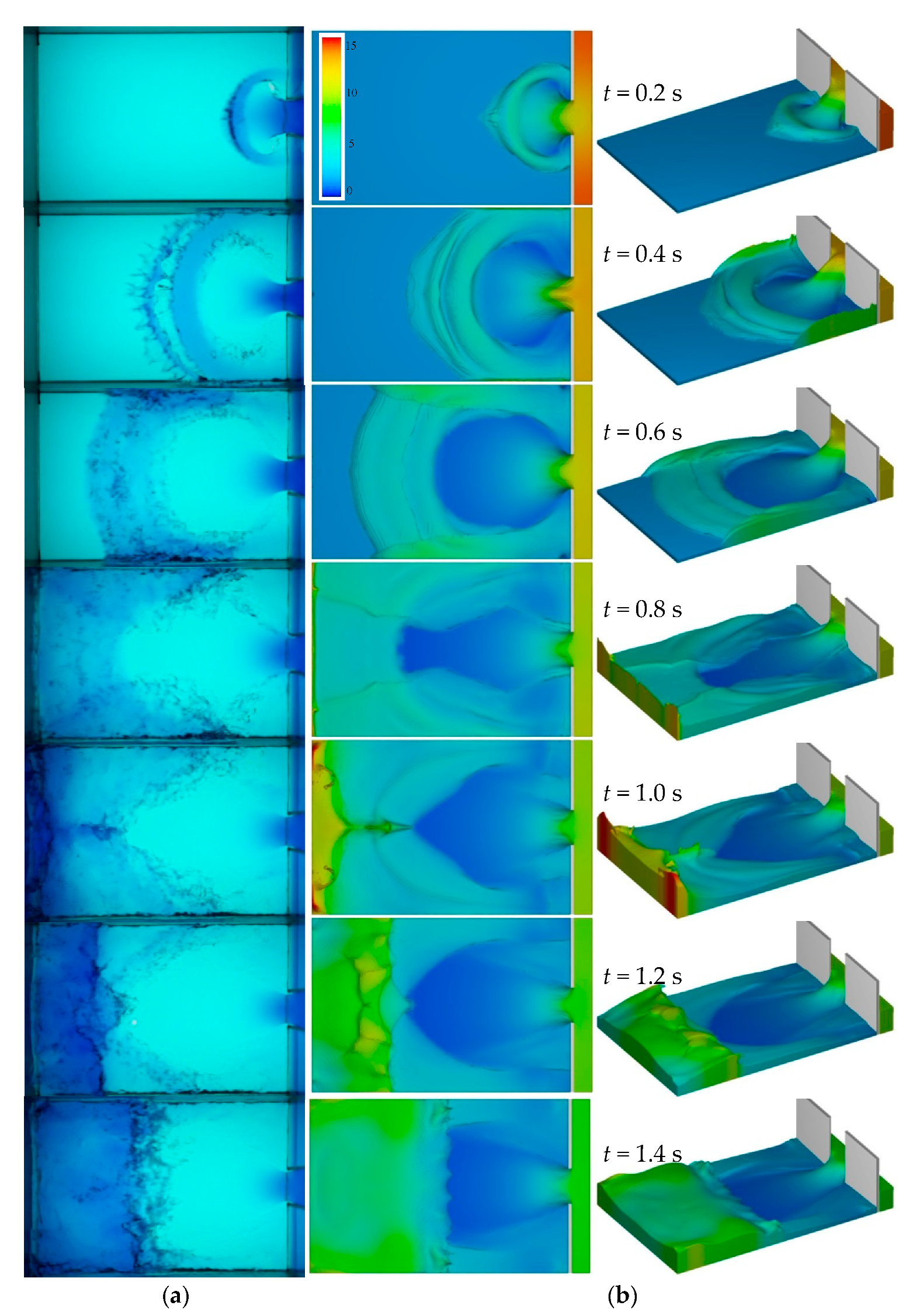
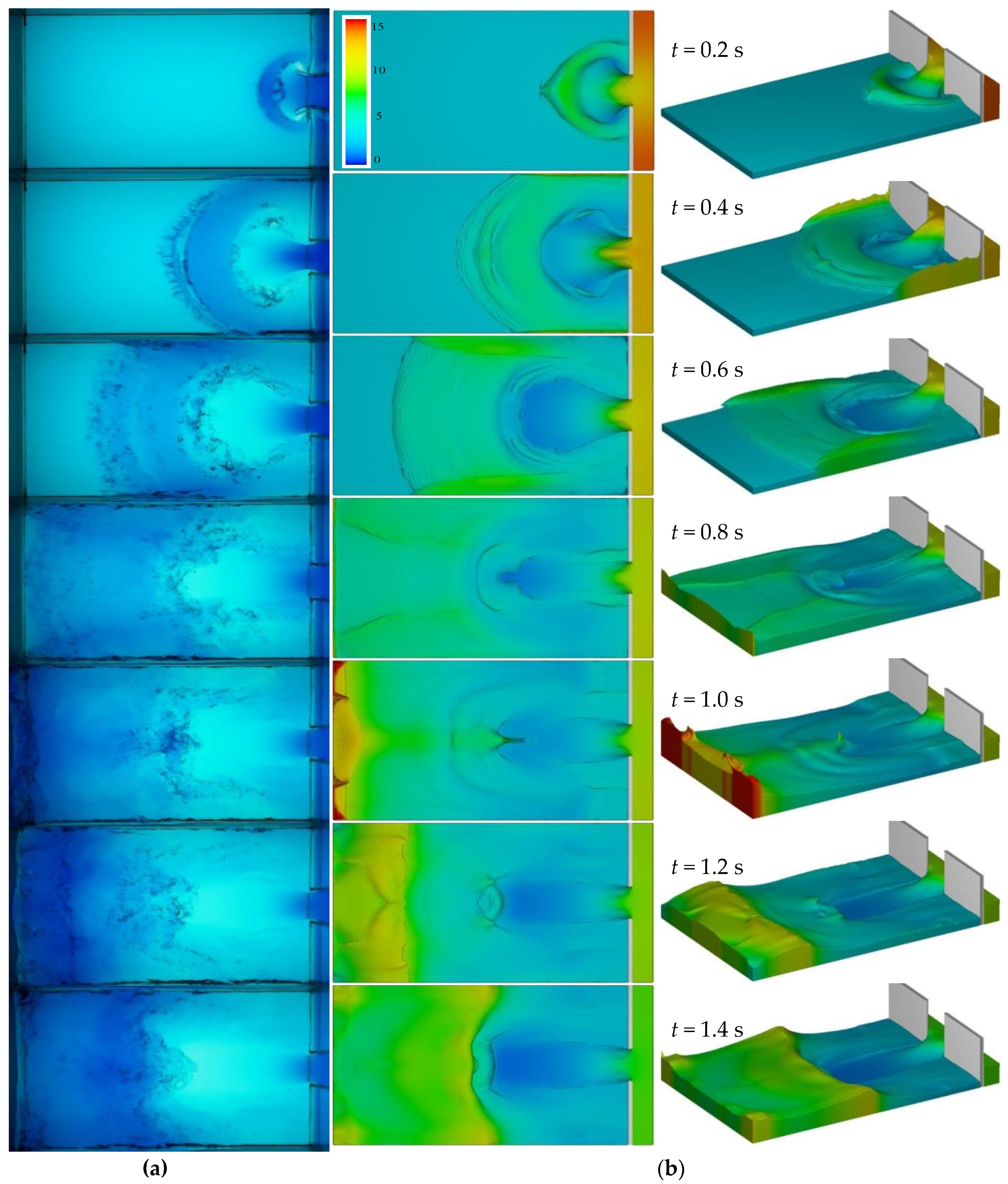
4.1. Experimental Results
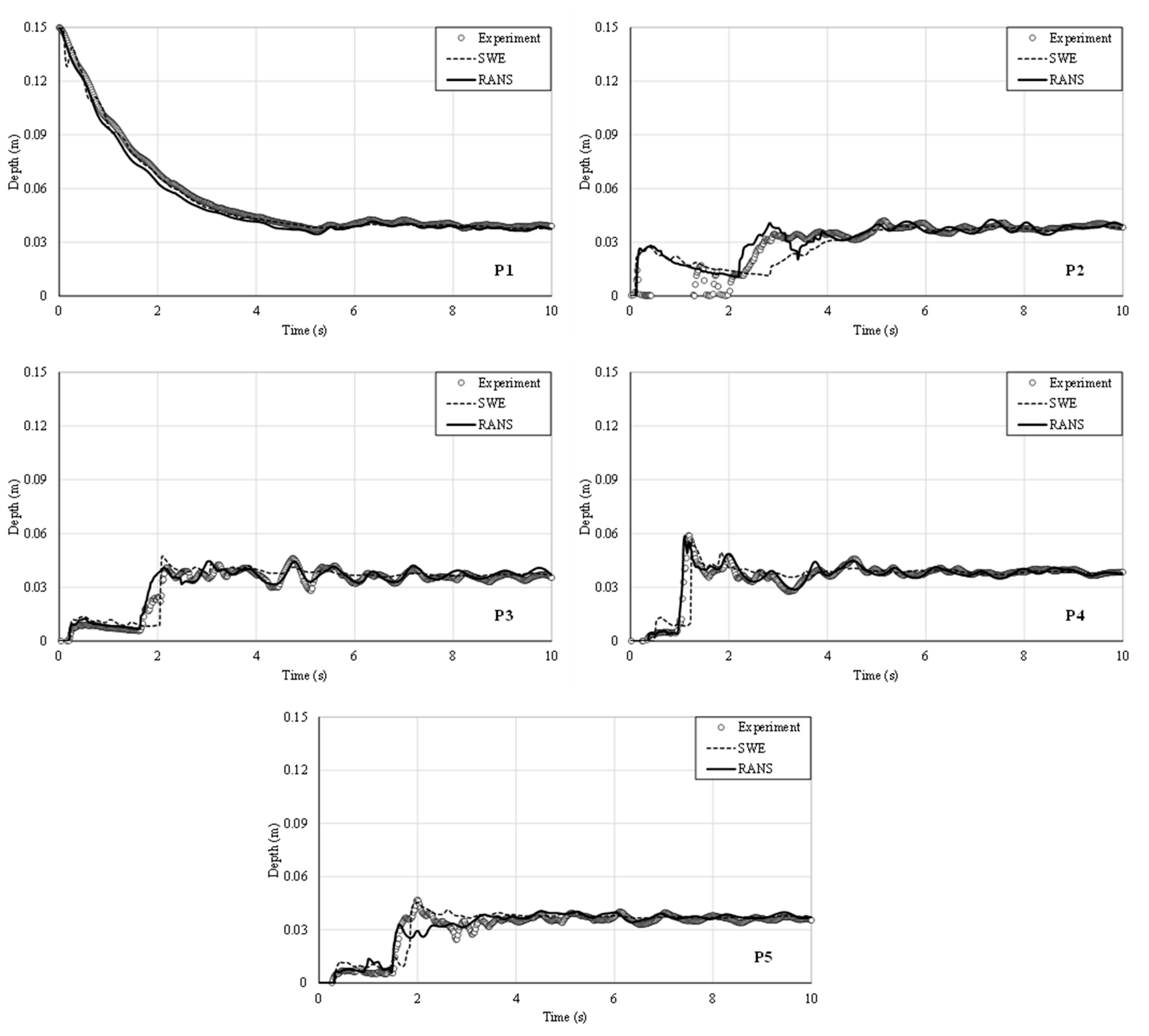
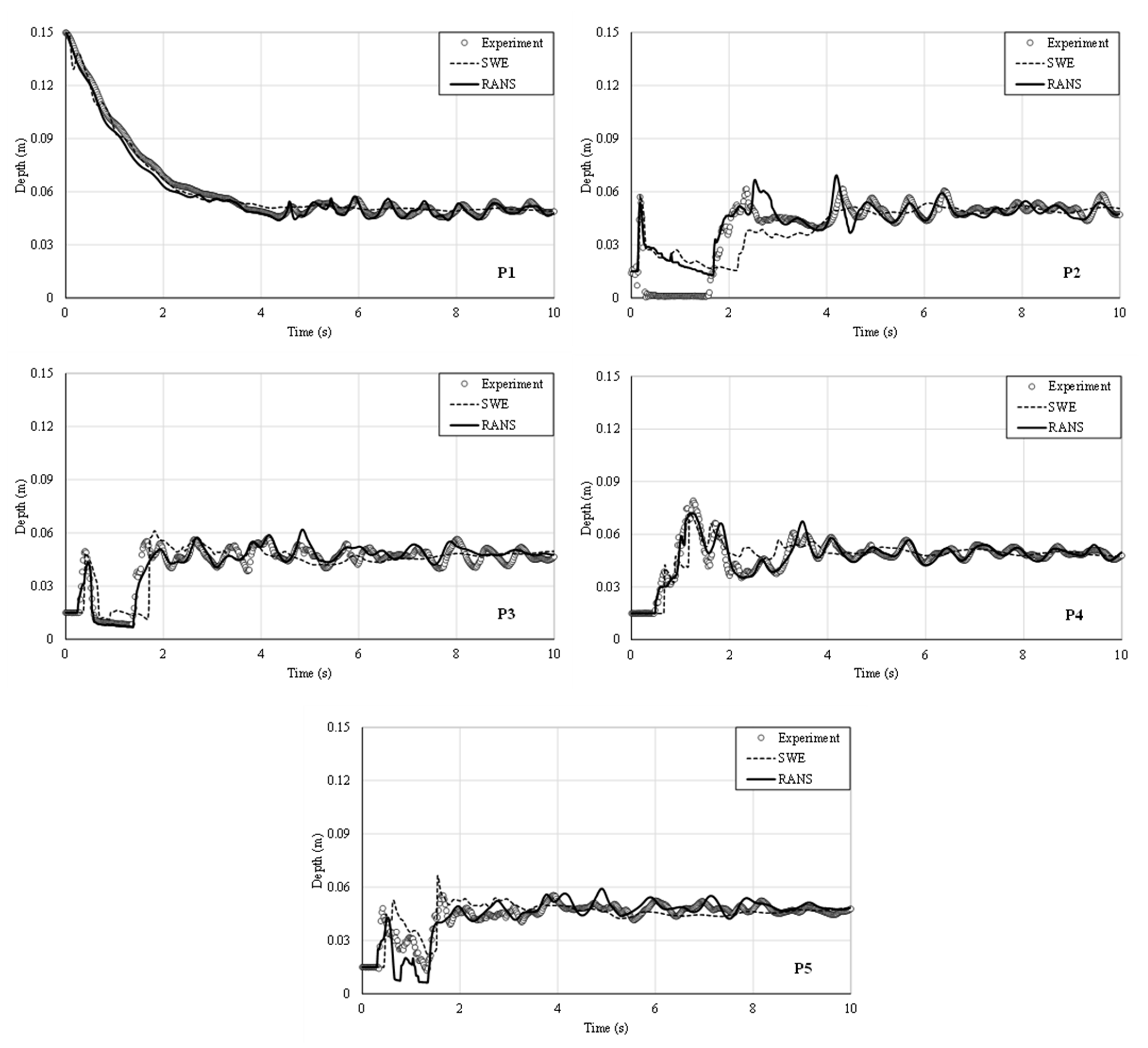
4.2. Comparison between Measured and Computed Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rendina, I.; Viccione, G.; Cascini, L. Kinematics of flow mass movements on inclined surfaces. Theor. Comput. Fluid Dyn. 2019, 33, 107–123. [Google Scholar] [CrossRef]
- Evangelista, S.; Altinakar, M.S.; Di Cristo, C.; Leopardi, A. Simulation of dam-break waves on movable beds using a multi-stage centered scheme. Int. J. Sediment Res. 2013, 28, 269–284. [Google Scholar] [CrossRef]
- Pohle, F.V. Motion of Water Due to Breaking of a Dam and Related Problems; USNBS: Washington, DC, USA, 1952; pp. 47–53. [Google Scholar]
- Kosorin, K. Hydraulic characteristics of some dam-break wave singularities. In Proceedings of the 20th IAHR Congress, International Association for Hydraulic Research, Moscow, Russia, 5–9 September 1983; pp. 520–528. [Google Scholar]
- Stoker, J.J. Water Waves. In Water Waves; Wiley: Hoboken, NJ, USA, 1992; pp. 291–449. [Google Scholar]
- Ritter, A. Die Fortpflanzung der Wassarwellen, Z. Vereines Deutsh. Ing. 1892, 36, 947–954. [Google Scholar]
- Dressler, R.F. Comparison of theories and experiments for the hydraulic dam-break wave. In Assoc Int d’Hydrol Sci, Assemblee Generale De Rome, 1st ed.; National Bureau of Standards: Washington, DC, USA, 1954; Volume 38, pp. 319–328. [Google Scholar]
- Whitham, G.B. The effects of hydraulic resistance in the dam-break problem. In Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences; The Royal Society: London, UK, 1955; Volume 227, Issue 1170; pp. 399–407. [Google Scholar] [CrossRef]
- Schmidgall, T.; Strange, J.N. Floods Resulting from Suddenly Breached Dams. Conditions of High Resistance. Hydraulic Model Investigation; Army Engineer Waterways Experiment Station: Vicksburg, MS, USA, 1961; Miscellaneous Paper N. 2-374; Available online: https://apps.dtic.mil/dtic/tr/fulltext/u2/268411.pdf (accessed on 3 August 2020).
- Bellos, C.V.; Soulis, V.; Sakkas, J.G. Experimental investigation of two-dimensional dam-break induced flows. J. Hydraul. Res. 1992, 30, 47–63. [Google Scholar] [CrossRef]
- Bell, S.W.; Elliot, R.C.; Chaudhry, M.H. Experimental results of two-dimensional dam-break flows. J. Hydraul. Res. 1992, 30, 225–252. [Google Scholar] [CrossRef]
- Fraccarollo, L.; Toro, E.F. Experimental and numerical assessment of the shallow water model for two-dimensional dam-break type problems. J. Hydraul. Res. 1995, 33, 843–864. [Google Scholar] [CrossRef]
- Lauber, G.; Hager, W.H. Experiments to dambreak wave: Horizontal channel. J. Hydraul. Res. 1998, 36, 291–307. [Google Scholar] [CrossRef]
- Stansby, P.K.; Chegini, A.; Barnes, T.C.D. The initial stages of dam-break flow. J. Fluid Mech. 1998, 374, 407–424. [Google Scholar] [CrossRef]
- Bukreev, V.I.; Gusev, A.V. Initial stage of the generation of dam-break waves. Dokl. Phys. 2005, 50, 200–203. [Google Scholar] [CrossRef]
- Korobkin, A.; Yilmaz, O. The initial stage of dam-break flow. J. Eng. Math. 2008, 63, 293–308. [Google Scholar] [CrossRef]
- Leal, J.G.A.B.; Ferreira, R.M.L.; Cardoso, A.H. Dambreak waves on movable bed. In Proceedings of the River Flow 2002, Louvain-la-Neuve, Belgium, 4–6 September 2002; Bousmar, D., Zech, Y., Eds.; Balkema: Rotterdam, The Netherlands, 2002; Volume 2, pp. 981–990. [Google Scholar]
- Di Cristo, C.; Evangelista, S.; Greco, M.; Iervolino, M.; Leopardi, A.; Vacca, A. Dam-break waves over an erodible embankment: Experiments and simulations. J. Hydraul. Res. 2017, 56, 196–210. [Google Scholar] [CrossRef]
- Soares-Frazao, S.; Zech, Y. Experimental study of dam-break flow against an isolated obstacle. J. Hydraul. Res. 2007, 45, 27–36. [Google Scholar] [CrossRef]
- Ozmen-Cagatay, H.; Kocaman, S. Experimental study of tail water level effects on dam-break flood wave propagation. In Proceedings of the International Conference River Flow 2008, Cesme, Turkey, 3–5 September 2008; Al-tinakar, M.S., Kokpinar, M.A., Aydin, I., Cokgor, S., Kirkgoz, S., Eds.; Volume 1, pp. 635–644, ISBN 978-605-60136-1-4. [Google Scholar]
- Aureli, F.; Maranzoni, A.; Mignosa, P.; Ziveri, C. An image processing technique for measuring free surface of dam-break flows. Exp. Fluids 2010, 50, 665–675. [Google Scholar] [CrossRef]
- Kocaman, S.; Ozmen-Cagatay, H. Investigation of dam-break induced shock waves impact on a vertical wall. J. Hydrol. 2015, 525, 1–12. [Google Scholar] [CrossRef]
- Amicarelli, A.; Manenti, S.; Albano, R.; Agate, G.; Paggi, M.; Longoni, L.; Mirauda, D.; Ziane, L.; Viccione, G.; Todeschini, S.; et al. SPHERA v.9.0.0: A Computational Fluid Dynamics research code, based on the Smoothed Particle Hydrodynamics mesh-less method. Comput. Phys. Commun. 2020, 250, 107157. [Google Scholar] [CrossRef]
- Crespo, A.; Domínguez, J.; Rogers, B.; Gómez-Gesteira, M.; Longshaw, S.; Canelas, R.; Vacondio, R.; Barreiro, A.; García-Feal, O. DualSPHysics: Open-source parallel CFD solver based on Smoothed Particle Hydrodynamics (SPH). Comput. Phys. Commun. 2015, 187, 204–216. [Google Scholar] [CrossRef]
- Flow Science, Inc. FLOW-3D® Version 11; Flow Science, Inc.: Santa Fe, NM, USA, 2019. [Google Scholar]
- BOSS International, BOSS DAMBRK. Hydrodynamics Flooding Routing User’s Manual; BOSS International, BOSS DAMBRK: Madison, WI, USA, 1999. [Google Scholar]
- HEC-RAS. River Analysis System. US Army Corps of Engineers. Hydrologic Engineering Center. Hydraulic Reference Man-ual. Version 5.0. 2016. Available online: https://www.hec.usace.army.mil/software/hec-ras/documentation/HEC-RAS%205.0%20Reference%20Manual.pdf (accessed on 17 June 2021).
- Toro, E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics; Springer Science and Business Media LLC: Berlin, Germany, 2009. [Google Scholar]
- LeVeque, R.J. Finite Volume Methods for Hyperbolic Problems; Cambridge University Press: Cambridge, UK, 2002; Volume 31. [Google Scholar]
- Lai, J.-S.; Lin, G.-F.; Guo, W.-D. An upstream flux-splitting finite-volume scheme for 2D shallow water equations. Int. J. Numer. Methods Fluids 2005, 48, 1149–1174. [Google Scholar] [CrossRef]
- Aliparast, M. Two-dimensional finite volume method for dam-break flow simulation. Int. J. Sediment Res. 2009, 24, 99–107. [Google Scholar] [CrossRef]
- Ahmada, M.F.; Mamat, M.; Wan Nik, W.B.; Kartono, A. Numerical method for dam break problem by using Godunov approach. Appl. Math. Comp. Intel. 2013, 2, 95–107. [Google Scholar]
- Mirauda, D.; Albano, R.; Sole, A.; Adamowski, J. Smoothed Particle Hydrodynamics Modeling with Advanced Boundary Conditions for Two-Dimensional Dam-Break Floods. Water 2020, 12, 1142. [Google Scholar] [CrossRef]
- Viccione, G.; Bovolin, V. Simulating Triggering and Evolution of Debris-Flows with Smoothed Particle Hydrodynamics (SPH). Ital. J. Eng. Geo. Environ. 2011, 523–532. [Google Scholar] [CrossRef]
- Ferrari, A.; Fraccarollo, L.; Dumbser, M.; Toro, E.F.; Armanini, A. Three-dimensional flow evolution after a dam break. J. Fluid Mech. 2010, 663, 456–477. [Google Scholar] [CrossRef]
- Larocque, L.A.; Imran, J.; Chaudhry, M.H. 3D numerical simulation of partial breach dam-break flow using the LES and k–ϵ turbulence models. J. Hydraul. Res. 2012, 51, 145–157. [Google Scholar] [CrossRef]
- Marsooli, R.; Wu, W. 3-D finite-volume model of dam-break flow over uneven beds based on VOF method. Adv. Water Resour. 2014, 70, 104–117. [Google Scholar] [CrossRef]
- Issakhov, A.; Imanberdiyeva, M. Numerical Study of the Movement of Water Surface of Dam Break Flow by VOF Methods for Various Obstacles. Int. J. Nonlinear Sci. Numer. Simul. 2020, 21, 475–500. [Google Scholar] [CrossRef]
- Wu, W.; Marsooli, R.; He, Z. Depth-Averaged Two-Dimensional Model of Unsteady Flow and Sediment Transport due to Noncohesive Embankment Break/Breaching. J. Hydraul. Eng. 2012, 138, 503–516. [Google Scholar] [CrossRef]
- Wu, G.; Yang, Z.; Zhang, K.; Dong, P.; Lin, Y.-T. A Non-Equilibrium Sediment Transport Model for Dam Break Flow over Moveable Bed Based on Non-Uniform Rectangular Mesh. Water 2018, 10, 616. [Google Scholar] [CrossRef]
- Rodi, W. Turbulence Modeling and Simulation in Hydraulics: A Historical Review. J. Hydraul. Eng. 2017, 143, 03117001. [Google Scholar] [CrossRef]
- Shigematsu, T.; Liu, P.L.-F.; Oda, K. Numerical modeling of the initial stages of dam-break waves. J. Hydraul. Res. 2004, 42, 183–195. [Google Scholar] [CrossRef]
- Yang, C.; Lin, B.; Jiang, C.; Liu, Y. Predicting near-field dam-break flow and impact force using a 3D model. J. Hydraul. Res. 2010, 48, 784–792. [Google Scholar] [CrossRef]
- Ozmen-Cagatay, H.; Kocaman, S. Dam-Break Flow in the Presence of Obstacle: Experiment and CFD Simulation. Eng. Appl. Comput. Fluid Mech. 2011, 5, 541–552. [Google Scholar] [CrossRef]
- Ozmen-Cagatay, H.; Kocaman, S. Investigation of Dam-Break Flow Over Abruptly Contracting Channel with Trapezoidal-Shaped Lateral Obstacles. J. Fluids Eng. 2012, 134, 081204. [Google Scholar] [CrossRef]
- Hu, H.; Zhang, J.; Li, T. Dam-Break Flows: Comparison between Flow-3D, MIKE 3 FM, and Analytical Solutions with Experimental Data. Appl. Sci. 2018, 8, 2456. [Google Scholar] [CrossRef]
- Munoz, D.H.; Constantinescu, G. 3-D dam break flow simulations in simplified and complex domains. Adv. Water Resour. 2020, 137, 103510. [Google Scholar] [CrossRef]
- Kocaman, S.; Güzel, H.; Evangelista, S.; Ozmen-Cagatay, H.; Viccione, G. Experimental and Numerical Analysis of a Dam-Break Flow through Different Contraction Geometries of the Channel. Water 2020, 12, 1124. [Google Scholar] [CrossRef]
- Brufau, P.; Garcia-Navarro, P. Two-dimensional dam-break flow simulation. Int. J. Numer. Meth. Fluids 2000, 33, 35–57. [Google Scholar] [CrossRef]
- Wang, J.S.; Ni, H.G.; He, Y.S. Finite-Difference TVD Scheme for Computation of Dam-Break Problems. J. Hydraul. Eng. 2000, 126, 253–262. [Google Scholar] [CrossRef]
- Quecedo, M.; Pastor, M.; Herreros, M.; Merodo, J.F.; Zhang, Q. Comparison of two mathematical models for solving the dam break problem using the FEM method. Comput. Methods Appl. Mech. Eng. 2005, 194, 3984–4005. [Google Scholar] [CrossRef]
- Ozmen-Cagatay, H.; Kocaman, S. Dam-break flows during initial stage using SWE and RANS approaches. J. Hydraul. Res. 2010, 48, 603–611. [Google Scholar] [CrossRef]
- Evangelista, S. Experiments and Numerical Simulations of Dike Erosion due to a Wave Impact. Water 2015, 7, 5831–5848. [Google Scholar] [CrossRef]
- Mohapatra, P.K.; Eswaran, V.; Bhallamudi, S.M. Two-Dimensional Analysis of Dam-Break Flow in Vertical Plane. J. Hydraul. Eng. 1999, 125, 183–192. [Google Scholar] [CrossRef][Green Version]
- Alcrudo, F.; Garcia-Navarro, P. A high-resolution Godunov-type scheme in finite volumes for the 2D shallow-water equations. Int. J. Numer. Methods Fluids 1993, 16, 489–505. [Google Scholar] [CrossRef]
- Kuiry, S.N.; Pramanik, K.; Sen, D. Finite Volume Model for Shallow Water Equations with Improved Treatment of Source Terms. J. Hydraul. Eng. 2008, 134, 231–242. [Google Scholar] [CrossRef]
- Morris, M.W. CADAM-Concerted Action on Dam-Break Modelling; HR: Wallingford, UK, 2000. [Google Scholar]
- Murzyn, F.; Chanson, H. Free-Surface, Bubbly Flow and Turbulence Measurements in Hydraulic Jumps. Research Report N° CH 63/07; Department of Civil Engineering, The University of Queensland: Brisbane, Australia, 2007; p. 118. ISBN 9781864998917. [Google Scholar]
- Murzyn, F.; Chanson, H. Free-surface fluctuations in hydraulic jumps: Experimental observations. Exp. Therm. Fluid Sci. 2009, 33, 1055–1064. [Google Scholar] [CrossRef]
- Chachereau, Y.; Chanson, H. Free-surface fluctuations and turbulence in hydraulic jumps. Exp. Therm. Fluid Sci. 2011, 35, 896–909. [Google Scholar] [CrossRef]
- Kocaman, S.; Dal, K. A New Experimental Study and SPH Comparison for the Sequential Dam-Break Problem. J. Mar. Sci. Eng. 2020, 8, 905. [Google Scholar] [CrossRef]
- Dal, K.; Kocaman, S. Comparison of the experimental results with SPH method for sequential dam-break problem. In Proceedings of the 5th IAHR Europe Congress, Trento, Italy, 12–14 June 2018. [Google Scholar]
- Munir, M.M.; Salam, R.A.; Widiatmoko, E.; Supriadani, Y.; Rahmadhani, A.; Latief, H.; Khairurrijal, K. Web-Based Surface Level Measuring System Employing Ultrasonic Sensors and GSM/GPRS-Based Communication. Appl. Mech. Mater. 2015, 771, 92–95. [Google Scholar] [CrossRef]
- Fiorentino, A.; De Luca, G.; Rizzo, L.; Viccione, G.; Lofrano, G.; Carotenuto, M. Simulating the fate of indigenous antibiotic resistant bacteria in a mild slope wastewater polluted stream. J. Environ. Sci. 2018, 69, 95–104. [Google Scholar] [CrossRef]



| TEST | hd [m] | α |
|---|---|---|
| D1 | 0.00 | 0 |
| W1 | 0.015 | 0.1 |
| W2 | 0.030 | 0.2 |
| P1 | P3 | P4 | P5 | |||||
|---|---|---|---|---|---|---|---|---|
| RANS | SWEs | RANS | SWEs | RANS | SWEs | RANS | SWEs | |
| D1 | 5.17 | 2.91 | 9.45 | 14.74 | 4.99 | 12.57 | 12.54 | 15.37 |
| W1 | 3.99 | 4.01 | 8.08 | 16.71 | 4.42 | 9.03 | 10.79 | 11.50 |
| W2 | 3.90 | 3.84 | 8.83 | 13.01 | 3.63 | 7.16 | 8.16 | 10.67 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kocaman, S.; Evangelista, S.; Guzel, H.; Dal, K.; Yilmaz, A.; Viccione, G. Experimental and Numerical Investigation of 3D Dam-Break Wave Propagation in an Enclosed Domain with Dry and Wet Bottom. Appl. Sci. 2021, 11, 5638. https://doi.org/10.3390/app11125638
Kocaman S, Evangelista S, Guzel H, Dal K, Yilmaz A, Viccione G. Experimental and Numerical Investigation of 3D Dam-Break Wave Propagation in an Enclosed Domain with Dry and Wet Bottom. Applied Sciences. 2021; 11(12):5638. https://doi.org/10.3390/app11125638
Chicago/Turabian StyleKocaman, Selahattin, Stefania Evangelista, Hasan Guzel, Kaan Dal, Ada Yilmaz, and Giacomo Viccione. 2021. "Experimental and Numerical Investigation of 3D Dam-Break Wave Propagation in an Enclosed Domain with Dry and Wet Bottom" Applied Sciences 11, no. 12: 5638. https://doi.org/10.3390/app11125638
APA StyleKocaman, S., Evangelista, S., Guzel, H., Dal, K., Yilmaz, A., & Viccione, G. (2021). Experimental and Numerical Investigation of 3D Dam-Break Wave Propagation in an Enclosed Domain with Dry and Wet Bottom. Applied Sciences, 11(12), 5638. https://doi.org/10.3390/app11125638








