Gamma Ray Shielding Properties of Yb³⁺-Doped Calcium Borotellurite Glasses

Abstract

This research work aims to investigate the radiation shielding ability of a Yb³⁺-doped calcium borotellurite glass system. The system has the basic composition of CaF₂–CaO–B₂O₃–TeO₂–Yb₂O₃ but is denoted as TeBYbn for simplicity. The effect of increasing the TeO₂ content in the glasses from 10 to 54 mol% was investigated, with five different chosen compositions and densities. The Phy-X/PSD program was used to investigate the mass attenuation coefficient (µ/ρ) of the samples. The mass attenuation coefficients were theoretically determined by using an online software for the calculation of shielding parameters. Other parameters were then calculated and analyzed, such as the linear attenuation coefficient (µ), transmission factor (TF), radiation protection efficiency (RPE), effective atomic number (Z_eff), and mean free path (MFP). TeBYb5, the glass with the greatest TeO₂ content, was shown to have the greatest µ/ρ; however, at greater energies, the differences between the values are practically negligible. µ was shown to increase with density, such as from 0.386 cm⁻¹ to 0.687 cm⁻¹ for TeBYb1 and TeBYb5 at 0.284 MeV, respectively. The least TF was found for samples with a thickness of 1.5 cm, proving an inverse correlation between the thickness of the sample and the TF. The HVL and TVL of the glasses decreased as the density of the samples increased, which means that TeBYb1 is the least effective out of the investigated glasses. The five samples proved to have a lower MFP than some other shielding glasses, demonstrating their capabilities as radiation shields. Based on the calculated parameters, TeBYb5 indicated the greatest photon attenuation ability.

1. Introduction

In the past few years, researchers have conducted various studies to find the best materials for reducing exposure to radiation and thus protecting people working in the field of radiation, as well as people exposed to radiation due to side effects [1,2,3,4,5,6,7,8,9,10,11]. Glass has features that make it distinct from other materials, such as visible light being able to pass through it, the ease of preparing glass in different and simple ways, and the possibility of changing the density of the glass during the preparation of glass samples. For these reasons, glassy materials are considered some of the most important materials currently used in radiation protection [12,13,14,15]. In order to enhance the photons attenuation ability of any glassy materials, we must use a glass systems which possesses relatively high density, and this is achieved by utilizing heavy metal oxides such as PbO, TeO₂, etc. [16,17]. Recent studies have shown that tellurite glasses possess effective photon-shielding characteristics, since they have high density and atomic number in addition to their considerable distinguished properties, namely excellent transmission window, high linear refractive index, good stability, low-phonon energies, good chemical resistance and low melting temperature [18,19]. The aforementioned properties of the TeO₂-based glasses made researchers interested in studying the shielding properties and trying to develop new types of glass based on tellurite oxide as effective materials in radiation protection [20,21,22]. On the other hand, the calcium borotellurite glasses (CaBTe) have a wide optical window transparency and good thermal stability [23]. Previously, different researchers have examined the thermal and structural properties of CaBTe glasses [23,24]. To the best our knowledge, there are limited studies that report the gamma ray attenuation ability of CaBTe glasses. For this reason, we aimed in this study to investigate some radiation-shielding factors of CaBTe glasses with the composition CaF₂–CaO–B₂O₃–TeO₂–Yb₂O₃ [25]. To report the radiation-shielding factors for any glassy materials, and thus to understand the ability of this material to shield the incoming radiation, one must calculate the mass attenuation coefficient (µ/ρ). There are several ways to determine this quantity, such as Monte Carlo simulation [26] and theoretical calculations based on some computer programs such as WinXcom or Phy-X/PSD [27,28]. From the µ/ρ values, other shielding factors are calculated, and then we can understand the transmission of the photons through the glassy materials.

This study aims to report the radiation shielding ability of the Yb³⁺-doped calcium borotellurite glass system. The five glasses are numbered in increasing TeO₂ content, which varies from 10 mol% to 54 mol%, in order to determine the effect of increasing the amount of TeO₂ in the glasses with their attenuation capability. A program was used to calculate the attenuation factors of the glasses, and further parameters were evaluated and analyzed to determine the abilities of these glasses to be used in radiation shielding applications.

2. Materials and Methods

Gamma rays have been, to a large degree, utilized in several areas, and for that reason, gamma ray attenuation parameters—including the dose rate of photons, the radiation protection percentage of the sample, the tenth value thickness, the photon interaction cross sections and some other shielding factors—have gained great importance due to their applications in nuclear shielding and health physics [29,30,31]. It is necessary to report the aforementioned quantities for several glass systems in order to obtain the suitable glass that can supply a convenient safe shielding from the ionizing radiation. In our work, the photon attenuation factors of CaF₂–CaO–B₂O₃–TeO₂–Yb₂O₃ glass systems (for simplicity, we will use TeBYbX to denote the glass samples) were theoretically studied by the Phy-X/PSD program [28], and the influence of varying the amount of TeO₂ from 10 to 54 mol% on the attenuation effectiveness of these systems was examined. Previously, Lima et al. fabricated the chosen glasses. The full glass fabrication details, the optical and the spectroscopic features of the glasses are reported in [25]. The chosen glasses are coded as:

• 10TeO₂-54B₂O₃-25.5CaO-10CaF₂-0.5Yb₂O₃ (TeBYb1), the density is 3.08 g/cm³
• 16TeO₂-50.4B₂O₃-23.1CaO-10CaF₂- 0.5Yb₂O₃ (TeBYb2), the density is 3.25 g/cm³
• 22TeO₂-46.8B₂O₃-20.7CaO-10CaF₂- 0.5Yb₂O₃ (TeBYb3), the density is 3.43 g/cm³
• 31TeO₂-41.4B₂O₃-17.1CaO-10CaF₂- 0.5Yb₂O₃ (TeBYb4), the density is 3.71 g/cm³
• 54TeO₂-27.6B₂O₃-7.9CaO-10CaF₂- 0.5Yb₂O₃ (TeBYb5), the density is 4.46 g/cm³

For the above glasses, Phy-X/PSD was applied to generate the mass attenuation coefficient (µ/ρ) values, and we examined the influence of increasing the concentration of 10 to 54 mol% on the µ/ρ values of the glasses under study. In addition, we used the obtained µ/ρ values to determine the linear attenuation coefficient (µ), and from this parameter we can check the enhancement of the radiation shielding ability of the samples when the density increases from 3.08 g/cm³ (for TeBYb1) to 4.46 g/cm³ (for TeBYb5). Two other important factors that can be generated from µ are the transmission factor (TF) and the radiation protection percentage (RPP). The TF and RPP can be calculated via the following relations:

$$TF=e^{-\mathsf{\mu }\times t}$$

(1)

$$RPP=\left(1-\frac{I}{I_0}\right)\times 100\%$$

(2)

In Equation (1), t represents the thickness of the sample, while I and I₀ in Equation (2) are the attenuated and incident intensities of the photons. Moreover, the half value thickness (HVL) represents the width of glass that able to shield half of the initial radiation [32]. The smaller the sample thickness that is able to provide adequate radiation protection, the better it will be used in practical applications. The HVL for the chosen CaF₂–CaO–B₂O₃–TeO₂–Yb₂O₃ glass systems can be obtained from the next formula:

$$HVL=\frac{Ln2}{\mathsf{\mu }}$$

(3)

Additionally, the Phy-X/PSD program which was used in this study to calculate some of the shielding parameters is an accurate and quick tool for radiation shielding calculations. In this program, the users must first define the material by inputting the composition with the density of the material. Then, the users need to select the investigated energy value/range and select the parameter that they wish to calculate (µ/ρ, HVL, etc.). Then, they can obtain the results as an MS Excel file.

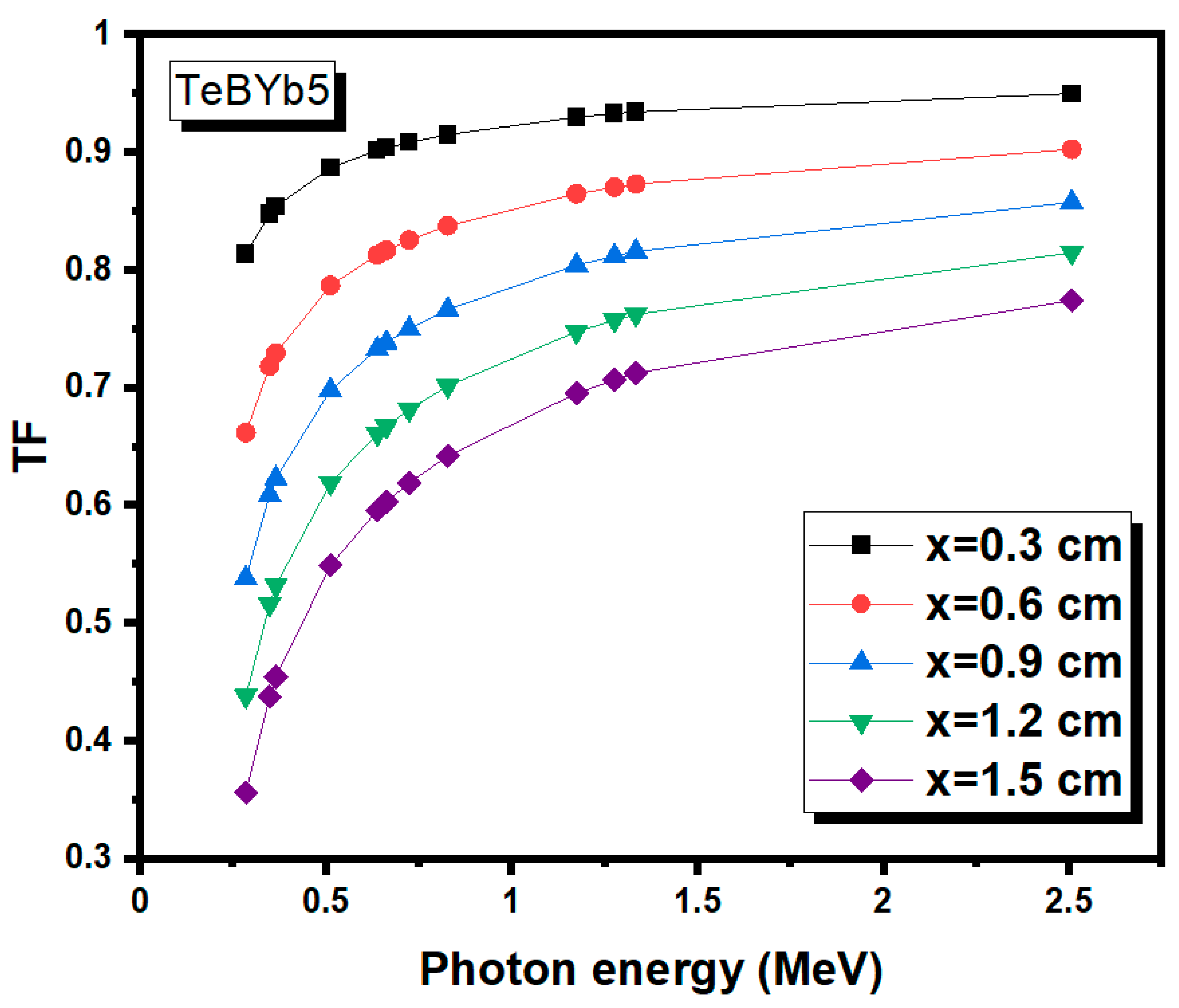
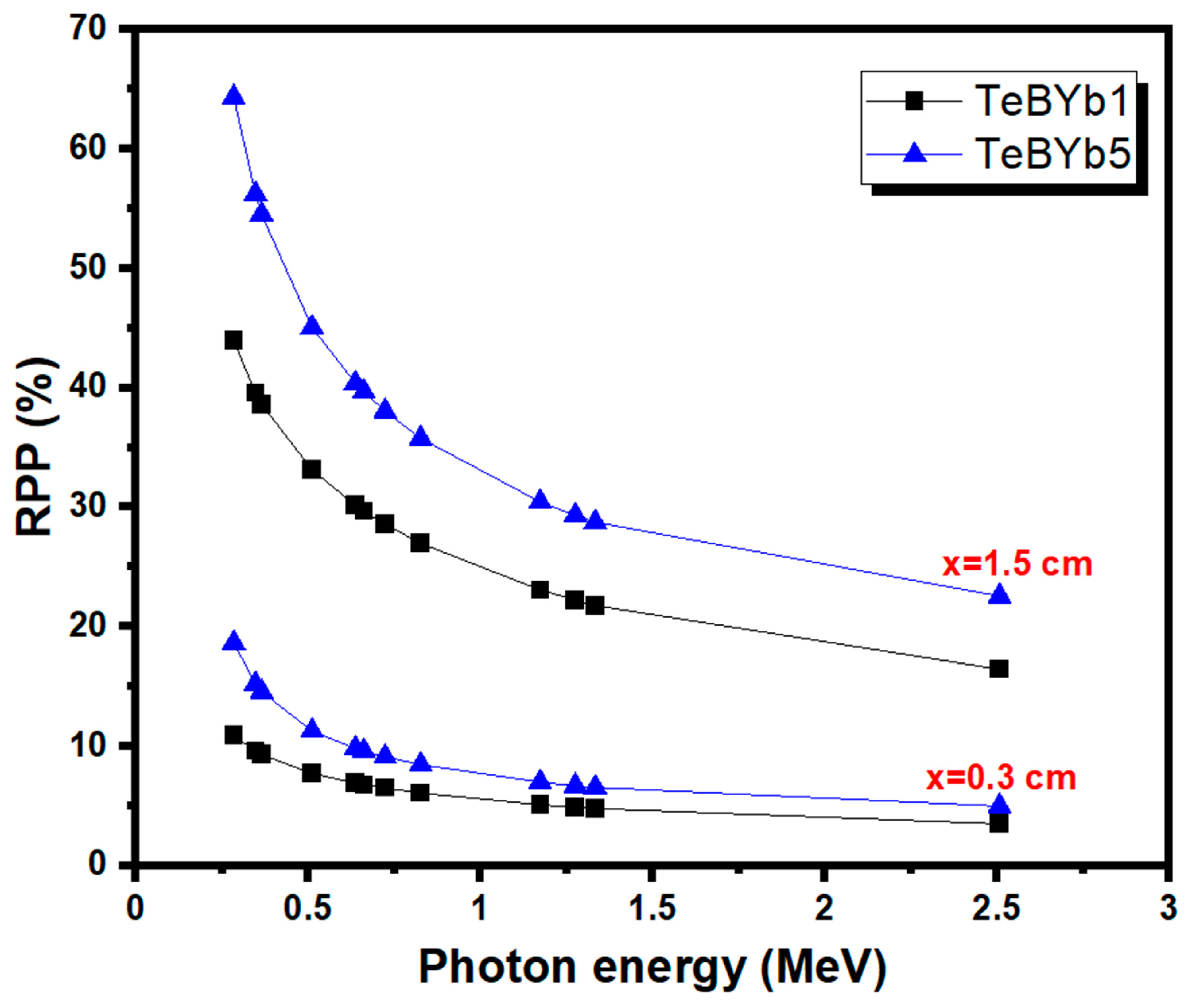
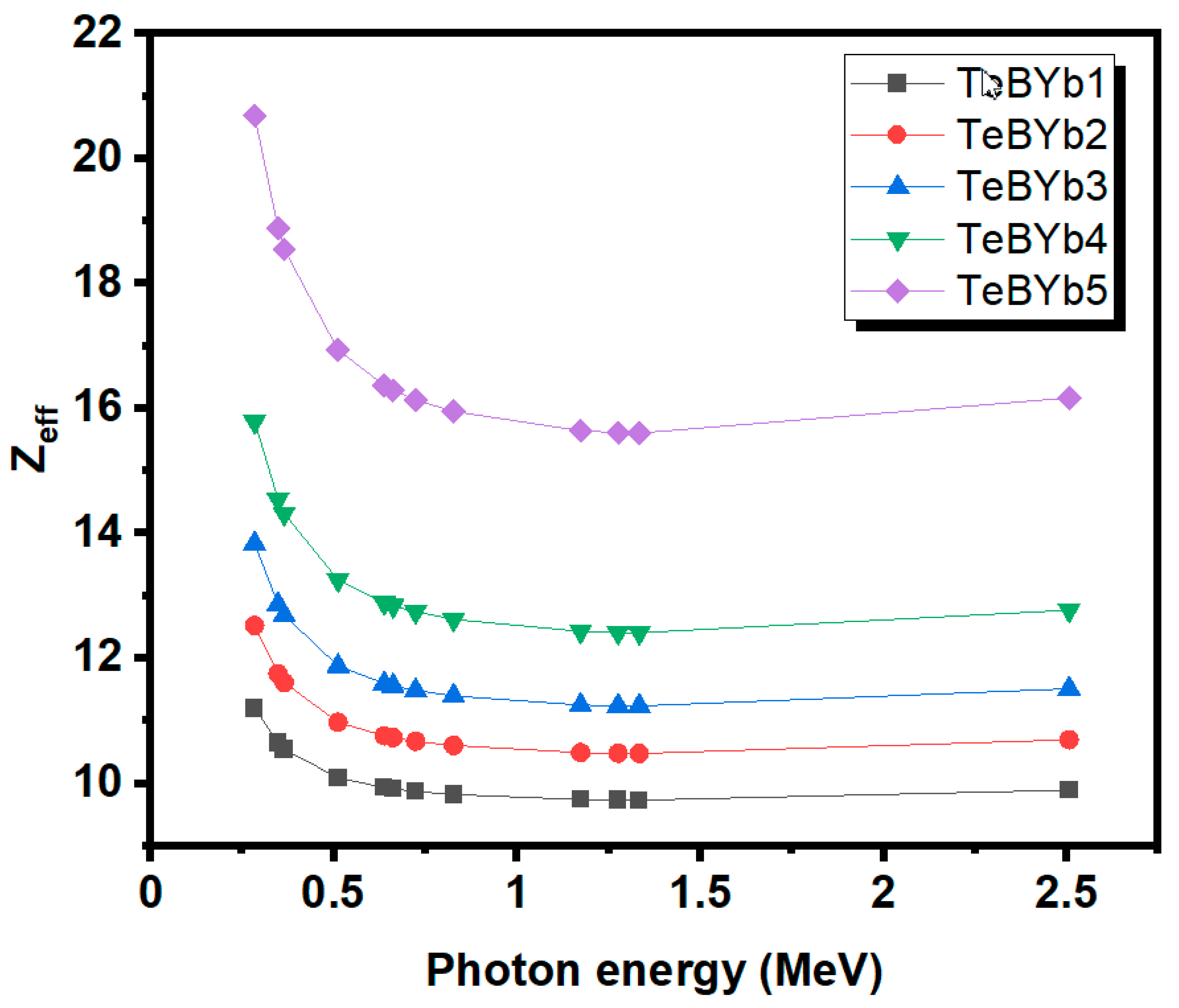
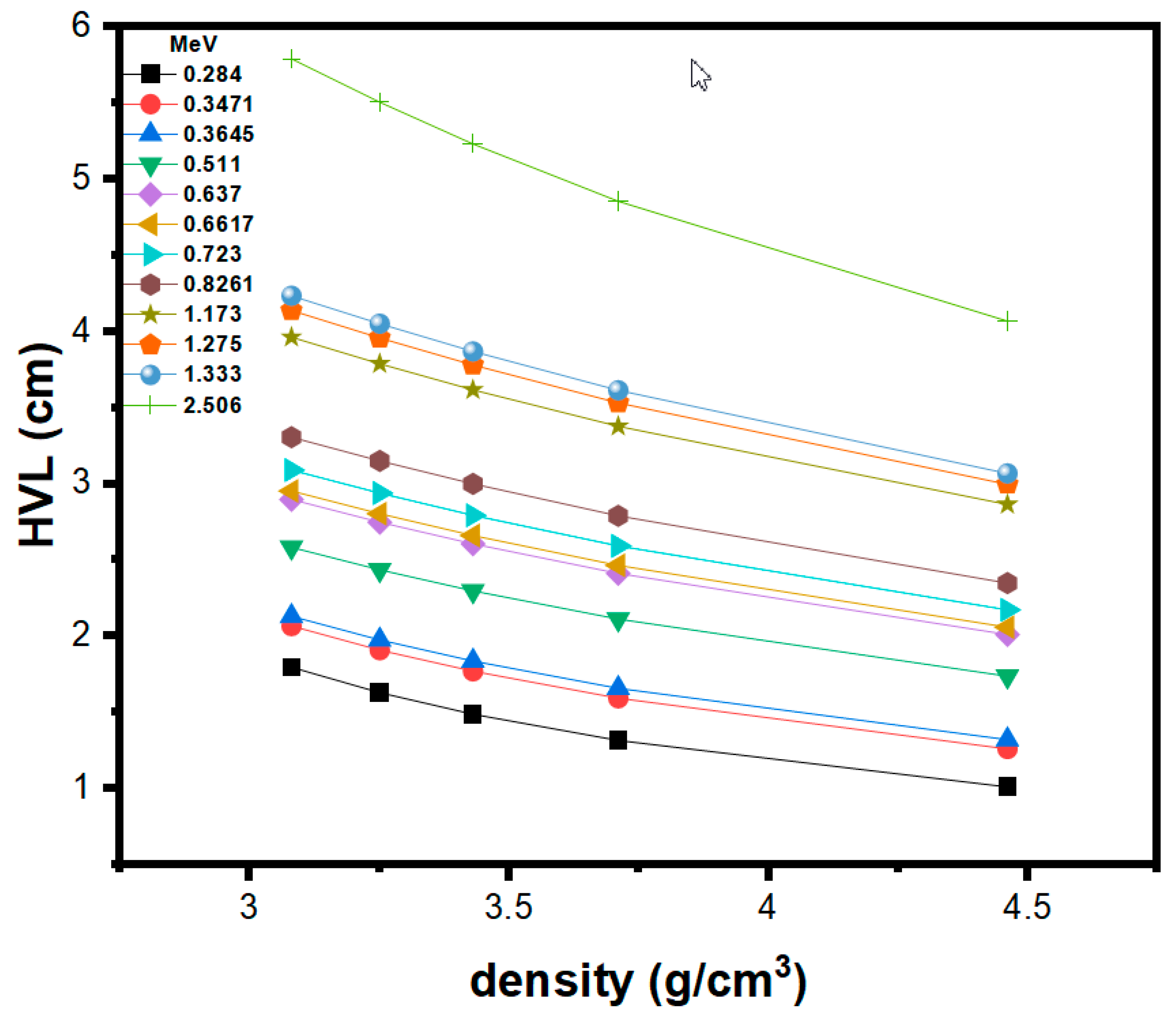
3. Results and Discussion

Figure 1 exhibits the µ/ρ for the five chosen TeBYbX samples. The following energy values were selected in the µ/ρ calculations: 0.284, 0.347, 0.356, 0.511, 0.637, 0.662, 0.723, 0.826, 1.173, 1.275, 1.333 and 2.506 MeV. These energies presented a variety of low, moderate and high energy ranges. The effect of the energy on the µ/ρ can first be investigated. Figure 1 shows that for all chosen TeBYbX samples, as energy increases, the µ/ρ reduces. However, the previous trend in the µ/ρ happens in two phases. In the first phase, the µ/ρ reduces sharply as energy increases between 0.284 to 0.637 MeV. In this case, the interactions of the photons with the TeBYbX atoms are mainly due to the photoelectric effect [33]. The µ/ρ for TeBYb1 reduces from 0.1255 to 0.0776 cm²/g when the energy changes from 0.248 to 0.637 MeV. In the second phase (for E > 0.637 MeV), we can see from Figure 1 that the rate at which the µ/ρ changes becomes less clear. This is because for higher energies, the Compton scattering starts to become increasingly more predominant. Additionally, we can observe from Figure 1 that the µ/ρ at high energies (for the last two energies) become almost constant. Next, the effect of the content of TeO₂ on the µ/ρ can be examined. At all the investigated energies, as the content of TeO₂ changes from 10 to 54 mol%, the µ/ρ increases with it. For example, at 0.347 MeV, the µ/ρ values are 0.109, 0.112, 0.114, 0.117 and 0.123 cm²/g for TeBYb1, TeBYb2, TeBYb3, TeBYb4 and TeBYb5 respectively. This is related to incorporating Te2, which has a higher mass attenuation coefficient than the B and Ca atoms. Accordingly, as the TeO₂ in the samples increases and the B₂O₃ and CaO decrease, the shielding ability of the TeBYbX samples is enhanced. Therefore, we can conclude that TeBYb5 with the highest amount of TeO2 is the more effective attenuator out of the chosen samples for the energy range of 0.284 and 2.506 MeV. The µ/ρ for the TeBYbX samples is compared with some traditional glasses used in practical shielding areas (see Figure 2). The compositions of these traditional glasses are given the references [34,35]. We selected only one energy for the comparison, namely 0.284 MeV, and we found the same trend at the other energies. It is to be noted that all the TeBYbX glasses have higher µ/ρ than that of Type A and B, glasses as well as lower µ/ρ than that of Osmania and rider glasses. Additionally, the TeBYb1 sample possesses almost the same µ/ρ as RS-253-G18. However, all the TeBYbX glasses have lower µ/ρ than the µ/ρ for RS-360 glass. It is important to mention that RS-360 contains a high content of PbO (45 w.t%) and this explains the high µ/ρ for this glass.

The interaction of gamma photons with constituent atoms of the selected TeBYbX glasses determines the linear attenuation coefficient (µ), and this quantity is dependent on the sample’s density as well as the radiation’s energy. The µ is an important factor of the attenuators, and it helps to estimate the applications in the radiation shielding field. Figure 3 exhibits the µ for the TeBYbX specimens. As can be seen, the µ is proportionally increased with increasing the TeO₂ content from 10 to 54 mol%. This is due to the fact that the µ is a parameter that is related directly to the density of the attenuator, and in our samples, the density increases from 3.08 to 4.46 g/cm³ when the TeO₂ changes from 10 to 54 mol%. For instance, the µ increased from 0.386 cm⁻¹ (for TeBYb1, ρ = 3.08 g/cm³) to 0.687 cm⁻¹ (for TeBYb5, ρ = 4.46 g/cm³) at 0.284 MeV. Furthermore, the µ increased from 0.336 cm⁻¹ (for TeBYb1) to 0.551 cm⁻¹ (for TeBYb5) at 0.347 MeV. These results show that there is a diminishing trend in the gamma radiation transmission corresponding with an increase in the density of the TeBYbX glasses (resulting from increased the TeO₂ content). According to the µ curves, we can conclude that the glass specimen with high percentage of TeO₂ can be developed in different shielding applications. Another important point that can be understood from Figure 3 is the dependence of the µ on the energy. It is clear that the energy affects the µ, and, accordingly, the shielding strength of the chosen TeBYbX glasses. The highest/lowest µ is found at 0.284/2.506 MeV. The highest µ values are 0.386, 0.426, 0.466, 0.527 and 0.687 cm⁻¹ for TeBYb1, TeBYb2, TeBYb3, TeBYb4 and TeBYb5 glasses respectively. In contrast, the smallest µ values are 0.120, 0.126, 0.132, 0.143 and 0.170 cm⁻¹ for the previous glasses, respectively.

Figure 4 graphs the transmission factor, or TF, of the TeBYb1 sample at five different thicknesses against energy. A smaller TF signifies a more effective shielding material. This sample was chosen as an example to investigate the effects of thickness and photon energy on the TF of the glass. Five thicknesses were chosen, 0.3, 0.6, 0.9, 1.2, and 1.5 cm, to test thinner and thicker samples. The energy varied from 0.284 MeV to 2.51 MeV to examine how low, mid, and high energies affect TF. The minimum TF can be observed at the minimum chosen energy, 0.284 MeV, where TF is equal to 0.891, 0.793, 0.707, 0.629, 0.560 for thicknesses of 0.3–1.5 cm, respectively. Additionally, as the thickness of the sample increases, the TF decreases. We can conclude that the greater the thickness of the shield, the more photons it will absorb. Therefore, if space is not a serious concern, a thicker material should be used to absorb the greatest number of photons possible. For any one thickness, as energy increases, TF increases. For instance, for a 1.5 cm sample of TeBYb1, the TF increases from 0.560 at 0.284 MeV, 0.714 at 0.723 MeV, and 0.836 at 2.506 MeV. The results also demonstrate that the glass is more successful in blocking the photons at lower energies and decreases in competence as energy increases.

The TF of TeBYb5 was plotted against energy at various thicknesses in Figure 5. The same five thicknesses and energy range were used as in the previous figure. Similar trends can be observed between this figure and the last. For example, TF decreases as the thickness of the sample increases. At 2.506 MeV, the TF is equal to 0.950 for a thickness of 0.3 cm, 0.858 for a thickness of 0.9 cm, and 0.774 for a thickness of 1.5 cm. In addition, for any one thickness, TF declines as energy increases. For 0.3 cm, the TF is equal to 0.814, 0.915, and 0.950 at energies of 0.284, 0.823, and 2.506 MeV, respectively. When comparing the two figures, for any one thickness at any one energy, TeBYb1 has a greater TF than TeBYb5. For a thickness of 0.3 cm, the TF of TeBYb1 at 0.284 MeV is 0.891, while it is 0.814 for TeBYb5 at this energy. For the same thickness and at an energy of 2.506 MeV, the TF of TeBYb1 is 0.965, while the TF of TeBYb5 is 0.950. From these results, it can be determined that TeBYb5 is a more effective shield than TeBYb1, since it has a lower TF at all energies and thicknesses. Accordingly, increasing the TeO₂ content in the glasses improves its attenuation properties.

Figure 6 illustrates the radiation protection efficiency, or RPE, of TeBY1 and TeBYb5 against energy at two thicknesses. RPE measures how effective a material is at shielding radiation and is calculated as a percentage, with a greater percent meaning a better shield. The same energy range was used as previous figures. These two glasses were chosen to evaluate the effect of the TeO₂ content in the glasses, or the density of the glasses, on RPE. The lowest and highest thicknesses were investigated to determine if thickness has an impact on RPE. At the lowest investigated energy, 0.284 MeV, for both thicknesses, TeBYb1 has a lesser RPE than TeBYb5. For instance, for a thickness of 0.3 cm at this energy, TeBYb1 has an RPE of 10.94%, while TeBYb5 has an RPE of 18.63%. At 1.5 cm, the RPE values are 43.96% and 64.33% for TeBYb1 and TeBYb5, respectively. The results demonstrate that TeBYb5 is the more effective attenuator since it has the greater RPE at both thicknesses. This trend occurs since more photons are absorbed when the thickness of the material increases. In addition, when observing a glass at a certain thickness, its RPE value decreases as energy increases. For the TeBYb5 at 1.5 cm, the RPE decreases from 64.33% at 0.284 MeV, to 35.77% at 0.826 MeV, and 22.55% at 2.506 MeV. This decrease signifies that the protection abilities of the samples decline with the increase in photon energy, which is consistent with the results for TF. Nevertheless, TeBYb5 proves to be the better shield even at higher energies.

We can also present the effective atomic number (Z_eff) as an important factor used in the radiation shielding field to understand the effectiveness of the TeBYbX glasses in blocking the incoming radiation. Manohara et al. [36] explained the methods for the calculations of this parameter for all materials for E > 1 keV. From the Z_eff we can give a conclusion about the performance of the materials against gamma radiation. The high Z_eff for a specific attenuator implies that it is more capable at shielding the incoming radiation. Figure 7 presents the variations in Z_eff with energy for the TeBYbX glasses. It is to be noted from Figure 7 that the Z_eff takes the maximum values at 0.284 MeV (11.20 for TeBYb1, 12.52 for TeBYb2, 13.84 for TeBYb3, 15.79 for TeBYb4 and 20.69 for TeBYb5). These values decrease rapidly between 0.284 to 0.723 MeV. The Z_eff varies between 9.87 and 16.14 at 0.723 MeV. The previous trend in the Z_eff can be demonstrated by the photoelectric effect which is important at these energies. A constant trend in the Z_eff can be seen between 0.826 and 1.333 MeV. For instance, the Z_eff for TeBYb1 at these two energies are 9.73 and 9.82. For TeBYb5, the Z_eff values are 15.61 and 15.95 (at 0.826 and 1.333 MeV respectively). Between these energies, Compton scattering becomes very important and it doesn’t depend on the atomic number of the medium, therefore we found that the Z_eff seems to be almost constant with the energy. Finally, at the last chosen energy (E = 2.506 MeV), the Z_eff shows a small increase. For TeBYb1, the Z_eff increases from 9.73 to 9.89, while it increases from 15.61 to 16.17 for TeBYb5. Moreover, we can understand from Figure 7 that the addition of TeO₂ causes an enhancement in the Z_eff values. This is because TeBYb5 shows the highest values of this quantity and in contrast TeBYb1 shows the lowest Z_eff, and from

Table 1. Samples’ codes, composition (mol%) for the TeBYb-X glasses.

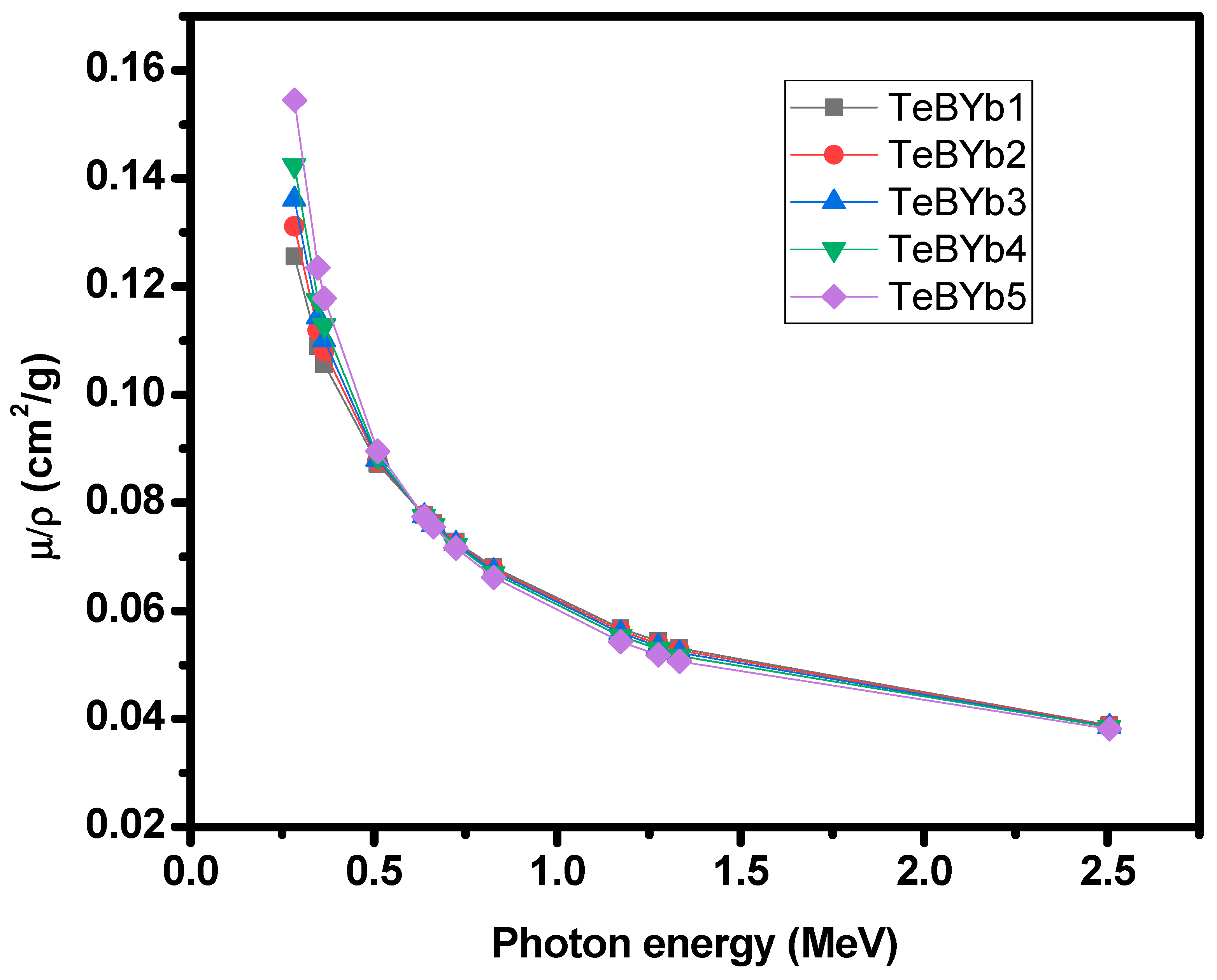
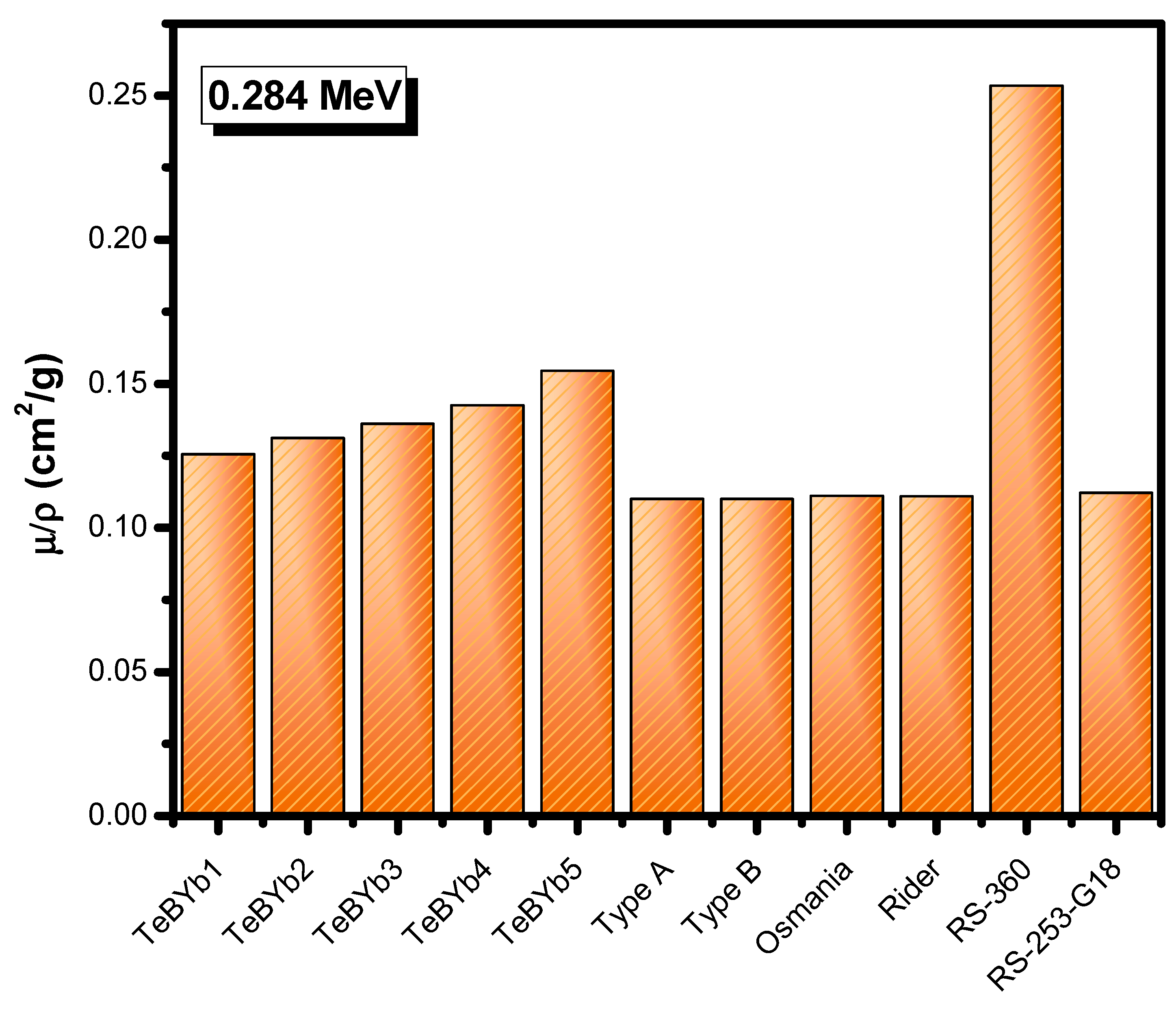
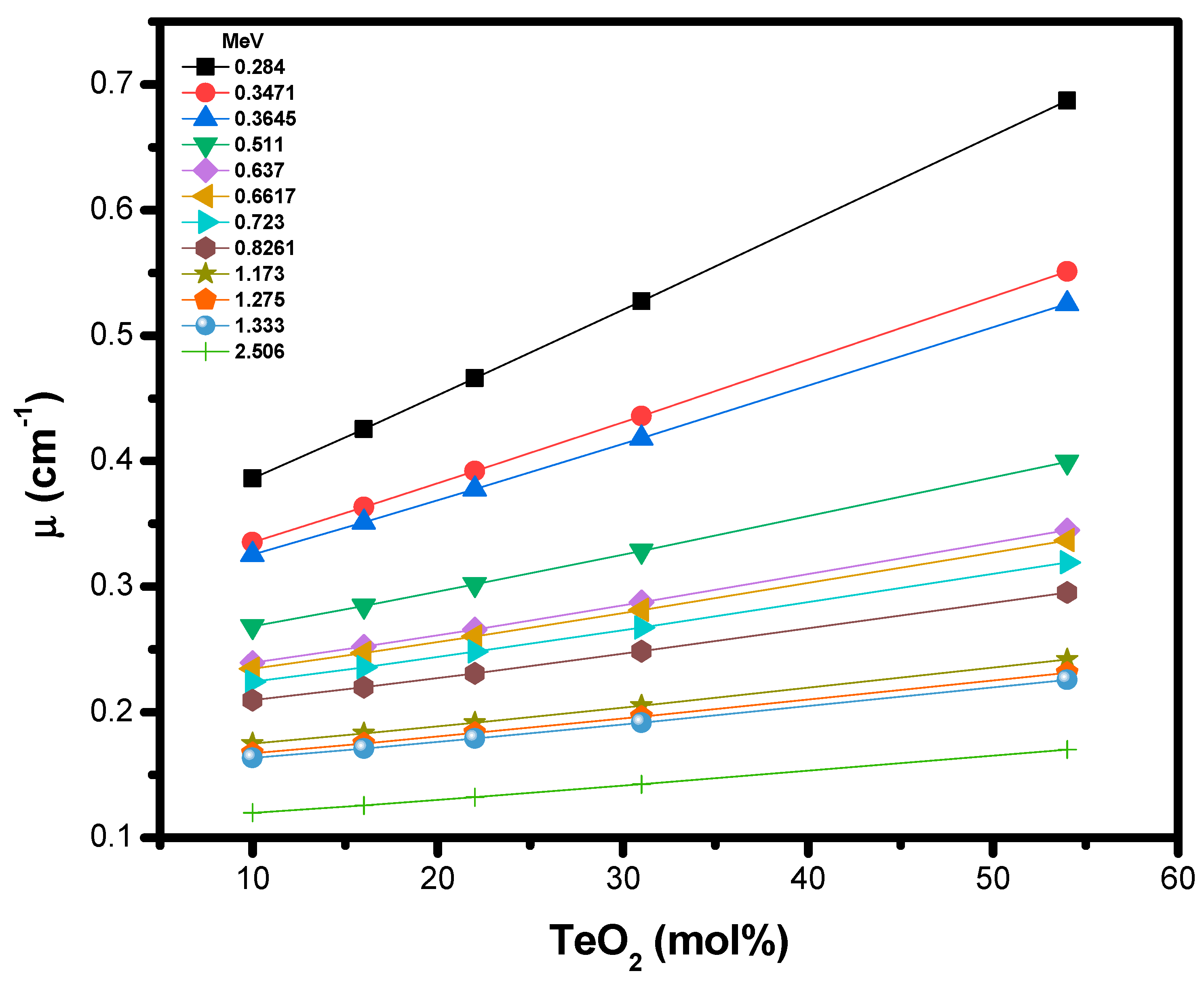
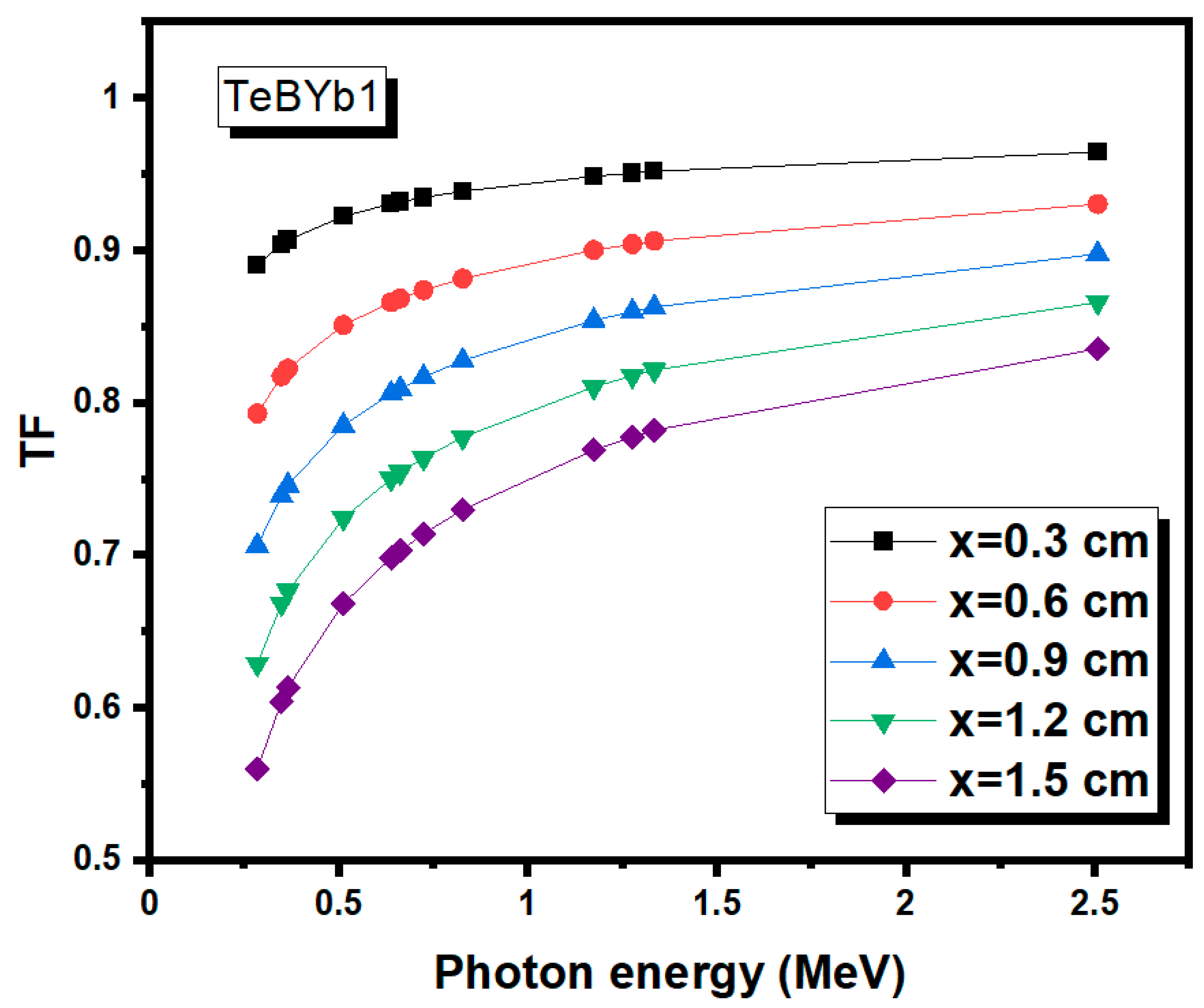
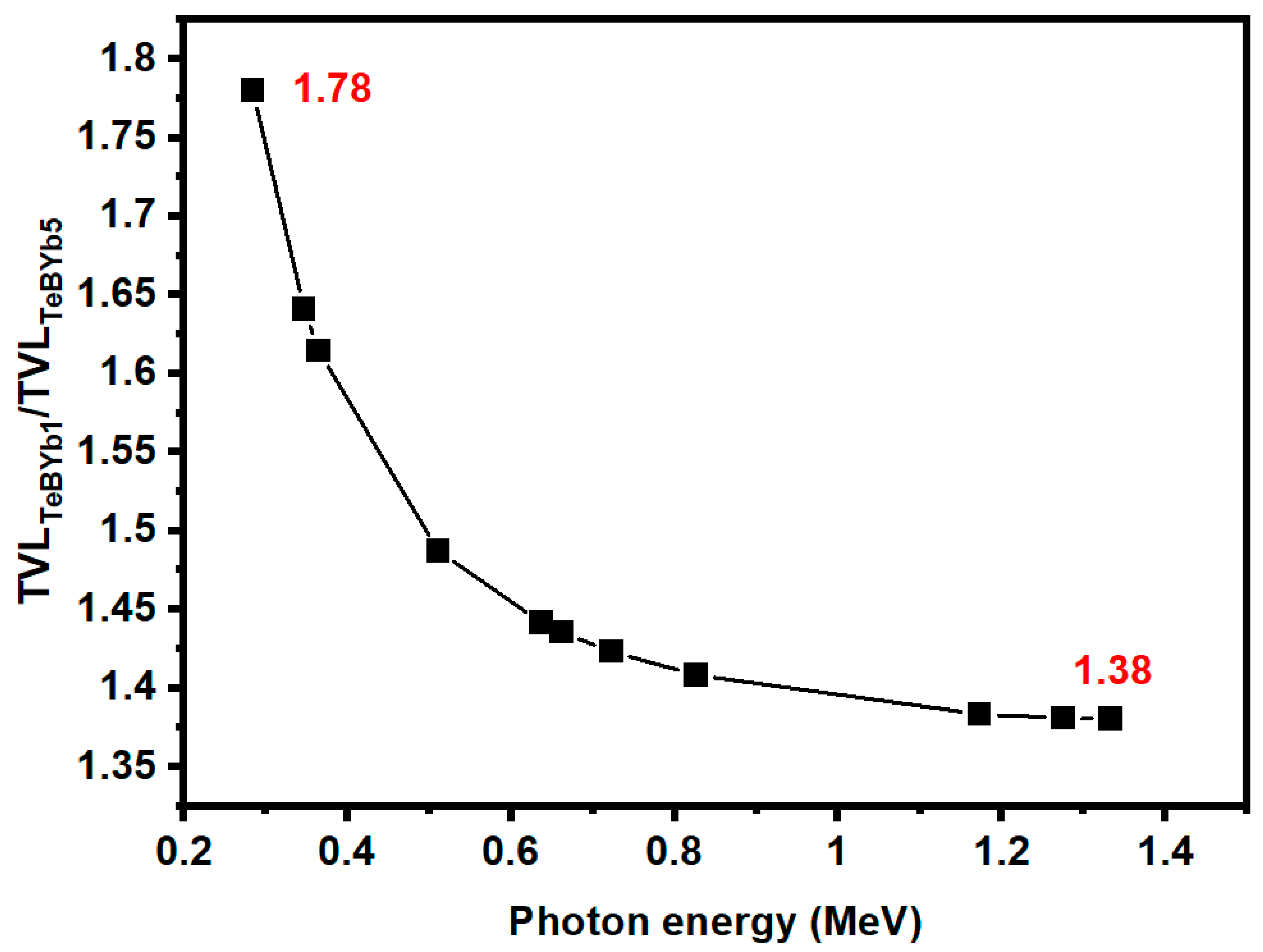
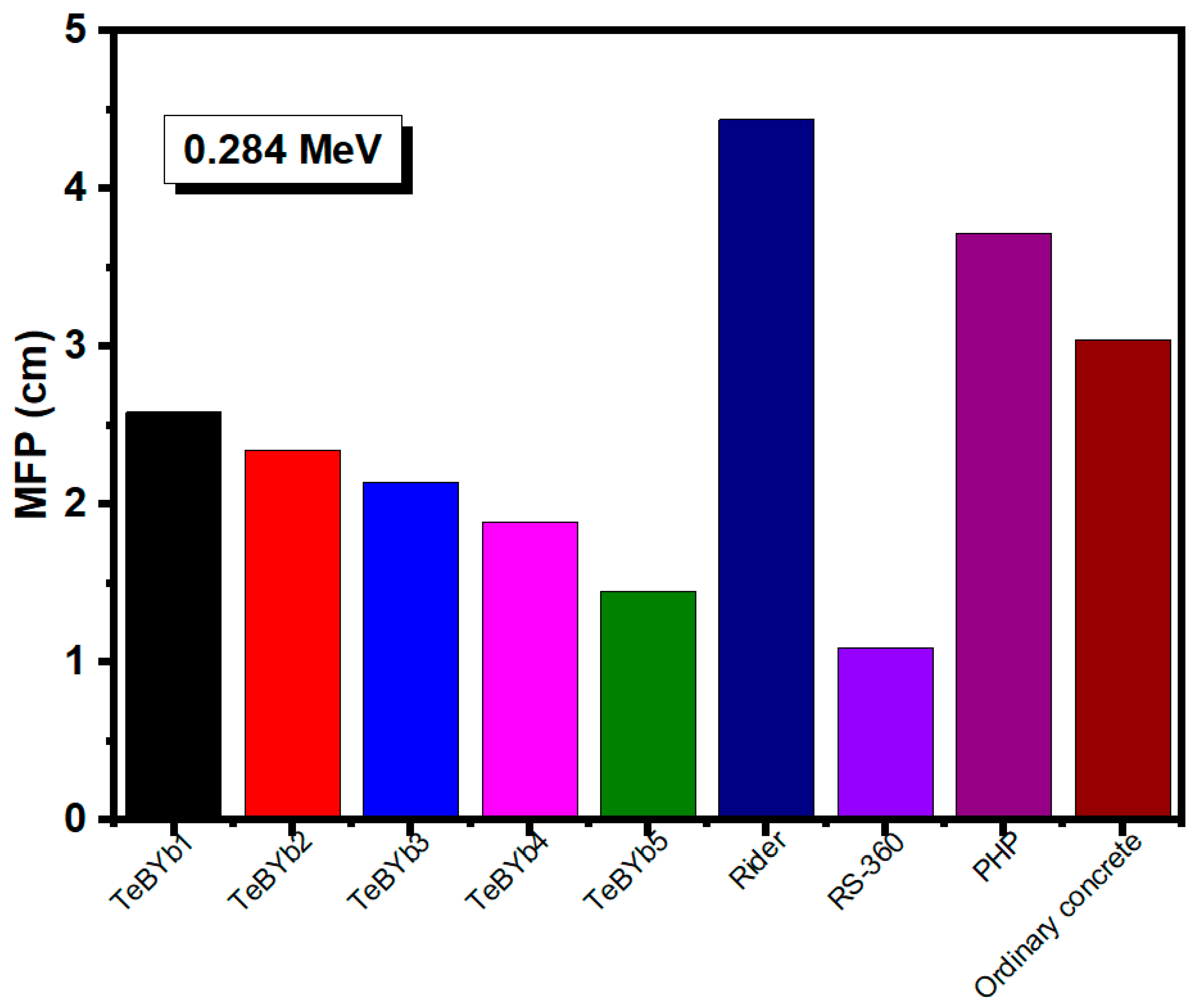
Sample Code	TeO2	B2O3	CaO	CaF2	Yb2O3	Density (g/cm3)
TeBYb1	10	54	25.5	10	0.5	3.08
TeBYb2	16	50.4	23.1	10	0.5	3.25
TeBYb3	22	46.8	20.7	10	0.5	3.43
TeBYb4	31	41.4	17.1	10	0.5	3.71
TeBYb5	54	27.6	7.9	10	0.5	4.46

, it can be seen that TeBYb1 and TeBYb5 have 10 and 54 mol% of TeO₂. The Z_eff results emphasis that the glass with the composition of 54TeO₂-27.6B₂O₃-7.9CaO-10CaF₂-0.5Yb₂O₃ is the best attenuator out of the chosen glasses.

Furthermore, the efficiency of the photon shielding is characterized in terms of the HVL. It describes the thickness at which the attenuator will reduce the radiation to half of its initial intensity. The HVL as a function of the density of the TeBYbX glasses is exhibited in Figure 8. From Figure 8, it is clear that the HVL of the chosen samples has a downward trend as the density of the glasses increases. This tendency in the HVL implies that among the TeBYbX glasses, TeBYb5, the sample with the highest content of TeO₂ as well as the greatest density, is the most efficient at shielding the photons, whereas TeBYb1, the sample with the lowest content of TeO₂ and lowest density, is the least efficient at shielding the photons. We can explain the previous relationship between the HVL and the density of the TeBYbX glasses according to the following: when the gamma photons pass through the low density glass, there is a space between the atoms, hence the probability of photon-glass atom interaction is relatively small, and thus it is much easier for the photons to pass through the glass, therefore we need to increase the thickness of the sample to attenuate the 50% of the initial photons, so the HVL for the low density materials is high. In contrast, the probability of the photons interacting with the high density glass is high, and thus the penetration of the photons through the glass decreased, and this reduced the HVL for the high density glass samples. Moreover, as seen in Figure 8, the HVL varied between 1.796 and 1.009 cm at 0.284 MeV and increased to 5.791 cm (for TeBYb1) and 4.068 cm (for TeBYb5) at 2.506 MeV. The previous results imply that, as the energy increases from 0.284 to 2.506 MeV, the attenuation by the TeBYbX glasses decreases. This can also be understood from the types of radiation-matter interaction; as we go from low to high energy, the probability of the photoelectric effect decreases and the probability of Compton scattering increases [37].

For the chosen calcium borotellurite glasses (TeBYbX), we determined the tenth value layer for the samples with lowest and highest TeO₂ contents, namely TeBYb1 and TeBYb5, then we calculated the ratio between the TVL for the TeBYb1 and TeBYb5 glasses (TVL_TeBYb1/TVL_TeBYb5). The results are presented in Figure 9. The aim of this figure is to understand the influence of the 10 and 54 mol% of TeO₂ on the thickness of the TeBYbX samples that can attenuate the gamma rays. By examining the data presented in Figure 9, one can easily understand that TeBYb1 has a higher TVL than TeBYb5, because the ratio is almost larger than 1. The TVL_TeBYb1/TVL_TeBYb5 decreases with the increasing energy; it starts with maximum value of 1.78 at 0.284 MeV, then reduces quickly with a further increase in energy. The TVL_TeBYb1/TVL_TeBYb5 at 0.347 and 0.511 MeV are 1.64 and 1.61. We can conclude from this figure that increasing the amount of TeO₂ from 10 to 54 mol% in the selected calcium borotellurite glasses (TeBYbX) leads to a decrease in the TVL by a factor of 1.48 (on average). This findings agrees with the obtained findings in the µ and Z_eff figures. The rapid reduction in the TVL in the low energy zone implies that the TeO₂ content has a remarkable influence on the attenuation competence of the TeBYbX glasses, and this is due to the domination of the photoelectric effect. However, as we see from the ratio figure, the amount of TeO₂ has a lower effect on the TVL at higher energies.

The mean free path, or MFP, was determined at 0.284 MeV and graphed in Figure 10. A smaller value is more desirable. An energy of 0.284 MeV was chosen as an example since all other energies obtained similar results. In addition to the five glass samples, the MFP of three commercial glasses and one concrete were plotted at the same energy for comparison, namely Rider, RS-360, PHP, and ordinary concrete. The results demonstrated that the five Yb³⁺-doped calcium borotellurite glasses had a lower MFP than Rider and PHP glass and ordinary concrete, with Rider having the greatest MFP at 4.44 cm, which indicates that the investigated glasses have greater shielding capabilities than the other three materials. However, RS-360 has the lowest MFP out of all the tested materials at 1.10 cm, which means it is a better shield than the Yb³⁺-doped calcium borotellurite glasses. When only comparing these glasses, TeBYb5 has the lowest MFP at 1.45 cm, while TeBYb1 has the greatest at 2.59 cm. The figure indicates that as the TeO₂ content in the glasses increases, and the density with it, the MFP decreases, improving the shielding abilities of the glasses. This trend is consistent with the other investigated parameters. From this graph, it can be concluded that TeBYb5 and RS-360 have the greatest potential to be used in radiation shielding applications.

4. Conclusions

The gamma ray shielding properties of five calcium borotellurite glasses were theoretically investigated using the Phy-X/PSD. All the glasses had different compositions and were numbered from TeBYb1 to TeBYb5 in order of their densities. µ/ρ was found to increase as the TeO₂ content in the glasses increased, as it was equal to 0.109, 0.112, 0.114, 0.117, and 0.123 cm²/g at 0.347 MeV for TeBYb1, TeBYb2, TeBYb3, TeBYb4, and TeBYb5, respectively. TeBYb5 also had the greatest µ, such as 0.687 cm⁻¹ at 2.506 MeV. The smallest TF values were observed at 0.284 MeV, since the incoming photons have a harder time penetrating through the glasses at low energies. TeBYb1 had a greater TF than TeBYb5 at all thicknesses and energies, demonstrating that TeBYb5 is more effective than TeBYb1 at shielding radiation. In terms of RPE, TeBYb5 had the greater percentages at all energies and thicknesses, such as 18.63% at 0.284 MeV and a thickness of 0.3 cm, compared to 10.94% for TeBYb1 in the same conditions. Z_eff was shown to have a positive correlation with the TeO₂ content in the glasses, and since TeBYb5 has the greatest amount of TeO₂, 54 mol%, it naturally had the greatest Z_eff. The HVL varied between 5.791 cm (for TeBYb1) and 4.068 cm (for TeBYb5) at 2.506 MeV. Since the ratio between the TVL values of TeBYb1 and TeBYb5 is always greater than one, TeBYb1 requires a greater thickness to shield radiation at all energies. The MFP of the samples were compared against other radiation shields and were found to be more effective than Rider, PHP, and ordinary concrete, but a worse attenuator than RS-360. The results from the parameters proved the potential of the glass samples in radiation applications, with TeBYb5 having the greatest potential as a radiation shield.