Complex Systems, Emergence, and Multiscale Analysis: A Tutorial and Brief Survey
Abstract
:1. Introduction
2. Basics of Complex Systems and Emergence
2.1. Complex Systems and Emergence: Working Definitions
2.2. Power Law and Heavy-Tailed Distributions
2.2.1. Pareto Principle or the 80/20 Rule
2.2.2. Simulation and Parameter Estimation
2.2.3. Reasons Why the Power Law Is Favored in Modeling
2.2.4. Mechanisms for Power Laws
2.3. Essentials of Chaos Theory
2.3.1. Phase Space and Transformation
2.3.2. Defining Properties of Chaotic Systems
2.3.3. A Taste of Analysis
2.3.4. Bifurcations, Routes to Chaos, and Universality
2.3.5. Chaotic Time Series Analysis
- A.
- Optimal embedding
- (1)
- False nearest-neighbor method: This is a geometrical method. Consider the situation in which an -dimensional delay reconstruction is embedded but an -dimensional reconstruction is not. Passing from to , self-intersection in the reconstructed trajectory is eliminated. This feature can be quantified by the sharp decrease in the number of nearest neighbors when m is increased from to . Therefore, the optimal value of m is . More precisely, for each reconstructed vector , its nearest neighbor is found (to ensure unambiguity, here the superscript is used to emphasize that this is an m-dimensional reconstruction). If m is not large enough, then may be a false neighbor of (something like both the north and south poles are mapped to the center of the equator, or multiple different objects have the same shadow). If embedding can be achieved by increasing m by 1, then the embedding vectors become and , and they will no longer be close neighbors. Instead, they will be far apart. The criterion for optimal embedding is thenwhere is a heuristic threshold value. Abarbanel [72] recommends .After m is determined, can be obtained by minimizing .While this method is intuitively appealing, it should be pointed out that it works less effectively in the noisy case. Partly, this is because nearest neighbors may not be well defined when data have noise.
- (2)
- Time-dependent exponent curves: This is a dynamical method developed by Gao and Zheng [73,74]. The basic idea is that false neighbors will fly apart rapidly if we follow them on the trajectory. Denote the reconstructed trajectory by . If and are false neighbors, then it is unlikely that points , where k is the evolution time, will remain close neighbors. That is, the distance between and will be much larger than that between and if the delay reconstruction is not an embedding. The metric recommended by Gao and Zheng isHere, for simplicity, the superscript in the reconstructed vectors is no longer indicated. The angle brackets denote the average of all possible pairs satisfying the conditionwhere and are more or less arbitrarily chosen small distances. Geometrically speaking, Equation (40) defines a shell, with being the diameter of the shell and the thickness of the shell. When , the shell becomes a ball; in particular, if the embedding dimension m is 2, then the ball is a circle. Note that the computation is carried out for a series of shells, , and may depend on the index i. With this approach, the effect of noise can be greatly suppressed.
- B.
- Estimation of the largest positive Lyapunov exponent
- C.
- Estimation of fractal dimension and Kolmogorov entropy
2.3.6. Chaos-Based Communications and Effect of Noise on Dynamical Systems
- an emitter generates a chaotic signal ,
- a message signal is superimposed onto ,
- the signal is sent to the receiver through the communication channel,
- a receiver is synchronized to the emitter so that ,
- signal is retrieved at the receiver by taking the difference between and .
2.4. Basics of Random Fractal Theory
2.4.1. Introduction to Fractal Theory
2.4.2. Overview of Random Fractal Theory
Basic Definitions and Equations
The Fractional Brownian Motion (fBm) Process
Structure Function Based Multifractal Analysis
Singular Measure Based Multifractal Analysis
The Random Cascade Model
- The weights at stage N are log-normally distributed. To see this, one can take logarithm on both sides of Equation (87), then the multiplication becomes summation, and one can use the central limit theorem.
- We can readily derive that
- We can also derive thatand
2.5. Going from Distinguishing Chaos from Noise to Fully Understanding the System Dynamics
3. Adaptive Detrending, Denoising, Multiscale Decomposition, and Fractal Analysis
3.1. Adaptive Detrending, Denoising, and Multiscale Decomposition
3.2. Adaptive Fractal Analysis (AFA)
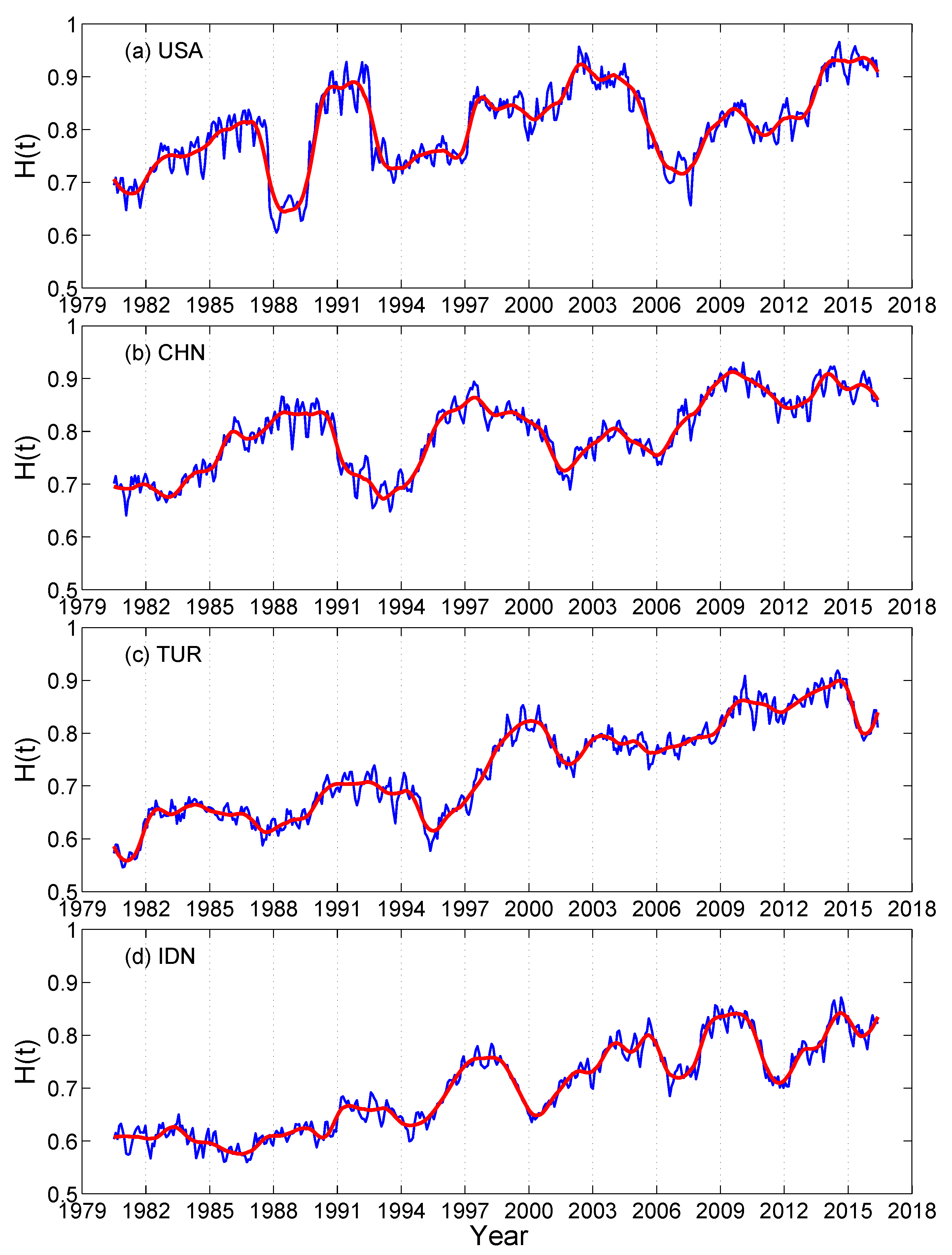
4. Multiscale Analysis with the Scale-Dependent Lyapunov Exponent (SDLE)
- For deterministic chaos,Amazingly, this property can even be observed in finite high-dimensional data, including the Lorenz’96 system, which has dimensions close to 30 [193], and in turbulent isotropic fluid with an integral scale Reynolds number reaching 6200 [203]. In such systems, estimation of dimensions is infeasible.
- As observational data are always contaminated by noise, it is important to have a scaling law for noisy chaos and noise-induced chaos [82,118]. The law readsThe law pertains to small scales, and controls the speed of information loss.
- For processes,
- For -stable Levy processes,
- For stochastic oscillations, both scaling laws and can be observed when different embedding parameters are used.
- When the dynamics of a system are very complicated, one or more of the above scaling laws may manifest themselves on different ranges.
5. Toward a Theory of Social Complexity
6. Concluding Remarks and Future Directions
- In Section 2.3.5, we find that citations to the original works on chaos synchronization decay exponentially. We also know that the general citation of scientific works decay as a power law. Can a model be developed that not only reconciles this marked difference but also finds a causal connection between them?
- We have observed in Figure 3 that the distribution of forest fires in USA and China is very different. It is known that casualties in fire fighting are much bigger in China than in the USA. Can the information in the distribution of forest fires be used to design better fire fighting strategies so that casualty and property loss can be both minimized?
- What is the fundamental difference between nation states with and without negative feedbacks?
- Which kinds of data are better in modeling the fundamental dynamics of cultural changes, the sparse data from poll/survey or massive real-time data streams acquired through sensors, mobile platforms, and the Internet?
- Will chaos theory in the strict mathematical sense be relevant to social emergent behaviors such as popular uprising? For this purpose, reading some fascinating descriptions from Victor Hugo’s Les Miserables (Penguin Classics, Translated and with an introduction by Norman Denny) could be stimulating:“Nothing is more remarkable than the first stir of a popular uprising. Everything, everywhere happens at once. It was foreseen but is unprepared for; it springs up from pavements, falls from the clouds, looks in one place like an ordered campaign and in another like a spontaneous outburst. A chance-comer may place himself at the head of a section of a crowd and lead it where he chooses. This first phase is filled with terror mingled with a sort of terrible gaiety …”
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Manyika, J.; Chui, M.; Brown, B.; Bughin, J.; Dobbs, R.; Roxburgh, C.; Byers, A.H. Big Data: The Next Frontier for Innovation, Competition, and Productivity. 2011. Available online: https://www.mckinsey.com/business-functions/mckinsey-digital/our-insights/big-data-the-next-frontier-for-innovation (accessed on 17 June 2021).
- Boyd, D.; Crawford, K. Six Provocations for Big Data; The Center for Open Science: Charlottesville, VA, USA, 2017. [Google Scholar] [CrossRef]
- Sakaki, T.; Okazaki, M.; Matsuo, Y. Earthquake shakes Twitter users: Real-time event detection by social sensors. In Proceedings of the 19th International Conference on World Wide Web, Raleigh, NC, USA, 26–30 April 2010. [Google Scholar]
- Ginsberg, J.; Mohebbi, M.H.; Patel, R.S.; Brammer, L.; Smolinski, M.S.; Brilliant, L. Detecting influenza epidemics using search engine query data. Nature 2009, 457, 1012–1014. [Google Scholar] [CrossRef] [PubMed]
- Butler, D. When Google got flu wrong. Nature 2013, 494, 155–156. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Available online: http://baike.baidu.com/link?url=zP_UWpBFHUI5PYen8cvlzKsXUhprdWaw97tSQ3L7ffOjjUYCTfnq_NMnxZG6IsKS5t0y85b2vMuIPa02atZFjStLmWoJMAFEvlfGlfvJ7zK#f-comment (accessed on 17 June 2021).
- Dash, S.; Shakyawar, S.K.; Sharma, M.; Kaushik, S. Big data in healthcare: Management, analysis and future prospects. J. Big Data 2019, 6, 1–25. [Google Scholar] [CrossRef] [Green Version]
- Raghupathi, W.; Raghupathi, V. Big data analytics in healthcare: Promise and potential. Health Inf. Sci. Syst. 2014, 2, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Reichman, O.J.; Jones, M.B.; Schildhauer, M.P. Challenges and opportunities of open data in ecology. Science 2011, 331, 703–705. [Google Scholar] [CrossRef] [Green Version]
- O’Donovan, P.; Leahy, K.; Bruton, K.; O’Sullivan, D.T.J. Big data in manufacturing: A systematic mapping study. J. Big Data 2015, 2, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Karakatsanis, L.P.; Pavlos, E.G.; Tsoulouhas, G.; Stamokostas, G.L.; Mosbruger, T.; Duke, J.L.; Pavlos, G.P.; Monos, D.S. Spatial constrains and information content of sub-genomic regions of the human genome. Iscience 2021, 24, 102048. [Google Scholar] [CrossRef]
- Rosenhead, J.; Franco, L.A.; Grint, K.; Friedland, B. Complexity theory and leadership practice: A review, a critique, and some recommendations. Leadersh. Q. 2019, 30, 101304. [Google Scholar] [CrossRef]
- Rusoja, E.; Haynie, D.; Sievers, J.; Mustafee, N.; Nelson, F.; Reynolds, M.; Sarriot, E.; Williams, B.; Swanson, R.C. Thinking about complexity in health: A systematic review of the key systems thinking and complexity ideas in health. J. Eval. Clin. Pract. 2018, 24, 600–606. [Google Scholar] [CrossRef]
- Lecun, Y. How does the brain learn so much so quickly? In Proceedings of the Cognitive Computational Neuroscience (CCN), New York, NY, USA, 6–8 September 2017. [Google Scholar]
- Shannon, C.E.; Weaver, W. The Mathematical Theory of Communication; The University of Illinois Press: Champaign, IL, USA, 1949. [Google Scholar]
- Kolmogorov, A.N. Entropy per unit time as a metric invariant of automorphism. Dokl. Russ. Acad. Sci. 1959, 124, 754–755. [Google Scholar]
- Sinai, Y.G. On the Notion of Entropy of a Dynamical System. Dokl. Russ. Acad. Sci. 1959, 124, 768–771. [Google Scholar]
- Kolmogorov, A. On Tables of Random Numbers. Sankhy Indian J. Stat. Ser. A 1963, 25, 369–375. [Google Scholar]
- Kolmogorov, A. On Tables of Random Numbers. Theor. Comput. Sci. 1998, 207, 387–395. [Google Scholar] [CrossRef] [Green Version]
- Chaitin, G.J. On the Simplicity and Speed of Programs for Computing Infinite Sets of Natural Numbers. J. ACM 1969, 16, 407–422. [Google Scholar] [CrossRef]
- Ziv, J.; Lempel, A. Compression of individual sequences via variable-rate coding. IEEE Trans. Inf. Theory 1978, 24, 530–536. [Google Scholar] [CrossRef] [Green Version]
- Kastens, K.A.; Manduca, C.A.; Cervato, C.; Frodeman, R.; Goodwin, C.; Liben, L.S.; Mogk, D.W.; Spangler, T.C.; Stillings, N.A.; Titus, S. How geoscientists think and learn. Eos Trans. Am. Geophys. Union 2009, 90, 265–272. [Google Scholar] [CrossRef]
- Goldstein, J. Emergence as a Construct: History and Issues. Emergence 1999, 1, 49–72. [Google Scholar] [CrossRef]
- Corning, P.A. The Re-Emergence of “Emergence”: A Venerable Concept in Search of a Theory. Complexity 2002, 7, 18–30. [Google Scholar] [CrossRef]
- Lin, C.C.; Shu, F.H. On the spiral structure of disk galaxies. Astrophys. J. 1964, 140, 646–655. [Google Scholar] [CrossRef]
- Vasavada, A.R.; Showman, A. Jovian atmospheric dynamics: An update after Galileo and Cassini. Rep. Prog. Phys. 2005, 68, 1935–1996. [Google Scholar] [CrossRef] [Green Version]
- Zhang, G.M.; Yu, L. Emergent phenomena in physics. Physics 2010, 39, 543. (In Chinese) [Google Scholar]
- Hemelrijk, C.K.; Hildenbrandt, H. Some Causes of the Variable Shape of Flocks of Birds. PLoS ONE 2011, 6, e22479. [Google Scholar] [CrossRef]
- Hildenbrandt, H.; Carere, C.; Hemelrijk, C.K. Self-organized aerial displays of thousands of starlings: A model. Behav. Ecol. 2010, 21, 1349–1359. [Google Scholar] [CrossRef]
- Shaw, E. Schooling fishes. Am. Sci. 1978, 66, 166–175. [Google Scholar] [CrossRef]
- Reynolds, C.W. Flocks, herds and schools: A distributed behavioral model. Comput. Graph. 1987, 21, 25–34. [Google Scholar] [CrossRef] [Green Version]
- D’Orsogna, M.R.; Chuang, Y.L.; Bertozzi, A.L.; Chayes, L.S. Self-Propelled Particles with Soft-Core Interactions: Patterns, Stability, and Collapse. Phys. Lett. 2006, 96, 10. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hemelrijk, C.K.; Hildenbrandt, H. Self-Organized Shape and Frontal Density of Fish Schools. Ethology 2007, 114, 3. [Google Scholar] [CrossRef] [Green Version]
- Kroy, K.; Sauermann, G.; Herrmann, H.J. Minimal model for sand dunes. Phys. Rev. Lett. 2002, 88, 054301. [Google Scholar] [CrossRef] [Green Version]
- Manson, S.M. Simplifying complexity: A review of complexity theory. Geoforum 2001, 32, 405–414. [Google Scholar] [CrossRef]
- Tang, L.; Lv, H.; Yang, F.; Yu, L. Complexity testing techniques for time series data: A comprehensive literature review. Chaos Solitons Fractals 2015, 81, 117–135. [Google Scholar] [CrossRef]
- Newman, M.E.J. Power laws, Pareto distributions and Zipf’s law. Contemp. Phys. 2005, 46, 323–351. [Google Scholar] [CrossRef] [Green Version]
- Gao, J.B.; Cao, Y.H.; Tung, W.W.; Hu, J. Multiscale Analysis of Complex Time Series—Integration of Chaos and Random Fractal Theory, and Beyond; Wiley: Hoboken, NJ, USA, August 2007. [Google Scholar]
- Pareto, V. La legge della domanda. In Ecrits d’Economie Politique Pure; Pareto, Ed.; Librairie Droz: Geneve, Switzerland, 1895; Chapter 11; pp. 295–304. [Google Scholar]
- Benford, F. The Law of Anomalous Numbers. Proc. Am. Philos. Soc. 1938, 78, 551–572. [Google Scholar]
- Pietronero, L.; Tosatti, E.; Tosatti, V.; Vespignani, A. Explaining the uneven distribution of numbers in nature: The laws of Benford and Zipf. Phys. A 2011, 293, 297–304. [Google Scholar] [CrossRef] [Green Version]
- Varian, H. Benford’s Law (Letters to the Editor). Am. Stat. 1972, 26, 65. [Google Scholar]
- From Benford to Erdös. Radio Lab. Episode 2009-10-09. 30 September 2009. Available online: https://www.wnycstudios.org/podcasts/radiolab/segments/91699-from-benford-to-erdos (accessed on 19 June 2021).
- Election forensics, The Economist (22 February 2007). Available online: https://www.economist.com/science-and-technology/2007/02/22/election-forensics (accessed on 19 June 2021).
- Deckert, J.; Myagkov, M.; Ordeshook, P.C. Benford’s Law and the Detection of Election Fraud. Political Anal. 2011, 19, 245–268. [Google Scholar] [CrossRef]
- Mebane, W.R. Comment on Benford’s Law and the Detection of Election Fraud. Political Anal. 2011, 19, 269–272. [Google Scholar] [CrossRef]
- Goodman, W. The promises and pitfalls of Benford’s law. Significance R. Stat. Soc. 2016, 13, 38–41. [Google Scholar] [CrossRef]
- Sehity, T.; Hoelzl, E.; Kirchler, E. Price developments after a nominal shock: Benford’s Law and psychological pricing after the euro introduction. Int. J. Res. Mark. 2005, 22, 471–480. [Google Scholar] [CrossRef]
- Durant, W.; Durant, A. The Story of Civilization, The Age of Louis XIV; Simon & Schuster: New York, NY, USA, 1963; p. 720. [Google Scholar]
- Durant, W.; Durant, A. The Story of Civilization, Rousseau and Revolution; Simon & Schuster: New York, NY, USA, 1967; p. 643. [Google Scholar]
- Gao, J.B.; Hu, J.; Mao, X.; Zhou, M.; Gurbaxani, B.; Lin, J.W.-B. Entropies of negative incomes, Pareto-distributed loss, and financial crises. PLoS ONE 2011, 6, e25053. [Google Scholar] [CrossRef]
- Fan, F.L.; Gao, J.B.; Liang, S.H. Crisis-like behavior in China’s stock market and its interpretation. PLoS ONE 2015, 10, e0117209. [Google Scholar] [CrossRef] [Green Version]
- Bowers, M.C.; Tung, W.W.; Gao, J.B. On the distributions of seasonal river flows: Lognormal or powerlaw? Water Resour. Res. 2012, 48, W05536. [Google Scholar] [CrossRef]
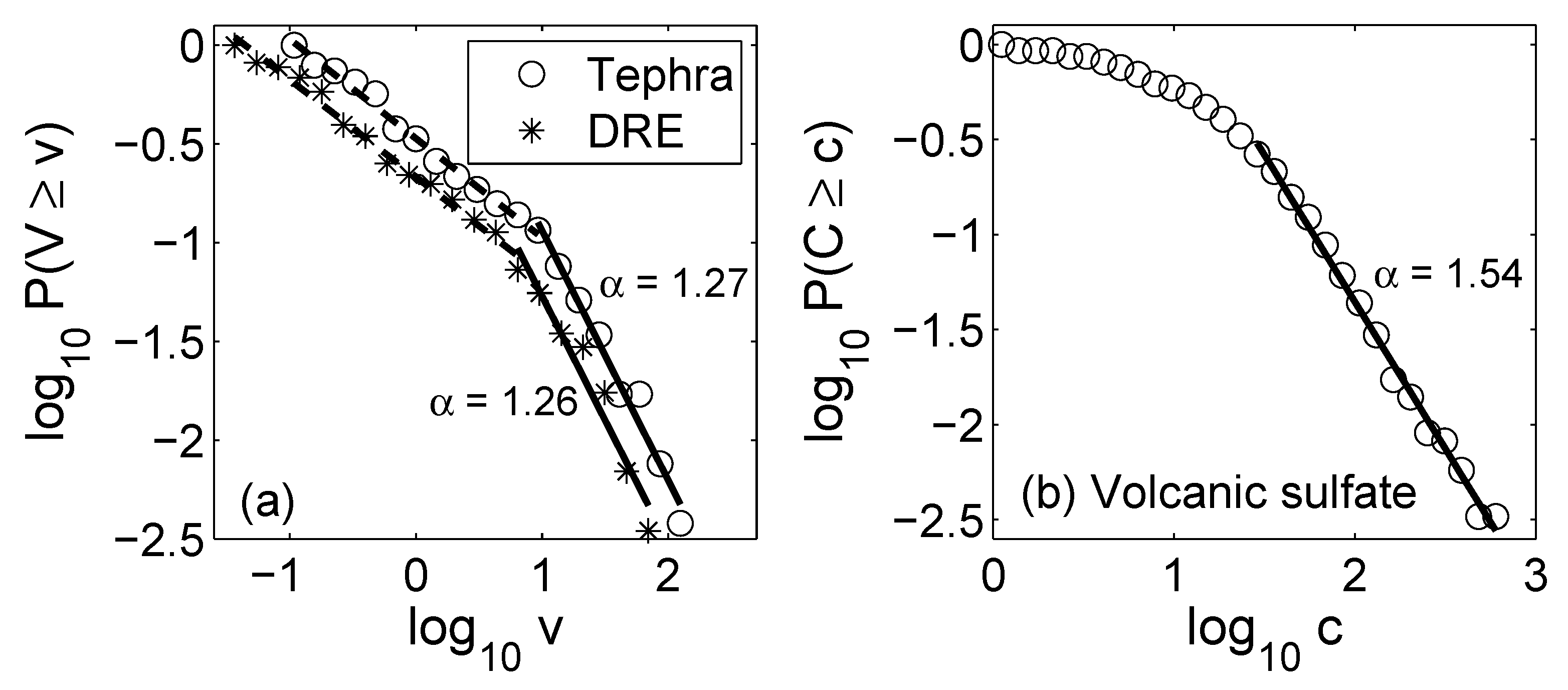
- Deligne, N.; Coles, S.; Sparks, R. Recurrence rates of large explosive volcanic eruptions. J. Geophys. Res. 2010, 115, B06203. [Google Scholar] [CrossRef] [Green Version]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics: Approaching a Complex World; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Pavlos, G.P.; Karakatsanis, L.P.; Xenakis, M.N.; Pavlos, E.G.; Iliopoulos, A.C.; Sarafopoulos, D.V. Universality of non-extensive Tsallis statistics and time series analysis: Theory and applications. Phys. A Stat. Mech. Appl. 2014, 395, 58–95. [Google Scholar] [CrossRef]
- Barabasi, A.L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gao, J.B.; Han, Q.; Lu, X.L.; Yang, L.; Hu, J. Self organized hotspots and social tomography. EAI Endorsed Trans. Complex Syst. 2013, 13, e1. [Google Scholar] [CrossRef]
- Jones, M. Phase space: Geography, relational thinking, and beyond. Prog. Hum. Geogr. 2009, 33, 487–506. [Google Scholar] [CrossRef]
- Henon, M. A two-dimensional mapping with a strange attractor. Commun. Math. Phys. 1976, 50, 69–77. [Google Scholar] [CrossRef]
- Shields, P. The Theory of Bernoulli Shifts; Univ. Chicago Press: Chicago, IL, USA, 1973. [Google Scholar]
- Atmanspacher, H.; Scheingraber, H. A fundamental link between system theory and statistical mechanics. Found. Phys. 1987, 17, 939–963. [Google Scholar] [CrossRef]
- Grassberger, P.; Procaccia, I. Estimation of the Kolmogorov entropy from a chaotic signal. Phys. Rev. A 1983, 28, 2591–2593. [Google Scholar] [CrossRef] [Green Version]
- Feigenbaum, M.J. Universal behavior in nonlinear systems. Phys. D 1983, 7, 16–39. [Google Scholar] [CrossRef]
- Ruelle, D.; Takens, F. On the nature of turbulence. Commun. Math. Phys. 1971, 20, 167. [Google Scholar] [CrossRef]
- Pomeau, Y.; Manneville, P. Intermittent transition to turbulence in dissipative dynamical systems. Commun. Math. Phys. 1980, 74, 189–197. [Google Scholar] [CrossRef]
- Gao, J.B.; Rao, N.S.V.; Hu, J.; Jing, A. Quasi-periodic route to chaos in the dynamics of Internet transport protocols. Phys. Rev. Lett. 2005, 94, 198702. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Packard, N.H.; Crutchfield, J.P.; Farmer, J.D.; Shaw, R.S. Geometry from a time series. Phys. Rev. Lett. 1980, 45, 712–716. [Google Scholar] [CrossRef]
- Takens, F. Detecting strange attractors in turbulence. In Dynamical Systems and Turbulence, Lecture Notes in Mathematics; Rand, D.A., Young, L.S., Eds.; Springer: Berlin/Heidelberg, Germany, 1981; Volume 898, p. 366. [Google Scholar]
- Sauer, T.; Yorke, J.A.; Casdagli, M. Embedology. J. Stat. Phys. 1991, 65, 579–616. [Google Scholar] [CrossRef]
- Abarbanel, H.D.I. Analysis of Observed Chaotic Data; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Gao, J.B.; Zheng, Z.M. Local exponential divergence plot and optimal embedding of a chaotic time series. Phys. Lett. A 1993, 181, 153–158. [Google Scholar] [CrossRef] [Green Version]
- Gao, J.B.; Zheng, Z.M. Direct dynamical test for deterministic chaos and optimal embedding of a chaotic time series. Phys. Rev. E 1994, 49, 3807–3814. [Google Scholar] [CrossRef] [Green Version]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D 1985, 16, 285–317. [Google Scholar] [CrossRef] [Green Version]
- Gao, J.B.; Hu, J.; Tung, W.W.; Zheng, Y. Multiscale analysis of economic time series by scale-dependent Lyapunov exponent. Quant. Financ. 2013, 13, 265–274. [Google Scholar] [CrossRef]
- Rosenstein, M.T.; Collins, J.J.; De Luca, C.J. Reconstruction expansion as a geometry-based framework for choosing proper delay times. Phys. D 1994, 73, 82–98. [Google Scholar] [CrossRef]
- Kantz, H. A robust method to estimate the maximal Lyapunov exponent of a time series. Phys. Lett. A 1994, 185, 77–87. [Google Scholar] [CrossRef]
- Gao, J.B.; Zheng, Z.M. Direct dynamical test for deterministic chaos. Europhys. Lett. 1994, 25, 485–490. [Google Scholar] [CrossRef] [Green Version]
- Gao, J.B.; Tung, W.W. Pathological tremors as diffusional processes. Biol. Cybern. 2002, 86, 263–270. [Google Scholar] [CrossRef]
- Gao, J.B. Recognizing randomness in a time series. Phys. D 1997, 106, 49–56. [Google Scholar] [CrossRef]
- Gao, J.B.; Chen, C.C.; Hwang, S.K.; Liu, J.M. Noise-induced chaos. Int. J. Mod. Phys. B 1999, 13, 3283–3305. [Google Scholar] [CrossRef]
- Hu, S.Q.; Raman, A. Chaos in Atomic Force Microscopy. Phys. Rev. Lett. 2006, 96, 036107. [Google Scholar] [CrossRef] [Green Version]
- Grassberger, P.; Procaccia, I. Characterization of strange attractors. Phys. Rev. Lett. 1983, 50, 346–349. [Google Scholar] [CrossRef]
- Theiler, J. Spurious dimension from correlation algorithms applied to limited time-series data. Phys. Rev. A 1986, 34, 2427–2432. [Google Scholar] [CrossRef]
- Gao, J.B.; Hu, J.; Liu, F.Y.; Cao, Y.H. Multiscale entropy analysis of biological signals: A fundamental bi-scaling law. Front. Comput. Neurosci. 2015, 9, 64. [Google Scholar] [CrossRef] [Green Version]
- Theiler, J.; Eubank, S.; Longtin, A.; Galdrikian, B.; Farmer, J.D. Testing for nonlinearity in time series: The method of surrogate data. Phys. D Nonlinear Phenom. 1992, 58, 77–94. [Google Scholar] [CrossRef] [Green Version]
- Lancaster, G.; Iatsenko, D.; Pidde, A.; Ticcinelli, V.; Stefanovska, A. Surrogate data for hypothesis testing of physical systems. Phys. Rep. 2018, 748, 1–60. [Google Scholar] [CrossRef]
- Cuomo, K.M.; Oppenheim, A.V. Circuit implementation of synchronized chaos with applications to communications. Phys. Rev. Lett. 1993, 71, 65–68. [Google Scholar] [CrossRef] [PubMed]
- Uchida, A.; Amano, K.; Inoue, M.; Hirano, K.; Naito, S.; Someya, H.; Oowada, I.; Kurashige, T.; Shiki, M.; Yoshimori, S.; et al. Fast physical random bit generation with chaotic semiconductor lasers. Nat. Photon. 2008, 2, 728. [Google Scholar] [CrossRef]
- Sciamanna, M.; Shore, K. Physics and applications of laser diode chaos. Nat. Photon. 2015, 9, 151. [Google Scholar] [CrossRef] [Green Version]
- Soriano, M.C.; Garcia-Ojalvo, J.; Mirasso, C.R.; Fischer, I. Complex photonics: Dynamics and applications of delay-coupled semiconductors lasers. Rev. Modern Phys. 2013, 85, 421. [Google Scholar] [CrossRef] [Green Version]
- Harayama, T.; Sunada, S.; Yoshimura, K.; Muramatsu, J.; Arai, K.-i.; Uchida, A.; Davis, P. Theory of fast nondeterministic physical random-bit generation with chaotic lasers. Phys. Rev. E 2012, 85, 046215. [Google Scholar] [CrossRef]
- Mikami, T.; Kanno, K.; Aoyama, K.; Uchida, A.; Ikeguchi, T.; Harayama, T.; Sunada, S.; Arai, K.-i.; Yoshimura, K.; Davis, P. Estimation of entropy rate in a fast physical random-bit generator using a chaotic semiconductor laser with intrinsic noise. Phys. Rev. E 2012, 85, 016211. [Google Scholar] [CrossRef]
- Sunada, S.; Harayama, T.; Davis, P.; Tsuzuki, K.; Arai, K.; Yoshimura, K.; Uchida, A. Noise amplification by chaotic dynamics in a delayed feedback laser system and its application to nondeterministic random bit generation. Chaos 2012, 22, 047513. [Google Scholar] [CrossRef]
- Durt, T.; Belmonte, C.; Lamoureux, L.P.; Panajotov, K.; Van den Berghe, F.; Thienpont, H. Fast quantum-optical random-number generators. Phys. Rev. A 2013, 87, 022339. [Google Scholar] [CrossRef] [Green Version]
- Yoshimura, K.; Muramatsu, J.; Davis, P.; Harayama, T.; Okumura, H.; Morikatsu, S.; Aida, H.; Uchida, A. Secure Key Distribution Using Correlated Randomness in Lasers Driven by Common Random Light. Phys. Rev. Lett. 2012, 108, 070602. [Google Scholar] [CrossRef] [PubMed]
- Kanno, K.; Uchida, A. Consistency and complexity in coupled semiconductor lasers with time-delayed optical feedback. Phys. Rev. E 2012, 86, 066202. [Google Scholar] [CrossRef] [PubMed]
- Li, X.-Z.; Zhuang, J.-P.; Li, S.-S.; Gao, J.B.; Chan, S.C. Randomness evaluation for an optically injected chaotic semiconductor laser by attractor reconstruction. Phys. Rev. E 2016, 94, 042214. [Google Scholar] [CrossRef] [Green Version]
- Pecora, L.M.; Carroll, T.L. Synchronization in chaotic systems. Phys. Rev. Lett. 1990, 64, 821–824. [Google Scholar] [CrossRef]
- Fujisaka, H.; Yamada, T. Stability theory of synchronized motion in coupled-oscillator systems. Prog. Theor. Phys. 1983, 69, 32. [Google Scholar] [CrossRef]
- Carroll, T.L.; Pecora, L.M. Synchronizing chaotic circuits. IEEE Trans. Circ. Syst. 1991, 38, 453–456. [Google Scholar] [CrossRef] [Green Version]
- Afraimovich, V.S.; Verichev, N.N.; Rabinovich, M.I. Stochastic synchronization of oscillations in dissipative systems. Radiophys. Quantum Electron. 1986, 29, 795. [Google Scholar] [CrossRef]
- Yamada, T.; Fujisaka, H. Stability theory of synchronized motion in coupled-oscillator systems. II. Prog. Theor. Phys. 1983, 70, 1240. [Google Scholar] [CrossRef] [Green Version]
- Afraimovich, V.S.; Verichev, N.N.; Rabinovich, M.I. Stochastic synchronization of oscillations in dissipative systems. Izv. Vyssh. Uchebn. Zaved. Radiofiz. 1986, 29, 1050. [Google Scholar]
- Yamada, T.; Fujisaka, H. Stability theory of synchronized motion in coupled-oscillator systems. III. Prog. Theor. Phys. 1984, 72, 885. [Google Scholar] [CrossRef] [Green Version]
- Fujisaka, H.; Yamada, T. Stability theory of synchronized motion in coupled-oscillator systems. IV. Prog. Theor. Phys. 1985, 74, 918. [Google Scholar] [CrossRef] [Green Version]
- Pikovskii, A.S. Synchronization and stochastization of array of selfexcited oscillators by external noise. Radiophys. Quantum Electron. 1984, 27, 390. [Google Scholar] [CrossRef]
- Volkovskii, A.R.; Rulkov, N.F. Experimental study of bifurcations at the threshold for stochastic locking. Sov. Tech. Phys. Lett. 1989, 15, 249. [Google Scholar]
- Aranson, I.S.; Rulkov, N.F. Nontrivial structure of synchronization zones in multidimensional systems. Phys. Lett. A 1989, 139, 375. [Google Scholar] [CrossRef]
- Pikovskii, A. On the interaction of strange attractors. Z. Phys. B 1984, 55, 149. [Google Scholar] [CrossRef]
- Locquet, A. Chaos-Based secure optical communications using semiconductor lasers. In Handbook of Information and Communication Security; Stavroulakis, P., Stamp, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 451–478. [Google Scholar]
- Argyris, A.; Syvridis, D.; Larger, L.; Annovazzi- Lodi, V.; Colet, P.; Fischer, I.; Garcia-Ojalvo, J.; Mirasso, C.R.; Pesquera, L.; Shore, K.A. Chaos-based communications at high bit rates using commercial fibre-optic links. Nature 2005, 438, 343–346. [Google Scholar] [CrossRef]
- Crutchfield, J.P.; Huberman, B.A. Fluctuationa and the onset of chaos. Phys. Lett. 1980, 74, 407. [Google Scholar] [CrossRef]
- Crutchfield, J.P.; Farmer, J.D.; Huberman, B.A. Fluctuations and simple chaotic dynamics. Phys. Rep. 1982, 92, 45–82. [Google Scholar] [CrossRef] [Green Version]
- Kautz, R.L. Chaos and thermal noise in the RF-biased Josephson junction. J. Appl. Phys. 1985, 58, 424. [Google Scholar] [CrossRef]
- Hwang, K.; Gao, J.B.; Liu, J.M. Noise-induced chaos in an optically injected semiconductor laser. Phys. Rev. E 2000, 61, 5162–5170. [Google Scholar] [CrossRef] [Green Version]
- Gao, J.B.; Hwang, S.K.; Liu, J.M. When can noise induce chaos? Phys. Rev. Lett. 1999, 82, 1132. [Google Scholar] [CrossRef] [Green Version]
- Alexandrov, D.V.; Bashkirtseva, I.A.; Ryashko, L.B. Noise-induced chaos in non-linear dynamics of El Ninos. Phys. Lett. A 2018, 382, 2922–2926. [Google Scholar] [CrossRef]
- Lei, Y.M.; Hua, M.J.; Du, L. Onset of colored-noise-induced chaos in the generalized Duffing system. Nonlinear Dyn. 2017, 89, 1371–1383. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; Freeman: San Francisco, CA, USA, 1982. [Google Scholar]
- Bassingthwaighte, J.B.; Liebovitch, L.S.; West, B.J. Fractal Physiology; Oxford University Press: Oxford, UK, 1994. [Google Scholar]
- Pandey, A. Practical Microstrip and Printed Antenna Design; Artech House: Norwood, MA, USA, 2019; pp. 253–260. ISBN 9781630816681. [Google Scholar]
- Gao, J.B.; Cao, Y.H.; Lee, J.M. Principal Component Analysis of 1/f Noise. Phys. Lett. A 2003, 314, 392–400. [Google Scholar] [CrossRef]
- Li, W.; Kaneko, K. Long-range correlation and partial 1/f-alpha spectrum in a noncoding DNA-sequence. Europhys. Lett. 1992, 17, 655–660. [Google Scholar] [CrossRef] [Green Version]
- Voss, R.F. Evolution of long-range fractal correlations and 1/f noise in DNA base sequences. Phys. Rev. Lett. 1992, 68, 3805. [Google Scholar] [CrossRef]
- Peng, C.K.; Buldyrev, S.V.; Goldberger, A.L.; Havlin, S.; Sciortino, F.; Simons, M.; Stanley, H.E. Long-range correlations in nucleotide sequences. Nature 1992, 356, 168. [Google Scholar] [CrossRef] [PubMed]
- Gao, J.; Qi, Y.; Cao, Y.; Tung, W.W. Protein coding sequence identification by simultaneously characterizing the periodic and random features of DNA sequences. J. Biomed. Biotechnol. 2005, 2005, 139–146. [Google Scholar] [CrossRef]
- Hu, J.; Gao, J.B.; Cao, Y.H.; Bottinger, E.; Zhang, W.J. Exploiting noise in array CGH data to improve detection of DNA copy number change. Nucleic Acids Res. 2007, 35, e35. [Google Scholar] [CrossRef] [Green Version]
- Gilden, D.L.; Thornton, T.; Mallon, M.W. 1/f noise in human cognition. Science 1995, 267, 1837–1839. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Ding, M.; Kelso, J.A.S. Long Memory Processes (1/fα type) in Human Coordination. Phys. Rev. Lett. 1997, 79, 4501. [Google Scholar] [CrossRef]
- Collins, J.J.; Luca, C.J.D. Random Walking during Quiet Standing. Phys. Rev. Lett. 1994, 73, 764. [Google Scholar] [CrossRef]
- Furstenau, N. A nonlinear dynamics model for simulating long range correlations of cognitive bistability. Biol. Cybern. 2010, 103, 175–198. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gao, J.B.; Billock, V.A.; Merk, I.; Tung, W.W.; White, K.D.; Harris, J.G.; Roychowdhury, V.P. Inertia and memory in ambiguous visual perception. Cogn. Process. 2006, 7, 105–112. [Google Scholar] [CrossRef]
- Ivanov, P.C.; Rosenblum, M.G.; Peng, C.K.; Mietus, J.; Havlin, S.; Stanley, H.E.; Goldberger, A.L. Scaling behaviour of heartbeat intervals obtained by wavelet-based time-series analysis. Nature 1996, 383, 323. [Google Scholar] [CrossRef]
- Amaral, L.A.N.; Goldberger, A.L.; Ivanov, P.C.; Stanley, H.E. Scale-independent measures and pathologic cardiac dynamics. Phys. Rev. Lett. 1998, 81, 2388. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ivanov, P.C.; Rosenblum, M.G.; Amaral, L.A.N.; Struzik, Z.R.; Havlin, S.; Goldberger, A.L.; Stanley, H.E. Multifractality in human heartbeat dynamics. Nature 1999, 399, 461. [Google Scholar] [CrossRef] [Green Version]
- Bernaola-Galvan, P.; Ivanov, P.C.; Amaral, L.A.N.; Stanley, H.E. Scale invariance in the nonstationarity of human heart rate. Phys. Rev. Lett. 2001, 87, 168105. [Google Scholar] [CrossRef] [Green Version]
- Gao, J.B. Analysis of Amplitude and Frequency Variations of Essential and Parkinsonian Tremors. Med. Biol. Eng. Comput. 2004, 52, 345–349. [Google Scholar] [CrossRef]
- Kuznetsov, N.; Bonnette, S.; Gao, J.B.; Riley, M.A. Adaptive fractal analysis reveals limits to fractal scaling in center of pressure trajectories. Ann. Biomed. Eng. 2012, 41, 1646–1660. [Google Scholar] [CrossRef]
- Gao, J.B.; Hu, J.; Buckley, T.; White, K.; Hass, C. Shannon and Renyi Entropies To Classify Effects of Mild Traumatic Brain Injury on Postural Sway. PLoS ONE 2011, 6, e24446. [Google Scholar] [CrossRef]
- Gao, J.B.; Gurbaxani, B.M.; Hu, J.; Heilman, K.J.; Emauele, V.A.; Lewis, G.F.; Davila, M.; Unger, E.R.; Lin, J.S. Multiscale analysis of heart rate variability in nonstationary environments. Front. Comput. Physiol. Med. 2013, 4, 119. [Google Scholar]
- Gao, J.B.; Hu, J.; Tung, W.W. Complexity measures of brain wave dynamics. Cogn. Neurodynamics 2011, 5, 171–182. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zheng, Y.; Gao, J.B.; Sanchez, J.C.; Principe, J.C.; Okun, M.S. Multiplicative multifractal modeling and discrimination of human neuronal activity. Phys. Lett. A 2005, 344, 253–264. [Google Scholar] [CrossRef]
- Hu, J.; Zheng, Y.; Gao, J.B. Long-range temporal correlations, multifractality, and the causal relation between neural inputs and movements. Front. Neurol. 2013, 4, 158. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhu, H.B.; Gao, J.B. Fractal behavior in the headway fluctuation simulated by the NaSch model. Phys. A 2014, 398, 187–193. [Google Scholar] [CrossRef]
- Bowers, M.; Gao, J.B.; Tung, W.W. Long-Range Correlations in Tree Ring Chronologies of the USA: Variation within and Across Species. Geophys. Res. Lett. 2013, 40, 568–572. [Google Scholar] [CrossRef]
- Gao, J.B.; Fang, P.; Liu, F.Y. Empirical scaling law connecting persistence and severity of global terrorism. Phys. A 2017, 482, 74–86. [Google Scholar] [CrossRef]
- Gao, J.B.; Hu, J.; Mao, X.; Perc, M. Culturomics meets random fractal theory: Insights into long-range correlations of social and natural phenomena over the past two centuries. J. R. Soc. Interface 2012, 9, 1956–1964. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wolf, M. 1/f noise in the distribution of prime numbers. Phys. A 1997, 241, 493. [Google Scholar] [CrossRef]
- Gao, J.; Hu, J.; Tung, W.W.; Cao, Y.; Sarshar, N.; Roychowdhury, V.P. Assessment of long range correlation in time series: How to avoid pitfalls. Phys. Rev. E 2006, 73, 016117. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Peng, C.K.; Buldyrev, S.V.; Havlin, S.; Simons, M.; Stanley, H.E.; Goldberger, A.L. Mosaic organization of dna nucleotides. Phys. Rev. E 1994, 49, 1685–1689. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Arneodo, A.; Bacry, E.; Muzy, J.F. The thermodynamics of fractals revisited with wavelets. Phys. A 1995, 213, 232–275. [Google Scholar]
- Gao, J.B.; Hu, J.; Tung, W.W. Facilitating joint chaos and fractal analysis of biosignals through nonlinear adaptive filtering. PLoS ONE 2011, 6, e24331. [Google Scholar] [CrossRef] [Green Version]
- Tung, W.W.; Gao, J.B.; Hu, J.; Yang, L. Recovering chaotic signals in heavy noise environments. Phys. Rev. E 2011, 83, 046210. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gao, J.B.; Sultan, H.; Hu, J.; Tung, W.W. Denoising nonlinear time series by adaptive filtering and wavelet shrinkage: A comparison. IEEE Signal Process. Lett. 2010, 17, 237–240. [Google Scholar]
- Riley, M.A.; Kuznetsov, N.; Bonnette, S.; Wallot, S.; Gao, J.B. A Tutorial Introduction to Adaptive Fractal Analysis. Front. Fractal Physiol. 2012, 3, 371. [Google Scholar] [CrossRef] [Green Version]
- Frisch, U. Turbulence—The Legacy of A.N. Kolmogorov; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Gouyet, J.F. Physics and Fractal Structures; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Frederiksen, R.D.; Dahm, W.J.A.; Dowling, D.R. Experimental assessment of fractal scale similarity in turbulent flows—Multifractal scaling. J. Fluid Mech. 1997, 338, 127–155. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Intermittent turbulence in self-similar cascades: Divergence of high moments and dimension of carrier. J. Fluid Mech. 1974, 62, 331–358. [Google Scholar] [CrossRef]
- Parisi, G.; Frisch, U. On the singularity structure of fully developed turbulence. In Turbulence and Predictability in Geophysical Fluid Dynamics and Climate Dynamics; Ghil, M., Benzi, R., Parisi, G., Eds.; North-Holland: Amsterdam, The Netherlands, 1985; pp. 71–84. [Google Scholar]
- Gao, J.B.; Rubin, I. Multifractal modeling of counting processes of long-range-dependent network traffic. Comput. Commun. 2001, 24, 1400–1410. [Google Scholar] [CrossRef]
- Gao, J.B.; Rubin, I. Multiplicative multifractal modeling of long-range-dependent network traffic. Int. J. Commun. Syst. 2001, 14, 783–801. [Google Scholar] [CrossRef]
- Tung, W.W.; Moncrief, M.W.; Gao, J.B. A systemic view of the multiscale tropical deep convective variability over the tropical western Pacific warm pool. J. Clim. 2004, 17, 2736–2751. [Google Scholar] [CrossRef] [Green Version]
- Hu, J.; Tung, W.W.; Gao, J.B. Detection of low observable targets within sea clutter by structure function based multifractal analysis. IEEE Trans. Antennas Propag. 2006, 54, 135–143. [Google Scholar] [CrossRef]
- Osborne, A.R.; Provenzale, A. Finite correlation dimension for stochastic-systems with power-law spectra. Phys. D 1989, 35, 357–381. [Google Scholar] [CrossRef]
- Provenzale, A.; Osborne, A.R.; Soj, R. Convergence of the K2 entropy for random noises with power law spectra. Phys. D 1991, 47, 361–372. [Google Scholar] [CrossRef]
- Hu, J.; Gao, J.B.; Principe, J.C. Analysis of biomedical signals by the Lempel-Ziv complexity: The effect of finite data size. IEEE Trans. Biomed. Eng. 2006, 53, 2606–2609. [Google Scholar]
- Galatolo, S.; Hoyrup, M.; Rojas, C. Effective symbolic dynamics, random points, statistical behavior, complexity and entropy. Inf. Comput. 2010, 208, 23–41. [Google Scholar] [CrossRef] [Green Version]
- Gao, J.B.; Hu, J.; Tung, W.W. Entropy measures for biological signal analysis. Nonlinear Dyn. 2012, 68, 431–444. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef]
- Cao, Y.H.; Tung, W.W.; Gao, J.B.; Protopopescu, V.A.; Hively, L.M. Detecting dynamical changes in time series using the permutation entropy. Phys. Rev. E 2004, 70, 1539–3755. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, J.; Wei, H.; Ye, C.; Ding, Y. Fractal behavior of traffic volume on urban expressway through adaptive fractal analysis. Phys. A 2016, 443, 518–525. [Google Scholar]
- Shen, S.; Ye, S.J.; Cheng, C.X.; Song, C.Q.; Gao, J.B.; Yang, J.; Ning, L.X.; Su, K.; Zhang, T. Persistence and Corresponding Time Scales of Soil Moisture Dynamics During Summer in the Babao River Basin, Northwest China. J. Geophys. Res. Atmos. 2018, 123, 8936–8948. [Google Scholar] [CrossRef]
- Zhang, T.; Shen, S.; Cheng, C.; Song, C.Q.; Ye, S.J. Long range correlation analysis of soil temperature and moisture on A’rou hillsides, Babao River basin. J. Geophys. Res. Atmos. 2018, 123, 12606–12620. [Google Scholar] [CrossRef]
- Yang, J.; Su, K.; Ye, S. Stability and long-range correlation of air temperature in the Heihe River Basin. J. Geogr. Sci. 2019, 29, 1462–1474. [Google Scholar] [CrossRef] [Green Version]
- Gao, J.B.; Fang, P.; Yuan, L.H. Analyses of geographical observations in the HeiheRiver Basin: Perspectives from complexity theory. J. Geogr. Sci. 2019, 29, 1441–1461. [Google Scholar] [CrossRef] [Green Version]
- Jiang, A.; Gao, J. Fractal analysis of complex power load variations through adaptive multiscale filtering. In Proceedings of the International Conference on Behavioral, Economic and Socio-Cultural Computing (BESC—2016), Durham, NC, USA, 11–13 November 2016. [Google Scholar]
- Li, Q.; Gao, J.B.; Zhang, Z.W.; Huang, Q.; Wu, Y.; Xu, B. Distinguishing Epileptiform Discharges from normal Electroencephalograms Using Adaptive Fractal and Network Analysis: A Clinical Perspective. Front. Physiol. 2020, 11, 828. [Google Scholar] [CrossRef] [PubMed]
- Zheng, F.; Chen, L.; Gao, J.; Zhao, Y. Fully Quantum Modeling of Exciton Diffusion in Mesoscale Light Harvesting Systems. Materials 2021, 14, 3291. [Google Scholar] [CrossRef]
- Gao, J.B.; Jockers, M.L.; Laudun, J.; Tangherlini, T. A multiscale theory for the dynamical evolution of sentiment in novels. In Proceedings of the International Conference on Behavioral, Economic and Socio-Cultural Computing (BESC—2016), Durham, NC, USA, 11–13 November 2016. [Google Scholar]
- Hu, Q.Y.; Liu, B.; Thomsen, M.R.; Gao, J.B.; Nielbo, K.L. Dynamic evolution of sentiments in Never Let Me Go: Insights from multifractal theory and its implications for literary analysis. Digit. Scholarsh. Humanit. 2020. [Google Scholar] [CrossRef]
- Wever, M.; Nielbo, K.L.; Gao, J.B. Tracking the Consumption Junction: Temporal Dependencies in Dutch Newspaper Articles and Advertisements. Digit. Humanit. Q. 2020, 14, 2. Available online: http://www.digitalhumanities.org/dhq/vol/14/2/000445/000445.html (accessed on 19 June 2021).
- Nielbo, K.L.; Baunvig, K.F.; Liu, B.; Gao, J.B. A curious case of entropic decay: Persistent complexity in textual cultural heritage. Digit. Scholarsh. Humanit. 2018. [Google Scholar] [CrossRef]
- Hu, J.; Gao, J.B.; Wang, X.S. Multifractal analysis of sunspot time series: The effects of the 11-year cycle and Fourier truncation. J. Stat. Mech. 2009, 2009, P02066. [Google Scholar] [CrossRef]
- Wu, Z.H.; Huang, N.E.; Long, S.R.; Peng, C.K. On the trend, detrending, and variability of nonlinear and nonstationary time series. Proc. Natl. Acad. Sci. USA 2007, 104, 14889–14894. [Google Scholar] [CrossRef] [Green Version]
- Podobnik, B.; Stanley, H.E. Detrended cross-correlation analysis: A new method for analyzing two non-stationary time series. Phys. Rev. Lett. 2008, 100, 84–102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gao, J.B.; Hu, J.; Tung, W.W.; Cao, Y.H. Distinguishing chaos from noise by scale-dependent Lyapunov exponent. Phys. Rev. E 2006, 74, 066204. [Google Scholar] [CrossRef] [Green Version]
- Torcini, A.; Grassberger, P.; Politi, A. Error Propagation in Extended Chaotic Systems. J. Phys. A Math. Gen. 1995, 28, 4533. [Google Scholar] [CrossRef] [Green Version]
- Aurell, E.; Boffetta, G.; Crisanti, A.; Paladin, G.; Vulpiani, A. Growth of non-infinitesimal perturbations in turbulence. Phys. Rev. Lett. 1996, 77, 1262. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aurell, E.; Boffetta, G.; Crisanti, A.; Paladin, G.; Vulpiani, A. Predictability in the large: An extension of the concept of Lyapunov exponent. J. Phys. A 1997, 30, 1–26. [Google Scholar] [CrossRef] [Green Version]
- Gao, J.B.; Tung, W.W.; Hu, J. Quantifying dynamical predictability: The pseudo-ensemble approach (in honor of Professor Andrew Majda’s 60th birthday). Chin. Ann. Math. Ser. B 2009, 30, 569–588. [Google Scholar] [CrossRef]
- Gao, J.B.; Hu, J.; Mao, X.; Tung, W.W. Detecting low-dimensional chaos by the “noise titration” technique: Possible problems and remedies. Chaos Solitons Fractals 2012, 45, 213–223. [Google Scholar] [CrossRef] [Green Version]
- Hu, J.; Gao, J.B.; Tung, W.W.; Cao, Y.H. Multiscale analysis of heart rate variability: A comparison of different complexity measures. Ann. Biomed. Eng. 2010, 38, 854–864. [Google Scholar] [CrossRef]
- Hu, J.; Gao, J.B.; Tung, W.W. Characterizing heart rate variability by scale-dependent Lyapunov exponent. Chaos Interdiscip. J. Nonlinear Sci. 2009, 19, 028506. [Google Scholar] [CrossRef] [Green Version]
- Ryan, D.A.; Sarson, G.R. The geodynamo as a low-dimensional deterministic system at the edge of chaos. EPL 2008, 83, 49001. [Google Scholar] [CrossRef]
- Fan, Q.B.; Wang, Y.X.; Zhu, L. Complexity analysis of spatial—Ctemporal precipitation system by PCA and SDLE. Appl. Math. Model. 2013, 37, 4059–4066. [Google Scholar] [CrossRef]
- Hu, J.; Gao, J.B. Multiscale characterization of sea clutter by scale-dependent Lyapunov exponent. Math. Probl. Eng. 2013, 2013, 584252. [Google Scholar] [CrossRef]
- Blasch, E.; Gao, J.B.; Tung, W.W. Chaos-based Image Assessment for THz Imagery. In Proceedings of the 2012 11th International Conference on Information Science, Signal Processing and Their Applications, Montreal, QC, Canada, 3–5 July 2012. [Google Scholar]
- Li, Q.; Gao, J.B.; Huang, Q.; Wu, Y.; Xu, B. Distinguishing Epileptiform Discharges from Normal Electroencephalograms Using Scale-Dependent Lyapunov Exponent. Front. Bioeng. Biotechnol. 2020, 8, 1006. [Google Scholar] [CrossRef]
- Gao, J.B.; Hu, J.; Tung, W.W.; Blasch, E. Multiscale analysis of physiological data by scale-dependent Lyapunov exponent. Front. Fractal Physiol. 2012, 2, 110. [Google Scholar] [CrossRef] [Green Version]
- Berera, A.; Ho, R.D.J.G. Chaotic Properties of a Turbulent Isotropic Fluid. Phys. Rev. Lett. 2018, 120, 024101. [Google Scholar] [CrossRef] [Green Version]
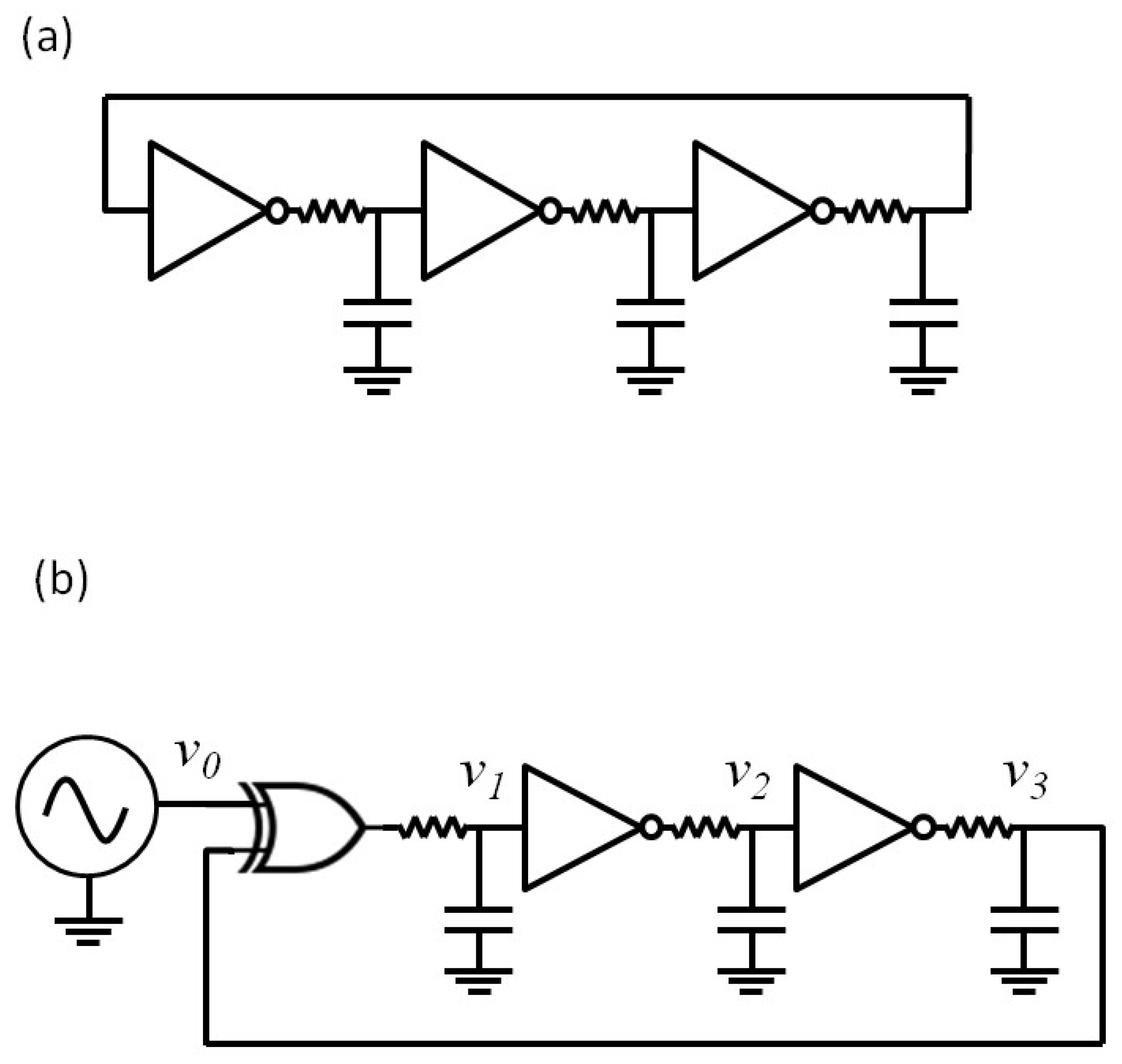
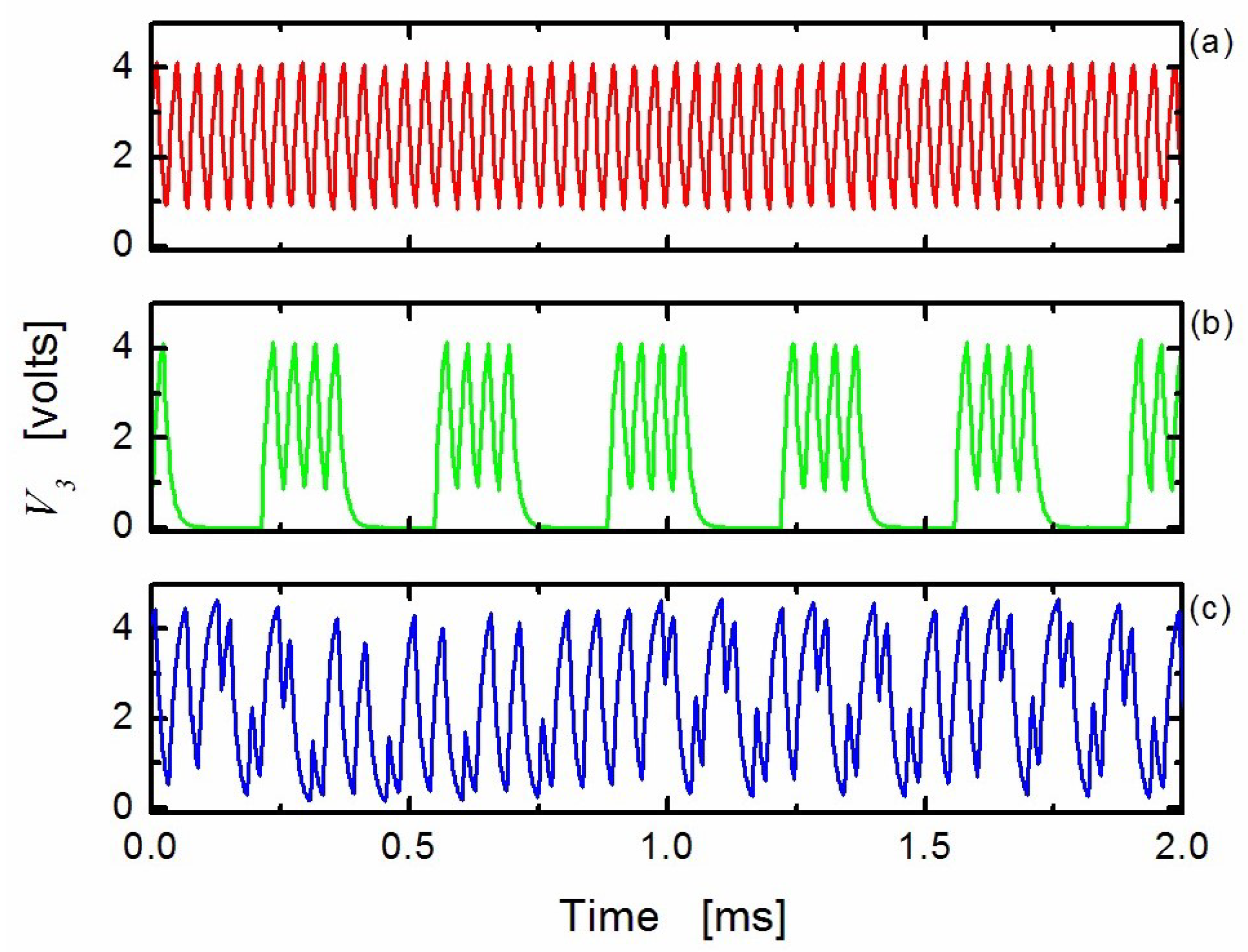
- Blakely, J.N.; Corron, N.J.; Pethel, S.D.; Stahl, M.T.; Gao, J.B. Non-autonomous Boolean chaos in a driven ring oscillator. In New Research Trends in Nonlinear circuits—Design, Chaotic Phenomena and Applications; Kyprianidis, I., Stouboulos, I., Volos, C., Eds.; Nova Publishers: New York, NY, USA, 2014; Chapter 8; pp. 153–168. [Google Scholar]
- Lazer, D.; Pentland, A.; Adamic, L.; Aral, S.; Barabasi, A.L.; Brewer, D.; Christakis, N.; Contractor, N.; Fowler, J.; Van Alstyne, M.; et al. Computational social science. Science 2009, 323, 721–723. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Goldstein, J.S. A Conflict-Cooperation Scale for WEIS Events Data. J. Confl. Resolut. 1992, 36, 369–385. [Google Scholar] [CrossRef]
- Schrodt, P.A.; Gerner, D.J.; Ömür, G. Conflict and Mediation Event Observations (CAMEO): An Event Data Framework for a Post Cold War World. In International Conflict Mediation: New Approaches and Findings; Bercovitch, J., Gartner, S., Eds.; Routledge: New York, NY, USA, 2009. [Google Scholar]
- O’Brien, S.P. Crisis Early Warning and Decision Support: Contemporary Approaches and Thoughts on Future Research. Int. Stud. Rev. 2010, 12, 87–104. [Google Scholar] [CrossRef]
- Turchin, P. Historical Dynamics: Why States Rise and Fall; Princeton University Press: Princeton, NJ, USA, 2003. [Google Scholar]
- Turchin, P. Arise ‘cliodynamics’. Nature 2008, 454, 34–35. [Google Scholar] [CrossRef] [PubMed]































Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, J.; Xu, B. Complex Systems, Emergence, and Multiscale Analysis: A Tutorial and Brief Survey. Appl. Sci. 2021, 11, 5736. https://doi.org/10.3390/app11125736
Gao J, Xu B. Complex Systems, Emergence, and Multiscale Analysis: A Tutorial and Brief Survey. Applied Sciences. 2021; 11(12):5736. https://doi.org/10.3390/app11125736
Chicago/Turabian StyleGao, Jianbo, and Bo Xu. 2021. "Complex Systems, Emergence, and Multiscale Analysis: A Tutorial and Brief Survey" Applied Sciences 11, no. 12: 5736. https://doi.org/10.3390/app11125736
APA StyleGao, J., & Xu, B. (2021). Complex Systems, Emergence, and Multiscale Analysis: A Tutorial and Brief Survey. Applied Sciences, 11(12), 5736. https://doi.org/10.3390/app11125736






