The Effects of Compression on the Detection of Atrial Fibrillation in ECG Signals
Abstract
:1. Introduction
2. Methods
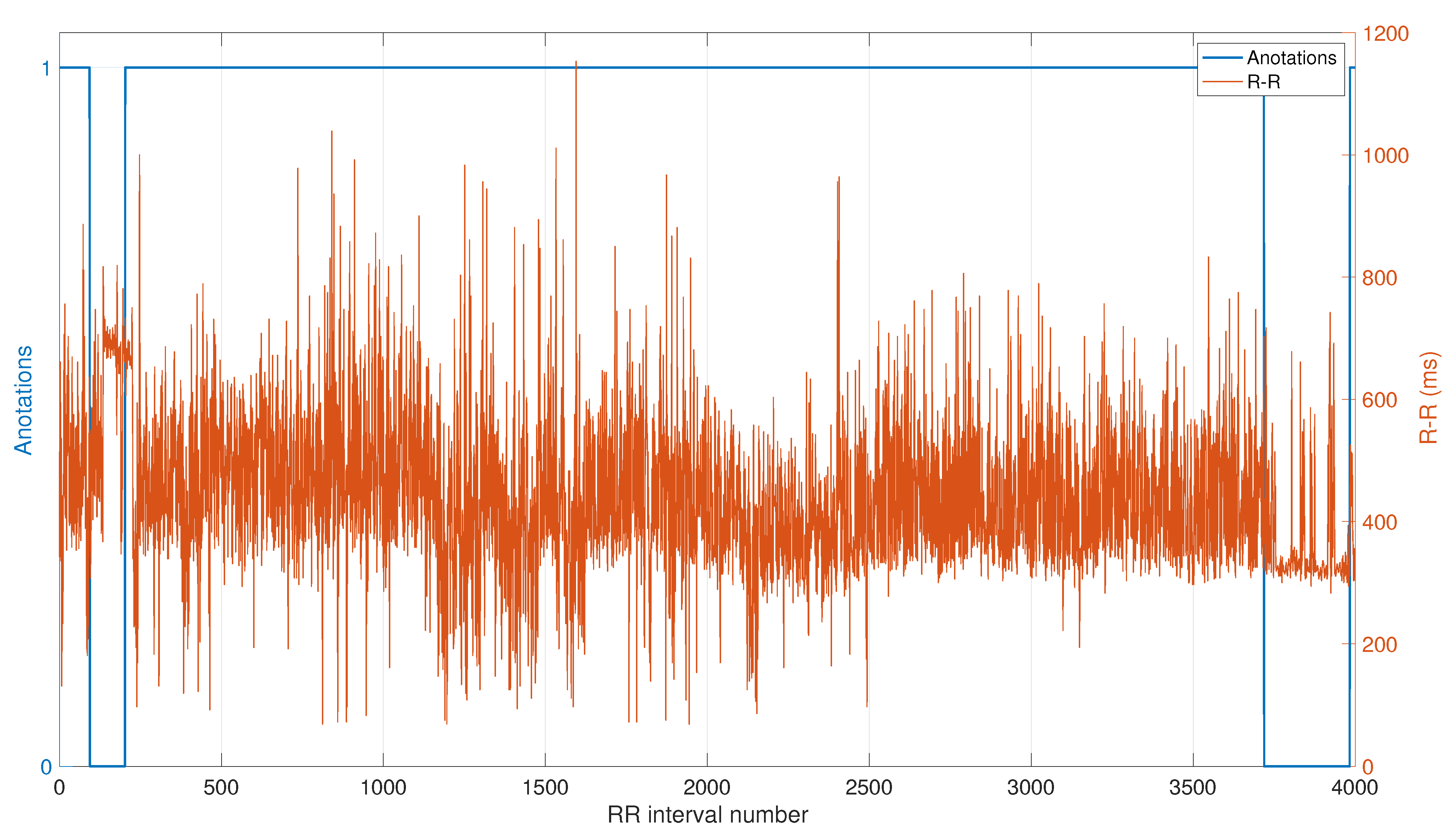
2.1. ECG Database
2.2. Compression Method
2.3. Detection Based on Shannon Entropy Calculation
2.4. Performance Metrics
3. Results
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Benjamin, E.J.; Wolf, P.A.; D’Agostino, R.B.; Silbershatz, H.; Kannel, W.B.; Levy, D. Impact of atrial fibrillation on the risk of death: The Framingham Heart Study. Circulation 1998, 98, 946–952. [Google Scholar] [CrossRef] [Green Version]
- Chugh, S.S.; Blackshear, J.L.; Shen, W.K.; Hammill, S.C.; Gersh, B.J. Epidemiology and natural history of atrial fibrillation: Clinical implications. J. Am. Coll. Cardiol. 2001, 37, 371–378. [Google Scholar] [CrossRef] [Green Version]
- Patel, N.J.; Deshmukh, A.; Pant, S.; Singh, V.; Patel, N.; Arora, S.; Shah, N.; Chothani, A.; Savani, G.T.; Mehta, K.; et al. Contemporary trends of hospitalization for atrial fibrillation in the United States, 2000 through 2010: Implications for healthcare planning. Circulation 2014, 129, 2371–2379. [Google Scholar] [CrossRef] [Green Version]
- Lip, G.Y.H.; Brechin, C.M.; Lane, D.A. The global burden of atrial fibrillation and stroke: A systematic review of the epidemiology of atrial fibrillation in regions outside North America and Europe. Chest 2012, 142, 1489–1498. [Google Scholar] [CrossRef]
- Ball, J.; Carrington, M.J.; McMurray, J.J.V.; Stewart, S. Atrial fibrillation: Profile and burden of an evolving epidemic in the 21st century. Int. J. Cardiol. 2013, 167, 1807–1824. [Google Scholar] [CrossRef]
- Chugh, S.S.; Havmoeller, R.; Narayanan, K.; Singh, D.; Rienstra, M.; Benjamin, E.J.; Gillum, R.F.; Kim, Y.H.; McAnulty, J.H., Jr.; Zheng, Z.J.; et al. Worldwide epidemiology of atrial fibrillation: A Global Burden of Disease 2010 Study. Circulation 2014, 129, 837–847. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Plasek, J.; Taborsky, M. Subclinical atrial fibrillation—What is the risk of stroke? Biomed. Pap. 2019, 163, 107–113. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Go, A.S.; Hylek, E.M.; Phillips, K.A.; Chang, Y.; Henault, L.E.; Selby, J.V.; Singer, D.E. Prevalence of diagnosed atrial fibrillation in adults: National implications for rhythm management and stroke prevention: The AnTicoagulation and Risk Factors in Atrial Fibrillation (ATRIA) Study. JAMA 2001, 285, 2370–2375. [Google Scholar] [CrossRef] [PubMed]
- Argulian, E.; Conen, D.; Messerli, F.H. Misconceptions and Facts about Atrial Fibrillation. Am. J. Med. 2015. [Google Scholar] [CrossRef] [PubMed]
- Du, X.; Rao, N.; Qian, M.; Liu, D.; Li, J.; Feng, W.; Yin, L.; Chen, X. A novel method for real-time atrial fibrillation detection in electrocardiograms using multiple parameters. Ann. Noninvasive Electrocardiol. 2014, 19, 217–225. [Google Scholar] [CrossRef]
- Huang, A.; Chen, C.; Bian, K.; Duan, X.; Chen, M.; Gao, H.; Meng, C.; Zheng, Q.; Zhang, Y.; Jiao, B.; et al. WE-CARE: An intelligent mobile telecardiology system to enable mHealth applications. IEEE J. Biomed. Health Inf. 2014, 18, 693–702. [Google Scholar] [CrossRef] [PubMed]
- Bayasi, N.; Tekeste, T.; Saleh, H.; Mohammad, B.; Khandoker, A.; Ismail, M. Low-power ECG-based processor for predicting ventricular arrhythmia. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2015, 24, 1962–1974. [Google Scholar] [CrossRef]
- Lewis, T. Report CXIX. auricular fibrillation: A common clinical condition. Br. Med. J. 1909, 2, 1528. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Asgari, S.; Mehrnia, A.; Moussavi, M. Automatic detection of atrial fibrillation using stationary wavelet transform and support vector machine. Comput. Biol. Med. 2015, 60, 132–142. [Google Scholar] [CrossRef]
- Tateno, K.; Glass, L. Automatic detection of atrial fibrillation using the coefficient of variation and density histograms of RR and deltaRR intervals. Med. Biol. Eng. Comput. 2001, 39, 664–671. [Google Scholar] [CrossRef]
- Lee, S.; Kim, J.; Lee, M. A real-time ECG data compression and transmission algorithm for an e-health device. IEEE Trans. Biomed. Eng. 2011, 58, 2448–2455. [Google Scholar] [PubMed]
- Mamaghanian, H.; Khaled, N.; Atienza, D.; Vandergheynst, P. Compressed sensing for real-time energy-efficient ECG compression on wireless body sensor nodes. IEEE Trans. Biomed. Eng. 2011, 58, 2456–2466. [Google Scholar] [CrossRef] [Green Version]
- Mazomenos, E.B.; Biswas, D.; Acharyya, A.; Chen, T.; Maharatna, K.; Rosengarten, J.; Morgan, J.; Curzen, N. A low-complexity ECG feature extraction algorithm for mobile healthcare applications. IEEE J. Biomed. Health Inform. 2013, 17, 459–469. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Jung, T.P.; Makeig, S.; Rao, B.D. Compressed sensing for energy-efficient wireless telemonitoring of noninvasive fetal ECG via block sparse Bayesian learning. IEEE Trans. Biomed. Eng. 2012, 60, 300–309. [Google Scholar] [CrossRef] [Green Version]
- Izumi, S.; Yamashita, K.; Nakano, M.; Kawaguchi, H.; Kimura, H.; Marumoto, K.; Fuchikami, T.; Fujimori, Y.; Nakajima, H.; Shiga, T.; et al. A Wearable Healthcare System with a 13.7 μ A Noise Tolerant ECG Processor. IEEE Trans. Biomed. Circuits Syst. 2014, 9, 733–742. [Google Scholar] [CrossRef]
- Craven, D.; McGinley, B.; Kilmartin, L.; Glavin, M.; Jones, E. Adaptive Dictionary Reconstruction for Compressed Sensing of ECG Signals. IEEE J. Biomed. Health Inform. 2017, 21, 645–654. [Google Scholar] [CrossRef]
- Kannan, R.; Eswaran, C. Lossless compression schemes for ECG signals using neural network predictors. EURASIP J. Adv. Signal Process. 2007, 035641. [Google Scholar] [CrossRef] [Green Version]
- Luo, K.; Li, J.; Wu, J. A dynamic compression scheme for energy-efficient real-time wireless electrocardiogram biosensors. IEEE Trans. Instrum. Meas. 2014, 63, 2160–2169. [Google Scholar] [CrossRef]
- Craven, D.; McGinley, B.; Kilmartin, L.; Glavin, M.; Jones, E. Compressed Sensing for Bioelectric Signals: A Review. IEEE Trans. Biomed. Health Inform. 2014, 19, 529–540. [Google Scholar] [CrossRef]
- Twomey, N.; Walsh, N.; Doyle, O.; McGinley, B.; Glavin, M.; Jones, E.; Marnane, W.P. The Effect of Lossy ECG Compression on QRS and HRV Feature Extraction. In Proceedings of the Engineering in Medicine and Biology Society (EMBC), 2010 Annual International Conference of the IEEE, Buenos Aires, Argentina, 31 August–4 September 2010; pp. 634–637. [Google Scholar]
- Ku, C.T.; Hung, K.C.; Wu, T.C.; Wang, H.S. Wavelet-based ECG data compression system with linear quality control scheme. IEEE Trans. Biomed. Eng. 2010, 57, 1399–1409. [Google Scholar]
- Bendifallah, A.; Benzid, R.; Boulemden, M. Improved ECG compression method using discrete cosine transform. Electron. Lett. 2011, 47, 87–89. [Google Scholar] [CrossRef]
- Ma, J.; Zhang, T.; Dong, M. A novel ECG data compression method using adaptive fourier decomposition with security guarantee in e-health applications. IEEE J. Biomed. Health Inform. 2014, 19, 986–994. [Google Scholar] [CrossRef] [PubMed]
- Said, A.; Pearlman, W.A. A new, fast, and efficient image codec based on set partitioning in hierarchical trees. IEEE Trans. Circuits Syst. Video Technol. 1996, 6, 243–250. [Google Scholar] [CrossRef]
- Miaou, S.G.; Lin, C.L. A quality-on-demand algorithm for wavelet-based compression of electrocardiogram signals. IEEE Trans. Biomed. Eng. 2002, 49, 233–239. [Google Scholar] [CrossRef]
- Moody, G. A new method for detecting atrial fibrillation using RR intervals. Comput. Cardiol. 1983, 227–230. [Google Scholar]
- Goldberger, A.L.; Amaral, L.A.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.K.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet: Components of a new research resource for complex physiologic signals. Circulation 2000, 101, E215–E220. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Higgins, G.; McGinley, B.; Walsh, N.; Glavin, M.; Jones, E. Lossy compression of EEG signals using SPIHT. Electron. Lett. 2011, 47, 1017–1018. [Google Scholar] [CrossRef]
- Cervigón, R.; Sánchez, C.; Castells, F.; Blas, J.; Millet, J. Wavelet analysis of electrocardiograms to characterize recurrent atrial fibrillation. J. Frankl. Inst. 2007, 344, 196–211. [Google Scholar] [CrossRef]
- Afonso, V.X.; Tompkins, W.J.; Nguyen, T.Q.; Luo, S. ECG beat detection using filter banks. IEEE Trans. Biomed. Eng. 1999, 46, 192–202. [Google Scholar] [CrossRef] [PubMed]
- Shannon, C.E.; Weaver, W. The Mathematical Theory of Communication; University of Illinois Press: Urbana, IL, USA, 1998. [Google Scholar]
- Lian, J.; Wang, L.; Muessig, D. A simple method to detect atrial fibrillation using RR intervals. Am. J. Cardiol. 2011, 107, 1494–1497. [Google Scholar] [CrossRef]
- Petrėnas, A.; Sörnmo, L.; Lukoševičius, A.; Marozas, V. Detection of occult paroxysmal atrial fibrillation. Med. Biol. Eng. Comput. 2015, 53, 287–297. [Google Scholar] [CrossRef] [PubMed]
- Meijler, F.L.; Janse, M.J. Morphology and electrophysiology of the mammalian atrioventricular node. Physiol. Rev. 1988, 68, 608–647. [Google Scholar] [CrossRef] [Green Version]
- Cervigón, R.; Moreno, J.; Reilly, R.B.; Pérez-Villacastín, J.; Castells, F. Ventricular rhythm in atrial fibrillation under anaesthetic infusion with propofol. Physiol. Meas. 2009, 30, 833–845. [Google Scholar] [CrossRef]
- Faust, O.; Ciaccio, E.J.; Acharya, U.R. A Review of Atrial Fibrillation Detection Methods as a Service. Int. J. Environ. Res. Public Health 2020, 17, 3093. [Google Scholar] [CrossRef] [PubMed]
- Cervigón, R.; Moreno, J.; Reilly, R.B.; Millet, J.; Pérez-Villacastín, J.; Castells, F. Entropy measurements in paroxysmal and persistent atrial fibrillation. Physiol. Meas. 2010, 31, 1011–1020. [Google Scholar] [CrossRef]
- Mian Qaisar, S.; Fawad Hussain, S. Arrhythmia Diagnosis by Using Level-Crossing ECG Sampling and Sub-Bands Features Extraction for Mobile Healthcare. Sensors 2020, 20, 2252. [Google Scholar] [CrossRef] [Green Version]
- Pelc, M.; Khoma, Y.; Khoma, V. ECG Signal as Robust and Reliable Biometric Marker: Datasets and Algorithms Comparison. Sensors 2019, 19, 2350. [Google Scholar] [CrossRef] [Green Version]
- Ambadkar, M.; Leonelli, F.M.; Sankar, R. Signal processing techniques for atrial fibrillation source detection. Conf. Proc. IEEE Eng. Med. Biol. Soc. 2014, 2014, 2821–2824. [Google Scholar] [CrossRef]
- Freedman, B.; Camm, J.; Calkins, H.; Healey, J.S.; Rosenqvist, M.; Wang, J.; Albert, C.M.; Anderson, C.S.; Antoniou, S.; Benjamin, E.J.; et al. Screening for Atrial Fibrillation: A Report of the AF-SCREEN International Collaboration. Circulation 2017, 135, 1851–1867. [Google Scholar] [CrossRef]
- Kirchhof, P.; Benussi, S.; Kotecha, D.; Ahlsson, A.; Atar, D.; Casadei, B.; Castella, M.; Diener, H.C.; Heidbuchel, H.; Hendriks, J.; et al. 2016 ESC Guidelines for the management of atrial fibrillation developed in collaboration with EACTS. Europace 2016, 18, 1609–1678. [Google Scholar] [CrossRef] [PubMed]
- Hartikainen, S.; Lipponen, J.A.; Hiltunen, P.; Rissanen, T.T.; Kolk, I.; Tarvainen, M.P.; Martikainen, T.J.; Castren, M.; Väliaho, E.S.; Jäntti, H. Effectiveness of the Chest Strap Electrocardiogram to Detect Atrial Fibrillation. Am. J. Cardiol. 2019, 123, 1643–1648. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, X.; Ding, H.; Ung, B.; Pickwell-MacPherson, E.; Zhang, Y. Automatic online detection of atrial fibrillation based on symbolic dynamics and Shannon entropy. Biomed. Eng. Online 2014, 13, 18. [Google Scholar] [CrossRef] [Green Version]
- Lake, D.E.; Moorman, J.R. Accurate estimation of entropy in very short physiological time series: The problem of atrial fibrillation detection in implanted ventricular devices. Am. J. Physiol. Heart Circ. Physiol. 2011, 300, H319–H325. [Google Scholar] [CrossRef]
- Lindsberg, P.J.; Toivonen, L.; Diener, H.C. The atrial fibrillation epidemic is approaching the physician’s door: Will mobile technology improve detection? BMC Med. 2014, 12, 180. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Glotzer, T.V.; Ziegler, P.D. Does atrial fibrillation detected by cardiac implantable electronic devices have clinical relevance? Cardiol. Clin. 2014, 32, 271–281. [Google Scholar] [CrossRef]
- Andersson, O.; Chon, K.H.; Sornmo, L.; Rodrigues, J.N. A 290 mV Sub- VT ASIC for Real-Time Atrial Fibrillation Detection. IEEE Trans. Biomed. Circuits Syst. 2014. [Google Scholar] [CrossRef]





| CR | PRD (%) | AUC | Specificity |
|---|---|---|---|
| 0 | 0 | 0.947 | 0.717 |
| 0.953 | 0.006 | 0.946 | 0.714 |
| 5.002 | 5.236 | 0.948 | 0.728 |
| 10.004 | 9.194 | 0.951 | 0.751 |
| 14.010 | 12.437 | 0.950 | 0.739 |
| 20.007 | 17.765 | 0.951 | 0.746 |
| 25.031 | 22.239 | 0.952 | 0.764 |
| 30.037 | 26.532 | 0.954 | 0.775 |
| 35.090 | 30.468 | 0.950 | 0.750 |
| 40.085 | 34.193 | 0.948 | 0.732 |
| 45.056 | 37.485 | 0.941 | 0.705 |
| 50.062 | 40.499 | 0.935 | 0.678 |
| 60.235 | 46.081 | 0.921 | 0.624 |
| 70.400 | 50.922 | 0.909 | 0.569 |
| 80.457 | 54.997 | 0.904 | 0.559 |
| 90.112 | 58.228 | 0.901 | 0.554 |
| 100.571 | 61.067 | 0.881 | 0.491 |
| 110.431 | 63.204 | 0.865 | 0.477 |
| 121.128 | 65.018 | 0.848 | 0.457 |
| 150.187 | 68.510 | 0.746 | 0.040 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cervigón, R.; McGinley, B.; Craven, D.; Glavin, M.; Jones, E. The Effects of Compression on the Detection of Atrial Fibrillation in ECG Signals. Appl. Sci. 2021, 11, 5908. https://doi.org/10.3390/app11135908
Cervigón R, McGinley B, Craven D, Glavin M, Jones E. The Effects of Compression on the Detection of Atrial Fibrillation in ECG Signals. Applied Sciences. 2021; 11(13):5908. https://doi.org/10.3390/app11135908
Chicago/Turabian StyleCervigón, Raquel, Brian McGinley, Darren Craven, Martin Glavin, and Edward Jones. 2021. "The Effects of Compression on the Detection of Atrial Fibrillation in ECG Signals" Applied Sciences 11, no. 13: 5908. https://doi.org/10.3390/app11135908






