Analyzing and Modeling of Water Transport Phenomena in Open-Cathode Polymer Electrolyte Membrane Fuel Cell
Abstract
:1. Introduction
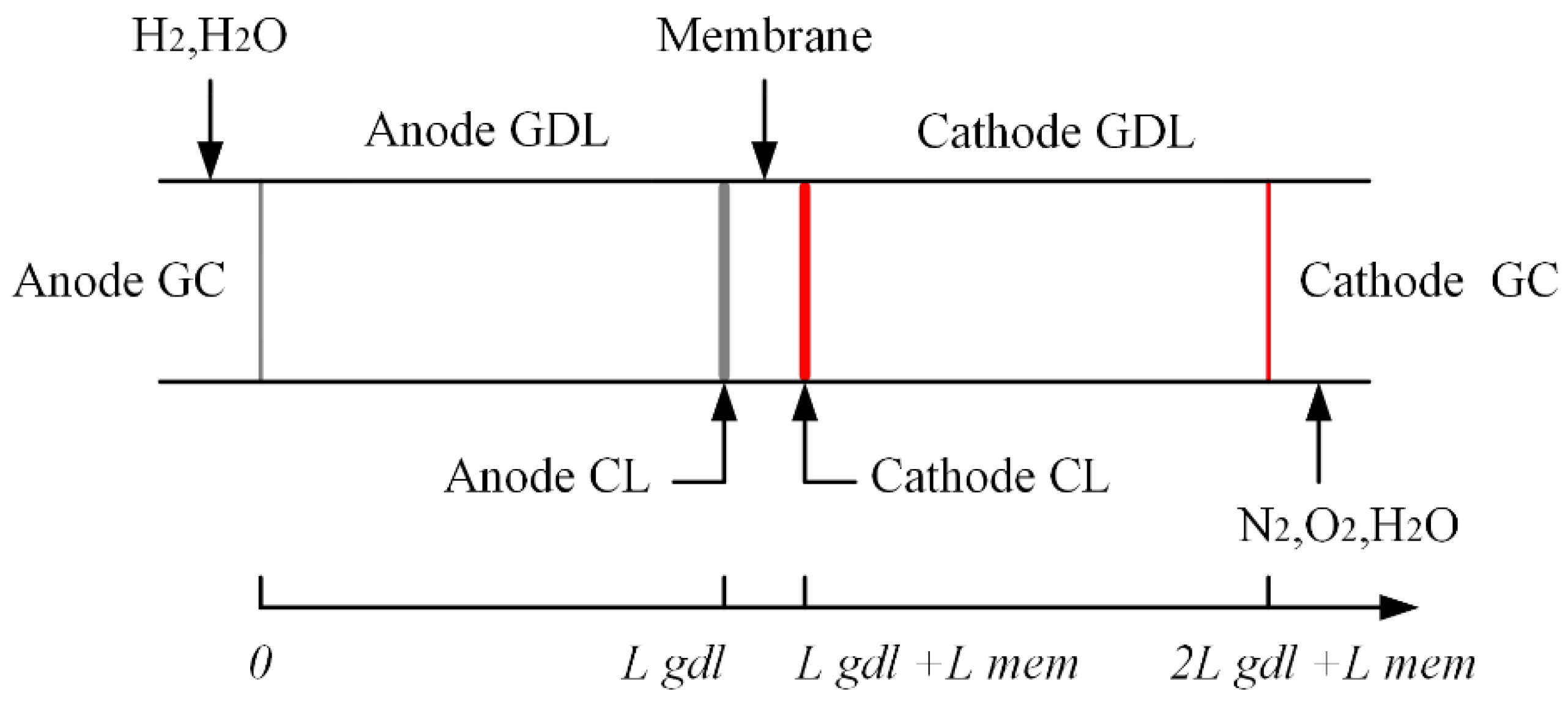
2. Mathematical Description
Electrochemical Model
3. Results
3.1. Gas Diffusion Layer
3.2. Catalyst Layers
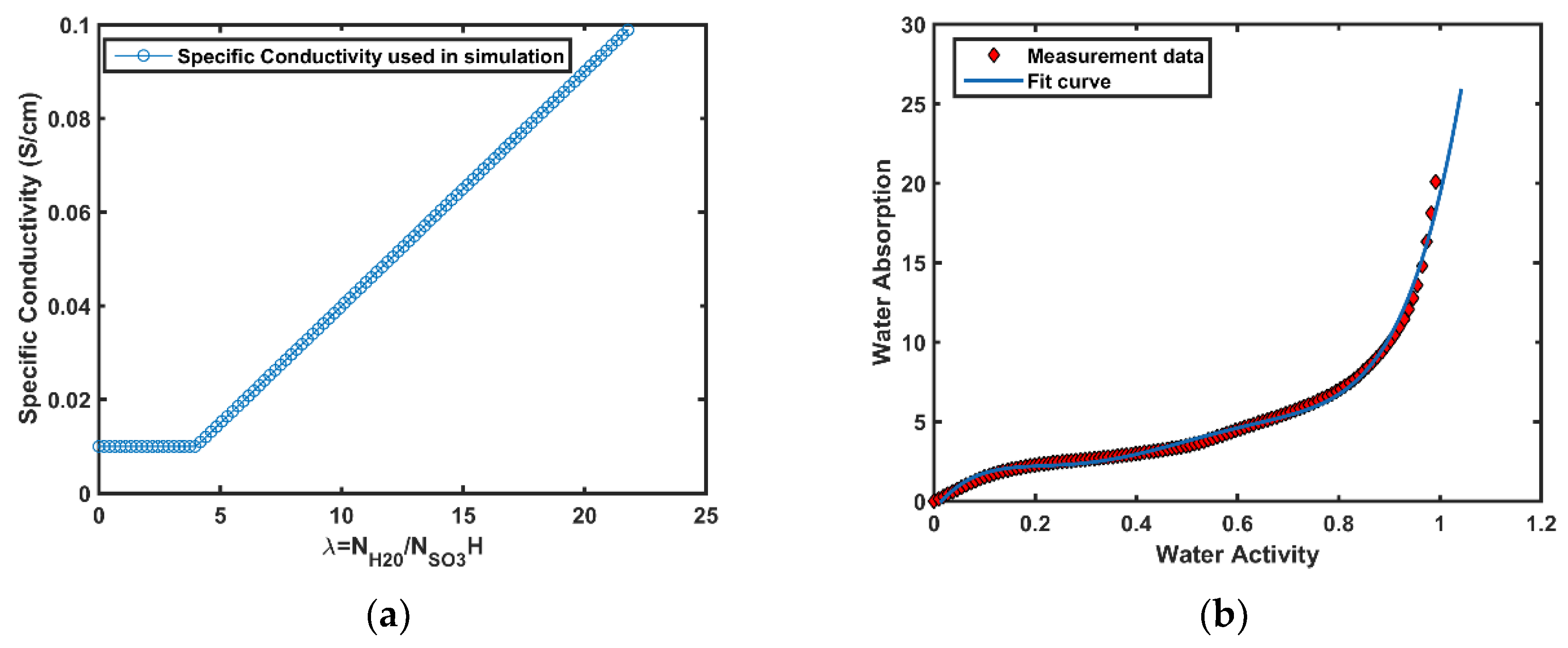
3.3. Water Transport in Membrane
3.4. Source Terms
3.5. Boundary Conditions and Initial Values
4. Mathematical Description
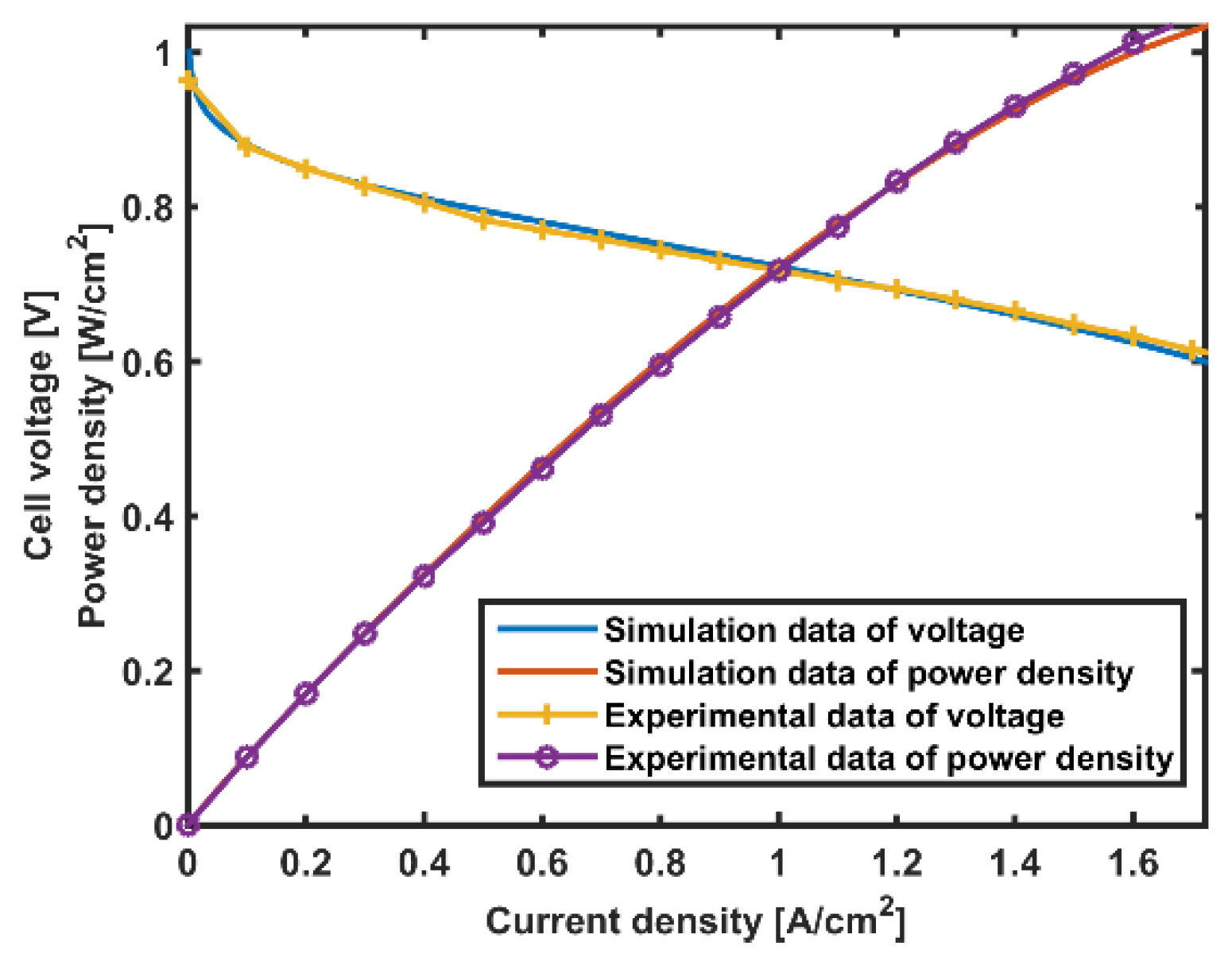
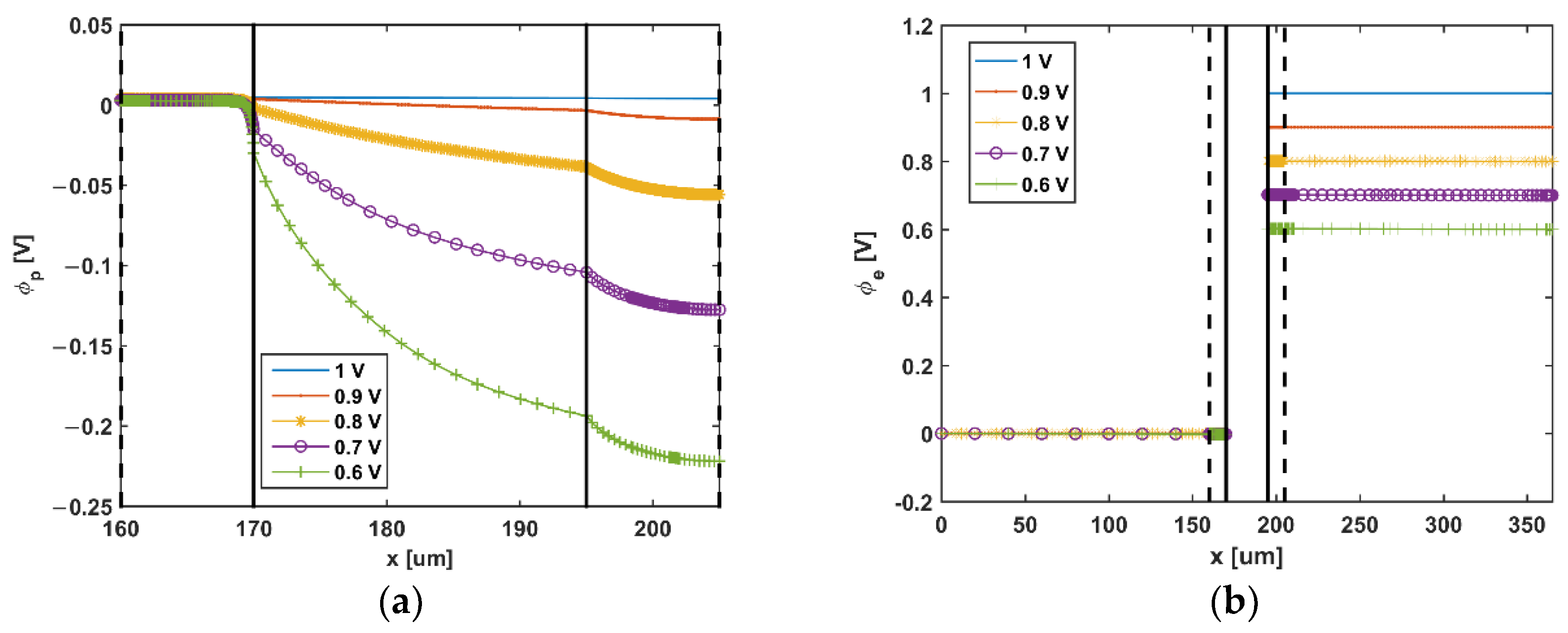
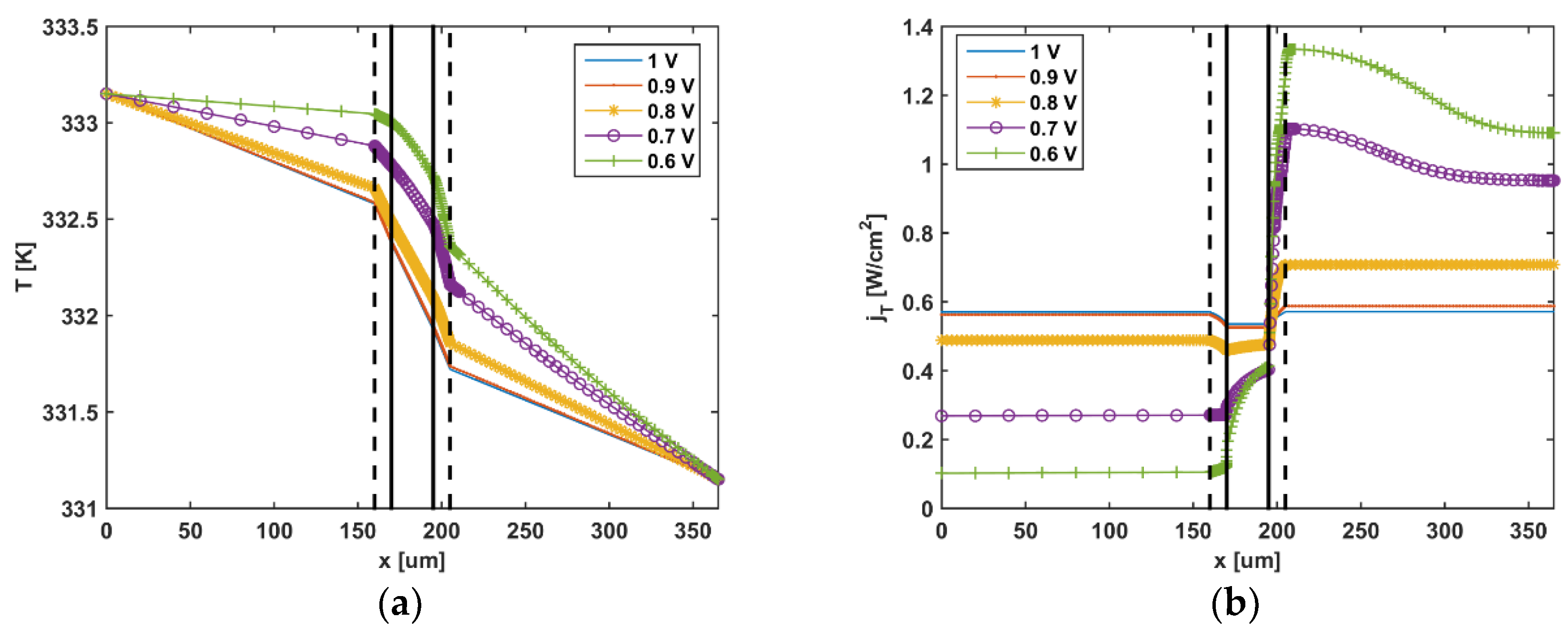
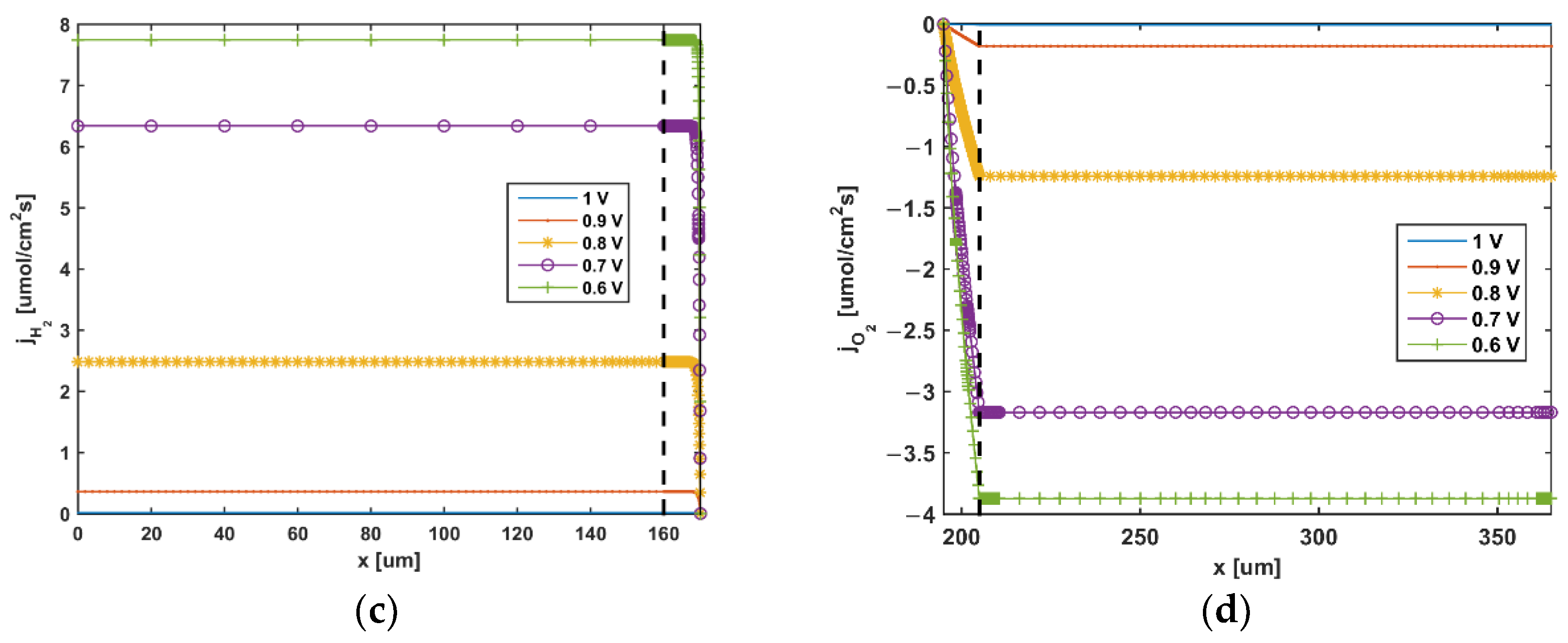
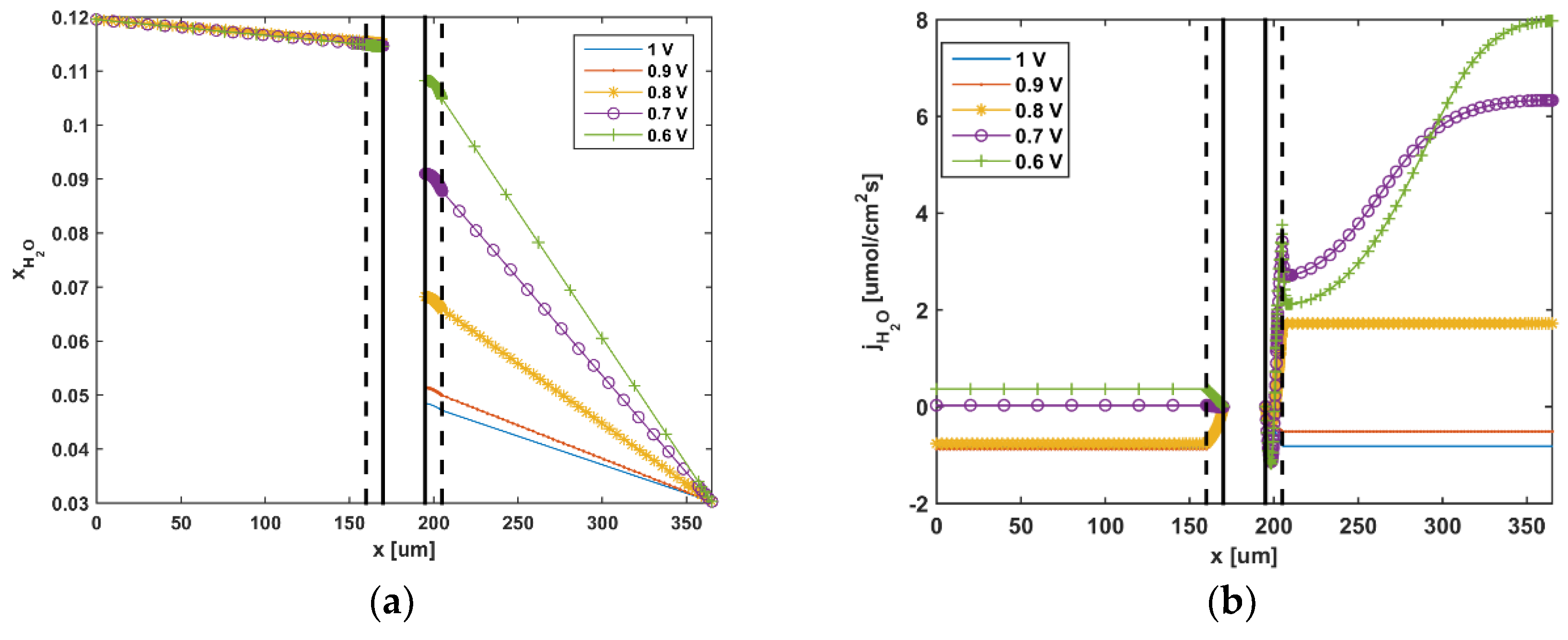
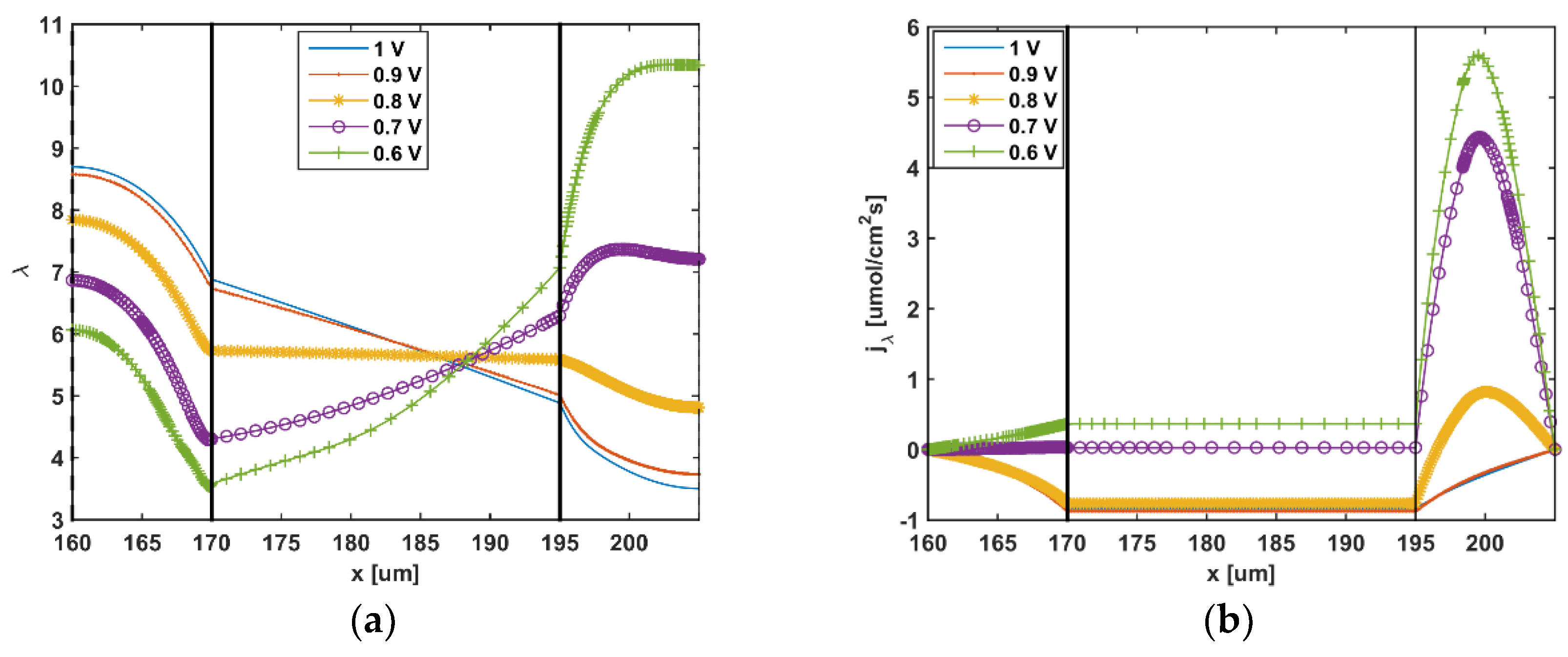
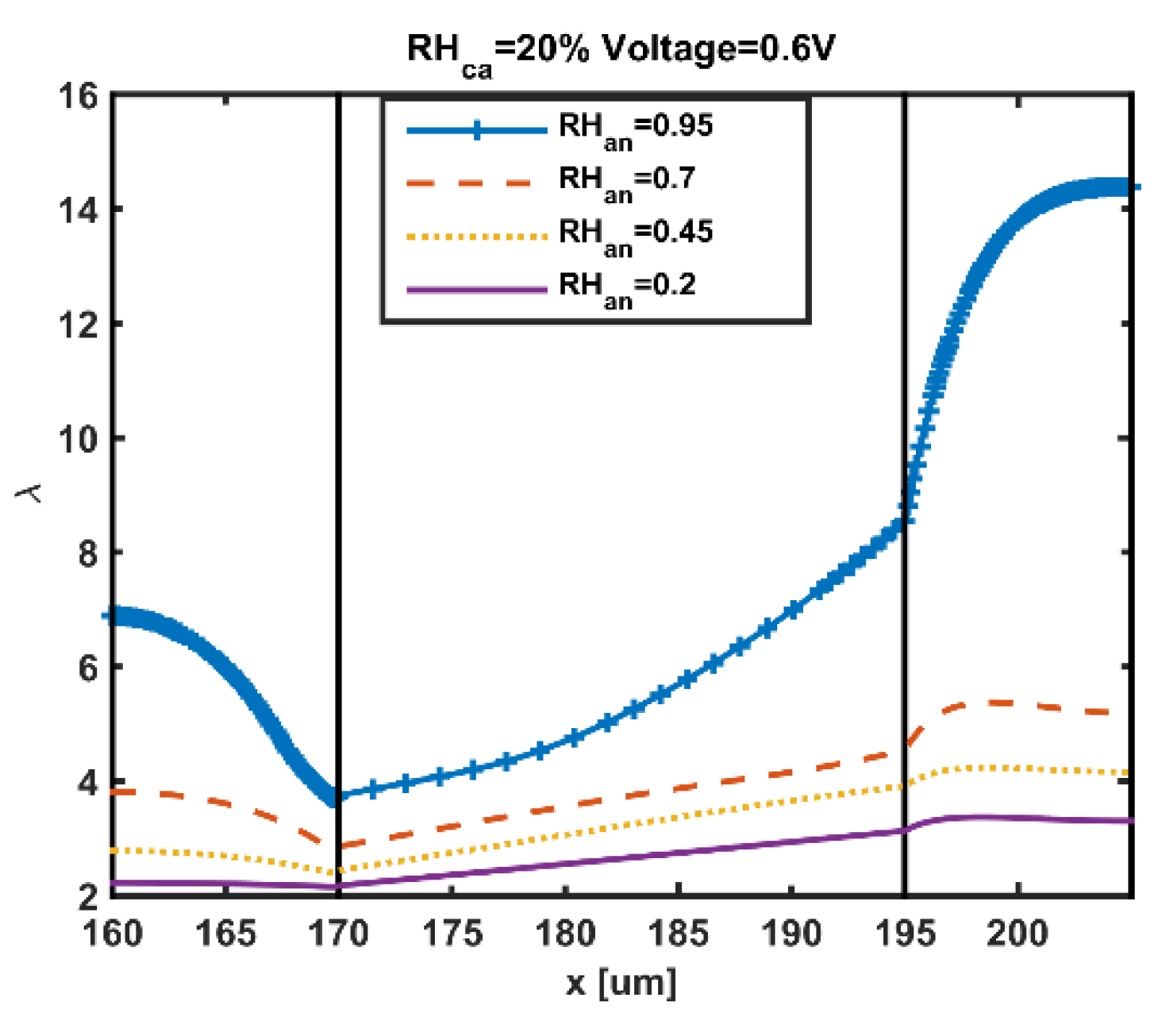
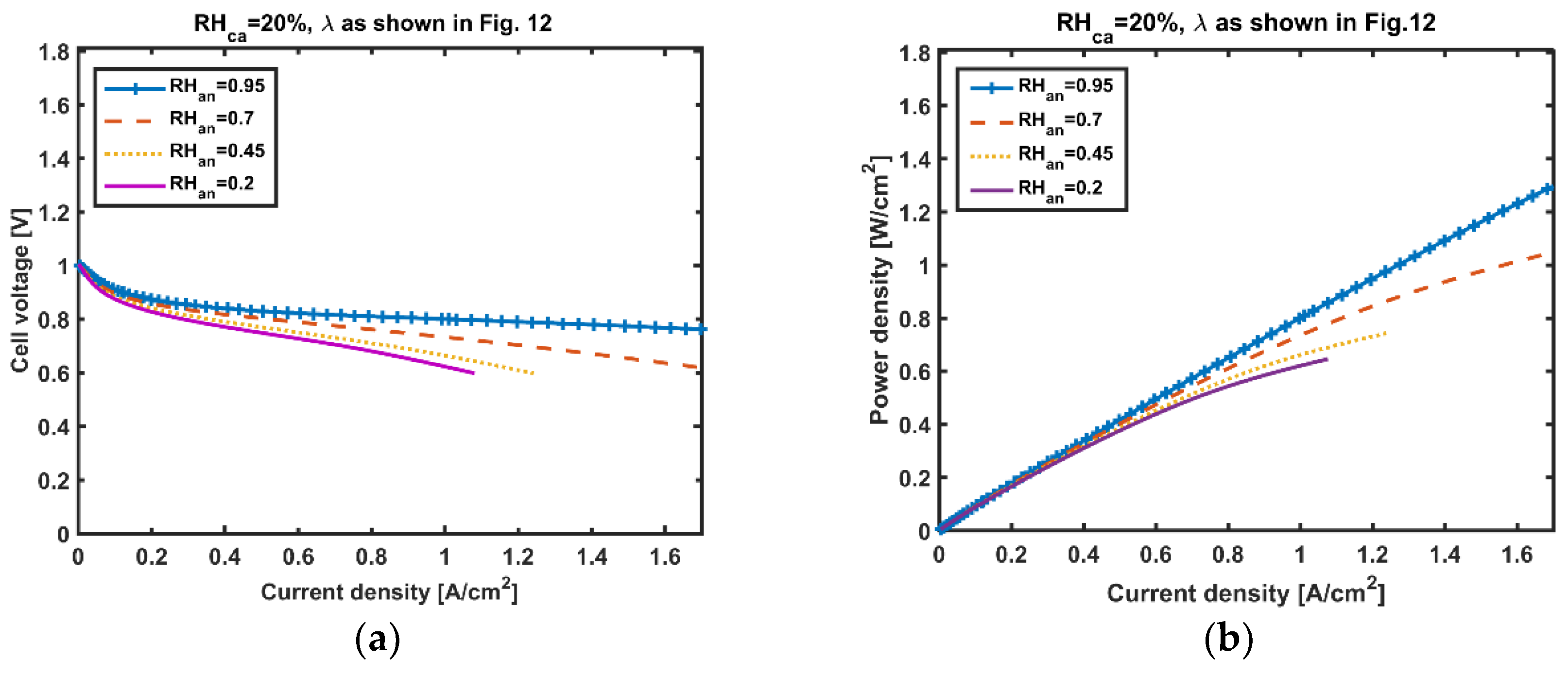
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviations | |
| ACL | Anode catalyst layer |
| CCL | Cathode catalyst layer |
| CL | Catalyst layer |
| EW | Equivalent weight |
| GC | Gas channel |
| GDE | Gas-diffusion electrode |
| GDL | Gas diffusion layer |
| HOR | Hydrogen oxidation reaction |
| MEA | Membrane-electrode assembly |
| MPL | Microporous layer |
| ORR | Oxygen reduction reaction |
| PEM | Polymer electrolyte membrane |
| PDE | Partial differential equation |
| Symbols | |
| C | Total interstitial gas concentration [mol/m3] |
| Cv,an | Water concentration on the surface area of the membrane at the anode side [mol/m3] |
| Cv,ca | Water concentration on the surface area of the membrane at the cathode side [mol/m3] |
| Di | Diffusivity of O2, H2, and H2O in the gas mixture [m2/s] |
| Di,ref | Diffusivity of i at reference conditions [m2/s] |
| Dcl | Knudsen diffusion coefficient [m2/s] |
| Dλ | Diffusion coefficient of dissolved water [m2/s] |
| Dw | Water diffusion coefficient related to the water activity [m2/s] |
| F | Faraday’s constant (96,485 C mol−1) |
| Had | Water ab-/desorption enthalpy [J/mol] |
| Hec | Evaporation/condensation enthalpy [J/mol] |
| J | Flux [A/m2] |
| L | Layer thickness [m] |
| Mw | Molar mass of water [kg/mol] |
| Mm,dry | Molar mass of water [kg/mol] |
| Nelectro | The net transport water caused by electro-osmotic drag [mol/(s∙cm2)] |
| Ndiffusion | The net transport water caused by back-diffusion [mol/(s∙cm2)] |
| P | Absolute gas pressure [Pa] |
| Pref | Reference pressure (1 atm, 101,325 Pa) |
| Psat | Saturation water vapor pressure [Pa] |
| Pa | Gas pressure in anode gas channel [Pa] |
| Pc | Gas pressure in cathode gas channel [Pa] |
| R | Gas constant (8.31446 J/mol K) |
| RH | Relative gas humidity [–] |
| RHa | Relative humidity in anode gas channel [–] |
| RHc | Relative humidity in cathode gas channel [–] |
| SH2O | Source term of hydrogen |
| SO2 | Source term of oxygen |
| Selectron | Source term of electrons |
| Sproton | Source term of protons |
| Swater | Source term of water |
| Sλ | Dissolved water reaction rate [mol/m3s] |
| ST | Heat source [W/m3] |
| Sred | Reduced liquid water saturation [–] |
| T | Absolute temperature [K] |
| Tref | Reference temperature [K] |
| Tst | Stack temperature [K] |
| Ta | Temperature of anode plate and GC [K] |
| Tc | Temperature of cathode plate and GC [K] |
| U | Open voltage of single fuel cell [V] |
| VW | Molar volume of liquid water [m3/mol] |
| Vm | Acid equivalent volume of membrane [m3/mol] |
| a | Active surface area density [1/m] |
| alg | Liquid–gas interfacial area density prefactor [1/m] |
| i | Electrochemical reaction rate [A/m3] |
| i0 | Exchange current density [A/m2] |
| ki | Water absorption/desorption transfer coefficient [m/s] |
| ke | Water evaporation transfer coefficient [m/s] |
| kc | Water condensation transfer coefficient [m/s] |
| nd | Electro-osmotic drag coefficient |
| Equivalent capillary radius [m] | |
| s | Liquid water saturation [–] |
| tm | Membrane thickness |
| ΔE | Galvani potential difference [V] |
| ΔE0 | Reversible potential difference [V] |
| ΔG | Gibbs free energy difference [J/mol] |
| ΔH | Enthalpy of formation of liquid water [J/mol] |
| ΔSHOR | Hydrogen oxidation reaction entropy [J/mol K] |
| ΔSORR | Oxygen reduction reaction entropy [J/mol K] |
| Greek letters | |
| αH2 | Mole fraction of hydrogen in dry fuel gas [–] |
| αO2 | Mole fraction of oxygen in dry oxidant gas [–] |
| β | Half-reaction symmetry factor [–] |
| γi | Water evaporation/condensation rate [1/s] |
| σe | Electric conductivity [S/m] |
| σp | Protonic conductivity [S/m] |
| εP | Porosity of the GDLs [–] |
| η | Activation overpotential [V] |
| κ | Hydraulic permeability [m2] |
| λ | Ionomer water content [–] |
| λan | Ionomer water content in anode [–] |
| λca | Ionomer water content in cathode [–] |
| λeq | Equilibrium ionomer water content [–] |
| μ | Dynamic viscosity of liquid water [Pa s] |
| ξ | Electro-osmotic drag coefficient [–] |
| π | Ratio of circumference to diameter [–] |
| ρm,dry | Dry density of membrane [kg m−3] |
| ϕe | Electrode phase potential [V] |
| ϕp | Electrolyte phase potential [V] |
| Water vapor mole fraction [–] | |
| Saturation water vapor mole fraction [–] | |
| Hydrogen mole fraction in anode GC [–] | |
| Water vapor mole fraction in anode GC [–] | |
| Oxygen mole fraction in cathode GC [–] | |
| Water vapor mole fraction in cathode GC [–] | |
| ψ | Empirical coefficient |
References
- Weber, A.Z.; Borup, R.L.; Darling, R.M.; Das, P.K.; Dursch, T.J.; Gu, W.; Harvey, D.B.; Kusoglu, A.; Litster, S.; Mench, M.M.; et al. A Critical Review of Modeling Transport Phenomena in Polymer-Electrolyte Fuel Cells. J. Electrochem. Soc. 2014, 161, F1254–F1299. [Google Scholar] [CrossRef] [Green Version]
- Uddin, K.M.S.; Saha, L.K.; Oshima, N. Water Transport through the Membrane of PEM Fuel Cell. Am. J. Comput. Appl. Math. 2014, 4, 225–238. [Google Scholar] [CrossRef]
- Omasta, T.J.; Wang, L.; Peng, X.; Lewis, C.A.; Varcoe, J.R.; Mustain, W.E. Importance of balancing membrane and electrode water in anion exchange membrane fuel cells. J. Power Sources 2018, 375, 205–213. [Google Scholar] [CrossRef] [Green Version]
- Iranzo, A.; Boillat, P. Liquid water distribution patterns featuring back-diffusion transport in a PEM fuel cell with neutron imaging. Int. J. Hydrogen Energy 2014, 39, 17240–17245. [Google Scholar] [CrossRef]
- Zhang, G.; Jiao, K. Multi-phase models for water and thermal management of proton exchange membrane fuel cell: A review. J. Power Sources 2018, 391, 120–133. [Google Scholar] [CrossRef]
- Jiao, K.; Li, X. Water transport in polymer electrolyte membrane fuel cells. Prog. Energy Combust. 2011, 37, 221–291. [Google Scholar] [CrossRef]
- Wiley, D.; Weihs, G.F. Electroosmotic Drag in Membranes. Encycl. Membr. 2016. [Google Scholar] [CrossRef]
- Kalantari, H. Numerical Analysis of Water Distribution in the Various Layers of Proton Exchange Membrane Fuel Cells. Comput. Chem. Eng. 2018, 118, 14–24. [Google Scholar] [CrossRef]
- Kim, S.; Mench, M.M. Investigation of temperature-driven water transport in polymer electrolyte fuel cell: Thermo-osmosis in membranes. J. Membr. Sci. 2009, 328, 113–120. [Google Scholar] [CrossRef]
- Gandomi, Y.A.; Edmundson, M.D.; Busby, F.C.; Mench, M.M. Water Management in Polymer Electrolyte Fuel Cells through Asymmetric Thermal and Mass Transport Engineering of the Micro-Porous Layers. J. Electrochem. Soc. 2016, 163, F933. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Sundén, B. Effects of gas diffusion layer deformation on the transport phenomena and performance of PEM fuel cells with interdigitated flow fields. Int. J. Hydrogen Energy 2018, 43, 16279–16292. [Google Scholar] [CrossRef]
- Iranzo, A.; Boillat, P. CFD simulation of the transient gas transport in a PEM fuel cell cathode during AC impedance testing considering liquid water effects. Energy 2018, 158, 449–457. [Google Scholar] [CrossRef]
- Muirhead, D.; Banerjee, R.; Lee, J.; George, M.G.; Ge, N.; Liu, H.; Chevalier, S.; Hinebaugh, J.; Han, K.; Bazylak, A. Simultaneous characterization of oxygen transport resistance and spatially resolved liquid water saturation at high-current density of polymer electrolyte membrane fuel cells with varied cathode relative humidity. Int. J. Hydrogen Energy 2017, 42, 29472–29483. [Google Scholar] [CrossRef]
- Gholizadeh, M.; Ghazikhani, M.; Khazaee, I. Effect of changing the water balance on electro-osmotic flow in an elliptical single proton exchange membrane fuel cell. Energy Convers. Manag. 2016, 120, 44–50. [Google Scholar] [CrossRef]
- AlRwashdeh, S.S.; Markötter, H.; Haußmann, J.; Arlt, T.; Klages, M.; Scholta, J.; Banhart, J.; Manke, I. Investigation of water transport dynamics in polymer electrolyte membrane fuel cells based on high porous micro porous layers. Energy 2016, 102, 161–165. [Google Scholar] [CrossRef]
- Yan, Q.; Toghiani, H.; Wu, J. Investigation of water transport through membrane in a PEM fuel cell by water balance experiments. J. Power Sources 2006, 158, 316–325. [Google Scholar] [CrossRef]
- Sanchez, D.G.; Ruiu, T.; Friedrich, K.A.; Sanchez-Monreal, J.; Vera, M. Analysis of the Influence of Temperature and Gas Humidity on the Performance Stability of Polymer Electrolyte Membrane Fuel Cells. J. Electrochem. Soc. 2015, 163, F150. [Google Scholar] [CrossRef] [Green Version]
- Bezmalinović, D.; Strahl, S.; Roda, V.; Husar, A. Water transport study in a high temperature proton exchange membrane fuel cell stack. Int. J. Hydrogen Energy 2014, 39, 10627–10640. [Google Scholar] [CrossRef] [Green Version]
- Edwards, R.L. Simplified, Alternative Formulation of Numerical Simulation of Proton Exchange Membrane Fuel Cell. Ph.D. Thesis, Doctor of Philosophy, Department of Mechanical Aerospace Engineering, Old Dominion University, Norfolk, VA, USA, 2018. [Google Scholar] [CrossRef]
- Zamel, N.; Li, X. Effective transport properties for polymer electrolyte membrane fuel cells—With a focus on the gas diffusion layer. Prog. Energy Combust. 2013, 39, 111–146. [Google Scholar] [CrossRef]
- Kurnia, J.C.; Chaedir, B.A.; Sasmito, A.P.; Shamim, T. Progress on open cathode proton exchange membrane fuel cell: Performance, designs, challenges and future directions. Appl. Energy 2021, 283, 116359. [Google Scholar] [CrossRef]
- Vetter, R.; Schumacher, J.O. Free open reference implementation of a two-phase PEM fuel cell model. Comput. Phys. Commun. 2019, 234, 223–234. [Google Scholar] [CrossRef]
- Hu, J.; Li, J.; Xu, L.; Huang, F.; Ouyang, M. Analytical calculation and evaluation of water transport through a proton exchange membrane fuel cell based on a one-dimensional model. Energy 2016, 111, 869–883. [Google Scholar] [CrossRef]
- Rakhshanpouri, S.; Rowshanzamir, S. Water transport through a PEM (proton exchange membrane) fuel cell in a seven-layer model. Energy 2013, 50, 220–231. [Google Scholar] [CrossRef]
- Song, G.H.; Meng, H. Numerical modeling and simulation of PEM fuel cells: Progress and perspective. Acta Mech. Sin. 2013, 29, 318–334. [Google Scholar] [CrossRef]
- Wang, Z.; Zeng, Y.; Sun, S.; Shao, Z.; Yi, B. Improvement of PEMFC water management by employing water transport plate as bipolar plate. Int. J. Hydrogen Energy 2017, 42, 21922–21929. [Google Scholar] [CrossRef]
- Wawdee, P.; Limtrakul, S.; Vatanatham, T.; Fowler, M.W. Water transport in a PEM fuel cell with slanted channel flow field plates. Int. J. Hydrogen Energy 2015, 40, 3739–3748. [Google Scholar] [CrossRef]
- Jeon, D.H. The impact of rib structure on the water transport behavior in gas diffusion layer of polymer electrolyte membrane fuel cells. J. Energy Inst. 2019, 92, 755–767. [Google Scholar] [CrossRef]
- Aslam, R.M.; Ingham, D.B.; Ismail, M.S.; Hughes, K.J.; Ma, L.; Pourkashanian, M. Simultaneous thermal and visual imaging of liquid water of the PEM fuel cell flow channels. J. Energy Inst. 2019, 92, 311–318. [Google Scholar] [CrossRef]
- Huo, S.; Jiao, K.; Park, J.W. On the water transport behavior and phase transition mechanisms in cold start operation of PEM fuel cell. Appl. Energy 2019, 233–234, 776–788. [Google Scholar] [CrossRef]
- Bhaiya, M.; Putz, A.; Secanell, M. Analysis of non-isothermal effects on polymer electrolyte fuel cell electrode assemblies. Electrochim. Acta 2014, 147, 294–309. [Google Scholar] [CrossRef]
- Yoshimune, W.; Kato, S.; Yamaguchi, S. Multi-scale pore morphologies of a compressed gas diffusion layer for polymer electrolyte fuel cells. Int. J. Heat Mass Transf. 2020, 152, 119537. [Google Scholar] [CrossRef]
- Liu, X.; Peng, F.; Lou, G.; Wen, Z. Liquid water transport characteristics of porous diffusion media in polymer electrolyte membrane fuel cells: A review. J. Power Sources 2015, 299, 85–96. [Google Scholar] [CrossRef]
- Martinez, N.; Peng, Z.; Morin, A.; Porcar, L.; Gebel, G.; Lyonnard, S. Real time monitoring of water distribution in an operando fuel cell during transient states. J. Power Sources 2017, 365, 230–234. [Google Scholar] [CrossRef]
- Duan, Q.; Wang, H.; Benziger, J. Transport of liquid water through Nafion membranes. J. Membr. Sci. 2012, 392–393, 88–94. [Google Scholar] [CrossRef]
- Wijmans, J.G.; Baker, R.W. The solution-diffusion model: A review. J. Membr. Sci. 1995, 107, 1–21. [Google Scholar] [CrossRef]
- Cha, D.; Ahn, J.H.; Kim, H.S.; Kim, Y. Effects of clamping force on the water transport and performance of a PEM (proton electrolyte membrane) fuel cell with relative humidity and current density. Energy 2015, 93, 1338–1344. [Google Scholar] [CrossRef]
- Sundén, B. Transport phenomena in fuel cells. In Hydrogen, Batteries and Fuel Cells, 1st ed.; Jones, G., Ed.; Academic Press: Cambridge, MA, USA, 2019; Chapter 9; pp. 145–166. [Google Scholar]
- Jithin, M.; Siddharth, S.; Das, M.K.; De, A. Simulation of coupled heat and mass transport with reaction in PEM fuel cell cathode using lattice Boltzmann method. Therm. Sci. Eng. Prog. 2017, 4, 85–96. [Google Scholar] [CrossRef]





| Description | Symbol | Flux Equation | Continuity Equation |
|---|---|---|---|
| Fourier’s heat conduction | |||
| Water transport in ionomer | |||
| Ohm’s law of electrons | |||
| Ohm’s law of proton | |||
| Fickian oxygen diffusion | |||
| Fickian hydrogen diffusion | |||
| Fickian water vapor diffusion | |||
| Liquid water transport (Darcy’s law) |
| Symbol | Explanation | AGDL&CGDL | ACL&CCL | PEM |
|---|---|---|---|---|
| L | Layer thickness | 160 μm | 10 μm | 25 μm |
| Symbol | Explanation | Value |
|---|---|---|
| RHC | Relative humidity in cathode GC | 20% |
| SC | Liquid saturation at CGDL/GC interface | 0.12 |
| TA | Temperature of anode plate and GC | 60 °C |
| TC | Temperature of cathode plate and GC | 58 °C |
| αH2 | Hydrogen mole fraction in dry fuel gas | 1.00 |
| αO2 | Oxygen mole fraction in dry oxidant gas | 0.21 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, W.-W.; Ou, K.; Jung, S.; Kim, Y.-B. Analyzing and Modeling of Water Transport Phenomena in Open-Cathode Polymer Electrolyte Membrane Fuel Cell. Appl. Sci. 2021, 11, 5964. https://doi.org/10.3390/app11135964
Yuan W-W, Ou K, Jung S, Kim Y-B. Analyzing and Modeling of Water Transport Phenomena in Open-Cathode Polymer Electrolyte Membrane Fuel Cell. Applied Sciences. 2021; 11(13):5964. https://doi.org/10.3390/app11135964
Chicago/Turabian StyleYuan, Wei-Wei, Kai Ou, Seunghun Jung, and Young-Bae Kim. 2021. "Analyzing and Modeling of Water Transport Phenomena in Open-Cathode Polymer Electrolyte Membrane Fuel Cell" Applied Sciences 11, no. 13: 5964. https://doi.org/10.3390/app11135964
APA StyleYuan, W.-W., Ou, K., Jung, S., & Kim, Y.-B. (2021). Analyzing and Modeling of Water Transport Phenomena in Open-Cathode Polymer Electrolyte Membrane Fuel Cell. Applied Sciences, 11(13), 5964. https://doi.org/10.3390/app11135964






