A Novel Method for Intrinsic and Extrinsic Parameters Estimation by Solving Perspective-Three-Point Problem with Known Camera Position
Abstract
:1. Introduction
2. Materials and Methods
2.1. Pinhole Camera Model
2.2. P3P Problem
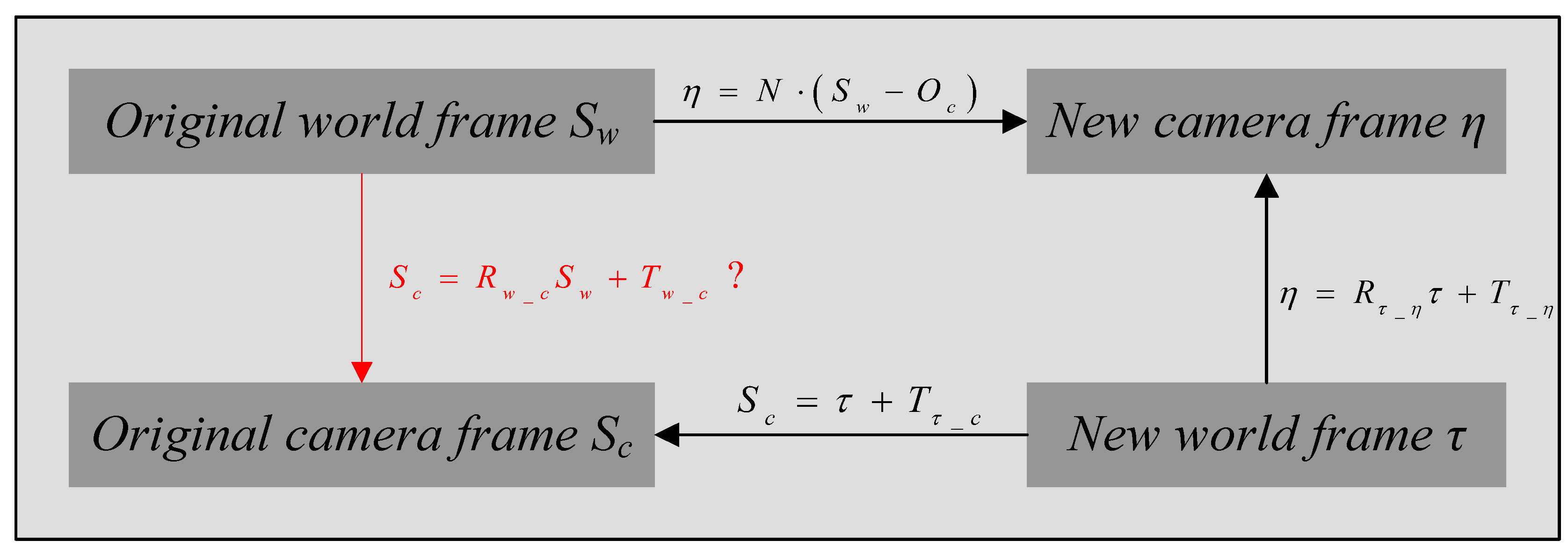
2.3. Problem Statement and Method
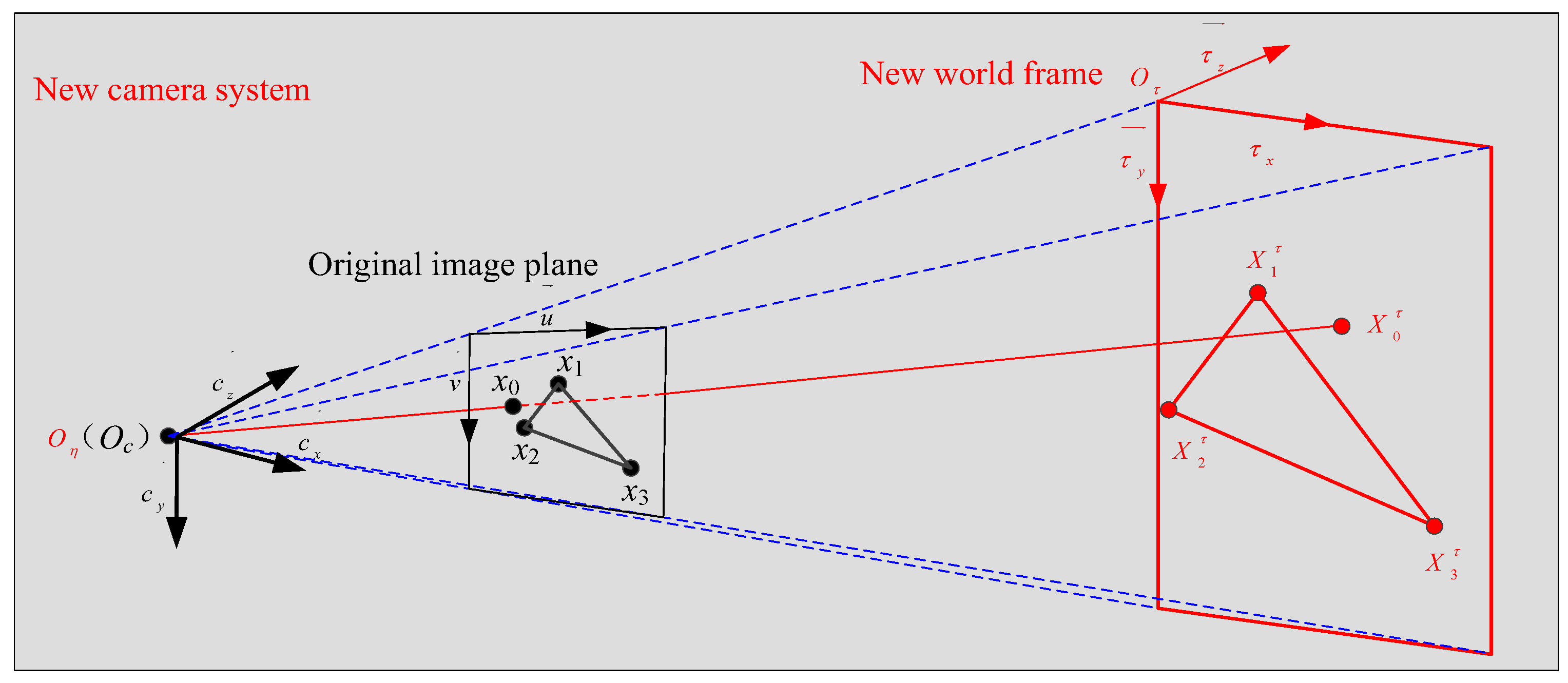
2.3.1. Problem Statement
2.3.2. Proposed Method
3. Experiments and Results
3.1. Synthetic Data
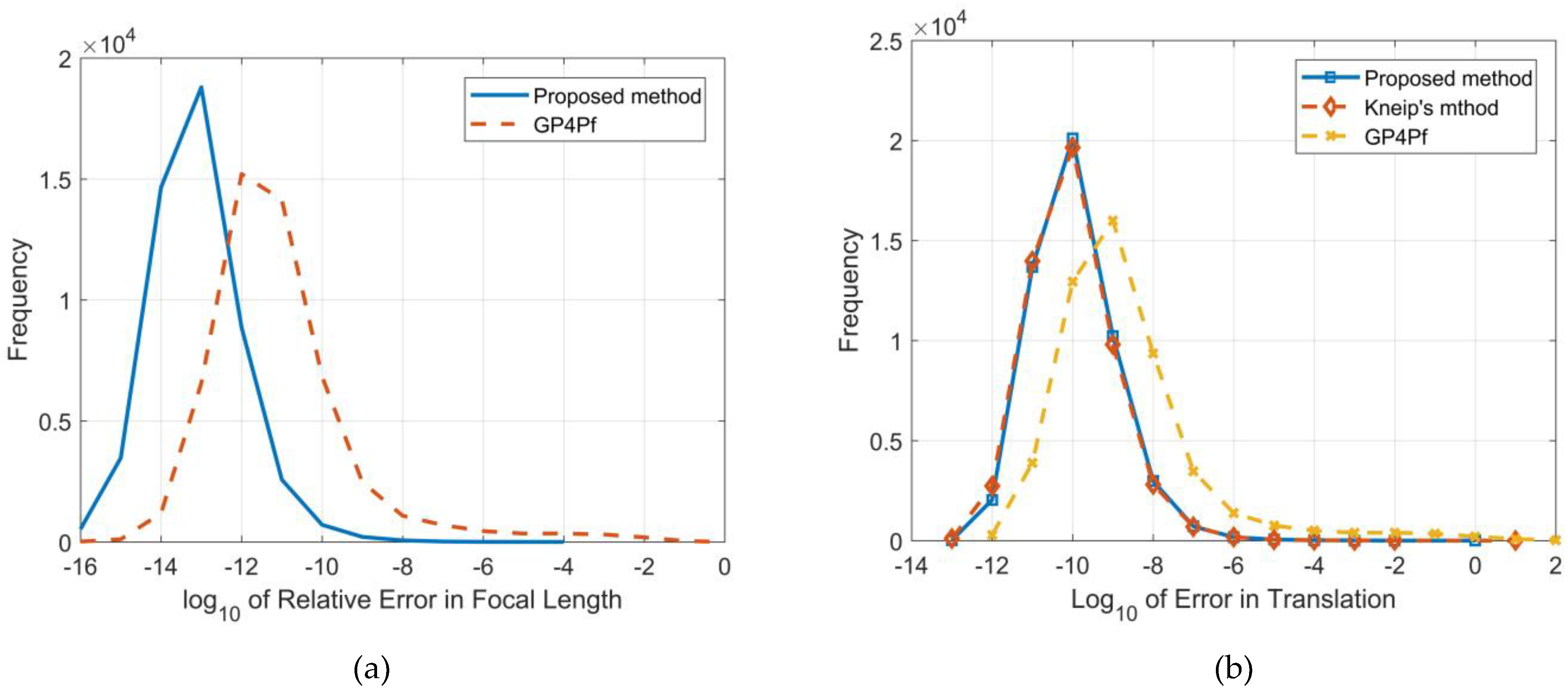
3.1.1. Numerical Stability
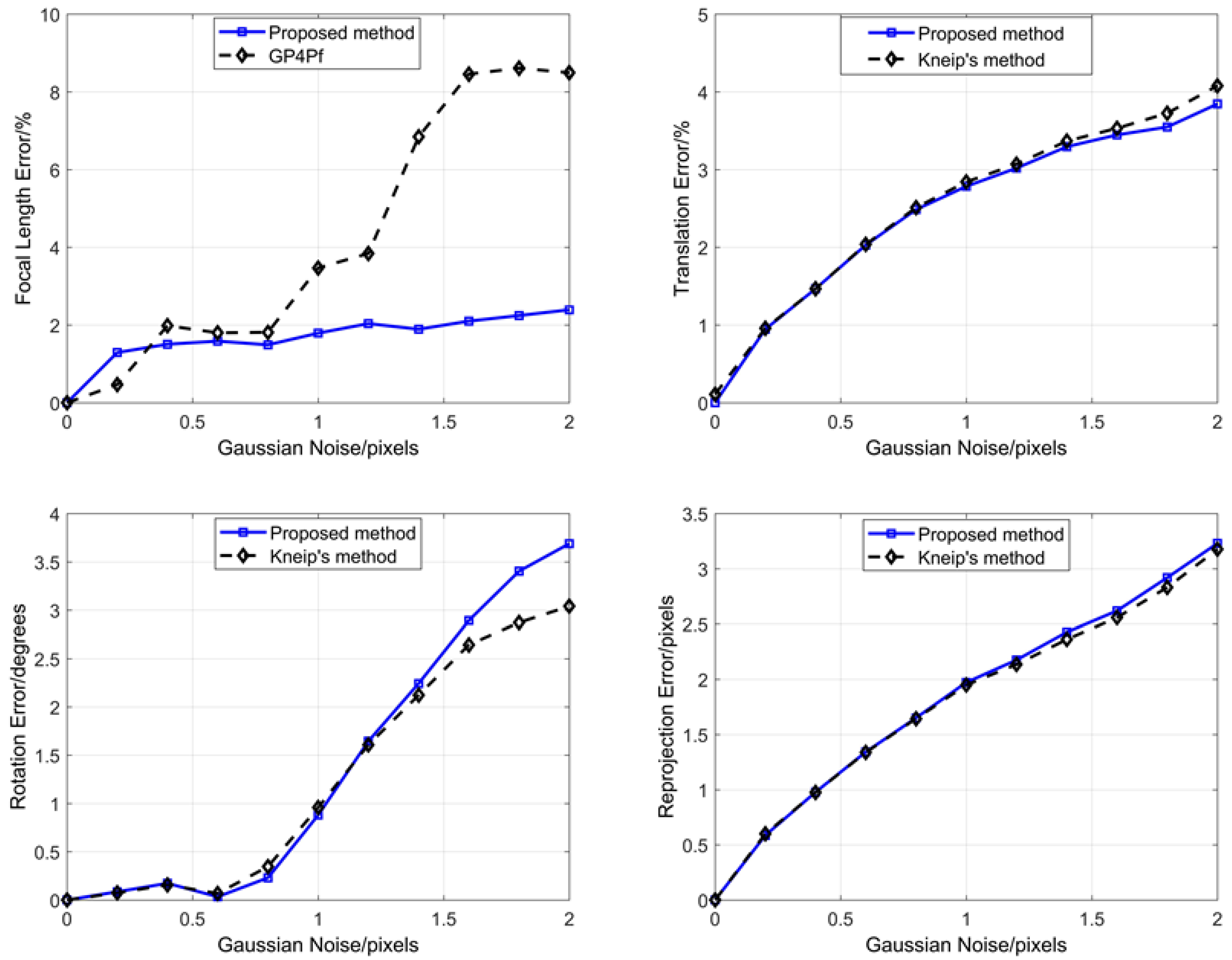
3.1.2. Noise Sensitivity
3.1.3. Computational Time
3.2. Real Images
4. Discussion
4.1. Difference and Advantage
4.2. Future Work
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lu, X.X. A Review of Solutions for Perspective-n-Point Problem in Camera Pose Estimation. J. Phys. Conf. Ser. 2018, 1087, 052009. [Google Scholar] [CrossRef]
- Nakano, G. A versatile approach for solving PnP, PnPf, and PnPfr problems. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016; pp. 338–352. [Google Scholar]
- Zhou, L.; Kaess, M. An efficient and accurate algorithm for the perspective-n-point problem. In Proceedings of the International Conference on Intelligent Robots and Systems, Macau, China, 3–8 November 2019; pp. 6245–6252. [Google Scholar]
- Zheng, Y.; Kuang, Y.; Sugimoto, S.; Astrom, K.; Okutomi, M. Revisiting the pnp problem: A fast, general and optimal solution. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013; pp. 2344–2351. [Google Scholar]
- Ferraz, L.; Binefa, X.; Moreno-Noguer, F. Very fast solution to the PnP problem with algebraic outlier rejection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 501–508. [Google Scholar]
- Lourakis, M.; Terzakis, G. A globally optimal method for the PnP problem with MRP rotation parameterization. In Proceedings of the International Conference on Pattern Recognition, Milan, Italy, 10–15 January 2021; pp. 3058–3063. [Google Scholar]
- Yu, Q.; Xu, G.; Zhang, L.; Shi, J. A consistently fast and accurate algorithm for estimating camera pose from point correspondences. Measurement 2021, 172, 108914. [Google Scholar] [CrossRef]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision, 2nd ed.; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Wu, Y.; Tang, F.; Li, H. Image-based camera localization: An overview. Vis. Comput. Ind. Biomed. Art 2018, 1, 1–13. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yuan, J.S.C. A general photogrammetric method for determining object position and orientation. IEEE Trans. Robot. Autom. 1989, 5, 129–142. [Google Scholar] [CrossRef]
- Wang, P.; Xu, G.; Wang, Z.; Cheng, Y. An efficient solution to the perspective-three-point pose problem. Comput. Vis. Image Underst. 2018, 166, 81–87. [Google Scholar] [CrossRef]
- Wolfe, W.; Mathis, D.; Sklair, C.; Magee, M. The perspective view of three points. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 13, 66–73. [Google Scholar] [CrossRef]
- Kneip, L.; Scaramuzza, D.; Siegwart, R. A novel parametrization of the perspective-three-point problem for a direct computation of absolute camera position and orientation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Colorado Springs, CO, USA, 20–25 June 2011; pp. 2969–2976. [Google Scholar]
- Ke, T.; Roumeliotis, S.I. An efficient algebraic solution to the perspective-three-point problem. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 7225–7233. [Google Scholar]
- Masselli, A.; Zell, A. A new geometric approach for faster solving the perspective-three-point problem. In Proceedings of the International Conference on Pattern Recognition, Stockholm, Sweden, 24–28 August 2014; pp. 2119–2124. [Google Scholar]
- Gao, X.-S.; Hou, X.-R.; Tang, J.; Cheng, H.-F. Complete solution classification for the perspective-three-point problem. IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 930–943. [Google Scholar]
- Grunert, J.A. Das pothenotische problem in erweiterter gestalt nebst über seine anwendungen in der geodäsie. Grunerts Archiv für Mathematik und Physik. 1841, Band 1, 238–248. [Google Scholar]
- Fischler, M.A.; Bolles, R.C. Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography. Read. Comput. Vis. 1987, 24, 726–740. [Google Scholar]
- Camposeco, F.; Cohen, A.; Pollefeys, M.; Sattler, T. Hybrid camera pose estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 136–144. [Google Scholar]
- Taketomi, T.; Okada, K.; Yamamoto, G.; Miyazaki, J.; Kato, H. Camera pose estimation under dynamic intrinsic parameter change for augmented reality. Comput. Graph. 2014, 44, 11–19. [Google Scholar] [CrossRef] [Green Version]
- Zheng, Y.; Sugimoto, S.; Sato, I.; Okutomi, M. A general and simple method for camera pose and focal length determination. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 430–437. [Google Scholar]
- Wu, C. P3.5p: Pose estimation with unknown focal length. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 2440–2448. [Google Scholar]
- Bujnak, M.; Kukelova, Z.; Pajdla, T. A general solution to the P4P problem for camera with unknown focal length. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AL, USA, 23–28 June 2008; pp. 1–8. [Google Scholar]
- Kanaeva, E.; Gurevich, L.; Vakhitov, A. Camera Pose and Focal Length Estimation Using Regularized Distance Constraints. In Proceedings of the British Machine Vision Conference, Swansea, UK, 7–10 September 2015; pp. 162.1–162.12. [Google Scholar]
- Triggs, B. Camera pose and calibration from 4 or 5 known 3d points. In Proceedings of the Seventh IEEE International Conference on Computer Vision, Corfu, Greece, 20–25 September 1999; Volume 1, pp. 278–284. [Google Scholar]
- Abidi, M.A.; Chandra, T. A new efficient and direct solution for pose estimation using quadrangular targets: Algorithm and evaluation. IEEE Trans. Pattern Anal. Mach. Intell. 1995, 17, 534–538. [Google Scholar] [CrossRef] [Green Version]
- Bujnak, M.; Kukelova, Z.; Pajdla, T. New efficient solution to the absolute pose problem for camera with unknown focal length and radial distortion. In Proceedings of the Asian Conference on Computer Vision, Queenstown, New Zealand, 8–12 November 2010; pp. 11–24. [Google Scholar]
- Josephson, K.; Byrod, M. Pose estimation with radial distortion and unknown focal length. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Miami Beach, FL, USA, 20–25 June 2009; pp. 2419–2426. [Google Scholar]
- Guo, Y. A Novel Solution to the P4P Problem for an Uncalibrated Camera. J. Math. Imaging Vis. 2013, 45, 186–198. [Google Scholar] [CrossRef]
- Wu, Y.; Hu, Z. PnP Problem Revisited. J. Math. Imaging Vis. 2005, 24, 131–141. [Google Scholar] [CrossRef]
- Tsai, R. A versatile camera calibration technique for high-accuracy 3D machine vision metrology using off-the-shelf TV cameras and lenses. IEEE J. Robot. Autom. 1987, 3, 323–344. [Google Scholar] [CrossRef] [Green Version]




| Method | Proposed Method | GP4Pf | Kneip’s Method |
|---|---|---|---|
| Computational Time | 0.538 ms | 2.565 ms | 0.525 ms |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, K.; Ye, H.; Gu, J.; Chen, H. A Novel Method for Intrinsic and Extrinsic Parameters Estimation by Solving Perspective-Three-Point Problem with Known Camera Position. Appl. Sci. 2021, 11, 6014. https://doi.org/10.3390/app11136014
Guo K, Ye H, Gu J, Chen H. A Novel Method for Intrinsic and Extrinsic Parameters Estimation by Solving Perspective-Three-Point Problem with Known Camera Position. Applied Sciences. 2021; 11(13):6014. https://doi.org/10.3390/app11136014
Chicago/Turabian StyleGuo, Kai, Hu Ye, Junhao Gu, and Honglin Chen. 2021. "A Novel Method for Intrinsic and Extrinsic Parameters Estimation by Solving Perspective-Three-Point Problem with Known Camera Position" Applied Sciences 11, no. 13: 6014. https://doi.org/10.3390/app11136014
APA StyleGuo, K., Ye, H., Gu, J., & Chen, H. (2021). A Novel Method for Intrinsic and Extrinsic Parameters Estimation by Solving Perspective-Three-Point Problem with Known Camera Position. Applied Sciences, 11(13), 6014. https://doi.org/10.3390/app11136014






