Design and Analysis of Cam Wave Generator Based on Free Deformation in Non-Working Area of the Flexspline
Abstract
:1. Introduction
2. Background
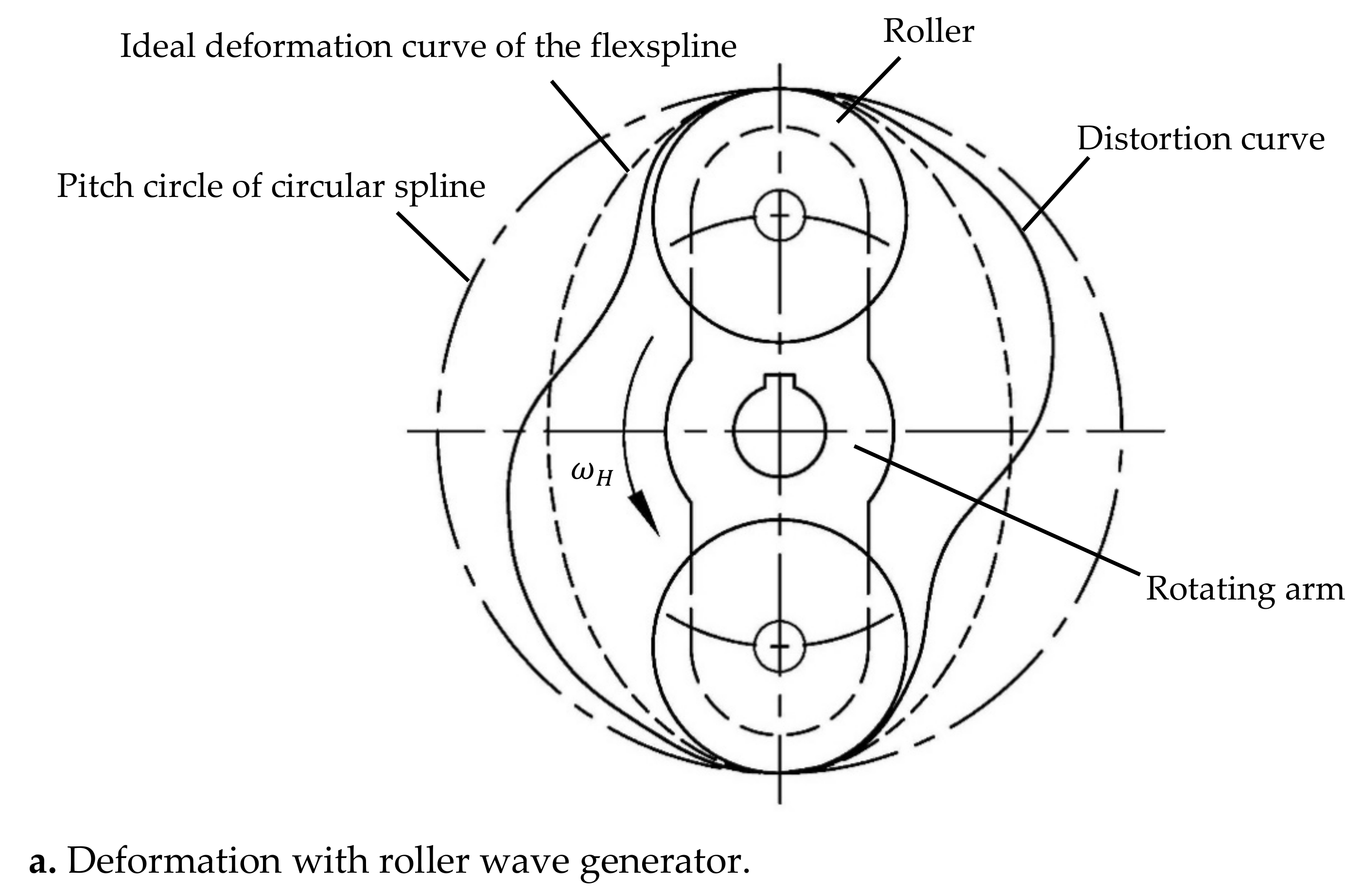
2.1. Free Deformation
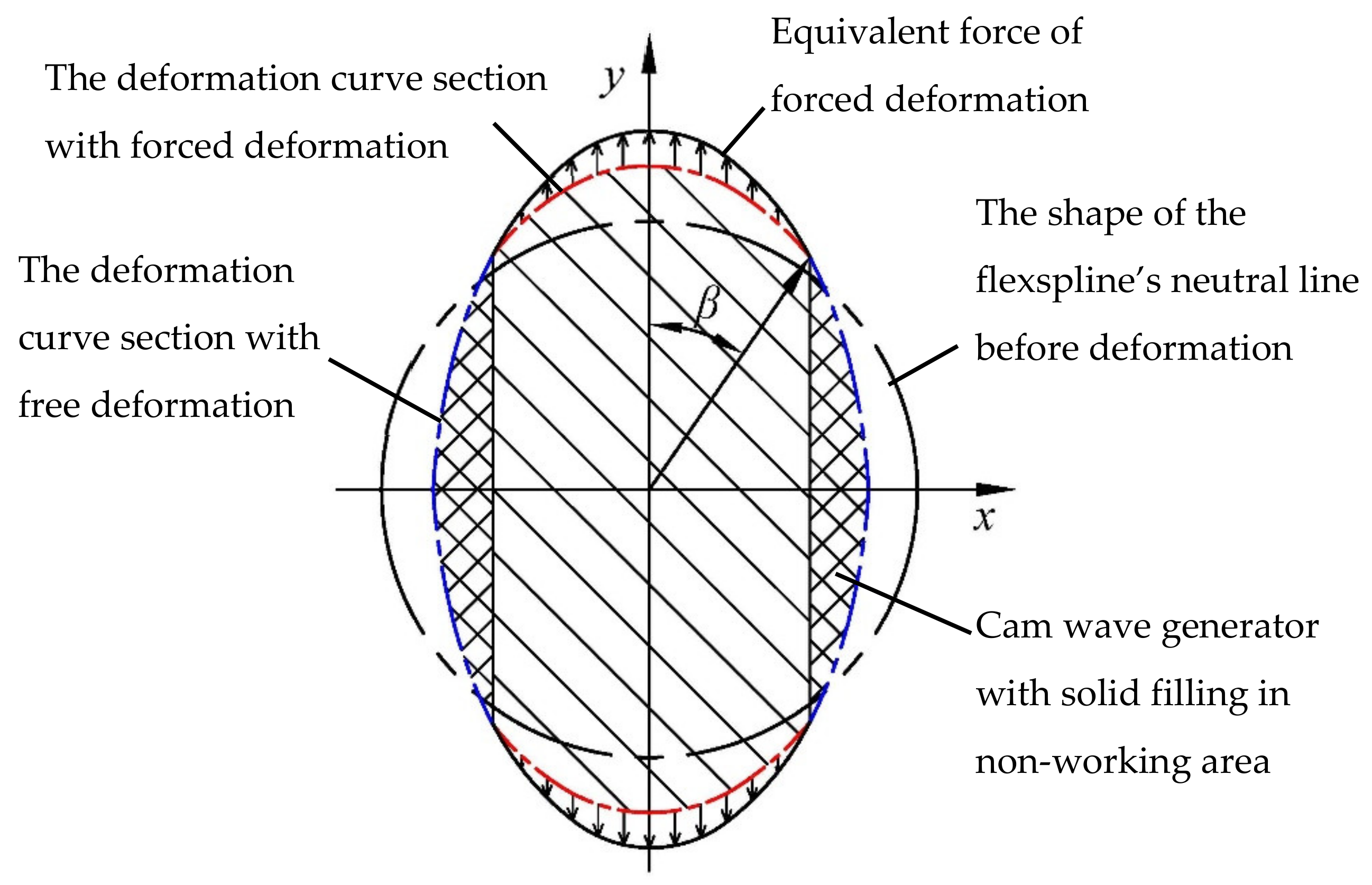
2.2. Forced Deformation
3. Cam Wave Generators with Free Deformation in Non-Working Area
3.1. Mathematical Model
3.2. Design of Cam Wave Generator
3.3. Sample Design with Double Eccentric Arc Cam Wave Generator
4. Numerical Examples and Discussion
4.1. Parameter Selection
4.2. Result Presentation
5. Conclusions
- (1)
- When the forced deformation in the non-working area is released, the stress distribution of the flexspline in working area is smoother, and the overall basic deformation stress of the flexspline is obviously reduced.
- (2)
- With increasing the wrap angle, the basic stress of the flexspline would also increase. Moreover, when the wrap angle increases to a certain value determined by cam parameters, the flexspline’s deflect causes stress concentration.
- (3)
- Solid filling in the non-working area of the cam according to the deflection curve of the flexspline is an effective method to keep the deformation shape of the flexspline unchanged during rotating, which ensures high meshing quality without increasing the basic stress.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hasl, C.; Liu, H.; Oster, P.; Tobie, T.; Stahl, K. Method for calculating the tooth root stress of plastic spur gears meshing with steel gears under consideration of deflection-induced load sharing. Mech. Mach. Theory 2017, 111, 152–163. [Google Scholar] [CrossRef]
- Zhou, Y.; Wu, Y.; Wang, L.; Tang, J. A new closed-form calculation of envelope surface for modeling face gears. Mech. Mach. Theory 2019, 137, 211–226. [Google Scholar] [CrossRef]
- Tang, J.; Yang, B.; Shi, Z. Influence on center distance by measurement force in double-flank gear rolling test. Measurement 2021, 168, 108321. [Google Scholar] [CrossRef]
- Bhabani, S.M.; Vineet, S.; Rathindranath, M. Effect of cam insertion on stresses in harmonic drive in industrial robotic joints. Procedia Comput. Sci. 2018, 133, 432–439. [Google Scholar] [CrossRef]
- Han, S.J.; Se, H.O. A study on stress and vibration analysis of a steel and hybrid flexspline for harmonic drive. Compos. Struct. 1999, 47, 827–833. [Google Scholar] [CrossRef]
- Ostapski, W. Analysis of the stress state in the harmonic drive generator-flexspline system in relation to selected structural parameters and manufacturing deviations. Bull. Pol. Acad. Sci. Tech. Sci. 2010, 58, 683–698. [Google Scholar] [CrossRef] [Green Version]
- Ostapski, W.; Mukha, I. Stress state analysis of harmonic drive elements by FEM. Bull. Pol. Acad. Sci. 2007, 55, 115–123. [Google Scholar]
- Sahoo, V.; Maiyi, R. Load sharing by tooth pairs in involute toothed harmonic drive with conventional wave generator cam. Meccanica 2018, 53, 373–394. [Google Scholar] [CrossRef]
- Xin, H.; Mo, H.; Gao, J.; Wang, W.; Cui, D.; Liu, L.; Wang, T.; Xin, Y. Study on the gear tooth influence coefficients of flexspline of harmonic drive. Adv. Mater. Res. 2013, 774–776, 144–147. [Google Scholar] [CrossRef]
- Fan, Y.; Wang, H. Study on the deformation of flexspline in the engagement out put harmonic drive. J. Nanjing Univ. Sci. Technol. Soc. Sci. Ed. 1996, 20, 38–42. [Google Scholar]
- Zhang, L.; Liu, X.; Wang, C.; Wei, L.; Qiao, X.; Wang, R. Influence of radial deformation on stress of flexspline and meshing characteristic of harmonic reducer. Mech. Transm. 2017, 41, 166–169. [Google Scholar] [CrossRef]
- Hu, S.; Yao, T.; Qin, H.; Zhang, Y.; Yang, B. Research of internal stress distribution of double arc flexspline. Mech. Transm. 2020, 44, 29–34. [Google Scholar] [CrossRef]
- Dong, H.; Wang, D. Elastic deformation characteristic of the flexspline in harmonic drive. In Proceedings of the ASME/IFTOMM, International Conference on Reconfigurable Mechanisms and Robots, London, UK, 22–24 July 2009; pp. 363–369. [Google Scholar]
- Yang, P. Harmonic Gear Driving Device and the Short Flexspline Study. Ph.D. Thesis, China Academy of Machinery Science and Technology, Beijing, China, 2006. [Google Scholar]
- Xia, T.; Jiang, P.; Ma, C.; Chen, W.; Yan, R. Research advance of the failure mechanism and friction wear of flexible wheel of harmonic reducer. J. Mech. Transm. 2016, 40, 173–176. [Google Scholar] [CrossRef]
- Routh, B.; Maiti, R.; Ray, A.K. Analysis of coning and lubrication at flexspline cup and cam interface in conventional harmonic drives. Ind. Lubr. Tribol. 2017, 69, 817–827. [Google Scholar] [CrossRef]
- Federico, G.; Victor, H.M.; Ettore, P. Influence of wave generator profile on the pure kinematic error and centrodes of harmonic drive. Mech. Mach. Theory 2016, 104, 100–117. [Google Scholar] [CrossRef]
- Pacana, J.; Witkowski, W.; Mucha, J. FEM analysis of stress distribution in the hermetic harmonic drive flexspline. Strength Mater. 2017, 49, 388–398. [Google Scholar] [CrossRef]
- Ma, D.; Wu, J.; Liu, T.; Yan, S. Deformation analysis of the flexspline of harmonic drive gears considering the driving speed effect using laser sensors. Sci. China 2017, 60, 1175–1187. [Google Scholar] [CrossRef]
- Song, G.; Chen, S. Study on the profile equation of the rigid gear of the harmonic chain drive. J. Mech. Transm. 2004, 28, 7–9. [Google Scholar] [CrossRef]
- Yao, Y.; Chen, X.; Xing, J. Tooth effects on assembling bending stress of flexible tooth rim in harmonic drive. Mech. Mach. Theory 2020, 150, 103871. [Google Scholar] [CrossRef]
- Yang, C.; Hu, Q.; Liu, Z.; Zhao, Y.; Cheng, Q.; Zhang, C. Analysis of the partial axial load of a very thin-walled spur-gear (flexspline) of a harmonic drive. Int. J. Precis. Eng. Manuf. 2020, 21. [Google Scholar] [CrossRef]
- Tang, T.; Jia, H.; Li, J.; Wang, J.; Zeng, X. Modeling of transmission compliance and hysteresis considering degradation in a harmonic drive. Appl. Sci. 2021, 11, 665. [Google Scholar] [CrossRef]
- Shen, Y.; Ye, Q. Theory and Design of Harmonic Gear Transmission; China Machine Press: Beijing, China, 1985. [Google Scholar]
- Li, F.; Li, X.; Guo, Y.; Shang, D. Analysis of contact mechanical characteristics of flexible parts in harmonic gear reducer. Shock Vib. 2021, 2021, 5521320. [Google Scholar] [CrossRef]
- Yang, S. Calculating the deformations and the internal forces of the ring and the wheel rim. J. Chengdu Univ. Nat. Sci. Ed. 1995, 2, 16–23. [Google Scholar]
- Bulte, C.H.F. The differential equation of the deflection curve. Int. J. Math. Educ. Sci. Technol. 1992, 23, 51–63. [Google Scholar] [CrossRef]
- Chen, X.; Liu, Y.; Xing, J.; Xu, W. Neutral line stretch of flexspline in harmonic driver. J. Mech. Eng. 2014, 50, 189–196. [Google Scholar] [CrossRef]
- Gao, H.; Li, Z.; Deng, Z. Sensitivity analysis of cup-shaped flexible gear parameters to its stress based on ANSYS. J. Mech. Eng. 2010, 46, 1–7. [Google Scholar] [CrossRef]
- Fu, J.; Dong, H.; Shen, Y. Stress analysis of the flexspline in harmonic gearing by using FEM. China Mech. Eng. 2007, 18, 2210–2214. [Google Scholar] [CrossRef]









| Parameters | Symbols | Values |
|---|---|---|
| Diameter of neutral line (mm) | 41.98 | |
| Wall thickness (mm) | 0.26 | |
| Width of tooth ring (mm) | 8 | |
| Width of cup (mm) | 23.5 | |
| Thickness of cup bottom (mm) | 3 | |
| Outside diameter of cup bottom (mm) | 80 |
| Parameters | Symbols | Values |
|---|---|---|
| Radius of the eccentric arc (mm) | 20.868 | |
| Eccentric distance (mm) | 0.39 | |
| The wrap angle (°) | 30~67.89 |
| Material Parameters | Wave Generator | Flexspline |
|---|---|---|
| Steel type | 42CrMo | SNCM439 |
| Density | 7850 kg/m3 | 7870 kg/m3 |
| Yield strength | 930 MPa | 835 MPa |
| Tensile strength | 1080 MPa | 980 MPa |
| Young’s modulus | 2.12 × 1011 Pa | 2.09 × 1011 Pa |
| Poisson’s ratio | 0.28 | 0.295 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Li, D.; Mao, S.; Chen, B. Design and Analysis of Cam Wave Generator Based on Free Deformation in Non-Working Area of the Flexspline. Appl. Sci. 2021, 11, 6049. https://doi.org/10.3390/app11136049
Wang S, Li D, Mao S, Chen B. Design and Analysis of Cam Wave Generator Based on Free Deformation in Non-Working Area of the Flexspline. Applied Sciences. 2021; 11(13):6049. https://doi.org/10.3390/app11136049
Chicago/Turabian StyleWang, Shuyan, Dongliang Li, Shiteng Mao, and Bingkui Chen. 2021. "Design and Analysis of Cam Wave Generator Based on Free Deformation in Non-Working Area of the Flexspline" Applied Sciences 11, no. 13: 6049. https://doi.org/10.3390/app11136049
APA StyleWang, S., Li, D., Mao, S., & Chen, B. (2021). Design and Analysis of Cam Wave Generator Based on Free Deformation in Non-Working Area of the Flexspline. Applied Sciences, 11(13), 6049. https://doi.org/10.3390/app11136049






