4.1. Aerodynamic Responses
Figure 7 shows the time-varying aerodynamic coefficients of each car during the train’s run, from 100 m before the crosswind region to 100 m after the tail car exits. The speeds of the train and the crosswind were 83.33 m/s and 20 m/s, respectively, giving a yaw angle of 13.5°. The time points when the corresponding car entered and left the crosswind region were given in each figure to explore the transient influence of the crosswind on the aerodynamics of the train. The results of the train with and without the consideration of posture were included in each figure to compare the aerodynamic differences. The range of the coefficient values of the sub-figures was maintained to facilitate the analysis of the different performances among various aerodynamic coefficients. The peak-to-peak value of the aerodynamic coefficients obtained when each car of the train entered and left the crosswind region was also calculated and shown in
Table 2 and
Figure 8, which quantified the transient fluctuations. The period when each car entered and left the crosswind region was captured—from 0.1 s before the corresponding car started to enter the crosswind region, to 0.1 s after it exited. Based on this, the periods for the leading, middle, and trailing cars entering the crosswind region were 1.100–1.609 s, 1.409–1.913 s, and 1.713–2.223 s, respectively, while the periods for exiting the region were at 3.500–4.010 s, 3.810–4.313 s, and 4.113–4.624 s, respectively.
As can be seen in
Figure 7a–c, the aerodynamic side force of different cars showed great differences. The value of
received from the head car to the tail car decreased in order. The
value of the head car in the crosswind region was increasing, and the growth rate was the fastest when it had just entered this region due to the increase in the blocking area against the crosswind. When the whole head car was in the crosswind region, the growth rate significantly decreased. When it left the crosswind region, the
value quickly dropped to 0, which was the same as before entering the region. The posture of the car head was proven to have a global effect on the
value of the leading car, whose rotations gave it a higher side force especially in the crosswind region; however, the
values during its exit from the crosswind region were almost the same. The same difference was found in the performance of the middle car, where the original car presented a slightly higher
value beyond the crosswind region, but showed a lower
value when it was within the crosswind region. Due to the development of the longitudinally flowing boundary layers, the intrusion of crosswind on the trailing car was protected to some extent, so that the trailing car gave much slighter fluctuations when it entered and left the crosswind region. From
Figure 8, the peak-to-peak transient fluctuations of the
value of the separated cars were always higher when the posture was considered, except for when the tail car exited the crosswind region.
There was no noticeable difference in the maximum lift acting on the leading, middle, and trailing cars, which was similar to that coming from the side force. A default posture combination weakened the aerodynamic lift force of the leading and middle cars, while it strengthened that of the tailing car. Additionally, the difference of
values between the trains with and without posture increased from the leading car to the trailing car. The peak-to-peak transient fluctuations of the
value of the separated cars were similar or slightly lower with a default posture, while that when the leading car entered the crosswind region increased, as can be seen in
Figure 8.
As a combined effect of the aerodynamic side and lift forces, the value of
acting on different cars passing through the crosswind region presented a similar trend to
values, as exhibited in
Figure 7g–i. Here, the combination of the side and lift forces shows a different law of overturning moment: a default posture increased the overturning moment of the leading car, while weakened that of the middle and trailing cars. According to
Figure 8,
is the smallest numerically, all distributed between –0.05 to 0.15, and the peak-to-peak difference is not obvious.
The most significant difference was found in the trend and the value of the pitching moments of different cars. The
value of the leading and trailing cars were always positive during the train run, while most of the time, the middle car showed a negative
value. As shown in
Figure 7j, the difference brought by the posture was not only significantly concentrated in the crosswind area, but the discrepancy of the
value was even higher at the region beyond the crosswind, while the posture caused the
value of the leading car inside the crosswind region to decrease. An obvious difference can be found in the
values when the middle car ran in the crosswind region, where a given posture weakened the negative
value that the origin train maintained. Therefore, the peak-to-peak value of the
value always had a noticeable difference, although they are relatively and numerically low.
A low yawing moment was found when the middle car passed through the crosswind region, and those of the head and the tail cars changed significantly because they were only connected to other vehicles at one end. The effect brought by the posture on the value was much simpler compared to the other aerodynamic coefficients: this difference law never changed according to the time, and a given posture always made the value of the leading and trailing cars greater, but that of the middle car lower. The peak-to-peak values of were the numerically largest at the leading and trailing cars, and increased at the leading car while decreased at the other cars due to the given posture. It should be noted that the reason why the middle car was obviously different from the head and the tail cars for and values is that it is geometrically symmetrical in the length direction, while the head and tail cars have a strong asymmetric flow due to the presence of streamlined structures so that different time-varying and values were generated.
4.2. Flow Patterns
Figure 9 shows the distribution of the dimensionless velocity
U the y-z planes at the middle length of the leading, middle, and trailing cars. Here, the value of
U can be calculated as:
where
u is the velocity of the flow in the domain obtained by numerical simulations. This comparison was based on the time when the train arrived in the middle of the crosswind region. Additionally, the velocity vector fields on these planes displayed in the form of line integral convolution are also given, helping to understand these flow structures.
According to
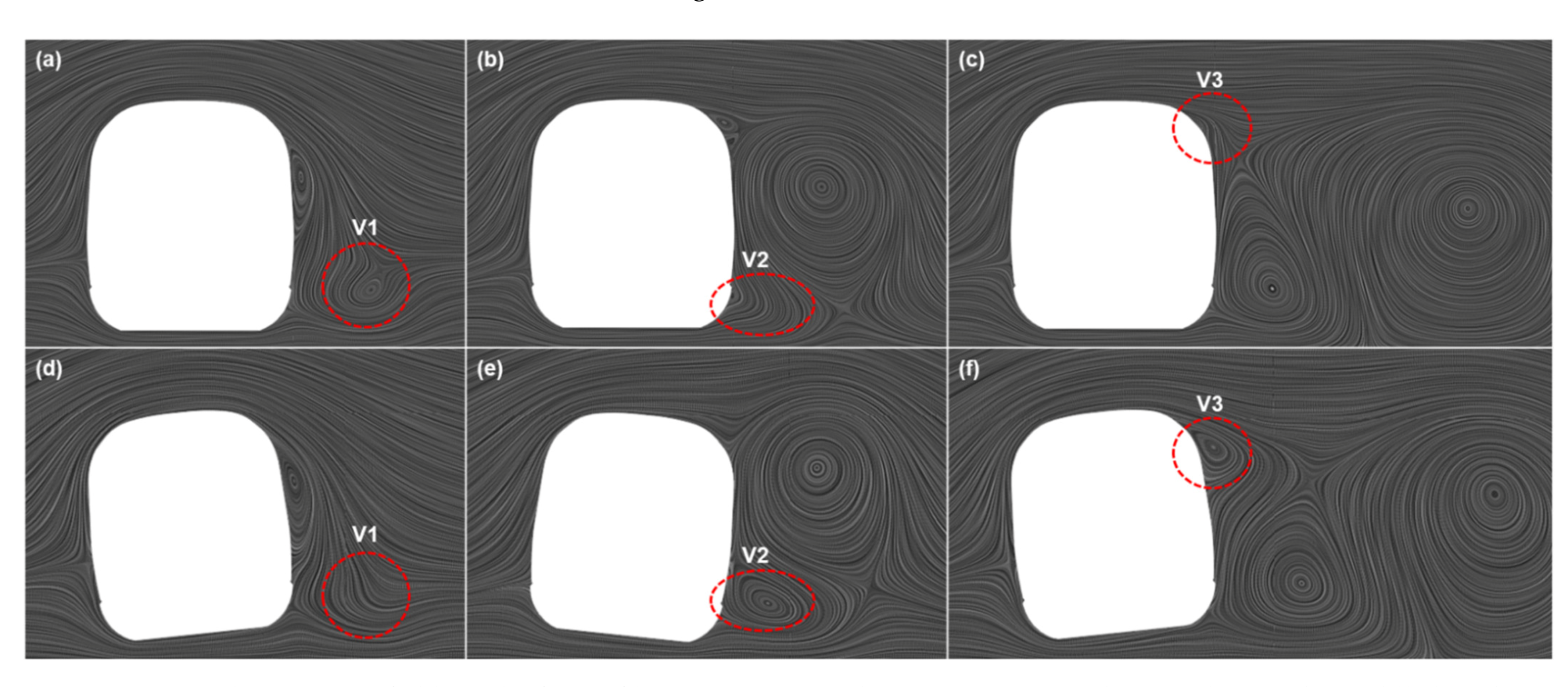
Figure 9a,d, the distribution patterns of the velocity field near the leading car were the same: a local high-speed flow was formed at the top and bottom of the vehicle, and a much higher-speed flow could be seen in the area near the ground downstream of the leading car. Due to an overturning posture, the entrance of the crosswind into the underbody of the vehicle shrunk, resulting in greater underbody flow, as seen in region A. On the contrary, the exit of the escaping flow from the bottom of the vehicle was larger due to the existence of this overturning posture, making the flow in area B greater, thus creating the low-speed area. In area C, an obvious vortex (V1 in
Figure 10) was generated at the leeward side of the original leading car, but no obvious swirling flow was found behind the train with posture. This is the reason for the difference in velocity flow in this area. Around the middle car, as shown in
Figure 9b,e, most of the flow fields around the vehicle body are similar, only the D area (the same as the C area in
Figure 9a,d) produced a different shape for the high-speed area, which is attributed to the additional vortex (V2 in
Figure 10) generated by the shrunk exit of the underbody flow of the middle car with posture. The overturning posture of the trailing car not only caused the roof airflow to form a stronger flow separation (V3 in
Figure 10) on the leeward side of the vehicle, but also a main large-scale vortex structure on the backward side.
Figure 11 shows the pressure distribution on the longitudinal and horizontal planes around the two trains to understand the difference in flow patterns along the train length. The longitudinal plane was located at y = 0 m, and the horizontal plane was located at z = 1.5 m. From
Figure 11a,b, the pressure distribution on the symmetry plane of the train was almost unaffected by the posture change, and only the near-wake area had a relatively obvious difference, where the streamlined structure of the trailing car of the train with posture bore large positive pressure, and smaller negative pressure was found in the center of the wake plume flow. An even smaller difference was found in the pressure distribution pattern on the horizontal plane, seen in
Figure 11c,d. Since different postures were applied to separated cars, there were quite local and slight differences due to geometric discontinuities at the car joints.
Figure 12 presents the surface pressure distribution of the train with and without the posture when it was located in the same position as
Figure 9,
Figure 10 and
Figure 11 from four different perspectives. Similar to the findings in
Figure 11, no significant differences in pressure distribution patterns were found on different surfaces of the train, such as the accumulation of positive pressure on the nose tip of the leading car and the accumulation of negative pressure on the nose tip of the trailing car. The pressure difference was mainly reflected on the edge structure of the vehicle, such as the transition area between the side surface and the top surface, the transition area between the side surface and the bottom surface, and the connection of different vehicles. The pressure difference on the edge area of the vehicle is due to the flow difference guided by different train postures, and that of the connection of vehicles resulted from the flow stagnation or separation caused by geometric dislocation.
To obtain further quantitative difference in pressure distribution from the distribution pattern in
Figure 12, the profiles of the
value on the same cross-section as in
Figure 9 and
Figure 10 are given in
Figure 13. The top of the train body often distributed the greatest pressure value, but the largest pressure difference appeared at the junction between the train surfaces. Regardless of whether it is the leading car, middle car, or the trailing car, a general rule can be drawn: the corner where the flow tends to be accelerated instead of being blocked will produce lower pressure than the original situation, as shown in corner 2 and corner 4 in
Figure 13b, as well as corner 3 in
Figure 13a; when the posture tends to block the airflow, greater pressure will be formed, such as in corner 4 in
Figure 13a and corner 3 in
Figure 13b. In addition, there was almost no difference in the pressure generated on the windward and leeward sides of the leading car in different postures, though this difference gradually became larger with the development of the longitudinal airflow, which was prominent on the leeward side of the trailing car.
4.3. Running Safety
The transient aerodynamic load of the running train was inputted into the train-track coupled dynamic model to conduct a dynamic analysis of the running safety. The coupled model consists of three sub-models: train subsystem, track subsystem, and wheel–rail contact model. Every train carriage is modelled as a set of seven rigid bodies, including one carriage body, two bogies, four wheelsets, and bottom and top suspensions, without taking into account the longitudinal interaction between carriages. The track structure subsystem’s 3D model must be created using the finite element approach. The spring-damper unit simulates the rubber pad between the rail and the rail slab, and the track slab is regarded as totally fixed. Track irregularity, which includes vertical, directional, level, and gauge irregularity, is a major cause of train vibration interference. The geometry contact relationship between wheel and rail is solved using the 3D space trace approach. For the sake of simplicity, the current study did not describe the dynamic system model specifically, which can be seen in Deng’s research [
23]. According to the previous studies, the leading car was generally exposed to higher running safety risks than the middle and trailing cars due to much more terrible aerodynamic fluctuations. However, considering the influence of posture, whether this is still correct or not is unknown. Therefore, the running safety of all cars were given and analyzed here, which means studying the effect of the given posture on DC, WLRR, and the posture changes of the train.
4.3.1. Derailment Coefficient
The derailment coefficient of the train can be calculated by the contact force of the wheels according to the TB10621-2009 standard, which is given as:
where
Q and
P are the lateral and vertical forces acting on the wheels, respectively.
Figure 14 shows the time-varying
DC values of the first wheelset of the leading car and the last wheelset of the trailing car of the train, with and without the given posture.
As trains passed the crosswind region, the DC values on these two wheelsets showed different performances. After the first wheelset of the leading car entered the crosswind region, the DC value began to rise and fluctuated at a high level. When it left the crosswind region at about
t = 4 s, the value of DC began to fall. The highest value appeared at about
t = 2.6 s. As shown in
Figure 14b, the DC development trend of the train with and without the designated posture over time was the same, but the consideration of posture gave a larger peak value, which meant that the safety situation of the train with posture was highly threatened. For the trailing car, same as the lateral force performance in
Figure 7c, the fully developed boundary layer weakened the impact of the crosswind to a certain extent, resulting in a significant reduction of difference of the DC value of two different trains. The trailing car of the train with posture only produced a slightly higher global sub-peak value than that of the train without posture when the time was at about 3.4 s, and there was no significant difference at the other time.
4.3.2. Wheel Load Reduction Rate
When a train runs at a high speed, the wheels do not stay horizontal but move up and down due to the vibration, and the wheel weight of the wheelset increase or decrease. Even if the lateral force on the side of the reduced wheel weight is small (or even none), there may be lateral relative displacement with the wheels, which leads to a derailment. Hence, the WLRR was also considered in the evaluation of the running safety in terms of:
where Δ
P is the load reduction in the wheel load,
P is the average static wheel load of the wheelset, and
is the maximum overrun duration. The same as
Figure 14,
Figure 15 shows the time-varying WLRR values of the first wheelset of the leading car and the last wheelset of the trailing car of the train, with and without the given posture. According to the definition of WLRR, its theoretical maximum value is +1, which means that the wheel–rail contact force is 0 and the wheel–rail disengagement state is at this time, so the maximum value of WLRR cannot exceed 1. However, its lowest value is not −1. In the process of high-speed train operation, if there is irregularity on the rail surface (the rail surface is slightly arched upwards) or a transient aerodynamic impact at a certain moment. The wheels will have a transient impact on the rail, where the impact force can even reach several times the static wheel weight, which is why WLRR can reach a value higher than −1.
No remarkable difference in the WLRR value could be found when the train with and without a designed posture passed the crosswind region. Their distributions, peak values, and the developing mode were all the same, saying that a slightly given posture cannot significantly influence the performance of WLRR.
4.3.3. Running Posture
Furthermore, the coupled dynamic system provides the posture changes of the train passing through the crosswind region with and without the given posture. The running posture is a part of the safety analysis and was studied by a previous study [
26], while only the posture of the leading vehicle was investigated. In the present study, the posture changes of the leading, middle, and trailing cars of the trains with and without the initial posture in five degrees of freedom (lateral and vertical displacement and rotation in three directions) were compared and analyzed.
Figure 16 shows the changes of different degrees of freedom indexes when the train passed the crosswind region with regard to two different initial postures. In the figure, Dy, Dz, Rx, Ry, Rz are the lateral and vertical displacements (unit: m) and the rotation of the x, y, and z axes (unit: rad). The diagram of the running posture of the train is also given in each figure, where the transparent one represents the original position, and another is the posture caused by the crosswind. The same range of the y axis was kept constant for a single degree of freedom to understand the different performances of separated cars.
According to
Figure 16a–c, there were obvious differences in the displacement characteristics of the three cars in the lateral direction, and the magnitude of the displacement decreased from the leading car to the trailing car, which could be attributed to the differences in their lateral forces, as described in
Figure 7a–c. In addition, the influence of the given posture on the lateral displacement of the train is consistent with the law of lateral force: the preset posture tended to push the leading car and the middle car further in the direction of the crosswind; while the lateral displacement of the trailing car that did not consider the posture in the crosswind area fluctuated slightly around 0, and that of the trailing car with posture increased, whether same or opposite to the direction of the crosswind. From
Figure 16d–f, all three cars had downward vertical displacements, and they all showed two humps with similar peak values within the crosswind region. Only a slight difference can be found in the leading car, while relatively larger differences were formed in the vertical displacement of the middle and the trailing cars. For the overturning angle shown in
Figure 16g,i, due to the similarity of the preset attitude on the lateral and vertical displacements of the leading car (see
Figure 16a,d), the overturning angles shown by the two leading cars were almost the same, but the middle car was different: the middle car with posture was found to have a reverse overturning trend much larger than the original car. The overturning rotation of the trailing car was similar to the change in lateral displacement (see
Figure 16c). The pitching rotation changes of the three cars were the most active, and the difference caused by the preset posture was not limited to the crosswind region. The most obvious difference was also found in the middle car: the preset posture reduced the pitching angle not only inside but also beyond the crosswind region to around 0. For the leading and trailing vehicles with a streamlined structure, the preset posture slightly increased their maximum values. As shown in
Figure 16m–o, the influence of a given posture on the yawing angle is clear and simple, which made the positive yawing rotation of the leading and trailing cars larger and increased the negative yawing rotation of the middle car in reverse.
4.3.4. Safety Domain
Analyses of critical speeds of trains traveling in various crosswinds define the safety domain of trains running in a crosswind with attitude change taken into account. In the present study, the values of DC and WLRR are employed as the running safety indices, based on which
Figure 17 shows the running safety domain in terms of the relationship between the speed of crosswind and train. A train’s critical speed is higher when there is a weaker crosswind, and it is lower when there is a stronger crosswind. The train’s ability to overcome crosswind decreases as it speeds up. With the consideration of posture, a train is proven to withstand a weaker crosswind. As a result, for high-speed and super-speed trains, extra attention should be given to the wind environment.