Application Study on Fiber Optic Monitoring and Identification of CRTS-II-Slab Ballastless Track Debonding on Viaduct
Abstract
:1. Introduction
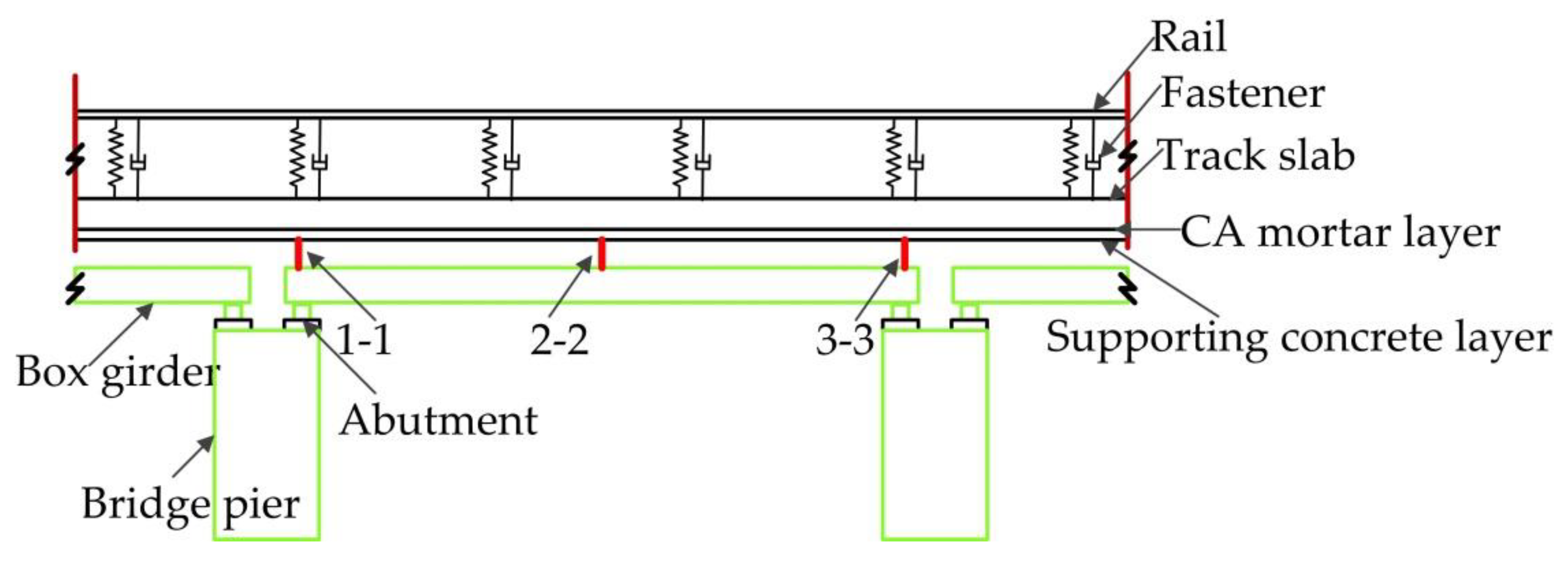
2. Monitoring Scheme
2.1. Instantaneous Baseline Establishment for Comparative Monitoring
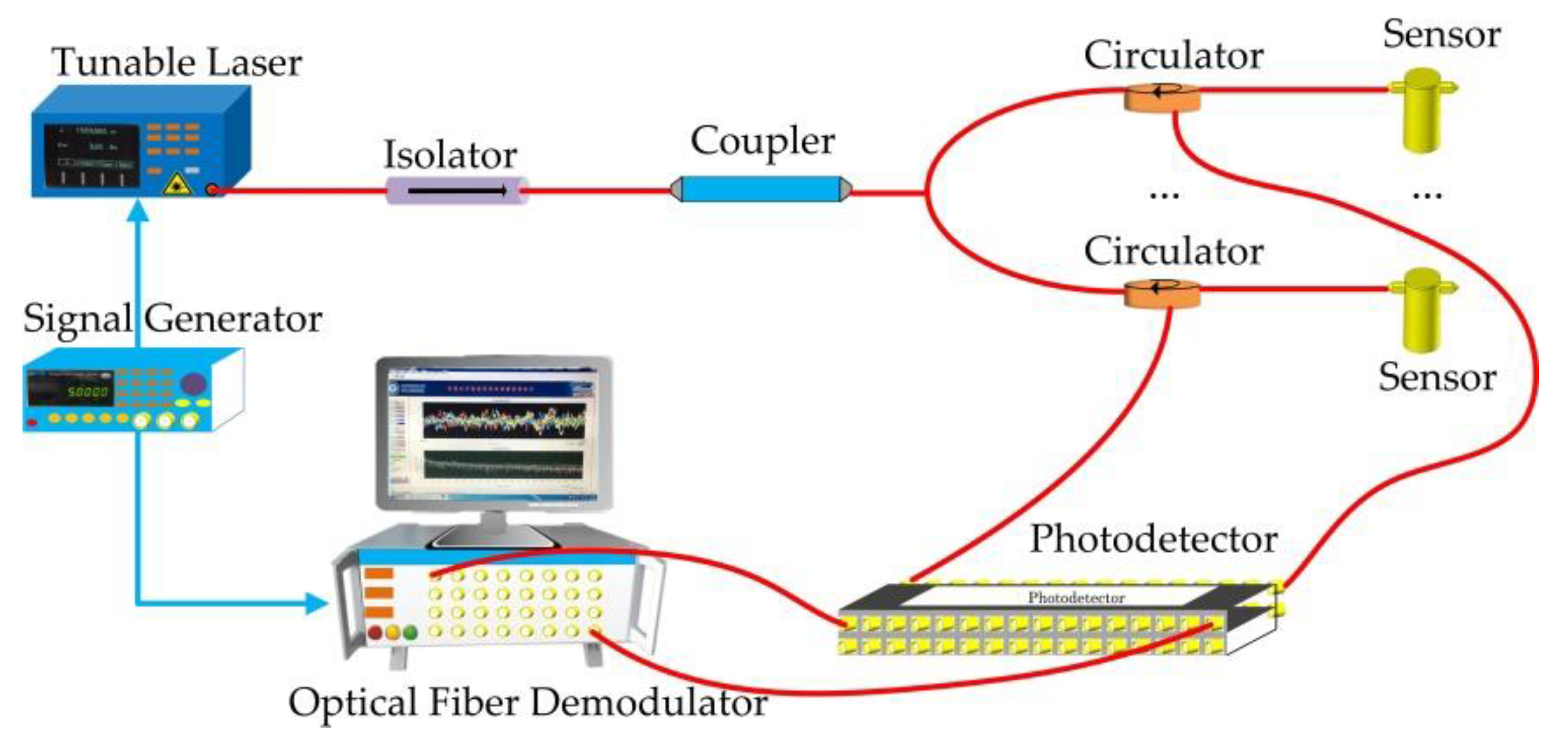
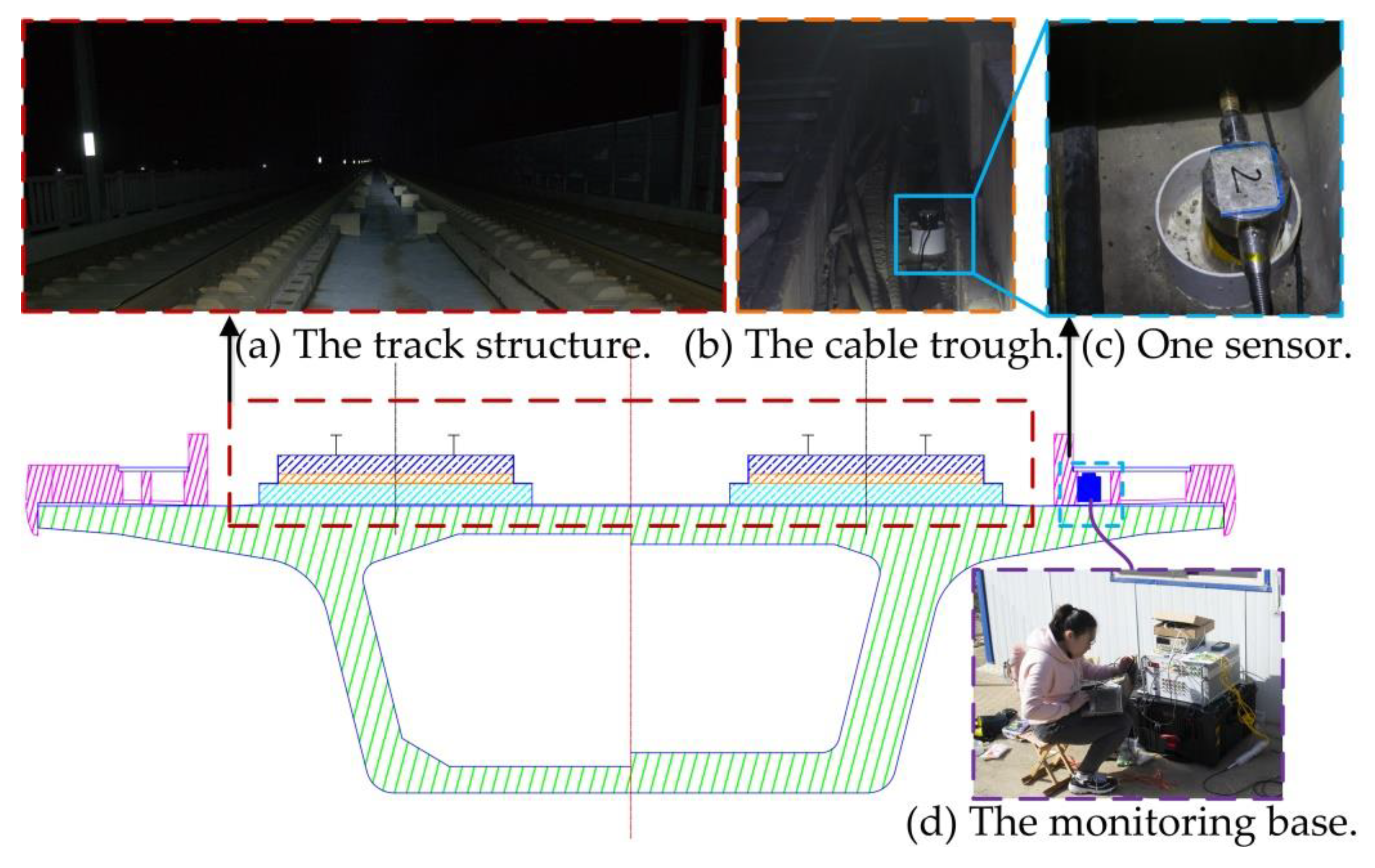
2.2. Fiber Optic Monitoring System and Deployment
3. Feature Extraction Methods and Indicator Development
3.1. Multi-Feature Extraction Methods in Time Domain
3.2. Multi-Feature Extraction Method in Frequency Domain
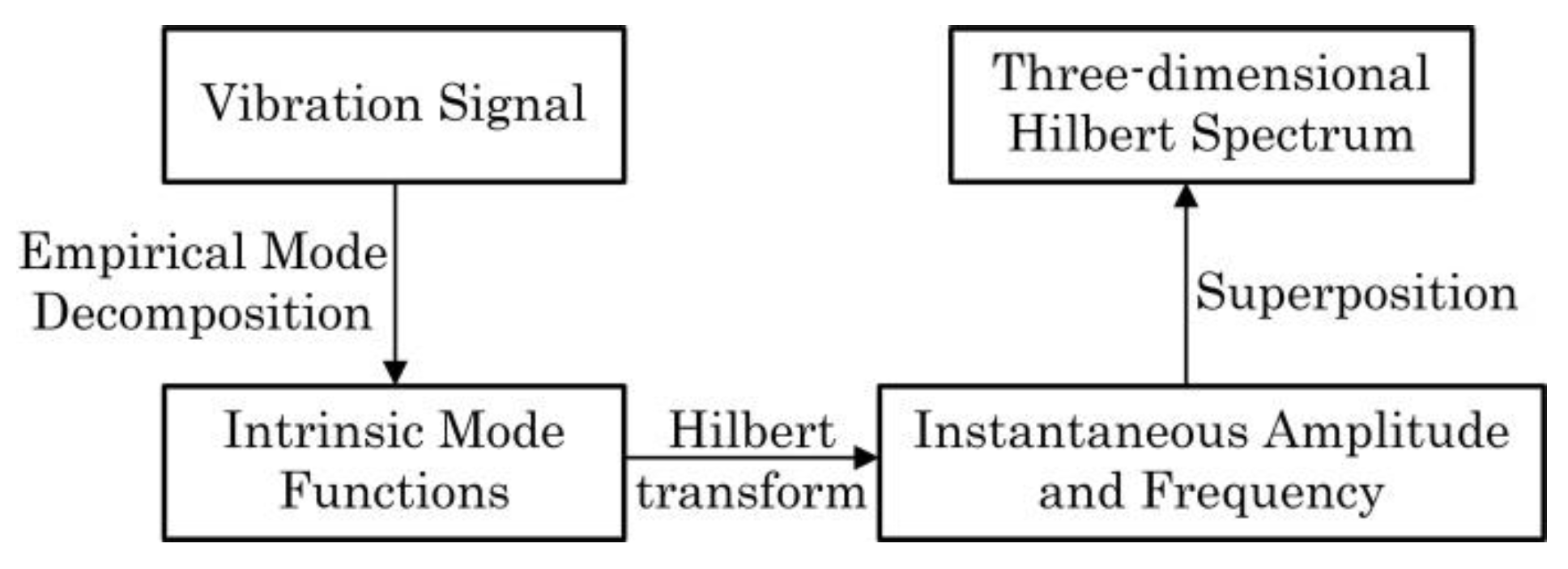
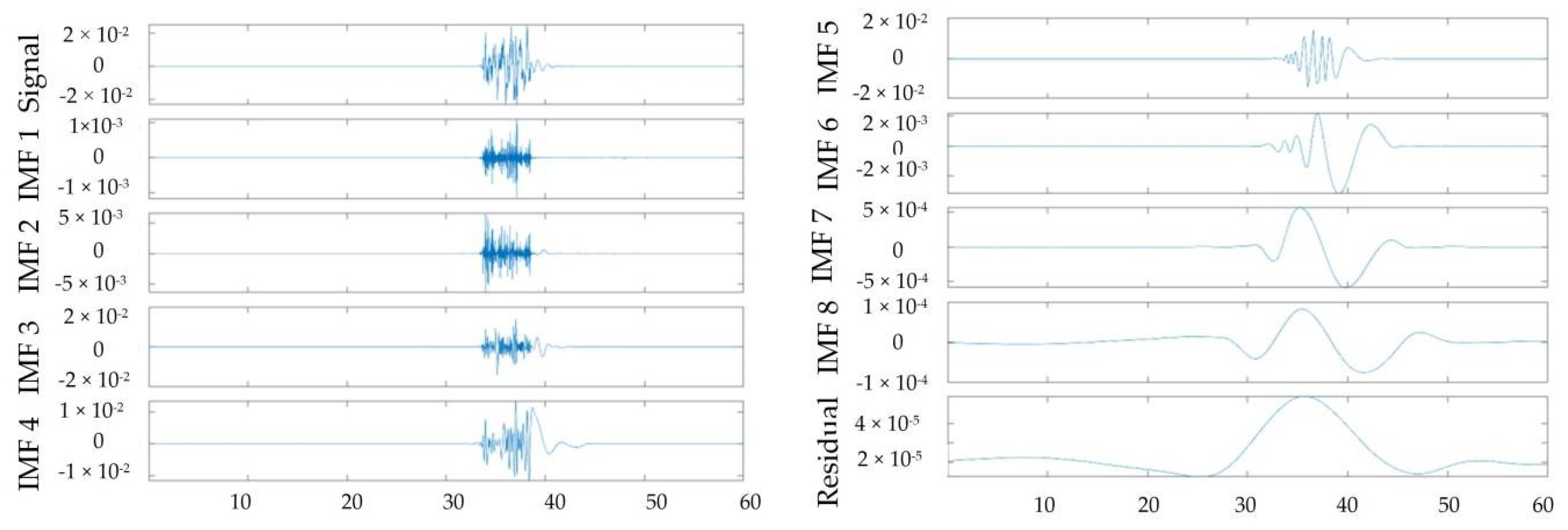
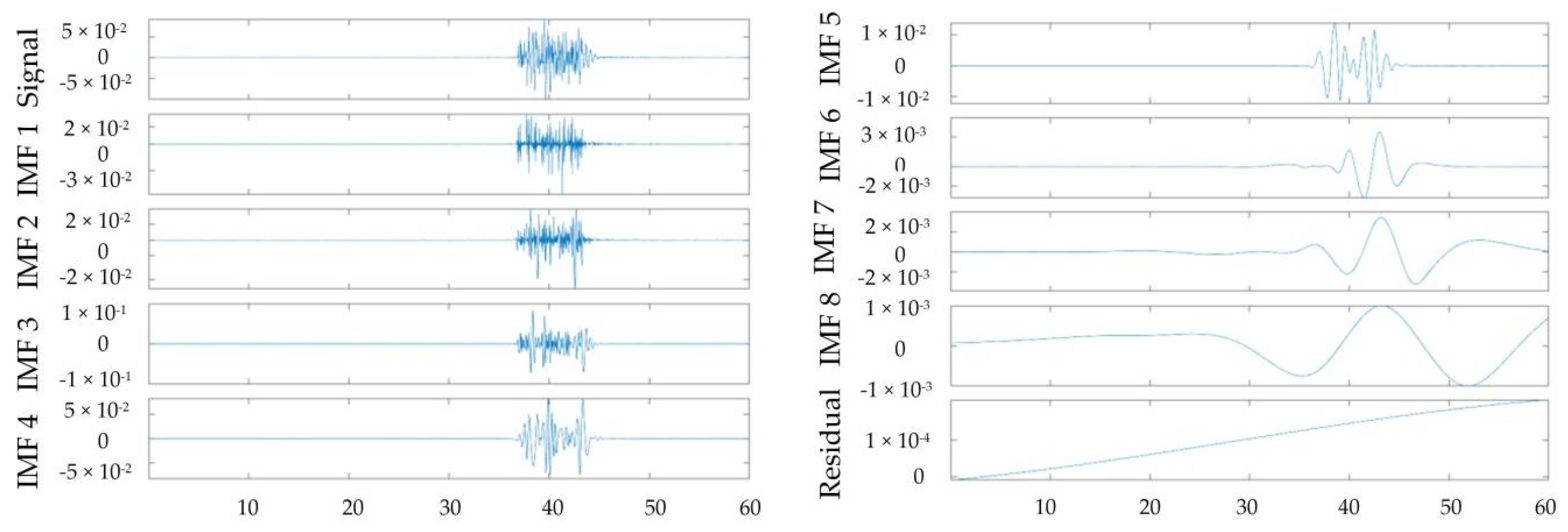
3.3. Multi-Feature Extraction Method in the Time–Frequency Domain
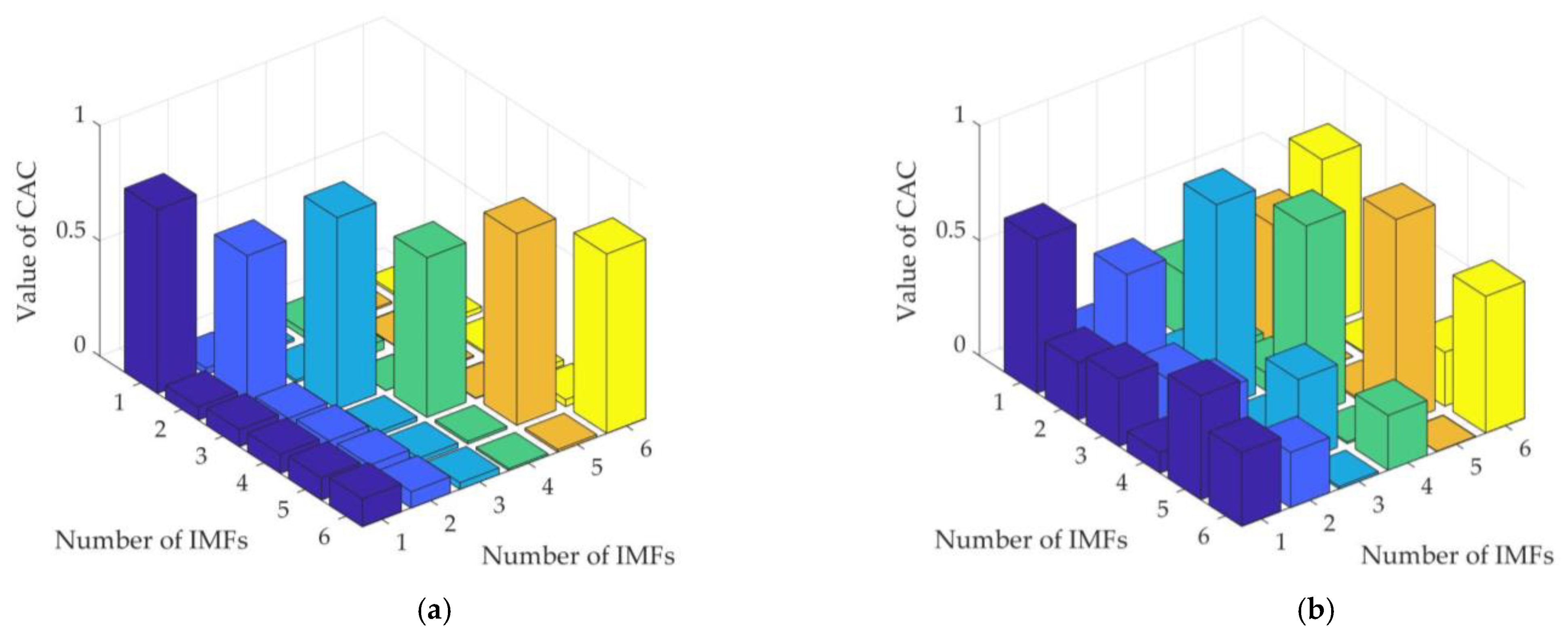
3.4. Development of a Similarity-Based Indicator
4. Analysis and Discussion
4.1. Validation of Instantaneous Baseline
4.2. Time-Domain Analysis for Multi-Feature Extraction and Assessment
4.3. Frequency-Domain Analysis for Multi-Feature Extraction and Assessment
4.4. Time–Frequency-Domain Analysis for Multi-Feature Extraction and Assessment
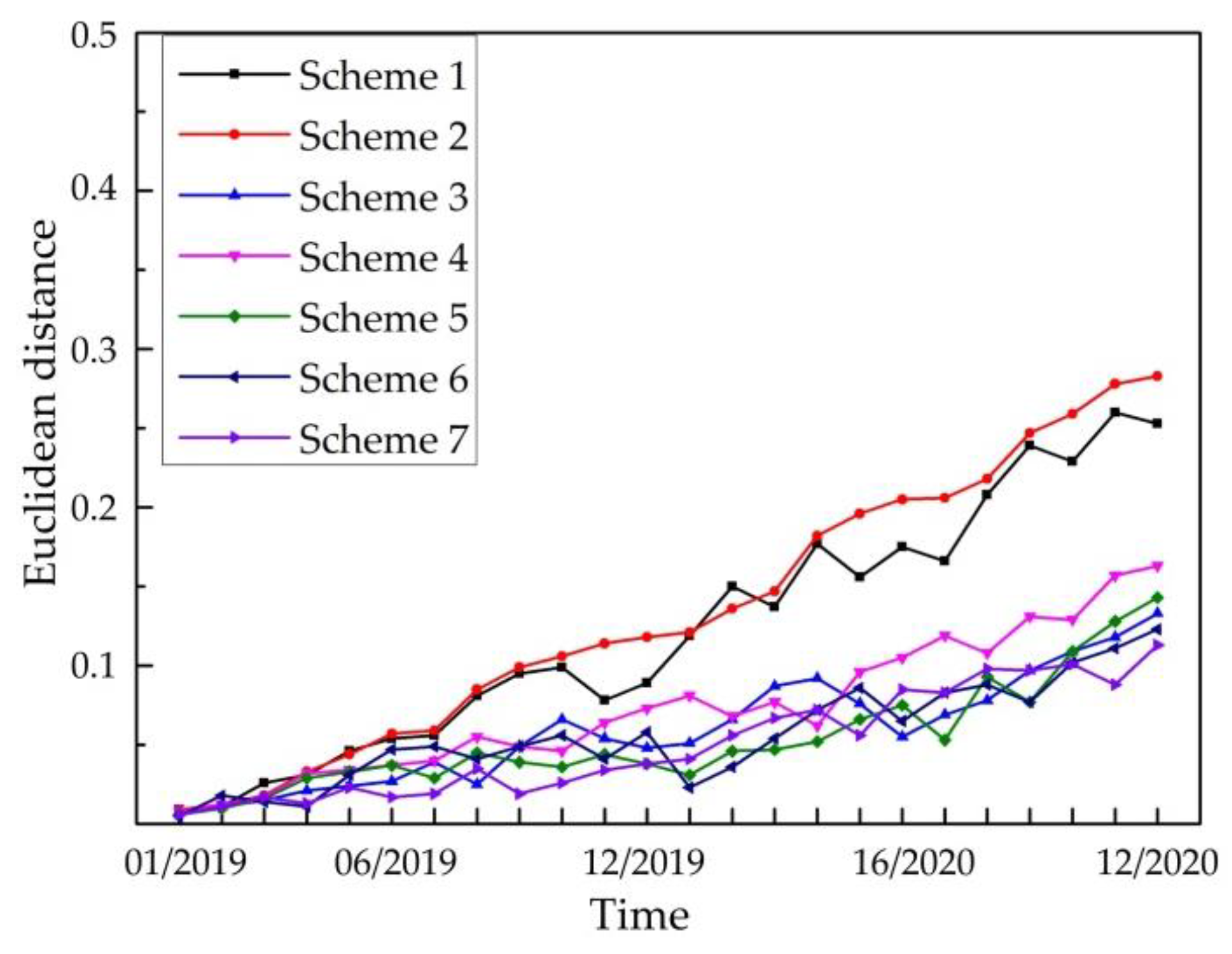
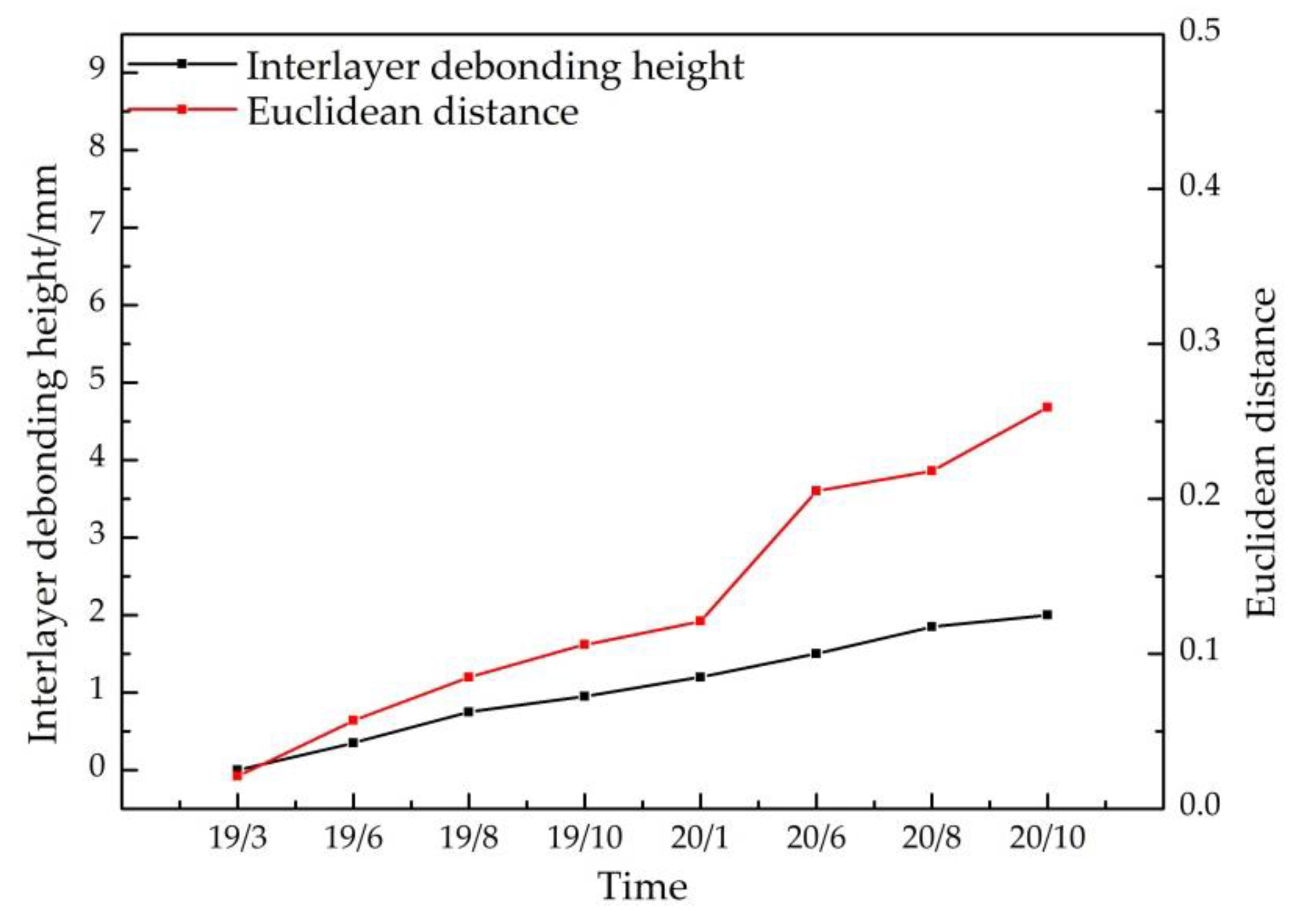
4.5. Quantitative Assessment Using the Similarity-Based Indicator
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, N.; Guo, W.W.; Xia, H. Dynamic Interaction of Train-Bridge Systems in High-Speed Railway, 1st ed.; Beijing Jiaotong University Press: Beijing, China, 2018; Volume 1, pp. 13–14. [Google Scholar]
- Luo, J.; Zhu, S.Y.; Zhai, W.M. An efficient model for vehicle-slab track coupled dynamic analysis considering multiple slab cracks. Constr. Build. Mater. 2019, 215, 557–568. [Google Scholar] [CrossRef]
- Wang, P.; Xu, H.; Chen, R. Effect of cement asphalt mortar debonding on dynamic properties of CRTS-II- slab ballastless track. Adv. Mater. Sci. Eng. 2014, 8, 193128. [Google Scholar] [CrossRef] [Green Version]
- Shi, H.; Yu, Z.J.; Shi, H.M.; Zhu, L.Q. Recognition algorithm for the disengagement of cement asphalt mortar based on dynamic responses of vehicles. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2019, 233, 270–282. [Google Scholar] [CrossRef]
- Yu, C.Y.; Xiang, J.; Mao, J.H. Influence of slab arch imperfection of double-block ballastless track system on vibration response of high-speed train. J. Braz. Soc. Mech. Sci. 2018, 109, 1–14. [Google Scholar] [CrossRef]
- Ke, Y.T.; Cheng, C.C.; Ni, Y.Q.; Hsu, K.T.; Wai, T.T. Preliminary study on assessing delaminated cracks in cement asphalt mortar layer of high-speed rail track using traditional and normalized impact—Echo methods. Seonsors 2020, 30, 3022. [Google Scholar] [CrossRef]
- Hoda, A.; Soheil, N.; Deren, Y. Assessing sensitivity of impact echo and ultrasonic surface waves methods for nondestructive evaluation of concrete structures. Constr. Build. Mater. 2014, 71, 384–391. [Google Scholar]
- Taekeun, O.; Jongil, P. Comparison of Data-Processing Methods by Air-Coupled Impact Echo Testing for the Assessment of a Concrete Slab. J. Test Eval. 2014, 42, 921–930. [Google Scholar]
- Lutz, A.; Samir, S. Track-Soil Dynamics-Calculation and Measurement of Damaged and Repaired Slab Tracks. Transp. Geotech. 2017, 12, 1–14. [Google Scholar]
- Xu, J.M.; Wang, P.; Liu, H. Identification of internal damage in ballastless tracks based on Gaussian curvature mode shapes. J. Vibroeng. 2016, 18, 1392–8716. [Google Scholar]
- Nikolaos, Z.; Efthymios, T.; Christos, V. Inspection, evaluation and repair monitoring of cracked concrete floor using NDT methods. Constr. Build. Mater. 2013, 48, 1302–1308. [Google Scholar]
- Che, A.L.; Tang, Z.; Feng, S.K. An elastic-wave-based full-wavefield imaging method for investigating defects in a high speed railway under track structure. Soil Dyn. Earthq. Eng. 2015, 77, 299–308. [Google Scholar] [CrossRef]
- Varnavina, A.V.; Khamzin, A.K.; Torgashow, E.V. Data acquisition and processing parameters for concrete bridge deck condition assessment using ground-coupled ground penetrating radar: Some considerations. J. Appl. Geophys. 2015, 114, 123–133. [Google Scholar] [CrossRef]
- Yang, Y.; Zhao, W.G. Curvelet transform-based identification of void diseases in ballastless track by ground-penetrating radar. Struct. Control Health Monit. 2019, 26, 1–18. [Google Scholar] [CrossRef]
- Yong, J.X.; Hua, J.L.; Zhong, W.F. Concrete crack case and its damage in ballastless track structure. Int. J. Rail 2009, 2, 30–36. [Google Scholar]
- Lichtberger, B. Track Compendium, 1st ed.; Eurorail Press: Hamburg, Germany, 2005. [Google Scholar]
- Yin, F. Research on detection method of gap cause by camber of CRTS -II- track slab. Railw. Eng. 2018, 58, 117–133. [Google Scholar]
- Tian, X.S.; Zhao, W.G.; Du, Y.L. Detection of mortar defects in ballastless tracks of high-speed railway using transient elastic wave method. J. Civ. Struct. Health 2018, 8, 151–160. [Google Scholar] [CrossRef]
- Lin, J.F.; Xu, Y.L.; Zhan, S. Experimental investigation on multi-objective multi-type sensor optimal placement for structural damage detection. Struct. Health Monit. 2019, 18, 882–901. [Google Scholar] [CrossRef]
- Wang, Y.W.; Ni, Y.Q.; Wang, X. Real-Time Defect Detection of High-Speed Train Wheels by Using Bayesian Forecasting and Dynamic Model. Mech. Syst. Signal Process. 2002, 139, 106654. [Google Scholar] [CrossRef]
- Ni, Y.Q.; Wang, J.F.; Chan, T.H.T. Structural damage alarming and localization of cable-supported bridges using multi-novelty indices: A feasibility study. Struct. Eng. Mech. 2015, 54, 337–362. [Google Scholar] [CrossRef]
- Wan, H.P.; Ni, Y.Q. A new approach for interval dynamic analysis of train-bridge system based on Bayesian optimization. J. Eng. Mech. 2020, 146, 04020029. [Google Scholar] [CrossRef]
- Wang, J.F.; Liu, X.Z.; Ni, Y.Q. Bayesian probabilistic approach for acoustic emission based rail condition assessment. Comput. Aided Civ. Inf. 2018, 33, 21–34. [Google Scholar] [CrossRef]
- Liu, X.Z.; Xu, C.; Ni, Y.Q. Wayside detection of wheel minor defects in high-speed trains by a Bayesian blind source separation method. Sensors 2019, 19, 3981. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.W.; He, Y.L.; Liu, X.Z. Long-Term monitoring for track slab in high speed rail via vision sensing. IEEE Access 2020, 8, 156043–156052. [Google Scholar] [CrossRef]
- Karakose, M.; Yaman, O.; Murat, K. A new approach for condition monitoring and detection of rail components and rail track in railway. Int. J. Comput. Int. Syst. 2018, 11, 830–845. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.; Wei, J.H.; Zhang, Z.X. Design and evaluation of a remote measurement system for the online monitoring of rail vibration signals. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2014, 230, 724–733. [Google Scholar]
- Cosimo, S.; Alessandro, N.; Pietro, S. GNSS integrity monitoring for rail applications: Two-tiers method. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 1850–1863. [Google Scholar]
- Victoria, J.H.; Simon, O.K.; Michael, W.; Anthony, M. Wireless sensor networks for condition monitoring in the railway industry: A Survey. IEEE Trans. Intell. Transp. 2015, 16, 1088–1106. [Google Scholar]
- Guo, Y.X.; Liu, W.L.; Xiong, L. Fiber Bragg Grating Displacement Sensor with High Abrasion Resistance for a Steel Spring Floating Slab Damping Track. Sensors 2018, 18, 1899. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.A.; Ni, Y.Q. Measurement and Forecasting of High-Speed Rail Track Slab Deformation under Uncertain SHM Data Using Variational Heteroscedastic Gaussian Process. Sensors 2019, 19, 3311. [Google Scholar] [CrossRef] [Green Version]
- Hussaini, S.K.K.; Indraratna, B.; Vinod, J.S. Application of Optical-Fiber Bragg Frating Sensors in Monitoring the Rail Track Deformations. Geotech. Test J. 2015, 38, 387–396. [Google Scholar] [CrossRef] [Green Version]
- Yucel, M.; Ozturk, N.F. Real-Time Monitoring of Railroad Track Tension Using a Fiber Bragg Grating-Based Strain Sensor. Instrum. Sci. Technol. 2018, 46, 519–533. [Google Scholar] [CrossRef]
- Milne, D.; Masoudi, A.; Ferro, E. An analysis of railway track behaviour based on distributed optical fibre acoustic sensing. Mech. Syst. Signal Process. 2020, 142, 1–4. [Google Scholar] [CrossRef]
- Chapeleau, X.; Sedran, T.; Cottineau, L.M.; Cailliau, J.; Taillade, F.; Gueguen, I.; Henault, J.M. Study of ballastless track structure monitoring by distributed optical fiber sensors on a real-scale mockup in laboratory. Eng. Struct. 2013, 56, 1751–1757. [Google Scholar] [CrossRef]
- Wang, C.Y.; Tsai, H.C.; Chen, C.S. Railway track performance monitoring and safety warning system. J. Perform. Constr. Fac. 2011, 25, 577–586. [Google Scholar] [CrossRef]
- Philippe, V.; Tiziano, N.; Alessandro, S. Monitoring large railways infrastructures using hybrid optical fibers sensor systems. IEEE Trans. Intell. Transp. 2020, 21, 5177–5188. [Google Scholar]
- Xu, H.B.; Zheng, X.Y.; Zhao, W.G. High precision, small size and flexible FBG strain sensor for slope model monitoring. Sensors 2019, 19, 2716. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiang, D.S.; Zhang, W.T.; Li, F. All-Metal Optical Fiber Accelerometer with Low Transverse Sensitivity for Seismic Monitoring. IEEE Sens. J. 2013, 13, 4556–4560. [Google Scholar] [CrossRef]
- Zhang, J.X.; Huang, W.Z.; Zhang, W.T. Train-Induced Vibration Monitoring of Track Slab Under Long-Term Temperature Load Using Fiber-Optic Accelerometers. Sensors 2021, 21, 1–11. [Google Scholar]
- Anton, S.R.; Inman, D.J.; Park, G. Reference-Free Damage Detection Using Instantaneous Baseline Measurements. AIAA J. 2009, 47, 1952–1964. [Google Scholar] [CrossRef]
- Park, S.; Anton, S.R.; Kim, J.K.; Inman, D.J.; Ha, D.S. Instantaneous baseline structural damage detection using a miniaturized piezoelectric guided waves system. KSCE J. Civ. Eng. 2010, 14, 889–895. [Google Scholar] [CrossRef]
- Rao, R.M.; Lakshmi, A. Detection of delamination in laminated composites with limited measurements combining PCA and dynamic QPSO. Adv. Eng. Softw. 2015, 86, 85–106. [Google Scholar] [CrossRef]
- Wang, P.; Vachtsevanos, G. Fault prognostics using dynamic wavelet neural networks, artificial intelligence for engineering design. Anal. Manuf. 2001, 15, 349–365. [Google Scholar]
- Feng, S.J.; Zhang, X.L.; Wang, L. In Situ Experimental Study on High Speed Train Induced Ground Vibrations with the Ballast-less Track. Soil Dyn. Earthq. Eng. 2017, 102, 195–214. [Google Scholar] [CrossRef]
- Jiang, H.W.; Gao, L. Analysis of the vibration characteristics of ballastless track on bridges using an energy method. Appl. Sci. 2020, 10, 2289. [Google Scholar] [CrossRef] [Green Version]
- Huang, N.E.; Zheng, S. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. A Math. Phys. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Yang, Y.Q.; Yao, J.C.; Meng, X.; Liu, P.; Yin, J.; Dong, Z.; Wang, W. Experimental study on dynamic behaviors of bridges for 300~350 km/h high speed railway. China Railw. Sci. 2013, 34, 14–19. [Google Scholar]
- Wang, S.R.; Sun, L.; Li, Q.Y.; Wu, Y.S. Temperature measurement and temperature stress analysis of ballastless track slab. J. Railw. Eng. Soc. 2009, 2, 52–55. [Google Scholar]
- Fang, J.; Lei, X.Y.; Lian, S.L. Experimental study on the vibration characteristics of elevated track structures for passenger dedicated lines. Noise Vib. Control 2019, 39, 142–146. [Google Scholar]
- Wang, G.Q.; Xu, T.W.; Li, F. PGC demodulation technique with high stability and low harmonic distortion. IEEE Photonic Tech. Lett. 2012, 24, 2093–2096. [Google Scholar] [CrossRef]
- Zhang, B.; Liu, X.B.; Ma, S. Local deformation identification method for high speed railway subgrade based on time–frequency analysis. Railw. Eng. 2019, 59, 95–98. [Google Scholar]
- Xu, L.; Chen, X.M.; Xu, W.C. Application of wavelet energy spectrum in railway track detection. J. Vib. Eng. 2014, 27, 605–612. [Google Scholar]
- Li, Z.W.; Lian, S.L.; Zhou, J.L. Time–Frequency Analysis of Track Irregularity Based on Improved Empirical Mode Decomposition Method. J. Tongji Univ. Nat. Sci. 2012, 40, 702–707. [Google Scholar]
- Chen, Y.J.; Wang, X.L.; Zhang, Y. Fault diagnosis of train wheels based on empirical mode decomposition generalized energy. In Proceedings of the 3rd International Conference on Electrical Engineering and Information Technologies for Rail Transportation (EITRT), Changsha, China, 20–22 October 2017. [Google Scholar]
- Ho, H.H.; Chen, P.L.; Chang, T.T.; Tseng, C.H. Rail structure analysis by Empirical Mode Decomposition and Hilbert Huang Transform. Tamkang J. Sci. Eng. 2010, 13, 267–279. [Google Scholar]
- Cui, J.W.; Niu, Y.Z.; Dang, H. Demodulation method of F-P sensor based on wavelet transform and polarization low coherence interferometry. Sensors 2020, 20, 4249. [Google Scholar] [CrossRef] [PubMed]
- Lu, C.F.; He, H.W.; Zheng, J.; An, G.D.; Zhao, G.T. TB 10621-2014 Code for Design of High Speed Railway; Railway Publishing House: Beijing, China, 2014. [Google Scholar]
- Wang, L.; Wang, P.; Wu, R.Y. Common deterioration phenomena and effect analysis of mortar bed on CRTS -II- track structure. Railw. Stand. Des. 2012, 11, 11–14. [Google Scholar]
- Bracciali, A.; Cascini, G.; Ciuffi, R. Time domain model of the vertical dynamics of a railway track up to 5 kHz. Veh. Syst. Dyn. 1998, 30, 1–15. [Google Scholar] [CrossRef]
- Vittorio, M.; Natalino, D.B.; Leandro, M.; Ernesto, M.; Fabrizio, R. Damage localization in composite structures using a guided waves based multi-parameter approach. Aerospace 2018, 5, 21–26. [Google Scholar]
- Tian, X.S. Detection and Identification of Mortar Void in Ballastless Track Based on Elastic Wave Method. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2020. [Google Scholar]
- Fryba, L. Vibration of Solids and Structures under Moving Loads; Thomas Telford Ltd.: London, UK, 1999; Volume 1, pp. 339–342. [Google Scholar]
- Ren, B. Experimental Research on Vibration Characteristics of Vibration Reducing CRTS III Slab Ballastless Track. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2016. [Google Scholar]
- Lin, T.; Chen, G.; Zhang, Q.D.; Wang, H.W.; Chen, L.B. Fault sensitivity analysis and fusion technology for vibration features of aero-engine rolling bearings. J. Aerosp. Power 2017, 32, 2205–2217. [Google Scholar]


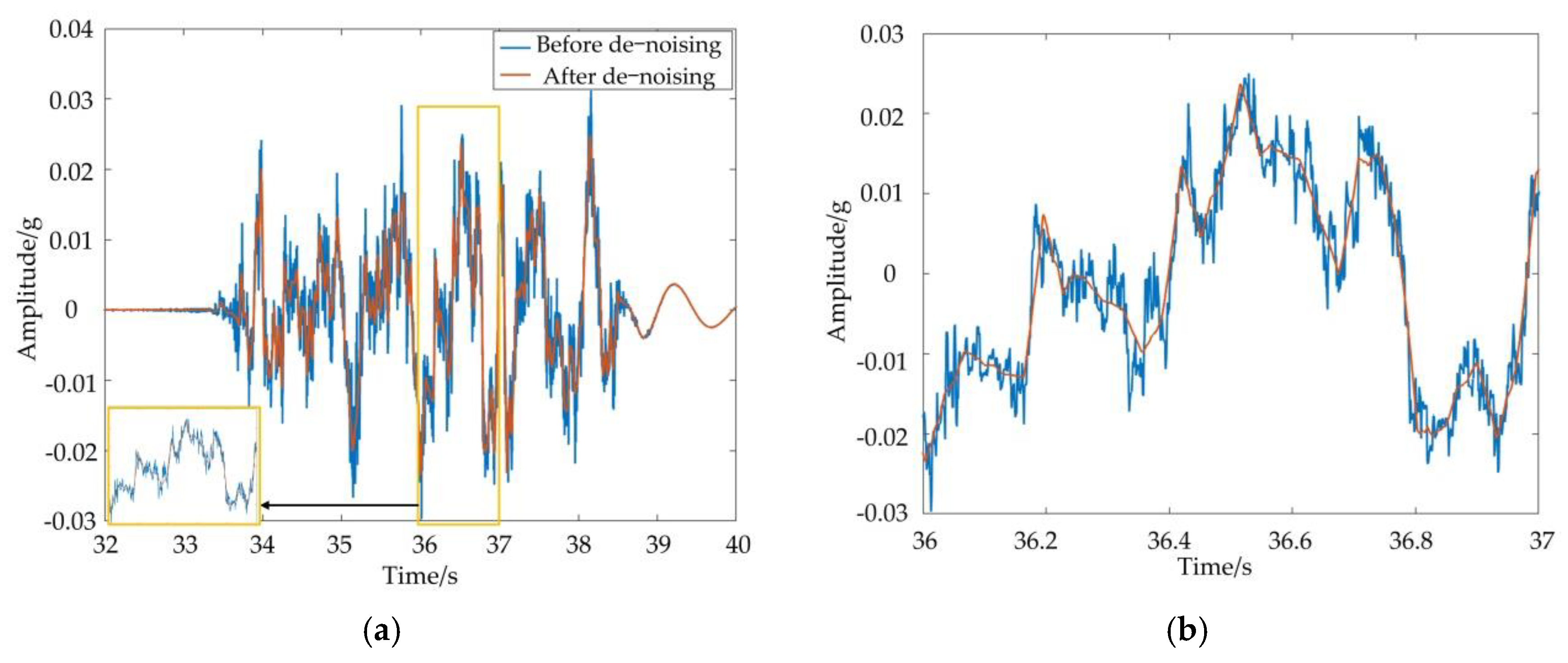
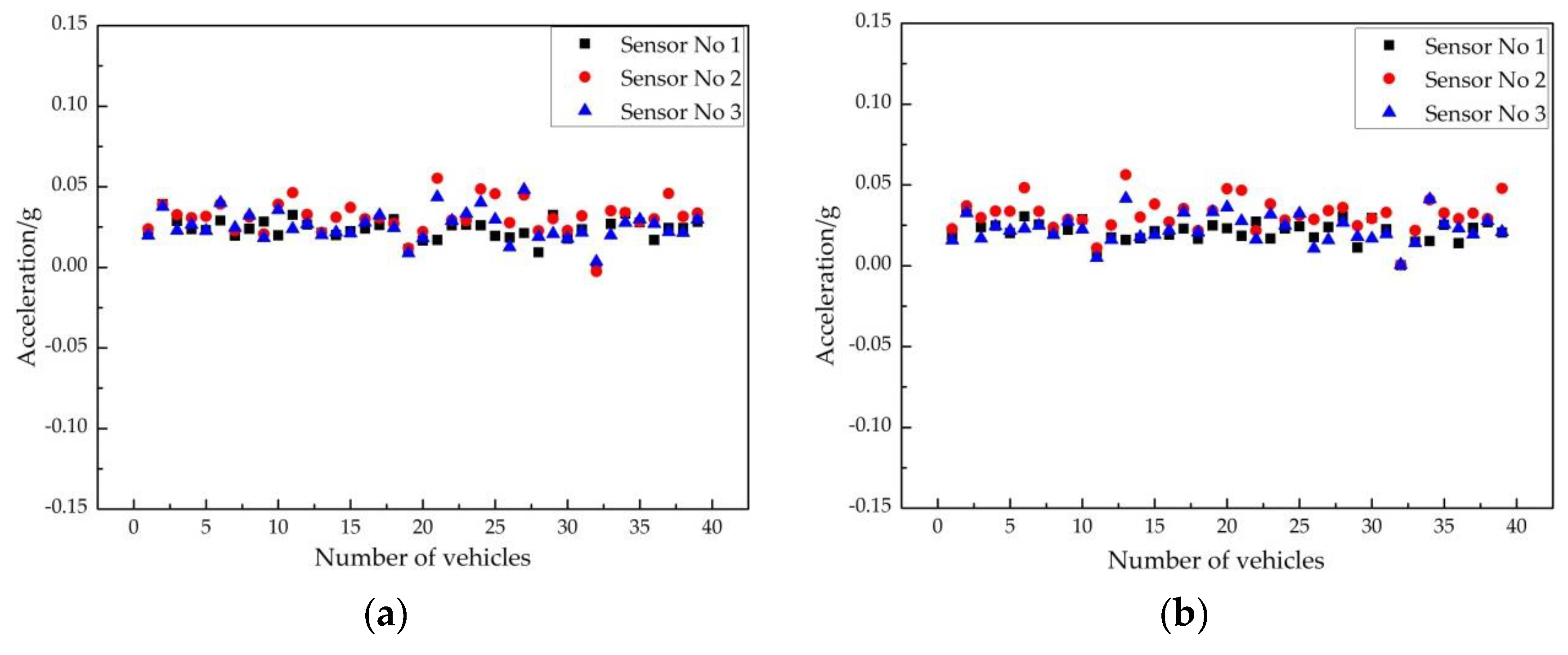

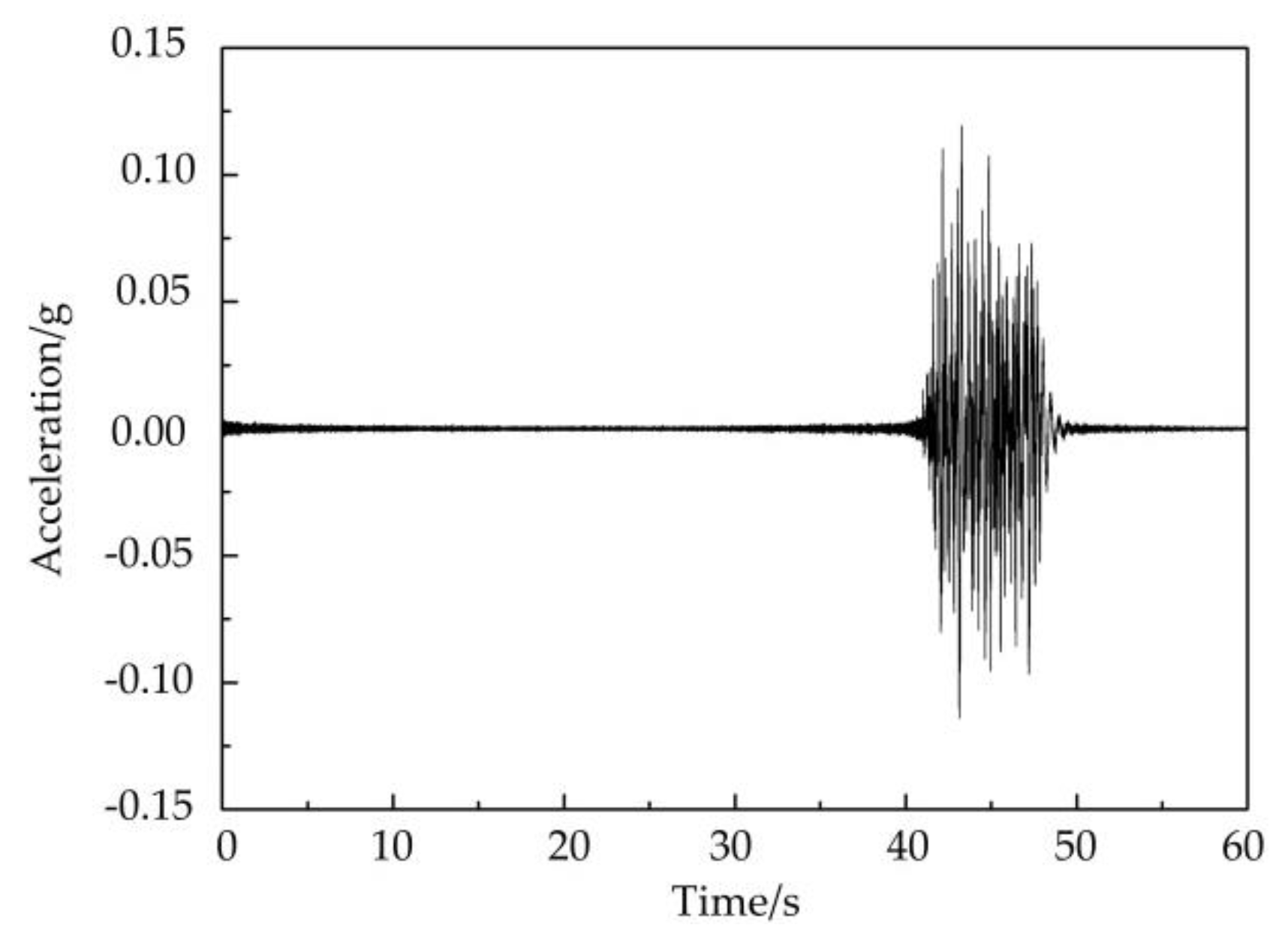

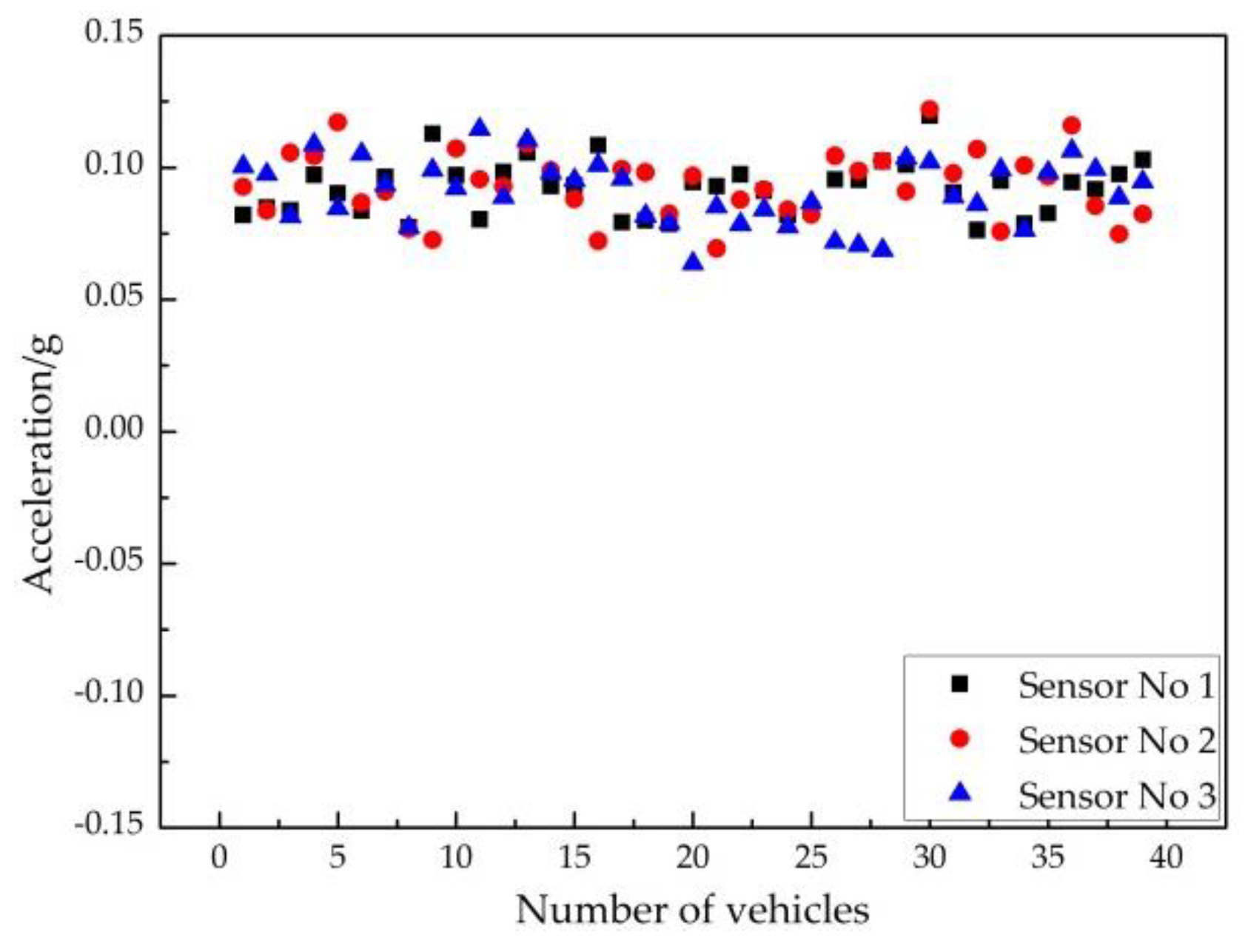






| Name | Expression | Description |
|---|---|---|
| Peak acceleration | Max value of the amplitude of signals. | |
| Shape factor | Shape factor refers to a value that is affected by the shape of waveforms. In this equation, mean value and root mean square (RMS) | |
| Crest factor | Crest factor is the measure of a waveform to show the ratio of the peak value to RMS | |
| Impulse factor | Impulse factor is the measure of a waveform to show the ratio of the peak value to the mean value. | |
| Clearance factor | Clearance factor is the measure of a waveform to show the ratio of the peak value to the . | |
| Kurtosis factor | Kurtosis factor is the ratio of kurtosis () to the fourth power of RMS. |
| Features | Segment 1 (a) | Segment 2 (b) | Difference |
|---|---|---|---|
| Peak acceleration | 0.0268 | 0.0336 | 2.537 × 10−1 |
| Shape factor | 3.560 | 3.548 | 3.371 × 10−3 |
| Crest factor | 17.509 | 17.503 | 3.427 × 10−4 |
| Impulse factor | 68.832 | 68.797 | 5.085 × 10−4 |
| Clearance factor | 517.106 | 517.055 | 9.863 × 10−5 |
| Kurtosis factor | 17,616.660 | 17,616.722 | 3.519 × 10−6 |
| Features | Segment 1 (a) | Segment 2 (b) | Difference |
|---|---|---|---|
| Peak acceleration | 0.0257 | 0.0910 | 2.541 |
| Shape factor | 3.584 | 3.749 | 0.0460 |
| Crest factor | 17.517 | 19.391 | 0.107 |
| Impulse factor | 68.984 | 75.490 | 0.0943 |
| Clearance factor | 517.051 | 560.485 | 0.0840 |
| Kurtosis factor | 17,616.587 | 17,360.558 | 0.0145 |
| Number | Feature | Segment 1 (a) | Segment 2 (b) | Difference |
|---|---|---|---|---|
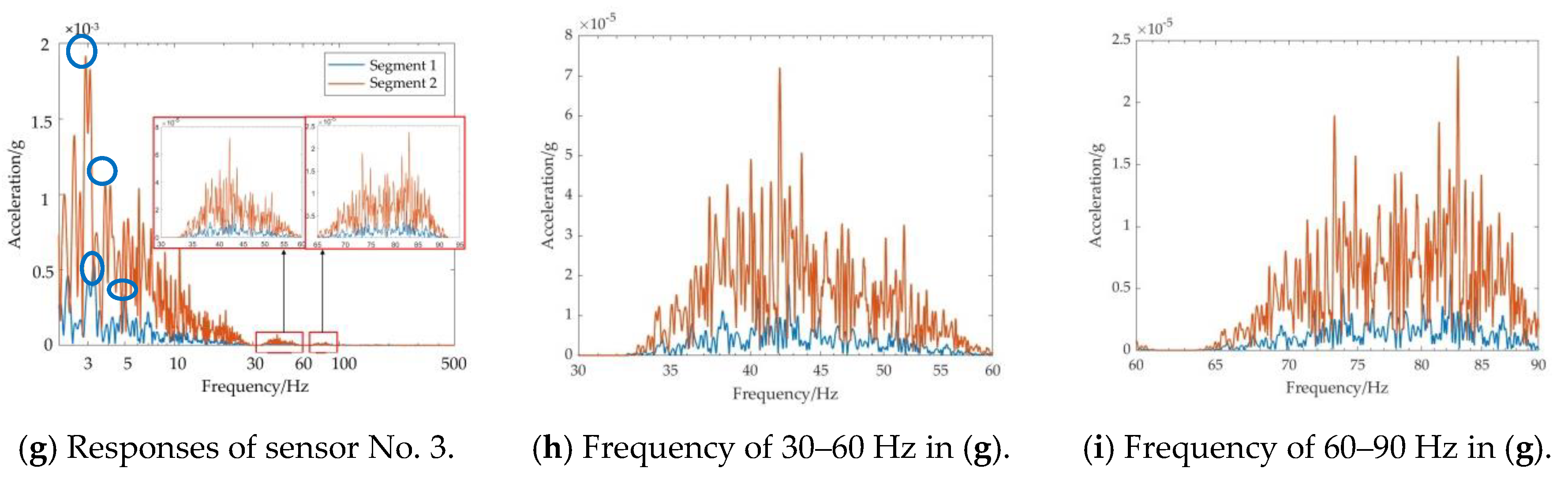
| Sensor 1 | Peak frequency 1/Hz | 2.56 | 2.46 | 0.039 |
| Peak frequency 2/Hz | 3.63 | 3.43 | 0.055 | |
| Peak amplitude 1/10−4 g | 4.32 | 15.8 | 2.66 | |
| Peak amplitude 2/10−4 g | 5.73 | 14.7 | 1.57 | |
| Sensor 2 | Peak frequency 1/Hz | 2.66 | 2.58 | 0.030 |
| Peak frequency 2/Hz | 3.74 | 3.63 | 0.029 | |
| Peak amplitude 1/10−4 g | 3.01 | 23.2 | 6.71 | |
| Peak amplitude 2/10−4 g | 2.81 | 15.3 | 4.44 | |
| Sensor 3 | Peak frequency 1/Hz | 2.49 | 2.37 | 0.048 |
| Peak frequency 2/Hz | 3.80 | 3.67 | 0.034 | |
| Peak amplitude 1/10−4 g | 4.61 | 10.9 | 1.36 | |
| Peak amplitude 2/10−4 g | 5.76 | 19.1 | 2.32 |
| Characteristic length/m | L1 | L2 | L3 | L4 |
| 2.5 | 17.5 | 7.5 | 25.0 | |
| Characteristic frequency/Hz | 25.78 | 3.68 | 8.59 | 2.58 |
| Category | Segment 1/dB | Segment 2/dB |
|---|---|---|
| Sensor No 1 | 283.63 | 357.44 |
| Sensor No 2 | 298.42 | 375.63 |
| Sensor No 3 | 284.51 | 357.55 |
| Number | Working Conditions | Frequency Band | Local Peak | Local Energy | Maximum Local Peak | Maximum Local Energy |
|---|---|---|---|---|---|---|
| Sensor 1 | Segment 1 | 0–11 | 28.99 | 1.88 | 28.99 | 4.64 |
| 11–80 | 8.55 | 4.64 | ||||
| Segment 2 | 0–35 | 439.70 | 115.00 | 439.70 | 115.00 | |
| 35–60 | 131.70 | 23.00 | ||||
| 60–80 | 89.20 | 45.30 | ||||
| Sensor 2 | Segment 1 | 0–25 | 41.00 | 8.96 | 88.55 | 33.70 |
| 25–80 | 88.55 | 33.70 | ||||
| Segment 2 | 36–80 | 445.00 | 125.00 | 445.00 | 125.00 | |
| Sensor 3 | Segment 1 | 0–34 | 28.92 | 6.36 | 28.92 | 6.36 |
| 34–80 | 8.50 | 5.66 | ||||
| Segment 2 | 0–4 | 434.70 | 12.70 | 434.70 | 99.70 | |
| 8–74 | 231.40 | 99.70 | ||||
| 74–80 | 74.32 | 22.80 |
| Scheme | Fused Features | ||||
|---|---|---|---|---|---|
| Time-Domain Feature | Frequency-Domain Feature | Time–Frequency-Domain Features | |||
| 1 | Peak acceleration | Peak frequency | Local peak | Local energy | CAC values |
| 2 | Peak acceleration | Peak frequency | Local peak | Local energy | Active CAC values |
| 3 | - | Peak frequency | Local peak | Local energy | Active CAC values |
| 4 | Peak acceleration | - | Local peak | Local energy | Active CAC values |
| 5 | Peak acceleration | Peak frequency | - | Local energy | Active CAC values |
| 6 | Peak acceleration | Peak frequency | Local peak | - | Active CAC values |
| 7 | Peak acceleration | Peak frequency | Local peak | Local energy | - |
| Scheme | Weights (%) | ||||
|---|---|---|---|---|---|
| Time-Domain Feature | Frequency-Domain Feature | Time–Frequency-Domain Features | |||
| 1 | 18.63 | 10.27 | 14.82 | 19.43 | 36.85 |
| 2 | 16.29 | 8.57 | 15.29 | 17.54 | 42.31 |
| 3 | - | 10.97 | 18.27 | 22.93 | 47.83 |
| 4 | 19.27 | - | 20.82 | 19.26 | 40.65 |
| 5 | 22.52 | 9.69 | - | 24.51 | 43.28 |
| 6 | 23.05 | 10.29 | 22.49 | - | 44.17 |
| 7 | 36.28 | 15.84 | 21.57 | 26.31 | - |
| Scheme | Sensitivity |
|---|---|
| 1 | 2.87 |
| 2 | 3.58 |
| 3 | 2.23 |
| 4 | 2.67 |
| 5 | 2.01 |
| 6 | 1.99 |
| 7 | 1.32 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, G.; Wang, J.; Du, B.; Du, Y. Application Study on Fiber Optic Monitoring and Identification of CRTS-II-Slab Ballastless Track Debonding on Viaduct. Appl. Sci. 2021, 11, 6239. https://doi.org/10.3390/app11136239
Guo G, Wang J, Du B, Du Y. Application Study on Fiber Optic Monitoring and Identification of CRTS-II-Slab Ballastless Track Debonding on Viaduct. Applied Sciences. 2021; 11(13):6239. https://doi.org/10.3390/app11136239
Chicago/Turabian StyleGuo, Gaoran, Junfang Wang, Bowen Du, and Yanliang Du. 2021. "Application Study on Fiber Optic Monitoring and Identification of CRTS-II-Slab Ballastless Track Debonding on Viaduct" Applied Sciences 11, no. 13: 6239. https://doi.org/10.3390/app11136239
APA StyleGuo, G., Wang, J., Du, B., & Du, Y. (2021). Application Study on Fiber Optic Monitoring and Identification of CRTS-II-Slab Ballastless Track Debonding on Viaduct. Applied Sciences, 11(13), 6239. https://doi.org/10.3390/app11136239






