An Artificial Intelligence Solution for Predicting Short-Term Degradation Behaviors of Proton Exchange Membrane Fuel Cell
Abstract
:1. Introduction
2. Methods
2.1. Data Acquisition
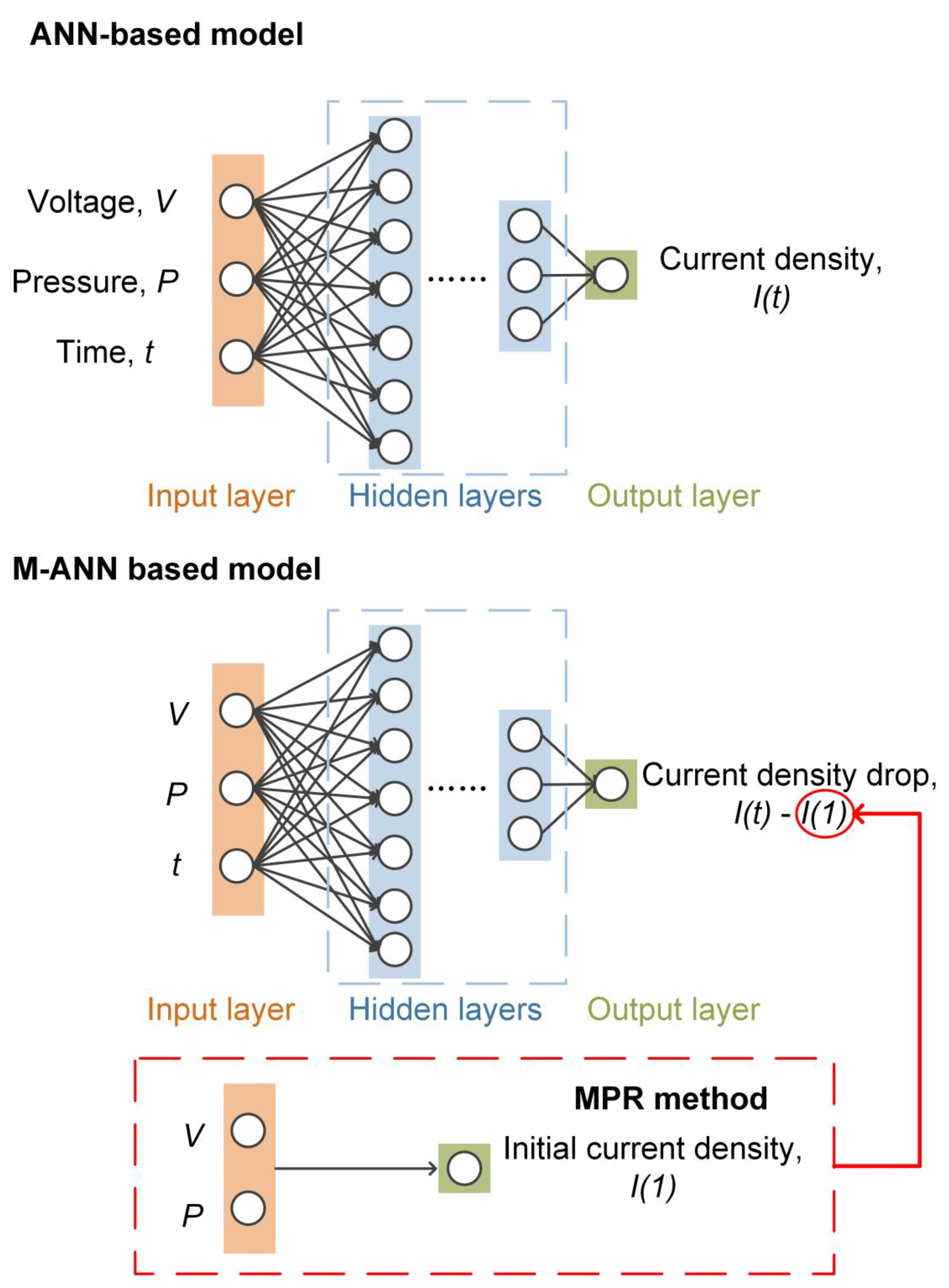
2.2. ANN Model Development
- Voltage;
- Inlet pressure;
- Time.
- Current density;
- Anode stoichiometry;
- Time.
2.3. Multivariate Polynomial Regression (MPR) Method
3. Results and Discussion
3.1. Performance Decay Prediction of the DEA Mode
3.1.1. Comparison of the ANN and M-ANN
- The MPR method solves the problem of initial current density prediction under various working conditions. This is because each operating condition has a different starting point for its current density due to different initial conditions, which is the reason for the poor effectiveness of ANN in predicting the overall degraded current density. ANN can also be used to predict initial current density at various operating conditions. the initial current density dataset has only 12 samples. It is well known that the ANN model needs a large amount of data to be trained to get better results. Therefore, when the amount of data is small, it is a wise choice to use the MPR method to predict results.
- The ANN solves the problem of predicting current density change. After eliminating the influence of the initial point, the current density changes under various operating conditions are similar. However, this change is relatively complex, not only rise or fall, but also the magnitude and time of rise and fall are uncertain. Therefore, with a large number of samples, a relatively complex ANN is more effective in learning the current density change. Figure 6 shows the result of MPR method predicting current density change. MPR-MPR means to use MPR to predict the initial current density and then MPR to predict the current density change. Compared with Figure 5 and Figure 6, ANN is better at predicting the current density change than MPR.
3.1.2. Comparison of Hidden Layer Numbers and Activation Functions
- The sigmoid activation function is computationally intensive while the ReLU activation function is much less so when the backpropagation algorithm is solving for the gradient.
- For deep neural networks with sigmoid activation function, the vanishing gradient problem can easily occur when the backpropagation algorithm is solving for the gradient.
- The ReLU activation function can make the output of some neurons zero, which will cause the sparsity of the neural network, reduces the interdependence of parameters and alleviates the overfitting problem.
3.2. Performance Decay Prediction of the Anode Recirculation Mode
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| T | temperature, K |
| u | flow rate, m·s−1 |
| RH | relative humidity |
| GDL | gas diffusion layer |
| MPL | micro-porous layer |
| CL | catalyst layer |
| L | length of the channel, cm |
| W | width of the channel, mm |
| d | depth of the channel, mm |
| A | area, m2 |
| K | permeability, mol·m−1·s−1·Pa−1 |
| I | current density, A·m−2 |
| c | reactant concentration, mol·m−3 |
| S | source term, mol·m−2·s−1 |
| N | the number of control volumes along the channel |
| J | the convection flux along the channel, mol·m−2·s−1 |
| M | molar weight, kg·mol−1 |
| s | liquid volume fraction |
| EW | equivalent weight of the membrane, kg·mol−1 |
| Cp | specific heat capacity, J·kg−1·K−1 |
| P | pressure, Pa |
| V | voltage, V |
| E | potential, V |
| R | area resistance, ; universal gas constant, 8.314 J·K−1·mol−1 |
| n | the number of electron transfer |
| F | Faraday constant, 96,485 C·mol−1 |
| ReLU | rectified linear unit |
| Greek Letter | |
| δ | thickness, m |
| porosity | |
| contact angle, ◦ | |
| ionomer volume fraction of the catalyst layer | |
| transfer coefficient | |
| diffusion flux, mol·m−2·s−1 | |
| density, kg·m−3 | |
| membrane water content | |
| Subscript and Superscript | |
| 0 | reference value |
| a | anode |
| c | cathode |
| GDL | gas diffusion layer |
| MPL | micro-porous layer |
| CL | catalyst layer |
| m | membrane |
| act | activation |
| CH | channel |
| in | flow inlet; inlet surface of the control volume |
| out | flow outlet |
| ref | reference |
| k | time step |
| n | control volume along the channel |
| i | gas species |
| CH-GDL | interface between the channel and gas diffusion layer |
| lq | liquid water |
| w | water |
| p | components of the electrode |
| m | membrane |
| mw | membrane water |
| T | Energy |
| eff | effective coefficient |
| cro | crossover |
| rev | reversible |
| Abbreviation | |
| DEA | dead-ended anode |
| PEM | proton exchange membrane |
| MPR | multivariate polynomial regression |
| ANN | artificial neural network |
| CFD | computational fluid dynamics |
| BO | bonobo optimizer |
| LSTM | long short-term memory |
| RNN | recurrent neural network |
| GRU | gated recurrent unit |
| ESN | echo state network |
| GNNM | grey neural network model |
| PSO | particle swarm optimization |
References
- Jiao, K.; Ni, M. Challenges and opportunities in modelling of proton exchange membrane fuel cells (PEMFC). Int. J. Energy Res. 2017, 41, 1793–1797. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Seo, B.; Wang, B.; Zamel, N.; Jiao, K.; Adroher, X.C. Fundamentals, materials, and machine learning of polymer electrolyte membrane fuel cell technology. Energy AI 2020, 1, 100014. [Google Scholar] [CrossRef]
- Wang, Y.; Yuan, H.; Martinez, A.; Hong, P.; Bockmiller, F.R. Polymer electrolyte membrane fuel cell and hydrogen station networks for automobiles: Status, technology, and perspectives. Adv. Appl. Energy 2021, 2, 100011. [Google Scholar] [CrossRef]
- Luo, Y.; Jiao, K. Cold start of proton exchange membrane fuel cell. Prog. Energy Combust. Sci. 2018, 64, 29–61. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, X.; Guo, L.; Liu, H. Local degradation in proton exchange membrane fuel cells with dead-ended anode. J. Power Sources 2020, 477, 229021. [Google Scholar] [CrossRef]
- Wang, B.; Deng, H.; Jiao, K. Purge strategy optimization of proton exchange membrane fuel cell with anode recirculation. Appl. Energy 2018, 225, 1–13. [Google Scholar] [CrossRef]
- Rabbani, A.; Rokni, M.; Hosseinzadeh, E.; Mortensen, H.H. The Start-Up Analysis of a PEM Fuel Cell System in Vehicles. Int. J. Green Energy 2014, 11, 91–111. [Google Scholar] [CrossRef]
- Pei, P.; Chen, H. Main factors affecting the lifetime of Proton Exchange Membrane fuel cells in vehicle applications: A review. Appl. Energy 2014, 125, 60–75. [Google Scholar] [CrossRef]
- He, L.; Zhan, Z.; Chen, H.; Jiang, P.; Yu, Y.; Yang, X.; Sun, Y.; Wan, X.; Liao, L.; Li, S.; et al. A quick evaluation method for the lifetime of the fuel cell MEA with the particle filter algorithm. Int. J. Green Energy 2021, 18, 1–14. [Google Scholar] [CrossRef]
- Ren, P.; Pei, P.; Li, Y.; Wu, Z.; Chen, D.; Huang, S. Degradation mechanisms of proton exchange membrane fuel cell under typical automotive operating conditions. Prog. Energy Combust. Sci. 2020, 80, 100859. [Google Scholar] [CrossRef]
- Jiao, K.; Li, X. Water transport in polymer electrolyte membrane fuel cells. Prog. Energy Combust. Sci. 2011, 37, 221–291. [Google Scholar] [CrossRef]
- Kurnia, J.C.; Sasmito, A.P.; Shamim, T. Advances in proton exchange membrane fuel cell with dead-end anode operation: A review. Appl. Energy 2019, 252, 113416. [Google Scholar] [CrossRef]
- Hou, J.; Yang, M.; Zhang, J. Active and passive fuel recirculation for solid oxide and proton exchange membrane fuel cells. Renew. Energy 2020, 155, 1355–1371. [Google Scholar] [CrossRef]
- Wang, B.; Wu, K.; Xi, F.; Xuan, J.; Xie, X.; Wang, X.; Jiao, K. Numerical analysis of operating conditions effects on PEMFC with anode recirculation. Energy 2019, 173, 844–856. [Google Scholar] [CrossRef]
- Peng, Y.; Mahyari, H.M.; Moshfegh, A.; Javadzadegan, A.; Toghraie, D.; Shams, M.; Rostami, S. A transient heat and mass transfer CFD simulation for proton exchange membrane fuel cells (PEMFC) with a dead-ended anode channel. Int. Commun. Heat Mass Transf. 2020, 115, 104638. [Google Scholar] [CrossRef]
- Rizvandi, O.B.; Yesilyurt, S. A Transient Pseudo-3D model of the PEM Fuel Cell for the Analysis of Dead-Ended Anode and Anode Bleeding Operation Modes. Electrochim. Acta. 2019, 324, 134866. [Google Scholar] [CrossRef]
- Xu, L.; Fang, C.; Li, J.; Ouyang, M.; Lehnet, W. Nonlinear dynamic mechanism modeling of a polymer electrolyte membrane fuel cell with dead-ended anode considering mass transport and actuator properties. Appl. Energy 2018, 230, 106–121. [Google Scholar] [CrossRef]
- Luo, Y.; Jiao, K.; Jia, B. Elucidating the constant power, current and voltage cold start modes of proton exchange membrane fuel cell. Int. J. Heat Mass Transf. 2014, 77, 489–500. [Google Scholar] [CrossRef]
- Zhou, Y.; Luo, Y.; Yu, S.; Jiao, K. Modeling of cold start processes and performance optimization for proton exchange membrane fuel cell stacks. J. Power Sources 2014, 247, 738–748. [Google Scholar] [CrossRef]
- Sultan, H.M.; Menesy, A.S.; Kamel, S.; Tostado-Véliz, Z.; Jurado, F. Parameter identification of proton exchange membrane fuel cell stacks using bonobo optimizer. In Proceedings of the 2020 IEEE International Conference on Environment and Electrical Engineering and 2020 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Milan, Italy, 9–12 June 2020; pp. 1–7. [Google Scholar]
- Wang, B.; Wu, K.; Yang, Z.; Jiao, K. A quasi-2D transient model of proton exchange membrane fuel cell with anode recirculation. Energy Convers. Manag. 2016, 129, 108–121. [Google Scholar] [CrossRef]
- Kheirandish, A.; Motlagh, F.; Shafiabady, N.; Dahari, M. Dynamic modelling of PEM fuel cell of power electric bicycle system. Int. J. Hydrogen Energy 2016, 41, 9585–9594. [Google Scholar] [CrossRef]
- Zou, W.; Froning, D.; Shi, Y.; Lehnert, W. A least-squares support vector machine method for modeling transient voltage in polymer electrolyte fuel cells. Appl. Energy 2020, 271, 115092. [Google Scholar] [CrossRef]
- Gu, X.; Hou, Z.; Cai, J. Data-based flooding fault diagnosis of proton exchange membrane fuel cell systems using LSTM networks. Energy AI 2021, 4, 100056. [Google Scholar] [CrossRef]
- Lin, T.; Hu, L.; Wisely, W.; Gu, X.; Litster, S.; Kara, L.B. Prediction of high frequency resistance in polymer electrolyte membrane fuel cells using long short term memory based model. Energy AI 2021, 3, 100045. [Google Scholar] [CrossRef]
- Wang, B.; Xie, B.; Xuan, J.; Jiao, K. AI-based optimization of PEM fuel cell catalyst layers for maximum power density via data-driven surrogate modeling. Energy Convers. Manag. 2020, 205, 112460. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, G.; Wang, H.; Xuan, J.; Jiao, K. Multi-physics-resolved digital twin of proton exchange membrane fuel cells with a data-driven surrogate model. Energy AI 2020, 1, 100004. [Google Scholar] [CrossRef]
- Xie, R.; Ma, R.; Pu, S.; Xu, L.; Zhao, D.; Huangfu, Y. Prognostic for fuel cell based on particle filter and recurrent neural network fusion structure. Energy AI 2020, 2, 100017. [Google Scholar] [CrossRef]
- Zuo, J.; Lv, H.; Zhou, D.; Xue, Q.; Jin, L.; Zhou, W.; Yang, D.; Zhang, C. Deep learning based prognostic framework towards proton exchange membrane fuel cell for automotive application. Appl. Energy 2021, 281, 115937. [Google Scholar] [CrossRef]
- Vichard, L.; Harel, F.; Ravey, A.; Venet, P.; Hissel, D. Degradation prediction of PEM fuel cell based on artificial intelligence. Int. J. Hydrogen Energy 2020, 45, 14953–14963. [Google Scholar] [CrossRef]
- Chen, K.; Laghrouche, S.; Djerdir, A. Degradation prediction of proton exchange membrane fuel cell based on grey neural network model and particle swarm optimization. Energy Convers. Manag. 2019, 195, 810–818. [Google Scholar] [CrossRef]
- Buzau, M.M.; Tejedor-Aguilera, J.; Cruz-Romero, P.; Gómez-Expósito, A. Hybrid deep neural networks for detection of non-technical losses in electricity smart meters. IEEE Trans. Power Syst. 2019, 35, 1254–1263. [Google Scholar] [CrossRef]
- Elisseeff, A.; Paugam-Moisy, H. Size of multilayer networks for exact learning: Analytic approach. Adv. Neural Inf. Process. Syst. 1996, 9, 162–168. [Google Scholar]









| Parameter | Value |
|---|---|
| Temperature, | 353.15 K |
| Cathode inlet velocity, | 10.0 m·s−1 |
| Cathode relative humidity, | 1.0 |
| Thickness of the GDL; MPL; CL; membrane, ; ; ; | 300.0 ; 40.0 ; 10.0 ; 25.4 |
| Length; Width; Depth of the channel, L; W; d | 10 cm; 1 mm; 1 mm |
| Activation area, | 2.0 × 10−4 m2 |
| Contact area between the GDL and channel, | 1.0 × 10−4 m2 |
| Inlet area, | 1.0 × 10−6 m2 |
| Porosity of the GDL; MPL; CL ; ; | 0.6; 0.4; 0.3 |
| Contact angle of the GDL; MPL; CL, ; ; | 110°; 120°; 95° |
| Permeability of the GDL; MPL; CL; membrane, ; ; ; | 1.0 × 10−11 m2; 1.0 × 10−12 m2; 1.0 × 10−13 m2; 2.0 × 10−20 m2 |
| Ionomer fraction of the anode and cathode CL, ; | 0.25, 0.25 |
| Transfer coefficient, ; | 0.5 |
| Reference exchange current density of anode and cathode, ; | 2.0 × 103 A·m−2; 1.0 × 10−5 A·m−2 |
| Reference reactant concentration of anode and cathode, ; | 41 mol·m−3; 41 mol·m−3 |
| Train Set | ||||||
| Voltage, V | 0.7 | 0.6 | 0.6 | 0.7 | 0.5 | 0.4 |
| Inlet pressure, bar | 1.6 | 1.4 | 1.3 | 1.0 | 1.2 | 1.8 |
| Train Set | Validation Set | Test Set | ||||
| Voltage, V | 0.4 | 0.5 | 0.5 | 0.6 | 0.6 | 0.7 |
| Inlet pressure, bar | 1.3 | 2.0 | 1.6 | 1.6 | 1.1 | 1.3 |
| Train Set | ||||||
| Current density, A·cm−2 | 1.6 | 1.5 | 0.4 | 1.2 | 1.2 | 1.1 |
| Anode stoichiometry | 1.3 | 1.5 | 2.0 | 1.5 | 2.4 | 1.8 |
| Train Set | Validation Set | Test Set | ||||
| Current density, A·cm−2 | 0.8 | 1.0 | 0.8 | 1.3 | 1 | 0.6 |
| Anode stoichiometry | 1.2 | 3.0 | 2.4 | 1.4 | 1.6 | 1.8 |
| Mean/Maximum Relative Error, % | |||
|---|---|---|---|
| Train | Validation | Test | |
| one-hidden-layer ANN (ReLU) | 0.405/2.037 | 0.625/1.122 | 0.725/1.563 |
| one-hidden-layer M-ANN (ReLU) | 0.119/1.632 | 0.180/0.759 | 0.198/0.803 |
| two-hidden-layer ANN (ReLU) | 0.186/1.381 | 0.291/0.665 | 0.341/0.932 |
| two-hidden-layer M-ANN (ReLU) | 0.094/1.010 | 0.146/0.484 | 0.158/0.534 |
| MPR-MPR | 0.228/2.210 | 0.264/1.263 | 0.348/1.510 |
| two-hidden-layer M-ANN (sigmoid) | 0.074/0.822 | 0.122/0.444 | 0.157/0.617 |
| Mean/Maximum Relative Error, % | |||
|---|---|---|---|
| Train | Validation | Test | |
| two-hidden-layer M-ANN (ReLU) | 0.082/1.768 | 0.128/0.768 | 0.143/0.458 |
| two-hidden-layer M-ANN (sigmoid) | 0.051/1.351 | 0.139/0.518 | 0.155/0.359 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Wang, B.; Sheng, X.; Wang, Y.; Ren, Q.; He, S.; Xuan, J.; Jiao, K. An Artificial Intelligence Solution for Predicting Short-Term Degradation Behaviors of Proton Exchange Membrane Fuel Cell. Appl. Sci. 2021, 11, 6348. https://doi.org/10.3390/app11146348
Yang Z, Wang B, Sheng X, Wang Y, Ren Q, He S, Xuan J, Jiao K. An Artificial Intelligence Solution for Predicting Short-Term Degradation Behaviors of Proton Exchange Membrane Fuel Cell. Applied Sciences. 2021; 11(14):6348. https://doi.org/10.3390/app11146348
Chicago/Turabian StyleYang, Zijun, Bowen Wang, Xia Sheng, Yupeng Wang, Qiang Ren, Shaoqing He, Jin Xuan, and Kui Jiao. 2021. "An Artificial Intelligence Solution for Predicting Short-Term Degradation Behaviors of Proton Exchange Membrane Fuel Cell" Applied Sciences 11, no. 14: 6348. https://doi.org/10.3390/app11146348
APA StyleYang, Z., Wang, B., Sheng, X., Wang, Y., Ren, Q., He, S., Xuan, J., & Jiao, K. (2021). An Artificial Intelligence Solution for Predicting Short-Term Degradation Behaviors of Proton Exchange Membrane Fuel Cell. Applied Sciences, 11(14), 6348. https://doi.org/10.3390/app11146348





