1. Introduction
Deep learning is an ubiquitous machine learning approach which has been successfully used in many applications to find a practical solution for complicated problems, e.g., medical image segmentation [
1] and self-driving cars [
2]. Recently, deep learning has emerged as a cornerstone for safety and security-critical applications, like autonomous vehicles [
3] and malware detection [
4]. It even supports other applications, e.g., facial recognition, which may effect our daily lives.
One of the recent obstacles of using deep learning are adversarial attacks, which were first introduced in [
5]. The authors in [
5] present a case of a malevolent attacker who can exploit the high-dimensional inputs by slightly modifying the pixels approaching the border of the high-dimensional geometrical manifold of the original class [
6]. Although the attacks can be very strong, reaching more than
confidence for misclassified classes, the modification which has been applied to the original image is imperceptible to the naked eye. Minor perturbation over the entire image is the first adversarial attack which has been introduced by Goodfellow [
7]. Many threatening results have surfaced urging the research community to find some defense mechanisms, e.g., Ref. [
8] demonstrates a universal perturbation fooling a classifier on any image, Ref. [
9] showed the possibility of fooling a classifier with a 3D printed object.
The most commonly applied defenses against adversarial attacks depend on one of three approaches: adversarial training [
10], modifying the network [
11] or a detection-based approach [
12]. Adversarial training slows down the training and it has also been demonstrated by [
8] that you can form an adversarial attack against a network which has been trained with adversarial training. Most defenses which rely on modifying the network are too computationally infeasible to be applied on larger networks or they only work against specific attacks [
13]. Detection-based approaches lack any notion of security in safety and time-critical applications where an immediate decision has to be taken without any delay, e.g., object detection in self-driving cars. Detection of adversarial attacks can be a good first step, but, on its own, it is not enough to ensure safety in practical applications since detection will only render the autonomous system in complete doubt, preventing the AI from making a sound and reliable decision. The ultimate safe solution for adversarial attacks, in the case of accurate detection, is recovering the original class. We will introduce a novel algorithm restoring the original class of the attacked image. We will demonstrate the effectiveness of our algorithm on three different datasets MNIST, CIFAR10 and 10 randomly selected classes from ImageNet.
2. Adversarial Attacks
The term
adversarial example was coined by [
5], where attacks on neural networks trained for image classification were generated via a very low intensity additive noise, completely unobtrusive to the human eyes as in
Figure 1. An adversarial example is a misclassified sample which has been modified with unnoticeable perturbations drastically changing the response of a network.
The eminent high risk of adversarial attacks urged the science community to thoroughly investigate any potential attack enlarging the concept of adversarial attack. Three kind of attacks have been investigated (evasion attacks, poisoning attacks and exploratory attacks) where the first published adversarial attack [
5] belongs to the first category. Evasion attacks are the most common attack in an adversarial setting where malicious samples are created to fool the network during the testing phase, causing a misclassification [
7,
14]. Poisoning attacks [
15] contaminate the training dataset by injecting meticulously contrived samples compromising the training procedure. Exploratory attacks [
16] are used when we only have a black-box access to the model and, thus, the attacker tries to collect as much knowledge as possible about the distribution of the training dataset and the network response which can be used to build a network that is capable of building adversarial samples. We will concentrate on the widespread white-box gradient-based attacks which we will investigate in our paper and briefly describe in this chapter.
2.1. Adversarial Attack Algorithms
The first attacks [
7] were implemented by calculating the sign of the gradient of the cost function (
J) with respect to the input (
x) and expected output (
y), multiplied by a constant to scale the intensity of the noise (formally
, where
is the parameters of the model) where the calculated value is the perturbation which is added to the original sample creating the adversarial image. This method, which is called the fast gradient sign method (FGSM), allows for much faster generation of attacks.
An extension to FGSM by [
14] is to use not only the gradient’s sing of the loss, but rather a scaled version of the gradient’s raw value (
). In the same paper a targeted attack and an iterative basic method were proposed. A targeted attack can be achieved by steering the perturbation to the opposite direction of the gradient of the loss function (
) maximizing the probability of a specific class (
). Iterative-based method attack, which is also called projected gradient descent attack (PGD), is a targeted attack that can be applied
N number of times with a small step size, taking into account the intensity boundary where the perturbations calculated at each iteration are accumulated, leading to a misclassification.
Another extension to the iterative version of FGSM by [
17] was to incorporate momentum into the equation, hypothesizing that, similarly to regular optimization, momentum helps in stabilizing the direction of the update and avoiding poor local minima or maxima, narrow valleys and other non-convex patterns in the objective function’s landscape.
Ref. [
18] proposed DeepFool attack to calculate minimum norm adversarial perturbations, taking the image to the edge of the decision boundaries of the classifier. It is similar to the basic iterative method in a sense that it relies on gradients, but DeepFool normalizes the gradient by linearizing the boundaries of the manifold where the image resides.
Many other variations of PGD attack have been formulated enhancing the quality and the speed of the adversarial attack [
19,
20]. A general overview of adversarial attacks, containing most of the previously mentioned methods, can be found in the following survey papers [
13,
21].
2.2. Adversarial Attack Detection
Defenses against adversarial attacks are required to prevent security threats in real-world application of neural networks. Most defenses rely on one of the following three main approaches:
Modifying the training process, e.g., adding adversarial samples (adversarial training) [
18] or modifying the input before testing (decision making) [
22,
23].
Modifying the network, e.g., adding extra masking layer before the last layer [
24] and changing the loss function by penalizing the degree of variety per class in the output [
11].
Using external model as a detector, e.g., SafetyNet [
12] and convolutional filter statistics detector [
25].
Detectors can be a reliable choice providing the highest accuracy reaching
[
25] preventing most security breaches. There are a lot of other detectors [
26,
27] separating the clean image from the adversarial one by finding some distinguishable features and properties e.g., convolution filter statistics [
25] and manifolds [
26]. Although detectors are considered strong defenses against adversarial attacks, an attack can cause a halt in the system hindering the achievement of any task. In a time sensitive task e.g self-driving cars, where an on-the-spot decision has to be drawn, detectors are not sufficient and a retrieving approach has to be installed recovering the original class of the input.
3. Class Retrieval
Most non-detection defenses are vulnerable to counter-counter attacks [
28], rendering potential exposure and keeping the system in a state of being without any functioning protective shield. Detection-based defenses, on the other hand, can be continuously updated but lack the ability to steer the decision-making process obstructing the installation of any safety measure. Thus, a recovery algorithm has to be employed after the detection of adversarial attacks, providing robustness and resilience.
Ref. [
29] hypothesized that adversarial attacks exploit the edge of the decision boundary between classes, pushing the adversarial sample to the targeted class. Their idea stemmed from the speculation that training data will be pushed to the edge of the decision boundary once they are classified correctly. In [
30,
31], the authors assume that the reason behind the adversarial vulnerability of neural networks is the highly positively curved decision boundary where the curvature is very intricate near the classes borders. The high dimensionality of neural networks creates convoluted borders between all the classes, making a targeted adversarial attack highly possible. Taking into account the complexity of the curvature of the decision boundary, we hypothesize that the distance between the adversarial sample and the original class’s manifold in the feature space of the decision boundary is smaller than the distance between the adversarial sample and any other classes’ manifolds and, hence, all the adversarial samples and their counter attacks are in the vicinity of the original class manifold. We have implemented our idea, a class retrieval algorithm, on the notion of our former hypothesis to predict the original class by counter attacking the adversarial samples, targeting every class and then selecting the class with the minimum loss. What we can derive from our hypothesis is that during the counter attack, it would be the easiest to transform back the attacked image to its original class since the attacked sample still contains many features belonging to the original class, and the manifold of the attacked class is the closest to the decision boundary of the original class, as we can observe in
Figure 2. The counter attack can return the attacked sample to its original class easily since the adversarial sample is on the edge of the original class decision boundary. Due to the high dimensionality of the decision boundary curvature, there exist an intricate border between the manifold of each of the two randomly selected classes.
To illustrate this hypothesis, we conducted experiments on the MNIST dataset, where 100 randomly selected samples from the same class were attacked (we considered them to be a separate class) and the two-dimensional position of their manifolds were depicted using the UMAP algorithm. An example can be seen in
Figure 3, which confirms our assumptions that going back to the original class manifold can be achieved in fewer iterations than turning the sample to any other class, i.e., the cross entropy loss of a targeted class will be the smallest when targeting the original class.
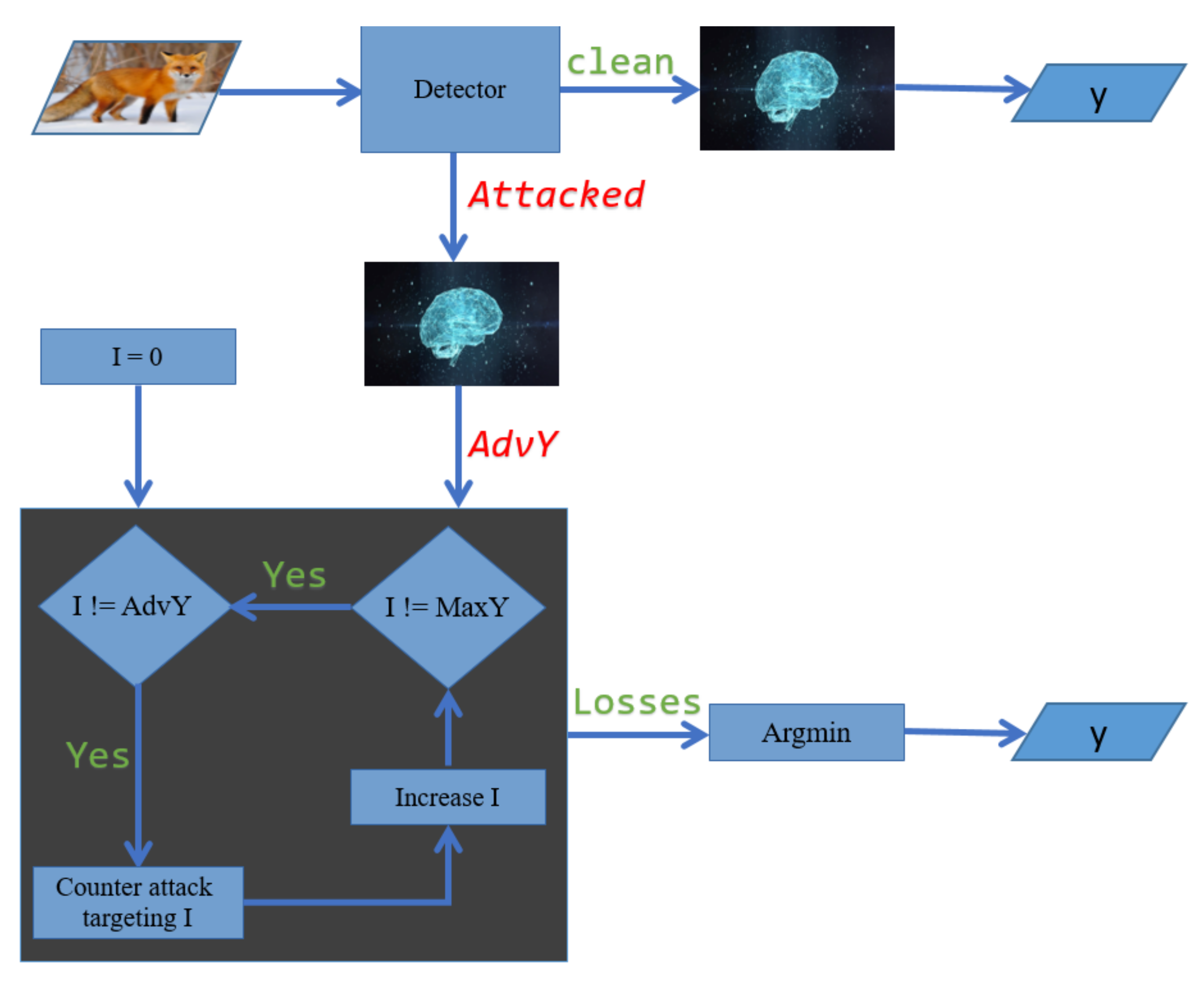
Our class retrieval algorithm for a detected adversarial attack is presented in Algorithm 1 as a pseudo-code, and explained as a flowchart in
Figure 4.
is the adversarial image which has been selected by an adversarial attack detector filtering any potential adversarial threat. The neural network prediction for the label of the adversarial image is
, which is a misclassification according to our detector.
is a fixed parameter representing the number of classes in our classification problem. We apply a counter targeted attack using
function where
is the number of iterations in the iterative adversarial attack and
is the targeted label. The loss function,
, calculates the cross entropy loss of the counter adversarial image,
, having
as a label. We exterminate the possibility of the adversarial label,
, being the original class by setting its loss to infinity. The original label,
, is the class with the minimum loss excluding the adversarial label where we used
function to return the index of the smallest loss.
| Algorithm 1: Class retrieval algorithm for a detected adversarial attack |
![Applsci 11 06438 i001]() |
To demonstrate the validity of our work, we assumed the existence of an optimal detector which can identify any adversarial attacks. We investigated four different adversarial attacks (projected gradient descent attack (PGD) [
32], MPGD [
17], Deepfool [
18], TPGD [
20], PGDDLR [
19]; most of the attacks were adopted from Torchattacks library [
33] while we used the codes of the original paper for the Deepfool attack) which were briefly explained in the previous section. Deepfool is not a targeted attack and the last two attacks are extended versions of the first attack; thus, we only used the first two previously mentioned attacks, PGD attack and PGD with momentum, as a counter adversarial attack. All the investigated adversarial attacks are white-box attacks, and this relies on the gradients to calculate the small perturbations fooling the classifier. For the sake of reproducibility, you can find our codes online
https://github.com/Al-Afandi/class_retrieval (accessed on 7 June 2021), which include the chosen investigated parameters.
4. Results
4.1. MNIST
To validate our hypotheses, detailed experiments were conducted using the MNIST and other datasets, as we will see in the next paragraphs. MNIST is a commonly investigated dataset with ten classes containing 70 thousand images of handwritten digits with a 28 × 28 resolution. We investigated five different adversarial attacks (PGD, MPGD, Deepfool, TPGD and PGDDLR) to create a matrix of success rate with another two counter attacks (PGD and MPGD). In each case, we attempted to retrieve the class of 1000 successfully attacked samples, which means 10,000 experiments altogether were conducted. The maximum distortion of the adversarial attack was set to 0.2. The number of iterations, , is 10 for the adversarial attacks insuring a successful attack, but we set it to 3 for the counter adversarial attack, illustrating the fast convergence to the original class.
AlexNet architecture was used throughout our experiments, providing a good baseline network where the average accuracy on clean samples is
(the original 28 × 28 images were rescaled to 224 × 224, ensuring the required input size).
Figure 5 demonstrates the high accuracy of the class retrieval algorithm investigating the usage of two counter attacks against the adversarial samples of five different attacks. On average,
of the attacked samples were correctly recovered, predicting their original class and averting misclassification.
4.2. CIFAR10
We investigated another simple but more intricate dataset, CIFAR10, to show the effectiveness of our novel approach. The same setup described in detail in the previous paragraph was used. The only parameters which were significantly modified were the adversarial attack maximum distortion and number of iterations
, where we set the former to 0.05 and the latter to 5. We opted to use these smaller values in comparison to our setup with MNIST due to the faster and easier conversion to adversarial samples.
Figure 6 shows the success rates using our class retrieval algorithm over the CIFAR10 dataset, engulfing ten different setups. We used the ResNet-18 architecture throughout our experiments, providing a good baseline with
accuracy in classifying clean samples. The overall averaged retrieval accuracy is
, which demonstrates the viability of our approach.
4.3. ImageNet
Our algorithm can be applied, in practice, with datasets that contain a limited number of classes
N, because of the nature of the algorithm (
number of counter attacks have to be made). To investigate complex and more practical datasets with high-resolution images, we have randomly selected 10 classes from ImageNet to execute similar experiments as in case of MNIST and CIFAR10. We did not use Deepfool as an adversarial attack because only targeted adversarial attacks can be used due to the fact that we can only target one of the ten selected classes. Altogether, 8000 attacks and retrievals were made and, to balance the effect of random class selection, we selected ten different classes for each 100 attacks. Throughout our investigation, we used the pretrained version of
architecture from the torchvision models library. The inception model has one thousand possible output classes, but our adversarial and counter attacks were only targeting the randomly selected ten classes. We can see the success rate on ImageNet in
Figure 7, where each cell represents the accuracy of a specific attack and counter attack investigating thousand cases with 10 different random classes for each hundred trials. There was a
average accuracy of recovering eight thousand attacked images from ImageNet using our class retrieval.
4.4. Parameters Investigating
Our class retrieval algorithm has two important parameters, number of iterations (
) and number of classes (
).
parameter does not have much effect on the algorithm according to our measurements, and it gave the same results after the first iteration, as we can observe in
Figure 3.
parameter is essential to the algorithm as we have to conduct (
) counter attacks. Statistically, the accuracy will drop when having a large number of classes preventing a correct retrieval. We conducted an extensive investigation over the CIFAR10 dataset, evaluating the success rate of adversarial attacks having different number of classes, from four to ten classes. We used AlexNet architecture to train a classifier for the randomly selected classes (4 to 10 classes), and we then calculated the average of the success rate of our class retrieval for each classifier (evaluating the retrieval of 10k adversarial attacks) to create a plot,
Figure 8, illustrating the relationship between the accuracy of our algorithm and
parameter. We can see that the algorithm is functioning effectively with a relatively high number of classes, but the accuracy will eventually decrease when processing a huge number of classes. Although a high number of classes is a limitation of our method due to time consumption and statistical probability, in most practical applications, only a few output classes are used.
Another parameter which can effect our method is the size of the input space. While low-resolution images, e.g., MNIST, are difficult to attack with small bounded unnoticeable perturbation, high-resolution images, e.g., ImageNet, are easy to attack because of their high dimensionality, rendering a complicated but vulnerable decision boundary curvature which can be easily compromised by slightly modifying the high number of pixels.
As we mentioned before, we assumed the existence of an optimal detector which can identify any adversarial attacks, and we implemented our experiments in light of this assumption. Unfortunately, practical detectors may result in false positive and false negative samples. False negative samples will not be processed by our method but false positive samples will, yielding bad classification and reducing the success rate of our method. In practice, the success rate of our method will drop slightly due to false positive detected samples, but we hope that with the rapid development of this field, a near optimal detector will be available soon.
5. Conclusions
We presented a novel problem, class retrieval and the recovery from adversarial attacks along with a proposed solution, which can be used as a baseline approach in further experiments. Our retriever is a self-evident addition to adversarial attack detectors and the combination of these two methods can enable the practical applicability of deep network even in case of attacks. We investigated four different adversarial attacks (PGD, MPGD, Deepfool, TPGD and PGDDLR) on three different datasets (MNIST, CIFAR10 and ImageNet). The results are promising and consistent across all attacks and datasets, where the average accuracy is , and , respectively. Our retrieval algorithm was not able to recover the original class in all cases but, as a preliminary concept, it clearly shows that it is possible to build an algorithm where the original class can be retrieved. We hope this can open the way for further development and fine tuning of class retrievals of adversarial attacks, which can increase the robustness of deep neural networks in real-world applications.