Effect of Vibration on Emergency Braking Tribological Behaviors of Brake Shoe of Deep Coal Mine Hoist
Abstract
:1. Introduction
2. Performance Parameters of the Brake Shoe
3. Vibration Behaviors of the Brake Shoe during Emergency Braking
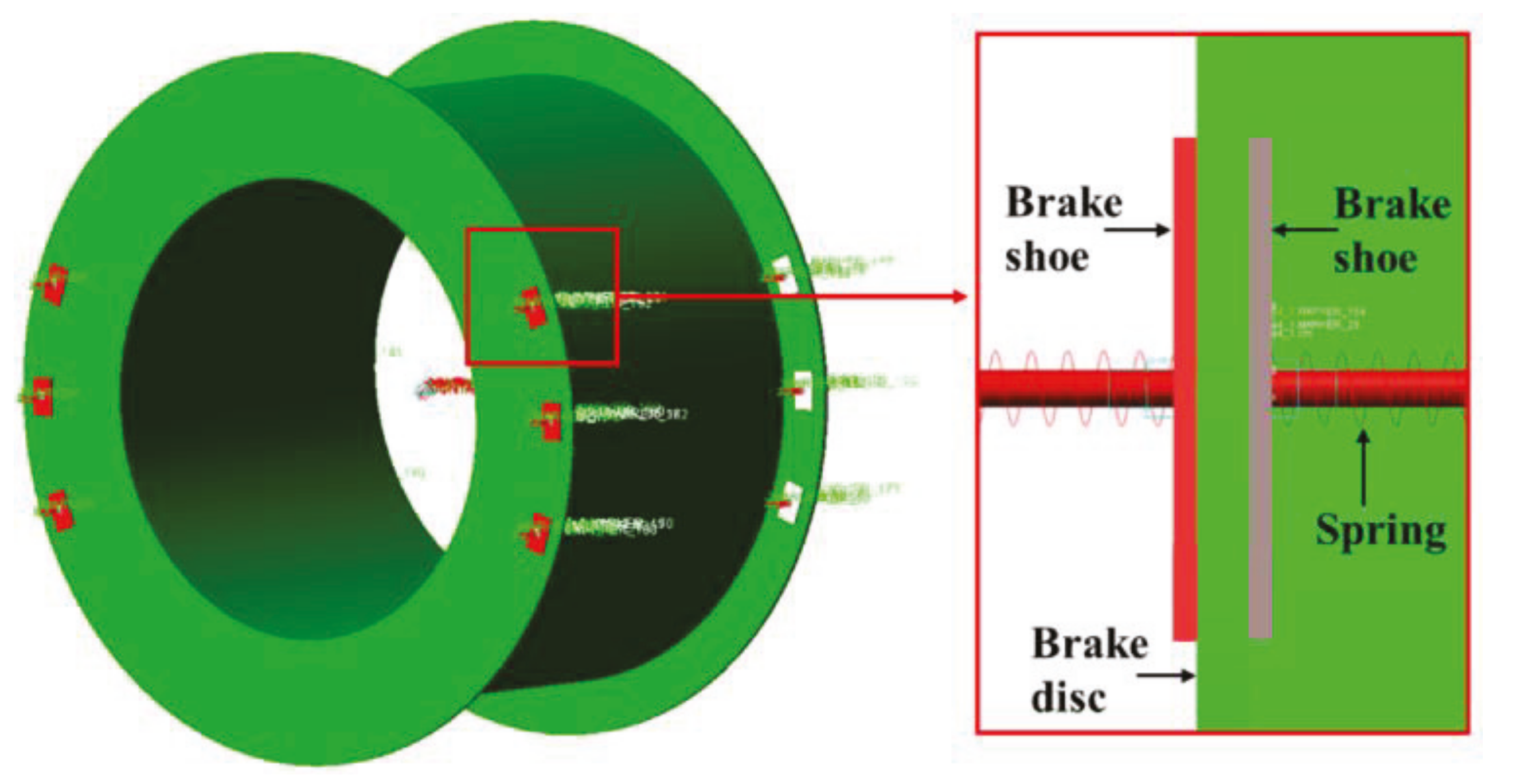
3.1. Dynamic Model of the Brake Shoe during Emergency Braking
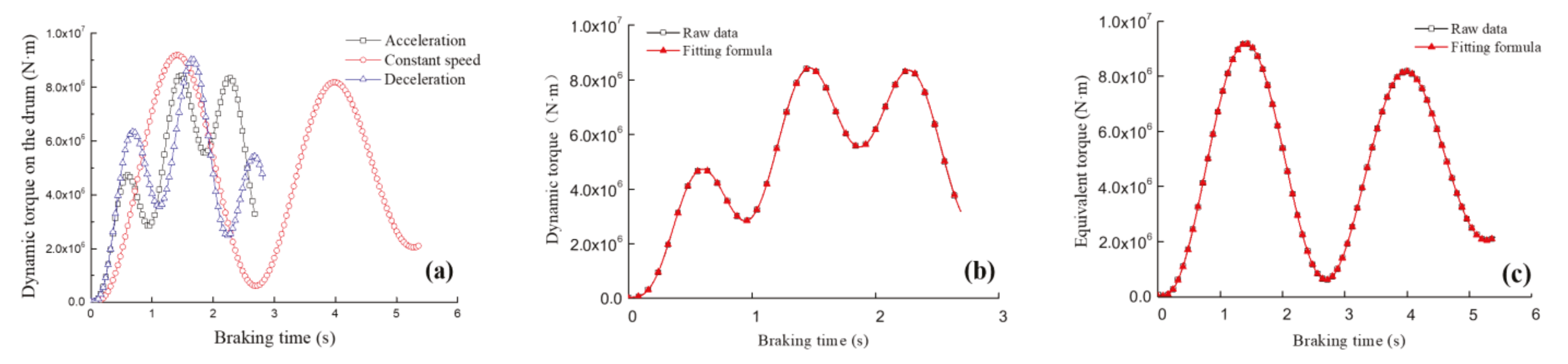
3.2. Dynamic Torque during Emergency Braking
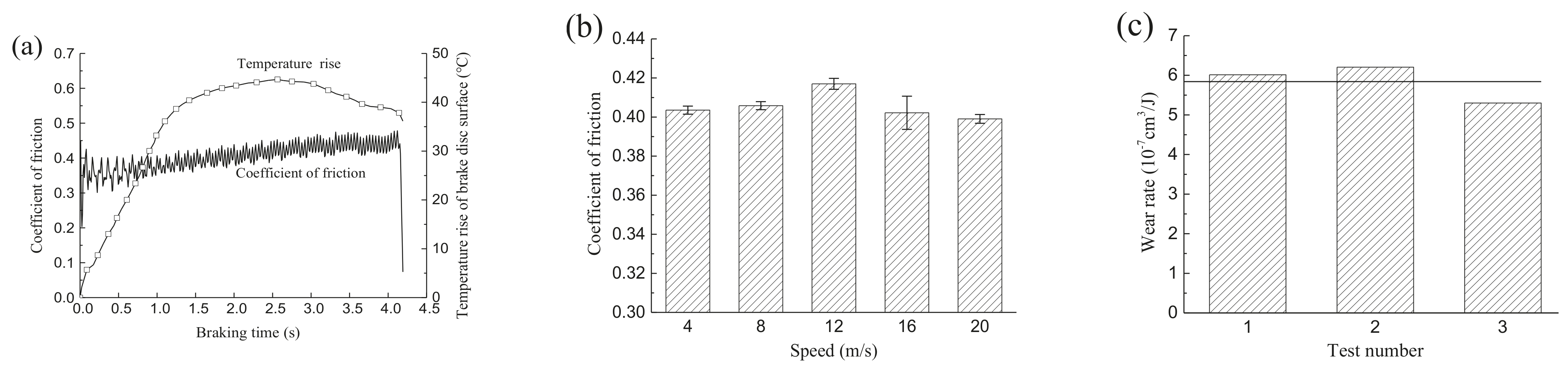
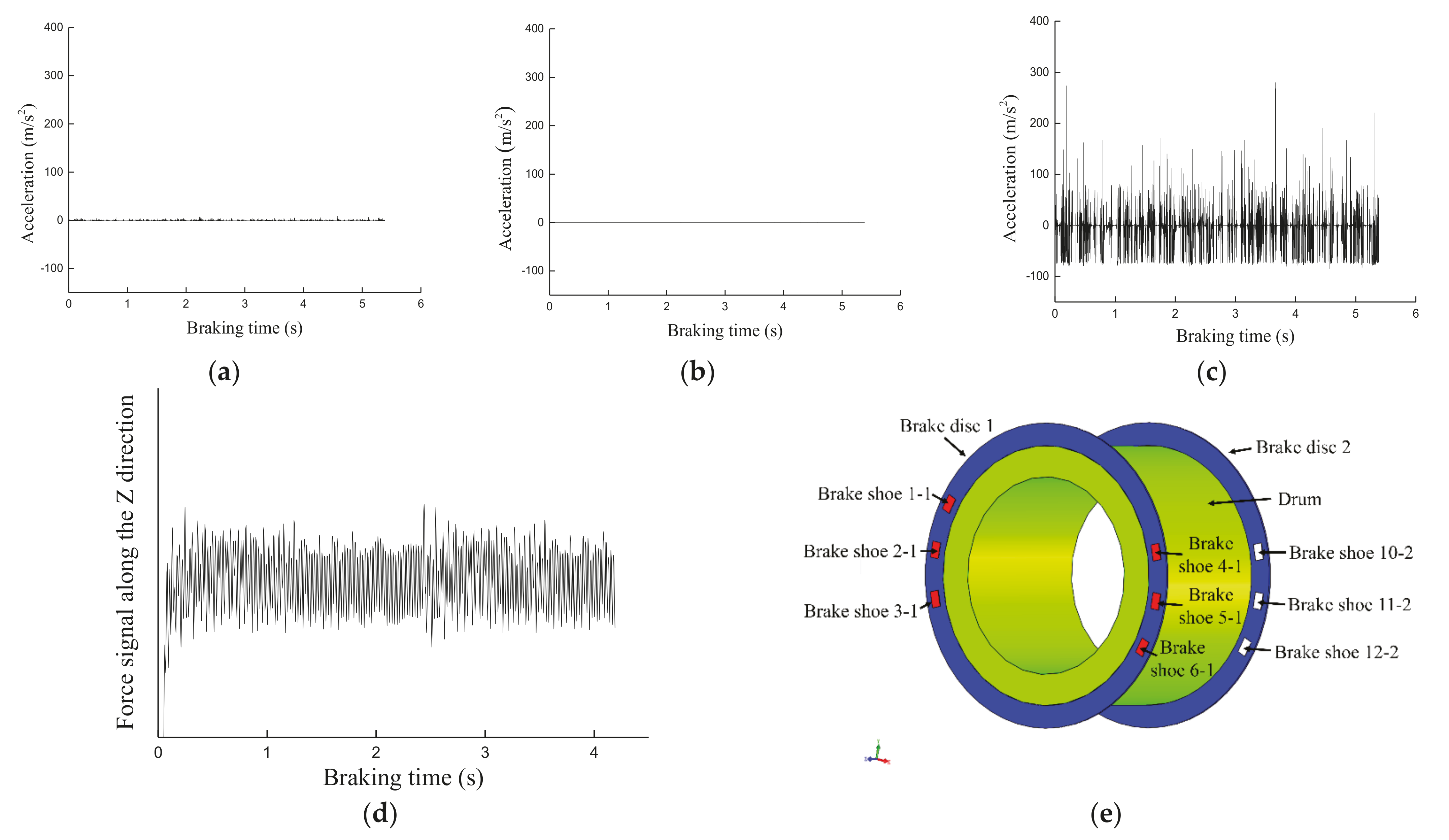
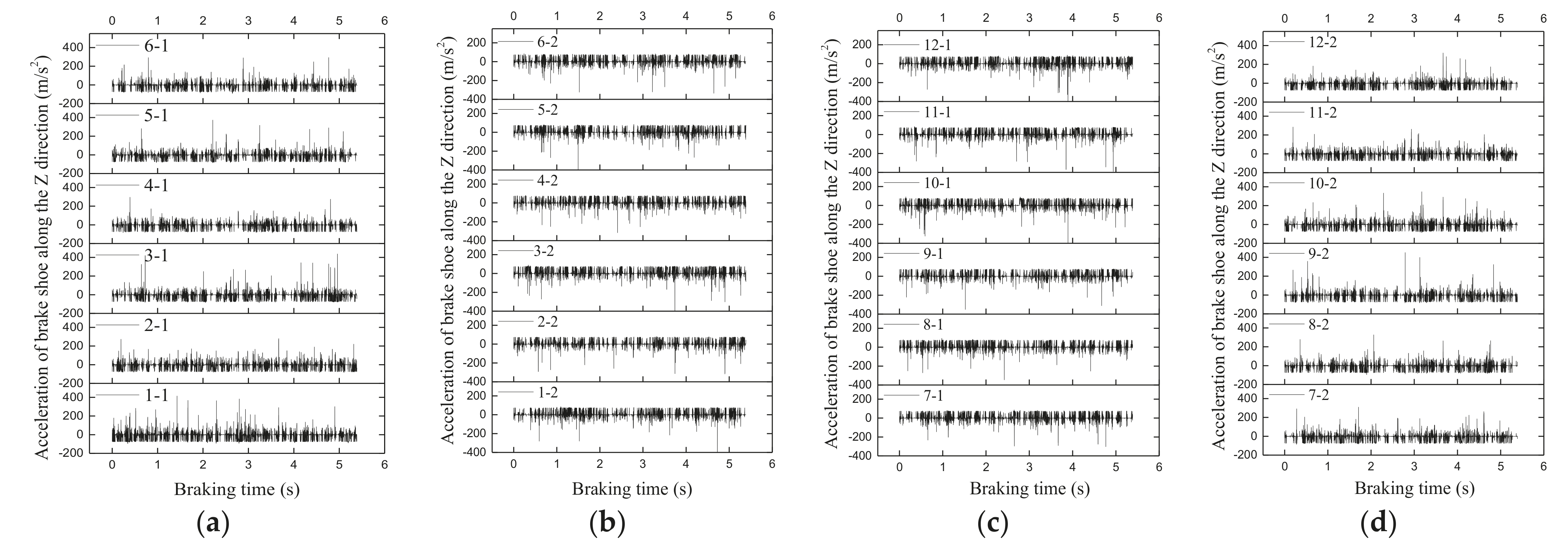
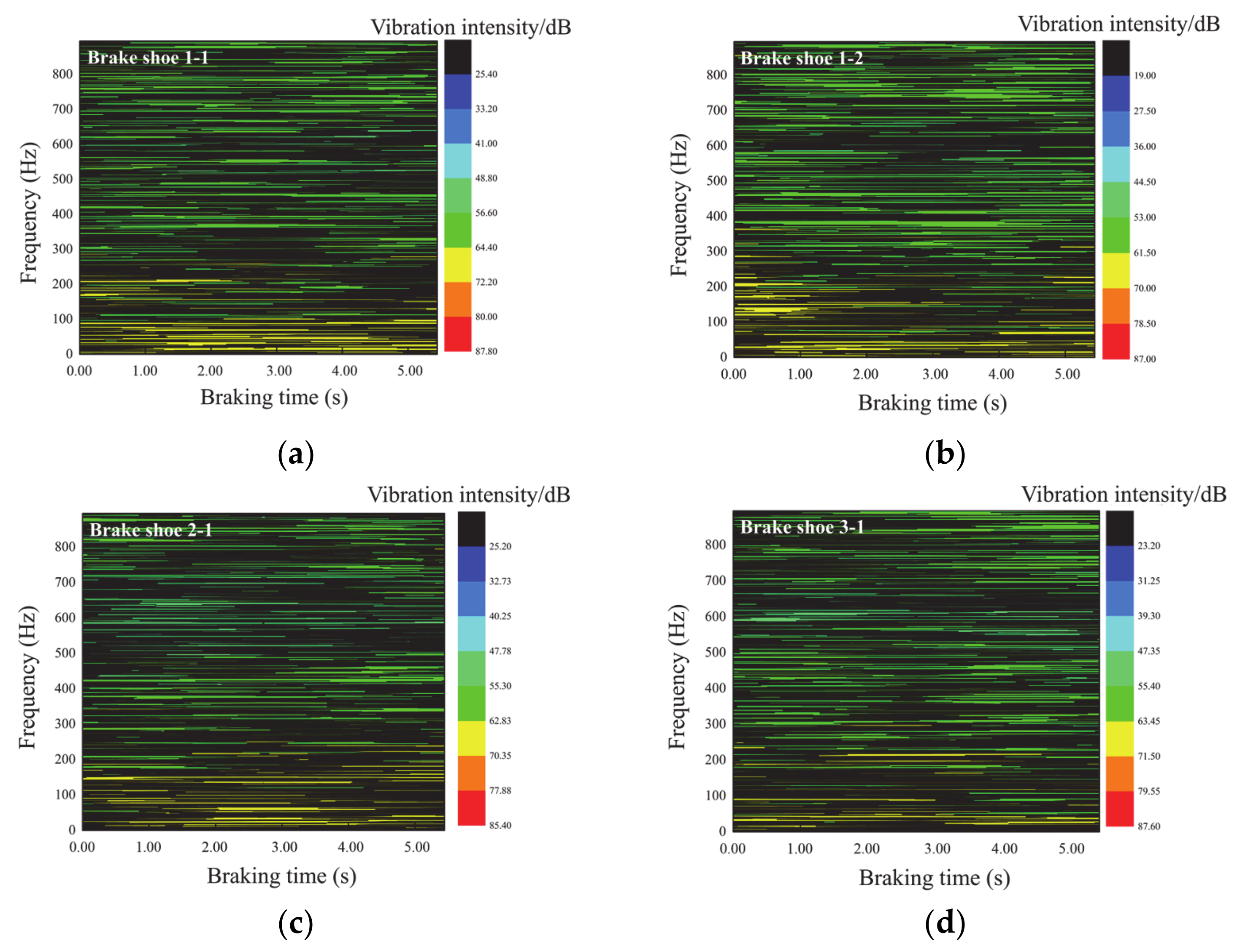
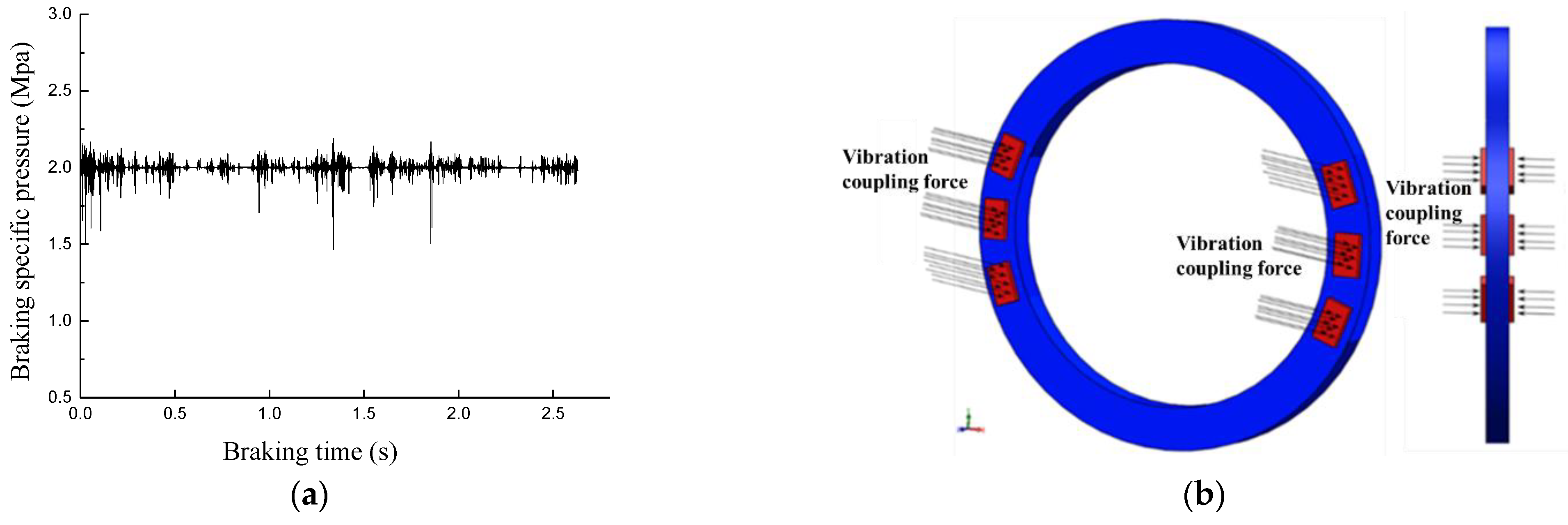
3.3. Vibration Characteristics of the Brake Shoe during Emergency Braking
4. Effect of Vibration on Emergency Braking Tribological Behaviors of Brake Interfaces
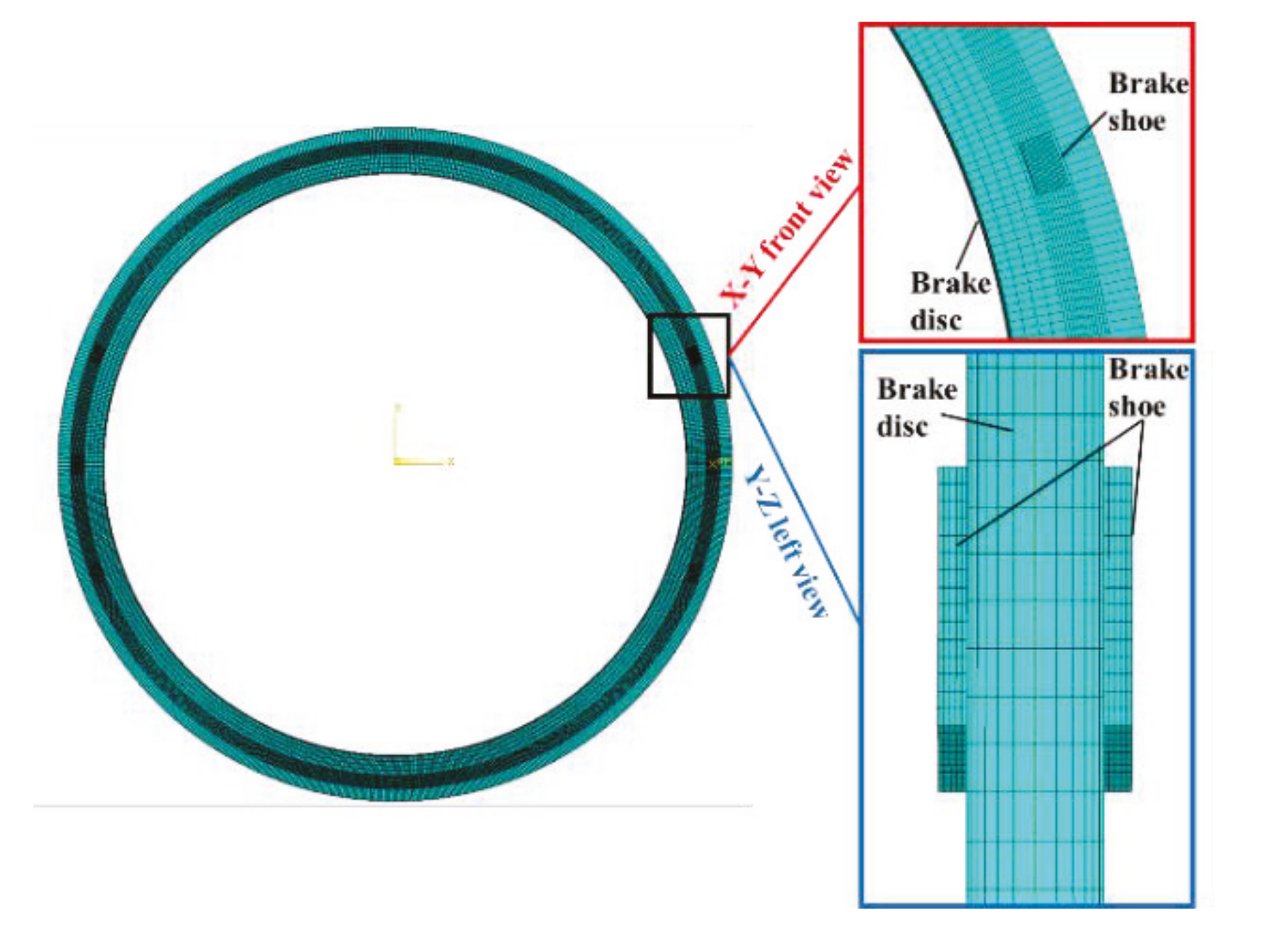
4.1. Emergency Braking Model of Brake Shoe under Vibration
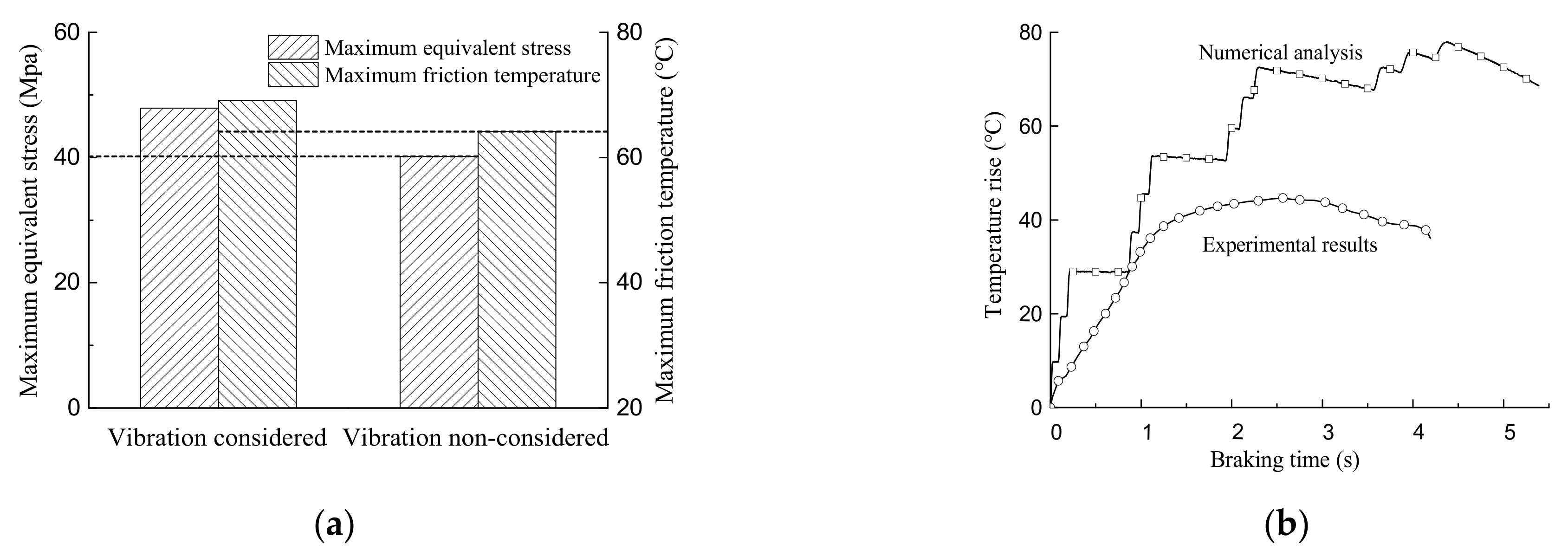
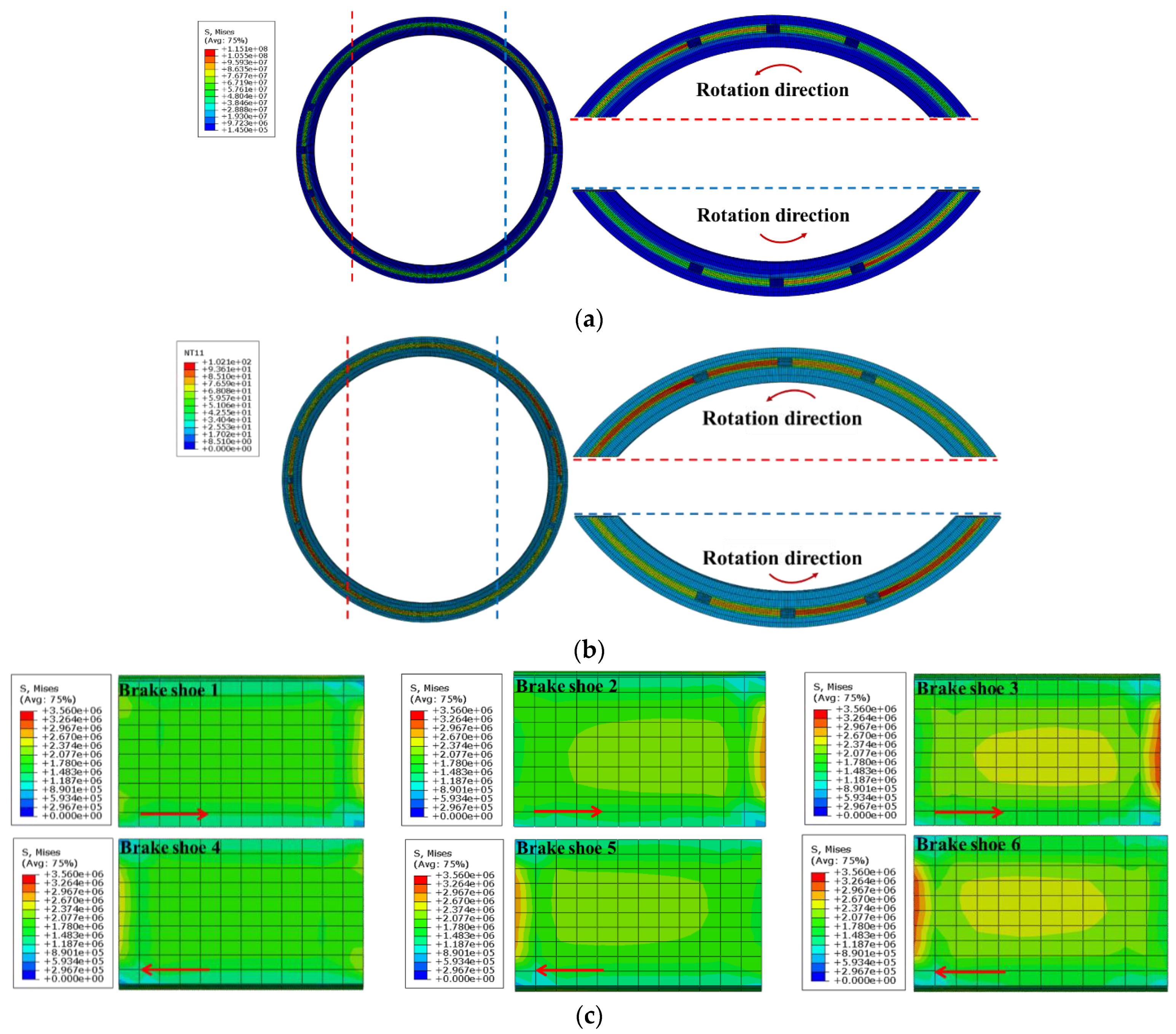
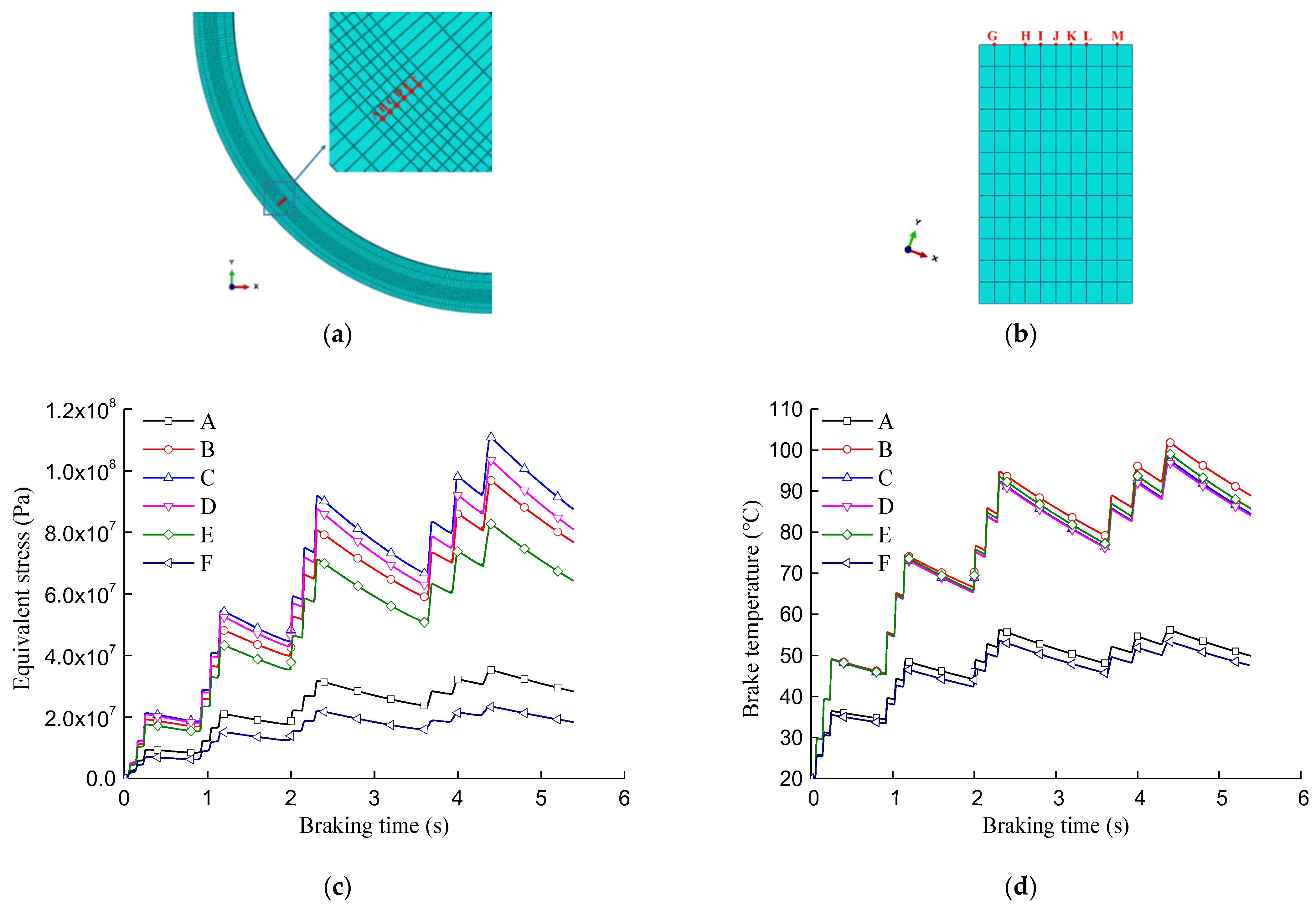
4.2. Effect of Vibration on Thermal Stress Fields of Braking Interfaces
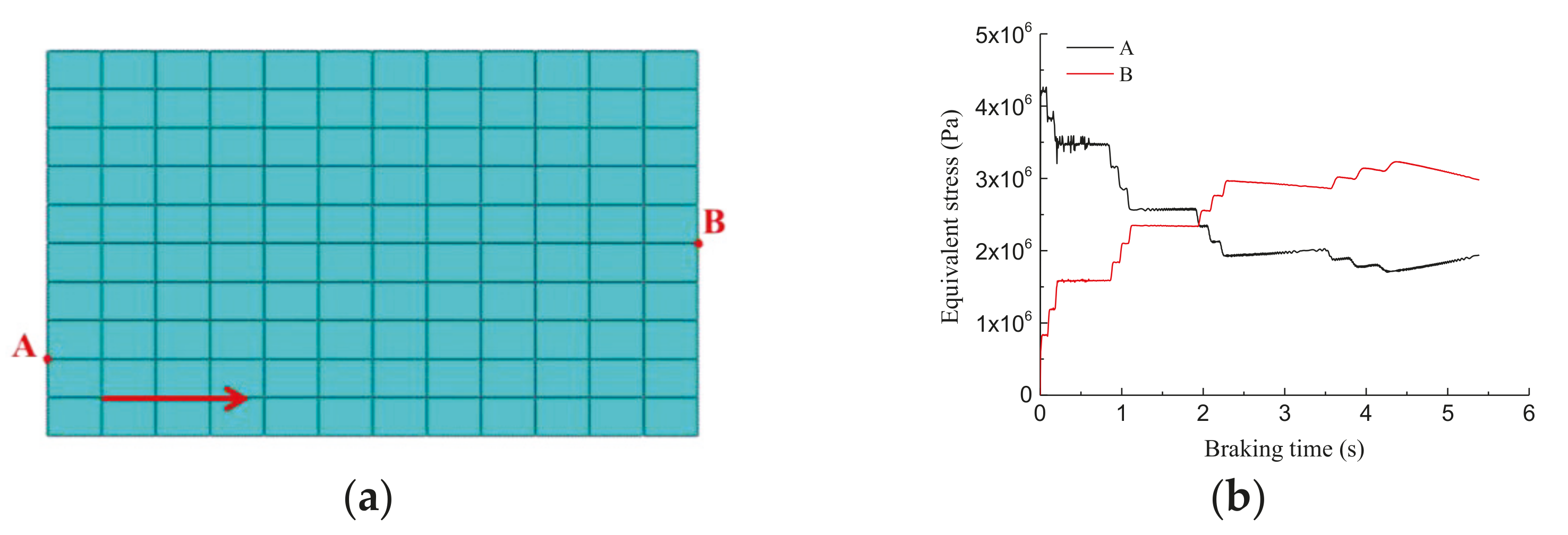
4.3. Evolutions of Thermal Stresses of Braking Interfaces under the Effect of Vibration
5. Friction Deterioration Behaviors of the Brake Shoe during Emergency Braking
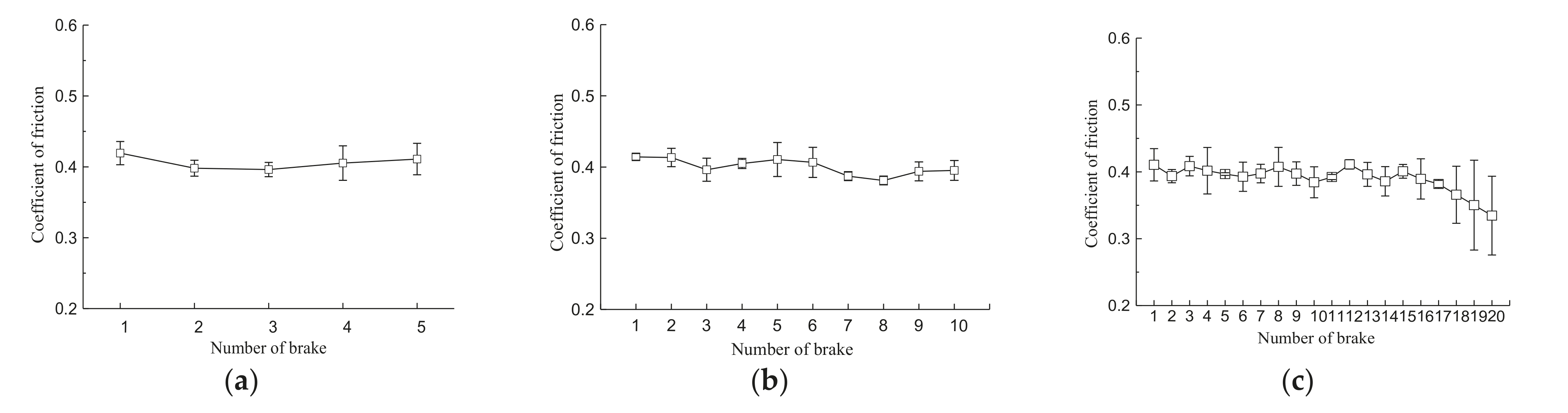
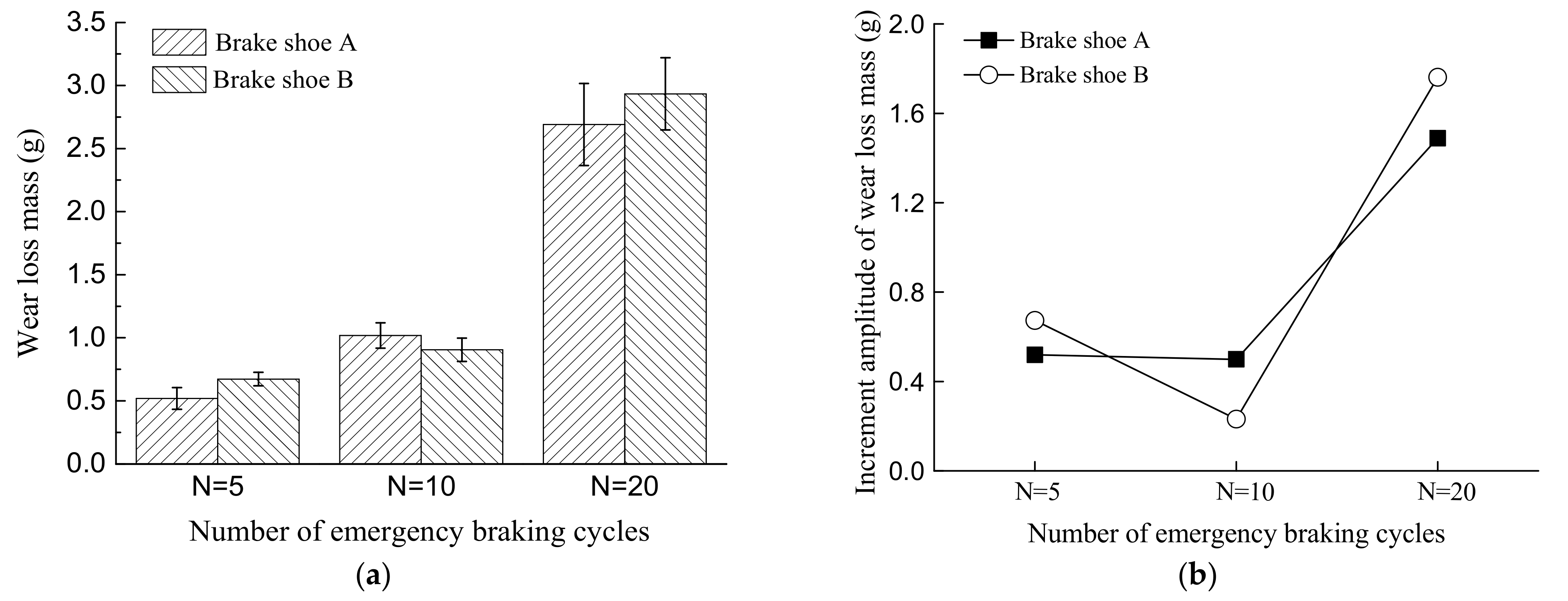
5.1. Effects of Emergency Braking Cycles
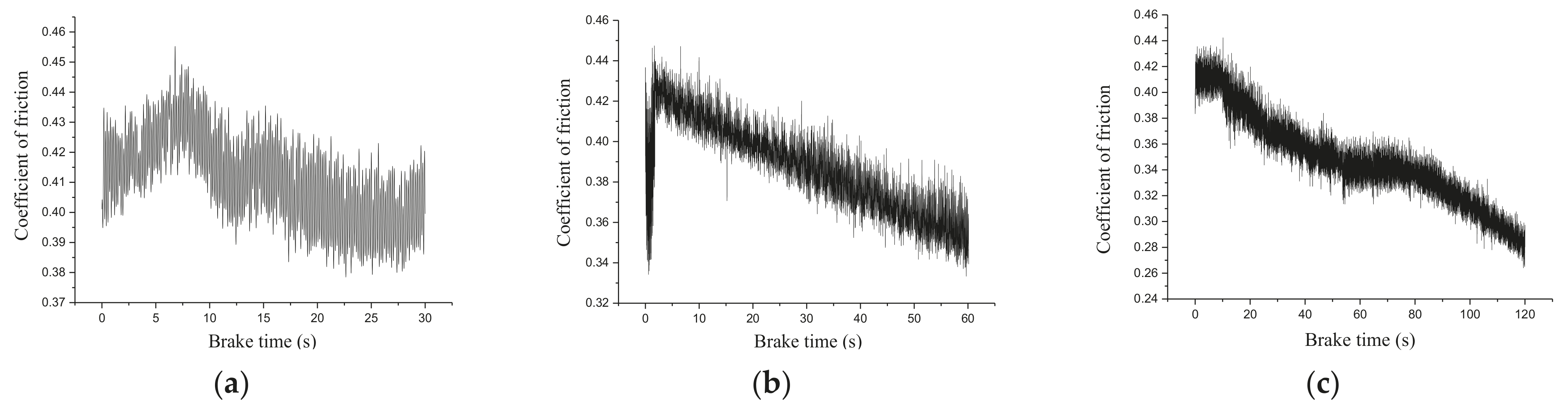
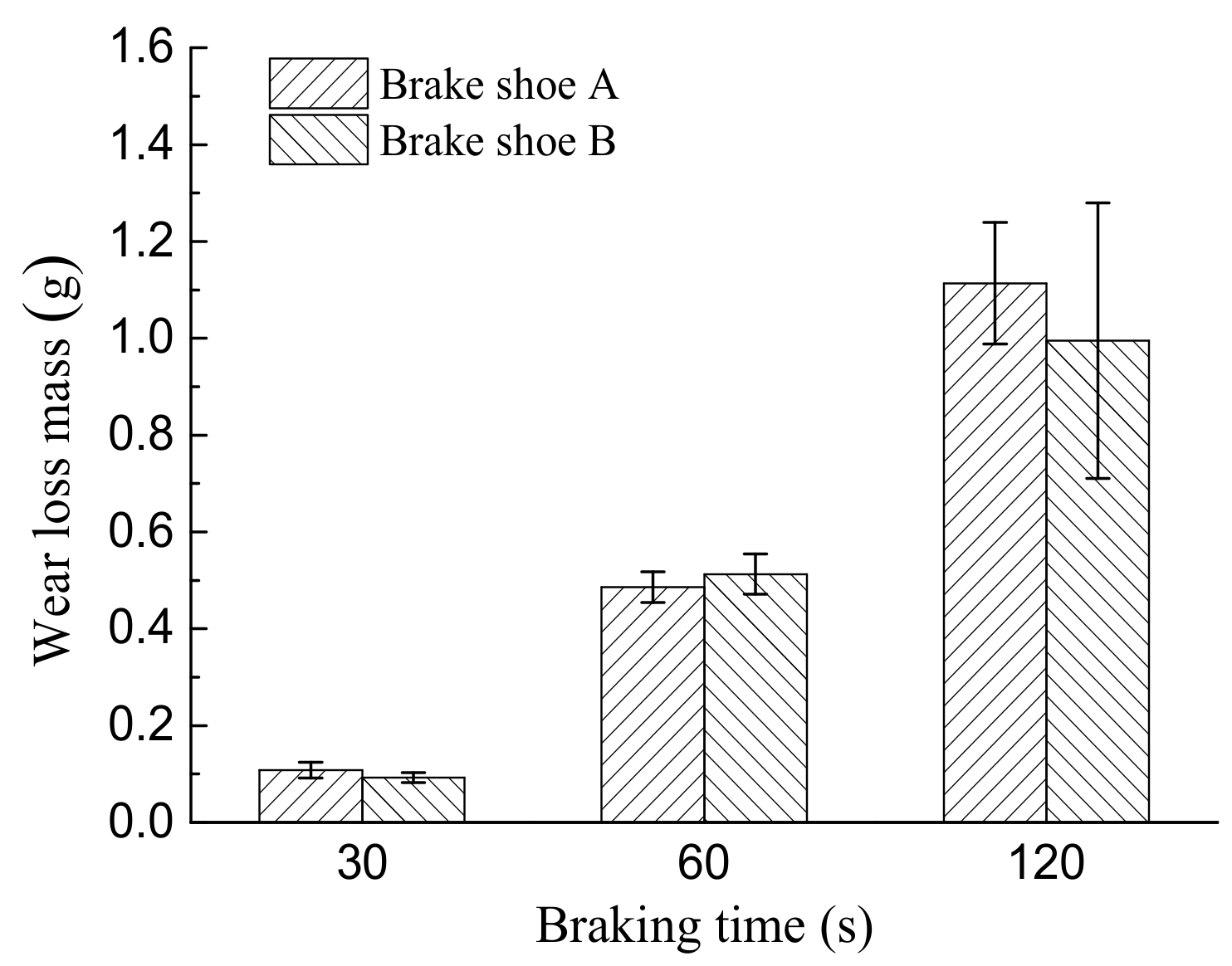
5.2. Effect of Continuous Emergency Braking Time
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Wang, D.G.; Yin, J.K.; Zhu, Z.C.; Zhang, D.K.; Liu, D.H.; Liu, H.W.; Sun, F.Q. Preparation of High Friction Brake Shoe Material and Its Tribological Behaviors during Emergency Braking in Ultra-Deep Coal Mine Hoist. Wear 2020, 458, 203391. [Google Scholar] [CrossRef]
- Wang, D.G.; Li, X.W.; Wang, X.R.; Shi, G.; Mao, X.; Wang, D. Effects of Hoisting Parameters on Dynamic Contact Characteristics between the Rope and Friction Lining in a Deep Coal Mine. Tribol. Int. 2016, 96, 31–42. [Google Scholar] [CrossRef]
- Wang, D.G.; Wang, R.X.; Zhang, J. Dynamic Brake Characteristics of Disc Brake during Emergency Braking of the Kilometer Deep Coal Mine Hoist. Adv. Mech. Eng. 2020, 12, 1–23. [Google Scholar] [CrossRef]
- Wang, D.G.; Zhang, J.; Ge, S.R.; Zhang, D.; Shi, G. Mechanical Behavior of Hoisting Rope in 2 Km Ultra Deep Coal Mine. Eng. Fail. Anal. 2019, 106, 104185. [Google Scholar] [CrossRef]
- Yun, C.K.; Min, H.C.; Kim, S.J.; Jang, H. The Effect of Phenolic Resin, Potassium Titanate, and Cnsl on the Tribological Properties of Brake Friction Materials. Wear 2008, 264, 204–210. [Google Scholar] [CrossRef]
- Satapathy, B.K.; Bijwe, J. Performance of Friction Materials Based on Variation in Nature of Organic Fibres: Part I. Fade and Recovery Behaviour. Wear 2004, 257, 585–589. [Google Scholar] [CrossRef]
- Wang, Z.J.; Wang, C.L.; Li, D. Study on the Influence Mechanism of the Temperature Rise and Frictional Coefficient of Brake Shoe on Braking of Mine Hoist. J. China Coal Soc. 2005, 30, 149–152. [Google Scholar]
- Bao, J.S.; Zhu, Z.C.; Tong, M.; Yin, Y.; Peng, Y. Influence of Braking Pressure on Tribological Performance of Non-Asbestos Brake Shoe for Mine Hoister During Emergency Braking. Ind. Lubr. Tribol. 2012, 64, 230–236. [Google Scholar] [CrossRef]
- Olesiak, Z.; Pyryev, Y.; Yevtushenko, A. Determination of Temperature and Wear during Braking. Wear 1997, 210, 120–126. [Google Scholar] [CrossRef]
- Zhu, Z.C.; Peng, Y.X.; Shi, Z.Y.; Cheng, G.-A. Three-Dimensional Transient Temperature Field of Brake Shoe during Hoist’s Emergency Braking. App. Therm. Eng. 2009, 29, 932–937. [Google Scholar] [CrossRef]
- Zhu, Z.C.; Bao, J.S.; Yin, Y.; Chen, G.A. Frictional Catastrophe Behaviors and Mechanisms of Brake Shoe for Mine Hoisters during Repetitious Emergency Brakings. Ind. Lubr. Tribol. 2013, 65, 245–250. [Google Scholar] [CrossRef]
- Pyryev, Y.; Yevtushenko, A. Influence of the Brakes Friction Elements Thickness on the Contact Temperature and Wear. Heat Mass Transf. 2000, 36, 319–323. [Google Scholar] [CrossRef]
- Wang, D.G.; Wang, R.X.; Heng, T.; Xie, G.; Zhang, D. Tribo-Brake Characteristics between Brake Disc and Brake Shoe during Emergency Braking of Deep Coal Mine Hoist with High Speed and Heavy Load. Energies 2020, 13, 5094. [Google Scholar] [CrossRef]
- Zhou, H.B.; Yao, P.P.; Xiao, Y.L.; Fan, K.; Zhang, Z.; Gong, T.; Zhao, L.; Deng, M.; Liu, C.; Ling, P. Friction and Wear Maps of Copper Metal Matrix Composites with Different Iron Volume Content. Tribol. Int. 2019, 132, 199–210. [Google Scholar] [CrossRef]
- Xing, J.H.; Huang, H.; Zhang, J.Y.; Yang, Q.S. Mechanical Properties of Disc Springs. J. Vib. Shock 2015, 22, 167–172. [Google Scholar] [CrossRef]
- Piao, G.; Zhang, B.L.; Gao, J.H.; Guo, B. An Experimental Research Method of Disc Spring’s Mechanical Properties. Mech. Eng. Autom. 2014, 3, 114–116. [Google Scholar] [CrossRef]
- Jin, M.J.; Yan, J.M.; Lu, Z.Q. Braking Moment and Oil Pressure of a Mine Hoist. J. Taiyuan Heavy Mach. Inst. 2001, 22, 214–216. [Google Scholar] [CrossRef]
- Pan, Y.; Xia, R. Dynamic Tension in Wire Ropes during Emergency Braking on Shaft Hoists. J. China Univ. Min. Technol. 1982, 3, 52–70. [Google Scholar]
- Liu, F.F. Study on Thermal-Stress Coupling Behavior of Brake Shoe during Emergency Braking of Hoist. Xuzhou, China. J. China Univ. Min. Technol 2011. [Google Scholar]
- Zhao, Y.J. Simulation and Analysis of Disc Brake Coupled Thermal-Stress Transient Temperature. J. Wuhan Huazhong Univ. Sci. Technol. 2013. [Google Scholar] [CrossRef]
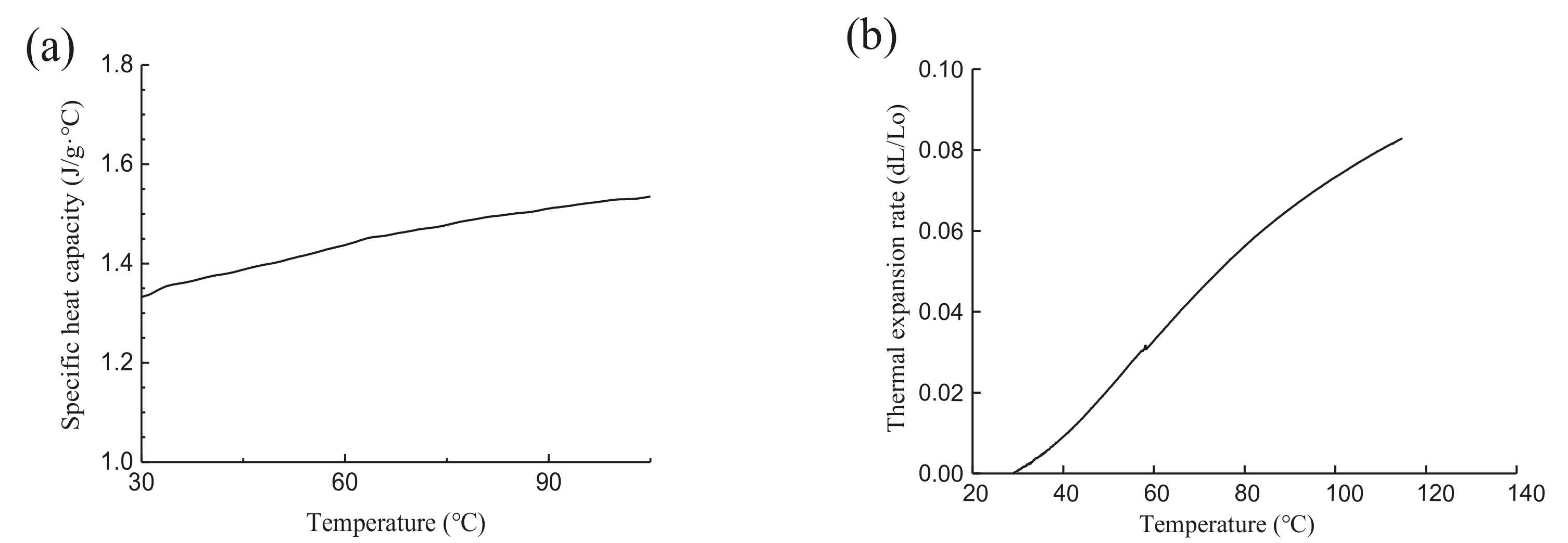





| Temperature Range (°C) | 30–40 | 40–50 | 50–60 | 60–70 | 70–80 | 80–90 | 90–100 | 100–114 |
| Thermal Expansion Coefficient (×10−6/°C) | 8.33 | 11.85 | 12 | 12.26 | 11.04 | 9.24 | 7.90 | 6.54 |
| Hoisting Stage | Equation Form | Fitting Coefficients |
|---|---|---|
| Acceleration | (5) | a0 = −7.438 × 106; a1 = −9.777 × 106; b1 = 2.117 × 107; a2 = 1.205 × 107; b2 = 1.018 × 107; a3 = 9.083 × 106, b3 = −4.612 × 106; a4 = −4.979 × 105, b4 = −5.407 × 106; a5 = −3.411 × 106, b5 = −9.719 × 105; w = 1.353 |
| Constant speed | (6) | a1 = 7.837 × 106, b1 = 0.6227, c1 = −0.1956; a2 = 3.538 × 106, b2 = 2.766, c2 = −2.755; a3 = 4.36 × 106, b3 = 1.278, c3 = 1.081; a4 = 1.034 × 106, b4 = 3.489, c4 = 4.363; a5 = 3.744 × 105, b5 = 3.853, c5 = 6.447 |
| Deceleration | (6) | a1 = 9.48 × 106, b1 = 1.279, c1 = −0.5925; a2 = 2.327 × 106, b2 = 6.504, c2 = 3.287; a3 = 9.069 × 106, b3 = 3.015, c3 = 2.71; a4 = 1.157 × 107, b4 = 2.62, c4 = 0.1908; a5 = 3.482 × 105, b5 = 7.563, c5 = 4.704 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, D.; Wang, R.; Wang, B.; Wahab, M.A. Effect of Vibration on Emergency Braking Tribological Behaviors of Brake Shoe of Deep Coal Mine Hoist. Appl. Sci. 2021, 11, 6441. https://doi.org/10.3390/app11146441
Wang D, Wang R, Wang B, Wahab MA. Effect of Vibration on Emergency Braking Tribological Behaviors of Brake Shoe of Deep Coal Mine Hoist. Applied Sciences. 2021; 11(14):6441. https://doi.org/10.3390/app11146441
Chicago/Turabian StyleWang, Dagang, Ruixin Wang, Bo Wang, and Magd Abdel Wahab. 2021. "Effect of Vibration on Emergency Braking Tribological Behaviors of Brake Shoe of Deep Coal Mine Hoist" Applied Sciences 11, no. 14: 6441. https://doi.org/10.3390/app11146441
APA StyleWang, D., Wang, R., Wang, B., & Wahab, M. A. (2021). Effect of Vibration on Emergency Braking Tribological Behaviors of Brake Shoe of Deep Coal Mine Hoist. Applied Sciences, 11(14), 6441. https://doi.org/10.3390/app11146441







