Optimization of Design Parameters in LSTM Model for Predictive Maintenance
Abstract
:1. Introduction
2. Literature Survey
2.1. Various Approaches for Predictive Maintenance
2.1.1. Physics Model-Based Approaches
2.1.2. Statistical Model-Based Approaches
2.1.3. Artificial Intelligence (AI)-Based Approaches
2.2. Tuning Hyperparameters of Deep Learning
3. Optimization of Design Parameters for an LSTM-Based Predictive Maintenance Model
3.1. Problem Definition and Optimization Procedure
3.2. Feature Selection for HI
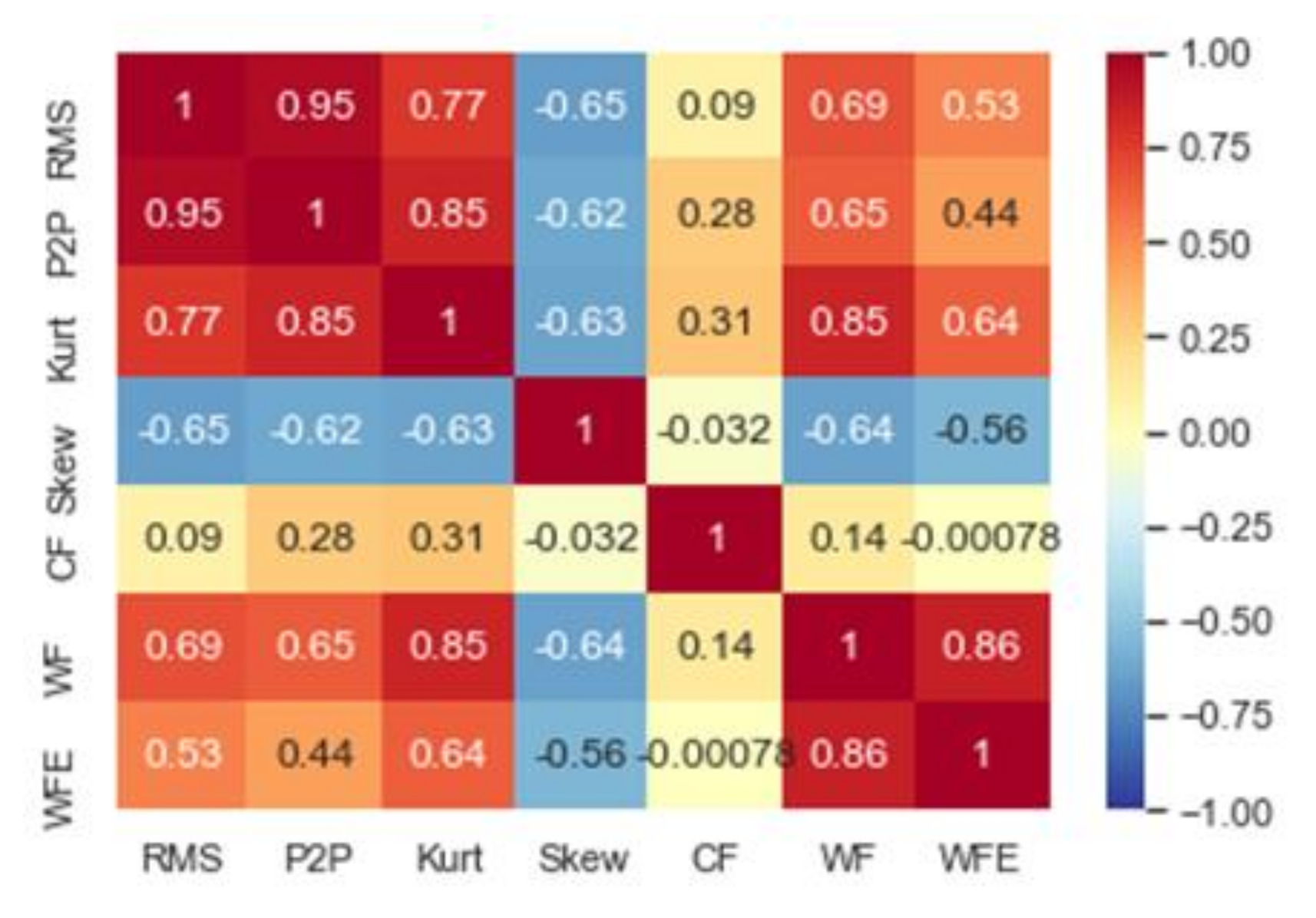
3.2.1. Filtering with Correlation Analysis
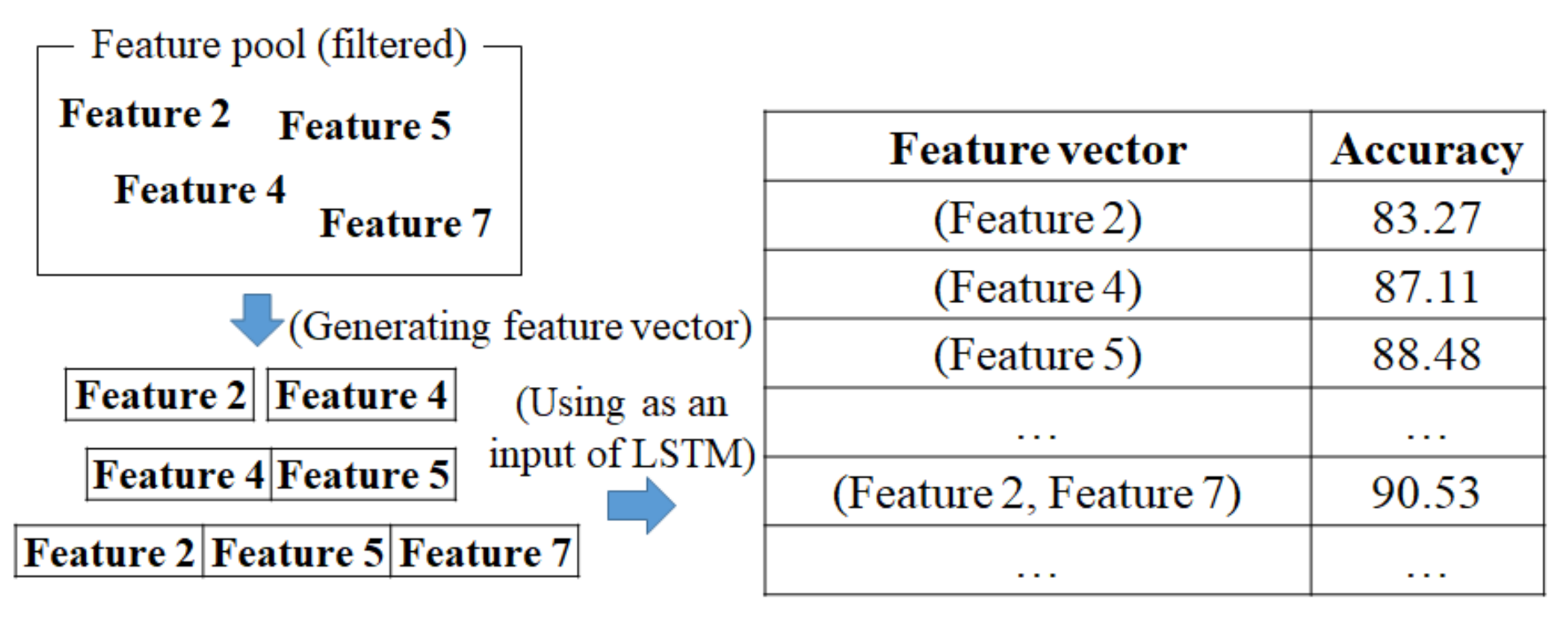
3.2.2. Choosing the Fittest Feature Vector
3.3. Design of GA for Exploring Optimal Hyperparameters of LSTM
3.3.1. Chromosome Structure and Initial Population
3.3.2. Fitness Function
3.3.3. Crossover Operator
3.3.4. Mutation Operator
3.3.5. Updating Population and Termination Criteria of GA
4. A Numerical Experiment
4.1. An Experimental Design
4.2. Experimental Results
4.2.1. Feature Selection for Defining HI
4.2.2. Exploring Optimal Hyperparameters of LSTM
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- GE Oil & Gas. The Impact of Digital on Unplanned Downtime—An Offshore Oil and Gas Perspective. 2016. Available online: https://www.gemeasurement.com/sites/gemc.dev/files/ge_the_impact_of_digital_on_unplanned_downtime_0.pdf (accessed on 14 July 2017).
- Lei, Y.; Li, N.; Guo, L.; Li, N.; Yan, T.; Lin, J. Machinery health prognostics: A systematic review from data acquisition to RUL prediction. Mech. Syst. Signal Process. 2018, 104, 799–834. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, S.; Li, W. Bearing performance degradation assessment using long short-term memory recurrent net-work. Comput. Ind. 2019, 106, 14–29. [Google Scholar] [CrossRef]
- Baraldi, P.; Mangili, F.; Zio, E. A Kalman Filter-Based Ensemble Approach with Application to Turbine Creep Prognostics. IEEE Trans. Reliab. 2012, 61, 966–977. [Google Scholar] [CrossRef]
- Paris, P.; Erdogan, F. A Critical Analysis of Crack Propagation Laws. J. Basic Eng. 1963, 85, 528–533. [Google Scholar] [CrossRef]
- Brighenti, R.; Carpinteri, A.; Corbari, N. Damage mechanics and Paris regime in fatigue life assessment of metals. Int. J. Press. Vessel. Pip. 2013, 104, 57–68. [Google Scholar] [CrossRef]
- Pais, M.J.; Kim, N.H. Predicting fatigue crack growth under variable amplitude loadings with usage monitoring data. Adv. Mech. Eng. 2015, 7, 1687814015619135. [Google Scholar] [CrossRef]
- Qian, Y.; Yan, R.; Hu, S. Bearing Degradation Evaluation Using Recurrence Quantification Analysis and Kalman Filter. IEEE Trans. Instrum. Meas. 2014, 63, 2599–2610. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, L.; Wang, X. Reliability estimation and remaining useful lifetime prediction for bearing based on proportional hazard model. J. Cent. South Univ. 2015, 22, 4625–4633. [Google Scholar] [CrossRef]
- Nielsen, J.S.; Sørensen, J.D. Bayesian Estimation of Remaining Useful Life for Wind Turbine Blades. Energies 2017, 10, 664. [Google Scholar] [CrossRef] [Green Version]
- Pei, H.; Hu, C.; Si, X.; Zheng, J.; Zhang, Q.; Zhang, Z.; Pang, Z. Remaining Useful Life Prediction for Nonlinear Degraded Equipment with Bivariate Time Scales. IEEE Access 2019, 7, 165166–165180. [Google Scholar] [CrossRef]
- Liu, J.; Zio, E. System dynamic reliability assessment and failure prognostics. Reliab. Eng. Syst. Saf. 2017, 160, 21–36. [Google Scholar] [CrossRef] [Green Version]
- Zhai, Q.; Ye, Z.-S. RUL Prediction of Deteriorating Products Using an Adaptive Wiener Process Model. IEEE Trans. Ind. Inform. 2017, 13, 2911–2921. [Google Scholar] [CrossRef]
- Loutas, T.; Eleftheroglou, N.; Zarouchas, D. A data-driven probabilistic framework towards the in-situ prognostics of fatigue life of composites based on acoustic emission data. Compos. Struct. 2017, 161, 522–529. [Google Scholar] [CrossRef]
- Lei, Y.; Li, N.; Gontarz, S.; Lin, J.; Radkowski, S.; Dybała, J. A Model-Based Method for Remaining Useful Life Prediction of Machinery. IEEE Trans. Reliab. 2016, 65, 1314–1326. [Google Scholar] [CrossRef]
- Marra, D.; Sorrentino, M.; Pianese, C.; Iwanschitz, B. A neural network estimator of Solid Oxide Fuel Cell performance for on-field diagnostics and prognostics applications. J. Power Sources 2013, 241, 320–329. [Google Scholar] [CrossRef]
- Bossio, J.M.; De Angelo, C.H.; Bossio, G.R. Self-organizing map approach for classification of mechanical and rotor faults on induction motors. Neural Comput. Appl. 2012, 23, 41–51. [Google Scholar] [CrossRef]
- Ren, L.; Cui, J.; Sun, Y.; Cheng, X. Multi-bearing remaining useful life collaborative prediction: A deep learning approach. J. Manuf. Syst. 2017, 43, 248–256. [Google Scholar] [CrossRef]
- Zhu, J.; Chen, N.; Peng, W. Estimation of Bearing Remaining Useful Life Based on Multiscale Convolutional Neural Network. IEEE Trans. Ind. Electron. 2019, 66, 3208–3216. [Google Scholar] [CrossRef]
- Guo, L.; Li, N.; Jia, F.; Lei, Y.; Lin, J. A recurrent neural network based health indicator for remaining useful life prediction of bearings. Neurocomputing 2017, 240, 98–109. [Google Scholar] [CrossRef]
- Widodo, A.; Yang, B.-S. Machine health prognostics using survival probability and support vector machine. Expert Syst. Appl. 2011, 38, 8430–8437. [Google Scholar] [CrossRef]
- Khelif, R.; Chebel-Morello, B.; Malinowski, S.; Laajili, E.; Fnaiech, F.; Zerhouni, N. Direct Remaining Useful Life Estimation Based on Support Vector Regression. IEEE Trans. Ind. Electron. 2017, 64, 2276–2285. [Google Scholar] [CrossRef]
- Chen, C.; Liu, Y.; Wang, S.; Sun, X.; Di Cairano-Gilfedder, C.; Titmus, S.; Syntetos, A.A. Predictive maintenance using cox proportional hazard deep learning. Adv. Eng. Inform. 2020, 44, 101054. [Google Scholar] [CrossRef]
- Nguyen, T.P.K.; Medjaher, K. A new dynamic predictive maintenance framework using deep learning for failure prognostics. Reliab. Eng. Syst. Saf. 2019, 188, 251–262. [Google Scholar] [CrossRef] [Green Version]
- Bampoula, X.; Siaterlis, G.; Nikolakis, N.; Alexopoulos, K. A Deep Learning Model for Predictive Maintenance in Cyber-Physical Production Systems Using LSTM Autoencoders. Sensors 2021, 21, 972. [Google Scholar] [CrossRef] [PubMed]
- Larochelle, H.; Erhan, D.; Courville, A.; Bergstra, J.; Bengio, Y. An Empirical Evaluation of Deep Architectures on Problems with Many Factors of Variation. In Proceedings of the 24th International Conference on Machine Learning, Association for Computing Machinery, New York, NY, USA, 20 June 2007; pp. 473–480. [Google Scholar]
- Bergstra, J.; Bengio, Y. Random Search for Hyper-Parameter Optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Wu, J.; Chen, X.-Y.; Zhang, H.; Xiong, L.-D.; Lei, H.; Deng, S.-H. Hyperparameter Optimization for Machine Learning Models Based on Bayesian Optimizationb. J. Electron. Sci. Technol. 2019, 17, 26–40. [Google Scholar] [CrossRef]
- Bergstra, J.; Bardenet, R.; Bengio, Y.; Kégl, B. Algorithms for Hyper-Parameter Optimization. In Proceedings of the 24th International Conference on Neural Information Processing Systems, Red Hook, NY, USA, 12 December 2011; Curran Associates Inc.: New York, NY, USA, 2011; pp. 2546–2554. [Google Scholar]
- Mattioli, F.; Caetano, D.; Cardoso, A.; Naves, E.; Lamounier, E. An Experiment on the Use of Genetic Algorithms for Topology Selection in Deep Learning. J. Electr. Comput. Eng. 2019, 2019, 1–12. [Google Scholar] [CrossRef]
- Camero, A.; Toutouh, J.; Alba, E. Random error sampling-based recurrent neural network architecture optimization. Eng. Appl. Artif. Intell. 2020, 96, 103946. [Google Scholar] [CrossRef]
- Yi, H.; Bui, K.-H.N. An Automated Hyperparameter Search-Based Deep Learning Model for Highway Traffic Prediction. IEEE Trans. Intell. Transp. Syst. 2020, 1–10. [Google Scholar] [CrossRef]
- Victoria, A.H.; Maragatham, G. Automatic tuning of hyperparameters using Bayesian optimization. Evol. Syst. 2021, 12, 217–223. [Google Scholar] [CrossRef]
- Haitovsky, Y. Multicollinearity in Regression Analysis: Comment. Rev. Econ. Stat. 1969, 51, 486. [Google Scholar] [CrossRef]
- Mäkinen, R.A.E.; Periaux, J.; Toivanen, J. Multidisciplinary Shape Optimization in Aerodynamics and Electromagnetics Us-ing Genetic Algorithms. Int. J. Numer. Methods Fluids 1999, 30, 149–159. [Google Scholar] [CrossRef]
- Sivanandam, S.N.; Deepa, S.N. Genetic Algorithm Optimization Problems. In Introduction to Genetic Algorithms; Sivanandam, S.N., Deepa, S.N., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 165–209. ISBN 978-3-540-73190-0. [Google Scholar]
- Qiu, H.; Lee, J.; Lin, J.; Yu, G. Wavelet filter-based weak signature detection method and its application on rolling element bearing prognostics. J. Sound Vib. 2006, 289, 1066–1090. [Google Scholar] [CrossRef]
- Caesarendra, W.; Tjahjowidodo, T. A Review of Feature Extraction Methods in Vibration-Based Condition Monitoring and Its Application for Degradation Trend Estimation of Low-Speed Slew Bearing. Machines 2017, 5, 21. [Google Scholar] [CrossRef]
- Yiakopoulos, C.; Gryllias, K.; Antoniadis, I. Rolling element bearing fault detection in industrial environments based on a K-means clustering approach. Expert Syst. Appl. 2011, 38, 2888–2911. [Google Scholar] [CrossRef]
- Ben Ali, J.; Chebel-Morello, B.; Saidi, L.; Malinowski, S.; Fnaiech, F. Accurate bearing remaining useful life prediction based on Weibull distribution and artificial neural network. Mech. Syst. Signal Process. 2015, 56–57, 150–172. [Google Scholar] [CrossRef]
- Zhou, Q.; Shen, H.; Zhao, J.; Liu, X.; Xiong, X. Degradation State Recognition of Rolling Bearing Based on K-Means and CNN Algorithm. Shock. Vib. 2019, 2019, 1–9. [Google Scholar] [CrossRef]
- Yu, J. Local and Nonlocal Preserving Projection for Bearing Defect Classification and Performance Assessment. IEEE Trans. Ind. Electron. 2012, 59, 2363–2376. [Google Scholar] [CrossRef]
- Roy, S.S.; Dey, S.; Chatterjee, S. Autocorrelation Aided Random Forest Classifier-Based Bearing Fault Detection Framework. IEEE Sens. J. 2020, 20, 10792–10800. [Google Scholar] [CrossRef]
- Saxena, A.; Goebel, K.; Simon, D.; Eklund, N. Damage propagation modeling for aircraft engine run-to-failure simulation. In Proceedings of the 2008 International Conference on Prognostics and Health Management, Denver, CO, USA, 6–9 October 2008. [Google Scholar]






| Steps | Design Parameters | Examples |
|---|---|---|
| Derivation of HI | Feature values used as HI to describe the state of machinery | Elementary statistics (mean, standard deviation), wavelet feature of time series data |
| Definition of HS | Characteristics of degradation model after fault | The number of degradation stages and linear/nonlinear degradation model assigned to each stage |
| Generation of Prediction and Monitoring model | Category of models to predict the state of machinery and hyperparameters of the model | The number of hidden layers and the number of neurons at each layer in deep learning model |
| Set | Recording Duration | Number of Files | Failure Occurs In |
|---|---|---|---|
| No. 1 | 10/22/2003 12:06:24 to 11/25/2003 23:39:56 | 2156 | Bearing 3, 4 |
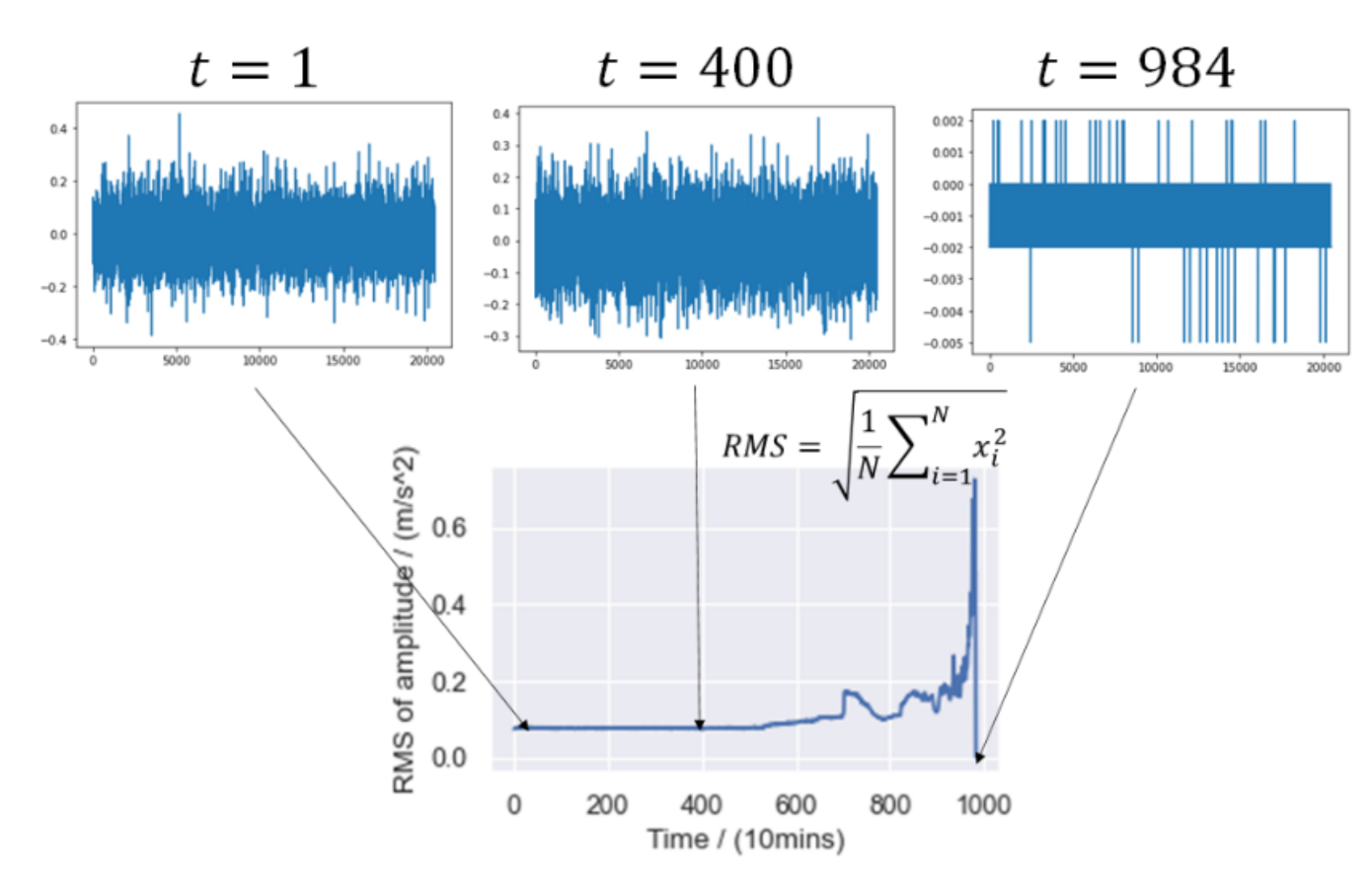
| No. 2 | 02/12/2004 10:32:39 to 02/19/2004 06:22:39 | 984 | Bearing 1 |
| No. 3 | 03/04/2004 09:27:46 to 04/04/2004 19:01:57 | 4448 | Bearing 3 |
| Features | Descriptions | Equations for Calculating Features |
|---|---|---|
| Root Mean Square (RMS) | Square root of mean square | |
| Peak-to-Peak | Difference between positive and negative peak | |
| Kurtosis | Steepness of distribution of samples | |
| Skewness | Asymmetry of distribution of samples | |
| Crest Factor (CF) | Extremeness of positive peak compared to other samples | |
| Waveform Factor (WF) | Coefficient affecting shape of vibration or wave | |
| Waveform Factor Entropy (WFE) | Entropy of WF to acquire robust values |
| Feature Vector | Training Accuracy | Validation Accuracy |
|---|---|---|
| Mean (std. dev.) | Mean (std. dev.) | |
| (Kurtosis) | 0.8043 (0.0079) | 0.7946 (0.0084) |
| (Skewness) | 0.8188 (0.0078) | 0.7950 (0.0098) |
| (CF) | 0.7432 (0.0194) | 0.7113 (0.0188) |
| (WFE) | 0.8341 (0.0125) | 0.8296 (0.0137) |
| (Kurtosis, Skewness) | 0.8703 (0.0114) | 0.8678 (0.0107) |
| (Kurtosis, CF) | 0.8654 (0.0123) | 0.8642 (0.0147) |
| (Kurtosis, WFE) | 0.8987 (0.0149) | 0.8413 (0.0188) |
| (Skewness, CF) | 0.8422 (0.0144) | 0.8063 (0.0164) |
| (Skewness, WFE) | 0.9011 (0.0129) | 0.8710 (0.0135) |
| (CF, WFE) | 0.9237 (0.0138) | 0.8823 (0.0156) |
| (Kurtosis, Skewness, CF) | 0.9568 (0.0124) | 0.9234 (0.0121) |
| (Kurtosis, Skewness, WFE) | 0.9612 (0.0110) | 0.9175 (0.0099) |
| (Kurtosis, CF, WFE) | 0.9301 (0.0105) | 0.8958 (0.0129) |
| (Skewness, CF, WFE) | 0.8939 (0.0149) | 0.8813 (0.0156) |
| Referred | Feature | Method | Validation Accuracy |
|---|---|---|---|
| (This paper) | Kurtosis, skewness, crest factor | LSTM with 8 time steps, 3 LSTM layers, 115 hidden neurons | 0.9814 (0.099) |
| Ali et al. [40] | RMS, kurtosis, RMSEE 1 | SFAM 2 (3 layers, 6 hidden neurons) | 0.7420 |
| Zhang et al. [3] | Kurtosis, waveform factor | LSTM with 8 time steps, 3 LSTM layers, 150 hidden neurons | 0.7846 |
| Kurtosis, waveform factor, waveform entropy | LSTM with 8 time steps, 3 LSTM layers, 150 hidden neurons | 0.9312 | |
| Back propagation (BP) network with 3 hidden layers containing 150 hidden neurons | 0.7841 | ||
| Stacked autoencoder (SAE) with 3 hidden layers containing 150, 100, 50 hidden neurons each | 0.8677 | ||
| Convolutional neural network (CNN) with 2 convolutional layers (5 × 5 × 32, 5 × 5 × 16) and 2 pooling layers | 0.9203 | ||
| Zhou et al. [41] | RMS, kurtosis, skewness, RMSEE 1, 8 frequency-based features (total 12 features used) | CNN with 5 convolutional layers, 3 pooling layers, and 3 additional fully connected layers except for one before output layer | 0.9858 |
| Yu [42] | Seven time-based features (including RMS, kurtosis, skewness, etc.) and 4 frequency and wavelet features (total 11 features) | k-NN with original features | 0.9167 |
| k-NN with features resulting from PCA | 0.9167 | ||
| k-NN with features resulting from LNPP 3 | 0.9444 | ||
| k-NN with features resulting from LDA 4 | 0.9722 | ||
| k-NN with features resulting from SLNPP 5 | 0.9722 | ||
| Roy et al. [43] | Five features (max. value, centroid, abs. centroid, kurtosis, and simple sign integral) among 36 features | Autocorrelation-aided random forest with feature selection and pre-processing including binary classification | 0.9790 |
| Five features (abs. centroid, RMS, impulse factor, 75th percentile, and approximate entropy) among 36 features | 0.9824 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, D.-G.; Choi, J.-Y. Optimization of Design Parameters in LSTM Model for Predictive Maintenance. Appl. Sci. 2021, 11, 6450. https://doi.org/10.3390/app11146450
Kim D-G, Choi J-Y. Optimization of Design Parameters in LSTM Model for Predictive Maintenance. Applied Sciences. 2021; 11(14):6450. https://doi.org/10.3390/app11146450
Chicago/Turabian StyleKim, Do-Gyun, and Jin-Young Choi. 2021. "Optimization of Design Parameters in LSTM Model for Predictive Maintenance" Applied Sciences 11, no. 14: 6450. https://doi.org/10.3390/app11146450
APA StyleKim, D.-G., & Choi, J.-Y. (2021). Optimization of Design Parameters in LSTM Model for Predictive Maintenance. Applied Sciences, 11(14), 6450. https://doi.org/10.3390/app11146450





