Damage Detection and Localization on Real Structures Subjected to Strong Motion Earthquakes Using the Curvature Evolution Method: The Navelli (Italy) Case Study
Abstract
:1. Introduction
2. Materials and Methods
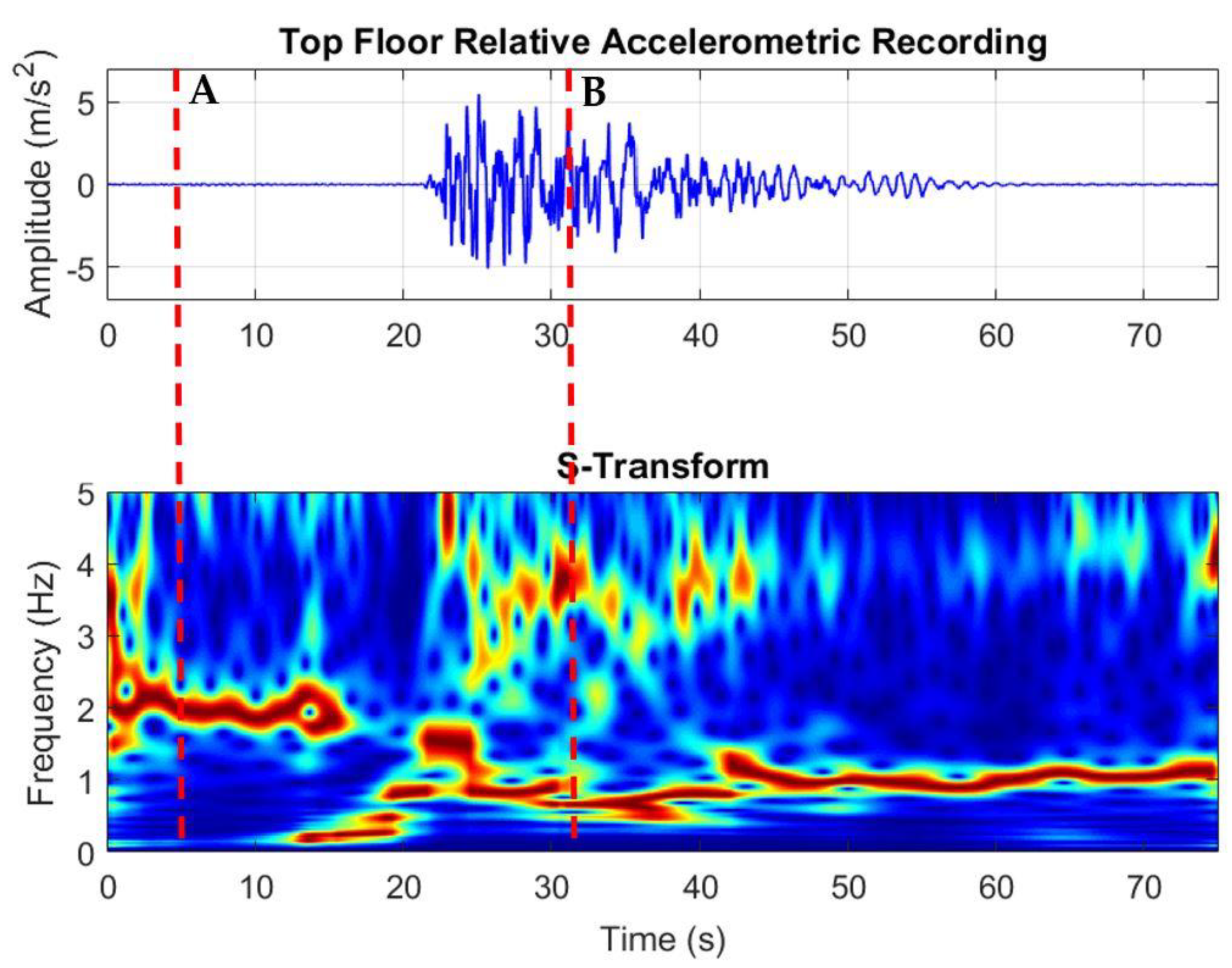
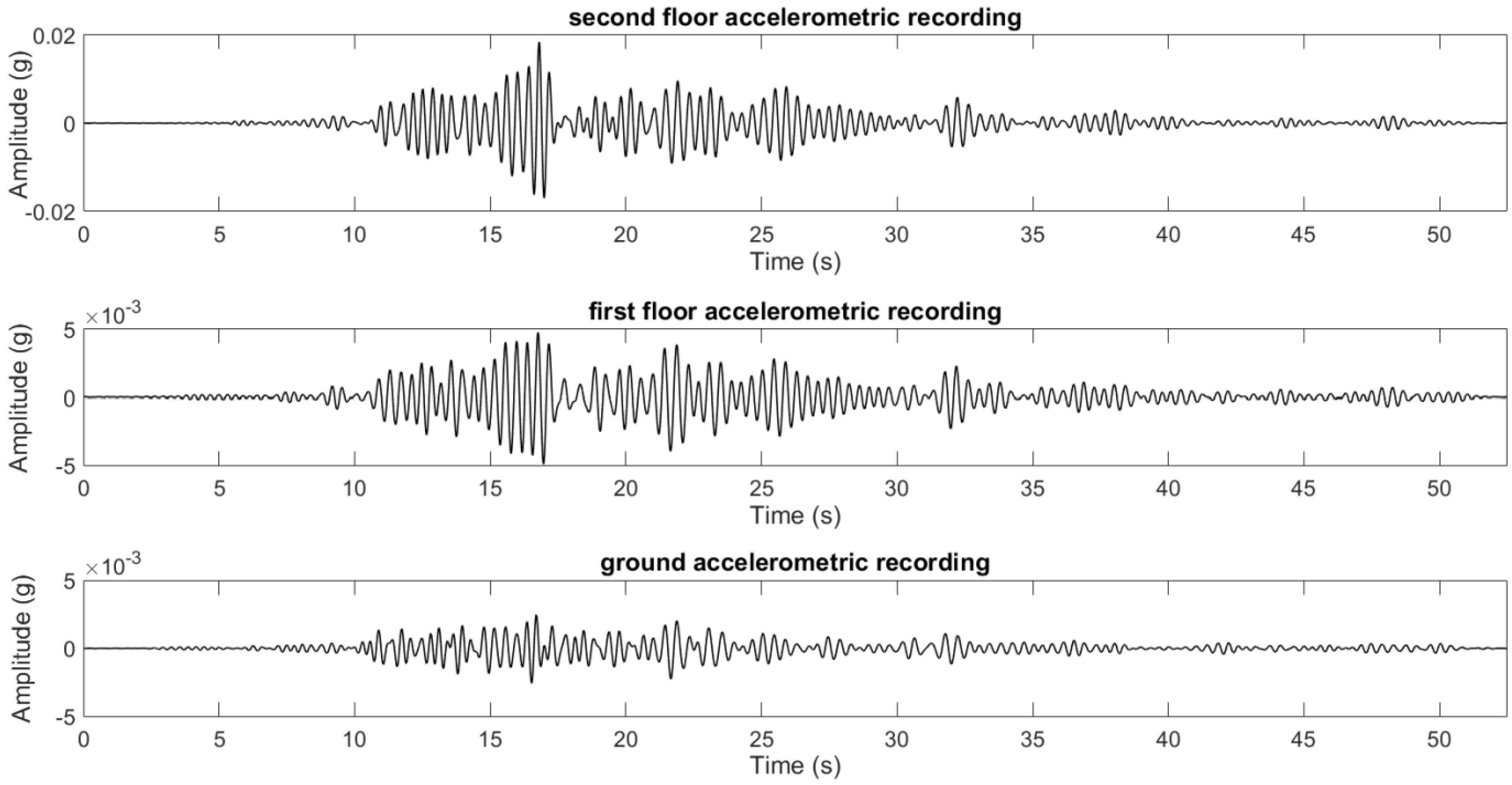
- Identification of the fundamental frequency of the structure in the time-frequency domain by analyzing the top floor’s relative accelerometric recordings (difference between top and bottom instant acceleration values, see Figure 1);
- definition of a filtering matrix, using the band-pass-time-variable filter, fitting the evolution over-time of the fundamental frequency of the monitored structure (evaluated in the previous step);
- convolution of the filtering matrix with the Stockwell Transform of the signal recorded at each floor, along the same direction for all floors;
- evaluation of the variation of the fundamental mode shape and related mode curvature over time (time instants A and B, see Figure 1);
- computation of the mode curvature differences among floors at different time steps (see Equations (2) and (3));
- selection of two different time instants (one immediately before the earthquake and one corresponding to the minimum fundamental frequency) and evaluation of the mode curvature difference between them (time instants A and B, see Figure 1).
3. Numerical Applications
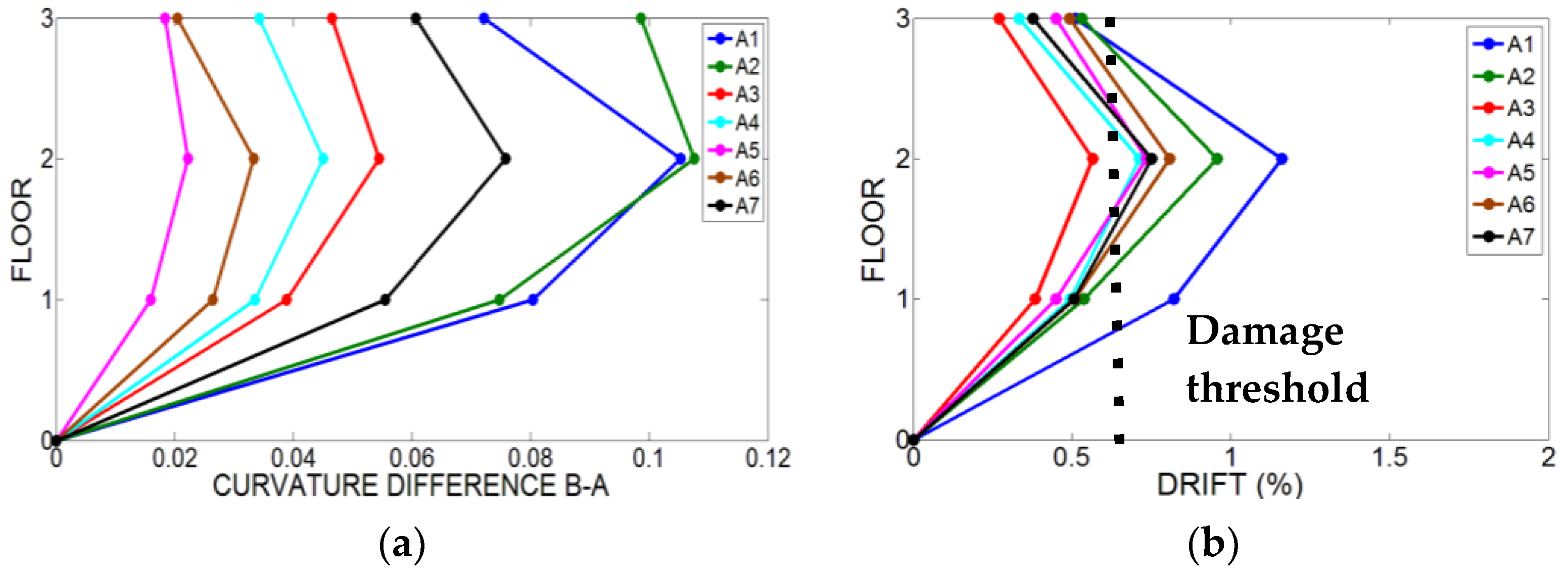
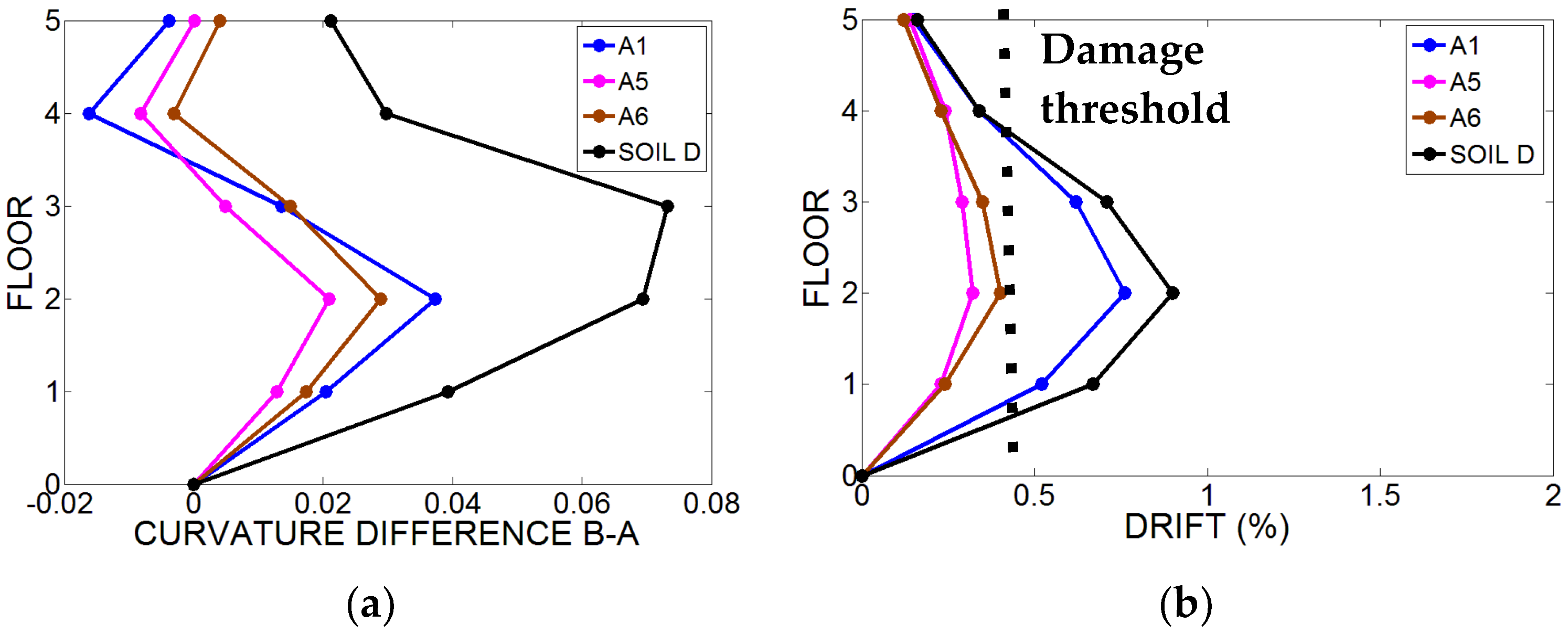
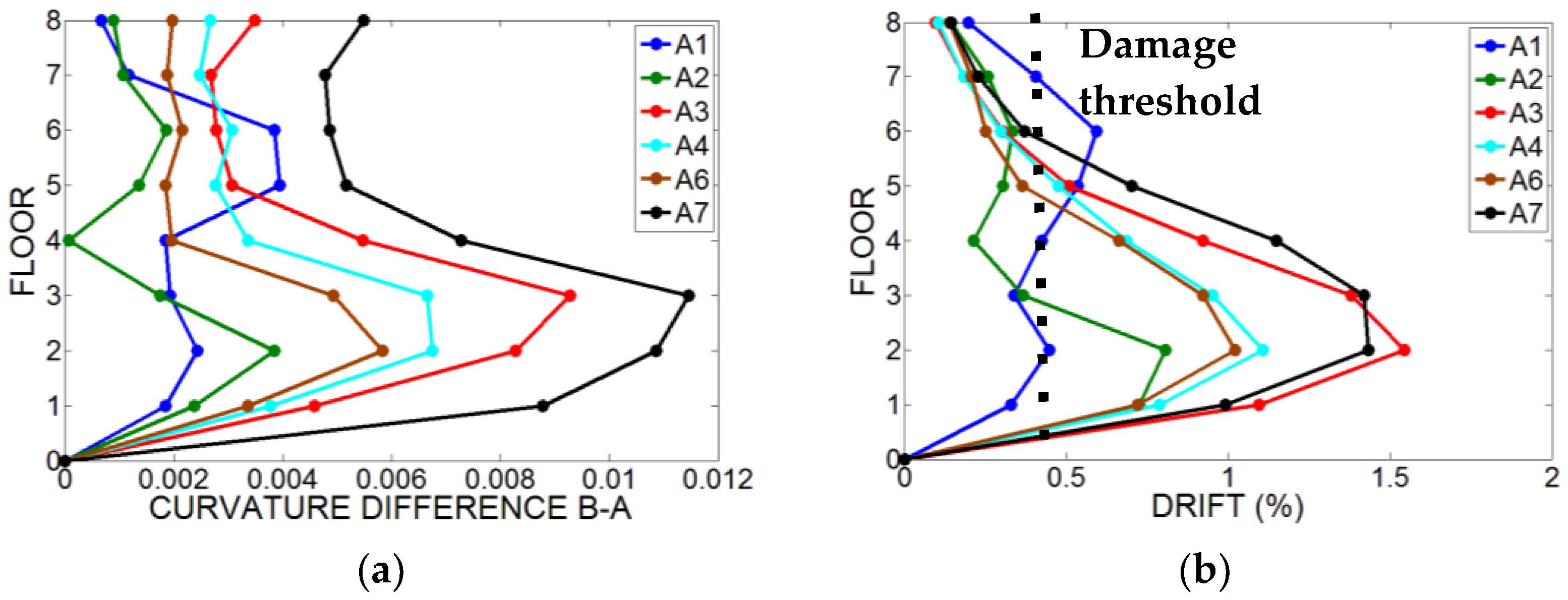
3.1. Numerical Results
3.2. Definition of Empirical “Curvature Variation-Maximum Inter-Story Drift” Relationships
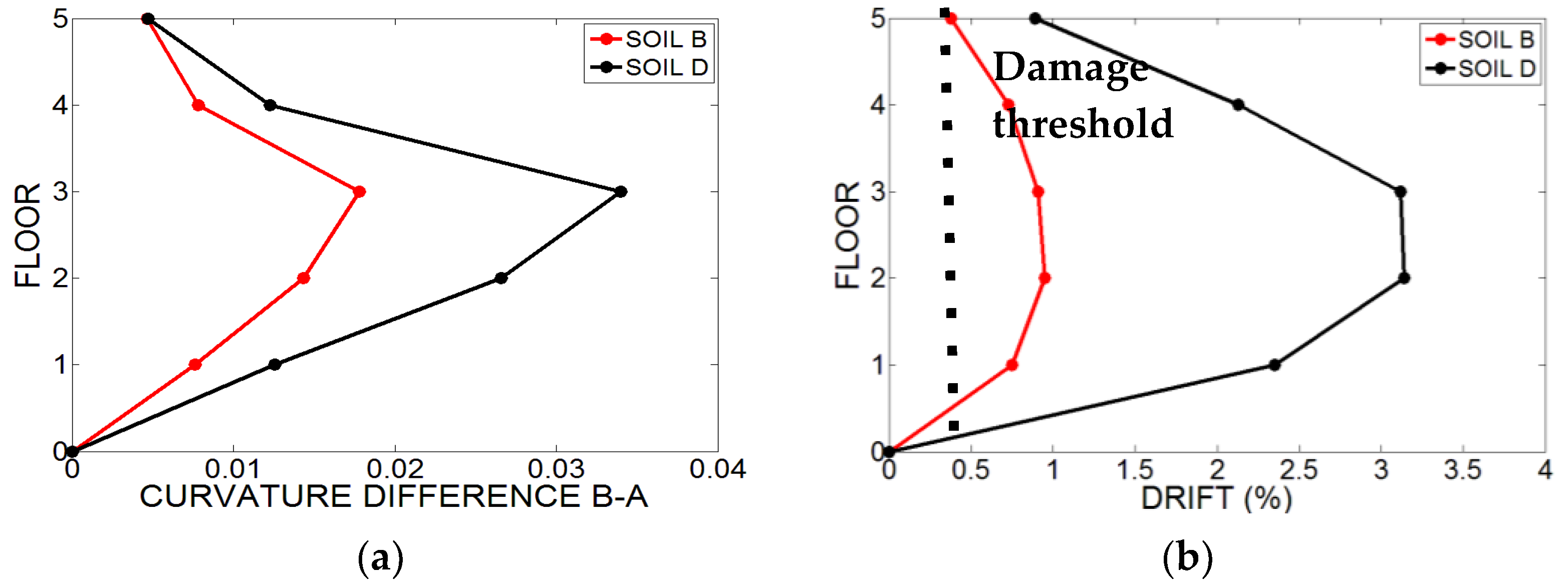
4. Experimental Case Study
Data Analysis and Experimental Results
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Time Instant A | Time Instant B | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Accelerogram PGA | No. of Floors | Inter-Story Drift (%) | Mode Shape | Mode Curvature | Curvature Difference | Mode Shape | Mode Curvature | Curvature Difference | Curvature Difference B-A |
| A1 (soil class B) 0.34 g | 0 | 0.00 | 0.000 | −0.013 | 0.000 | 0.000 | −0.067 | 0.000 | 0.000 |
| 1 | 0.82 | 0.351 | 0.026 | 0.051 | 0.331 | −0.002 | 0.132 | 0.080 | |
| 2 | 1.16 | 0.763 | 0.072 | 0.060 | 0.796 | 0.097 | 0.165 | 0.105 | |
| 3 | 0.51 | 1.000 | 0.087 | 0.028 | 1.000 | 0.130 | 0.100 | 0.072 | |
| A2 (soil class B) 0.34 g | 0 | 0.00 | 0.000 | −0.025 | 0.000 | 0.000 | −0.091 | 0.000 | 0.000 |
| 1 | 0.54 | 0.359 | 0.018 | 0.068 | 0.281 | −0.039 | 0.143 | 0.075 | |
| 2 | 0.96 | 0.765 | 0.074 | 0.081 | 0.745 | 0.058 | 0.189 | 0.108 | |
| 3 | 0.53 | 1.000 | 0.086 | 0.038 | 1.000 | 0.104 | 0.136 | 0.099 | |
| A3 (soil class B) 0.13 g | 0 | 0.00 | 0.000 | −0.024 | 0.000 | 0.000 | −0.055 | 0.000 | 0.000 |
| 1 | 0.38 | 0.348 | 0.019 | 0.068 | 0.328 | −0.004 | 0.106 | 0.039 | |
| 2 | 0.57 | 0.759 | 0.075 | 0.080 | 0.767 | 0.075 | 0.134 | 0.055 | |
| 3 | 0.27 | 1.000 | 0.087 | 0.036 | 1.000 | 0.103 | 0.083 | 0.047 | |
| A4 (soil class B) 0.15 g | 0 | 0.00 | 0.000 | −0.031 | 0.000 | 0.000 | −0.053 | 0.000 | 0.000 |
| 1 | 0.50 | 0.341 | 0.011 | 0.072 | 0.331 | −0.002 | 0.105 | 0.034 | |
| 2 | 0.71 | 0.754 | 0.067 | 0.087 | 0.769 | 0.076 | 0.132 | 0.045 | |
| 3 | 0.33 | 1.000 | 0.082 | 0.046 | 1.000 | 0.103 | 0.080 | 0.034 | |
| A5 (soil class B) 0.22 g | 0 | 0.00 | 0.000 | −0.058 | 0.000 | 0.000 | −0.070 | 0.000 | 0.000 |
| 1 | 0.45 | 0.308 | −0.007 | 0.109 | 0.320 | −0.016 | 0.125 | 0.016 | |
| 2 | 0.73 | 0.747 | 0.072 | 0.138 | 0.737 | 0.074 | 0.160 | 0.022 | |
| 3 | 0.45 | 1.000 | 0.101 | 0.087 | 1.000 | 0.109 | 0.105 | 0.018 | |
| A6 (soil class B) 0.48 g | 0 | 0.00 | 0.000 | −0.036 | 0.000 | 0.000 | −0.049 | 0.000 | 0.000 |
| 1 | 0.51 | 0.358 | 0.006 | 0.077 | 0.340 | 0.005 | 0.103 | 0.026 | |
| 2 | 0.81 | 0.771 | 0.065 | 0.095 | 0.778 | 0.083 | 0.128 | 0.033 | |
| 3 | 0.49 | 1.000 | 0.083 | 0.053 | 1.000 | 0.108 | 0.074 | 0.021 | |
| A7 (soil class B) 0.35 g | 0 | 0.00 | 0.000 | −0.031 | 0.000 | 0.000 | −0.072 | 0.000 | 0.000 |
| 1 | 0.51 | 0.363 | 0.012 | 0.074 | 0.315 | −0.014 | 0.130 | 0.056 | |
| 2 | 0.75 | 0.769 | 0.070 | 0.090 | 0.774 | 0.080 | 0.166 | 0.076 | |
| 3 | 0.38 | 1.000 | 0.086 | 0.047 | 1.000 | 0.116 | 0.108 | 0.061 | |
| Time Instant A | Time Instant B | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Accelerogram PGA | No. of Floor | Inter-Story Drift (%) | Mode Shape | Mode Curvature | Curvature Difference | Mode Shape | Mode Curvature | Curvature Difference | Curvature Difference B-A |
| A1 (soil class B) 0.34 g | 0 | 0.00 | 0.000 | −0.049 | 0.000 | 0.000 | −0.056 | 0.000 | 0.0000 |
| 1 | 0.48 | 0.189 | −0.043 | 0.055 | 0.183 | −0.049 | 0.062 | 0.0071 | |
| 2 | 0.74 | 0.466 | 0.003 | 0.095 | 0.478 | 0.008 | 0.113 | 0.0179 | |
| 3 | 0.68 | 0.715 | 0.058 | 0.104 | 0.747 | 0.078 | 0.125 | 0.0214 | |
| 4 | 0.47 | 0.899 | 0.057 | 0.048 | 0.924 | 0.073 | 0.051 | 0.0028 | |
| 5 | 0.20 | 1.000 | 0.042 | 0.033 | 1.000 | 0.050 | 0.032 | −0.0012 | |
| A2 (soil class B) 0.34 g | 0 | 0.00 | 0.000 | −0.047 | 0.000 | 0.000 | −0.061 | 0.000 | 0.0000 |
| 1 | 0.33 | 0.186 | −0.040 | 0.055 | 0.166 | −0.057 | 0.064 | 0.0093 | |
| 2 | 0.59 | 0.464 | 0.007 | 0.095 | 0.452 | −0.002 | 0.116 | 0.0212 | |
| 3 | 0.58 | 0.714 | 0.061 | 0.101 | 0.724 | 0.071 | 0.133 | 0.0322 | |
| 4 | 0.38 | 0.898 | 0.057 | 0.044 | 0.910 | 0.070 | 0.059 | 0.0151 | |
| 5 | 0.18 | 1.000 | 0.041 | 0.031 | 1.000 | 0.048 | 0.039 | 0.0078 | |
| A3 (soil class B) 0.13 g | 0 | 0.00 | 0.000 | −0.047 | 0.000 | 0.000 | −0.054 | 0.000 | 0.0000 |
| 1 | 0.17 | 0.193 | −0.039 | 0.055 | 0.169 | −0.049 | 0.059 | 0.0043 | |
| 2 | 0.29 | 0.472 | 0.009 | 0.095 | 0.447 | 0.000 | 0.103 | 0.0082 | |
| 3 | 0.28 | 0.720 | 0.062 | 0.099 | 0.704 | 0.060 | 0.114 | 0.0153 | |
| 4 | 0.21 | 0.901 | 0.057 | 0.042 | 0.894 | 0.059 | 0.053 | 0.0109 | |
| 5 | 0.12 | 1.000 | 0.041 | 0.030 | 1.000 | 0.042 | 0.037 | 0.0073 | |
| A4 (soil class B) 0.15 g | 0 | 0.00 | 0.000 | −0.049 | 0.000 | 0.000 | −0.058 | 0.000 | 0.0000 |
| 1 | 0.32 | 0.176 | −0.044 | 0.054 | 0.176 | −0.051 | 0.066 | 0.0114 | |
| 2 | 0.50 | 0.450 | 0.001 | 0.095 | 0.469 | 0.007 | 0.116 | 0.0215 | |
| 3 | 0.43 | 0.704 | 0.058 | 0.106 | 0.732 | 0.072 | 0.123 | 0.0171 | |
| 4 | 0.29 | 0.894 | 0.058 | 0.050 | 0.908 | 0.064 | 0.050 | 0.0009 | |
| 5 | 0.15 | 1.000 | 0.042 | 0.034 | 1.000 | 0.043 | 0.037 | 0.0032 | |
| A5 (soil class B) 0.22 g | 0 | 0.00 | 0.000 | −0.049 | 0.000 | 0.000 | −0.058 | 0.000 | 0.0000 |
| 1 | 0.27 | 0.177 | −0.044 | 0.055 | 0.168 | −0.053 | 0.063 | 0.0078 | |
| 2 | 0.47 | 0.451 | 0.002 | 0.095 | 0.453 | 0.000 | 0.112 | 0.0166 | |
| 3 | 0.47 | 0.704 | 0.058 | 0.106 | 0.718 | 0.067 | 0.125 | 0.0191 | |
| 4 | 0.35 | 0.895 | 0.058 | 0.050 | 0.904 | 0.065 | 0.056 | 0.0060 | |
| 5 | 0.18 | 1.000 | 0.042 | 0.034 | 1.000 | 0.045 | 0.038 | 0.0043 | |
| A6 (soil class B) 0.48 g | 0 | 0.00 | 0.000 | −0.048 | 0.000 | 0.000 | −0.052 | 0.000 | 0.0000 |
| 1 | 0.31 | 0.179 | −0.041 | 0.055 | 0.189 | −0.042 | 0.062 | 0.0069 | |
| 2 | 0.51 | 0.459 | 0.006 | 0.096 | 0.482 | 0.014 | 0.108 | 0.0122 | |
| 3 | 0.53 | 0.711 | 0.061 | 0.103 | 0.734 | 0.070 | 0.108 | 0.0050 | |
| 4 | 0.38 | 0.897 | 0.058 | 0.046 | 0.907 | 0.060 | 0.042 | −0.0034 | |
| 5 | 0.19 | 1.000 | 0.042 | 0.032 | 1.000 | 0.040 | 0.032 | 0.0004 | |
| A7 (soil class B) 0.35 g | 0 | 0.00 | 0.000 | −0.050 | 0.000 | 0.000 | −0.059 | 0.000 | 0.0000 |
| 1 | 0.31 | 0.172 | −0.045 | 0.054 | 0.174 | −0.053 | 0.065 | 0.0112 | |
| 2 | 0.49 | 0.444 | −0.001 | 0.094 | 0.466 | 0.005 | 0.117 | 0.0233 | |
| 3 | 0.48 | 0.697 | 0.055 | 0.106 | 0.733 | 0.073 | 0.127 | 0.0216 | |
| 4 | 0.33 | 0.890 | 0.057 | 0.051 | 0.912 | 0.067 | 0.053 | 0.0022 | |
| 5 | 0.17 | 1.000 | 0.042 | 0.035 | 1.000 | 0.045 | 0.037 | 0.0023 | |
| Time Instant A | Time Instant B | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Accelerogram PGA | No. of Floor | Inter-Story Drift (%) | Mode Shape | Mode Curvature | Curvature Difference | Mode Shape | Mode Curvature | Curvature Difference | Curvature Difference B-A |
| A1 (soil class B) 0.34 g | 0 | 0.00 | 0.000 | −0.046 | 0.0000 | 0.000 | −0.054 | 0.000 | 0.000 |
| 1 | 0.52 | 0.169 | −0.045 | 0.0467 | 0.203 | −0.042 | 0.067 | 0.020 | |
| 2 | 0.76 | 0.430 | −0.007 | 0.0835 | 0.515 | 0.025 | 0.121 | 0.037 | |
| 3 | 0.62 | 0.687 | 0.051 | 0.1034 | 0.776 | 0.087 | 0.117 | 0.014 | |
| 4 | 0.34 | 0.888 | 0.058 | 0.0526 | 0.931 | 0.070 | 0.037 | −0.016 | |
| 5 | 0.15 | 1.000 | 0.044 | 0.0316 | 1.000 | 0.043 | 0.028 | −0.004 | |
| A5 (soil class B) 0.22 g | 0 | 0.00 | 0.000 | −0.046 | 0.0000 | 0.000 | −0.051 | 0.000 | 0.000 |
| 1 | 0.23 | 0.167 | −0.046 | 0.0465 | 0.185 | −0.043 | 0.059 | 0.013 | |
| 2 | 0.32 | 0.426 | −0.008 | 0.0831 | 0.472 | 0.009 | 0.104 | 0.021 | |
| 3 | 0.29 | 0.684 | 0.050 | 0.1045 | 0.727 | 0.067 | 0.109 | 0.005 | |
| 4 | 0.24 | 0.886 | 0.058 | 0.0540 | 0.906 | 0.062 | 0.046 | −0.008 | |
| 5 | 0.14 | 1.000 | 0.044 | 0.0323 | 1.000 | 0.043 | 0.032 | 0.000 | |
| A6 (soil class B) 0.48 g | 0 | 0.00 | 0.000 | −0.046 | 0.0000 | 0.000 | −0.057 | 0.000 | 0.000 |
| 1 | 0.24 | 0.165 | −0.047 | 0.0456 | 0.174 | −0.050 | 0.063 | 0.017 | |
| 2 | 0.40 | 0.422 | −0.010 | 0.0823 | 0.462 | 0.004 | 0.111 | 0.029 | |
| 3 | 0.35 | 0.681 | 0.049 | 0.1056 | 0.724 | 0.068 | 0.121 | 0.015 | |
| 4 | 0.23 | 0.885 | 0.058 | 0.0553 | 0.906 | 0.064 | 0.052 | −0.003 | |
| 5 | 0.12 | 1.000 | 0.045 | 0.0325 | 1.000 | 0.044 | 0.037 | 0.004 | |
| A2 (soil class D) 0.26 g | 0 | 0.00 | 0.000 | 0.000 | 0.0000 | 0.000 | −0.035 | 0.000 | 0.000 |
| 1 | 0.67 | 0.175 | 0.000 | 0.0001 | 0.180 | −0.030 | 0.039 | 0.039 | |
| 2 | 0.90 | 0.440 | 0.000 | 0.0003 | 0.476 | 0.006 | 0.070 | 0.069 | |
| 3 | 0.71 | 0.695 | 0.000 | 0.0003 | 0.739 | 0.045 | 0.074 | 0.073 | |
| 4 | 0.34 | 0.891 | 0.000 | 0.0002 | 0.914 | 0.040 | 0.030 | 0.030 | |
| 5 | 0.16 | 1.000 | 0.000 | 0.0001 | 1.000 | 0.027 | 0.021 | 0.021 | |
| Time Instant A | Time Instant B | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Accelerogram PGA | No. of Floor | Inter-Story Drift (%) | Mode Shape | Mode Curvature | Curvature Difference | Mode Shape | Mode Curvature | Curvature Difference | Curvature Difference B-A |
| A1 (soil class B) 0.34 g | 0 | 0.00 | 0.000 | −0.000036 | 0.000000 | 0.000 | −0.002 | 0.0000 | 0.0000 |
| 1 | 0.33 | 0.111 | −0.000036 | 0.000036 | 0.096 | −0.002 | 0.0019 | 0.0019 | |
| 2 | 0.45 | 0.276 | −0.000014 | 0.000058 | 0.241 | −0.001 | 0.0025 | 0.0024 | |
| 3 | 0.34 | 0.441 | 0.000010 | 0.000060 | 0.382 | −0.001 | 0.0020 | 0.0019 | |
| 4 | 0.42 | 0.593 | 0.000016 | 0.000043 | 0.534 | −0.001 | 0.0019 | 0.0019 | |
| 5 | 0.54 | 0.742 | 0.000032 | 0.000052 | 0.710 | 0.002 | 0.0040 | 0.0039 | |
| 6 | 0.59 | 0.864 | 0.000046 | 0.000050 | 0.864 | 0.004 | 0.0039 | 0.0038 | |
| 7 | 0.41 | 0.951 | 0.000028 | 0.000018 | 0.958 | 0.003 | 0.0012 | 0.0012 | |
| 8 | 0.20 | 1.000 | 0.000026 | 0.000034 | 1.000 | 0.002 | 0.0007 | 0.0007 | |
| A2 (soil class B) 0.34 g | 0 | 0.00 | 0.000 | −0.000022 | 0.000000 | 0.000 | −0.001 | 0.0000 | 0.0000 |
| 1 | 0.73 | 0.126 | −0.000019 | 0.000024 | 0.185 | 0.000 | 0.0024 | 0.0024 | |
| 2 | 0.81 | 0.303 | −0.000002 | 0.000039 | 0.416 | 0.002 | 0.0039 | 0.0039 | |
| 3 | 0.37 | 0.469 | 0.000011 | 0.000035 | 0.578 | 0.003 | 0.0018 | 0.0018 | |
| 4 | 0.21 | 0.617 | 0.000012 | 0.000023 | 0.697 | 0.001 | 0.0001 | 0.0001 | |
| 5 | 0.30 | 0.759 | 0.000020 | 0.000030 | 0.809 | 0.001 | 0.0014 | 0.0014 | |
| 6 | 0.34 | 0.874 | 0.000028 | 0.000030 | 0.903 | 0.002 | 0.0019 | 0.0019 | |
| 7 | 0.26 | 0.955 | 0.000022 | 0.000016 | 0.966 | 0.001 | 0.0011 | 0.0011 | |
| 8 | 0.14 | 1.000 | 0.000015 | 0.000014 | 1.000 | 0.001 | 0.0009 | 0.0009 | |
| A3 (soil class B) 0.13 g | 0 | 0.00 | 0.000 | −0.000013 | 0.000000 | 0.000 | −0.004 | 0.0000 | 0.0000 |
| 1 | 1.10 | 0.119 | −0.000013 | 0.000014 | 0.155 | −0.004 | 0.0046 | 0.0046 | |
| 2 | 1.55 | 0.289 | −0.000004 | 0.000022 | 0.382 | 0.000 | 0.0083 | 0.0083 | |
| 3 | 1.38 | 0.457 | 0.000005 | 0.000023 | 0.597 | 0.005 | 0.0093 | 0.0093 | |
| 4 | 0.92 | 0.609 | 0.000008 | 0.000016 | 0.764 | 0.006 | 0.0055 | 0.0055 | |
| 5 | 0.51 | 0.754 | 0.000013 | 0.000019 | 0.872 | 0.005 | 0.0031 | 0.0031 | |
| 6 | 0.31 | 0.871 | 0.000017 | 0.000018 | 0.940 | 0.004 | 0.0028 | 0.0028 | |
| 7 | 0.18 | 0.953 | 0.000014 | 0.000010 | 0.979 | 0.002 | 0.0027 | 0.0027 | |
| 8 | 0.10 | 1.000 | 0.000009 | 0.000009 | 1.000 | 0.001 | 0.0035 | 0.0035 | |
| A4 (soil class B) 0.15 g | 0 | 0.00 | 0.000 | −0.000023 | 0.000000 | 0.000 | −0.003 | 0.0000 | 0.0000 |
| 1 | 0.79 | 0.119 | −0.000023 | 0.000024 | 0.149 | −0.003 | 0.0038 | 0.0038 | |
| 2 | 1.11 | 0.290 | −0.000006 | 0.000040 | 0.368 | 0.000 | 0.0068 | 0.0068 | |
| 3 | 0.95 | 0.457 | 0.000009 | 0.000039 | 0.569 | 0.004 | 0.0067 | 0.0067 | |
| 4 | 0.69 | 0.608 | 0.000012 | 0.000027 | 0.720 | 0.004 | 0.0034 | 0.0034 | |
| 5 | 0.48 | 0.754 | 0.000022 | 0.000033 | 0.835 | 0.003 | 0.0028 | 0.0028 | |
| 6 | 0.30 | 0.871 | 0.000030 | 0.000032 | 0.918 | 0.003 | 0.0031 | 0.0031 | |
| 7 | 0.18 | 0.953 | 0.000024 | 0.000017 | 0.971 | 0.002 | 0.0025 | 0.0025 | |
| 8 | 0.11 | 1.000 | 0.000016 | 0.000016 | 1.000 | 0.001 | 0.0027 | 0.0027 | |
| A5 (soil class B) 0.22 g | 0 | 0.00 | 0.000 | −0.000034 | 0.000000 | 0.000 | −0.009 | 0.0000 | 0.0000 |
| 1 | 3.63 | 0.114 | −0.000034 | 0.000034 | 0.190 | −0.007 | 0.0111 | 0.0111 | |
| 2 | 4.86 | 0.279 | 0.000012 | 0.000080 | 0.483 | 0.004 | 0.0196 | 0.0195 | |
| 3 | 4.10 | 0.444 | 0.000010 | 0.000032 | 0.722 | 0.014 | 0.0184 | 0.0184 | |
| 4 | 2.62 | 0.596 | 0.000016 | 0.000040 | 0.866 | 0.012 | 0.0069 | 0.0069 | |
| 5 | 1.03 | 0.744 | 0.000031 | 0.000049 | 0.930 | 0.006 | 0.0032 | 0.0032 | |
| 6 | 0.35 | 0.865 | 0.000044 | 0.000048 | 0.968 | 0.003 | 0.0054 | 0.0054 | |
| 7 | 0.23 | 0.951 | 0.000036 | 0.000026 | 0.990 | 0.002 | 0.0074 | 0.0074 | |
| 8 | 0.13 | 1.000 | 0.000025 | 0.000023 | 1.000 | 0.001 | 0.0081 | 0.0081 | |
| A6 (soil class B) 0.48 g | 0 | 0.00 | 0.000 | −0.000032 | 0.000000 | 0.000 | −0.003 | 0.0000 | 0.0000 |
| 1 | 0.72 | 0.122 | −0.000030 | 0.000034 | 0.173 | −0.002 | 0.0034 | 0.0034 | |
| 2 | 1.02 | 0.298 | −0.000007 | 0.000055 | 0.408 | 0.002 | 0.0059 | 0.0058 | |
| 3 | 0.92 | 0.468 | 0.000016 | 0.000055 | 0.604 | 0.004 | 0.0050 | 0.0049 | |
| 4 | 0.66 | 0.620 | 0.000020 | 0.000036 | 0.745 | 0.003 | 0.0020 | 0.0020 | |
| 5 | 0.37 | 0.761 | 0.000030 | 0.000042 | 0.851 | 0.003 | 0.0019 | 0.0019 | |
| 6 | 0.25 | 0.875 | 0.000039 | 0.000041 | 0.925 | 0.002 | 0.0022 | 0.0022 | |
| 7 | 0.21 | 0.955 | 0.000031 | 0.000024 | 0.973 | 0.002 | 0.0019 | 0.0019 | |
| 8 | 0.14 | 1.000 | 0.000021 | 0.000022 | 1.000 | 0.001 | 0.0020 | 0.0020 | |
| A7 (soil class B) 0.35 g | 0 | 0.00 | 0.000 | −0.000020 | 0.000000 | 0.000 | −0.006 | 0.0000 | 0.0000 |
| 1 | 0.99 | 0.121 | −0.000018 | 0.000022 | 0.159 | −0.004 | 0.0088 | 0.0088 | |
| 2 | 1.43 | 0.290 | −0.000004 | 0.000035 | 0.389 | 0.001 | 0.0109 | 0.0109 | |
| 3 | 1.42 | 0.452 | 0.000008 | 0.000032 | 0.601 | 0.006 | 0.0115 | 0.0115 | |
| 4 | 1.15 | 0.598 | 0.000009 | 0.000021 | 0.762 | 0.007 | 0.0073 | 0.0073 | |
| 5 | 0.70 | 0.742 | 0.000017 | 0.000028 | 0.871 | 0.005 | 0.0052 | 0.0052 | |
| 6 | 0.37 | 0.863 | 0.000026 | 0.000029 | 0.939 | 0.004 | 0.0049 | 0.0049 | |
| 7 | 0.23 | 0.950 | 0.000022 | 0.000016 | 0.979 | 0.002 | 0.0048 | 0.0048 | |
| 8 | 0.14 | 1.000 | 0.000015 | 0.000013 | 1.000 | 0.001 | 0.0055 | 0.0055 | |
| Time Instant A | Time Instant B | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Accelerogram PGA | No. of Floor | Inter-Story Drift (%) | Mode Shape | Mode Curvature | Curvature Difference | Mode Shape | Mode Curvature | Curvature Difference | Curvature Difference B-A |
| A1 (soil class B) 0.34 g | 0 | 0.00 | 0.000 | −0.032 | 0.00000 | 0.000 | −0.047 | 0.000 | 0.000 |
| 1 | 0.34 | 0.146 | −0.042 | 0.02220 | 0.102 | −0.064 | 0.030 | 0.008 | |
| 2 | 0.65 | 0.354 | −0.024 | 0.05010 | 0.298 | −0.051 | 0.060 | 0.010 | |
| 3 | 0.88 | 0.602 | 0.015 | 0.07080 | 0.561 | 0.005 | 0.103 | 0.032 | |
| 4 | 0.88 | 0.803 | 0.014 | 0.03110 | 0.798 | 0.024 | 0.066 | 0.035 | |
| 5 | 0.68 | 1.000 | 0.002 | 0.02020 | 1.000 | 0.017 | 0.041 | 0.020 | |
| A2 (soil class D) 0.26 g | 0 | 0.00 | 0.000 | −0.030 | 0.00000 | 0.000 | −0.037 | 0.000 | 0.000 |
| 1 | 1.74 | 0.159 | −0.038 | 0.02280 | 0.181 | −0.041 | 0.033 | 0.010 | |
| 2 | 2.37 | 0.378 | −0.016 | 0.05200 | 0.437 | −0.006 | 0.073 | 0.021 | |
| 3 | 2.54 | 0.625 | 0.023 | 0.06890 | 0.708 | 0.059 | 0.101 | 0.033 | |
| 4 | 2.14 | 0.817 | 0.019 | 0.02580 | 0.896 | 0.063 | 0.041 | 0.015 | |
| 5 | 1.42 | 1.000 | 0.004 | 0.01610 | 1.000 | 0.042 | 0.016 | 0.000 | |
References
- Ditommaso, R.; Ponzo, F.C.; Auletta, G. Damage detection on framed structures: Modal curvature evaluation using Stockwell Transform under seismic excitation. Earthq. Eng. Eng. Vib. 2015, 14, 265–274. [Google Scholar] [CrossRef]
- Ditommaso, R.; Parolai, S.; Mucciarelli, M.; Eggert, S.; Sobiesiak, M.; Zschau, J. Monitoring the response and the back-radiated energy of a building subjected to ambient vibration and impulsive action: The Falkenhof Tower (Potsdam, Germany). Bull. Earthq. Eng. 2009, 8, 705–722. [Google Scholar] [CrossRef] [Green Version]
- Mucciarelli, M.; Bianca, M.; Ditommaso, R.; Gallipoli, M.R.; Masi, A.; Milkereit, C.; Parolai, S.; Picozzi, M.; Vona, M. Far field damage on RC buildings: The case study of Navelli during the L’Aquila (Italy) seismic sequence, 2009. Bull. Earthq. Eng. 2010, 9, 263–283. [Google Scholar] [CrossRef]
- Mallat, S. A Wavelet Tour of Signal Processing; Academic Press: New York, NY, USA, 1998. [Google Scholar]
- Şafak, E. Wave propagation formulation of seismic response of multi-story buildings. J. Struct. Eng. ASCE 1999, 125, 426–437. [Google Scholar] [CrossRef]
- Şafak, E. Propagation of seismic waves in tall buildings. Struct. Des. Tall Build. 1998, 7, 295–306. [Google Scholar] [CrossRef]
- Şafak, E. Detection of seismic damage in multi-story buildings by using wave propagation analysis. In Proceedings of the 6th National Conference on Earthquake Engineering, Oakland, CA, USA, 31 May–4 June 1998; p. 12, Paper No. 171. [Google Scholar]
- Parolai, S. Denoising of Seismograms Using the S Transform. Bull. Seism. Soc. Am. 2009, 99, 226–234. [Google Scholar] [CrossRef]
- Petrovic, B.; Parolai, S.; Pianese, G.; Dikmen, S.U.; Moldobekov, B.; Orunbaev, S.; Paolucci, R. Joint deconvolution of building and downhole seismic recordings: An application to three test cases. Bull. Earthq. Eng. 2017, 16, 613–641. [Google Scholar] [CrossRef]
- Ditommaso, R.; Mucciarelli, M.; Ponzo, F.C. Analysis of non-stationary structural systems by using a band-variable filter. Bull. Earthq. Eng. 2012, 10, 895–911. [Google Scholar] [CrossRef]
- Iacovino, C.; Ditommaso, R.; Ponzo, F.; Limongelli, M. The Interpolation Evolution Method for damage localization in structures under seismic excitation. Earthq. Eng. Struct. Dyn. 2018, 47, 2117–2136. [Google Scholar] [CrossRef]
- Michel, C.; Guéguen, P. Interpretation of the velocity measured in buildings by seismic interferometry based on Timoshenko beam theory under weak and moderate motion. Soil Dyn. Earthq. Eng. 2018, 104, 131–142. [Google Scholar] [CrossRef]
- Serra, M.; Festa, G.; Vassallo, M.; Zollo, A.; Quattrone, A.; Ceravolo, R. Damage detection in elastic properties of masonry bridges using coda wave interferometry. Struct. Control. Health Monit. 2016, 24, e1976. [Google Scholar] [CrossRef]
- Todorovska, M. Seismic Interferometry of a Soil-Structure Interaction Model with Coupled Horizontal and Rocking Response. Bull. Seism. Soc. Am. 2009, 99, 611–625. [Google Scholar] [CrossRef]
- Pinnegar, C.R.; Eaton, D.E. The S-transform with windows of arbitrary and varying shape. Geophysics 2003, 68, 381–385. [Google Scholar] [CrossRef]
- Askari, R.; Siahkoohi, H.R. Ground roll attenuation using the S and x-f-k transforms. Geophys. Prospect. 2007, 56, 105–114. [Google Scholar] [CrossRef]
- Simon, C.; Ventosa, S.; Schimmel, M.; Heldring, A.; Danobeitia, J.J.; Gallart, J.; Mànuel, A. The S-Transform and Its Inverses: Side Effects of Discretizing and Filtering. IEEE Trans. Signal Process. 2007, 55, 4928–4937. [Google Scholar] [CrossRef] [Green Version]
- Snieder, R.; Şafak, E. Extracting the Building Response Using Seismic interferometry: Theory and Application to the Millikan Library in Pasadena. California. Bull. Seism. Soc. Am. 2006, 96, 586–598. [Google Scholar] [CrossRef] [Green Version]
- Limongelli, M.P. Seismic health monitoring of an instrumented multistory building using the interpolation method. Earthq. Eng. Struct. Dyn. 2014, 43, 1581–1602. [Google Scholar] [CrossRef]
- Gerardi, V.; Ditommaso, R.; Auletta, G.; Ponzo, F.C. Reinforced concrete framed structures: Numerical validation of two physical models capable to consider the stiffness contribution of infill panels on framed structures in operative conditions. Ing. Sismica 2018, 35, 1–21. [Google Scholar]
- Serlenga, V.; Gallipoli, M.R.; Ditommaso, R.; Ponzo, C.F.; Tragni, N.; Perrone, A.; Stabile, T.A.; Calamita, G.; Vignola, L.; Carso, R.F.; et al. An integrated approach for structural behavior characterization of the Gravina Bridge (Matera, Southern Italy). Struct. Health Monit. 2021. [Google Scholar] [CrossRef]
- Doebling, S.; Farrar, C.; Prime, M.; Shevitz, D. Damage Identification and Health Monitoring of Structural and Mechanical Systems from Changes in Their Vibration Characteristics: A Literature Review; Los Alamos National Laboratory Report; USDOE: Washington, DC, USA, 1996. [Google Scholar]
- Dinh, H.M.; Nagayama, T.; Fujino, Y. Structural parameter identification by use of additional known masses and its experimental application. Struct. Control. Health Monit. 2011, 19, 436–450. [Google Scholar] [CrossRef]
- Chelidze, D. Identifying Multidimensional Damage in a Hierarchical Dynamical System. Nonlinear Dyn. 2004, 37, 307–322. [Google Scholar] [CrossRef]
- Foti, D.; Diaferio, M.; Giannoccaro, N.I.; Mongelli, M. Ambient vibration testing, dynamic identification and model updating of a historic tower. NDT E Int. 2012, 47, 88–95. [Google Scholar] [CrossRef]
- Choi, S.; Park, S.; Yoon, S.; Stubbs, N. Nondestructive damage identification in plate structures using changes in modal compliance. NDT E Int. 2005, 38, 529–540. [Google Scholar] [CrossRef]
- Rytter, A. Vibrational Based Inspection of Civil Engineering Structures. Ph.D. Thesis, Aalborg University, Aalborg, Denmark, 1993. [Google Scholar]
- Pandey, A.; Biswas, M.; Samman, M.; Pandey, A.; Biswas, M.; Samman, M. Damage detection from changes in curvature mode shapes. J. Sound Vib. 1991, 145, 321–332. [Google Scholar] [CrossRef]
- Ponzo, F.C.; Iacovino, C.; Ditommaso, R.; Bonano, M.; Lanari, R.; Soldovieri, F.; Cuomo, V.; Bozzano, F.; Ciampi, P.; Rompato, M. Transport Infrastructure SHM Using Integrated SAR Data and on Site Vibrational Acquisitions: “Ponte Della Musica–Armando Trovajoli” Case Study. Appl. Sci. 2021, 11, in press. [Google Scholar]
- Pai, P.; Young, L.G. Damage detection of beams using operational deflection shapes. Int. J. Solids Struct. 2001, 38, 3161–3192. [Google Scholar] [CrossRef]
- Ponzo, F.C.; DiTommaso, R.; Auletta, G.; Mossucca, A. A fast method for structural health monitoring of Italian reinforced concrete strategic buildings. Bull. Earthq. Eng. 2010, 8, 1421–1434. [Google Scholar] [CrossRef]
- Amezquita-Sanchez, J.P.; Adeli, H. Signal Processing Techniques for Vibration-Based Health Monitoring of Smart Structures. Arch. Comput. Methods Eng. 2016, 23, 1–15. [Google Scholar] [CrossRef]
- Iacovino, C.; DiTommaso, R.; Limongelli, M.P.; Ponzo, F.C. Experimental damage localization in a full-scale 7 story benchmark building under seismic excitation. In Proceedings of the SPIE—The International Society for Optical Engineering, Conference on Nondestructive Characterization and Monitoring of Advanced Materials, Aerospace, Civil Infrastructure, and Transportation XI 2017, Portland, OR, USA, 26–29 March 2017; Volume 10169, p. 101691B. [Google Scholar]
- Limongelli, M. The interpolation damage detection method for frames under seismic excitation. J. Sound Vib. 2011, 330, 5474–5489. [Google Scholar] [CrossRef]
- Roy, K.; Ray-Chaudhuri, S. Fundamental mode shape and its derivatives in structural damage localization. J. Sound Vib. 2013, 332, 5584–5593. [Google Scholar] [CrossRef]
- Xiang, J.; Matsumoto, T.; Wang, Y.; Jiang, Z. Detect damages in conical shells using curvature mode shape and wavelet finite element method. Int. J. Mech. Sci. 2013, 66, 83–93. [Google Scholar] [CrossRef]
- Radzieński, M.; Krawczuk, M.; Palacz, M. Improvement of damage detection methods based on experimental modal parameters. Mech. Syst. Signal Process. 2011, 25, 2169–2190. [Google Scholar] [CrossRef]
- Xin, Y.; Li, J.; Hao, H. Damage Detection in Initially Nonlinear Structures Based on Variational Mode Decomposition. Int. J. Struct. Stab. Dyn. 2020, 20. [Google Scholar] [CrossRef]
- Quqa, S.; Landi, L.; Diotallevi, P.P. Instantaneous modal identification under varying structural characteristics: A decentralized algorithm. Mech. Syst. Signal Process. 2020, 142. [Google Scholar] [CrossRef]
- Hsu, T.Y.; Shih, Y.C.; Pham, Q.-V. Damage detection of a thin plate using modal curvature via macrostrain measurement. Earthq. Engineering and Engineering Vibration 2019, 18, 409–424. [Google Scholar] [CrossRef]
- Katunin, A. Identification of structural damage using S-transform from 1D and 2D mode shapes. Meas. J. Int. Meas. Confed. 2021, 173. [Google Scholar] [CrossRef]
- Ghahremani, B.; Bitaraf, M.; Ghorbani-Tanha, A.K. Structural damage identification based on fast S-transform and convolutional neural networks. Structures 2021, 29, 1199–1209. [Google Scholar] [CrossRef]
- Stockwell, R.G.; Mansinha, L.; Lowe, R.P. Localization of the complex spectrum: The S transform. IEEE Trans. Signal Process. 1996, 44, 998–1001. [Google Scholar] [CrossRef]
- Pianese, G.; Petrovic, B.; Parolai, S.; Paolucci, R. Identification of the nonlinear seismic response of buildings by a combined Stockwell Transform and deconvolution interferometry approach. Bull. Earthq. Eng. 2018, 16, 3103–3126. [Google Scholar] [CrossRef]
- Ditommaso, R.; Ponzo, F.C. Automatic evaluation of the fundamental frequency variations and related damping factor of reinforced concrete framed structures using the Short Time Impulse Response Function (STIRF). Eng. Struct. 2015, 82, 104–112. [Google Scholar] [CrossRef]
- Cao, M.; Xu, W.; Ostachowicz, W.; Su, Z. Damage identification for beams in noisy conditions based on Teager energy operator-wavelet transform modal curvature. J. Sound Vib. 2014, 333, 1543–1553. [Google Scholar] [CrossRef]
- SAP2000. Computers & Structures. Available online: https://www.csiamerica.com/products/sap2000 (accessed on 13 July 2021).
- Mainstone, R.J. Supplementary Note on the Stiffness and Strength of Infilled Frames, Current Paper CP13/74; Building Research Establishment: London, UK, 1974. [Google Scholar]
- Ministero delle Infrastrutture e dei Trasporti. Nuove Norme Tecniche per le Costruzioni (Italian Seismic CODE). Supplemento ordinario alla “Gazzetta Ufficiale, n. 42 del 20 febbraio 2018-Serie generale. 2018. Available online: https://www.studiopetrillo.com/ntc2018.html (accessed on 31 May 2021).
- Calvi, G.M. Alternative choices and criteria for seismic strengthening. Progettazione Sismica 2013, 4. [Google Scholar] [CrossRef]
- Picozzi, M.; Ditommaso, R.; Parolai, S.; Mucciarelli, M.; Milkereit, C.; Sobiesiak, M.; Di Giacomo, D.; Gallipoli, M.R.; Pilz, M.; Vona, M.; et al. Real time monitoring of structures in task force missions: The example of the Mw = 6.3 Central Italy Earthquake, April 6, 2009. Nat. Hazards 2009, 52, 253–256. [Google Scholar] [CrossRef]
- Picozzi, M.; Parolai, S.; Mucciarelli, M.; Milkereit, C.; Bindi, D.; Ditommaso, R.; Vona, M.; Gallipoli, M.; Zschau, J. Interferometric Analysis of Strong Ground Motion for Structural Health Monitoring: The Example of the L’Aquila, Italy, Seismic Sequence of 2009. Bull. Seism. Soc. Am. 2011, 101, 635–651. [Google Scholar] [CrossRef]
- Fleming, K.; Picozzi, M.; Milkereit, C.; Kühnlenz, F.; Lichtblau, B.; Fischer, J.; Zulfikar, C.; Özel, O.; The SAFER and EDIM Working Groups. The Self-organizing Seismic Early Warning Information Network (SOSEWIN). Seismol. Res. Lett. 2009, 80, 755–771. [Google Scholar] [CrossRef]
- Chris, G.; Maria, J.; Favvataa, D.J. Kakaletsisb Seismic behaviour of infilled and pilotis RC frame structures with beam–column joint degradation effect. Eng. Struct. 2011, 33, 2821–2831. [Google Scholar]
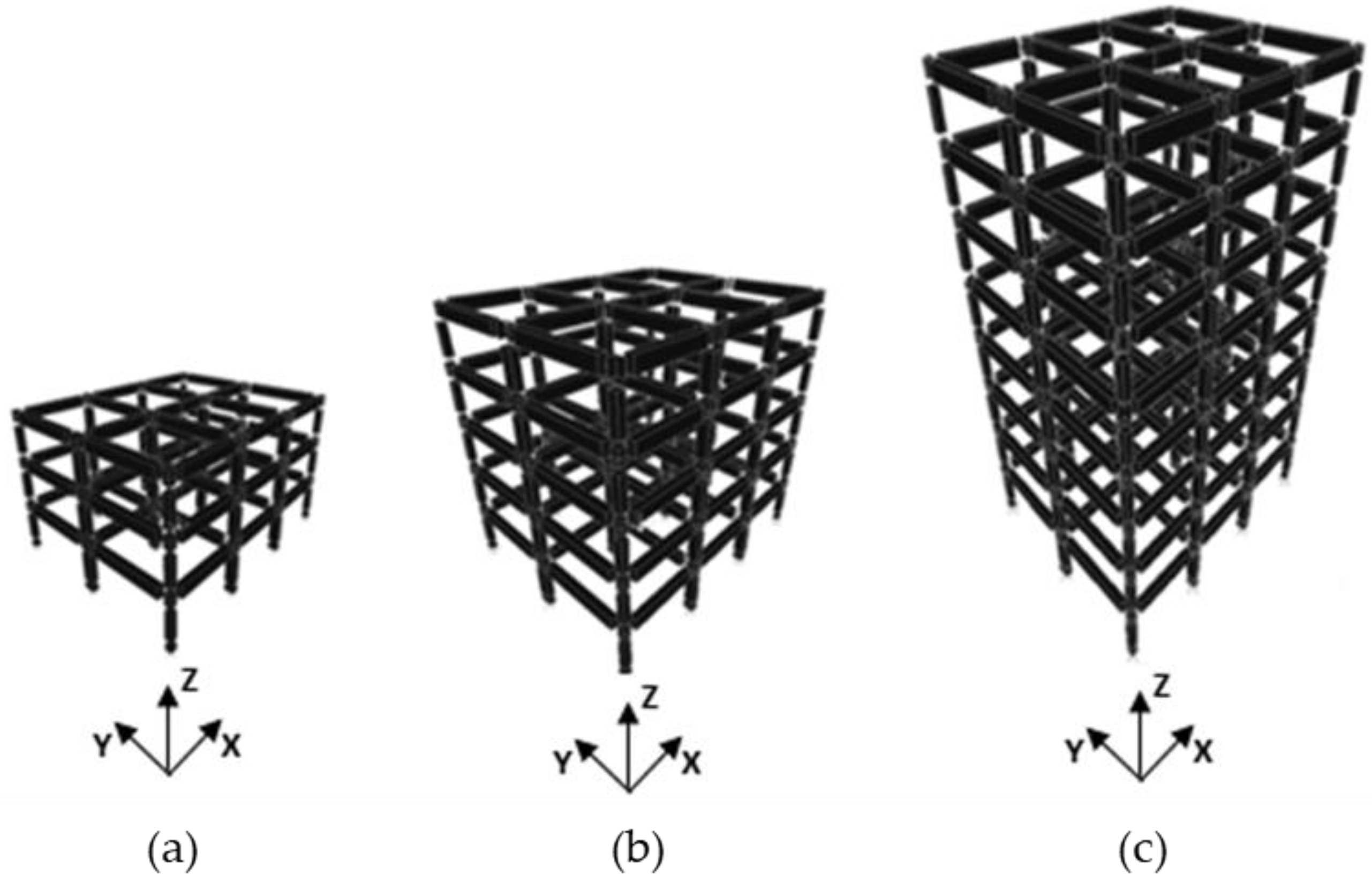
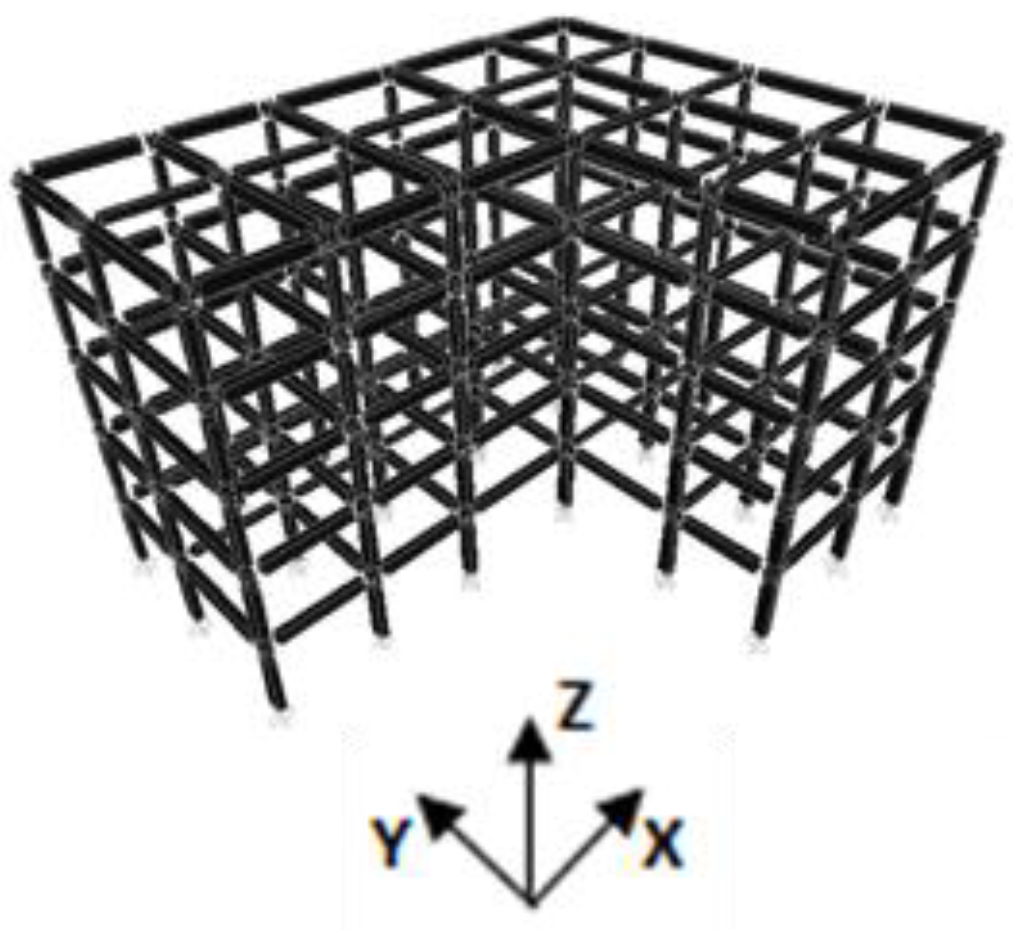
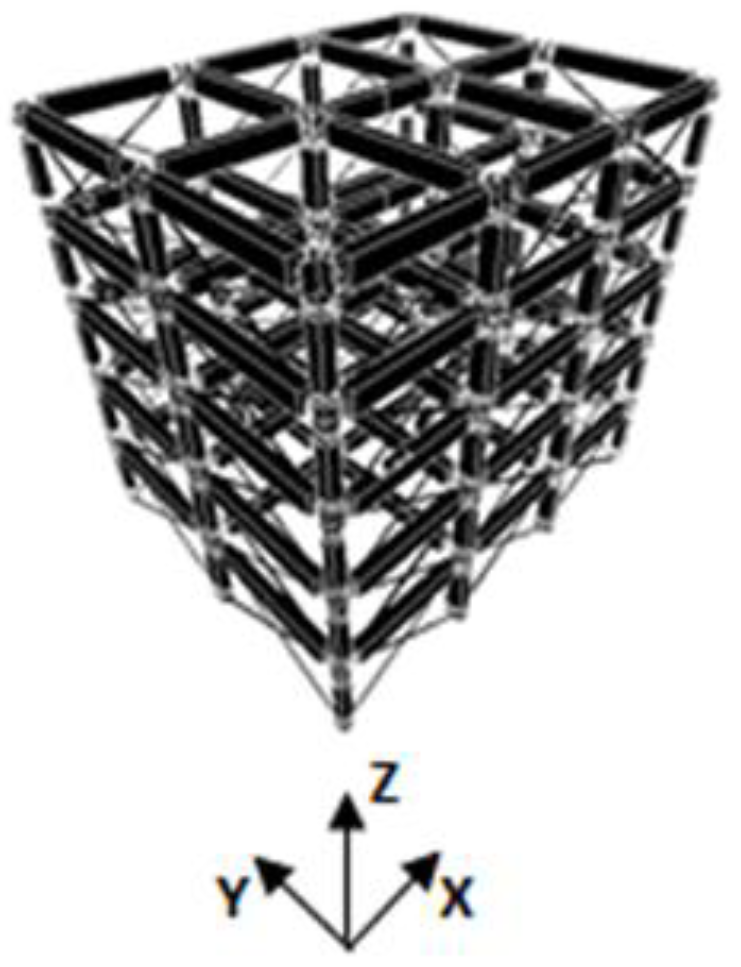
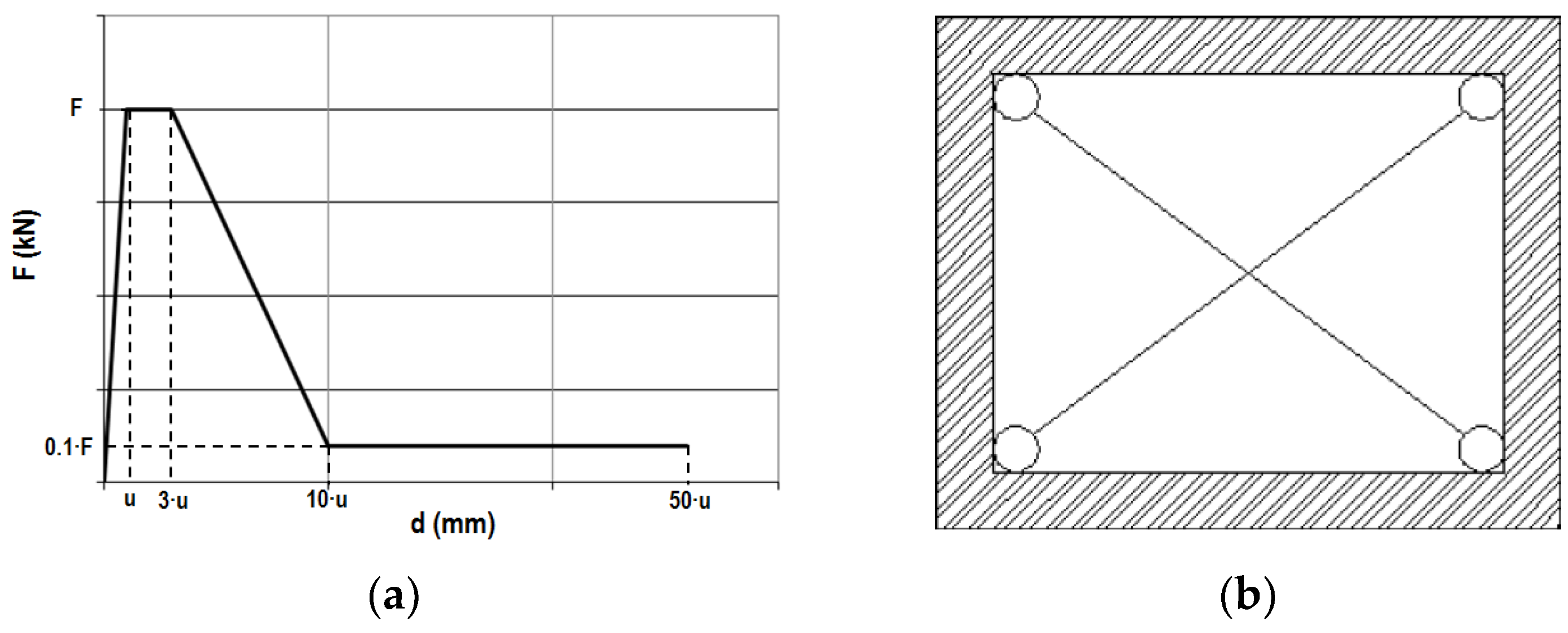
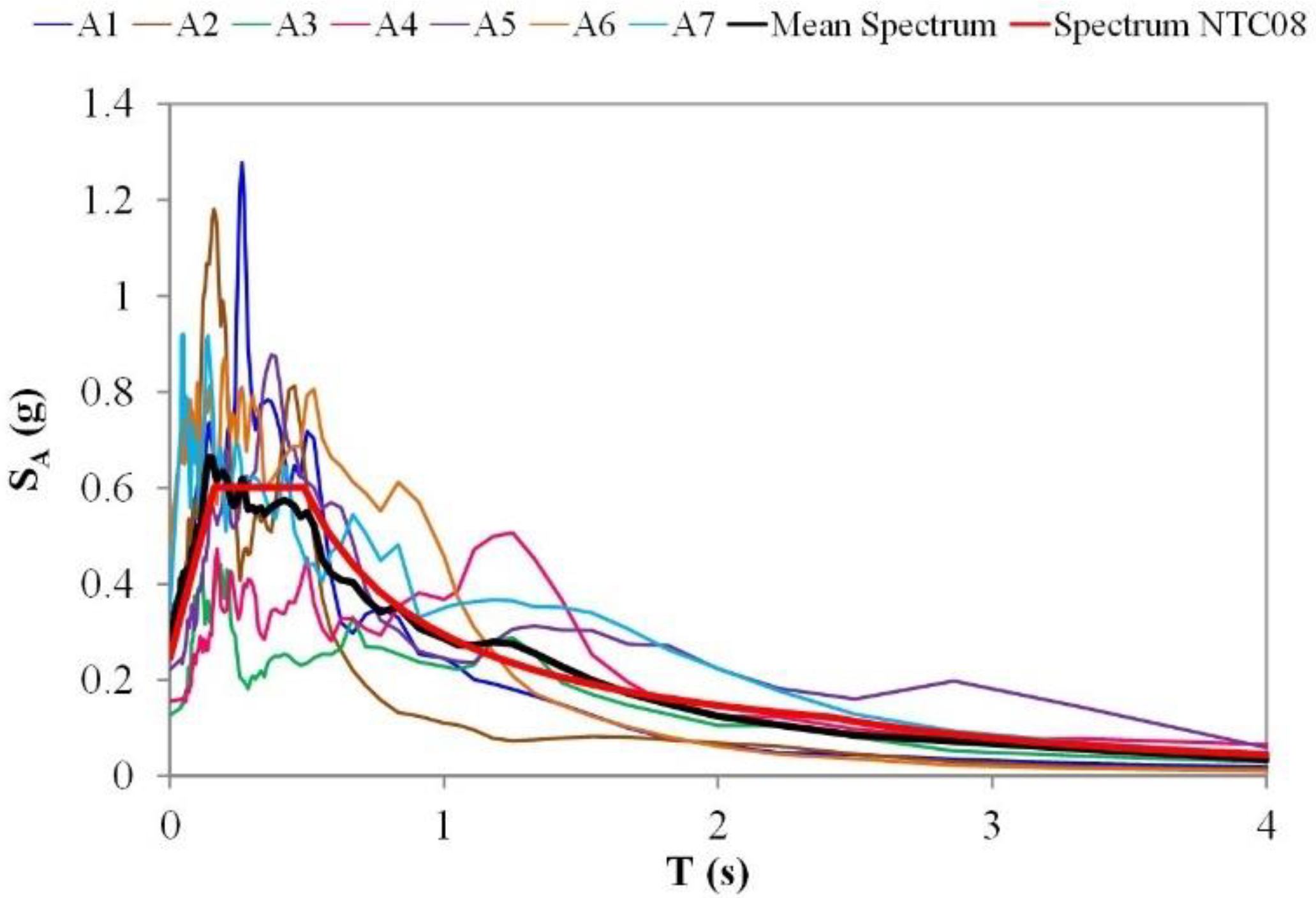
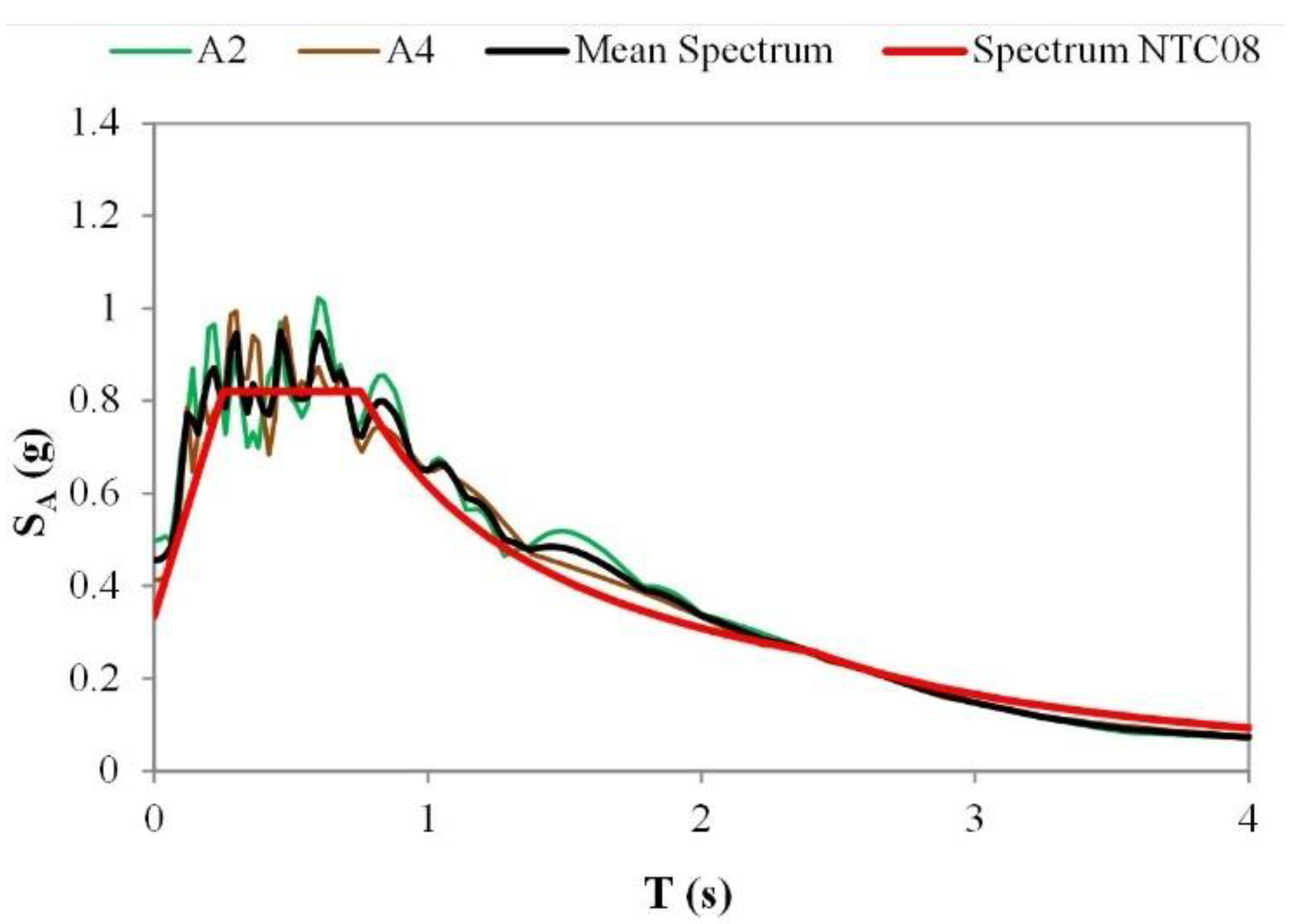


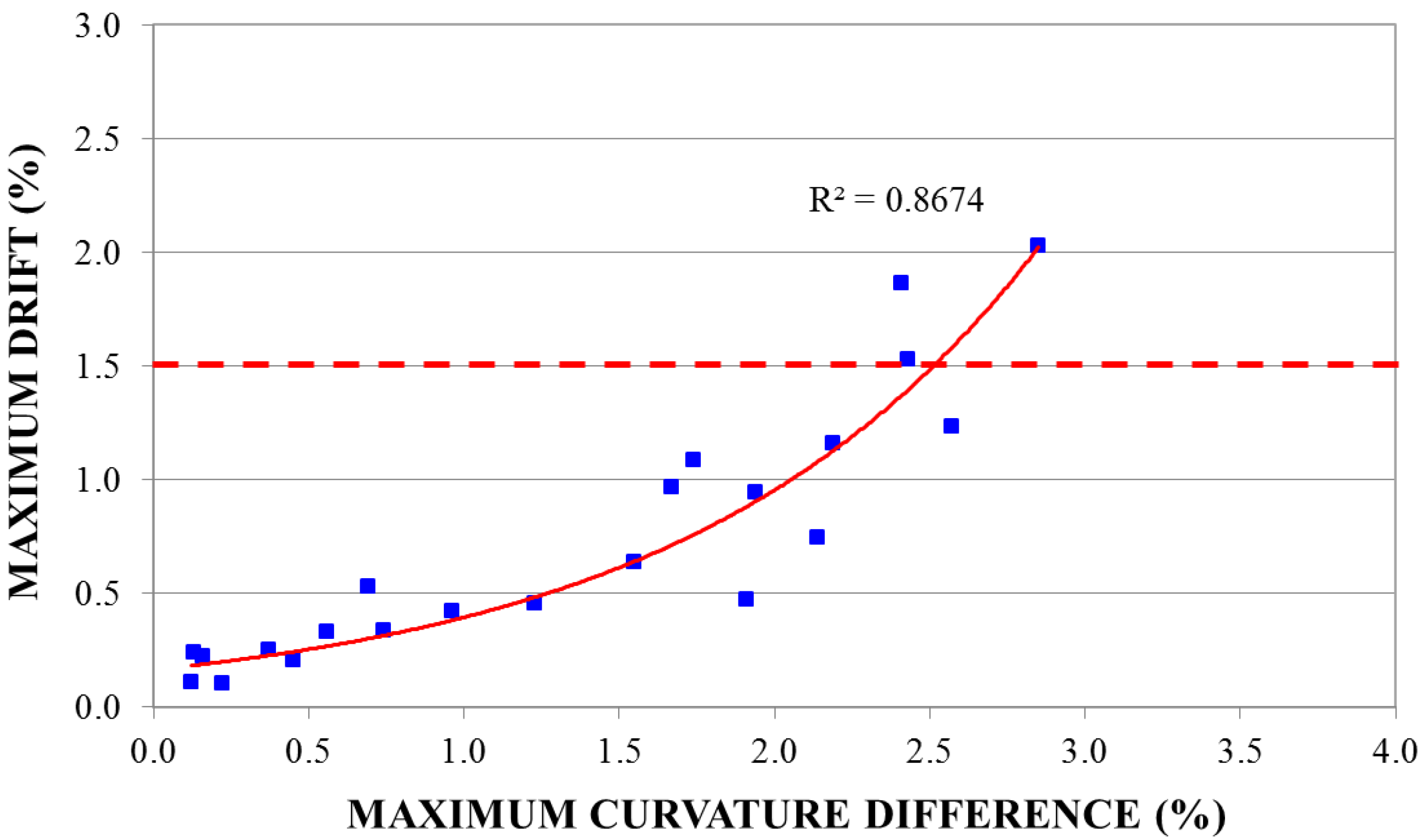
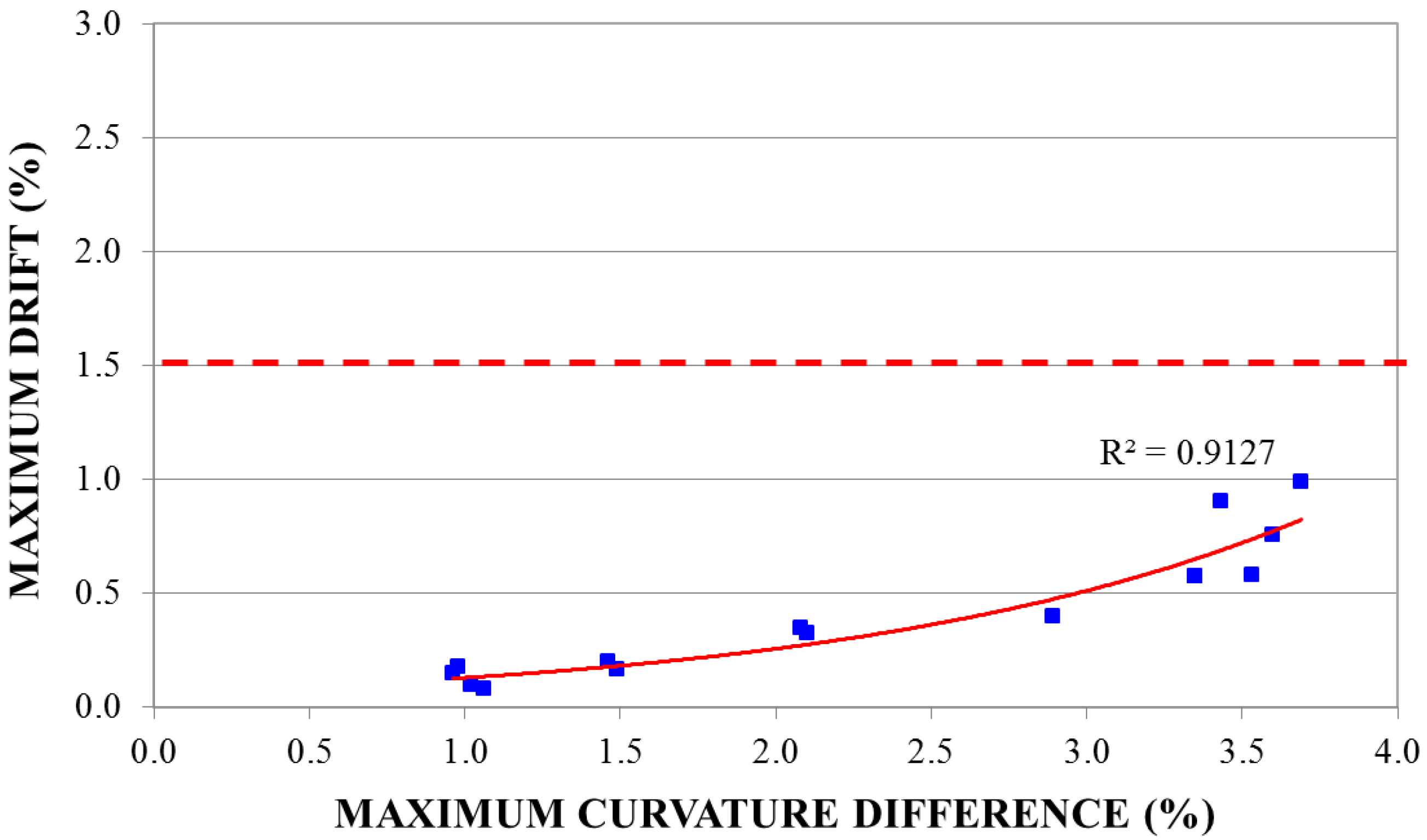
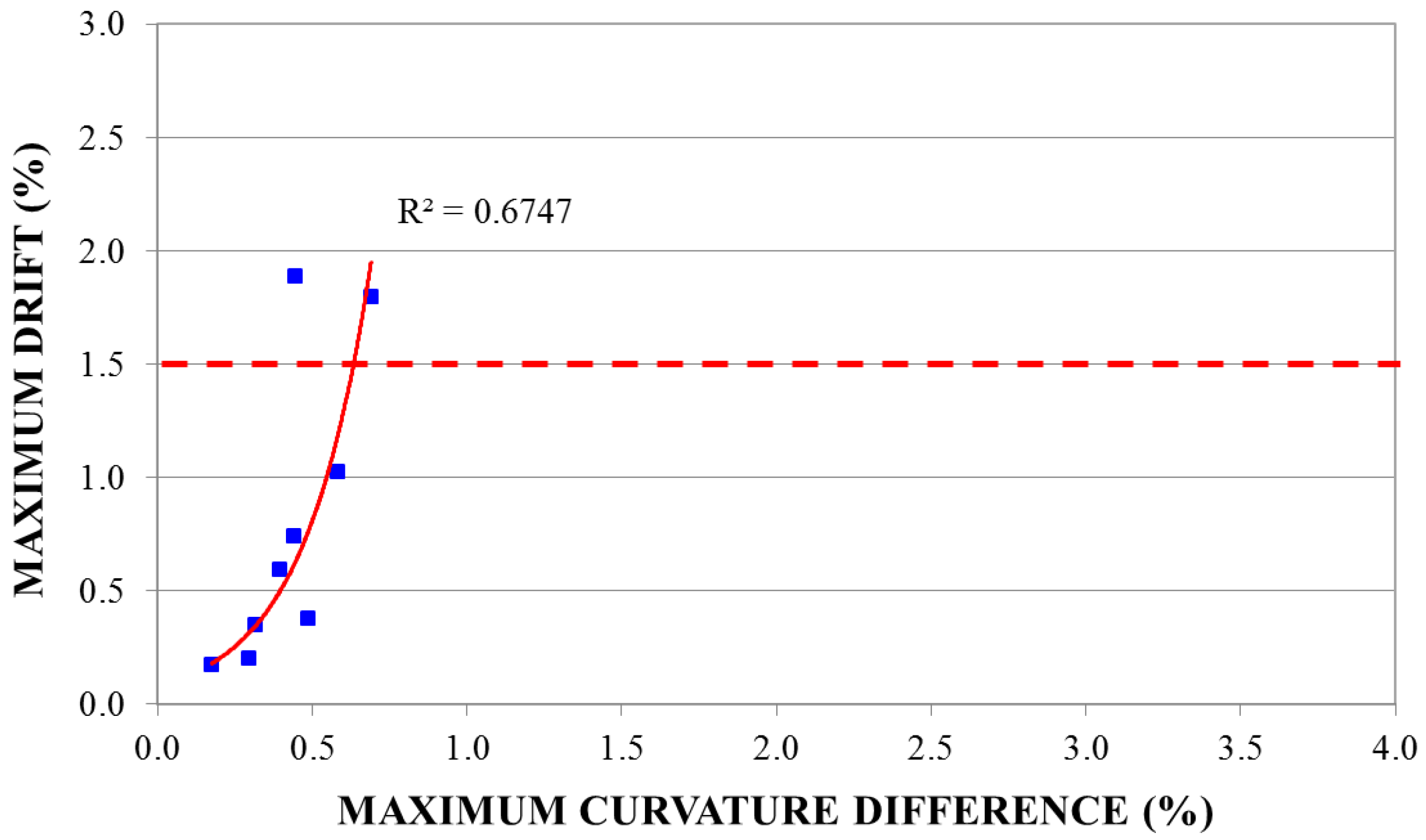



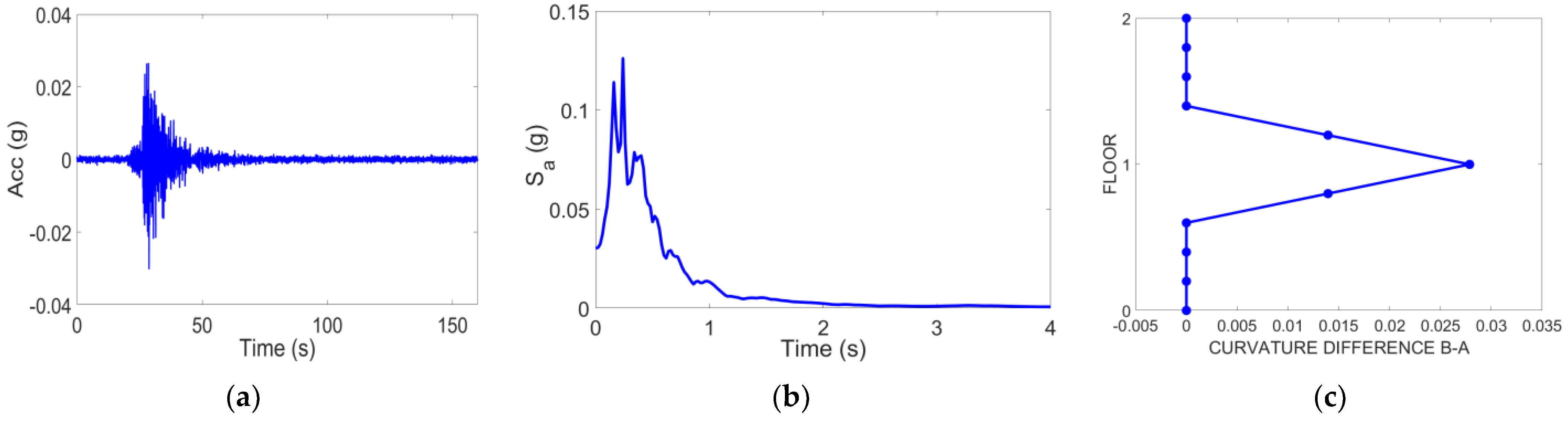
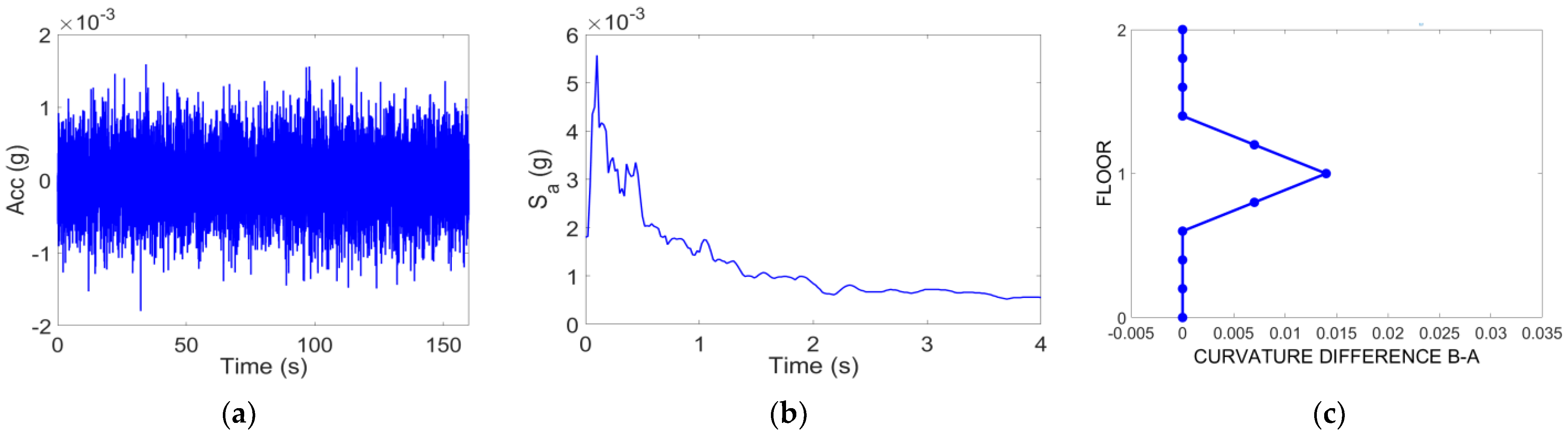
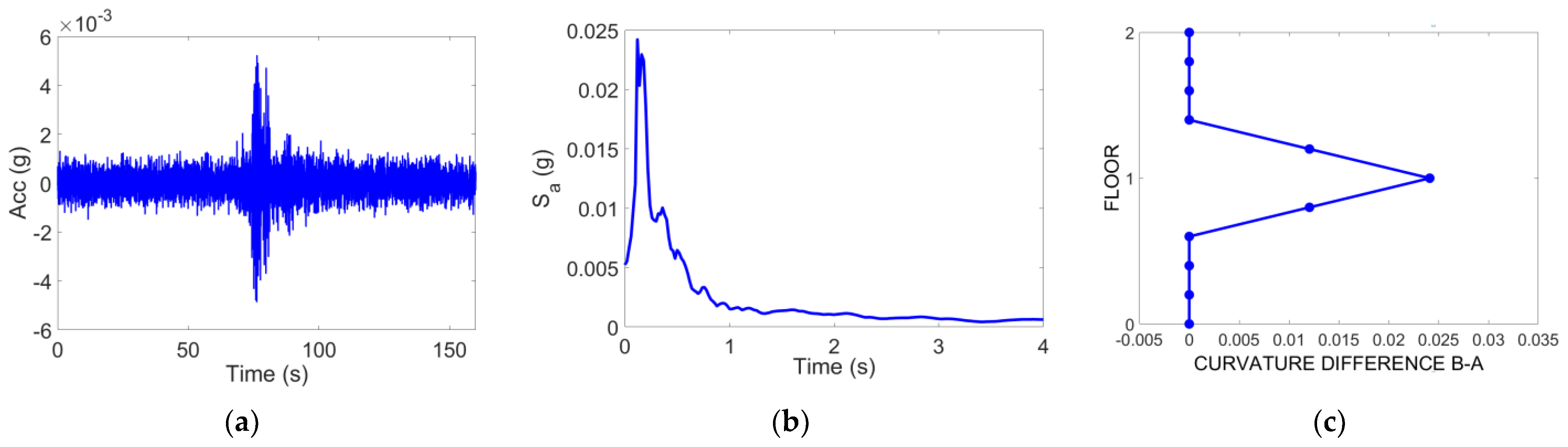

| 3-Story Model | 5-Story Model | 5-Story Model with Infill Panel | 8-Story Model | 5-Story Model Irregular in Plan | |
|---|---|---|---|---|---|
| T (s) | 0.65 | 0.84 | 0.51 | 1.50 | 1.28 |
| Performance Level | Inter-Story Drift (%) |
|---|---|
| Fully Operational (FO) | 0.2 |
| Operational (DC) | 0.5 |
| Life Safety (LS) | 1.5 |
| Near Collapse (NC) | 2.5 |
| N. Event | Date (dd/mm/yyyy) | Time (UTC) | Magnitude (ML) |
|---|---|---|---|
| 1 | 8 April 2009 | 22:59 | 4.3 |
| 2 | 9 April 2009 | 00:53 | 5.1 |
| 3 | 9 April 2009 | 02:34 | 3.1 |
| 4 | 9 April 2009 | 03:14 | 4.2 |
| 5 | 9 April 2009 | 04:32 | 4.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ditommaso, R.; Iacovino, C.; Auletta, G.; Parolai, S.; Ponzo, F.C. Damage Detection and Localization on Real Structures Subjected to Strong Motion Earthquakes Using the Curvature Evolution Method: The Navelli (Italy) Case Study. Appl. Sci. 2021, 11, 6496. https://doi.org/10.3390/app11146496
Ditommaso R, Iacovino C, Auletta G, Parolai S, Ponzo FC. Damage Detection and Localization on Real Structures Subjected to Strong Motion Earthquakes Using the Curvature Evolution Method: The Navelli (Italy) Case Study. Applied Sciences. 2021; 11(14):6496. https://doi.org/10.3390/app11146496
Chicago/Turabian StyleDitommaso, Rocco, Chiara Iacovino, Gianluca Auletta, Stefano Parolai, and Felice Carlo Ponzo. 2021. "Damage Detection and Localization on Real Structures Subjected to Strong Motion Earthquakes Using the Curvature Evolution Method: The Navelli (Italy) Case Study" Applied Sciences 11, no. 14: 6496. https://doi.org/10.3390/app11146496
APA StyleDitommaso, R., Iacovino, C., Auletta, G., Parolai, S., & Ponzo, F. C. (2021). Damage Detection and Localization on Real Structures Subjected to Strong Motion Earthquakes Using the Curvature Evolution Method: The Navelli (Italy) Case Study. Applied Sciences, 11(14), 6496. https://doi.org/10.3390/app11146496








