Dynamical Analysis of Biological Signals with the 0–1 Test: A Case Study of the PhotoPlethysmoGraphic (PPG) Signal
Abstract
:1. Introduction
2. 0–1 Test Description
3. Method and Materials
3.1. 0–1 Test Algorithm
- 1.
- Equation (1) is solved for a given .
- 2.
- 3.
- The asymptotic growth rate of , makes it possible to distinguish between regular behavior and chaotic behavior. There are two suggested methods for determining : regression method and correlation method. However, the correlation method provides better results than the regression method, according to the analyses carried out, for different dynamic systems, by Gottwald and Melbourne [32]. In our study, we have used both types of methods, and we have verified that the correlation method yields better results.
- 4.
- Steps 1 to 3 are repeated for several values of c; with 100 c values, selected randomly, it is enough [32], to ensure a higher degree of convergence of the statistic. The final result, K, attends to the median of the computed values, that is, . In this study, we introduce a slight modification to the original method, our modified version of the test, taking the median of the absolute value of the calculated values, after removing outliers values, i.e., , since the interest is focused not so much on the numerical values as on the strength of the correlation. It also enables us to identify intermediate dynamics, as we shall see below.
3.2. Reference Signals
3.2.1. Periodic
3.2.2. Quasi-Periodic
3.2.3. Aperiodic
3.2.4. Chaotic
3.2.5. Random
3.3. Biological Signal
PPG Signal
4. Results and Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Appendix A. Accompanying Material

References
- Seely, A.J.E.; Macklem, P. Fractal variability: An emergent property of complex dissipative systems. Chaos Interdiscip. J. Nonlinear Sci. 2012, 22, 013108. [Google Scholar] [CrossRef]
- Hertzman, A.B. Photoelectric Plethysmography of the Fingers and Toes in Man. Exp. Biol. Med. 1937, 37, 529–534. [Google Scholar] [CrossRef]
- Murray, W.B.; Foster, P.A. The peripheral pulse wave: Information overlooked. J. Clin. Monit. 1996, 12, 365–377. [Google Scholar] [CrossRef] [PubMed]
- Goh, C.H.; Tan, L.K.; Lovell, N.H.; Ng, S.C.; Tan, M.P.; Lim, E. Robust PPG motion artifact detection using a 1-D convolution neural network. Comput. Methods Programs Biomed. 2020, 196, 105596. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.H.; Li, R.X.; Wang, J.J.; Chen, W.; Su, C.H. Classification of Photoplethysmographic Signal Quality with Deep Convolution Neural Networks for Accurate Measurement of Cardiac Stroke Volume. Appl. Sci. 2020, 10, 4612. [Google Scholar] [CrossRef]
- Cannesson, M.; Talke, P. Recent advances in pulse oximetry. F1000 Med. Rep. 2009, 1. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, J.; Kim, M.; Park, H.K.; Kim, I.Y. Motion Artifact Reduction in Wearable Photoplethysmography Based on Multi-Channel Sensors with Multiple Wavelengths. Sensors 2020, 20, 1493. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Seok, D.; Lee, S.; Kim, M.; Cho, J.; Kim, C. Motion Artifact Removal Techniques for Wearable EEG and PPG Sensor Systems. Front. Electron. 2021, 2. [Google Scholar] [CrossRef]
- Kim, B.; Yoo, S. Motion Artifact Reduction in Photoplethysmography Using Independent Component Analysis. IEEE Trans. Biomed. Eng. 2006, 53, 566–568. [Google Scholar] [CrossRef]
- Hanyu, S.; Xiaohui, C. Motion artifact detection and reduction in PPG signals based on statistics analysis. In Proceedings of the IEEE 2017 29th Chinese Control And Decision Conference (CCDC), Chongqing, China, 28–30 May 2017. [Google Scholar] [CrossRef]
- Majeed, I.A.; Jos, S.; Arora, R.; Choi, K.; Bae, S. Motion Artifact Removal of Photoplethysmogram (PPG) Signal. In Proceedings of the 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019. [Google Scholar] [CrossRef]
- Pollreisz, D.; TaheriNejad, N. Detection and Removal of Motion Artifacts in PPG Signals. Mob. Netw. Appl. 2019. [Google Scholar] [CrossRef] [Green Version]
- Tamura, T. Current progress of photoplethysmography and SPO2 for health monitoring. Biomed. Eng. Lett. 2019, 9, 21–36. [Google Scholar] [CrossRef]
- Islam, T.T.; Ahmed, M.S.; Hassanuzzaman, M.; Amir, S.A.B.; Rahman, T. Blood Glucose Level Regression for Smartphone PPG Signals Using Machine Learning. Appl. Sci. 2021, 11, 618. [Google Scholar] [CrossRef]
- Cosoli, G.; Iadarola, G.; Poli, A.; Spinsante, S. Learning classifiers for analysis of Blood Volume Pulse signals in IoT-enabled systems. In Proceedings of the 2021 IEEE International Workshop on Metrology for Industry 4.0 & IoT, Roma, Italy, 7–9 June 2021. [Google Scholar]
- Cosoli, G.; Scalise, L.; Poli, A.; Spinsante, S. Wearable devices as a valid support for diagnostic excellence: Lessons from a pandemic going forward. Health Technol. 2021, 11, 673–675. [Google Scholar] [CrossRef] [PubMed]
- Sprott, J.C. Chaos and Time-Series Analysis; Oxford University Press: New York, NY, USA, 2003. [Google Scholar]
- Kantz, H.; Schreiber, T. Nonlinear Time Series Analysis, 2nd ed.; Cambridge Nonlinear Science Series; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Tsonis, A.A. Chaos: From Theory to Applications; Springer: New York, NY, USA, 2012. [Google Scholar]
- Toker, D.; Sommer, F.T.; D’Esposito, M. A simple method for detecting chaos in nature. Commun. Biol. 2020, 3. [Google Scholar] [CrossRef] [Green Version]
- Bhattacharya, J.; Kanjilal, P.P.; Muralidhar, V. Analysis and characterization of photo-plethysmographic signal. IEEE Trans. Biomed. Eng. 2001, 48, 5–11. [Google Scholar] [CrossRef] [PubMed]
- Martin-Martinez, D.; de-la Higuera, P.C.; Martin-Fernandez, M.; Alberola-Lopez, C. Stochastic Modeling of the PPG Signal: A Synthesis-by-Analysis Approach With Applications. IEEE Trans. Biomed. Eng. 2013, 60, 2432–2441. [Google Scholar] [CrossRef]
- Sviridova, N.; Zhao, T.; Aihara, K.; Nakamura, K.; Nakano, A. Photoplethysmogram at green light: Where does chaos arise from? Chaos Solitons Fractals 2018, 116, 157–165. [Google Scholar] [CrossRef]
- Gottwald, G.A.; Melbourne, I. A new test for chaos in deterministic systems. Proc. R. Soc. A Math. Phys. Eng. Sci. 2004, 460, 603–611. [Google Scholar] [CrossRef] [Green Version]
- de Pedro-Carracedo, J.; Fuentes-Jimenez, D.; Ugena, A.M.; Gonzalez-Marcos, A.P. Phase Space Reconstruction from a Biological Time Series: A Photoplethysmographic Signal Case Study. Appl. Sci. 2020, 10, 1430. [Google Scholar] [CrossRef] [Green Version]
- Czegledy, F.; Katz, J. Biological systems: Stochastic, deterministic or both. Open Syst. Inf. Dyn. 1995, 3, 179–188. [Google Scholar] [CrossRef]
- Aguiló, J.; Ferrer-Salvans, P.; García-Rozo, A.; Armario, A.; Corbi, A.; Cambra, F.J.; Bailón, R.; González-Marcos, A.; Caja, G.; Aguiló, S.; et al. Project ES3: Attempting to quantify and measure the level of stress. Rev. Neurol. 2015, 61, 405–415. [Google Scholar]
- Arza, A.; Garzón-Rey, J.M.; Lázaro, J.; Gil, E.; López-Antón, R.; de la Cámara, C.; Laguna, P.; Bailón, R.; Aguiló, J. Measuring acute stress response through physiological signals: Towards a quantitative assessment of stress. Med. Biol. Eng. Comput. 2018, 57, 271–287. [Google Scholar] [CrossRef] [Green Version]
- Gottwald, G.A.; Melbourne, I. Testing for chaos in deterministic systems with noise. Phys. D Nonlinear Phenom. 2005, 212, 100–110. [Google Scholar] [CrossRef] [Green Version]
- Gottwald, G.A.; Melbourne, I. Comment on “Reliability of the 0–1 test for chaos”. Phys. Rev. E 2008, 77. [Google Scholar] [CrossRef] [Green Version]
- Skokos, C.; Gottwald, G.A.; Laskar, J. Chaos Detection and Predictability; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Gottwald, G.A.; Melbourne, I. On the validity of the 0–1 test for chaos. Nonlinearity 2009, 22, 1367–1382. [Google Scholar] [CrossRef]
- Grassberger, P. Toward a quantitative theory of self-generated complexity. Int. J. Theor. Phys. 1986, 25, 907–938. [Google Scholar] [CrossRef]
- Badii, R.; Politi, A.; Remo, B. Complexity; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Fluid Mechanics, 2nd ed.; Pergamon Press: Oxford, UK, 1987. [Google Scholar]
- Enderle, J.; Bronzino, J. Introduction to Biomedical Engineering, 3rd ed.; Biomedical Engineering; Elsevier Science: Burlington, MA, USA, 2011. [Google Scholar]
- Chen, M.; Zhu, Q.; Wu, M.; Wang, Q. Modulation Model of the Photoplethysmography Signal for Vital Sign Extraction. IEEE J. Biomed. Health Inform. 2021, 25, 969–977. [Google Scholar] [CrossRef]
- Mendes, J.J.A., Jr.; Vieira, M.E.M.; Pires, M.B.; Stevan, S.L., Jr. Sensor Fusion and Smart Sensor in Sports and Biomedical Applications. Sensors 2016, 16, 1569. [Google Scholar] [CrossRef] [PubMed]
- Allen, J. Photoplethysmography and its application in clinical physiological measurement. Physiol. Meas. 2007, 28, R1–R39. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Meredith, D.J.; Clifton, D.; Charlton, P.; Brooks, J.; Pugh, C.W.; Tarassenko, L. Photoplethysmographic derivation of respiratory rate: A review of relevant physiology. J. Med. Eng. Technol. 2011, 36, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Glass, L. Multistable spatiotemporal patterns of cardiac activity. Proc. Natl. Acad. Sci. USA 2005, 102, 10409–10410. [Google Scholar] [CrossRef] [Green Version]
- Goldberger, A.L. Giles F. Filley Lecture. Complex Systems. Proc. Am. Thorac. Soc. 2006, 3, 467–471. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wessel, N.; Riedl, M.; Kurths, J. Is the normal heart rate “chaotic” due to respiration? Chaos Interdiscip. J. Nonlinear Sci. 2009, 19, 028508. [Google Scholar] [CrossRef] [PubMed]
- Bartsch, R.P.; Schumann, A.Y.; Kantelhardt, J.W.; Penzel, T.; Ivanov, P.C. Phase transitions in physiologic coupling. Proc. Natl. Acad. Sci. USA 2012, 109, 10181–10186. [Google Scholar] [CrossRef] [Green Version]
- Khreis, S.; Ge, D.; Carrault, G. Estimation of Breathing Rate From the Photoplethysmography Using Respiratory Quality Indexes. In Proceedings of the 2018 Computing in Cardiology Conference (CinC), Maastricht, The Netherlands, 23–26 September 2018; Volume 45, pp. 1–4. [Google Scholar] [CrossRef]
- Pedro-Carracedo, J.D.; Fuentes-Jimenez, D.; Ugena, A.M.; Gonzalez-Marcos, A.P. Is the PPG Signal Chaotic? IEEE Access 2020, 8, 107700–107715. [Google Scholar] [CrossRef]
- Ram, M.R.; Madhav, K.V.; Krishna, E.H.; Komalla, N.R.; Reddy, K.A. A Novel Approach for Motion Artifact Reduction in PPG Signals Based on AS-LMS Adaptive Filter. IEEE Trans. Instrum. Meas. 2012, 61, 1445–1457. [Google Scholar] [CrossRef]
- Ganeshapillai, G.; Guttag, J. Real time reconstruction of quasiperiodic multi parameter physiological signals. EURASIP J. Adv. Signal Process. 2012, 2012. [Google Scholar] [CrossRef] [Green Version]
- Grebogi, C.; Ott, E.; Pelikan, S.; Yorke, J.A. Strange attractors that are not chaotic. Phys. D Nonlinear Phenom. 1984, 13, 261–268. [Google Scholar] [CrossRef]
- Brindley, J.; Kapitaniak, T. Existence and characterization of strange nonchaotic attractors in nonlinear systems. Chaos Solitons Fractals 1991, 1, 323–337. [Google Scholar] [CrossRef]
- Pikovsky, A.S.; Feudel, U. Characterizing strange nonchaotic attractors. Chaos Interdiscip. J. Nonlinear Sci. 1995, 5, 253–260. [Google Scholar] [CrossRef]
- Prasad, A.; Negi, S.S.; Ramaswamy, R. Strange Nonchaotic Attractors. Int. J. Bifurc. Chaos 2001, 11, 291–309. [Google Scholar] [CrossRef] [Green Version]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of biological signals. Phys. Rev. E 2005, 71, 021906. [Google Scholar] [CrossRef] [Green Version]
- Hurst, H.E. Long-Term Storage of Reservoirs: An Experimental Study. Trans. Am. Soc. Civ. Eng. 1951, 116, 770–799. [Google Scholar] [CrossRef]
- Zhou, T.; Moss, F.; Bulsara, A. Observation of a strange nonchaotic attractor in a multistable potential. Phys. Rev. A 1992, 45, 5394–5400. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ding, M.; Kelso, J.A.S. Phase-resetting map and the dynamics of quasi-periodically forced biological oscillators. Int. J. Bifurc. Chaos 1994, 4, 553–567. [Google Scholar] [CrossRef]
- de Pedro-Carracedo, J.; Fuentes-Jimenez, D.; Ugena, A.M.; Gonzalez-Marcos, A.P. Transcending conventional biometry frontiers: Diffusive Dynamics PPG Biometry. arXiv 2020, arXiv:2007.15060. [Google Scholar]



| Step 1: From Equation (1) | Resolve: and , ; |
Number of observations: N |
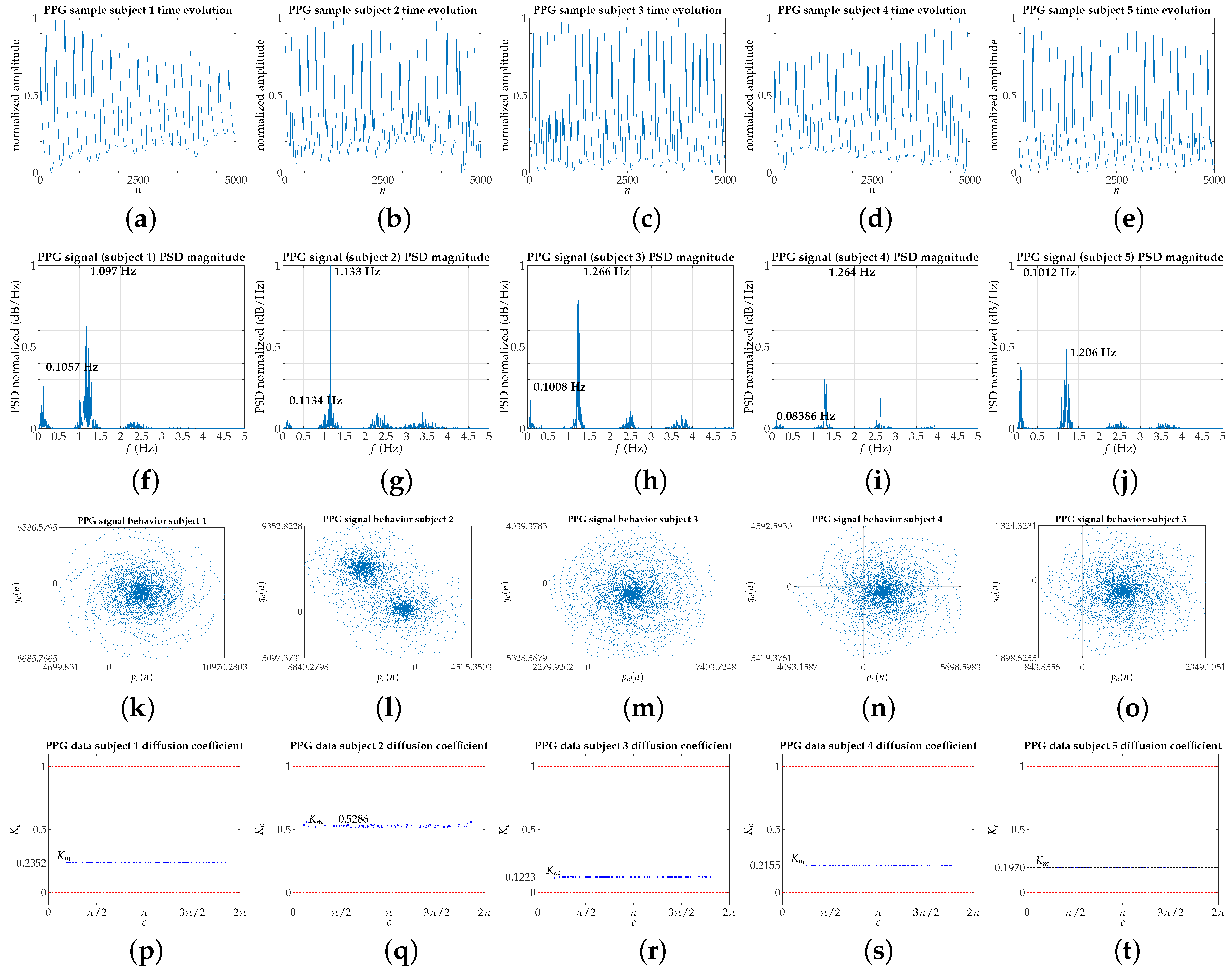
Plots: Figure 1k–o, Figure 2k–o |
| Step 2: Analyze the diffusive, or non-diffusive, behavior of and | The plot of this step is not relevant in this work | ||
| Step 3: Grown rate | Regression or correlation method | ||
| Step 4: Steps 1–3 must be executed for various values of c (randomly selected) | In practice, 100 choices of are sufficient; moreover, in our case, once outliers of have been removed |
Plots: Figure 1p–t, Figure 2p–t | |
| Evaluated Signal | Averaged (600,000 Points) | Averaged (150,000 Points) | Trend (up to 60,000 Points ) | ||
|---|---|---|---|---|---|
| subject number 1 (PPG1) | |||||
| subject number 2 (PPG2) | |||||
| subject number 3 (PPG3) | 0.1619 | ||||
| subject number 4 (PPG4) | |||||
| subject number 5 (PPG5) | |||||
| Evaluated Signal | Maximal Lyapunov Exponent (MLE) | Fractal Dimension |
|---|---|---|
| subject number 1 (PPG1) | ||
| subject number 2 (PPG2) | ||
| subject number 3 (PPG3) | ||
| subject number 4 (PPG4) | ||
| subject number 5 (PPG5) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Pedro-Carracedo, J.; Ugena, A.M.; Gonzalez-Marcos, A.P. Dynamical Analysis of Biological Signals with the 0–1 Test: A Case Study of the PhotoPlethysmoGraphic (PPG) Signal. Appl. Sci. 2021, 11, 6508. https://doi.org/10.3390/app11146508
de Pedro-Carracedo J, Ugena AM, Gonzalez-Marcos AP. Dynamical Analysis of Biological Signals with the 0–1 Test: A Case Study of the PhotoPlethysmoGraphic (PPG) Signal. Applied Sciences. 2021; 11(14):6508. https://doi.org/10.3390/app11146508
Chicago/Turabian Stylede Pedro-Carracedo, Javier, Ana María Ugena, and Ana Pilar Gonzalez-Marcos. 2021. "Dynamical Analysis of Biological Signals with the 0–1 Test: A Case Study of the PhotoPlethysmoGraphic (PPG) Signal" Applied Sciences 11, no. 14: 6508. https://doi.org/10.3390/app11146508
APA Stylede Pedro-Carracedo, J., Ugena, A. M., & Gonzalez-Marcos, A. P. (2021). Dynamical Analysis of Biological Signals with the 0–1 Test: A Case Study of the PhotoPlethysmoGraphic (PPG) Signal. Applied Sciences, 11(14), 6508. https://doi.org/10.3390/app11146508






