Vibration Error Correction for the FOGs-Based Measurement in a Drilling System Using an Extended Kalman Filter
Abstract
:1. Introduction
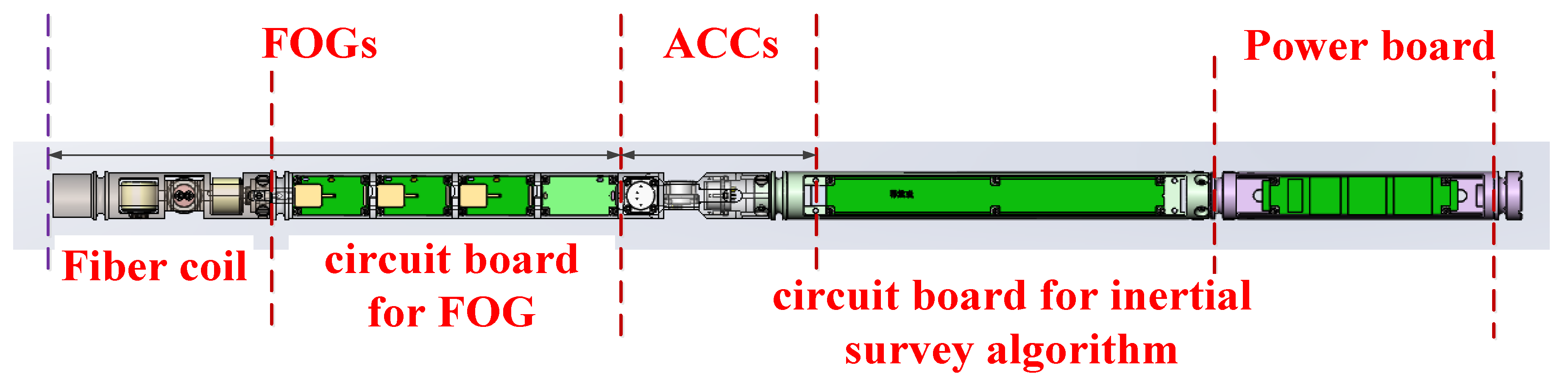
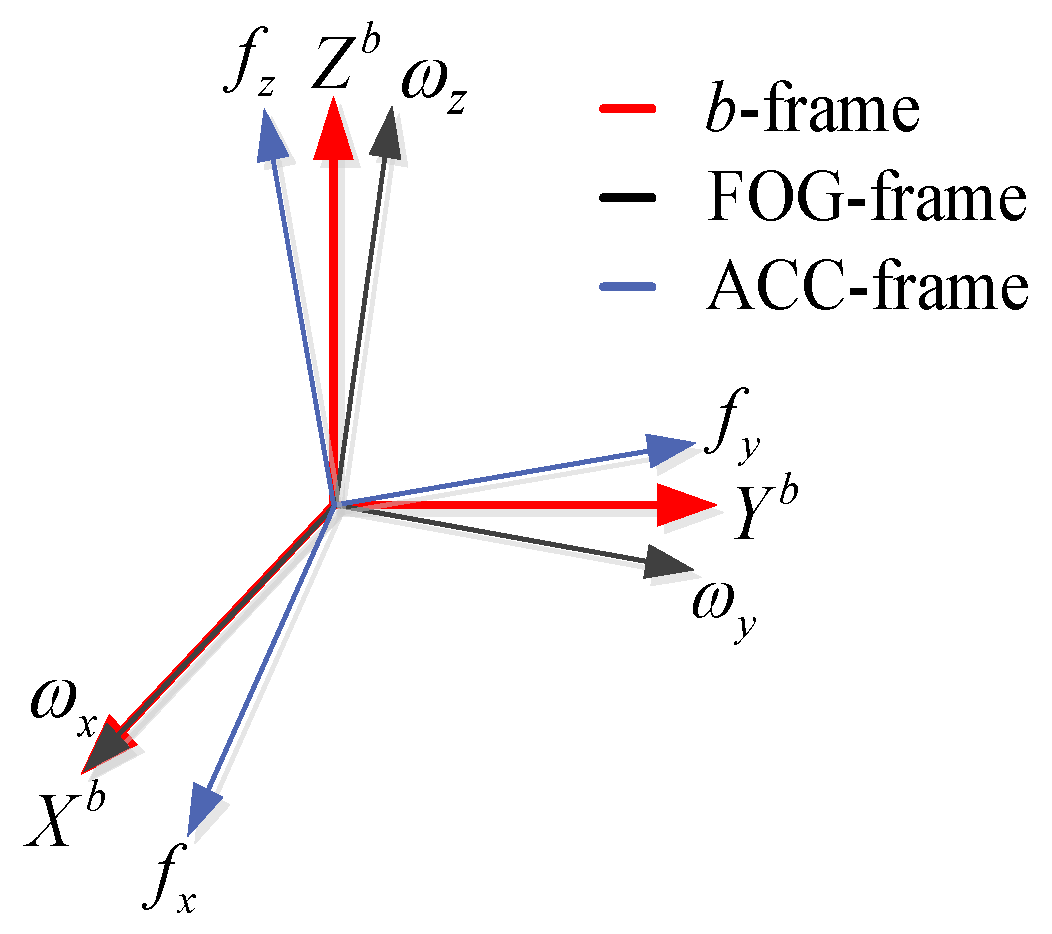
2. Principle of the FOG-Based MWD
3. Establish of the Nonlinear Error Model
4. Recognition of the Coefficient of the Vibration Error
4.1. The 36-Order EKF
4.2. Calibration Design
5. An Iterative Calibration Method
6. Simulation Experiment
6.1. Simulation Data
6.2. Simulation Results
7. Experiment
7.1. Calibration Experiment
7.2. Vibration Experiment
7.2.1. The Periodic Vibration
7.2.2. The Random Vibration
8. Discussion
8.1. Repeatability of Nonlinear Error
8.2. Error Terms Related to Acceleration in FOG
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Appendix A. The Estimated Results of the Bias Error for FOG-Based MWD

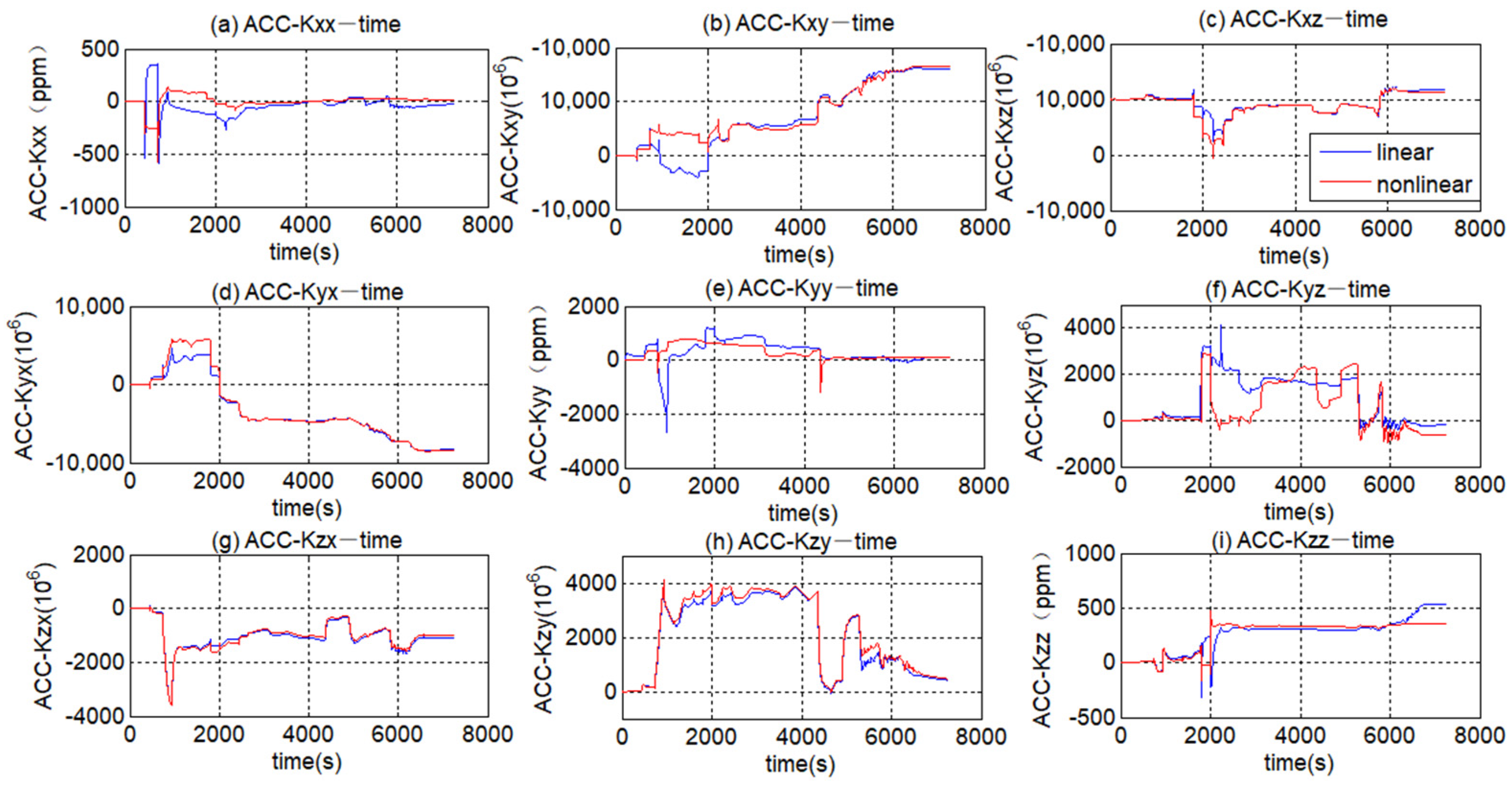
Appendix B. Estimated Results of the Scale Factor Error and Misalignment Error (ACCs)
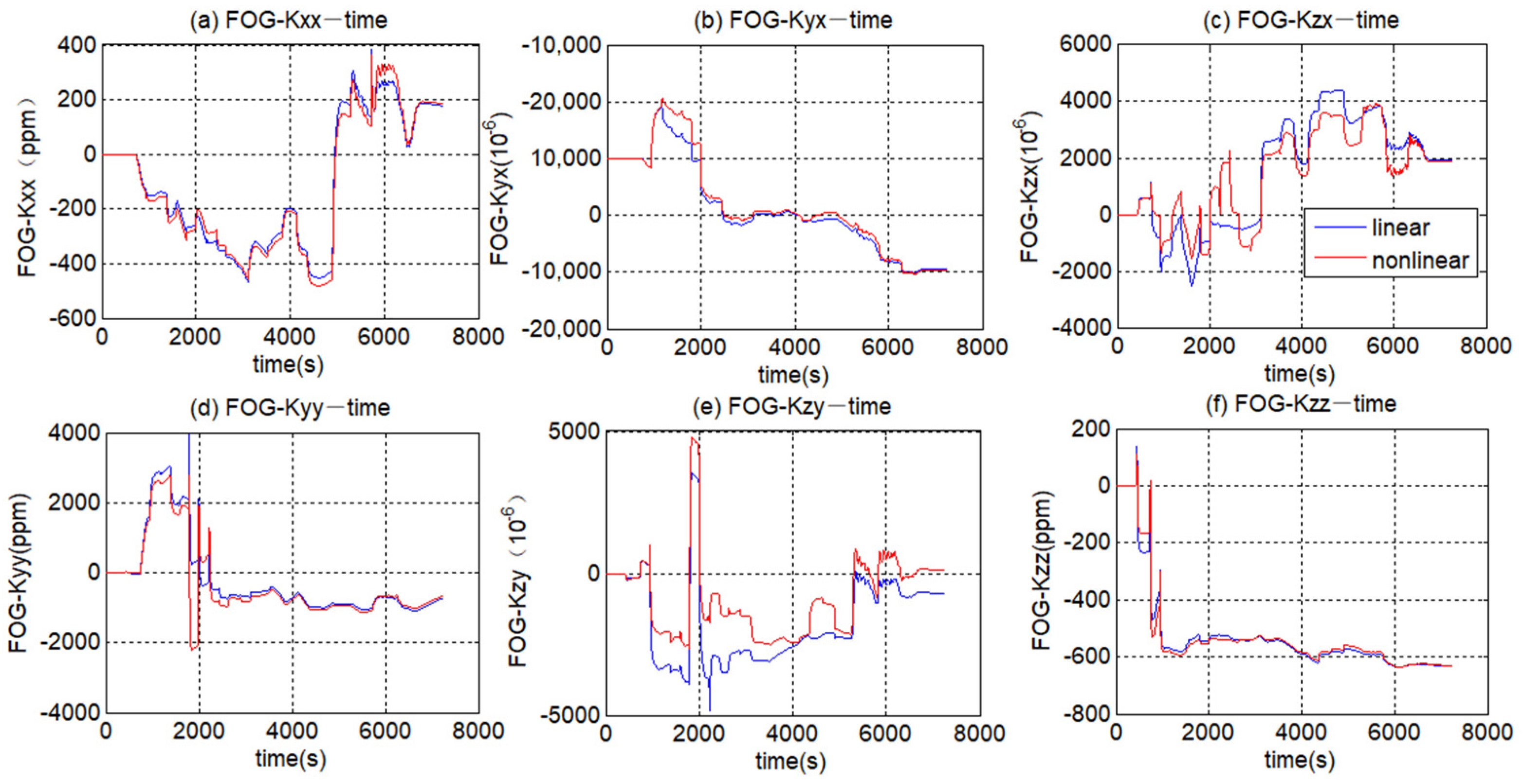
Appendix C. Estimated Results of the Scale Factor Error and Misalignment Error (FOGs)
References
- Qilong, X.; Ruihe, W.; Feng, S.; Leilei, H.; Laiju, H. Continuous Measurement-While-Drilling Utilizing Strap-Down Multi-Model Surveying System. IEEE Trans. Instrum. Meas. 2014, 63, 650–657. [Google Scholar] [CrossRef]
- Yang, Y.; Li, F.; Gao, Y.; Mao, Y. Multi-Sensor Combined Measurement While Drilling Based on the Improved Adaptive Fading Square Root Unscented Kalman Filter. Sensors 2020, 20, 1897. [Google Scholar] [CrossRef] [Green Version]
- ElGizawy, M.L. Continuous Measurement-While-Drilling Surveying System Utilizing MEMS Inertial Sensors; Department of Geomatics Engineering, University of Calgary: Calgary, AB, Canada, 2009. [Google Scholar]
- Silva, T.; Batista, P. Long baseline navigation filter with clock offset estimation. Nonlinear Dyn. 2020, 100, 2557–2573. [Google Scholar] [CrossRef]
- De Celis, R.; Cadarso, L. GNSS/IMU laser quadrant detector hybridization techniques for artillery rocket guidance. Nonlinear Dyn. 2018, 91, 2683–2698. [Google Scholar] [CrossRef]
- Dorveaux, E.; Vissiere, D.; Martin, A.-P.; Petit, N. Iterative calibration method for inertial and magnetic sensors. In Proceedings of the Joint 48h IEEE Conference on Decision and Control (CDC) and 28th Chinese Control Conference, Shanghai, China, 15–18 December 2009; pp. 8296–8303. [Google Scholar] [CrossRef] [Green Version]
- Lefevre, H.C. The fiber-optic gyroscope: Actually better than the ring-laser gyroscope? In Proceedings of the OFS2012 22nd International Conference on Optical Fiber Sensor, Beijing, China, 15–17 October 2012. [Google Scholar] [CrossRef]
- Noureldin, A.; Irvine-Halliday, D.; Mintchev, M.P. Accuracy limitations of fog-based continuous measurement-while-drilling surveying instruments for horizontal wells. IEEE Trans. Instrum. Meas. 2002, 51, 1177–1191. [Google Scholar] [CrossRef]
- Xu, X.; Gu, H.; Kan, Z.; Zhang, Y.; Cheng, J.; Li, Z. Properties of Drillstring Vibration Absorber for Rotary Drilling Rig. Arab. J. Sci. Eng. 2020, 45, 5849–5858. [Google Scholar] [CrossRef]
- Xue, Q.; Leung, H.; Huang, L.; Zhang, R.; Liu, B.; Wang, J.; Li, L. Modeling of torsional oscillation of drillstring dynamics. Nonlinear Dyn. 2019, 96, 267–283. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, C.; Lin, T.; Li, X.; Wang, T. Characterization of a fiber optic gyroscope in a measurement while drilling system with the dynamic Allan variance. Measurement 2015, 75, 263–272. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, C.; Gao, S.; Lin, T.; Li, X. Influence of linear vibration on the errors of three-axis FOGs in the measurement while drilling systems. Optik 2018, 156, 204–223. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, L.; Gao, S.; Lin, T.; Li, X. Vibration Noise Modeling for Measurement While Drilling System Based on FOGs. Sensors 2017, 17, 2367. [Google Scholar] [CrossRef] [Green Version]
- Volynskii, D.V.; Odintsov, A.A.; Dranitsyna, E.V.; Untilov, A.A. Calibration of fiber-optic gyros within strapdown inertial measurement units. Gyroscopy Navig. 2012, 3, 194–200. [Google Scholar] [CrossRef]
- Dzhashitov, V.E.; Pankratov, V.M.; Barulina, M.A. Mathematical models of thermal stress-strain state and scale factor error of fiber optic gyro sensors. J. Mach. Manuf. Reliab. 2013, 42, 124–131. [Google Scholar] [CrossRef]
- Nikolaev, S.; Golota, A.; Ivshina, I. Identification modeling of inertial sensors’ parameters of strapdown inertial navigation systems. In Proceedings of the 2nd International Ural Conference on Measurements (UralCon), Chelyabinsk, Russia, 16–19 October 2017; pp. 149–155. [Google Scholar] [CrossRef]
- IEEE Recommended Practice for Precision Centrifuge Testing of Linear Accelerometers. In IEEE Std 836-2001; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2001; pp. 1–96. [CrossRef]
- Ren, S.-Q.; Liu, Q.-B.; Zeng, M.; Wang, C.-H. Calibration Method of Accelerometer’s High-Order Error Model Coefficients on Precision Centrifuge. IEEE Trans. Instrum. Meas. 2019, 69, 2277–2286. [Google Scholar] [CrossRef]
- Kau, D.S.; Boutelle, J.; Lawdermilt, L. Accelerometer input axis angular acceleration sensitivity. IEEE Aerosp. Electron. Syst. Mag. 2005, 14, 449–456. [Google Scholar] [CrossRef]
- Wang, S.; Ren, S. Calibration of cross quadratic term of gyro accelerometer on centrifuge and error analysis. Aerosp. Sci. Technol. 2015, 43, 30–36. [Google Scholar] [CrossRef]
- Einicke, G.A.; White, L.B. Robust extended Kalman filtering. IEEE Trans. Signal Process. 1999, 47, 2596–2599. [Google Scholar] [CrossRef]
- Schwarz, K.P.; Wei, M. INS/GPS Integration for Geodetic Applications; Lecture Notes of ENGO 623; Department of Geomatics Engineering at the University of Calgary: Calgary, AB, Canada, 1999. [Google Scholar]
- Peng, H.; Zhi, X.; Wang, R.; Liu, J.; Zhang, C. A new dynamic calibration method for IMU deterministic errors of the INS on the Hypersonic Cruise Vehicles. Aerosp. Sci. Technol. 2014, 32, 121–130. [Google Scholar] [CrossRef]
- Yu, Z. Design and implementation of linear error modelling in a wireless inertial localization system. In Proceedings of the 2014 Asia-Pacific Conference on Computer Aided System Engineering (APCASE), South Kuta, Indonesia, 10–12 February 2014; pp. 71–75. [Google Scholar] [CrossRef]
- Yu, H.; Lv, X.; Tang, J.; Wei, G.; Wang, Y.; Rao, G. Establishment and analysis of high-order error model of laser gyro SINS. Infrared Laser Eng. 2013, 42, 2375–2379. [Google Scholar]
- Li, B.G.; Lu, J.Z.; Xiao, W.H.; Lin, T. In-field fast calibration of FOG-based MWD IMU for horizontal drilling. Meas. Sci. Technol. 2015, 26, 7. [Google Scholar] [CrossRef]
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef] [Green Version]
- Jiang, C.; Wang, S.; Wu, B.; Fernandez, C.; Xiong, X.; Coffie-Ken, J. A state-of-charge estimation method of the power lithium-ion battery in complex conditions based on adaptive square root extended Kalman filter. Energy 2021, 219, 119603. [Google Scholar] [CrossRef]
- Gustafsson, F.; Hendeby, G. Some Relations Between Extended and Unscented Kalman Filters. IEEE Trans. Signal Process. 2012, 60, 545–555. [Google Scholar] [CrossRef] [Green Version]
- Chao, D.; Zhuang, Y.; El-Sheimy, N. An Innovative MEMS-Based MWD Method for Directional Drilling. In Proceedings of the SPE/CSUR Unconventional Resources Conference, Calgary, AB, Canada, 20–22 October 2015. [Google Scholar] [CrossRef]
- Wang, W.; Liu, Z.-Y.; Xie, R.-R. Quadratic extended Kalman filter approach for GPS/INS integration. Aerosp. Sci. Technol. 2006, 10, 709–713. [Google Scholar] [CrossRef]
- Zhang, X.; Mu, X.; Liu, H.; He, B.; Yan, T. Application of Modified EKF Based on Intelligent Data Fusion in AUV Navigation. In Proceedings of the 2019 IEEE Underwater Technology Conference, Kaohsiung, Taiwan, 16–19 April 2019. [Google Scholar] [CrossRef]
- Ribas, D.; Ridao, P.; Carreras, M.; Cufi, X. An EKF vision-based navigation of an UUV in a structured environment. IFAC Proc. Vol. 2003, 36, 287–292. [Google Scholar] [CrossRef]
- IEEE Standard for Inertial Systems Terminology. In IEEE Std 1559-2009; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2009; pp. 1–30. [CrossRef]

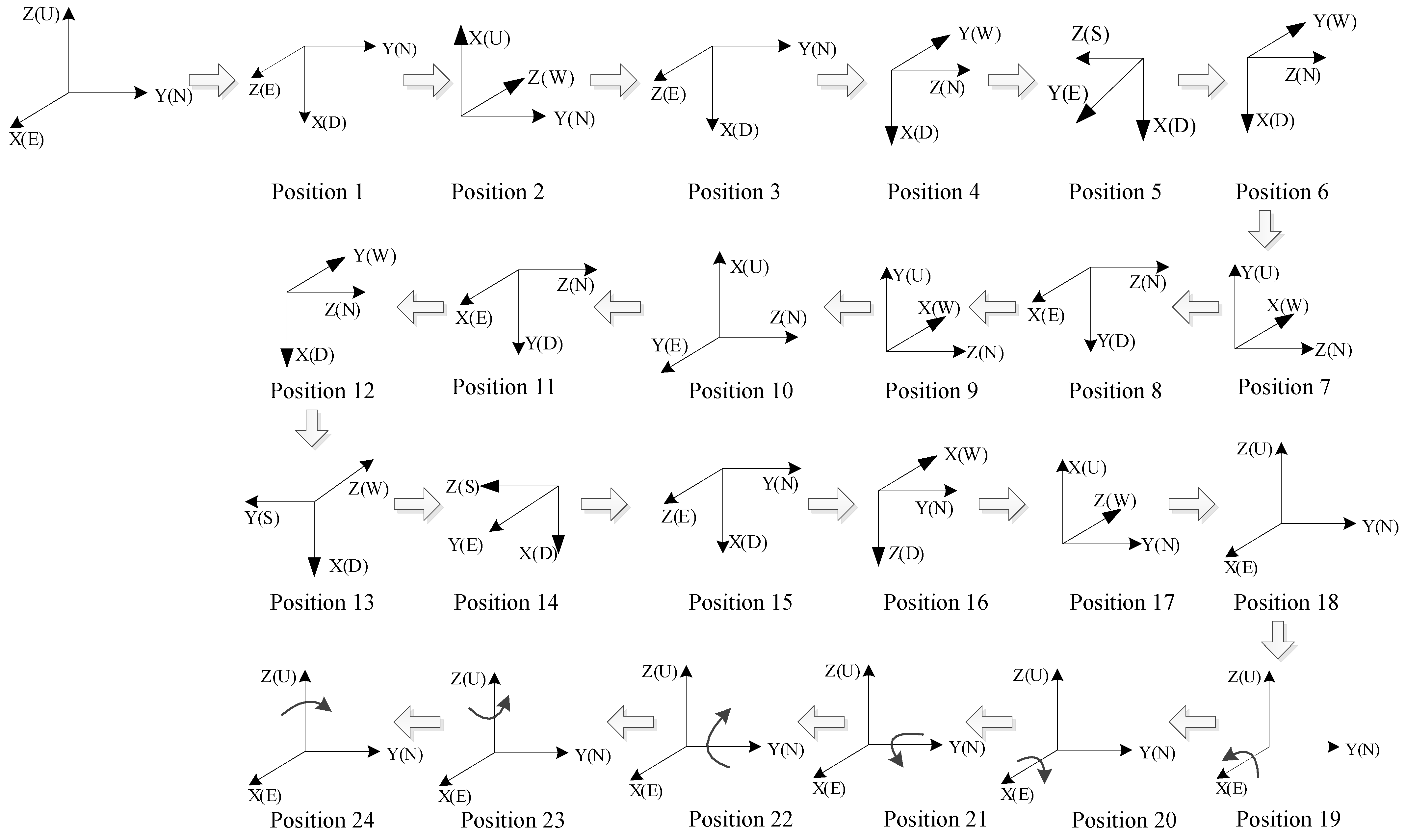
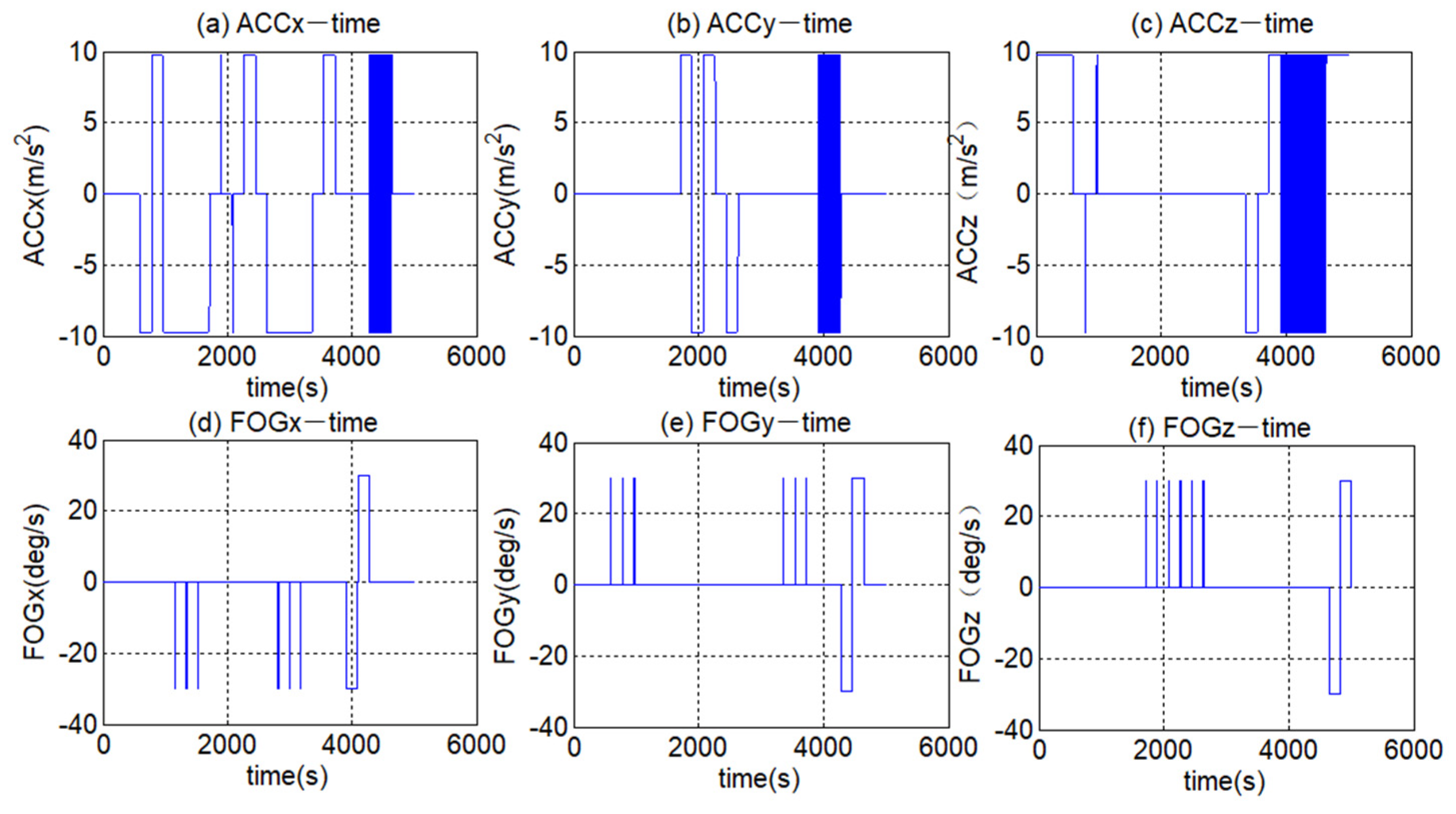






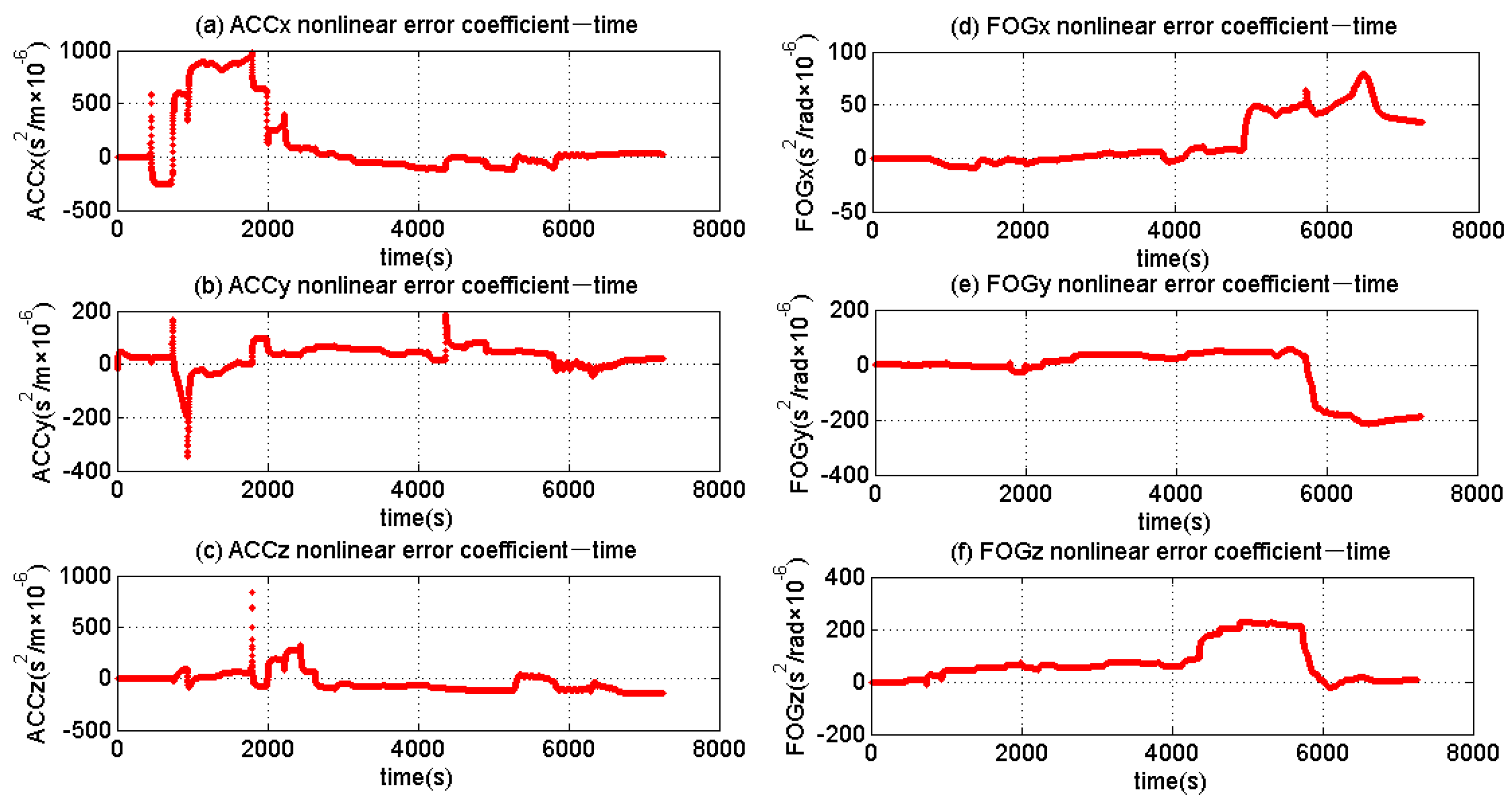



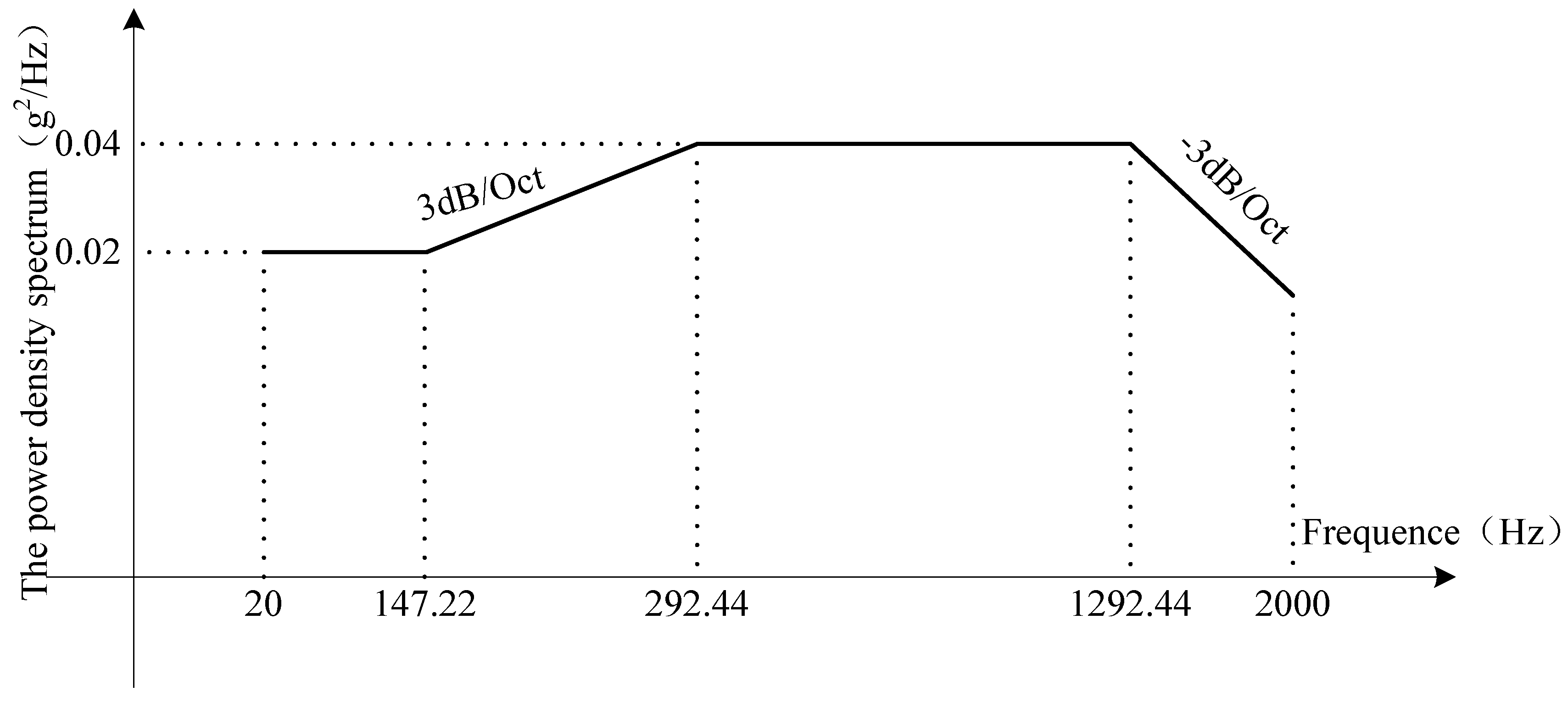
| Number | Transfer Process | Keep Time after Transfer (s) | Number | Transfer Process | Keep Time after Transfer (s) |
|---|---|---|---|---|---|
| 0 | Static | 0~600 | / | / | / |
| 1 | Rotate Y-axis by +90° | 603~783 | 13 | Rotate X-axis by −90° | 2817~2997 |
| 2 | Rotate Y-axis by +180° | 789~969 | 14 | Rotate X-axis by −90° | 3000~3180 |
| 3 | Rotate Y-axis by +180° | 975~1155 | 15 | Rotate X-axis by −90° | 3183~3363 |
| 4 | Rotate X-axis by −90° | 1158~1338 | 16 | Rotate Y-axis by +90° | 3366~3546 |
| 5 | Rotate X-axis by −180° | 1344~1524 | 17 | Rotate Y-axis by +90° | 3549~3729 |
| 6 | Rotate X-axis by −180° | 1530~1710 | 18 | Rotate Y-axis by +90° | 3732~3912 |
| 7 | Rotate Z-axis by +90° | 1713~1893 | 19 | Keep rotating X-axis at +30°/s | 3912s~4092 |
| 8 | Rotate Z-axis by +180° | 1899~2079 | 20 | Keep rotating X-axis at −30°/s | 4095~4275 |
| 9 | Rotate Z-axis by +180° | 2085~2265 | 21 | Keep rotating X-axis at +30°/s | 4278~4458 |
| 10 | Rotate Z-axis by +90° | 2268~2448 | 22 | Keep rotating X-axis at −30°/s | 4461~4641 |
| 11 | Rotate Z-axis by +90° | 2451~2631 | 23 | Keep rotating X-axis at +30°/s | 4644~5004 |
| 12 | Rotate Z-axis by +90° | 2634~2814 | 24 | Keep rotating X-axis at −30°/s | 5034~5394 |
| Error Item | Symbol | Value | Error Item | Symbol | Value |
|---|---|---|---|---|---|
| FOG Bias error | Bgx = Bgy = Bgz | 0.02°/h | ACC Misalignment error | Kaxy = Kaxz = Kayx = Kayz = Kazx = Kazy | 10 × 10−6 rad |
| ACC Bias error | Bax = Bay = Baz | 100 × 10−6 g | FOG Random noise | The mean is zero and the standard deviation is 0.02°/h | |
| FOG scale factor error | Kgxx = Kgyy = Kgzz | 50 × 10−6 | ACC Random noise | The mean is zero and the standard deviation is 50 × 10−6 g | |
| ACC scale factor error | Kaxx = Kayy = Kazz | 100 × 10−6 | FOG Nonlinear error | dgx = dgy = dgz | 10 × 10−6 s/rad |
| FOG Misalignment error | Kgyx = Kgzx = Kgzy | 10 × 10−6 rad | ACC Nonlinear error | dax = day = daz | 10 × 10−6 s2/m |
| Error Item | True Value | Linear EKF | Nonlinear EKF | |||
|---|---|---|---|---|---|---|
| Results | Relative Error | Results | Relative Error | |||
| Bias error of FOGs (°/h) | Bgx | 0.02 | 0.2867 | 1333.50% | 0.0199 | −0.50% |
| Bgy | 0.02 | \ | \ | 0.0200 | 0 | |
| Bgz | 0.02 | \ | \ | 0.0197 | −1.50% | |
| Bias error of ACCs (μg) | Bax | 100 | 133.3151 | 33.32% | 99.8489 | −0.15% |
| Bay | 100 | 153.9846 | 53.98% | 99.7889 | −0.21% | |
| Baz | 100 | \ | \ | 99.8027 | −0.20% | |
| Scale factor of FOGs (ppm) | Kgxx | 50 | 47.6136 | −4.77% | 45.4885 | −9.02% |
| Kgyy | 50 | 45.0199 | −9.96% | 45.4232 | −9.15% | |
| Kgzz | 50 | \ | \ | 45.4936 | −9.01% | |
| Misalignment error of FOGs (μrad) | Kgyx | −50 | \ | \ | −49.6124 | −0.78% |
| Kgzx | 50 | \ | \ | 50.2019 | 0.40% | |
| Kgzy | −50 | \ | \ | −50.9442 | 1.89% | |
| Scale factor of ACCs (ppm) | Kaxx | 100 | 69.7489 | 30.25% | 115.5479 | 15.55% |
| Kayy | 100 | 96.5638 | 3.44% | 115.1622 | 15.16% | |
| Kazz | 100 | \ | \ | 114.9464 | 14.95% | |
| Misalignment error of ACCs (μrad) | Kayx | −100 | \ | \ | −99.2220 | −0.78% |
| Kazx | 100 | \ | \ | 100.4671 | 0.47% | |
| Kaxy | 100 | \ | \ | 99.9669 | −0.03% | |
| Kazy | −100 | \ | \ | −100.4243 | 0.42% | |
| Kaxz | −100 | \ | \ | −99.8454 | −0.15% | |
| Kayz | 100 | 95.4444 | 4.56% | 100.5597 | 0.56% | |
| Nonlinear error of FOGs (10−6 s/rad) | dgx | 10 | \ | \ | 9.9872 | −0.13% |
| dgy | 10 | \ | \ | 10.0211 | 0.21% | |
| dgz | 10 | \ | \ | 10.3901 | 3.90% | |
| Nonlinear error of ACCs (10−6 s/m2) | dax | 10 | \ | \ | 10.05221 | 0.52% |
| day | 10 | \ | \ | 10.03140 | 0.31% | |
| daz | 10 | \ | \ | 10.0589 | 0.59% | |
| Items | Parameters |
|---|---|
| Size of mounting surface | Φ500 mm |
| Flatness of mounting surface | 0.02 mm |
| Biaxial inclination turning error | ≤±5″ |
| Non-perpendicularity of the two axes | ≤±5″ |
| Angular resolution | 0.0001° |
| Angular measurement accuracy | ±5″ |
| Angular Measurement repeatability | ±1″ |
| Range of Angular rate | 0.01°/s~360°/s |
| Error Item | Original Data | Compensated the Linear Errors | Compensated the Linear and Nonlinear Errors | ||
|---|---|---|---|---|---|
| Error | The Ratio of Error Reduction | Error | The Ratio of Error Reduction | ||
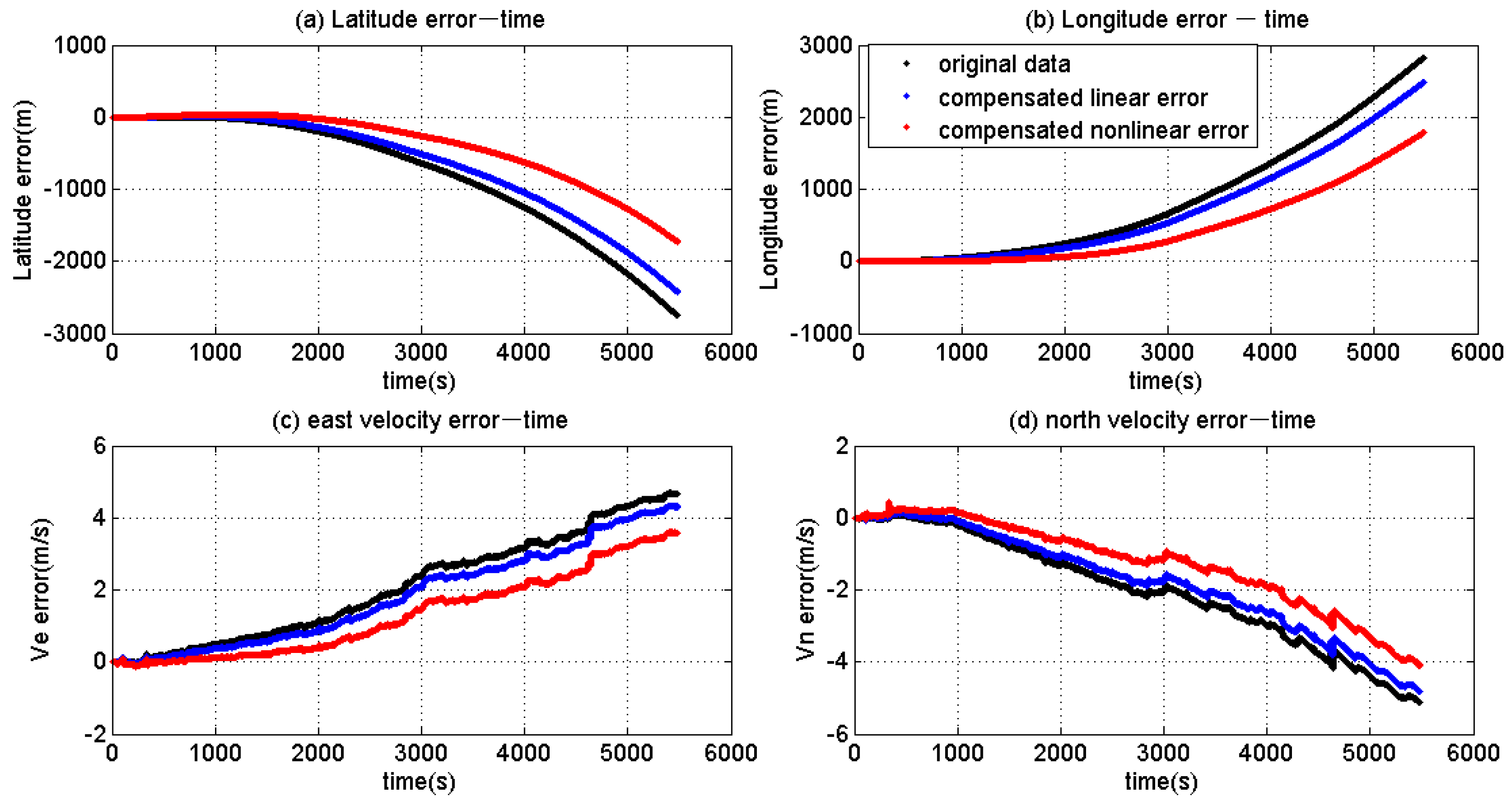
| Latitude error (m) | 86,500 | 56,700 | 34.45% | 2402 | 97.22% |
| Longitude error (m) | 62,200 | 53,800 | 13.50% | 4089 | 93.42% |
| East velocity error (m/s) | 27.72 | 24.56 | 11.40% | 15.40 | 44.44% |
| North velocity error (m/s) | 34.54 | 21.88 | 36.65% | 6.72 | 80.54% |
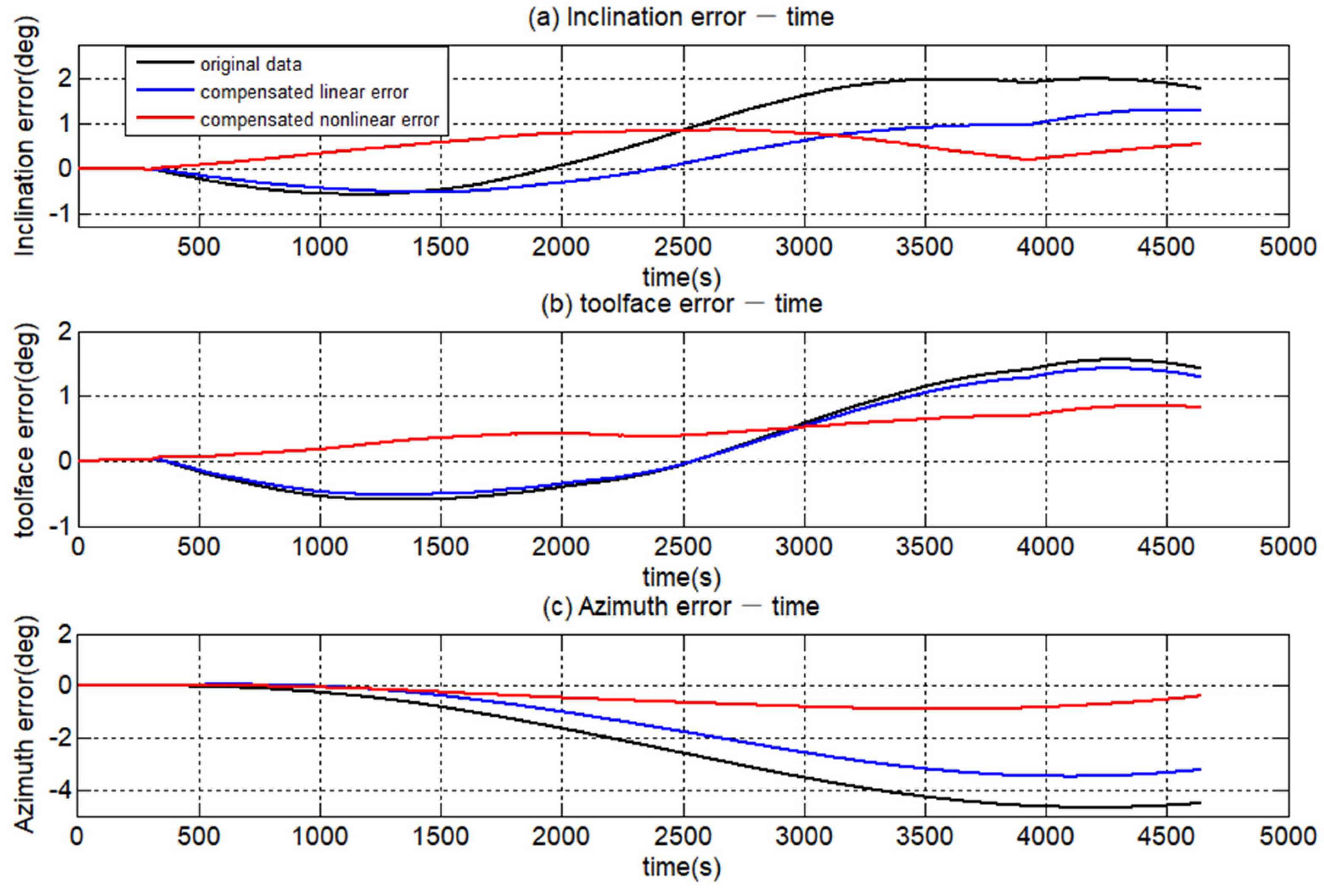
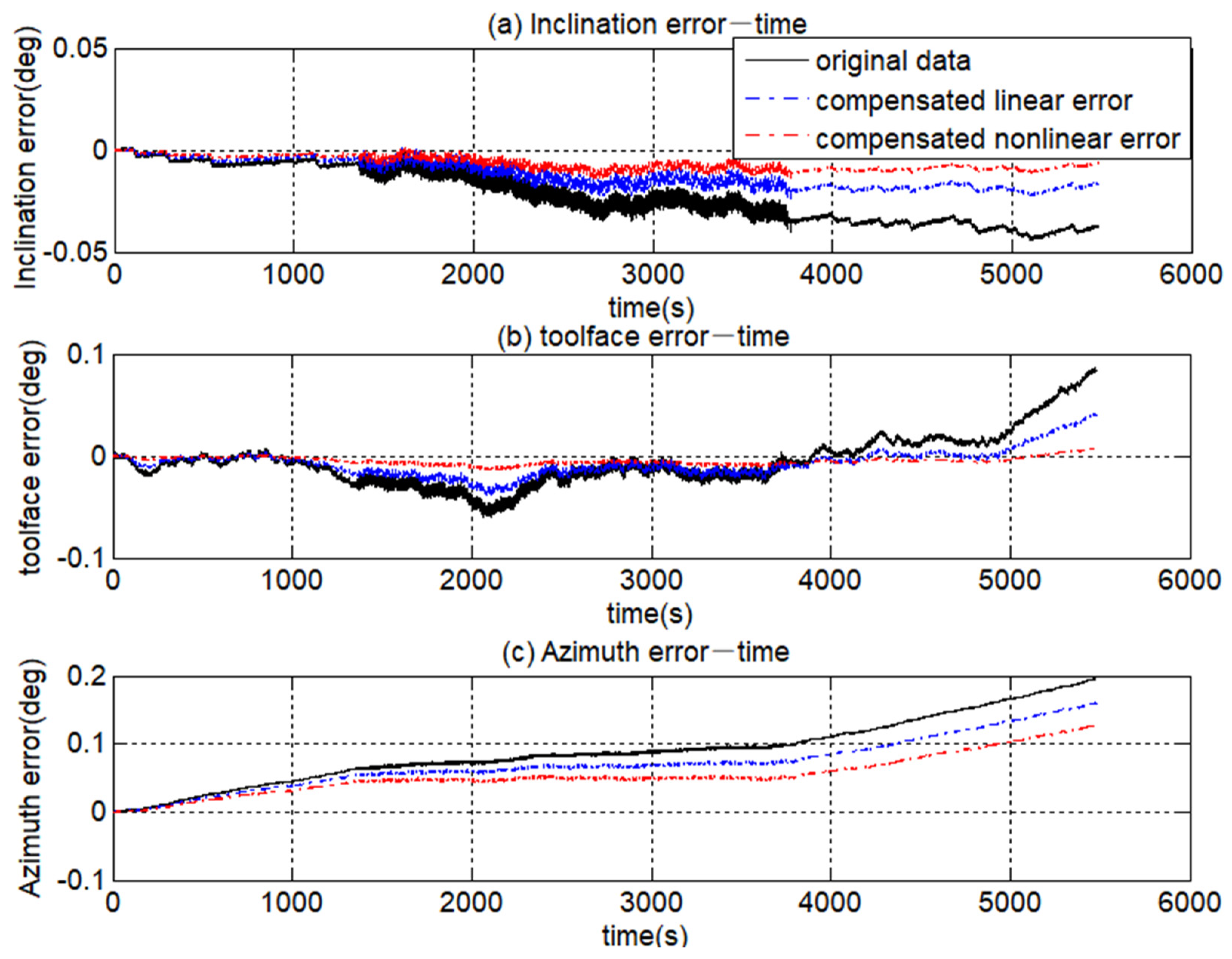
| Inclination (°) | 1.77 | 1.29 | 27.61% | 0.55 | 69.13% |
| Toolface angle (°) | 1.42 | 1.28 | 11.72% | 0.81 | 44.13% |
| azimuth (°) | 4.53 | 3.23 | 28.79% | 0.42 | 90.74% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Hu, Y.; Wang, T.; Liu, B. Vibration Error Correction for the FOGs-Based Measurement in a Drilling System Using an Extended Kalman Filter. Appl. Sci. 2021, 11, 6514. https://doi.org/10.3390/app11146514
Wang L, Hu Y, Wang T, Liu B. Vibration Error Correction for the FOGs-Based Measurement in a Drilling System Using an Extended Kalman Filter. Applied Sciences. 2021; 11(14):6514. https://doi.org/10.3390/app11146514
Chicago/Turabian StyleWang, Lu, Yuanbiao Hu, Tao Wang, and Baolin Liu. 2021. "Vibration Error Correction for the FOGs-Based Measurement in a Drilling System Using an Extended Kalman Filter" Applied Sciences 11, no. 14: 6514. https://doi.org/10.3390/app11146514






