BHHO-TVS: A Binary Harris Hawks Optimizer with Time-Varying Scheme for Solving Data Classification Problems

Abstract

Data classification is a challenging problem. Data classification is very sensitive to the noise and high dimensionality of the data. Being able to reduce the model complexity can help to improve the accuracy of the classification model performance. Therefore, in this research, we propose a novel feature selection technique based on Binary Harris Hawks Optimizer with Time-Varying Scheme (BHHO-TVS). The proposed BHHO-TVS adopts a time-varying transfer function that is applied to leverage the influence of the location vector to balance the exploration and exploitation power of the HHO. Eighteen well-known datasets provided by the UCI repository were utilized to show the significance of the proposed approach. The reported results show that BHHO-TVS outperforms BHHO with traditional binarization schemes as well as other binary feature selection methods such as binary gravitational search algorithm (BGSA), binary particle swarm optimization (BPSO), binary bat algorithm (BBA), binary whale optimization algorithm (BWOA), and binary salp swarm algorithm (BSSA). Compared with other similar feature selection approaches introduced in previous studies, the proposed method achieves the best accuracy rates on 67% of datasets.

1. Introduction

Data mining is determined as an important step in the knowledge discovery process. It has become an active research domain due to the presence of huge collections of digital data that need to be explored and transformed into useful patterns. The main role of data mining is to develop methods that assist in finding potentially useful hidden patterns in huge data collections [1]. In data mining techniques such as classification, preprocessing of data has a great influence on the goodness of discovered patterns and the efficiency of machine learning classifiers [1,2]. Feature selection (FS) is one of the main preprocessing techniques to discover and retain informative features and eliminate noisy and irrelevant ones. Selecting the optimal or near-optimal subset of given features will enhance the performance of the classification models and reduce the computational cost [2,3,4].

Based on the evaluation criteria of the selected features subset, FS approaches are classified into two classes: filter and wrapper approaches [3]. Filter techniques depend on scoring matrices such as chi-square and information gain to estimate the quality of the picked subset of features. More accurately, in filter approaches, a filter approach (e.g., chi-square) is used to rank the features, and then the only ones that have weights greater than or equal to a predefined threshold are retained. In contrast, wrapper approaches mainly consider a machine learning classifier such as K-Nearest Neighbors (KNN) or Support Vector Machines (SVM) to evaluate the feature subset.

Another aspect for categorizing FS methods is based on the selection mechanism that is used to explore the feature space, searching for the most informative features. The search algorithm task is to generate subsets of features, and then the machine learning algorithm is applied to assess the generated subsets of features to find the optimal one [4,5,6]. Compared to filter approaches, wrappers have superior performance, especially in terms of accuracy since it considers the dependencies between features in the dataset, while filter FS may ignore such relations [7]. Although, filter FS is better than wrapper FS in terms of computational cost [4].

Commonly, for a wide range of data mining applications, reaching the optimal subset of features is a challenging task. The size of the search space grows exponentially with respect to the number of features (i.e., $2^K-1$ possible subsets can be generated for a dataset with k features). Accordingly, FS is an intractable NP-hard optimization problem in which exhaustive search and even conventional exact optimization methods are impractical. For that reason, the FS domain has been extensively investigated by many researchers [5,8]. For example, in  [9], an improved version of the binary Particle Swarm Optimization (PSO) algorithm was introduced for the FS problem. An unsupervised FS approach based on Ant Colony Optimization (ACO) was proposed by [10]. Moreover, an FS technique that hybrids Genetic Algorithm (GA) and PSO was introduced in [11]. Finally, a binary variant of the hybrid Grey Wolf Optimization (GWO) and PSO is presented in [12] to tackle the FS problem.

Meta-heuristic algorithms have been very successful in tackling many optimization problems such as data mining, machine learning, engineering design, production tasks, and FS [13]. Meta-heuristic algorithms are general-purpose stochastic methods that can find a near-optimal solution within a reasonable time. Lately, various Swarm Intelligence (SI) based meta-heuristics have been developed and proved a good performance for handling FS tasks in different fields [14,15]. Some examples include Whale Optimization Algorithm (WOA) [16], Slim Mould Algorithm (SMA) [17], Marine Predators Algorithm (MPA) [18], and Grey Wolf Optimizer (GWO) [19].

Recently, Heidari and his co-authors proposed a new nature-inspired meta-heuristic optimizer named Harris Hawks Optimization (HHO) [20]. HHO simulates the behavior of hawks when they surprisingly attack their prey from different directions. HHO has several merits; it is simple, flexible, and free of internal parameters. Furthermore, it has a variety of exploitation and exploration strategies that ensure good results favorable convergence speed [21]. The original real-valued version of the HHO algorithm has been applied in conjunction with various techniques to solve many optimization problems belonging to different domains [22,23,24,25,26]. HHO has also been applied for solving FS problems [27,28,29].

Broadly, several binarization schemes have been introduced to adapt real-valued meta-heuristics to deal with discrete search space. These approaches follow two major branches. The first branch is named continuous-binary operator, in which the meta-heuristic is adapted to work in binary search space by redefining the basic real values operators of its equations into binary operators [30]. However, in the second branch, which is named two-step binarization, real values operators of meta-heuristics are kept without adjustment. To conduct the binarization, the first stage involves employing a transfer function (TF) to convert the real-valued solution R${}^n$ into an intermediate probability vector [0, 1]${}^n$. Each element in the probability vector determines the probability of transforming its equivalent in R${}^n$ into 0 or 1. In the second stage, a binarization rule is applied to transform the output of TF into a binary solution [30]. In general, the second binarization scheme is commonly used for adapting meta-heuristics to work in binary search space. In this regard, Transfer Functions (TFs) are defined depending on their shapes into two types: S-shaped and V-shaped [31,32,33]. Traditional or time-independent TFs are not able to deliver a satisfactory balance between exploration and exploitation in the search space. To overcome this shortcoming, several time-varying TFs have been proposed and applied with many meta-heuristic algorithms for providing a good balance between exploration and exploitation over iterations [34,35,36].

In this work, to be utilized for FS tasks, the authors integrate time-varying versions of V-shaped TFs into the HHO algorithm to convert the continuous HHO into a binary version called BHHO. The benefit of using time-varying functions with the BHHO algorithm is to enhance its search ability by getting a better balance between exploration and exploitation phases. Time-varying functions also help in avoiding BHHO from getting stuck in local minima. The proposed approach is verified through eighteen benchmark datasets and revealed excellent performance compared to other state-of-the-art methods.

The rest of this article is organized as follows: Section 2 introduces the related works, whereas Section 3 presents the HHO algorithm. Section 4 presents the proposed BHHO variants. Section 5 outlines FS using the BHHO algorithm. Results and discussions are presented in Section 6, while the conclusion in Section 7 sums up the main findings of this work.

2. Related Works

The literature reveals that meta-heuristic algorithms have been very successful in tackling FS problems. GA and PSO algorithms have been utilized to develop effective FS methods for many problems. Several GA-based approaches have been proposed. Examples of these approaches are [37,38,39,40,41]. Moreover, many binary variants of PSO have been frequently applied in many FS methods. Some examples can be found in Chuang et al. [42], Chantar et al. [4], Mafarja et al. [43], and Moradi et al. [44]. For instance, in Chuang et al. [42], an improved version of Binary PSO named Chaotic BPSO was used for FS in which two chaotic maps called logistic and tent were embedded in BPSO for estimating the value of inertia weight in the velocity equation of PSO algorithm. Another example is the recent work of Mafarja et al. [43], where five strategies were used to update the value of the inertia weight parameter during the search process. The proposed approaches have shown better performance when compared to other similar FS approaches. ACO algorithm, which was introduced by Dorigo et al. [45] was also applied in FS. As examples, one can refer to the work of Deriche M. [46], Chen et al. [47], and Kashef et al. [48]. Artificial Bee Colony (ABC) optimizer [49]. An example of using the ABC algorithm for FS is presented in [50]. In addition, as shown in [51], the binary version of the well-known meta-heuristic Bat Algorithm (BA) was used as an FS method. Experiential results demonstrated the superiority of BA based FS method in contrast with GA and PSO-based methods. In addition to the algorithms mentioned above that have been applied for FS, many recently introduced meta-heuristic algorithms such as Slap Swarm Algorithm (SSA) [6], Moth-Flame Optimization (MFO) [52], Dragonfly Algorithm (DA) [53], and Ant Lion Optimization (ALO) [54] have been successfully utilized in FS for many classification problems.

Harris Hawks algorithm has been utilized to solve many optimization problems. For instance, as stated in [23], in the civil engineering domain, HHO was used to improve the performance of the artificial neural network classifier in predicting the soil slope stability. In addition, a hybrid model based on HHO and Differential Evaluation (DE) algorithms has been applied to tackle the task of color image segmentation. Using different measures for evaluation purposes, results prove that HHO-DE based approach is superior compared to several state-of-the-arts image segmentation techniques [24]. A novel automatic approach combining deep learning and optimization algorithms for nine control chart patterns (CCPs) recognition was proposed by [25]. An HHO algorithm was applied for the best tuning of ConvNet parameters. In addition, an improved version of the HHO algorithm that incorporates three strategies, including chaos, topological multi-population, and differential evolution (DE), was proposed by [26]. DE-driven multi-population HHO (CMDHHO) algorithm has shown its effectiveness in solving real-world optimization problems.

The investigated literature reveals that some binary versions of HHO have been proposed since the appearance of the HHO algorithm in 2019 for FS problems [27,28,29,55]. As presented in [27], a set of binary variants of the HHO algorithm was proposed as wrapper FS methods. Eight V-shaped and S-shaped TFs and four quadratic functions were used to transform the search space from continuous to binary. The performance of proposed variants of BHHO are compared with binary forms of different optimization algorithms, include DE algorithm, binary Flower Pollination Algorithm (FPA), binary Multi-Verse Optimizer (MVO), binary SSA, and GA. The experimental results show that the QBHHO approach can mostly perform the best in terms of classification accuracy, least fitness value, and the lowest number of selected features. As stated in [28], two binary variants of the HHO algorithm were proposed as wrapper FS approaches in which two transfer functions (S-shaped and V-shaped) were used to transform continuous search space into binary. Using several high dimension and low-sample challenging datasets along with different optimization algorithms (e.g., GA, BPSO, and BBA) for validating purposes, the S-shaped transfer function-based BHHO shows promising results in dealing with challenging datasets. Recently, Ref. [55] proposed a wrapper-based FS for text classification in the Arabic context utilizing four binary variants of the HHO algorithm. The proposed variants of BHHO confirmed excellent performance compared to seven wrapper-based methods.

The traditional time-independent TFs are the most commonly used ones for adapting meta-heuristic algorithms to work in binary search space. For example, Kennedy and Eberhart [31] used an S-shaped TF to convert PSO optimizer to deal with binary optimization problems. A V-shaped transfer function was adopted by [33] to introduce a binary version of the Gravitational Search Algorithm (GSA). In 2013, for converting the continuous version of the PSO algorithm into Binary, Mirjalili and Lewis [32] introduced six new V-shaped and S-shaped TFs for mapping continuous search space into a binary one. Experimental results approved that the new proposed V-shaped group of TFs can remarkably improve the performance of the classic version of PSO, especially in terms of convergence speed and avoiding local minima problems. In addition, the same set of TFs introduced by [32] was also applied by Mafarja et al. [56] to propose six versions of binary ALO. Results show that equipping ALO with V-shaped TFs can significantly improve its performance in terms of accuracy and preventing local minima.

Time-varying TFs were proposed by Islam et al. [34] for boosting the performance of BPSO in which a modified form of BPSO called TV${}_T$-BPSO that adopts a time-varying transfer function was introduced to overcome the drawbacks of traditional TFs by providing a better balance between exploration and exploitation for the BPSO through its optimization process. In addition, Mafarja et al. [35] was also applied several time-varying S-shaped and V-shaped TFs for improving the exploitation and exploration power of the Binary DA (BDA). The experimental results confirmed the superiority of time-varying S-shaped BDA approaches when compared to other tested approaches. Recently, Kahya et al. [36] investigated the use of a time-varying transfer function with a binary WOA for FS. The results confirmed that BWOA-TV2 has consistency in FS. It also provides high accuracy of the classification with better convergence over conventional algorithms such as Binary Firefly Algorithm (BFA) and BPSO.

3. Harris Hawks Optimization (HHO)

HHO is a new meta-heuristic optimization algorithm introduced by Heidari et al. in 2019 [20]. HHO mimics the hunting mechanism of Harris Hawks in nature. The study of Harris hawks’ behavior revealed that these birds use various sophisticated strategies in surprisingly attacking and hunting the fleeing prey (mostly a rabbit). As shown in the original publication of HHO, the mathematical modeling of this algorithm confirms its effectiveness in tackling diverse optimization problems. As any other population-based meta-heuristic optimizer, HHO generates a population of search agents and updates these search agents using exploration and exploitation phases. The exploration of this algorithm has two stages, while the exploitation consists of four stages [20]. Figure 1 depicts the stages of the HHO optimizer. The following subsections describe the phases and mathematical models of HHO.

3.1. Exploration Phase

In this phase, the search agents (Hawks) are updated through two strategies where both strategies have an equal chance to be selected. In HHO, agents perch with respect to the positions of other close individuals and the prey or perch on random positions (tall trees). These strategies can be mathematically formulated as in Equation (1)

$$X(t+1)=\left\{\begin{array}{cc}{X}_{rand}\left(t\right)-r_1\left|X_{rand}\left(t\right)-2r_{2}X\left(t\right)\right|& p\ge 0.5\\ (X_{prey}\left(t\right)-X_n\left(t\right))-r_3(LB+r_4(UB-LB))& p<0.5\end{array}\right.$$

(1)

where $X(t+1)$ denotes hawks’ position vector in the next generation t, $X_{prey}\left(t\right)$ refers to hawks’ current position, $r_1,r_2,r_3,r_p$, and p are randomly generated numbers within range (0, 1) in each generation, LB and UB mean the lower and upper boundaries of variables respectively, $X_{rand}\left(t\right)$ denotes a randomly picked individual (hawk) from the current generation, $X_n$ refers to the mean position of the current generation of individuals, which can be calculated using Equation (2):

$$X_n\left(t\right)=\frac{1}{N}\sum _{i=1}^N{X}_i\left(t\right)$$

(2)

where N indicates the size of the population of hawks, and $X_i\left(t\right)$ denotes the location of each individual at generation t.

3.2. Moving from Exploration to Exploitation

In general, to achieve a suitable balance between the core searching behaviors, an algorithm requires an appropriate way to transfer from exploration to exploitation. In HHO, the decreasing energy of a fleeing prey is used to control this part of the search process, where this energy decreases through the escaping behavior. The energy of the escaping prey is formulated as in Equation (3)

$$E=2E_0(1-\frac{t}{T})$$

(3)

where E denotes the escaping energy of the prey (rabbit), $E_0$ presents the initial value of the rabbit’s energy, and T indicates the maximum number of generations. For each iteration t, $E_0$ changes at random in range (−1, 1). The prey is physically strengthening when the value of $E_0$ increases from 0 to 1, while it is flagging if $E_0$ decreases from 0 to −1. The escaping energy is reduced over the generation. When $\left|E\right|\ge 1$, it means that the algorithm performs exploration by searching different regions to locate a rabbit, whilst the algorithm does exploitation when $\left|E\right|<1$.

3.3. Exploitation Phase

This phase comes after HHO completes the exploration of promising regions of the search space. At this stage, HHO puts more emphasis on intensifying better solutions to reach the optimal one. To achieve that, Harris’ Hawks perform what is called the surprise pounce in order to attack the prey. The prey always attempts to flee from a dangerous place. Consequently, various chasing strategies happen in reality. Depending on the escaping mechanisms of the prey and chasing behavior of hawks, four possible attaching behaviors are formulated in the HHO optimizer. Let r be the probability that a prey succeeds in escaping where ($r<0.5$) indicates that the prey succeeded in escaping and ($r\ge 0.5$) means it could not. One of two actions named soft and hard besiege is performed by hawks to catch the prey. In this way, the prey will be surrounded from various directions softly or hardly based on prey’s remaining energy. This process is modeled using the parameter $\left|E\right|$ where soft besiege takes place when $\left|E\right|\ge$ 0.5 and hard besiege happens if $\left|E\right|$ < 0.5.

3.3.1. Soft Besiege

If the values of the parameters ($r\ge$ 0.5) and ($\left|E\right|\ge$ 0.5), this means that the prey still has sufficient energy to run; thus, the hawks surround the prey softly in order to make it tired and then perform a surprise pounce. This is mathematically modeled using the following two rules:

$$X(t+1)=\Delta X\left(t\right)-E\left|J{X}_{prey}\left(t\right)-X\left(t\right)\right|$$

(4)

$$\Delta X\left(t\right)=X_{prey}\left(t\right)-X\left(t\right)$$

(5)

where $\Delta X\left(t\right)$ denotes the difference between the prey’s position vector and the current hawk, E denotes the escaping energy, $r_5$ is a randomly generated number in the range [0, 1], and $J=2(1-r_5)$ denotes the random jump strength of the prey during the escaping operation.

3.3.2. Hard Besiege

If ($r\ge$ 0.5) and ($\left|E\right|$ < 0.5), then the prey is extremely tired and its escaping energy is low. Consequently, the hawks surround the targeted prey hardly and do the surprise pounce. In this case, the following formula is used for updating the current positions:

$$X(t+1)=X_{prey}\left(t\right)-E\left|\Delta X\left(t\right)\right|$$

(6)

3.3.3. Soft Besiege with Progressive Rapid Dives

In the soft besiege stage, if ($r<0.5$) and still ($\left|E\right|\ge$ 0.5), this means that the prey still has sufficient energy to succeed in escaping. A more sophisticated soft besiege step is done prior to the surprise pounce. To model the escaping styles of the prey in this case, the HHO algorithm uses the levy flight strategy to simulate the actual movements of prey as well as the abrupt, rapid, and irregular movements of search agents (hawks) toward the escaping prey (rabbit). Based on the actual behavior of Harris hawks, it is assumed that they can decide their next motion according to the rule in Equation (7):

$$Y=X_{prey}\left(t\right)-E\left|J{X}_{prey}\left(t\right)-X\left(t\right)\right|$$

(7)

After that, they make a comparison between the movement and the previous dive to see which one is better. If the previous dive is still better, then the hawks will make rapid dive depending on the levy flight (LF) pattern using Equation (8):

$$Z=Y+S\times LF\left(D\right)$$

(8)

where D indicates the dimension of given search space, S denotes a random vector with size $1\times D$, and LF represents levy flight function. LF value is obtained using Equation (9):

$$LF\left(x\right)=0.01\times \frac{u\times \sigma }{{\left|v\right|}^{\frac{1}{\beta }}},\sigma ={\left(\frac{\mathsf{\Gamma }(1+\beta )\times sin\left(\frac{\pi \beta }{2}\right)}{\mathsf{\Gamma }\left(\frac{1+\beta }{2}\right)\times \beta \times 2^{\left(\frac{\beta -1}{2}\right)}}\right)}^{\frac{1}{\beta }}$$

(9)

where u, v are random numbers inside (0,1), $\beta$ equals to 1.5, and $\mathsf{\Gamma }\left(x\right)$ is the standard gamma function.

Finally, in the soft besiege stage, the updating strategy of the positions of hawks can be done by Equation (10):

$$X(t+1)=\left\{\begin{array}{cc}Y& ifF\left(Y\right)<F\left(X\right(t\left)\right)\\ Z& ifF\left(Z\right)<F\left(X\right(t\left)\right)\end{array}\right.$$

(10)

where $F\left(x\right)$ denotes the fitness function for the given solution X, Y and Z can be calculated using Equations (7) and (8).

3.3.4. Hard Besiege with Progressive Rapid Dives

If ($r<0.5$) and also ($\left|E\right|$ < 0.5), then the prey has no sufficient energy to flee. In this case, prior to the surprise pounce to capture the prey, a hard besiege is done by the hawks where they attempt to decrease the distances between their average location and the intended prey. Therefore, the rule presented in Equation (11) is used in a hard besiege case.

$$X(t+1)=\left\{\begin{array}{cc}{Y}^{\prime }& ifF\left(Y^{\prime }\right)<F\left(X\left(t\right)\right)\\ Z^{\prime }& ifF\left(Z^{\prime }\right)<F\left(X\left(t\right)\right)\end{array}\right.$$

(11)

where $Y^{\prime }$ and $Z^{\prime }$ can be calculated using Equations (12) and (13).

$$Y^{\prime }=X_{prey}\left(t\right)-E\left|J{X}_{prey}\left(t\right)-X_m\left(t\right)\right|$$

(12)

where $X_m\left(t\right)$ is calculated using Equation (2), E denotes the escaping energy, and J refers to the jump strength.

$$Z^{\prime }=Y^{\prime }+S\times LF\left(D\right)$$

(13)

where D indicates the dimension of a given search space, S denotes a random vector with size $1\times D$, and LF represents levy flight function. For more details about the HHO algorithm, please refer to the original paper [20].

4. Proposed Binary HHO

In general, optimization algorithms are initially developed for solving problems in the continuous search space. The basic forms of these algorithms can not be directly applied to deal with binary and discrete optimization problems. In the binary optimization field, the search space can be viewed as a hypercube in which a search agent can adjust its position in the search space by changing the bits of its position vector from 1 to 0 or vise versa [34,35]. In the literature, depending on the shape of function, two basic forms of TFs known as S-shaped and V-shaped are proposed for adapting continuous search into binary. The first S-shaped TF was proposed by Kennedy and Eberhart [31] to transform the continuous original version of the PSO algorithm into a discrete one while the initial V-shaped transfer function was proposed by Rashedi et al. [33] for developing a binary variant of GSA (BGSA). Although the sigmoid TF is simple, effective, cheap in terms of computational cost, and widely utilized for binary variants of optimization algorithms, it has some shortcomings. It is unable to provide sufficient balance between the two essential stages of the optimization process (exploration and exploitation). In addition, it also has difficulty in avoiding the stuck of the algorithm in local minima and controlling the convergence speed [32]. In the case of V-shaped TF, it is defined based on some principles to map continuous values of velocity vectors into probabilities. The main concept is that the search agents that have significant absolute values of velocity are potentially far from the optimal solution; hence the TF should provide a high probability for changing the positions of search agents. When the velocity vector has small absolute values, then the TF should present small probability values of changing the positions of the search agents [33].

To overcome the limitations of basic TFs in mapping velocity values to probability ones, Mirjalili and Lewis [32] extensively studied the influence of the available TFs on the performance of BPSO. Accordingly, six new transfer functions divided into two groups according to their forms, S-shaped and V-shaped, were introduced for mapping the continuous search to discrete search space. It was found that V-shaped family of TFs, in particular V4 TF, significantly improves the performance of binary algorithms compared to the sigmoid TF. Furthermore, the same families of TFs were employed by Mafarja et al. in [56] to develop six discrete forms of ALO for FS. It was observed that the V-shaped TFs, especially ALO-V3, significantly enhance the performance of binary ALO optimizer for FS tasks.

Following the appearance of various forms of TFs for adapting the optimization algorithms to work in discrete search space, in 2017, Islam et al. [34] studied and analyzed the behavior and performance of existing TFs with the PSO algorithm in dealing with low and high dimensional discrete optimization problems. It was demonstrated that current TFs still suffer from difficulty in controlling the balance between exploration and exploitation of the optimization process. As presented in [34], to overcome the limitations of current basic TFs, the authors defined some concepts in which the search process for an optimal solution should concentrate on the exploration in the early generations of the optimization process by letting the TF produce a high probability of changing the elements of the position vector of a search agent based on the value of the velocity vector (step). In later phases, the optimization process should move the focus of the search from exploration to exploitation by enabling the TF to provide a low probability of changing the position’s elements of a search agent. According to these concepts, a control parameter ($\tau$) was adopted in the TF, where this parameter starts with a large value and decreases gradually over the iteration to obtain a smooth shift from exploration to exploitation. In this way, the shape of the TF changes over time based on the value of the controlling parameter. The purpose of employing the time-varying scheme is to obtain a better balance between exploration and exploitation through the optimization process of a BPSO. Time-varying TFs demonstrated their superiority when compared to existing static TFs based on BPSO approaches over low-dimensional and high-dimensional discrete optimization problems.

Inspired by the work of [32,34], Mafarja et al. [35] proposed eight time-varying TFs related into two families (S-shaped and V-shaped) for developing binary versions of DA (BDA) to be used for FS. The authors demonstrated the efficiency of these time-varying TFs by comparing their performance with other static TFs as well as various wrapper-based FS approaches. In addition, three types of time-varying transfer functions were introduced in [36] for improving the performance of the binary WOA in the FS domain. WOA with time-varying TFs has shown higher effectiveness and efficiency than other popular approaches in the FS domain. In this work, considering the previous studies of the impact of TFs on the performance of binary optimization algorithms, we select the time-varying TFs, specifically V-shaped, proposed by [35], as shown in

Table 1. Original and time-varying V-shaped transfer functions.

Original Family		Time-Varying Family
Name	Transfer Function	Name	Transfer Function
V1	$T\left(x\right)=|\mathrm{erf}\left(\frac{\sqrt{\mathsf{\Pi }}}{2}x\right)|$	TV1	$T(x,\tau )=|\mathrm{erf}\left(\frac{\sqrt{\mathsf{\Pi }}}{2}\frac{x}{\tau }\right)|$
V2	$T\left(x\right)=|tanh(x\left)\right|$	TV2	$T(x,\tau )=|tanh\left(\frac{x}{\tau }\right)|$
V3	$T\left(x\right)=|\left(x\right)/\sqrt{1+x^2}|$	TV3	$T(x,\tau )=|\left(\frac{x}{\tau }\right)/\sqrt{1+{\left(\frac{x}{\tau }\right)}^2}|$
V4	$T\left(x\right)=|\frac{2}{\mathsf{\Pi }}\mathrm{arc}\tan \left(\frac{\mathsf{\Pi }}{2}x\right)|$	TV4	$T(x,\tau )=|\frac{2}{\mathsf{\Pi }}\arctan \left(\frac{\mathsf{\Pi }}{2}\frac{x}{\tau }\right)|$

, to convert HHO to binary and apply the binary variants of HHO to the FS problem. In the time-varying form of the TFs, $\tau$ represents a time-varying variable that begins with an initial value and progressively reduces over iterations, as shown in Equation (14).    

$$\tau ={\tau }_{max}-({\tau }_{max}-{\tau }_{min})\times \frac{t}{T}$$

(14)

where ${\tau }_{min}$ and ${\tau }_{max}$ represent the bounds of the $\tau$ parameter, t denotes the current iteration, and T represents the maximum number of iterations. In this study, ${\tau }_{min}$ and ${\tau }_{max}$ were selected to be 0.01 and 4, respectively [35]. The original time independent V-shaped TFs are shown in Figure 2, while the time varying variants of TFs are shown in Figure 3.

After employing the original or time-varying TFs as a first step in the binarization scheme, the real-valued solution R${}^n$ is converted into an intermediate probability vector [0, 1]${}^n$ such that each of its element determines the probability of transforming its equivalent in R${}^n$ into 0 or 1. In the second step, a binarization rule is applied to transform the output of TFs into a binary solution [30]. In this work, the complement binarization introduced by Rashedi et al. [33] is applied as given in Equation (15).

$$X_j(t+1)=\left\{\begin{array}{cc}\backsim b_j& r<T\left(X_j\left(t\right)\right)\\ b_j& Otherwise\end{array}\right.$$

(15)

where ∽ denotes the complement, $b_j$ is the current binary value for the jth element, and $X_j(t+1)$ is the new binary value. It is noted that the updated binary value is set considering the current binary solution, that is, based on the probability value $T(X_j\left(t\right)$, the jth element is either kept or flipped.

Algorithm 1 explains the pseudo-code of the Binary HHO algorithm.

Algorithm 1 Pseudo-code of the BHHO algorithm.

Inputs: Number of hawks (N) and maximum iterations (T) Outputs: $X_{prey}$ Generate the initial binary population $X_i(i=1,2,\dots ,N)$ while (t < T) do     Evaluate the fitness values of hawks     Find out the best search agent $X_{prey}$     for (each hawk ($X_i$)) do         Update $E_0$ and jump strength J                   ▹E${}_0$=2rand()−1, J=2(1−rand())         Update E by Equation (3)         if ($\left|E\right|\ge 1$) then                             ▹ Exploration phase            Update the position vector by Equation (1)            Calculate the probability vector using time-varying V-shaped TFs            Calculate the binary solution using Equation (15)         if ($\left|E\right|<1$) then                             ▹ Exploitation phase            if ($r\ge$0.5) then                if ($\left|E\right|\ge 0.5$ ) then                             ▹ Soft besiege                    Update the position vector by Equation (4)                else if ($\left|E\right|<0.5$ ) then                           ▹ Hard besiege                    Update the position vector by Equation (6)                Calculate the probability vector using time-varying V-shaped TFs                Calculate the binary solution using Equation (15)            if ($r<$0.5) then                if ($\left|E\right|\ge 0.5$ ) then                 ▹ Soft besiege with progressive rapid dives                    Calculate Y and Z using Equations (7) and (8)                    Convert Y and Z into binary using time-varying TF and binarization rule in Equation (15)                    Update the position vector by Equation (10)                else if ($\left|E\right|<0.5$ ) then               ▹ Hard besiege with progressive rapid dives                    Calculate Y’ and Z’ using Equations (12) and (13)                    Convert Y’ and Z’ into binary using time-varying TF and binarization rule in Equation (15)                    Update the position vector by Equation (11) Return$X_{prey}$

5. BHHO-Based FS

FS is recognized as a binary optimization task, where potential solutions (subsets of features) are encoded using binary values. Therefore, FS can be solved by employing a binary optimizer (e.g., BHHO). In this work, a wrapper FS approach that utilizes the binary version of HHO as a search algorithm and KNN classifier for evaluating the goodness of selected features generated by BHHO is introduced. In the FS problem, a binary vector is used to encode a solution where the vector’s length equals the number of features in the dataset. When the value of an element of the features vector is zero, that means the corresponding feature is omitted while one indicates that the feature is selected. In this paper, four FS methods using different binary versions of HHO are developed, where each method uses a different time-varying V-shaped TF to transform continuous values to binary. FS is considered a multi-objective optimization task where the highest classification accuracy and the least number of features are two criteria that need to be fulfilled. As shown in Equation (16), both classification accuracy and the number of selected features are included in the applied fitness function [35,36].

$$Fitness=(\propto \times err)+(\beta \times \left(\frac{R}{N}\right))$$

(16)

where err stands for the error rate of the KNN algorithm over a selected subset of features by the BHHO optimizer, ∝, and $\beta$ are two parameters for balancing between classification accuracy and the size of features subset, ∝ is a number within [0, 1], $\beta$ is equal to (1 −∝), N is the number of all features in the dataset, and R indicates the cardinality of the subset of features selected by a search agent.

6. Results and Discussion

In this section, we have conducted various experiments and tests to assess the performance of V-shaped time-varying-based HHO algorithms in solving the FS problem. The proposed BHHO algorithms were also compared to different optimizers. To achieve a fair comparison, the initial settings of all optimizers, such as population size, number of iterations, and number of independent runs, were unified by setting them to similar initials values.

Eighteen popular benchmark datasets obtained from the UCI data repository are applied for evaluating the performance of the proposed FS approaches.

Table 2. List of employed datasets.

Dataset	No. of Features	No. of Instances	No. of Classes
Breastcancer	9	699	2
BreastEW	30	569	2
Exactly	13	1000	2
Exactly2	13	1000	2
HeartEW	13	270	2
Lymphography	18	148	4
M-of-n	13	1000	2
PenglungEW	325	73	7
SonarEW	60	208	2
SpectEW	22	267	2
CongressEW	16	435	2
IonosphereEW	34	351	2
KrvskpEW	36	3196	2
Tic-tac-toe	9	958	2
Vote	16	300	2
WaveformEW	40	5000	3
WineEW	166	476	3
Zoo	16	101	7

shows the details of the datasets comprising a number of features, classes, and instances in each dataset. Following the hold-out method, each dataset is arbitrarily split into two portions (training/testing), where 80% of the data were preserved for training while the rest was employed for testing. Furthermore, each FS approach was run for 30 trials with a randomly set seed on a machine with an Intel Core i5, 2.2 GHz CPU, and 4 GB of RAM.

In this work, internal parameters of algorithms were set according to recommended settings in original papers as well as related works on FS problems, while common parameters were set based on the results of several trials.

Table 3. Common and internal parameters used in the experiments.

Common Parameters
Number of runs	30
population size	10
Number of iterations	100
Dimension	#features
Fitness function	$\alpha$ = 0.99, $\beta$ = 0.01
K for KNN classifier	5
Internal Parameters
GSA	$G_0$ = 10
	$c_1=c_2=2$
PSO	$\omega$: from 0.9 to 0.2
BA	$Q_{min}$ = 0, $Q_{max}$ = 2
	A loudness = 0.5, r Pulse rate = 0.5
WOA	a: from 2 to 0
	$a_2$: from −1 to −2
HHO	E: from 2 to 0

reveals the detailed parameters settings of each algorithm.

To study the impact of four types of time-varying V-shaped TFs on the efficiency of the BHHO optimizer, we provide comparisons between the results of HHO with four basic V-shaped TFs and those recorded by HHO with four time-varying V-shaped TFs. Furthermore, the best FS approach among tested basic and time-varying V-shaped based approaches was then compared to several state-of-the-art FS approaches comprising BGSA, BPSO, BBA, BSSA, and BWOA. The following criteria were used for the comparisons:

• The average of accuracy rates obtained from 30 trials.
• The average of best selected features rates recorded from 30 trials.
• The mean of best fitness values obtained from 30 trials.
• F-test method is used for ranking different FS methods to determine the best results.

Please note that in all reported tables, the best-obtained results are highlighted using a boldface format.

6.1. Comparison between Various Versions of BHHO with Basic and Time Varying V-Shaped TFs

In general, experimental results show that HHO with V-shaped time-varying transfer functions (TV-TFs) is better compared to those with classic V-shaped TFs. Inspecting the results in

Table 4. Comparison of BHHO with the basic and time-varying V-shaped variants in terms of accuracy rates.

Dataset	${\mathbf{BHHO}}_{\mathit{V}1}$	${\mathbf{BHHO}}_{\mathit{T}\mathit{V}1}$	${\mathbf{BHHO}}_{\mathit{V}2}$	${\mathbf{BHHO}}_{\mathit{T}\mathit{V}2}$	${\mathbf{BHHO}}_{\mathit{V}3}$	${\mathbf{BHHO}}_{\mathit{T}\mathit{V}3}$	${\mathbf{BHHO}}_{\mathit{V}4}$	${\mathbf{BHHO}}_{\mathit{T}\mathit{V}4}$
Breastcancer	0.9693	0.9783	0.9998	0.9924	0.9779	0.9848	0.9929	0.9781
BreastEW	0.9702	0.9819	0.9909	0.9883	0.9813	0.9918	0.9737	0.9792
CongressEW	0.9939	0.9801	0.9889	0.9992	0.9655	0.9816	0.9774	1.0000
Exactly	1.0000	0.9828	0.9135	0.9965	0.9997	0.9997	0.9993	0.9998
Exactly2	0.7918	0.8137	0.8148	0.7263	0.7565	0.7975	0.7712	0.7885
HeartEW	0.9370	0.8877	0.8988	0.9037	0.8704	0.8957	0.9074	0.9105
IonosphereEW	0.9620	0.9695	0.9418	0.9507	0.9596	0.9615	0.9531	0.9728
KrvskpEW	0.9735	0.9791	0.9724	0.9728	0.9735	0.9701	0.9735	0.9789
Lymphography	0.9822	0.9133	0.8878	0.9489	0.9511	0.9267	0.9656	0.9811
M-of-n	0.9998	0.9998	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000
penglungEW	1.0000	1.0000	1.0000	0.9444	0.9933	1.0000	1.0000	1.0000
SonarEW	0.9421	0.9556	0.9492	0.9833	0.9595	0.9341	0.9508	0.9754
SpectEW	0.9056	0.8883	0.8549	0.8778	0.8605	0.9296	0.9111	0.9093
Tic-tac-toe	0.8267	0.8542	0.8410	0.8594	0.8316	0.8418	0.8163	0.8333
Vote	0.9639	0.9994	0.9833	0.9872	0.9883	0.9861	0.9867	0.9872
WaveformEW	0.8023	0.7971	0.8036	0.8083	0.8056	0.7916	0.8003	0.7973
WineEW	1.0000	1.0000	1.0000	0.9926	1.0000	1.0000	1.0000	1.0000
Zoo	1.0000	0.9444	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000
$W\left|T\right|L$	$7\left|3\right|8$	$8\left|3\right|7$	$5\left|2\right|11$	$11\left|2\right|5$	$5\left|4\right|9$	$9\left|4\right|5$	$3\left|4\right|11$	$11\left|4\right|3$
Rank (F-Test)	4.56	4.61	4.83	4.44	5	4.53	4.61	3.42

, in the case of BHHO${}_{V1}$ and BHHO${}_{TV1}$, BHHO${}_{V1}$ has recorded higher accuracy rates on seven datasets while BHHO${}_{TV1}$ has found higher accuracy rates for eight cases. However, both approaches have the same accuracy rates in three cases. In addition, we see that BHHO${}_{TV2}$ has better accuracy measures than BHHO${}_{V2}$ on eleven datasets, whereas BHHO${}_{V2}$ outperforms BHHO${}_{TV2}$ in five cases. It can be observed that BHHO${}_{TV2}$ and BHHO${}_{V2}$ have maximum accuracy rates in two cases (M-of-N and Zoo). In the case of BHHO${}_{V3}$ and BHHO${}_{TV3}$, it can be noticed that BHHO${}_{TV3}$ outperforms BHHO${}_{V3}$ on nine datasets while BHHO${}_{V3}$ obtained higher accuracy rates on five datasets. It can be seen that both approaches obtained similar accuracy rates on the exactly dataset and the maximum accuracy measures on three datasets, including M-of-N, WineEW, and Zoo. As per results, BHHO${}_{TV4}$ outperforms BHHO${}_{V4}$ on eleven datasets in terms of accuracy rates, whereas BHHO${}_{V4}$ is superior in only three cases. However, both methods obtained similar maximum obtained maximum accuracy rates on four datasets. In terms of classification accuracy, as per F-test results, it can be seen that BHHO${}_{TV4}$ is ranked as the best, followed by the BHHO${}_{TV3}$ method. Based on the observed results, we can say that HHO with TV4 transfer function is able to obtain the best classification accuracy compared to its peers, including basic and time-varying TFs-based FS approaches.

In terms of selected features, as presented in

Table 5. Comparison of BHHO with the basic and time-varying V-shaped variants in terms of the number of selected features.

Dataset	${\mathbf{BHHO}}_{\mathit{V}1}$	${\mathbf{BHHO}}_{\mathit{T}\mathit{V}1}$	${\mathbf{BHHO}}_{\mathit{V}2}$	${\mathbf{BHHO}}_{\mathit{T}\mathit{V}2}$	${\mathbf{BHHO}}_{\mathit{V}3}$	${\mathbf{BHHO}}_{\mathit{T}\mathit{V}3}$	${\mathbf{BHHO}}_{\mathit{V}4}$	${\mathbf{BHHO}}_{\mathit{T}\mathit{V}4}$
Breastcancer	5.10	3.93	3.97	4.90	5.07	3.13	3.03	5.13
BreastEW	6.70	7.30	7.33	7.50	8.17	8.53	4.83	8.83
CongressEW	2.87	4.27	3.60	3.93	3.17	2.93	4.47	3.03
Exactly	6.00	6.23	5.30	6.07	6.03	6.07	6.03	6.07
Exactly2	4.67	5.37	3.83	6.27	6.37	5.33	5.93	4.43
HeartEW	4.87	3.20	5.80	5.20	5.60	5.67	5.27	6.13
IonosphereEW	4.17	5.30	5.07	4.87	4.87	4.23	4.07	3.63
KrvskpEW	13.80	14.87	18.90	13.37	16.10	17.07	13.43	13.73
Lymphography	4.13	5.90	5.43	5.77	4.33	4.13	5.63	4.97
M-of-n	6.07	6.03	6.00	6.03	6.00	6.07	6.07	6.00
penglungEW	11.30	8.17	11.83	20.67	9.60	8.23	12.67	11.07
SonarEW	13.67	14.37	14.20	11.13	16.43	11.50	13.10	14.57
SpectEW	6.97	4.77	6.30	5.20	4.77	7.70	5.40	5.17
Tic-tac-toe	5.00	8.20	7.83	6.17	6.47	7.93	5.90	5.13
Vote	4.57	3.20	4.30	4.63	5.50	5.37	4.20	1.70
WaveformEW	19.00	17.43	16.17	19.70	17.47	16.73	15.37	16.00
WineEW	4.03	4.33	4.10	6.77	3.53	3.27	3.00	4.27
Zoo	3.10	4.87	3.07	3.10	3.00	2.03	4.07	4.70
$W\left|T\right|L$	$11\left|0\right|7$	$7\left|0\right|11$	$12\left|0\right|6$	$6\left|0\right|12$	$7\left|0\right|11$	$11\left|0\right|7$	$9\left|0\right|9$	$9\left|0\right|9$
Rank (F-Test)	3.89	5.06	4.56	5.19	4.75	4.42	3.86	4.28

, it can be seen that the basic versions of V1 and V2 based approaches outperform the time-varying-based ones. In the case of BHHO${}_{V3}$ and BHHO${}_{TV3}$, it is clear that BHHO${}_{TV3}$ is dominant on 61.11% of cases while BHHO${}_{TV4}$ outperformed BHHO${}_{TV4}$ on 50% of the cases. According to recorded FS rates, F-test results show that BHHO${}_{V4}$ is ranked as the best method in terms of the least number of selected features. However, excessive feature reduction may not be the preferred option since it may exclude some relevant features, which degrade the classification performance. Although the basic versions of TFs-based approaches outperform the time-varying-based ones in terms of feature reduction, the latter can find the most relevant subset of features that provides better classification accuracy, as provided in Table 4.

To confirm the effectiveness of the competing algorithms, the fitness value that combines the two measures (i.e., accuracy and reduction rate) is adopted. In terms of fitness rates, as provided in

Table 6. Comparison of BHHO with the basic and time-varying V-shaped variants in terms of fitness rates.

Dataset	${\mathbf{BHHO}}_{\mathit{V}1}$	${\mathbf{BHHO}}_{\mathit{T}\mathit{V}1}$	${\mathbf{BHHO}}_{\mathit{V}2}$	${\mathbf{BHHO}}_{\mathit{T}\mathit{V}2}$	${\mathbf{BHHO}}_{\mathit{V}3}$	${\mathbf{BHHO}}_{\mathit{T}\mathit{V}3}$	${\mathbf{BHHO}}_{\mathit{V}4}$	${\mathbf{BHHO}}_{\mathit{T}\mathit{V}4}$
Breastcancer	0.0361	0.0258	0.0046	0.0130	0.0276	0.0186	0.0104	0.0274
BreastEW	0.0318	0.0204	0.0114	0.0141	0.0212	0.0110	0.0277	0.0235
CongressEW	0.0079	0.0224	0.0133	0.0032	0.0361	0.0200	0.0252	0.0019
Exactly	0.0046	0.0218	0.0897	0.0081	0.0050	0.0050	0.0053	0.0048
Exactly2	0.2097	0.1886	0.1863	0.2758	0.2460	0.2046	0.2311	0.2128
HeartEW	0.0661	0.1137	0.1047	0.0993	0.1326	0.1076	0.0957	0.0933
IonosphereEW	0.0389	0.0318	0.0591	0.0502	0.0414	0.0394	0.0477	0.0280
KrvskpEW	0.0300	0.0249	0.0326	0.0306	0.0307	0.0344	0.0300	0.0247
Lymphography	0.0199	0.0891	0.1141	0.0538	0.0508	0.0749	0.0372	0.0215
M-of-n	0.0048	0.0048	0.0046	0.0046	0.0046	0.0047	0.0047	0.0046
penglungEW	0.0003	0.0003	0.0004	0.0556	0.0069	0.0003	0.0004	0.0003
SonarEW	0.0596	0.0464	0.0527	0.0184	0.0428	0.0671	0.0509	0.0268
SpectEW	0.0967	0.1128	0.1465	0.1234	0.1403	0.0732	0.0905	0.0922
Tic-tac-toe	0.1771	0.1535	0.1661	0.1461	0.1739	0.1654	0.1884	0.1707
Vote	0.0386	0.0026	0.0192	0.0155	0.0150	0.0171	0.0158	0.0137
WaveformEW	0.2005	0.2053	0.1985	0.1947	0.1968	0.2105	0.2016	0.2047
WineEW	0.0031	0.0033	0.0032	0.0125	0.0027	0.0025	0.0023	0.0033
Zoo	0.0019	0.0580	0.0019	0.0019	0.0019	0.0013	0.0025	0.0029
$W\left|T\right|L$	$8\left|0\right|10$	$10\left|0\right|8$	$7\left|0\right|11$	$11\left|0\right|7$	$7\left|0\right|11$	$11\left|0\right|7$	$5\left|0\right|13$	$13\left|0\right|5$
Rank (F-Test)	4.44	4.75	4.92	4.33	5.03	4.31	4.75	3.47

, it is clear that all time-varying V-shaped TFs based methods outperform their peers (basic V-shaped-based techniques) in terms of fitness rates. Considering F-test results, BHHO${}_{TV4}$ is ranked as the best place compared to all other competitors. In this work, we consider that classification accuracy has higher importance compared to the number of selected features. Based on results, we found that HHO with time-varying V-shaped TV4 can realize the best performance.

6.2. Comparison with Other Optimization Algorithms

This section provides a comparison between the best approach BHHO${}_{TV4}$ and other well-known metaheuristic methods (BGSA, BPSO, BBA, BSSA, and BWOA). The comparison is made based on different criteria, including average classification accuracy, number of selected features, and fitness values.

As per results in

Table 7. Comparison of BHHO${}_{TV4}$ versus other optimizers in terms of average classification accuracy.

Dataset	BHHO${}_{\mathit{T}\mathit{V}4}$	BGSA	BPSO	BBA	BSSA	BWOA
Breastcancer	0.9781	0.9855	0.9783	0.9698	0.9700	0.9783
BreastEW	0.9792	0.9643	0.9734	0.9380	0.9661	0.9763
CongressEW	1.0000	0.9663	0.9877	0.9280	0.9816	0.9774
Exactly	0.9998	0.7227	0.9892	0.6815	0.9827	0.9952
Exactly2	0.7885	0.7908	0.8027	0.7313	0.7733	0.7465
HeartEW	0.9105	0.8488	0.9000	0.7864	0.9272	0.9037
IonosphereEW	0.9728	0.8507	0.9362	0.8681	0.9718	0.8681
KrvskpEW	0.9789	0.9182	0.9759	0.8267	0.9759	0.9749
Lymphography	0.9811	0.8220	0.8944	0.6867	0.9156	0.8933
M-of-n	1.0000	0.8815	0.9975	0.7665	0.9930	0.9993
penglungEW	1.0000	0.8832	0.9978	0.8867	0.9422	0.8044
SonarEW	0.9754	0.9397	0.9413	0.8468	0.9167	0.8714
SpectEW	0.9093	0.8265	0.8648	0.8222	0.9043	0.8482
Tic-tac-toe	0.8333	0.7941	0.8174	0.7024	0.9004	0.8594
Vote	0.9872	0.9294	1.0000	0.8800	0.9500	0.9683
WaveformEW	0.7973	0.7753	0.8167	0.7196	0.8000	0.8102
WineEW	1.0000	0.9843	0.9963	0.9111	0.9926	0.9815
Zoo	1.0000	0.9683	1.0000	0.8334	1.0000	0.9889
Rank (F-Test)	1.72	4.5	2.44	5.81	2.97	3.56

, it can be observed that BHHO${}_{TV4}$ outperforms other algorithms for 11 out of 18 datasets in terms of accuracy rates. It reached the maximum accuracy averages on five datasets. We see that BHHO${}_{TV4}$, BPSO, and BSSA reached maximum accuracy for the Zoo dataset. In addition, compared to BHHO${}_{TV4}$, it can be seen that BPSO obtained better results on Exactly2, Vote, and WaveformEW datasets. As per F-test results, we observe the BHHO${}_{TV4}$ is ranked one, followed by BPSO, BSSA, BWOA, BGSA, and BBA methods. To see whether the differences between obtained results from BHHO${}_{TV4}$ and other algorithms are statistically significant or not, a two-tailed Wilcoxon statistical test with 5% significance was used.

Table 8. The 2-tailed p-values of the Wilcoxon signed ranks test for accuracy results reported in Table 7 (p-values ≤ 0.05 are significant).

Dataset	BGSA	BPSO	BBA	BSSA	BWOA	BHHOTV4
Breastcancer	3.82E-09	5.70E-01	4.26E-01	3.33E-12	5.70E-01	1
BreastEW	1.15E-08	8.90E-04	2.45E-11	9.81E-10	1.78E-02	1
CongressEW	7.40E-13	2.50E-12	1.04E-12	4.17E-13	2.05E-13	1
Exactly	1.68E-12	3.98E-02	1.69E-12	1.02E-03	1.98E-02	1
Exactly2	8.30E-02	6.83E-11	1.79E-11	6.39E-11	1.53E-11	1
HeartEW	7.29E-11	2.67E-03	2.22E-10	3.43E-03	7.95E-03	1
IonosphereEW	1.30E-11	5.60E-09	1.69E-11	2.22E-01	1.21E-11	1
KrvskpEW	5.80E-11	1.24E-01	2.88E-11	1.05E-03	3.31E-04	1
Lymphography	1.12E-11	2.27E-11	1.57E-11	2.87E-11	5.19E-12	1
M-of-n	1.19E-12	8.15E-02	1.20E-12	1.37E-03	8.15E-02	1
penglungEW	2.54E-13	3.34E-01	6.09E-13	1.97E-11	4.16E-14	1
SonarEW	1.83E-08	3.52E-07	1.24E-11	6.77E-12	6.77E-12	1
SpectEW	1.07E-12	1.56E-12	2.87E-12	3.15E-02	4.70E-13	1
Tic-tac-toe	1.17E-12	8.26E-13	1.17E-12	4.16E-14	1.69E-14	1
Vote	2.73E-12	1.47E-09	7.07E-12	4.23E-13	2.60E-10	1
WaveformEW	2.06E-08	7.16E-10	5.72E-11	2.60E-01	4.18E-08	1
WineEW	1.06E-05	4.18E-02	3.70E-12	2.70E-03	5.88E-08	1
Zoo	5.88E-08	NaN	4.48E-12	NaN	5.47E-03	1

presents the p-values of the Wilcoxon test in terms of classification accuracy. It is clear that there are meaningful differences in terms of accuracy averages between BHHO${}_{TV4}$ and its competitors in most of the cases.

In terms of the least number of selected features, as stated in

Table 9. Comparison of BHHO${}_{TV4}$ versus other optimizers in terms of average selected features.

Dataset	BHHO${}_{\mathit{T}\mathit{V}4}$	BGSA	BPSO	BBA	BSSA	BWOA
Breastcancer	5.13	5.10	3.10	3.70	4.77	4.40
BreastEW	8.83	14.80	11.43	12.30	18.23	16.17
CongressEW	3.03	6.97	4.90	6.20	6.20	6.27
Exactly	6.07	7.87	6.17	6.30	6.87	6.57
Exactly2	4.43	4.47	2.43	4.93	8.83	7.67
HeartEW	6.13	6.50	5.17	4.77	7.53	6.37
IonosphereEW	3.63	13.57	9.47	12.50	17.40	12.83
KrvskpEW	13.73	19.93	19.00	15.57	25.30	25.50
Lymphography	4.97	8.53	5.97	6.73	9.03	9.77
M-of-n	6.00	7.90	6.20	6.20	7.10	6.80
penglungEW	11.07	149.87	126.50	123.07	174.27	120.83
SonarEW	14.57	28.27	24.37	25.63	36.30	31.27
SpectEW	5.17	10.90	8.37	9.37	11.63	13.33
Tic-tac-toe	5.13	6.13	6.20	4.33	7.13	9.00
Vote	1.70	7.57	2.63	6.57	7.07	6.00
WaveformEW	16.00	21.80	23.50	16.63	25.87	28.83
WineEW	4.27	6.47	5.97	5.90	5.93	6.17
Zoo	4.70	6.33	3.73	6.17	4.17	5.97
Rank (F-Test)	1.61	4.72	2.36	2.78	4.92	4.61

, it is observed that BHHO${}_{TV4}$ obtained the best averages on 13 out of 18 datasets while BPSO outperforms all other algorithms on three datasets. As per F-test results, we can see that the BHHO${}_{TV4}$ is ranked as the best one, followed by BPSO, and BBA methods, respectively. Inspecting the results of the p-value in

Table 10. The 2-tailed p-values of the Wilcoxon signed ranks test for the number of features reported in Table 9 (p-values ≤ 0.05 are significant).

Dataset	BGSA	BPSO	BBA	BSSA	BWOA	BHHOTV4
Breastcancer	6.18E-01	3.47E-11	4.06E-06	9.99E-03	2.63E-05	1
BreastEW	3.24E-08	4.08E-04	1.72E-05	3.16E-10	4.36E-09	1
CongressEW	6.51E-12	2.25E-10	2.96E-11	1.55E-12	1.47E-12	1
Exactly	9.70E-08	2.37E-01	2.10E-01	6.30E-07	9.34E-05	1
Exactly2	3.80E-01	8.67E-04	5.48E-01	1.98E-11	1.20E-08	1
HeartEW	4.58E-01	5.03E-02	1.72E-02	5.39E-03	3.01E-01	1
IonosphereEW	1.91E-11	2.43E-11	1.81E-11	1.71E-11	1.81E-11	1
KrvskpEW	4.74E-08	5.98E-07	2.64E-02	4.09E-11	5.47E-11	1
Lymphography	9.21E-10	9.16E-03	5.78E-04	1.93E-10	6.91E-11	1
M-of-n	2.03E-09	2.15E-02	8.10E-01	3.32E-10	2.64E-08	1
penglungEW	2.84E-11	2.86E-11	2.87E-11	2.86E-11	2.88E-11	1
SonarEW	9.02E-11	5.47E-10	8.76E-10	2.86E-11	4.53E-11	1
SpectEW	6.26E-11	7.97E-09	2.71E-09	7.11E-11	3.83E-11	1
Tic-tac-toe	9.22E-06	6.21E-03	1.53E-02	2.31E-12	1.17E-13	1
Vote	1.44E-11	4.31E-05	1.57E-10	4.00E-11	9.17E-11	1
WaveformEW	2.22E-06	8.70E-08	3.31E-01	1.62E-09	1.91E-10	1
WineEW	1.56E-08	7.13E-09	6.52E-06	1.98E-09	3.63E-11	1
Zoo	1.98E-07	3.82E-05	1.71E-03	3.27E-03	3.98E-06	1

, it is evident that the insignificant differences in terms of the lowest number of selected features between BHHO${}_{TV4}$ and other peers are limited.

Fitness rates are shown in

Table 11. Comparison of BHHO${}_{TV4}$ versus other optimizers in terms of average fitness values.

Dataset	BHHO${}_{\mathit{T}\mathit{V}4}$	BGSA	BPSO	BBA	BSSA	BWOA
Breastcancer	0.0274	0.0200	0.0249	0.0199	0.0350	0.0263
BreastEW	0.0235	0.0402	0.0302	0.0418	0.0397	0.0288
CongressEW	0.0019	0.0377	0.0152	0.0304	0.0221	0.0263
Exactly	0.0048	0.2806	0.0155	0.2846	0.0224	0.0098
Exactly2	0.2128	0.2105	0.1972	0.2299	0.2312	0.2569
HeartEW	0.0933	0.1547	0.1030	0.1235	0.0779	0.1002
IonosphereEW	0.0280	0.1518	0.0660	0.1102	0.0330	0.1344
KrvskpEW	0.0247	0.0865	0.0291	0.0828	0.0309	0.0319
Lymphography	0.0215	0.1809	0.1078	0.2088	0.0886	0.1110
M-of-n	0.0046	0.1234	0.0072	0.1353	0.0124	0.0059
penglungEW	0.0003	0.1203	0.0061	0.0739	0.0626	0.1973
SonarEW	0.0268	0.0644	0.0622	0.0996	0.0886	0.1325
SpectEW	0.0922	0.1767	0.1376	0.1296	0.1000	0.1564
Tic-tac-toe	0.1707	0.2107	0.1877	0.2296	0.1066	0.1492
Vote	0.0137	0.0746	0.0016	0.0715	0.0539	0.0351
WaveformEW	0.2047	0.2279	0.1873	0.2292	0.2045	0.1951
WineEW	0.0033	0.0206	0.0083	0.0167	0.0119	0.0231
Zoo	0.0029	0.0354	0.0023	0.0621	0.0026	0.0147
Rank (F-Test)	1.83	4.89	2.44	4.83	3.11	3.89

, and it can be noticed that BHHO${}_{TV4}$ reached the lowest fitness values compared with other algorithms on 11 out of 18 datasets. We can also see that BPSO is the best in four cases. Again, according to F-test results as in Table 11, it is clear that the BHHO${}_{TV4}$ is ranked as the best, followed by the BPSO method. In addition,

Table 12. The 2-tailed p-values of the Wilcoxon signed ranks test for fitness results reported in Table 11 (p-values ≤ 0.05 are significant).

Dataset	BGSA	BPSO	BBA	BSSA	BWOA	BHHOTV4
Breastcancer	6.84E-10	5.19E-11	6.86E-10	1.98E-12	2.60E-06	1
BreastEW	6.74E-10	9.17E-06	4.32E-10	5.38E-11	3.31E-06	1
CongressEW	1.67E-12	1.44E-12	1.68E-12	1.57E-12	1.52E-12	1
Exactly	2.35E-12	1.01E-01	2.35E-12	8.15E-07	1.03E-04	1
Exactly2	2.47E-03	8.79E-11	2.48E-11	2.56E-11	2.54E-11	1
HeartEW	3.76E-11	7.68E-02	1.64E-06	1.06E-02	1.85E-02	1
IonosphereEW	2.42E-11	4.80E-10	2.43E-11	7.52E-02	2.43E-11	1
KrvskpEW	4.97E-11	2.46E-02	3.33E-11	8.85E-06	5.84E-06	1
Lymphography	2.10E-11	2.64E-11	2.14E-11	2.09E-11	2.05E-11	1
M-of-n	1.21E-12	2.16E-02	4.57E-12	3.88E-10	2.65E-08	1
penglungEW	2.84E-11	2.86E-11	2.88E-11	2.86E-11	2.88E-11	1
SonarEW	1.76E-10	6.44E-09	3.80E-10	2.96E-11	2.98E-11	1
SpectEW	2.09E-11	2.09E-11	3.17E-10	4.79E-08	2.12E-11	1
Tic-tac-toe	1.67E-12	1.19E-12	1.66E-12	6.50E-14	2.71E-14	1
Vote	7.36E-12	4.57E-11	7.19E-12	6.91E-12	6.92E-12	1
WaveformEW	6.52E-09	2.44E-09	1.56E-08	9.76E-01	1.09E-05	1
WineEW	2.76E-11	6.44E-10	2.30E-10	7.63E-11	7.47E-12	1
Zoo	1.37E-11	3.82E-05	1.35E-11	3.27E-03	1.36E-07	1

shows the p-values of the Wilcoxon test in terms of best fitness rates. It can be observed that the differences between BHHO${}_{TV4}$ and others are not statistically significant in only four cases.

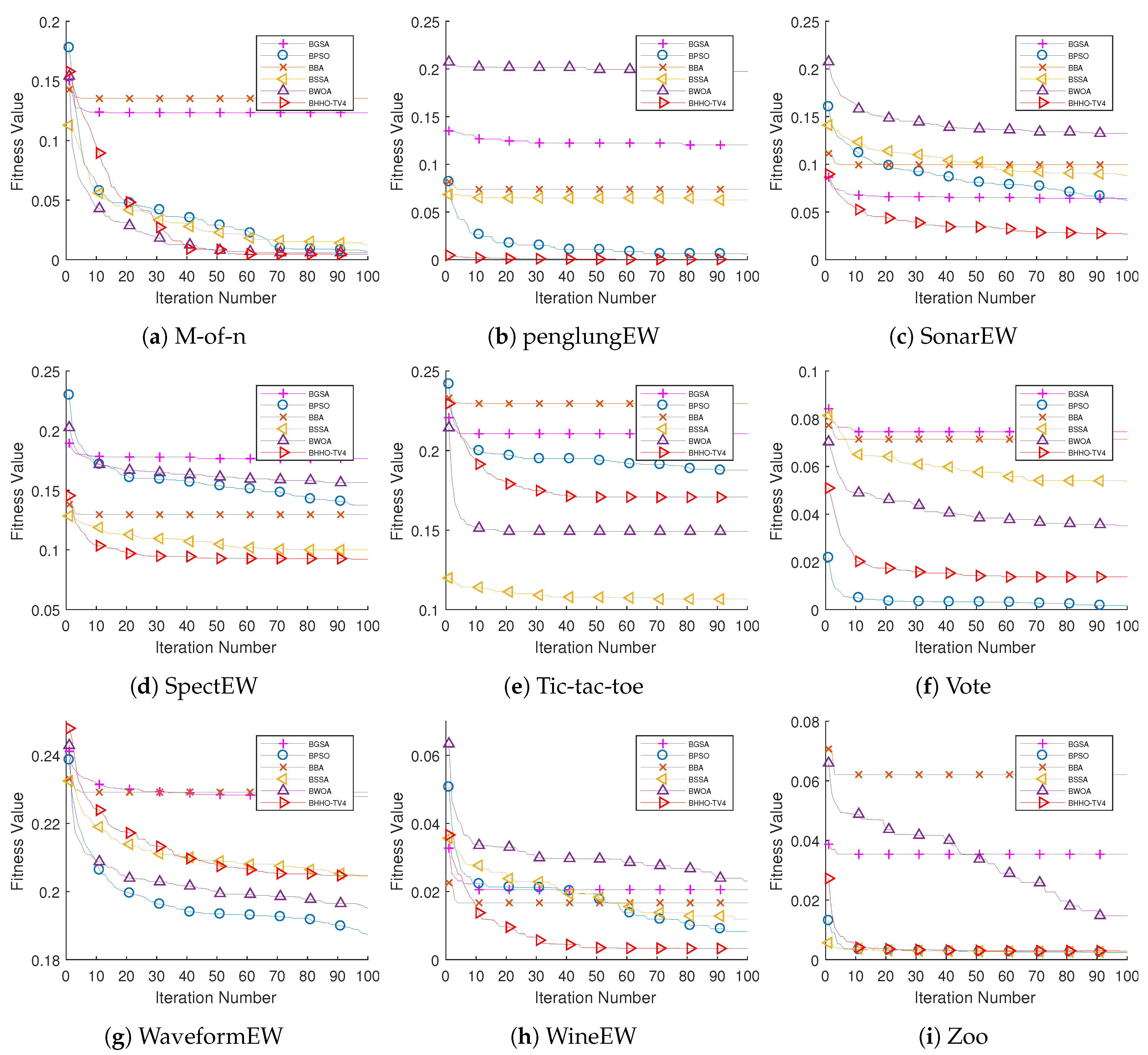
The convergence behaviors of BHHO${}_{TV4}$ and other algorithms were also investigated to assess their ability to make an adequate balance between exploration and exploitation by avoiding local optima and early convergence. The convergence behaviors of BHHO${}_{TV4}$ on 12 datasets compared to other optimizers are demonstrated in Figure 4 and Figure 5. In all tested cases, the superiority of BHHO${}_{TV4}$ can be seen in converging faster than other competitors towards the optimal solution.

6.3. Comparison with Results of Previous Works

This section provides comparisons of accuracy rates between optimal approach BHHO${}_{TV4}$ in this research and its similar FS approaches introduced in previous studies. Results of BHHO${}_{TV4}$ are compared with results of SSA in [58], WOA in [59], Grasshopper Optimization Algorithm (GOA) in [60], GSA boosted with evolutionary crossover and mutation operators in [61], GOA with Evolutionary Population Dynamics (EPD) stochastic search strategies in [62], BDA [35], hybrid approach based on Grey Wolf Optimization (GWO) and PSO in [12] and Binary Butterfly Optimization Algorithm (BOA) [63]. As in

Table 13. Comparison of the proposed $BHH{O}_{TV4}$ and other approaches from previous works in terms of accuracy rates.

Dataset	BHHOTV4	BSSA_S3_CP [58]	WOA-CM [59]	BGOA_EPD_Tour [60]	HGSA [61]	BGOA-M [62]	BDA-TVv4 [35]	BGWOPSO [12]	S-bBOA [63]
Breastcancer	0.978	0.977	0.968	0.980	0.974	0.974	0.977	0.980	0.9686
BreastEW	0.979	0.948	0.971	0.947	0.971	0.970	0.974	0.970	0.9709
CongressEW	1.000	0.963	0.792	0.964	0.966	0.976	0.995	0.980	0.9593
Exactly	1.000	0.980	0.956	0.999	1.000	1.000	0.929	1.000	0.9724
Exactly2	0.789	0.758	1.000	0.780	0.770	0.735	0.726	0.760	0.7596
HeartEW	0.910	0.861	0.742	0.833	0.856	0.836	0.886	0.850	0.8237
IonosphereEW	0.973	0.918	0.919	0.899	0.934	0.946	0.925	0.950	0.907
KrvskpEW	0.979	0.964	0.866	0.968	0.978	0.974	0.971	0.980	0.966
Lymphography	0.981	0.890	0.807	0.868	0.892	0.912	0.895	0.920	0.8676
M-of-n	1.000	0.992	0.926	1.000	1.000	1.000	0.973	1.000	0.972
penglungEW	1.000	0.878	0.972	0.927	0.956	0.934	0.807	0.960	0.8775
SonarEW	0.975	0.937	0.852	0.912	0.958	0.915	0.995	0.960	0.9362
SpectEW	0.909	0.836	0.991	0.826	0.919	0.826	0.877	0.880	0.8463
Tic-tac-toe	0.833	0.821	0.785	0.808	0.788	0.791	0.822	0.810	0.7983
Vote	0.987	0.951	0.939	0.966	0.973	0.963	0.962	0.970	0.9653
WaveformEW	0.797	0.734	0.753	0.737	0.815	0.751	0.749	0.800	0.7429
WineEW	1.000	0.993	0.959	0.989	0.989	0.989	0.999	1.000	0.9843
Zoo	1.000	1.000	0.980	0.993	0.932	0.958	0.983	1.000	0.9775
Rank (F-test)	1.78	6.00	6.78	5.92	4.28	5.50	4.86	3.03	6.86

, it can be seen that the proposed approach BHHO${}_{TV4}$ has achieved the best accuracy rates on twelve datasets compared to results presented in previous studies on the same datasets. We can also observe that BHHO${}_{TV4}$ reached the highest accuracy rates on six datasets. In addition, the F-test results indicate that BHHO${}_{TV4}$ is ranked as the best in comparison with results of other algorithms used in preceding works.

In general, the results reflect the impact of the adopted binarization scheme on the performance of HHO in scanning the binary search space for finding the optimal solution (e.g., the ideal or near to the ideal subset of features). It is evident that the utilized time-varying TFs, in particular, TV${}_{V4}$ can remarkably enhance the exploration and exploitation of the HHO algorithm. A potential key factor behind the superiority of BHHO${}_{TV4}$ is that changing the shape of TV${}_{V4}$ transfer function over generations has enabled the HHO algorithm to obtain an appropriate balance between exploration and exploitation phases and boosted the HHO algorithm to reach areas containing highly valuable features in the search space. Furthermore, similar to many materialistic algorithms, HHO suffers from the problem of sliding into local optima. The accuracy rates of BHHO${}_{TV4}$ compared to other algorithms prove its superior capability in preserving the population diversity during the search procedure. Hence, preventing the occurrence of an early convergence problem.

7. Conclusions and Future Directions

In this paper, various FS approaches were developed using a recently introduced swarm-based optimizer named HHO. The proposed methods integrate the HHO algorithm with V-shaped time-varying binarization schemes to enable HHO to work in a binary search space. Various well-known datasets from the UCI data repository were utilized for evaluating the introduced approaches, and the results of the best approach BHHO${}_{TV4}$ were compared with those obtained from several meta-heuristic-based FS approaches such as BGSA, BPSO, BBA, BSSA, and BWOA. It is clear from the obtained results that the efficiency of HHO in the FS domain is highly influenced by the binarization scheme used. The proposed BHHO${}_{TV4}$ can often overtake other FS approaches presented in previous studies. In future work, we will study the effect of using S-shaped time-varying binarization schemes on the performance of HHO in the FS problem.