Vortex Ring Theory—An Alternative to the Existing Actuator Disk and Rotating Annular Stream Tube Theories

Abstract

Currently, the actuator disk theory (ADT) and the rotating annular stream-tube theory (RAST), both of which predicate on the axial momentum and generalized momentum theories, among others, are commonly used in investigating the aerodynamic characteristics of horizontal axis wind turbines (HAWTs). These theories, which are based on a rotor with an infinite number of blades, typically do not properly capture the flow physics of wind blowing past the rotors of HAWTs. A vortex ring theory (VRT) that analyzes HAWTs based solely on the characteristics of fluids flowing past obstructions is proposed. The VRT is not predicated on the assertion that the induced velocity in the wake is twice the induced velocity at the rotor. On the contrary, it splits the axial induction factor in the wake into two components, namely, the induction or interference factor due to the solidity of the rotor and the induction factor due to the wake of the rotor a_w; a_w and its azimuthal counterpart are determined using the Biot–Savart law. The pressure differences across the rotor segments of a HAWT are derived from the Bernoulli equation for all the three theories. Blade segment/local areas based on the blade sectional geometry of the rotor are used in the case of the VRT to estimate the local forces. All the calculations in this study are based on the design parameters of the 5 MW National Renewable Energy Laboratory’s reference offshore wind turbine. Pressure differences are plotted as functions of local radii using the calculated axial and azimuthal induction factors for each theory. The local power coefficient is plotted as a function of the local tip-speed ratio, while the local thrust coefficient is plotted as a function of the local radii for all the three theories. There is piece-wise agreement between the VRT, the ADT, the RAST and numerical and experimental data available in the literature.

1. Introduction

This paper compares a vortex ring theory (VRT) that is not based on the general momentum theory to the existing actuator disk theory (ADT) [1] and the rotating annular stream-tube theory (RAST) [2,3]. The ADT and the RAST, whose origins are discussed hereafter, rely on the axial momentum balance in their formulation. The VRT is different from the ADT and the RAST in the sense that these two theories rely on the idealization that the wind speed at the wind turbine’s (WT) rotor is the average of the wind speed in the wake and the free-stream speed of the wind upstream of the WT. The VRT considers the fact that the wind slows down as it flows past the WT, resulting in an induction or interference factor due to solidity a_s, and that a further reduction in the wind speed occurs in the wake, resulting in an axial induction factor due to wake rotation a_w. There is also a tangential or azimuthal component of the induction factor due to wake rotation a’, commonly called the azimuthal or angular induction factor. The RAST also makes use of the angular induction factor. Thus, per the VRT, the axial induction factor at the WT wake is δ = a_s + a_w and not twice the induction factor at the WT rotor. It is worth noting that for a = 0.5, the freestream speed in the axial direction at the Trefftz plane is zero in the cases of the ADT and the RAST, whereas it is non-zero in the case of the VRT because a_s = 0.5 does not necessarily result in a δ = 1. The VRT represents the wake of a horizontal-axis WT (HAWT) with a conical control volume (CV) and applies the Biot–Savart law [4] to the CV to determine a’ and a_w. The CV is a conical helix since the flow past a WT rotor is solenoidal and a potential flow. This conical CV should not be misconstrued to be a diffuser, as is typical of shrouded WTs. The intent of this paper is to delve into the aerodynamics of commercial-scale unshrouded WTs. The axial momentum balance across the rotor of a HAWT forms the basis upon which Rankine formulated the ADT [1]. He represented the rotor with a permeable disk of cross-sectional area A, which extracts energy from the air flowing past it by reducing its pressure. Upstream the HAWT, the air pressure is above atmospheric due to the slowing down of the airstream. As the airstream passes through the WT, it loses pressure [1]. Improvements on this theory were made by Froude [5] who included the effects of the wake in his calculations and stated that the induced velocity at the wake of an actuator disk is twice the induced velocity at the disk.

Chattot [4] attempted to extend the ADT to unsteady fluid flow. In his treatise, he expatiated on both the steady and unsteady flow past a HAWT using a vortex tube as his CV. The vortex tube consisted of a continuous succession of vortex rings shed by the rotor and carried downstream by the flow. Suffice it to say, Chattot’s CV is quasi-cylindrical and does not seem to account for the expansion of the flow resulting from the slowing down of the air as it passes through the rotor. After rigorous mathematical manipulations, this researcher showed that at steady state, the induced velocity downstream the rotor at the Trefftz plane is twice the induced velocity at the rotor.

In his bid to estimate the maximum power extracted by a HAWT, Betz used the one-dimensional mass conservation and momentum conservation laws in conjunction with the ADT first developed by Rankine and Froude for propellers [5]. Other schools of thought [1] hold that the ADT is the brainchild of Rankine. The Betz model dwells on the premise that the power extracted by the WT is solely derived from the pressure drop across the rotor. This pressure drop results in a static thrust on the rotor [6]. Alternatively stated, a fluid particle passing through the WT rotor loses part of its kinetic energy (KE), viz, the flow through a WT slows down gradually from an upstream free-stream speed of U₀ to an average value far downstream in the wake U_w. The static pressure increases from its upstream value P_∞ to a value P_r⁺ just in front of the rotor and then drops to P_r⁻ behind the rotor. The difference in static pressure between the rotor inlet and its outlet results in an axial force exerted on the rotor. Recovery of the pressure lost by the wind as it flows past the WT occurs gradually in the wake until the initial free-stream pressure P_∞ is attained. It is worth noting that P_r⁺ − P_∞ > P_∞ − P_r⁻ [7].

The flow past a WT rotor is decelerated. Ideally, this deceleration of flow can result in a maximum power extraction of 59.26% of the initial KE per unit time of the wind by a WT rotor as established from the ADT, which is based on the conservation laws of flow as discussed in the foregoing paragraph. As stated earlier, the ADT replaces the WT rotor with a permeable disk with a distributed load, yielding the same overall thrust as the actual rotor. Despite this far-reaching abstraction, the ADT is the basis of WT aerodynamics. The maximum efficiency achievable by a HAWT is attributed to Betz by most German and British scholars, while Russians attribute it to Joukowsky [8]. In their bid to achieve good analytical results, Keane et al. [9] developed an analytical method predicated on the conservation of mass and linear momentum in the context of the ADT and the assumption that the velocity deficit in the wake follows a double Gaussian distribution.

Existing versions of the VRT, typically called ring vortex theories, predicate on the fact that the axial induction coefficient at the wake is 2a or in other words the wind speed at the wake of a WT is U_w = U₀(1− 2a). A case in point is the ring vortex actuator disk model by Bontempo et al. [10]. Bontempo et al. [10] proposed a ring-vortex actuator disk theory (RVADT) based on a uniformly loaded disk with no wake rotation, predicated on the axial and generalized momentum theories, respectively. They used their theory to numerically investigate the effects of the hub of HAWTs on the flow past a WT rotor. Per these researchers, the hub blockage effects are more pronounced in small HAWTs whose hub radius to rotor radius ratios range between 25 and 30% than in large HAWTs, which typically have hub radius to rotor radius ratios ranging between 4 and 5%. These researchers assert that hub blockage effects on large HAWTs are lower than those of smaller HAWTs such that neglecting these effects has little impact on the solution for large HAWTs than for smaller HAWTs. The RVADT models the flow induced by the rotor disk and hub with ring sheet vortices, which are discretized through a classical panel method by utilizing a homogeneous Dirichlet boundary condition for the velocity just beneath the hub vortex sheet, while a free force condition is imposed along the entire boundary [10].

These actuator disk-based ring vortex theories have a drawback in the sense that when a = 0.5, the axial component of the wind speed at the wake is zero, something that causes the air particles to stagnate at the Trefftz plane and undergo circular motion. This is not what occurs in real life. The proposed VRT does not result in a zero axial wind speed at the wake when the interference factor is 0.5 because the induction factor due to wake rotation a_w is not necessarily 0.5.

Other models have been used by numerical analysts to study WT wakes. Wake modeling approaches include empirical correlations, the ADT and full three-dimensional computational fluid dynamics (CFD) simulations. Analytical methods, such as Glauert’s blade element momentum theory (BEMT), have been extended to computational WT models, such as the vorticity–velocity model (VVM) [9]. The BEMT combines a CV conservation of momentum analysis with the blade sectional analysis [11]. The BEMT is an upshot of the general momentum theory developed by Glauert and Joukowsky [5,12]. Although interesting solutions of the general momentum equations were developed for special cases with simplifying assumptions, these researchers were not able to provide closure with an analytically determined axial force equation; later researchers determined that there was not enough information to account for an axial force balance [12]. According to the BEMT, the axial induction factor varies radially and azimuthally across the rotor [9]. Another numerical model is the actuator line model (ALM). The ALM represents the three rotor blades of a HAWT by a rotating body of forces. The force per unit span on a rotor blade is estimated and the total force on the rotor is calculated by multiplying the integral of the force per unit span by the number of rotor blades [13]. Typically, the overall forces on a WT rotor are calculated by adding up the aerodynamic forces of each cross-section using the strip or blade element theory. The centrifugal and Coriolis forces that appear in the laminar boundary layer (LBL) increase the aerodynamic lift forces as compared to those in a similar two-dimensional non-rotating disk. Centrifugal forces produce a span-wise outward velocity, which gives rise to the Coriolis forces that act as favorable pressure gradients in the chord-wise direction. They also tend to reduce the thickness of the LBL due to the outward movement of the fluid, viz, the centrifugal pumping effect. This secondary flow postpones the appearance of the separation point, allowing the airfoil to reach a higher angle of attack before stalling [14]. Glauert assumed that the angular speed of the wake is never greater than the angular speed of the rotor [12] but gave no justification for this assumption. On the contrary, in real life, even static rotors impart swirl on their wakes [12].

A setback of the ADT is the fact that it results in a discontinuity in pressure as air flows past the actuator disk. The Betz–Joukowsky limit was derived using a simple balance of axial momentum and remains the basis for the maximum power extracted by an ideal HAWT rotor [15]. Chamarro et al. [16] modified the ADT in their bid to account for the effects of the atmospheric boundary layer (ABL) on the maximum efficiency of an ideal HAWT by introducing modification factor β to account for the effects of Coriolis forces on the average KE per unit mass passing through the rotor and modification factor γ to account for the effects of velocity changes over a cross-section of the CV on the average momentum. They claimed that because of the effects of the ABL, the maximum power coefficient calculated is slightly higher than the Betz–Joukowsky limit—i.e., a 1–2% increase in the Betz limit was observed.

Simisiroglou et al. [17] in their study of the analytical methods for WT wake developed independently by Jensen and Larsen, discovered that though these models are fast in calculating wake velocity deficit, they rely solely on empirical coefficients that are case specific. For instance, Jensen’s model requires a wake expansion coefficient to be determined. These two models are modifications of the ADT. Larsen considered a turbulent wake state in developing his model, while Jensen used a steady wake state. Power predictions by the latter are higher than those of the former.

By revisiting the ALM discussed in a foregoing paragraph, it was first developed by Sorensen and Shen in 2002. It represents the HAWT rotor blades by a series of point forces acting along the span of each rotor blade at the quarter chord. The ALM allows for the flow effects on the rotor blades to be modeled using discrete rotor blades without requiring the discretization of the blade boundary layer, resulting in lower computational requirements than three-dimensional blade-resolved models, while preserving the principal effects of the rotor on the flow. The ALM is implemented by discretizing each rotor blade into span-wise segments. The blade element method (BEM) is used in conjunction with the flow field data returned by a Reynolds Average Navier–Stokes (RANS) solver to estimate the two-dimensional aerodynamic forces acting at the quarter chord of each span-wise segment. The force on each segment of radius r and length δr is the vector sum of the lift and drag. The ADT, the BEMT and three-dimensional blade-resolved methods are frequently used in the simulation of the flow past HAWT rotors. The ADT and the BEM allow for fast simulations but do not accurately simulate flow features, such as unsteady wake development [18]. The BEMT neither accurately predicts the axial velocity of flow past a HAWT rotor, especially around the inner part of the rotor where wake rotation accelerates the flow and the outer part where it decelerates the flow [19].

It is worth noting that the ABL is quite stable under nocturnal conditions, so much so that a considerable shear develops with an increase in wind speed as the height above the ground increases. Shear in the wind entering large HAWTs with mega-watt capacities is a frequent operational condition. Simulating such inflow conditions using the BEM, as is typically done using most common aero-elastic codes, is fraught with uncertainty. This uncertainty is the upshot of the lack of a well-documented procedure of the BEM model for sheared inflow [20]. Yet another method for simulating the flow past HAWTs is the actuator sector method (ASM). The ASM distributes the forces applied to the fluid azimuthally to maintain a continuous flow solution for increased time steps compared to the ALM. It is a hybrid actuator model that preserves the features of the ALM and reduces the computational expense associated with small time steps, which are typical of the latter. The ASM is the intermediary between the ALM and the ADT [21].

In this paper, a comparison is made between the ADT and the RAST derived by others [2,3] and the VRT. To carry out the comparison, the design parameters of the United States Department of Energy’s National Renewable Energy laboratory’s (NREL) 5 MW reference offshore WT (OWT) are used. The WT to be investigated in this work is an upwind, three-bladed, 5 MW NREL reference HAWT. The OWT has a swept radius of 63 m, a hub height of 90 m, a hub diameter of 3 m, a cut-in rotational speed of 6.9 RPM and a rated rotational speed of 12.1 RPM. Its cut-in wind speed at 90 m hub height is 3 m/s, its rated wind speed at hub height is 11.4 m/s and its cut off wind speed is 25 m/s [22].

This paper is structured as follows: Section 2 is a critique of the generalized momentum theory that forms the basis for the ADT and the RAST. Section 3 and its subsections consist of the derivation of the basic equations of fluid dynamics from which the aerodynamic equations are developed. Section 4 outlines the steps followed in coding the necessary equations into MATLAB and the subsequent plotting of curves. Section 4 consists of the parameters of the 5 MW reference NREL OWT. Section 5 consists of the results and discussion of the results of the analysis based on the three theories; subsection below Section 5 is a comparison between the VRT results and existing numerical and experimental results. Section 6 is the conclusion of the paper.

2. Critique of Generalized Momentum-Based Theories

The generalized momentum-based theories rely on assumptions that only make mathematical sense and defy the law of conservation of momentum. Elementary mechanics reveals that if a given mass of air m, moving with a speed $U_0$ in the axial direction, impinges on a rotor of mass $m_R$, it leaves the rotor with an axial speed of $U_R$ with $U_R<U_0$. Because of wake expansion, the speed of the air in the axial direction continues to reduce to $U_3$ at the Trefftz plane with $U_3<U_R$. Since the air loses linear momentum at the rotor due to the loss of translational KE, there is no linear momentum balance because the lost translational KE of the airstream is converted to rotational KE at the rotor, which results in an angular momentum on the rotor. The rotor does not move in the axial direction, viz, $m{U}_0>m(U_R+U_3)$. Instead, the rotor rotates about its axis with an angular momentum ${P^{\prime }}_R=I_R\omega$. The angular momentum acts tangentially to the rotor. All actuator disk-based theories predicate on the scientific fallacy that the loss in momentum at the rotor results solely in an axial thrust, which is entirely borne by the air flowing past the WT rotor. This therefore means that no energy is imparted on the rotor; thus, the rotor does not rotate. It is worth noting that the rotor does not move in the axial direction—something that renders its linear momentum null.

There are now two components of momentum at the rotor: the tangential component and the axial component. Just behind the rotor, the air exhibits a solenoidal flow that results from the swirl imparted on it by the rotor. If the air mass rotates with an angular speed ω_ar just behind the rotor, its angular speed at the wake is ${\omega }_{aw}$. Then, just behind the rotor, the momentum of the mass of air is $P_{air}=m{U}_R\widehat{i}+(I_{aR}{\omega }_{ar}/R)\widehat{k}$, where $\widehat{i}$ and $\widehat{k}$ are unit vectors along the x-axis and z-axis, respectively and $I_{aR}$ is the moment of inertia of the air at the rotor. At the wake, the momentum of the mass of air is $P_w=m{U}_3\widehat{i}+(I_{aw}{\omega }_{aw}/r_w)\widehat{k}$, where $I_{aw}$ is the moment of inertia of the air at the wake. The mere fact that the air is assumed to exert only an axial thrust or force on the rotor, which is idealized as a permeable disk, means that there is no torque on the rotor since there is no moment arm and hence no rotation on the rotor. Rotation can only occur if the rotor is directly coupled to a prime mover as is typical of propellers. WTs do not have such prime movers, as they are meant to generate power. The law of conservation of energy as stated in elementary mechanics warrants that the KE lost by the mass of air be equal to the rotational KE on the rotor; thus $\frac{1}{2}m{U}_0^2=\frac{1}{2}(I_R{\omega }_R^2+m{U}_3^2)$ or loss in KE is $\frac{1}{2}m(U_0^2-U_3^2)$. Clearly the KE lost by the air is linked to the rotation of the rotor. If the mass flow rate of the air is $\dot{m}$, where an overdot denotes a time derivative, then the rate of loss of KE by the air stream is $\frac{1}{2}\dot{m}(U_0^2-U_3^2)$. This is the power extracted from the air stream by the rotor. Glauert’s momentum theory assumes that the axial thrust on the rotor is given by the rate of change of the axial momentum of the air; $T=\dot{m}(U_0-U_3)$ and the KE lost per unit time by the airstream at the rotor is TU_R. Thus, $\dot{m}(U_0-U_3)U_R=\frac{1}{2}\dot{m}(U_0^2-U_3^2)$, which upon simplifying, yields $U_R=(U_0+U_3)/2$. In his generalized momentum theory, Glauert included a tangential velocity on the actuator disk but still relied on the axial momentum theory in the axial direction [23]. The actuator disk and rotating annular stream-tube theories rely on the above theory, while the VRT does not. On the contrary, the VRT considers the reduction in the speed of the air to be the result of the solidity of the rotor and the reduction in the air speed at the wake to result from an induced velocity due to wake rotation. Like the actuator disk and rotating annular stream-tube theories, the VRT uses the Bernoulli equation to determine the pressure drop across the rotor. The VRT uses a rotor with finite blades to determine the induced velocity components. Unlike the RAST that considers a one-dimensional state in state 0, a two-dimensional state in state 1, a three-dimensional state in state 2 and a two-dimensional state in state 3, the VRT considers a one-dimensional state in state 0 and three-dimensional states in states 1, 2 and 3.

3. Development of Basic Aerodynamic Theories

The basic equations governing the aerodynamics of HAWTs are derived in this section. The ADT, the RAST and the VRT are used in deriving useful equations for the analysis of the flow past HAWT rotors. It is assumed in all the three theories that the wind flows at right angles to the WT rotor. The WT analyzed in this work is an unshrouded commercial-scale WT and not a shrouded WT that in most cases is a small WT.

The ADT [1,2,3], first thought of by Rankine, considers the rotor of a HAWT as a uniformly loaded permeable disk of area A, or a rotor with an infinite number of blades. The basic equations underlying the theory have been derived in Reference [2]. In this work, it is sufficient to state the resulting equations without proof.

The pressure drop across the WT rotor is given by

$$p_{ad}=\frac{\rho (U_0^2-U_3^2)}{2}.$$

(1)

The axial thrust on the rotor is given by

$$T_{ax}=\pi R^2{P}_{ad}=\pi R^2\frac{\rho (U_0{}^2-U_3^2)}{2},$$

(2)

and the speed of the air flowing through the rotor is given by

$$U_R=\frac{U_0+U_3}{2}.$$

(3)

Thus, the speed of the air flowing through the actuator disk is the average of the free-stream speed far upstream the disk and the speed of the air in the wake of the disk. If the induced speed at the rotor is $\Delta U$, then $\Delta U=U_0-U_R$, the axial induction coefficient a is given by

$$a=\frac{\Delta U}{U_0}=\frac{U_0-U_R}{U_0},$$

(4)

from which one has

$$U_R=U_0(1-a).$$

(5)

The wind speed at the wake of the rotor is

$$U_3=U_0(1-2a).$$

(6)

For wind speeds that vary with the radial distance from the hub to the tip of the rotor, the actuator disk can be discretized as shown in Figure 1. If an element of the disk at radius r and thickness $dr$ is considered, then the area of the element is given by $A(r)=2\pi rdr$. The corresponding speeds for the elemental disk are $U_0(r)$, $U_R(r)$ and $U_3(r)$, respectively. The pressure drop across the disk element is

$$p_{ad}(r)=\frac{\rho (U_0^2(r)-U_3^2(r))}{2}.$$

(7)

The axial induction factor at each disk element a(r) is given by

$$a(r)=\frac{U_0(r)-U_R(r)}{U_0(r)},$$

(8)

from which one has

$$U_R(r)=U_0(r)(1-a(r)).$$

(9)

Additionally,

$$U_3(r)=U_0(r)(1-2a(r)).$$

(10)

The elemental or local axial thrust is given by

$$d{T}_{ad}=A(r)p_{ad}(r)=\pi r\rho (U_0^2(r)-U_3^2(r))dr,$$

(11)

and the local thrust coefficient per unit span is given by

$$d{C}_{Tad}/dr=\frac{2r(U_0^2(r)-U_3^2(r))}{R^2{U}_0^2}.$$

(12)

The local power captured is given by

$$d\dot{W}=U_R(r)d{T}_{ad}(r)=\rho \pi r{U}_R(r)(U_0^2(r)-U_3^2(r))dr.$$

(13)

The local power coefficient is given by

$$d{C}_p=\frac{2d\dot{W}}{\rho A{U}_0^3}=\frac{2r{U}_R(r)(U_0^2(r)-U_3^2(r))dr}{R^2{U}_0^3}.$$

(14)

The elemental or local tip speed ratio is

$$\lambda (r)=\frac{\omega r}{U_0(r)}.$$

(15)

The RAST predicates on the generalized momentum theory of Glauert (1929) [2,3,24]. It is assumed that the pressure head at the far wake is equal to the pressure head in the free-stream, that pressure, wake rotation and the induction factors depend on the elemental or local annular radius and that the rotor is uniformly loaded. Additionally, it is assumed that the torque generated by the rotor is equal to the change in the angular momentum per unit time of the wake. All the assumptions made for the ADT are valid for the flow in the axial direction. If the angular speed of the rotor is $\omega$ and the induced angular speed on the rotor by the wake is ω′, then the angular speed on the rotor relative to the wake-induced angular speed is $\omega +{\omega }^{\prime }$. It is worth noting that the wake rotates in the opposite direction to the rotor. It is shown in References [2,3] that the pressure drop across the WT rotor that results from the rotating annular stream tube theory is given by

$$p_1-p_2=2\rho a^{\prime }(1+a^{\prime }){\omega }^2{r}^2.$$

(16)

The elemental axial thrust is given by

$$dT=4\pi \rho a^{\prime }(1+a^{\prime }){\omega }^2{r}^{3}dr.$$

(17)

The elemental thrust coefficient per unit span is given by

$$d{C}_T/dr=\frac{8a^{\prime }(1+a^{\prime }){\omega }^2{r}^3}{R^2{U}_0^2}.$$

(18)

The local tip-speed ratio is

$$\lambda (r)=\sqrt{\frac{a(1-a)}{a^{\prime }(1+a^{\prime })}},$$

(19)

and the local power coefficient is

$$d{C}_p=\frac{8U_0(r)a^{\prime }(1-a){\omega }^2{r}^{3}dr}{R^2{U}_0^3}.$$

(20)

It is shown in References [2,3,24] that for maximum power capture at each elemental stream-tube,

$$a^{\prime }=\frac{1-3a}{4a-1}.$$

(21)

3.1. The VRT

Unlike the actuator disk and rotating annular stream tube theories, the VRT is not based on the axial momentum theory. It is predicated on the concept that the vortex sheet of free vortices is oriented in a helical path behind the WT rotor [24]. As stated in an earlier section, there is no linear momentum balance along the axis of the WT rotor because the momentum of the rotor is not included in the axial momentum balance—something that defies the law of conservation of linear momentum. The proposed VRT, among other assumptions, relies on the KE balance across the WT rotor and uses the Bernoulli equation to determine the pressure drop across the WT rotor. It is worth noting that the Bernoulli equation deals with energy per unit volume. Based on this, the flow past the WT rotor is assumed to be fully developed, inviscid, solenoidal and a potential flow. The VRT assumes that the wake of the WT rotor is conical, resulting in a conical helix. Additionally, it is assumed that each rotor segment generates a conical helix. In a nutshell, the WT rotor generates a family of conical helices, with the cone generated by the blade tip serving as an envelope. Worthy of re-iterating is the fact that the CV considered in this paper is not a duct, neither is it a shroud nor a diffuser. The CV considered in this paper does not result in an increase in the mass flow rate of the fluid as is typical of ducted flows [24]. It is also assumed that atmospheric conditions are neutral such that the wake remains conical and that the flow through the WT rotor is uniform. As is typical of any thermodynamic process, the beginning and end states are normally important in determining the process. Like the RAST, the VRT is predicated on the fact that the WT wake induces a rotational speed in opposition to the rotation of the rotor. Unlike the actuator disk and rotating annular stream-tube theories, the VRT utilizes the Biot–Savart law [4] to determine a wake-induced axial speed coupled with a wake-induced tangential speed on the WT rotor. The difference between the two methods arises from the fact that the RAST considers angular momentum conservation in deriving the wake angular velocity, while the VRT uses Kelvin’s circulation theorem and Helmholtz vortex theorem [25] in deriving the wake angular velocity. Helmholtz vortex theorem should not be misconstrued for the Helmholtz theorem that states: “A vector with both source and circulation densities vanishing at infinity may be written as the sum of two parts, one of which is irrotational, the other which is solenoidal” [26]. Consult Reference [26] for a mathematical statement of Helmholtz theorem. The VRT considers a segment of the rotor blade at a radius $r$ from the center of the hub of a WT rotor of radius $R$. The span of the rotor segment is dr. The angular speed of the WT rotor is $\omega$. Much like the lifting line theory for fixed aircraft wings, the VRT assumes that each segment of the rotor blade generates a combination of bound and trailing vortices, with the trailing vortices merging with the strong blade tip vortex to form a helical vortex filament (see Figures 3 and 10 in Reference [24]). It is worth noting that the VRT considers the static pressure developed at the rotor to be the resultant of the tangential and normal components, with the tangential component resulting in the driving force on the WT rotor. Additionally, made use of by the VRT is the blade sectional geometry in the calculation of the forces. The wind velocity at each station in Figure 2 below is expressed in vector form as follows:

• Station 0: ${\overrightarrow{V}}_0=U_0\widehat{i}$,
• Station 1: ${\overrightarrow{V}}_1=u_1\widehat{i}+v_1\widehat{j}+w_1\widehat{k}$,
• Station 2: ${\overrightarrow{V}}_2=u_2\widehat{i}+v_2\widehat{j}+w_2\widehat{k}$,
• Station 3: ${\overrightarrow{V}}_3=u_3\widehat{i}+v_3\widehat{j}+w_3\widehat{k}$,

where $\widehat{j}$ is the unit vector along the y-axis.

The equations of the proposed VRT have not been derived in existing textbooks; so every step in the derivation of its basic equations is important for the sake of lucidity. It is assumed that there is no swirl at the WT inlet. Thus, $w_1=0$ and for HAWTs facing the prevailing wind direction, in terms of the local radius, $v_1=v_2$, $w_2=\omega r(1+a^{\prime }(r))$, $w_3={\omega }_3{r}_3$, $u_1=u_2=u_r(r)$, $u_r(r)=U_0(r)(1-a_s(r))$ and $u_3=U_0(r)(1-\delta (r))$, where $a^{\prime }(r)$ is the local azimuthal induction factor, and the flow through the WT rotor is assumed to be uniform; $\delta (r)=a_s(r)+a_w(r)$, where a_s(r) is the local induction coefficient due to solidity given by $a_s(r)=\frac{U_0(r)-u_r(r)}{U_0(r)}$ and $a_w(r)$ is the local axial induction factor due to the wake. Note that $a^{\prime }(r)$ and $a_w(r)$ are determined using the Biot–Savart law [4,24,25,26,27].

3.1.1. The Biot–Savart Law and the Induction Factors of a HAWT Rotor

A three-dimensional representation of the flow of wind past a HAWT rotor of radius R is shown in Figure 3. Far from it, the flow investigated in this paper is not an axisymmetric flow that typically has the tangential component of its velocity $U_T=0$ [25]. On the contrary, the vortex sheet is a solenoid with an expanding cross-section because $U_T\ne 0$. The radius of the wake at a location x downstream the rotor is R(x), as depicted in Figure 3, while the axial and tangential components of the induced velocity $d\stackrel{\rightharpoonup }{V}$ on the WT rotor are $du$ and $dw$, respectively. The coordinates of the center of the rotor are $(0,0,0)$, the coordinates of the tip of the rotor at the point P are $(0,R,0)$ and the position vector of the line $\stackrel{\rightharpoonup }{OP}$ is $0\widehat{i}+R\widehat{j}+0\widehat{k}$. At the point x from the center of the rotor, the position vector of the wake radius at the point $P^{\prime }$ is given by $x\widehat{i}+0\widehat{j}+R(x)\widehat{k}$. The tangent at P’ to the arc subtending an elemental angle $\delta \theta$ is $\stackrel{\rightharpoonup }{T}$. As shown in Figure 3, the center of the wake is located at the point $(x,0,0)$. Since the strong tip vortices are located at the edge of the WT wake and the root vortices lie in a linear path along the axis of the rotor [24], it is worth estimating the induced velocity in terms of rotor parameters and then distributing its effects uniformly on each segment of the rotor blade. Emphasis is laid on the fact that for a convergent solution to be achieved, a_w < 1 and a’ < 1. All local counterparts of these factors must adhere to this rule. Only the local forces, local power and local power coefficients are integrated to obtain the corresponding rotor counterparts.

The position vector of the line $\overline{P{P}^{\prime }}$ $\overrightarrow{l}$ is $x\widehat{i}-R\widehat{j}+R(x)\widehat{k}$. From elementary vector algebra, the tangent at $P^{\prime }$ is given by

$$\stackrel{\rightharpoonup }{T}=\nabla \times {\stackrel{\rightharpoonup }{xP}}^{\prime },$$

(22)

leading to

$$\stackrel{\rightharpoonup }{T}=\nabla \times R(x)\widehat{k},$$

(23)

where $\nabla =\frac{d}{dx}\widehat{i}+\frac{d}{dy}\widehat{j}+\frac{d}{dz}\widehat{k}$. After solving for the cross product in Equation (23), the resulting tangent is

$$\stackrel{\rightharpoonup }{T}=\frac{d(r(x))\widehat{i}}{dy}-\frac{d(r(x))\widehat{j}}{dx},$$

(24)

leading to

$$\stackrel{\rightharpoonup }{T}=-\frac{d(r(x))\widehat{j}}{dx}.$$

(25)

The unit vector in the direction of $\stackrel{\rightharpoonup }{T}$ is

$$\widehat{T}=\frac{\stackrel{\rightharpoonup }{T}}{\left|\stackrel{\rightharpoonup }{T}\right|},$$

(26)

leading to

$$\widehat{T}=-\widehat{j}.$$

(27)

The length of the arc subtending the angle $\delta \theta$ is

$$ds=R(x)\delta \theta ,$$

(28)

and the position vector of the arc in the direction of the tangent is

$$\overrightarrow{ds}=-R(x)\delta \theta \widehat{j}.$$

(29)

The Biot–Savart law [4] states

$$d\stackrel{\rightharpoonup }{V}=\frac{\Gamma }{4\pi }{\displaystyle \oint \frac{\stackrel{\rightharpoonup }{l}\times \overrightarrow{ds}}{|\stackrel{\rightharpoonup }{l}{|}^3}},$$

(30)

where $\Gamma$ is the circulation and $\overrightarrow{l}$ is the position vector of $\stackrel{\rightharpoonup }{ds}$ relative to the rotor segment. Suffice it to say that during still weather conditions, when there is no wind, there is no wake behind the WT rotor and $\overrightarrow{l}=(0,0,0)$. Mathematically speaking, the Biot–Savart law becomes indeterminate in still weather condition, i.e., when $\overrightarrow{l}=(0,0,0)$. Applying the Biot–Savart law [4,24,25,26,27] to Figure 3 leads to

$$d\stackrel{\rightharpoonup }{V}=\frac{\Gamma }{4\pi }{\displaystyle \underset{-\pi }{\overset{\pi }{\int }}\frac{\stackrel{\rightharpoonup }{l}\times \overrightarrow{ds}}{|\stackrel{\rightharpoonup }{l}{|}^3}}.$$

(31)

Substituting for $\stackrel{\rightharpoonup }{l}$ and $\stackrel{\rightharpoonup }{ds}$ in Equation (31) yields

$$d\stackrel{\rightharpoonup }{V}=\frac{\Gamma }{4\pi }{\displaystyle \underset{-\pi }{\overset{\pi }{\int }}\frac{(x\widehat{i}-R\widehat{j}+R(x)\widehat{k})\times (-R(x)\delta \theta \widehat{j})}{{(x^2+R^2+R{(x)}^2)}^{3/2}}}.$$

(32)

But $(x\widehat{i}-R\widehat{j}+R(x)\widehat{k})\times (-R(x)\delta \theta \widehat{j})=R{(x)}^2\delta \theta \widehat{i}-xR(x)\delta \theta \widehat{k}$, which after substitution in Equation (32), yields

$$d\stackrel{\rightharpoonup }{V}=\frac{\Gamma }{4\pi }{\displaystyle \underset{-\pi }{\overset{\pi }{\int }}\frac{(R{(x)}^2\widehat{i}-xR(x)\widehat{k})\delta \theta }{{(x^2+R^2+R{(x)}^2)}^{3/2}}}=\frac{\Gamma }{4\pi }\frac{(R{(x)}^2\widehat{i}-xR(x)\widehat{k})}{{(x^2+R^2+R{(x)}^2)}^{3/2}}{\displaystyle \underset{-\pi }{\overset{\pi }{\int }}\delta \theta }.$$

(33)

Integrating Equation (33) and simplifying the resulting equation yield

$$d\stackrel{\rightharpoonup }{V}=\frac{\Gamma }{2}\frac{(R{(x)}^2\widehat{i}-xR(x)\widehat{k})}{{(x^2+R^2+R{(x)}^2)}^{3/2}}.$$

(34)

Clearly, the axial component of the induced velocity is

$$du=\frac{\Gamma R{(x)}^2}{2{(x^2+R^2+R{(x)}^2)}^{3/2}},$$

(35)

and the tangential component of the induced velocity is

$$dw=\frac{-\Gamma xR(x)}{2{(x^2+R^2+R{(x)}^2)}^{3/2}}.$$

(36)

Given that the axial component of the free stream speed is $U_0$ in the axial direction and the angular speed of the WT rotor is $\omega$, the circulation of the air in contact with the rotor is $\Gamma =2\pi R^2\omega$ and the tangential speed of the air particles on the WT rotor is expressed as $U_T=\omega R$. It should be noted that the air particles interacting with the rotor rotate at the same tangential speed as the rotor and that because there is no swirl at the WT inlet, the induced tangential velocity in the rotor plane is $d{V}_z=-a^{\prime }\omega R$ [24]. Substituting for the circulation in Equations (35) and (36) and dividing Equation (34) by $u_0$ and Equation (35) by $-\omega R$ yield the elemental induction coefficients due to the WT wake in the axial and tangential directions, respectively, as shown below:

$$a_w=\frac{d{V}_x}{U_0}=\frac{\pi r^2\omega R{(x)}^2}{U_0{(x^2+R^2+R{(x)}^2)}^{3/2}},$$

(37)

and

$$a^{\prime }=\frac{d{V}_z}{-\omega R}=\frac{\pi RxR(x)}{{(x^2+R^2+R{(x)}^2)}^{3/2}},$$

(38)

where $a_w$ is the axial induction factor due to the WT wake and $a^{\prime }$ is the azimuthal or angular induction factor. In wind energy engineering practice, trial values of these factors are used in calculations until suitable values are attained at which convergence is achieved. It is important to note that a′ is based on the tangential speed of the rotor because the tangential component of the induced velocity in the plane of the rotor is $a^{\prime }\omega R$ due to the absence of swirl in the flow upstream the WT, whereas the tangential component of the induced velocity at the WT’s wake is $2a^{\prime }\omega R$ [24]. Note that it would be erroneous to use $2a^{\prime }\omega R$ in calculating the azimuthal induction coefficient at the WT rotor. Cognizant of the fact that in real fluids, the trailing vortices curl up around the strong tip vortices, resulting in a vortex filament [24]; only the tip vortex is used in describing the CV in this paper. From the geometry of the CV, the radius of the wake at a distance x from the WT is given by

$$R(x)=R+x\tan \alpha ,$$

(39)

where α is half the cone angle of the CV. Similarly, for a segment of the rotor blade at a radius r from the center of the hub,

$$r(x)=\frac{r\eta +x\tan \alpha }{\eta },$$

(40)

where η is the number of rotor blade segments or elements. At station 3 in Figure 2, x is shown to lie within $3R\le x\le 4.5R$ [7]. Let $x=L$. Then, the radius of the wake at the Trefftz plane is given by

$$R_3=R+L\tan \alpha .$$

(41)

In terms of the section or local radius,

$$r_3=\frac{r\eta +L\tan \alpha }{\eta }.$$

(42)

Replacing $R(x)$ in Equations (37) and (38) with $r_3=\frac{r\eta +L\tan \alpha }{\eta }$, letting L = 4R and simplifying the resulting equations yield the following local induction factors:

$$a_w(r)=\frac{\pi r^2\eta \omega {(r\eta +4R\tan \alpha )}^2}{U_0{(16{\eta }^2{R}^2+2{\eta }^2{r}^2+8r\eta R\tan \alpha +16R^2{\tan }^2\alpha )}^{3/2}},$$

(43)

and

$$a^{\prime }(r)=\frac{2\pi R{\eta }^{2}r(\eta r+4R\tan \alpha )}{{(8{\eta }^2{R}^2+{\eta }^2{r}^2+4r\eta R\tan \alpha +8R^2{\tan }^2\alpha )}^{3/2}}.$$

(44)

Recalling Kelvin’s circulation theorem: “The circulation of an inviscid fluid around a loop moving with the fluid is constant with time if the body forces on the fluid are conservative” [25,27]. Mathematically stated,

$$\frac{d\Gamma }{dt}=0,$$

(45)

leading to

$$d\Gamma =0.$$

(46)

Integrating Equation (41) yields

$${\displaystyle \int d\Gamma }=\Gamma =\mathrm{constant}.$$

(47)

The above integral is in keeping with Helmholtz Vortex theorems [25,27] that state the following:

• Vortex lines move with the fluid. Otherwise stated, a vortex filament cannot start or end in a fluid; it must form a closed loop or extend to infinity [27].
• The circulation or strength of a vortex tube is always constant along the flow.
• Circulation does not vary with time.

Worthy of emphasizing here is the fact that the vortex filament at a distance x from the rotor forms a closed circular loop and does not extend to infinity. Applying the foregoing to stations 2 and 3 yields

$${\Gamma }_2={\Gamma }_3.$$

(48)

However, $\Gamma ={\displaystyle {\iint }_A\mathsf{\Omega }dA}=\mathsf{\Omega }A=\mathrm{constant}$, where Ω is the vorticity; Ω is twice the local angular speed. Substituting for ${\Gamma }_2={\mathsf{\Omega }}_2{A}_2$ and ${\Gamma }_3={\mathsf{\Omega }}_3{A}_3$ in Equation (48) yields

$${\mathsf{\Omega }}_2{A}_2={\mathsf{\Omega }}_3{A}_3,$$

(49)

where ${\mathsf{\Omega }}_2=2\omega (1+a^{\prime }(r))$, $A_2=\pi r^2$, ${\mathsf{\Omega }}_3=2{\omega }_3$ and $A_3=\pi r_3{}^2$. Substituting these parameters in Equation (44) yields $2\omega (1+a^{\prime }(r))\pi r^2=2{\omega }_3\pi r_3{}^2$, which after simplifying, leads to

$$\omega (1+a^{\prime }(r))\pi r^2={\omega }_3\pi r_3{}^2.$$

(50)

Equation (50) is an upshot of the application of Helmholtz vortex theorem to stations 2 and 3 in Figure 2. It is worth noting that station 2 is in the plane of the rotor such that the angular speed of the flow in station 2 is $\omega (1+a^{\prime }(r))$, while station 3 is in the wake. Solving Equation (50) for ${\omega }_3$ yields

$${\omega }_3=\omega (1+a^{\prime }(r)){(\frac{r_2}{r_3})}^2.$$

(51)

The Bernoulli equation can be cast in vector form as

$$p+\frac{1}{2}\rho \stackrel{\rightharpoonup }{V}•\stackrel{\rightharpoonup }{V}+\rho gz=\mathrm{constant}.$$

(52)

Applying the Bernoulli equation to stations 0, 1, 2 and 3 in Figure 4 yields $p_0+\frac{1}{2}\rho {\stackrel{\rightharpoonup }{V}}_0•\stackrel{\rightharpoonup }{V_0}+\rho g{z}_0-\rho g{h}_{1,2}=p_3+\frac{1}{2}\rho {\stackrel{\rightharpoonup }{V}}_3•{\stackrel{\rightharpoonup }{V}}_3+\rho g{z}_3$, which after appropriate substitution, leads to

$$p_0+\frac{1}{2}\rho U_0{}^2+\rho g{z}_0-\rho g{h}_{1,2}=p_3+\frac{1}{2}\rho (u_3^2+v_3^2+w_3^2)+\rho g{z}_3,$$

(53)

where $h_{1,2}$ is the head lost at the HAWT. Transposing Equation (53) to make the term containing $h_{1,2}$ the subject yields

$$\rho g{h}_{1,2}=p_0-p_3+\frac{1}{2}\rho (U_0{}^2-u_3^2-v_3^2-w_3^2)+\rho g(z_0-z_3).$$

(54)

For no slip in the radial direction, $v_3=0$. Substituting for $w_3={\omega }_3{r}_3$, $u_3=U_0(1-\delta )$ and $z_0=z_3$ in Equation (54) yields

$$\rho g{h}_{1,2}=p_0-p_3+\frac{1}{2}\rho (U_0{}^2-U_0^2{(1-\delta )}^2-{\omega }_3^2{r}_3^2).$$

(55)

Simplifying Equation (55) leads to

$$\rho g{h}_{1,2}=p_0-p_3+\frac{1}{2}\rho (U_0^2\delta (2-\delta )-{\omega }_3^2{r}_3^2).$$

(56)

Applying the Bernoulli equation between stations 1 and 2 yields

$$p_1+\frac{1}{2}\rho {\stackrel{\rightharpoonup }{V}}_1•\stackrel{\rightharpoonup }{V_1}+\rho g{z}_1-\rho g{h}_{1,2}=p_3+\frac{1}{2}\rho {\stackrel{\rightharpoonup }{V}}_2•{\stackrel{\rightharpoonup }{V}}_2+\rho g{z}_2,$$

(57)

leading to

$$p_1+\frac{1}{2}\rho {(u_1^2+v_1^2+w_1^2)}^2+\rho g{z}_1-\rho g{h}_{1,2}=p_2+\frac{1}{2}\rho (u_2^2+v_2^2+w_2^2)+\rho g{z}_2.$$

(58)

Transposing Equation (58) to make the term in $h_{1,2}$ the subject yields

$$\rho g{h}_{1,2}=p_1-p_2+\frac{1}{2}\rho (u_1^2+v_1{}^2+w_1^2-u_2^2-v_2^2-w_2^2)+\rho g(z_1-z_2).$$

(59)

However, $u_1=u_2=U_R$, $v_1=v_2$, $w_2=\omega (1+a^{\prime })r$, $z_1=z_2$ and $w_1=0$ in the case of a first row WT. Substituting these parameters in Equation (59) yields

$$\rho g{h}_{1,2}=p_1-p_2-\frac{1}{2}\rho {\omega }^2{r}^2{(1+a^{\prime })}^2.$$

(60)

Equating Equation (60) to Equation (56) and making $p_1-p_2$ the subject yield

$$p_1-p_2=p_0-p_3+\frac{1}{2}\rho [U_0^2\delta (2-\delta )+{\omega }^2{r}^2{(1+a^{\prime })}^2-{\omega }_3^2{r}_3^2].$$

(61)

Assuming that the turbulent ABL results in full recovery, $p_3\simeq p_0$ and Equation (61) becomes

$$p_1-p_2=\frac{1}{2}\rho [U_0^2\delta (2-\delta )+{\omega }^2{r}^2{(1+a^{\prime })}^2-{\omega }_3^2{r}_3^2].$$

(62)

In terms of blade segment parameters, $U_0=U_0(r)$, $\delta =\delta (r)$ and $a^{\prime }=a^{\prime }(r)$; thus,

$${\omega }_3=\omega (1+a^{\prime }(r)){(\frac{r_2}{r_3})}^2.$$

(63)

Substituting Equation (63) in Equation (62) yields the pressure drop across the WT rotor

$$p_1-p_2=\frac{1}{2}\rho (U_0^2(r)\delta (r)(2-\delta (r))+{\omega }^2{r}^2{(1+a^{\prime }(r))}^2(1-{(\frac{r}{r_3})}^2)).$$

(64)

Applying the continuity equation in the axial direction yields $r_3^2={(\frac{1-a_s(r)}{1-\delta (r)})}^2{r}^2$ and Equation (64) becomes

$$p_1-p_2=\frac{1}{2}\rho [\delta (r)U_0^2(r)(2-\delta (r))+{\omega }^2{r}^2{(1+a^{\prime }(r))}^2(1-{(\frac{1-\delta (r)}{1-a_s(r)})}^2))].$$

(65)

In terms of the local radius r, $p_1-p_2$ in Equation (65) becomes $p_1(r)-p_2(r)$.

3.1.2. Blade Sectional Parameters and Local Blade Forces

In a bid to calculate the forces on the rotor segment based on the static pressure determined using the VRT, the geometry and kinetics of the WT rotor blades must be taken into consideration. Some readers may be doubtful as to why the local planform area of the rotor is used in estimating the resultant force on the rotor blade; this is so because each rotor blade segment has a local twist angle such that the resultant static pressure does not act normally to the rotor blade but acts normally to the orthogonal projection of the rotor blade. Based on the local solidity ratio ${\sigma }^{\prime }(r)$, at a radius $r$ from the center of the rotor’s hub, the local projected or planform area of a k-blade rotor $A(r)$, where k is the number of rotor blades, is given by

$$A(r)=\pi {\sigma }^{\prime }(r)r^2.$$

(66)

However, ${\sigma }^{\prime }(r)=kc(r)/2\pi r$, where $c(r)$ is the local chord length of the rotor’s airfoil cross-section at a radius $r$ from the rotor hub [2,3]. Substituting for ${\sigma }^{\prime }(r)$ in Equation (62) and simplifying the resulting equation yield

$$A(r)=\frac{kc(r)r}{2}.$$

(67)

Differentiating Equation (67) with respect to r leads to

$$d(A(r))=\frac{kc(r)dr}{2}+\frac{krd(c(r))}{2}.$$

(68)

For very long slender rotor blades, $dc(r)$ is very small and $dc(r)\to 0$, leading to

$$\frac{dA(r)}{dr}=\frac{kc(r)}{2}.$$

(69)

Let $p_1(r)-p_2(r)$ be equal to $\Delta p$. Then, the elemental resultant force per unit span on the WT rotor, ${F^{\prime }}_R$ is given by ${F^{\prime }}_R=\frac{dA(r)}{dr}\Delta p$ and after substituting for $\frac{dA(r)}{dr}$ in the expression for ${F^{\prime }}_R$, one has

$${F^{\prime }}_R=k\Delta pc(r)/2.$$

(70)

Substituting the expression for $\Delta p$ from Equation (65) in Equation (70) yields

$${F^{\prime }}_R=\frac{1}{4}k\rho c(r)[\delta (r)U_0^2(r)(2-\delta (r))+{\omega }^2{r}^2{(1+a^{\prime }(r))}^2(1-{(\frac{1-\delta (r)}{1-a_s})}^2))].$$

(71)

The tangential force per unit span on the rotor segment is

$$\frac{d{F}_T}{dr}={F^{\prime }}_R\cos [\theta (r)],$$

(72)

leading to

$$\frac{d{F}_T}{dr}=\frac{1}{4}k\rho c(r)[\delta (r)U_0^2(r)(2-\delta (r))+{\omega }^2{r}^2{(1+a^{\prime }(r))}^2(1-{(\frac{1-\delta (r)}{1-a_s})}^2))]\cos [\theta (r)].$$

(73)

The normal force per unit span on the rotor segment is given by

$$\frac{d{F}_N}{dr}={F^{\prime }}_R\sin [\theta (r)],$$

(74)

leading to

$$\frac{d{F}_N}{dr}=\frac{1}{4}k\rho c(r)[\delta (r)U_0^2(r)(2-\delta (r))+{\omega }^2{r}^2{(1+a^{\prime }(r))}^2(1-{(\frac{1-\delta (r)}{1-a_s})}^2))]\sin [\theta (r)].$$

(75)

The local thrust coefficient per unit span is given by

$$\frac{d{C}_T}{dr}=\frac{1}{2\pi R^2{U}_0^2}kc(r)[\delta (r)U_0^2(r)(2-\delta (r))+{\omega }^2{r}^2{(1+a^{\prime }(r))}^2(1-{(\frac{1-\delta (r)}{1-a_s})}^2))]\sin [\theta (r)].$$

(76)

The local torque is given by

$$dQ=\frac{1}{4}k\rho rc(r)[\delta (r)U_0^2(r)(2-\delta (r))+{\omega }^2{r}^2{(1+a^{\prime }(r))}^3(1-{(\frac{1-\delta (r)}{1-a_s})}^2))]\cos [\theta (r)]dr.$$

(77)

The local power captured by the rotor segment is given by

$$d\dot{W}=\frac{1}{4}k\omega \rho rc(r)[\delta (r)U_0^2(r)(2-\delta (r))+{\omega }^2{r}^2{(1+a^{\prime }(r))}^2(1-{(\frac{1-\delta (r)}{1-a_s})}^2))]\cos [\theta (r)]dr.$$

(78)

The local power coefficient is given by

$$d{C}_p=\frac{1}{2\pi R^2{U}_0^3}k\omega c(r)[\delta (r)U_0^2(r)(2-\delta (r))r+{\omega }^2{r}^3{(1+a^{\prime }(r))}^2(1-{(\frac{1-\delta (r)}{1-a_s})}^2))]\cos [\theta (r)]dr,$$

(79)

where $\theta \left(r\right)$ is the angle of inclination of $F_R^{\prime }$ to the tangential force on each rotor segment. It is estimated from the tangential speed on the rotor and the axial wind speed at the rotor by expressing its tangent as

$$\tan \theta (r)=\frac{1-a_s(r)}{\lambda (r)(1+a^{\prime }(r))}.$$

(80)

It is evident from Equation (15) that the local tip-speed ratio is a function of r, and to reduce the number of equations, a’(r), a_w(r) and dC_p are expressed as functions of r instead of being expressed as functions of the local tip-speed ratio.

4. Methodology

The design parameters of the 5 MW NREL reference OWT outlined in Reference [22] as shown below, are used to validate the VRT in conjunction with the existing theories discussed in this paper:

• WT rating: 5 MW,
• Rotor diameter: 126 m,
• Rotor orientation: upwind,
• Hub diameter: 3 m,
• Number of blades: 3,
• Hub height: 90 m,
• Cut-in wind speed: 3 m/s,
• Rated tip-speed: 80 m/s,
• Cut-out wind speed: 25 m/s,
• Overhang: 5 m,
• Cut-in RPM: 6.9,
• Shaft tilt angle: 5°,
• Rated rotor RPM: 12.1,
• Pre-cone: 2.5°,
• Rated wind speed: 11.4 m/s.

Suffice it to emphasize that the present paper is solely a theoretical paper based on analytical methods as demonstrated in the previous section. Equations (7), (8), (12), (14), (15), (16), (18), (20), (21), (65), (73), (75), (79) and (80) are coded in MATLAB and graphs are plotted in Section 5. Based on the assertion that the axial induction factor of an optimum rotor lies within 1/4 ≤ a ≤ 1/3 [5], a value of a = 0.293 is used in determining U_R at the hub height. A value of U_R = 5.93 is estimated. The value a = 0.293 is the average of the range of optimum values. It is worth noting that based on Equation (21), a’ = ∞ at a = 1/4 and a’ = 0 at a = 1/3. To estimate the wind speed distribution across the rotor blade span, the wind shear equation is used. In this case, the WT rotor hub height h is the reference height. Based on 24-year data for the Maryland offshore wind farm, the average wind speed at a hub height of 90 m for the NREL OWT under investigation is estimated to be 8.37 m/s. The corresponding angular speed of the rotor is 0.93 rad/s. The wind speed distribution across the span of the rotor is given by

$$U_0(r)=U_h{(\frac{r+h}{h})}^{\epsilon },$$

(81)

where $U_h$ is the average wind speed at hub height and ε is the wind shear exponent estimated using Countian’s correlation formula:

$$\epsilon =0.096{\log }_{10}(z_0)+0.016{({\log }_{10}(z_0))}^2+0.24,$$

(82)

in which $z_0$ is the surface roughness. An average value of $z_0=3.5\times {10}^{-4}\mathrm{m}$ is used in this paper, which is estimated from corresponding values for calm open and blown seas [3]. A value of ε = 0.099 is obtained from the above value of z₀. Substituting for $U_h=8.37\hspace{0.33em}\mathrm{m}/\mathrm{s}$, $h=90$ and ε in Equation (81) yields

$$U_0(r)=8.37{(\frac{r+90}{90})}^{0.099}.$$

(83)

Similarly, the wind speed at the WT rotor is estimated using the wind shear equation:

$$U_R(r)=5.92{(\frac{r+90}{90})}^{0.099}.$$

(84)

The local axial induction factor due to solidity in the case of the VRT or the local axial induction factor in the cases of the actuator disk and rotating annular stream-tube theories are obtained using Equation (8). Trial values of the half cone angle within the range 0° ≤ α < 90°are used in estimating a_w(r), a’(r) and their corresponding pressure differences in the case of the VRT, while the value of a’ corresponding to a = 0.293 is estimated using Equation (21) in the case of the RAST, and their corresponding pressure differences are estimated. After iterating with trial values of α between 0° and 90°, an average half cone angle of 45° is adopted in this paper. The MATLAB curve fitting tool is used to obtain the best fit third-degree polynomials for the three theories; the resulting expressions for dC_p are integrated with respect to the local tip-speed ratio within the limits λ_h ≤ λ(r) ≤ λ to yield C_p for each theory. Trial values of the tip-speed ratio are used to ensure that the C_p values estimated from all the three theories do not exceed 0.593. To further validate the results of the VRT with existing theories, the existing numerical and experimental values of C_p estimated from Figure 13 in Reference [28] are plotted on the same plot with the C_p values of all the three theories for values of the tip-speed ratio corresponding to the existing C_p values obtained from the cited figure. Sarlak et al. [28] in their numerical simulations using a rectangular domain and the actuator line method, investigated the effects of blockage on the wake characteristics and power generated by a 0.894 m-diameter HAWT and plotted curves of power coefficient as a function of the tip-speed ratio for various blockage ratios at various flow regimes. They also used the results of a blind test experiment in their study. Consult Reference [28] for a detailed description of the methods implemented by these researchers. The local radii, local spans, and chord distribution for the NREL OWT are shown in

Table 1. Local data for the 5 MW NREL OWT (adopted from Reference [22]).

Segment	Local Radius (m)	Span of Segment (m)	Chord Length (m)
1	2.8667	2.7333	3.5420
2	5.6000	2.7333	3.8540
3	8.3330	2.7333	4.1670
4	11.7500	4.5570	4.5570
5	15.8500	4.1000	4.6520
6	19.9500	4.1000	4.5800
7	24.0500	4.1000	4.2490
8	28.1500	4.1000	4.0070
9	32.2500	4.1000	3.7480
10	36.3500	4.1000	3.5020
11	40.4500	4.1000	3.2560
12	44.5500	4.1000	3.0100
13	48.6500	4.1000	2.7640
14	52.7500	4.1000	2.5180
15	56.1667	2.7333	2.3130
16	58.9000	2.7333	20860
17	61.6333	2.7333	1.4190

.

5. Results and Discussion

The plot of the tangential force per unit span as a function of the blade segment radius or local radius estimated from the VRT is shown in Figure 4. It is discernible from the plot that the curve rises from a tangential force per unit span of about 50.98 N/m at a radius of about 2.867 m to a maximum of 8.23 kN/m at a radius of about 58.9 m after which it drops to a value of 6.23 kN/m near the tip of the rotor blade. The curve shows an upward concavity for local radii between 2.867 m and 58.89 m and a downward concavity for local radii between 58.9 m and 63 m. It is worth noting that the effects of drag on the tangential or driving force on the rotor blade were not taken into consideration at this stage of the research, an upshot of which is the relatively high values of the tangential force per unit span. The effects of drag shall be considered in a future study, where a comparison shall be made between the VRT and the BEMT.

Figure 4. Tangential force per unit span as a function of the local radius.

Figure 4. Tangential force per unit span as a function of the local radius.

The plot of the normal force per unit span as a function of the local radius estimated from the VRT is shown in Figure 5. It is discernible from the plot that the curve rises from a tangential force per unit span of about 113.56 N/m at a radius of about 2.867 m to a maximum of 969.29 N/m at a radius of about 58.9 m after which it drops to a value of 677.26 N/m near the tip of the rotor blade. The curve shows an upward concavity for local radii between 2.867 m and 58.89 m and a downward concavity for local radii between 58.9 m and 63 m. It is worth noting that the effects of drag on the normal force on the rotor blade were not taken into consideration at this stage of the research. It is discernible from the curves that the estimated values of the tangential force are relatively higher than those of the normal force. This is because the effects of the angle of attack, the local blade twist angle and the blade pitch angle were not considered in estimating the angle of inclination of the resultant of the tangential and normal forces to the tangential force.

Figure 6a depicts the plot of the curves of pressure difference as a function of local radius for the ADT, the RAST and the VRT. The three curves appear to coincide at local radii between 2.867 m and 5.6 m with the RAST curve leaving the rest of the curves and running above them. Despite the apparent coincidence between the ADT and VRT curves for local radii between 2.867 m and 45 m, Figure 6b reveals that both the VRT and ADT curves do not coincide within this range of local radii. Both curves intersect at r ≅ 43 m after which the VRT curve is seen to rise above the ADT curve. The apparent coincidence of the curves signifies an agreement between the three theories at these local radii. Suffice it to say that all the three curves have upward concavity, even though the VRT and ADT curves in Figure 6a appear to run parallel to the horizontal axis. This apparent flatness of the ADT and VRT curves is the result of the fact that the RAST values are higher than those of the other two theories. The ADT curve appears to be flat in Figure 6b because the pressure difference values for respective local radii are nearly equal. Suffice it to say that the pressure difference values of the ADT are higher than those of the VRT for local radii between 2.867 m and about 43 m. Even though both the actuator disk and rotating annular stream-tube theories consider the WT rotor as a disk, the pressure difference estimated using the RAST is the highest of all the three theories. It suffices to say that the RAST overestimates the pressure difference across the rotor compared to the VRT and the ADT. The low values resulting from the ADT are evident because only the flow in the axial direction is considered in its formulation. A closer look at the VRT curve reveals that for local radii between 2.867 m and 11.75 m, the values of the pressure difference are positive; for local radii between 11.75 m and 36.35 m, the pressure difference is negative; and for local radii between 36.35 m and 61.633 m, the pressure difference is positive, whereas the pressure difference is positive for all local radii in the cases of the ADT and the RAST.

The negative values of pressure difference exhibited by the VRT curve for local radii between 11.75 m and 36.35 m is the upshot of back pressure resulting from the acceleration of the flow within this region of the rotor blade. Suffice it to say that the mere fact that this negative pressure difference is exhibited by the VRT curve is proof that the VRT better captures the flow physics of the WT rotor than the actuator disk and rotating annular stream-tube theories. This phenomenon of the acceleration of flow within the inner parts of the WT rotor is like the one described by Dossing et al. [19] in which wake rotation accelerates the flow at the inner parts of the rotor and decelerates the flow at the outer parts of the rotor.

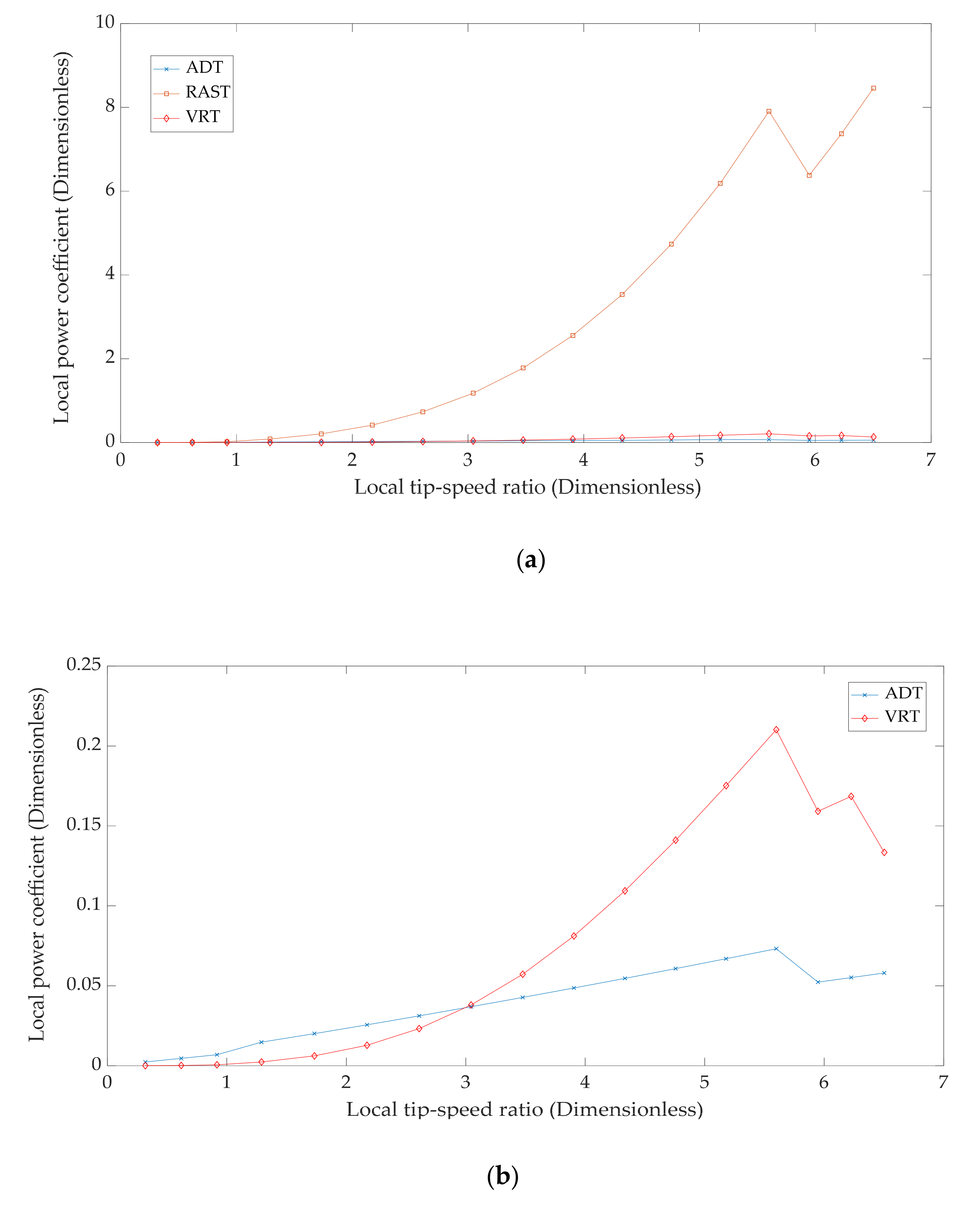
The curves of the local power coefficient dC_P as a function of the local tip-speed ratio λ(r) for the ADT, the RAST and the VRT are shown in Figure 7a. For clarity, the plot of the local power coefficient as a function of the local tip-speed ratio is plotted for the ADT and the VRT as depicted in Figure 7b. The three curves in Figure 7a appear to coincide at local tip-speed ratios ranging from about 0.32 to 0.918 after which the RAST curve leaves the ADT and VRT curves. Even though the ADT and VRT curves appear to coincide and run parallel to the horizontal axis at local tip-speed ratios between 0.918 and 4.33 as seen in Figure 7a, the two curves do intersect at local tip-speed ratios of about 0.32 and 2.900, respectively, as seen in Figure 7b. For local tip-speed ratios between 0.320 and 2.900, the ADT curve runs above the VRT curve because the dC_p values of the former are higher than those of the latter within this range of local tip-speed ratios. After this range of local tip speed-ratios, the VRT curve runs above the ADT curve as depicted in Figure 7b. The three theories appear to agree for local tip-speed ratios between 0.32 and 0.918, while the ADT and the VRT agree at local tip-speed ratios of 0.32 and 2.900. The RAST curve rises from values of dC_p slightly above zero to about 7.908 for 0.3 ≤ λ(r) ≤ 5.6 with an upward concavity after which it falls steeply to about 6.38 at a λ(r) of about 6.0 and rises thereafter. The VRT curve follows the same trend as the former within the same range of local tip-speed ratios, with a peak value of dC_p of about 0.21 at λ(r) ≅ 5.6 and a trough at dC_p ≅ 0.159 and λ(r) = 6.0. It then rises to another peak at λ(r) = 6.3 and drops thereafter. The ADT curve stays relatively flat for 0.3 ≤ λ(r) ≤ 5.6, even though this portion of the curve is supposed to have an upward concavity. It then exhibits a gently sloping peak at dC_p ≅ 0.073 and λ(r) = 5.6 followed by a drop to a trough at dC_p ≅ 0.052 and λ(r) = 6.0 and rises thereafter. It is worth noting that the values obtained from both the ADT and the VRT are low relative to those of the RAST, so much so that the concavity of their curves is adversely affected when plotted together with the curve of the RAST, a consequence of which is the flatness of their curves for 0.3 ≤ λ(r) ≤ 5.6. Also worthy of note is the fact that dC_p values for the VRT are higher than those estimated from the ADT, while the values estimated using the RAST are higher than those of the former two theories. This disparity in the magnitude of dC_p results from the fact that the RAST considers the local torque to be generated by the wake-induced angular speed on the rotor as stated in Equation (16), whereas the local torque estimated using the VRT results from the pressure difference across the WT rotor as expressed in Equation (64), while the power estimated from the ADT is the result of the product of the axial thrust expressed in Equation (2) and the wind speed at the rotor. The actuator disk and rotating annular stream-tube theories also consider the rotor as a disk.

The best fit curves for all the three theories are third-degree polynomials. The best fit curves are obtained with a 95% confidence interval using the MATLAB plotting tool. The best fit third-degree polynomial obtained for the ADT with a coefficient of determination of 0.9732, resulting in a correlation coefficient of 98.65%, is

$$d{C}_P=-5.842\times {10}^{-4}\lambda {(r)}^3+4.424\times {10}^{-3}\lambda {(r)}^2+4.424\times {10}^{-3}\lambda (r)+8.685\times {10}^{-4}.$$

(85)

After integrating Equation (85) with respect to λ(r) within the limits 0 ≤ λ(r) ≤ λ, the resulting expression is

$$C_P=-1.4605\times {10}^{-4}{\lambda }^4+1.4747\times {10}^{-3}{\lambda }^3+2.212\times {10}^{-3}{\lambda }^2+8.685\times {10}^{-4}\lambda ,$$

(86)

subject to the following constraints: $0.1\le \lambda \le 11.4$ and 0.0001104 < C_p ≤ 0.3102. The optimum C_p for the HAWT in this study using the ADT is $C_p=0.3102$ at $\lambda =8.377$.

The best fit third-degree polynomial obtained for the RAST with a coefficient of determination of 0.9755, resulting in a correlation coefficient of 98.76% is given by

$$d{C}_P=-5.037\times {10}^{-2}\lambda {(r)}^3+7.577\times {10}^{-1}\lambda {(r)}^2-1.633\lambda (r)+7.605\times {10}^{-1}.$$

(87)

After integrating Equation (87) with respect to λ(r) within the limits 0.155 ≤ λ(r) ≤ λ, the resulting expression is

$$C_P=-1.259\times {10}^{-2}{\lambda }^4+2.5257\times {10}^{-1}{\lambda }^3-8.165\times {10}^{-1}{\lambda }^2+7.605\times {10}^{-1}\lambda -0.1051,$$

(88)

subject to the following constraints: 2.2 ≤ λ ≤ 2.973 and $0.0105<C_p\le 0.5921$. The optimum C_p for the HAWT in this study using the RAST is $C_p=0.5921$ at λ = 2.973. Typically, wind farms are designed based on $C_p=0.34$, and this value is achieved at λ = 2.746 in the case of the RAST.

A best fit third-degree polynomial with a coefficient of determination of 0.952, resulting in a correlation coefficient of 97.57%, is obtained for the VRT using the MATLAB curve fitting tool:

$$d{C}_P=-3.507\times {10}^{-3}\lambda {(r)}^3+3.776\times {10}^{-2}\lambda {(r)}^2-7.889\times {10}^{-2}\lambda (r)+3.637\times {10}^{-2}.$$

(89)

After integrating Equation (89) with respect to λ(r) within the limits 0.155 ≤ λ(r) ≤ λ, the resulting expression is

$$C_P=-8.7675\times {10}^{-4}{\lambda }^4+1.2587\times {10}^{-2}{\lambda }^3-3.9495\times {10}^{-2}{\lambda }^2+3.637\times {10}^{-2}\lambda -0.0051,$$

(90)

subject to the following constraints: 1.6 ≤ λ ≤ 7.572, 8.7 ≤ λ ≤ 10.4 and 0.00022 < C_P ≤ 0.593. The optimum C_p for the HAWT in this study using the VRT is $C_p=0.593$ at λ = 7.572 and λ = 8.700. The typical design $C_p=0.34$ is obtained at λ = 5.777 in the case of the VRT. It is worth noting that the axial induction coefficient due to the wake and solidity are equal in the cases of the RAST and the ADT, whereas the VRT uses different values for the axial induction coefficients due to the wake and solidity of the WT rotor. An axial induction coefficient of a_s(r) = a(r)= 0.293 is used in this work, while the VRT uses a range of axial induction coefficients due to the wake of the rotor within 0.0201 ≤ a_w(r) ≤ 0.2566, resulting in 0.3129 ≤ δ(r) ≤ 0.5493. It can be inferred from the foregoing that the ADT is suitable for the analysis of WTs with high tip-speed ratios, whereas the RAST and the VRT are suitable for WTs with low tip-speed ratios. Typically, smaller WTs have higher tip-speed ratios than larger WTs, such as OWTs.

Figure 8 depicts the plot of the thrust coefficient per unit span dC_T/dr as a function of the local radius r for the vortex ring, rotating annular stream-tube and actuator disk theories. The VRT curve is seen to run almost parallel to the horizontal axis from dC_T/dr ≅ 0.00026 at r = 2.8667 m to a peak at dC_T/dr ≅ 0.00219 and r = 59 m and drops to dC_T/dr ≅ 0.0016 at r = 61.633 m. It is worth noting that despite the apparent flatness of the VRT curve, it has an upward concavity for local radii between 2.8667 m and 59 m. The ADT and RAST curves merge at all local radii. This merger is the upshot of the equality in the numerical values of dC_T/dr obtained from respective expressions for these theories. Despite the apparent cubic dependence of dC_T/dr in the case of the RAST on r and the linear dependence of dC_T/dr on r in the case of the ADT, both curves are linear and coincident, thus signifying a complete agreement of these two theories within this range of local radii. Equations (12) and (18) show the dependence of dC_T/dr on r for these two theories. The coincident curves rise linearly from dC_T/dr ≅ 0.0046 at r = 2.8667 m to dC_T/dr ≅ 0.1097 at r = 61.633 m. It is discernible from Figure 8 that the thrust coefficients estimated from both the actuator disk and rotating annular stream-tube theories are higher than those obtained from the VRT at all the local radii considered in this paper. This difference between the VRT and the other two theories is evident because the latter two theories use the entire cross-sectional area of the path swept by the rotor blades in estimating dC_T/dr, whereas the VRT uses the planform area of each rotor blade to estimate dC_T/dr. It can also be discerned from Figure 8 that the load on the WT rotor is linear as exhibited by the ADT and RAST curves, whereas the VRT curve shows that the load on the WT rotor blades is nonlinear.

Worthy of note is the fact that both the actuator disk and rotating annular stream-tube theories assume that the static pressure resulting from the pressure difference across the rotor acts in the axial direction with no component acting in the tangential direction. If this were the case, then there would be no rotation on the WT rotor unless there was another source of rotation coupled with the WT. This assertion that the entire static pressure extracted from the wind by the WT acts in the axial direction and is converted to the axial thrust defies the laws of mechanics because for there to be a rotation of the WT rotor, there must be a tangential component of the resultant force. Based on the foregoing, the actuator disk and rotating annular stream-tube theories are only suitable for the analysis of propellers and not WTs. On the contrary, the VRT is more suitable for WT analysis because it accounts for the tangential component of the static pressure in its initial formulation.

Comparison of the VRT Results to Existing Numerical and Experimental Results

Based on the results depicted in Figure 13 in Reference [28], the following data were estimated from the cited figure for a blockage ratio of 0.2 and laminar inflow conditions. The results of the numerical analysis and the experiment are shown in

Table 2. Existing values of the power coefficient (adopted from Reference [28]).

Tip-Speed Ratio	Numerical Cp	Experimental Cp
1.600	0.030	0.029
2.100	0.060	0.050
2.800	0.100	0.120
4.000	0.350	0.400
5.000	0.520	0.450
5.600	0.540	0.470
6.000	0.550	0.480
6.300	0.560	0.470
7.000	0.570	0.450
8.100	0.565	0.400
10.000	0.450	0.180
11.200	0.220	−0.020

. The data in Table 2 are plotted on the same plot as those from Equations (85), (87) and (89)—the expressions for the power coefficient obtained from the three theories and the resulting plots are shown in Figure 9. It is discernible from Figure 9 that both the curves of the vortex ring and actuator disk theories follow the same trend as both the existing numerical and experimental curves, even though for tip-speed ratios between 1.6 and about 6.5, the experimental values are higher than those of the VRT, while for tip-speed ratios between 1.6 and about 7.8, the numerical values are higher than those of the VRT. For tip-speed ratios between 1.6 and about 3, both the numerical and experimental curves nearly coincide after which the experimental curve leaves the numerical curve and runs above it up to a tip-speed ratio of about 4.3 and then runs below the numerical curve thereafter. For tip-speed ratios between about 7.8 and 8.5, the VRT curve runs above the numerical curve, while it runs above the experimental curve for tip-speed ratios between 6.5 and 10.2.

Beyond these limits of tip speed ratios, both the experimental and numerical curves run above the VRT curve. The VRT curve intersects with the experimental curve at tip-speed ratios of about 6.5 and 10.2, while it intersects with the numerical curve at tip-speed ratios of about 7.8 and 8.5. It is discernible from the plot that the RAST curve, even though a fourth-degree polynomial like the rest of the curves, is not valid for tip-speed ratios greater than 2.973 because beyond this limit, the power coefficients estimated from the RAST are greater than 0.593 in most cases; beyond this limit, they are greater than unity. On the contrary, both the curves of the vortex ring and actuator disk theories have upward concavity like the numerical and experimental curves. The values of the power coefficient estimated from the ADT are higher than those of the VRT at tip-speed ratios between 1.6 and 4, with both curves intersecting at tip-speed ratios of 4 and about 9.7, respectively. At tip-speed ratios between 4 and about 9.7, the values of the VRT are higher than those of the ADT, while the numerical values are higher than those of the ADT at all the tip-speed ratios considered. At tip-speed ratios greater than 9.7, the values of the power coefficient estimated from the ADT are higher than those of the VRT. It is worth noting that at tip-speed ratios below 2.2, the RAST curve shows negative values of the power coefficient, while at tip-speed ratios beyond 10.4, the VRT curve shows negative values of the power coefficient, and the experimental curve shows negative values of the power coefficient at a tip-speed ratio of 11.2 and beyond. Clearly, among the three theories, the VRT is the most reliable since the values predicted from the VRT lie between the numerical and experimental values and between the values predicted from the ADT and the experimental values within the range of tip-speed ratios at which the VRT is valid. Suffice it to say that the predictions of the VRT agree with the numerical and experimental results at the points of intersection of the curves.

6. Conclusions

Based on the foregoing, it can be deduced that there is piecewise agreement between the VRT and the two existing theories—the actuator disk and rotating annular stream-tube theories. There is no gainsaying that the VRT better captures the aerodynamics of HAWTs than the RAST and the ADT. Evidence of this assertion is the existence of negative values of the pressure difference across the WT rotor in the region between the hub of the rotor to somewhere beyond the midspan of the rotor blades as exhibited by the curve of the VRT, whereas the curves of the actuator disk and rotating annular stream-tube theories only show positive values throughout the span of the rotor blades. The negative values of pressure difference are consistent with the acceleration of the airstream around the region between the hub and the midspan of the rotor blades as it flows past the WT rotor. This acceleration of flow is in keeping with the assertions of Reference [19].

The optimum power coefficient predicted by the ADT occurs at a tip-speed ratio around 8.377, while the optimum power coefficient predicted by the RAST occurs at a tip-speed ratio of 2.973, whereas the optimum power coefficient predicted by the VRT occurs at tip-speed ratios of 7.572 and 8.700. This implies that the RAST is more suitable for the aerodynamic analysis of slowly rotating, large-diameter, megawatt HAWTs typical of OWTs, while the vortex ring and actuator disk theories are suitable for the aerodynamics of both low- and high-speed HAWTs. Comparison to the existing experimental and numerical results reveals that there is piecewise agreement between the VRT and existing results.

In a nutshell, the VRT’s ability to predict both negative and positive blade static pressure, mimicking the real-life state of stress on the rotor blades, renders it superior to the actuator disk and rotating annular stream-tube theories in the aero-elastic analysis of HAWTs. The VRT can be a useful tool in the aerodynamic analysis of WTs. Future work entails the use of an angle of inclination of the resultant of the blade forces to the tangential force that incorporates the effects of drag, lift and the relative wind speed angle. A comparison shall be made between the VRT and the BEMT.