Statistical Analysis for Transmission Error of Gear System with Mechanical and Thermal Deformation Uncertainties
Abstract
:1. Introduction
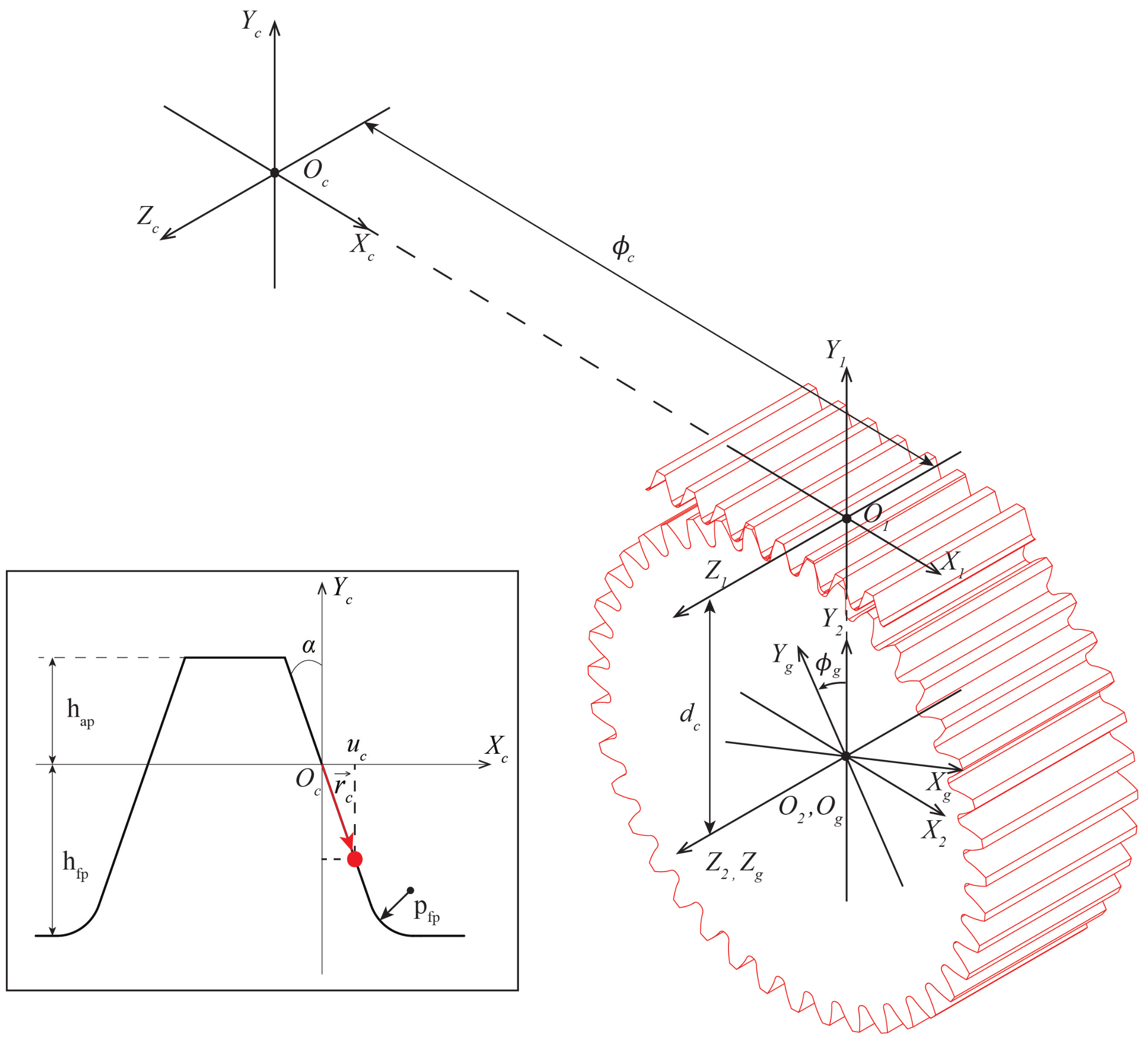
2. Rack Cutters and Gear Surfaces
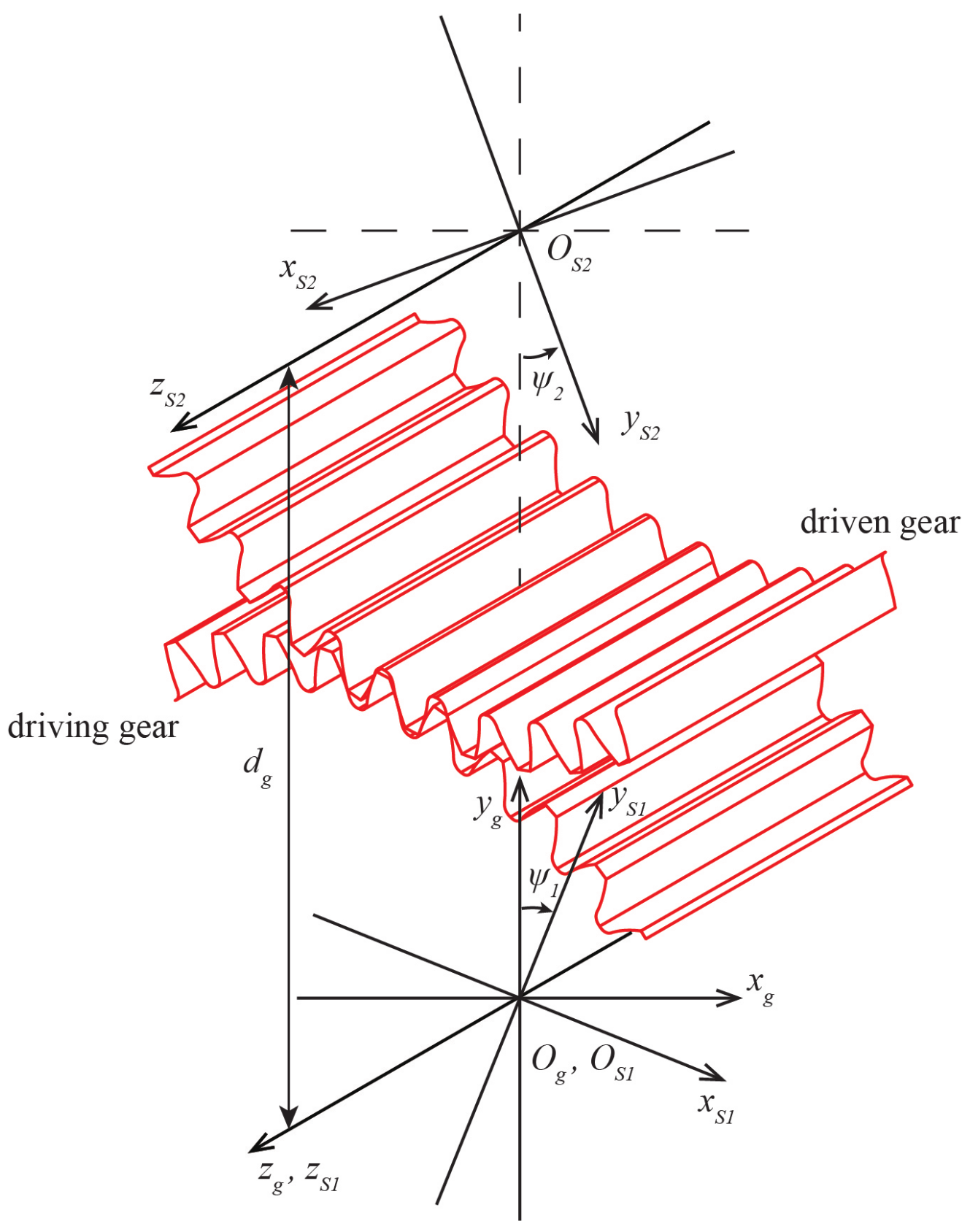
2.1. Tooth Contact Analysis (TCA)
2.2. Loaded Tooth Contact Analysis (LTCA)
3. Mathematical Modeling of Gears with Uncertainties
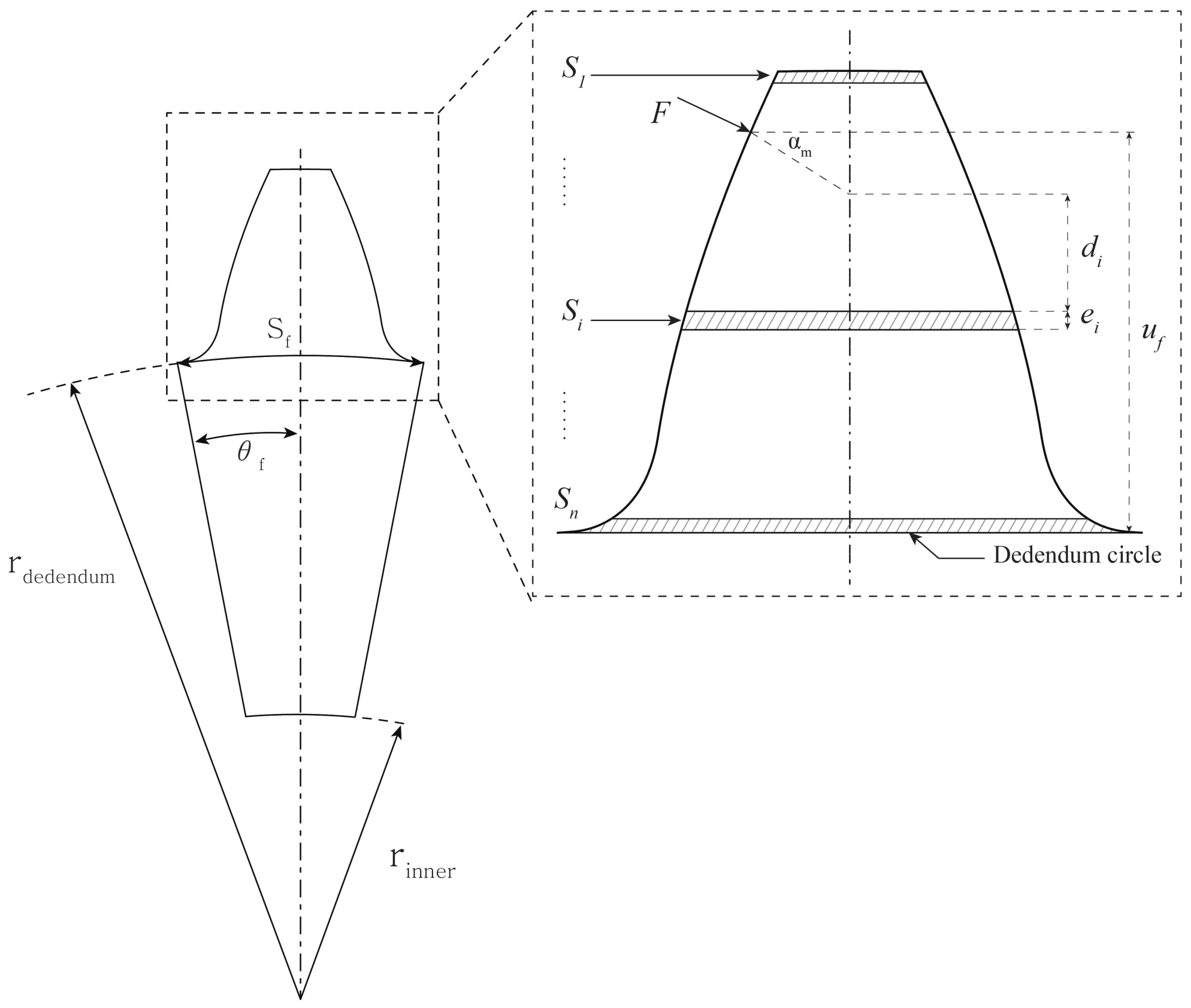
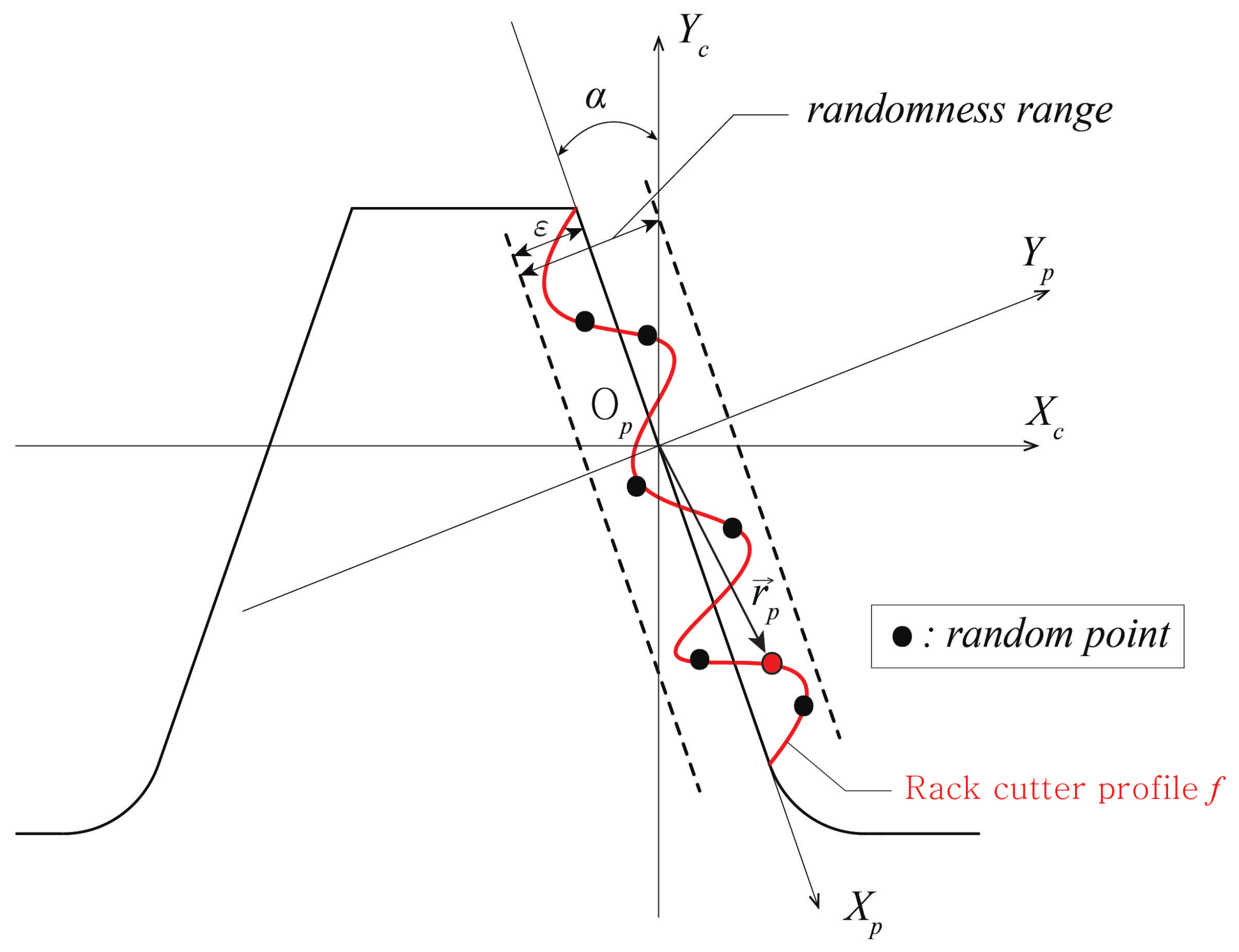
3.1. Mechanical Uncertainties
3.2. Thermal Deformation Uncertainties
4. Statistical Analysis for Gear System with Uncertainties
4.1. LTCA for Gear System with Uncertainties
4.2. Monte Carlo (MC) Simulation
| Algorithm 1 Gear model sampling with uncertainties. |
|
| Algorithm 2 Gear pair sampling. |
|
5. Numerical Studies
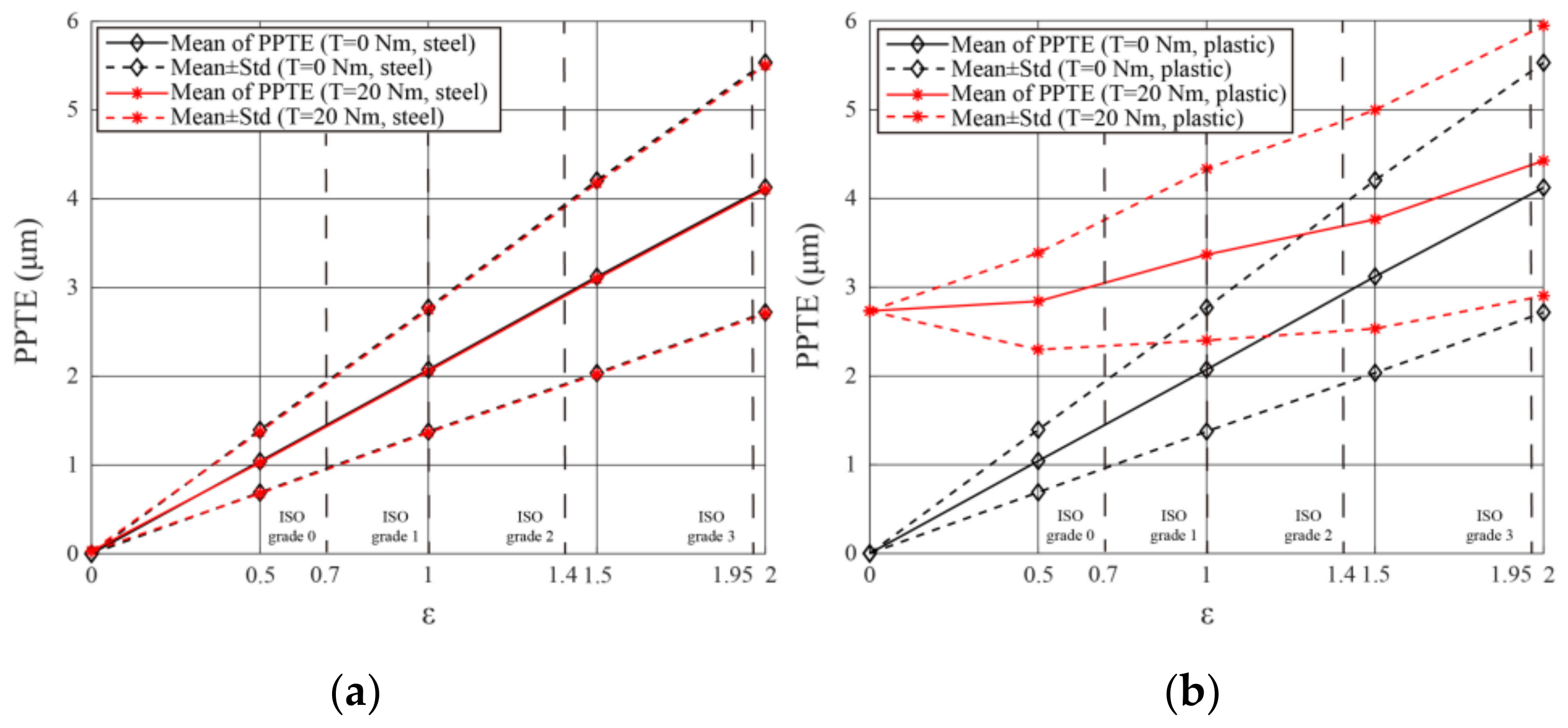
5.1. Effect of Machining Error (ME) on Transmission Error (TE)
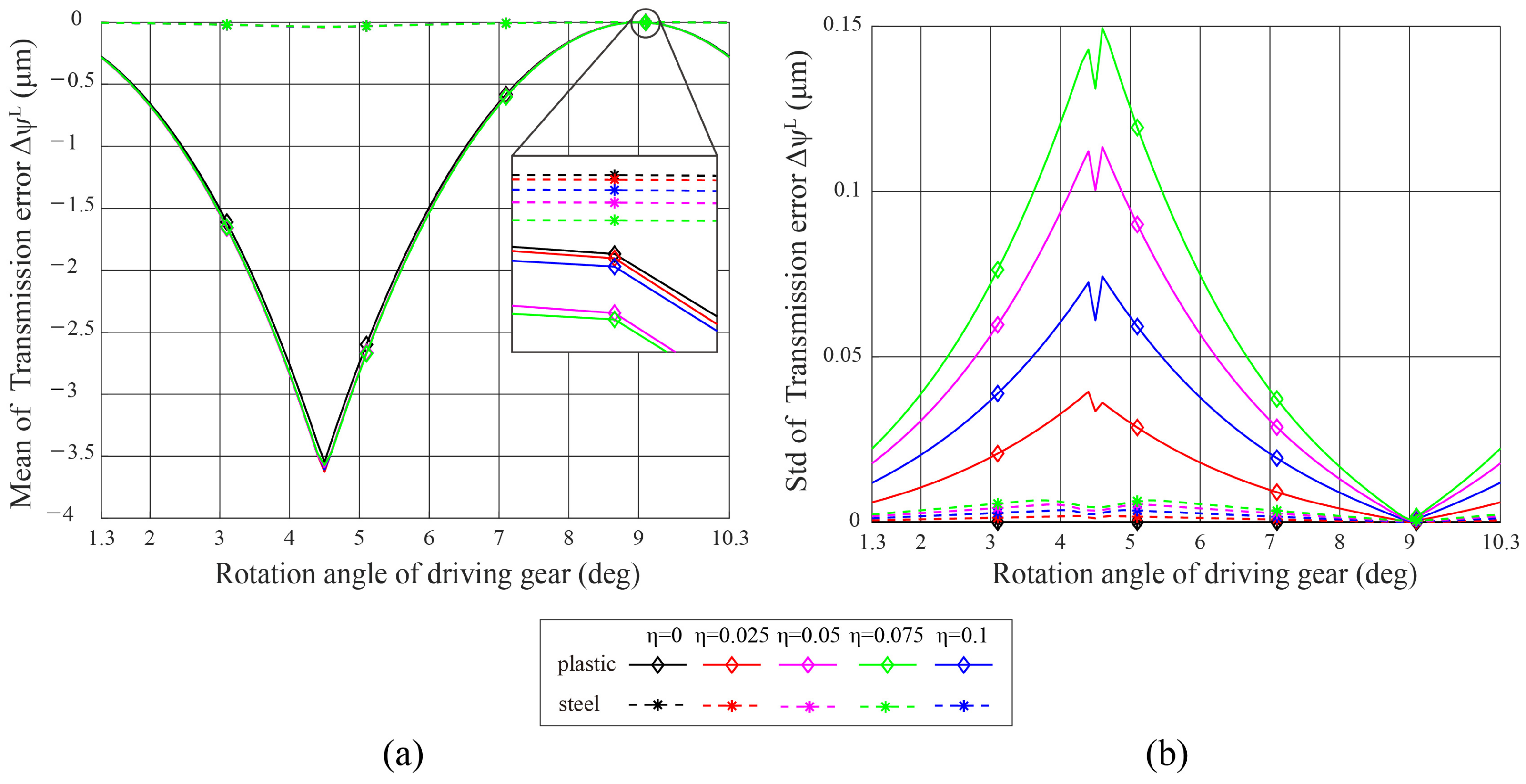
5.2. Effect of Thermal Deformation (TD) on Transmission Error (TE)
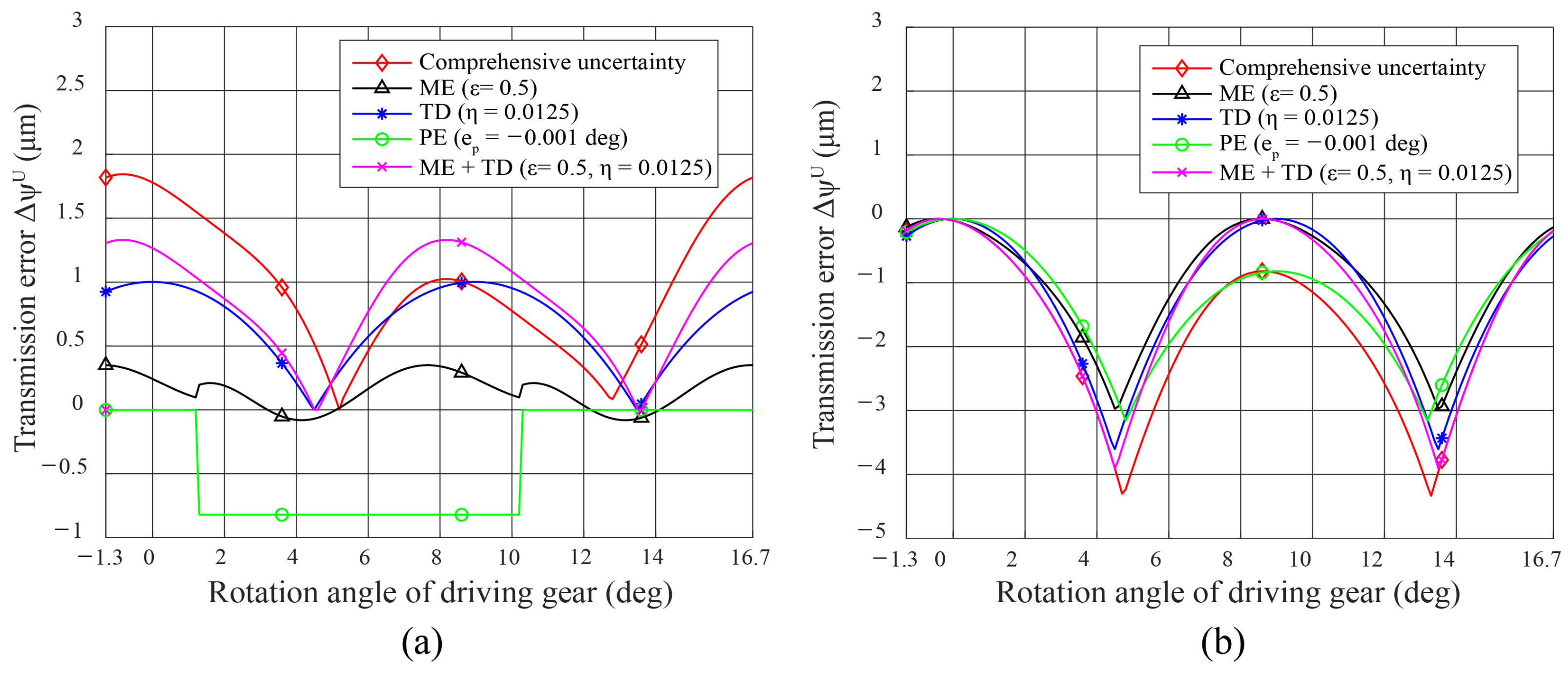
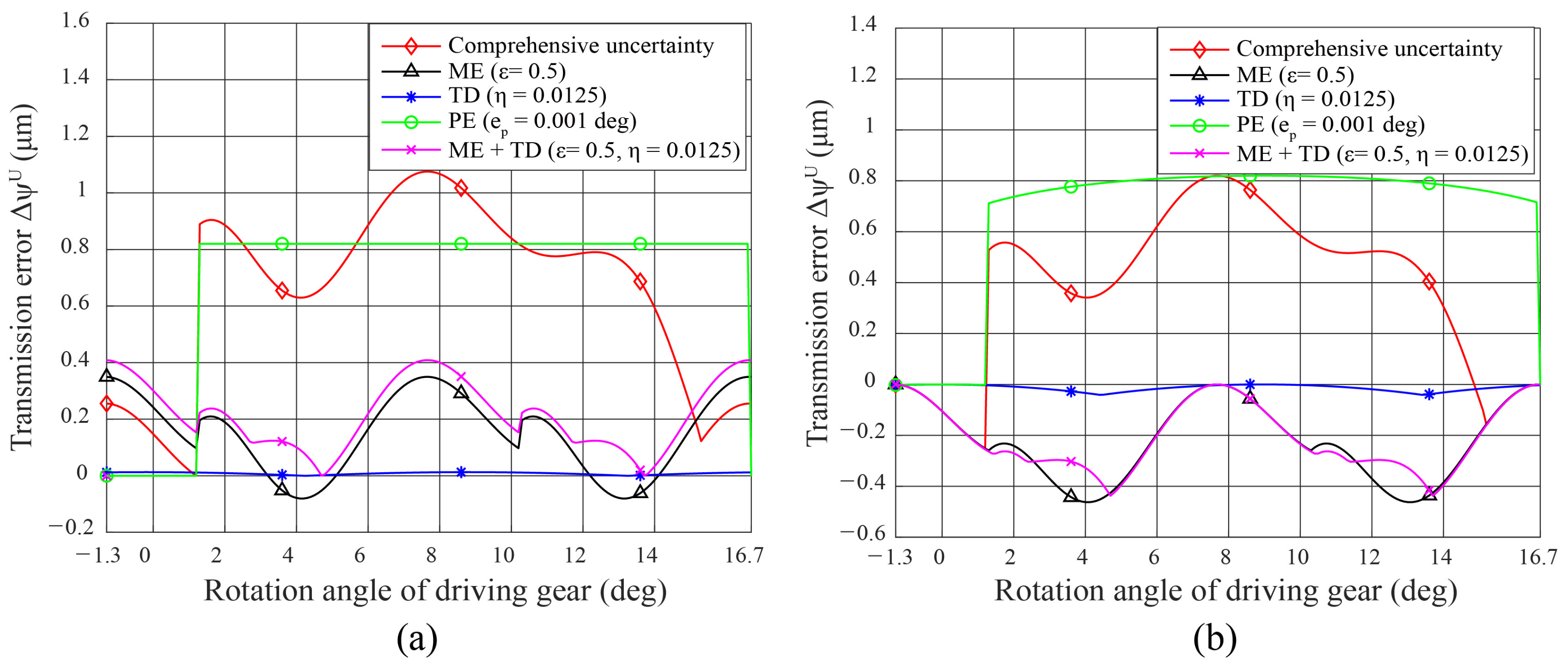
5.3. Effect of Comprehensive Error on Transmission Error (TE)
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Mesh Stiffness
| −5.574 × 10 | −1.9986 × 10 | −2.3015 × 10 | 4.7702 × 10 | 0.0271 | 6.8045 | |
| 60.111 × 10 | 28.100 × 10 | −83.431 × 10 | −9.9256 × 10 | 0.1624 | 0.9086 | |
| −50.952 × 10 | 185.50 × 10 | 0.0538 × 10 | 53.300 × 10 | 0.2895 | 0.9236 | |
| −6.2042 × 10 | 9.0889 × 10 | −4.0964 × 10 | 7.8297 × 10 | −0.1472 | 0.6904 |
References
- Krawiec, P.; Walus, K.; Warguła, Ł.; Adamiec, J. Wear evaluation of elements of V-belt transmission with the application of optical microscope. In Proceedings of the MATEC Web of Conferences Machine Modelling and Simulations, Sklené Teplice, Slovak Republic, 5–8 September 2017; Volume 157, p. 01009. [Google Scholar]
- Konczak, M.; Kukla, M.; Warguła, Ł.; Talaska, K. Determination of the vibration emission level for a chipper with combustion engine. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Kazimierz Dolny, Poland, 21–23 November 2019; Volume 776, p. 012007. [Google Scholar]
- Tang, J.; Zhang, Y.; Shi, Z. Radial and tangential error analysis of double-flank gear measurement. Precis. Eng. 2018, 51, 552–563. [Google Scholar] [CrossRef]
- Sato, O.; Osawa, S.; Kondo, Y.; Komori, M.; Takatsuji, T. Calibration and uncertainty evaluation of single pitch deviation by multiple-measurement technique. Precis. Eng. 2010, 34, 156–163. [Google Scholar] [CrossRef]
- Krawiec, P.; Warguła, Ł.; Walus, K.; Adamiec, J. Wear evaluation study of the multiple grooved pulleys with optical method. In Proceedings of the MATEC Web of Conferences XXIII Polish-Slovak Scientific Conference on Machine Modelling and Simulations, Rydzyna, Poland, 4–7 September 2018; Volume 254, p. 01004. [Google Scholar]
- Krawiec, P.; Domek, G.; Warguła, Ł.; Walus, K.; Adamiec, J. The application of the optical system ATOS II for rapid prototyping methods of non-classical models of cogbelt pulleys. In Proceedings of the MATEC Web of Conference, Machine Modelling and Simulations, Sklené Teplice, Slovak Republic, 5–8 September 2018; Volume 157, p. 01010. [Google Scholar]
- Krawiec, P.; Grzelka, M.; Kroczak, J.; Domek, G.; Kolodziej, A. A proposal of measurement methodology and assessment of manufacturing methods of nontypical cog belt pulleys. Measurement 2019, 132, 182–190. [Google Scholar] [CrossRef]
- Krawiec, P.; Czarnecka-Komorowska, D.; Warguła, Ł.; Wojciechowski, S. Geometric Specification of Non-Circular Pulleys Made with Various Additive Manufacturing Techniques. Materials 2021, 14, 1682. [Google Scholar] [CrossRef]
- Li, S. Effects of machining errors, assembly errors and tooth modifications on loading capacity, load-sharing ratio and transmission error of a pair of spur gears. Mech. Mach. Theory 2007, 42, 698–726. [Google Scholar] [CrossRef]
- Lin, T.; He, Z. Analytical method for coupled transmission error of helical gear system with machining errors, assembly errors and tooth modifications. Mech. Syst. Signal Process. 2017, 91, 167–182. [Google Scholar] [CrossRef]
- Liu, J.P.; Shu, X.B.; Kanazawa, H.; Imaoka, K.; Mikkola, A.; Ren, G.X. A model order reduction method for the simulation of gear contacts based on Arbitrary Lagrangian Eulerian formulation. Comput. Methods Appl. Mech. Eng. 2018, 338, 68–96. [Google Scholar] [CrossRef]
- Litvin, F.L.; Seol, I.H.; Kim, D.; Lu, J.; Wang, A.G.; Egelja, A.; Zhao, X.; Handschuh, R.F. Kinematic and geometric models of gear drives. J. Mech. Des. 1996, 118, 544–550. [Google Scholar] [CrossRef]
- Litvin, F.L.; Hsiao, C.-L. Computerized simulation of meshing and contact of enveloping gear tooth surfaces. Comput. Methods Appl. Mech. Eng. 1993, 102, 337–366. [Google Scholar] [CrossRef]
- Chaari, F.; Fakhfakh, H.; Haddar, M. Analytical modelling of spur gear tooth crack and influence on gearmesh stiffness. Eur. J. Mech. A-Solids. 2009, 28, 461–468. [Google Scholar] [CrossRef]
- Chen, Z.; Zhou, Z.; Zhai, W.; Wang, K. Improved analytical calculation model of spur gear mesh excitations with tooth profile deviations. Mech. Mach. Theory 2020, 149, 103838. [Google Scholar] [CrossRef]
- Wang, C. Study on 3-D modification for reducing vibration of helical gear based on TCA technology, LTCA technology and system dynamics. Mech. Syst. Signal Process. 2020, 146, 106991. [Google Scholar] [CrossRef]
- Letzelter, E.; Guingand, M.; Vaujany, J.-P.; Schlosser, P. A new experimental approach for measuring thermal behaviour in the case of nylon 6/6 cylindrical gears. Polym. Test. 2010, 29, 1041–1051. [Google Scholar] [CrossRef]
- Mao, K.; Li, W.; Hooke, C.J.; Walton, D. Polymer gear surface thermal wear and its performance prediction. Tribol. Int. 2010, 43, 433–439. [Google Scholar] [CrossRef]
- Krawiec, P.; Różański, L.; Czarnecka-Komorowska, D.; Warguła1, Ł. Evaluation of the Thermal Stability and Surface Characteristics of Thermoplastic Polyurethane V-Belt. Materials 2020, 13, 1502. [Google Scholar] [CrossRef] [Green Version]
- Krawiec, P.; Warguła, Ł.; Różański, L. Diagnostics of the Thermal Condition of the Cable Gear Used in the Drive of a Wood Chipper. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Lviv, Ukraine, 26–27 November 2020; Volume 1016, p. 012013. [Google Scholar]
- Kashyap, S.; Houser, D.; Smith, Z.; Selvaraj, S.; Casella, J.; Bradway, J. Methods of describing plastic gear geometry after a temperature change with application to the prediction of gear load distribution. In Proceedings of the ASME 2011 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Washington, DC, USA, 28–31 August 2021; Volume 8. [Google Scholar]
- Sohn, J.; Park, N. Geometric interference in cylindrical worm gear drives using oversized hob to cut worm gears. Mech. Mach. Theory 2016, 100, 83–103. [Google Scholar] [CrossRef]
- Chen, Y.-C.; Cheng, Y.-H.; Tseng, J.-T.; Hsieh, K.-J. Study of a harmonic drive with involute profile flexspline by two-dimensional finite element analysis. Eng. Comput. 2017, 34, 2107–2130. [Google Scholar] [CrossRef]
- Litvin, F.L.; Fuentes, A. Gear Geometry and Applied Theory; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Ypma, T.J. Historical development of the Newton–Raphson method. SIAM Rev. 1995, 37, 531–551. [Google Scholar] [CrossRef] [Green Version]
- Ben-Israel, A. A Newton–Raphson method for the solution of systems of equations. J. Math. Anal. Appl. 1966, 15, 243–252. [Google Scholar] [CrossRef] [Green Version]
- ISO 1328-1. Cylindrical Gears—ISO System of Flank Tolerance Classification Part 1: Definitions and Allowable Values of Deviations Relevant to Flanks of Gear Teeth. 2013. Available online: https://www.iso.org/obp/ui/#iso:std:iso:1328:-1:ed-2:v1:en (accessed on 1 June 2021).
- Li, W.; Zhai, P.; Ding, L. Analysis of thermal characteristic of spur/helical gear transmission. J. Therm. Sci. Eng. Appl. 2019, 11, 21003. [Google Scholar] [CrossRef]
- Abaqus Manual. Available online: http://dsk.ippt.pan.pl/docs/abaqus/v6.13/books/usi/default.htm (accessed on 1 June 2021).
- Zhang, H.; Mullen, R.; Muhanna, R. Interval Monte Carlo methods for structural reliability. Struct. Saf. 2010, 32, 183–190. [Google Scholar] [CrossRef]
- Zhang, H.; Dai, H.; Beer, M.; Wang, W. Structural reliability analysis on the basis of small samples: An interval quasi-Monte Carlo method. Mech. Syst. Signal Process. 2013, 37, 137–151. [Google Scholar] [CrossRef]
- Rost, K.; Wendt, K.; Härtig, F. Evaluating a task-specific measurement uncertainty for gear measuring instruments via Monte Carlo simulation. Precis. Eng. 2016, 44, 220–230. [Google Scholar] [CrossRef]
- Helton, J.C.; Davis, F.J. Latin hypercube sampling and the propagation of uncertainty in analyses of complex systems. Reliab. Eng. Syst. Saf. 2003, 81, 23–69. [Google Scholar] [CrossRef] [Green Version]
- Stein, M. Large sample properties of simulations using Latin hypercube sampling. Technometrics 1987, 29, 143–151. [Google Scholar] [CrossRef]
- Weber, C. The Deformation of Loaded Gears and the Effect on Their Load-Carrying Capacity; Sponsored Research (Germany); British Department of Scientific and Industrial Research: London, UK, 1949; Report No. 3. [Google Scholar]
- Muskhelishvili, N.L. Some Basic Problems of the Mathematical Theory of Elasticity; Springer: Berlin/Heidelberg, Germany, 1977. [Google Scholar]
- Sainsot, P.; Velex, P.; Duverger, O. Contribution of gear body to tooth deflections—A new bidimensional analytical formula. ASME J. Mec. Des. 2004, 126, 748–752. [Google Scholar] [CrossRef]
- Yang, D.C.H.; Sun, Z.S. A rotary model for spur gear dynamics. ASME J. Mech. Trans. Autom. Dec. 1985, 107, 529–535. [Google Scholar] [CrossRef]



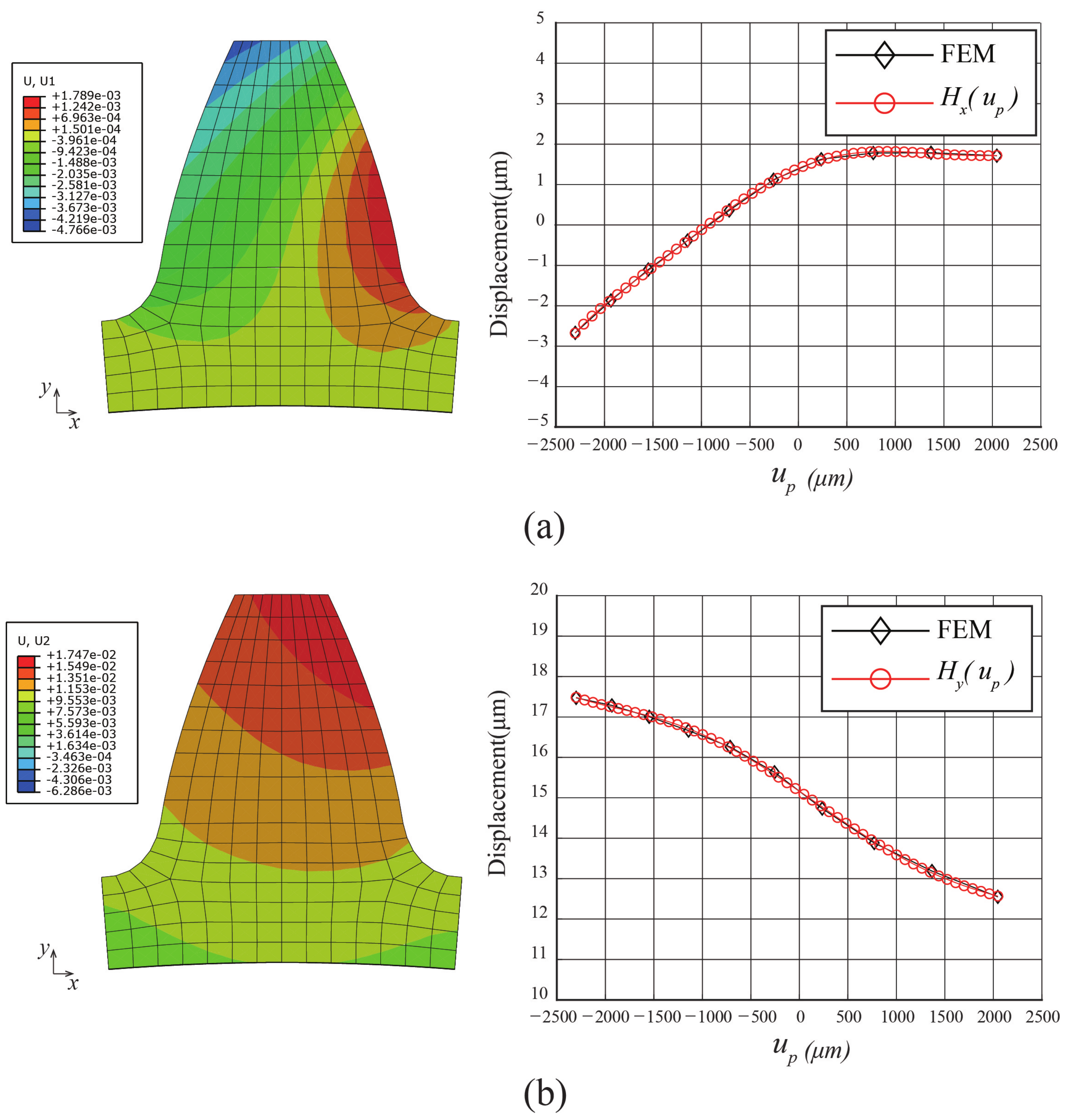
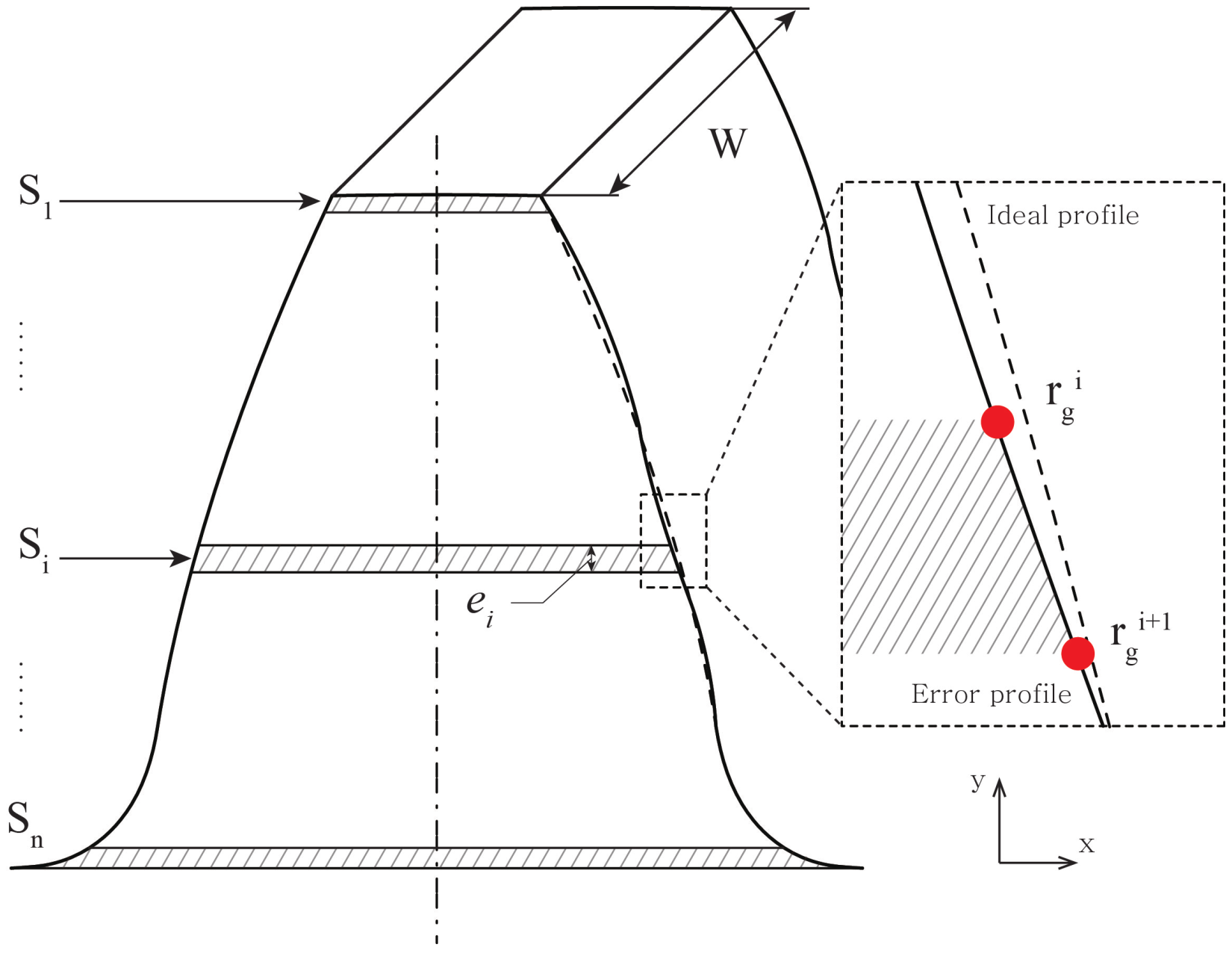

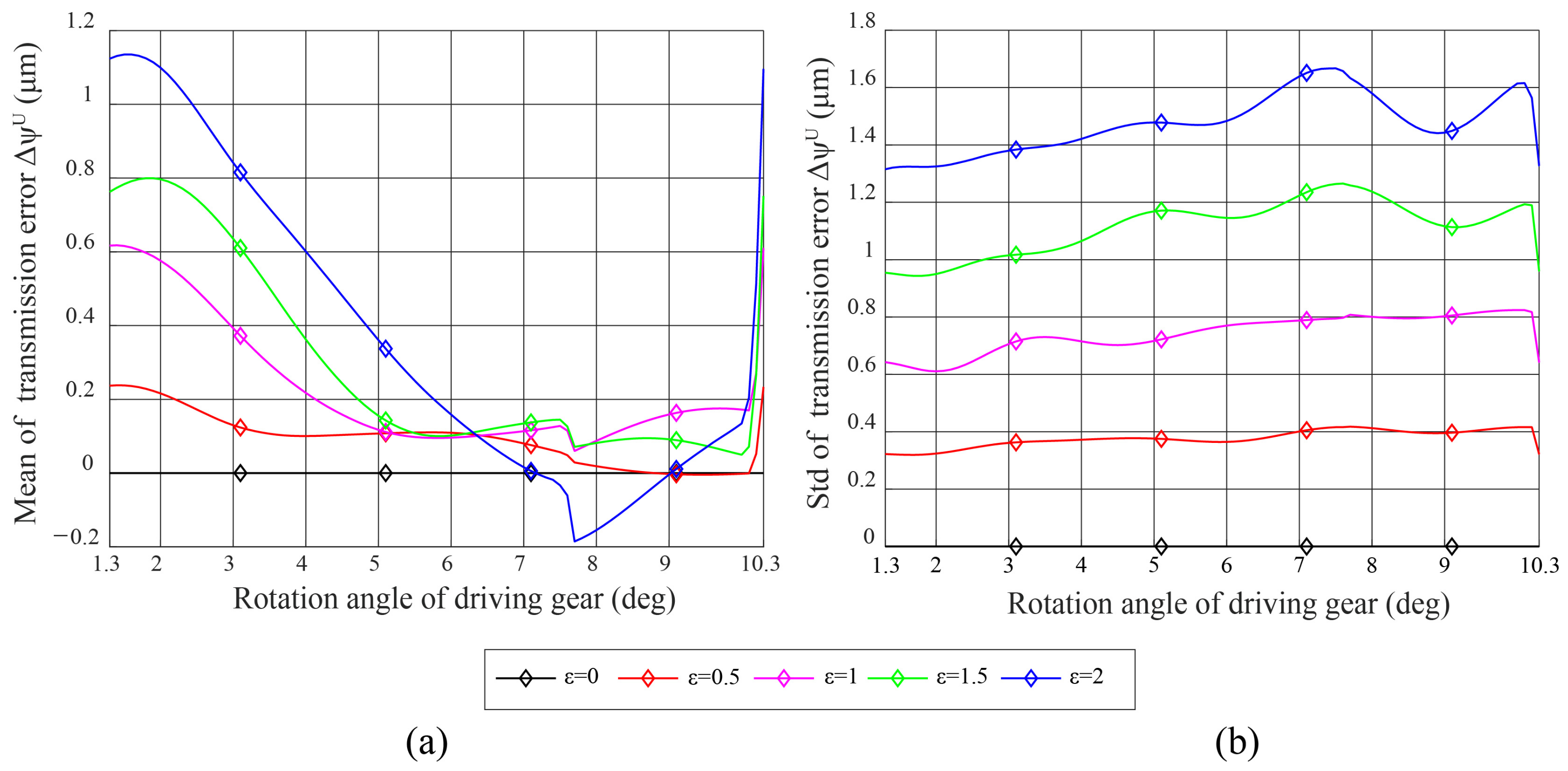
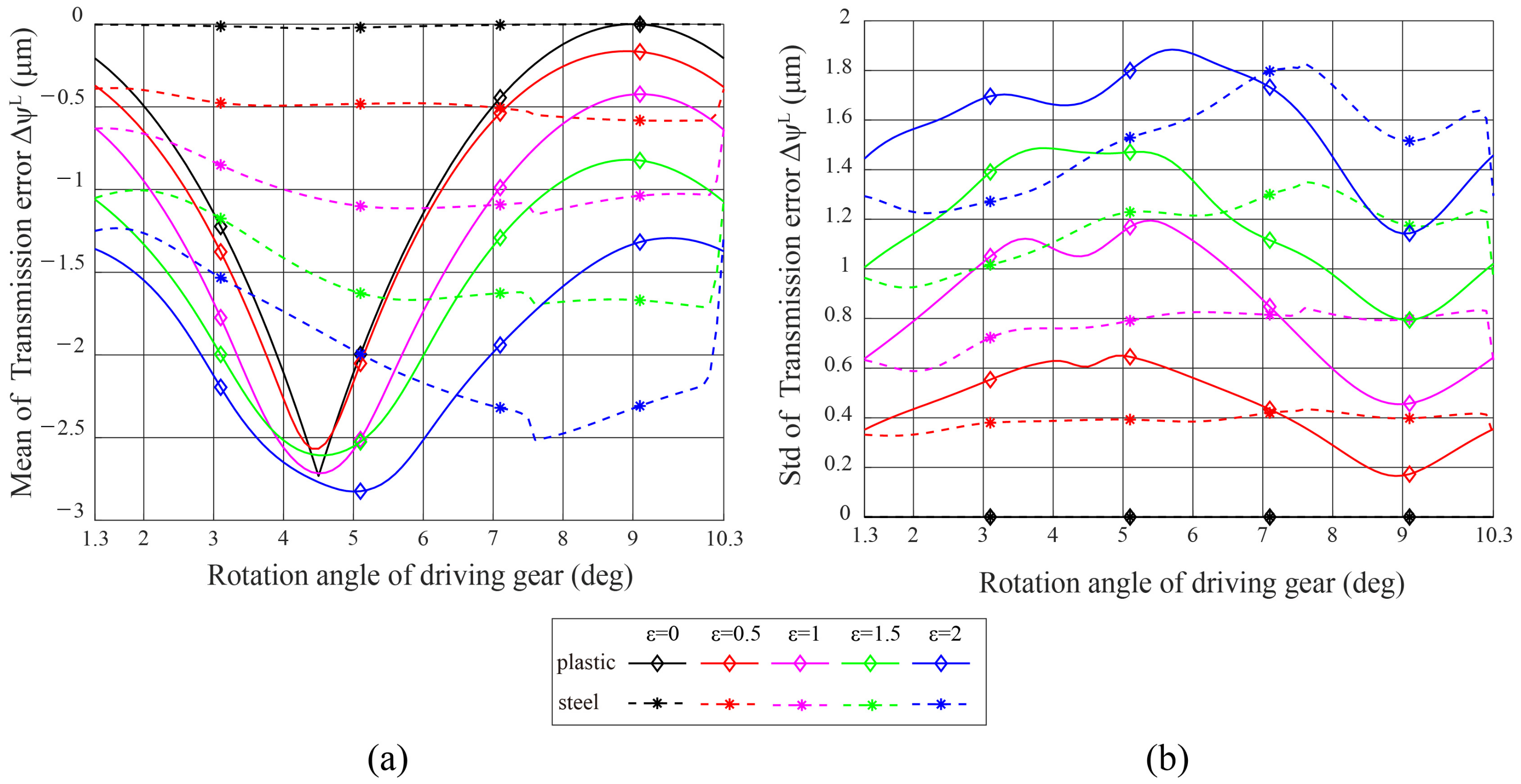





| Design Parameter | Gear1 | Gear2 |
|---|---|---|
| Number of teeth | 40 | 40 |
| Normal module (mm) | 2.5 | 2.5 |
| Normal pressure angle (deg) | 20 | 20 |
| Facewidth (mm) | 40 | 40 |
| Material | Steel, Plastic | Steel, plastic |
| Torque (Nm) | 20 | |
| Speed (r/min) | 200 | |
| Design Parameter | Rack | |
| Normal module (mm) | 2.5 | |
| Addendum (mm) | 2.5 | |
| Dedendum (mm) | 3.125 | |
| Fillet radius (mm) | 0.95 | |
| Material Property | Steel(18CrNiMo7-6) | Plastic(MC901) |
| Young’s modulus (MPa) | 206,000 | 2150 |
| Thermal expansion coefficient | 11.5 | 85 |
| Density (T/mm) | 7.83 × 10 | 1.13 × 10 |
| Conductivity (W/(m × K)) | 50 | 0.29 |
| Heat capacity (mJ/(T × K)) | 4.58 × 10 | 1.67 × 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.-H.; Choi, H.-S.; Sohn, J.-H.; Lee, G.-H.; Park, D.-I.; Kim, J.-G. Statistical Analysis for Transmission Error of Gear System with Mechanical and Thermal Deformation Uncertainties. Appl. Sci. 2021, 11, 6582. https://doi.org/10.3390/app11146582
Lee J-H, Choi H-S, Sohn J-H, Lee G-H, Park D-I, Kim J-G. Statistical Analysis for Transmission Error of Gear System with Mechanical and Thermal Deformation Uncertainties. Applied Sciences. 2021; 11(14):6582. https://doi.org/10.3390/app11146582
Chicago/Turabian StyleLee, Joon-Ho, Hee-Sun Choi, Jong-Hyeon Sohn, Geun-Ho Lee, Dong-Il Park, and Jin-Gyun Kim. 2021. "Statistical Analysis for Transmission Error of Gear System with Mechanical and Thermal Deformation Uncertainties" Applied Sciences 11, no. 14: 6582. https://doi.org/10.3390/app11146582
APA StyleLee, J.-H., Choi, H.-S., Sohn, J.-H., Lee, G.-H., Park, D.-I., & Kim, J.-G. (2021). Statistical Analysis for Transmission Error of Gear System with Mechanical and Thermal Deformation Uncertainties. Applied Sciences, 11(14), 6582. https://doi.org/10.3390/app11146582







