Lateral Resistance Requirement of Girder-Sleeper Fastener for CWR Track on an Open-Deck Steel Plate Girder Bridge
Abstract
:1. Introduction
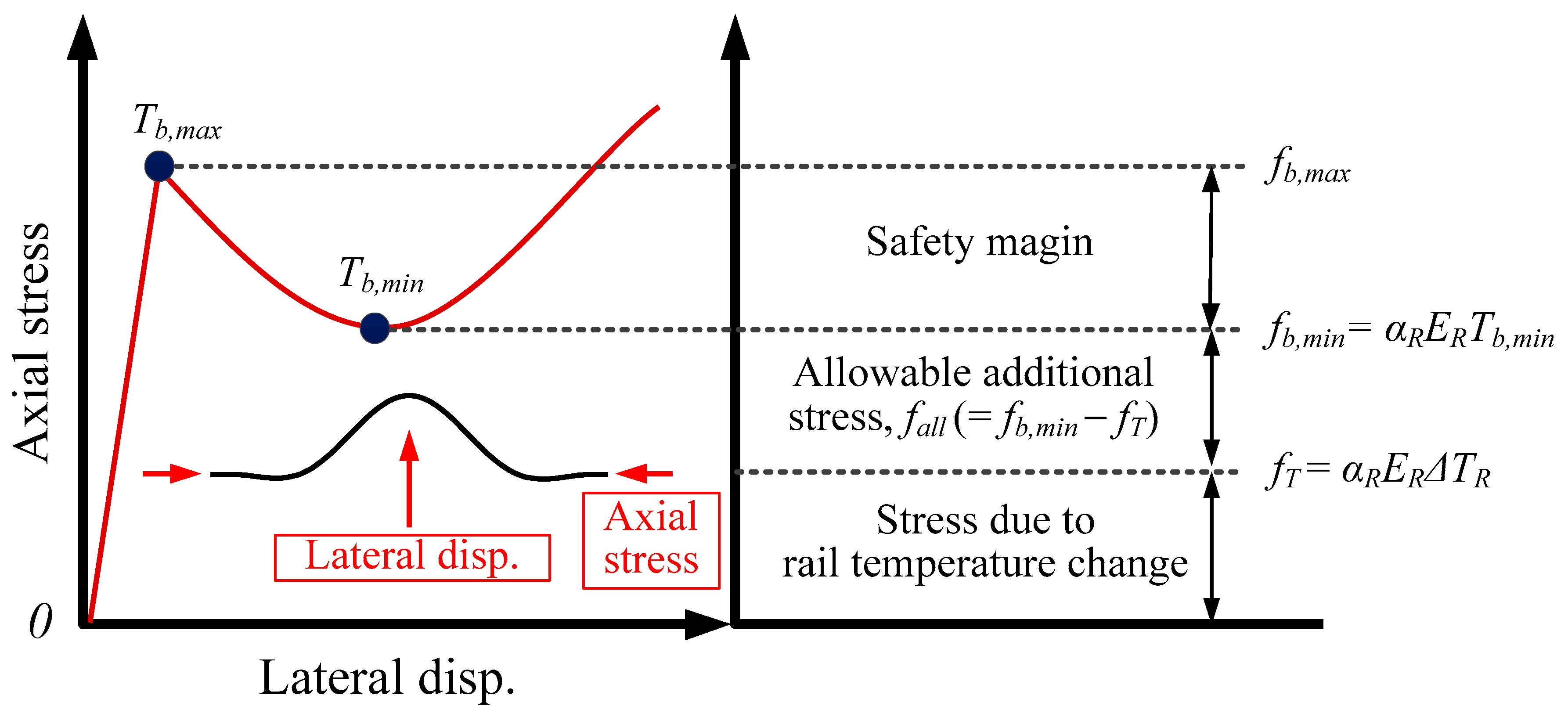
2. Theoretical Approach
3. Description of FE Model and Verification
3.1. Modeling Method
3.2. Verification
4. Parametric Study
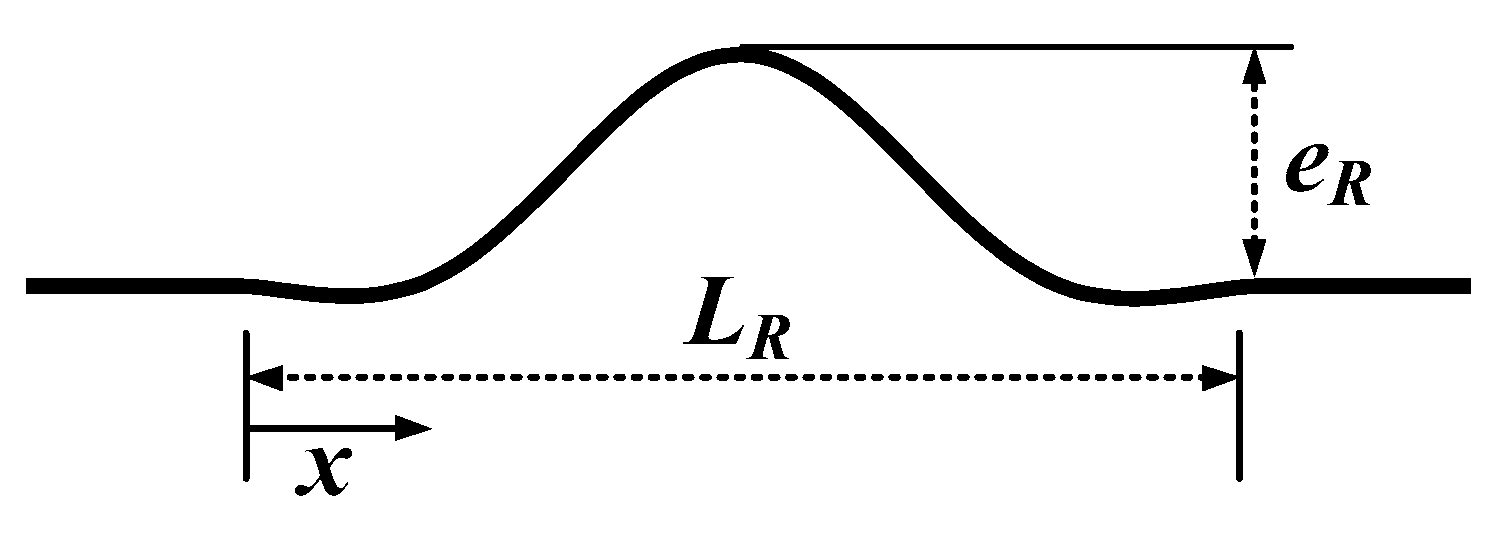
4.1. Parameters
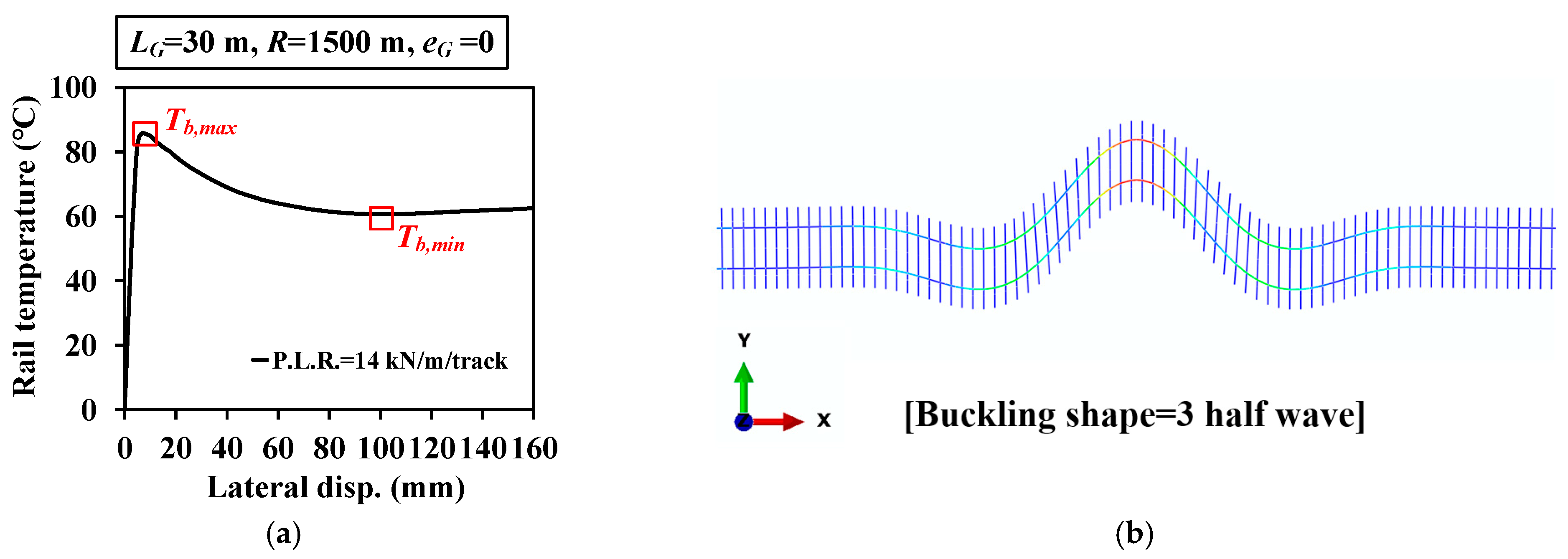
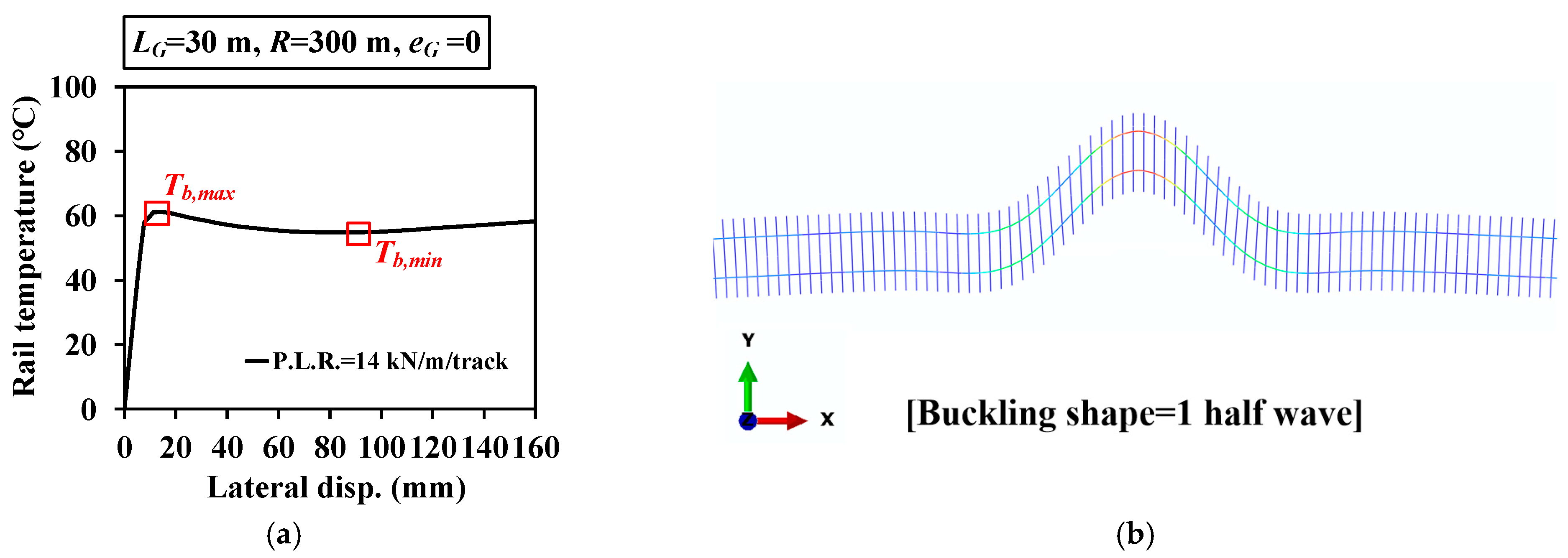
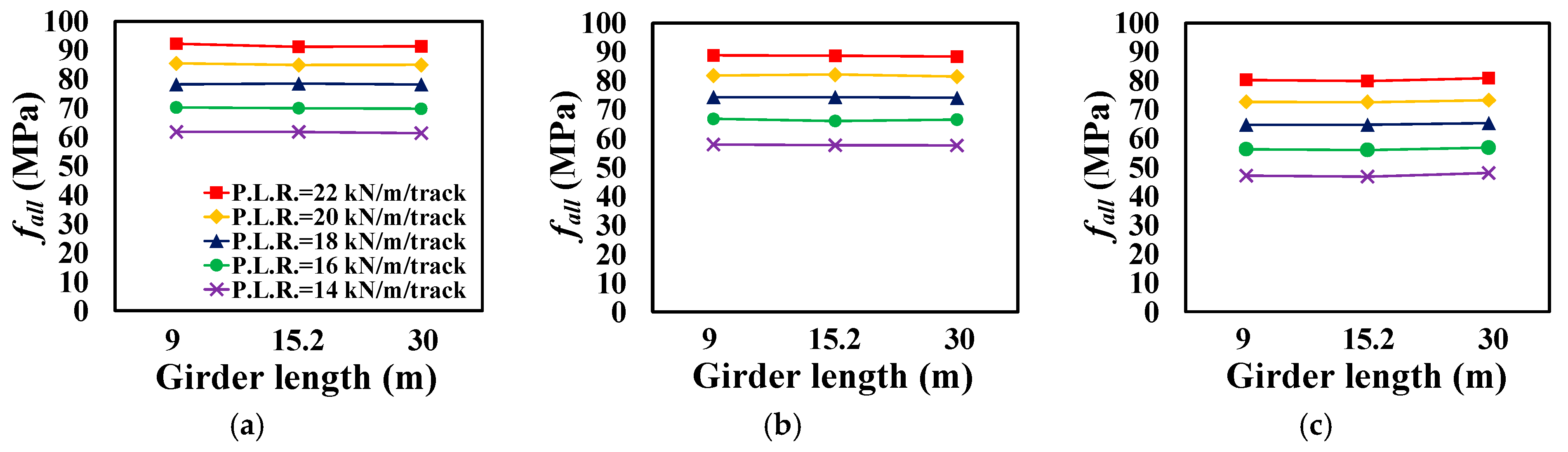
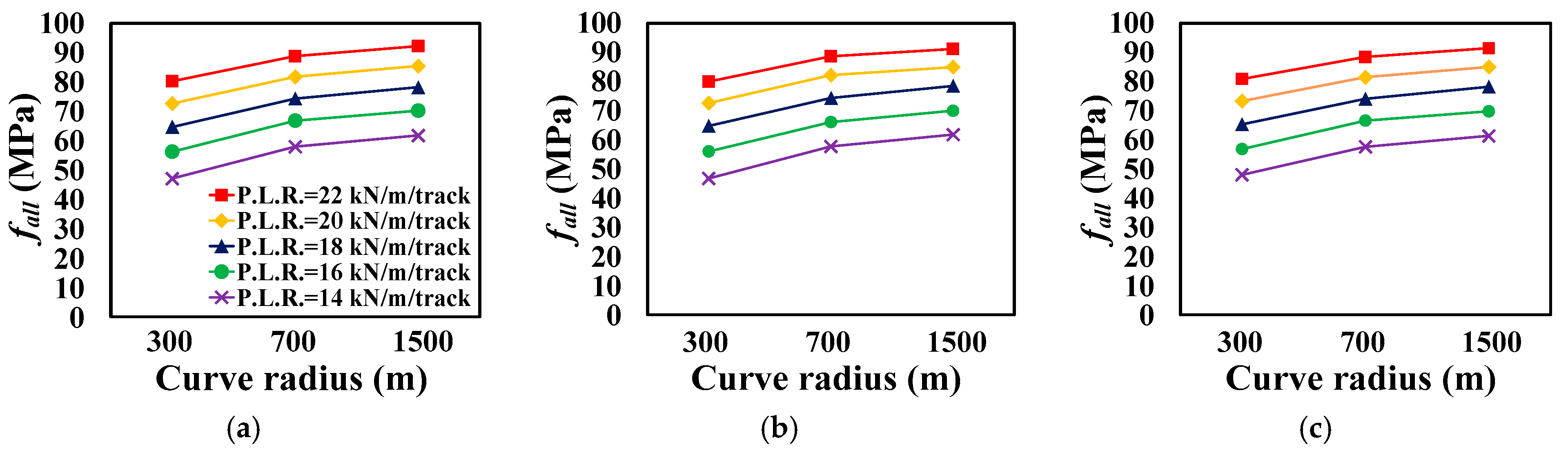
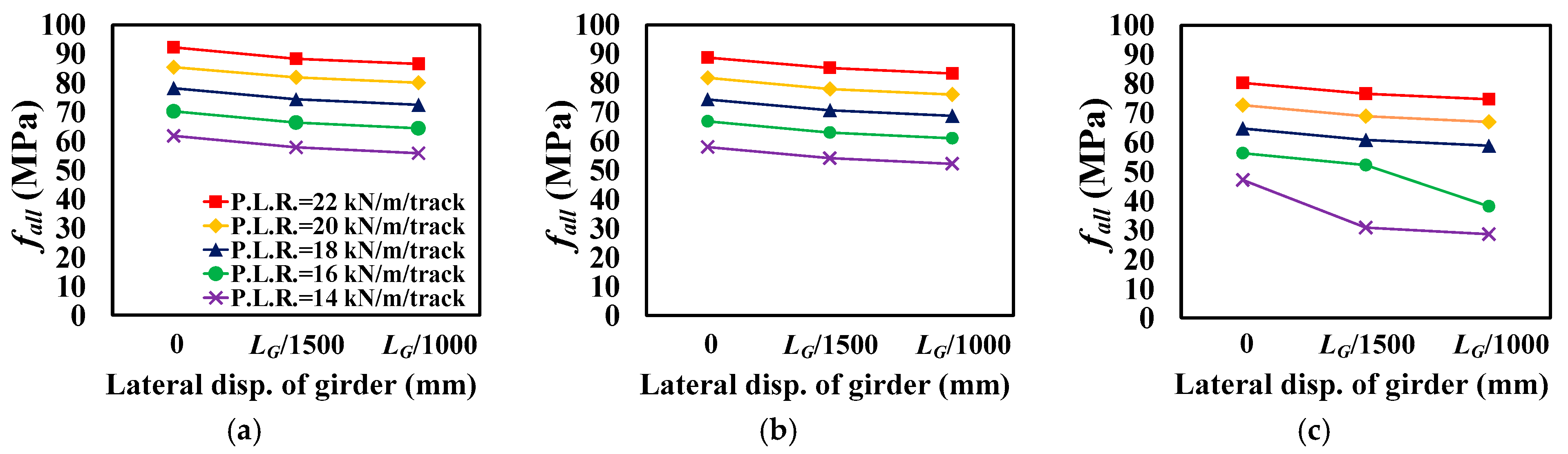
4.2. Analysis Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cai, W.; Wen, Z.; Jin, X.; Zhai, W. Dynamic stress analysis of rail joint with height difference defect using finite element method. Eng. Fail. Anal. 2007, 14, 1488–1499. [Google Scholar] [CrossRef]
- Chaboki, A. Assessment and Maintenance of Open Deck Railway Bridges. In Proceedings of the 9th Australian Small Bridges Conference, Gold Coast, QLD, Australia, 1–2 April 2019. [Google Scholar]
- Kish, A.; Samavedam, G. Track Buckling Prevention: Theory, Safety Concepts, and Applications (No. DOT/FRA/ORD-13/16); John, A., Ed.; Volpe National Transportation Systems Center: Washington, DC, USA, 2013. [Google Scholar]
- Chaudhary, K.R.; Sinha, A.N. A Study of Various Methods Adopted by World Railways to Continue LWR over Bridges. 1939. Available online: https://www.scribd.com/document/71782998/LWR (accessed on 6 November 2011).
- Lee, K.C.; Jang, S.Y.; Jung, D.K.; Byun, H.K.; Park, H.K.; Yang, T.S. Rail-Structure Interaction Analysis of Sliding Slab Track on Bridge. In Proceedings of the 2015 Joint Rail Conference, San Jose, CA, USA, 23–26 March 2015. [Google Scholar]
- Miri, A.; Thambiratnam, D.; Chan, T. Thermal challenges of replacing jointed rails with CWR on steel railway bridges. J. Constr. Steel Res. 2021, 181, 106627. [Google Scholar] [CrossRef]
- Miri, A.; Thambiratnam, D.; Weston, B.; Chan, T.H.T.; Dhanasekar, M. Lateral stability of CWR tracks in transition zones of open-deck steel bridges. Structures 2021, 33, 897–915. [Google Scholar] [CrossRef]
- Esveld, C. Modern Railway Track, 2nd ed.; MRT-Production: Delft, The Netherlands, 2001. [Google Scholar]
- International Union of Railway. UIC 774-3-R: Track/Bridge Interaction-Recommendation for Calculations, 2nd ed.; UIC International Union of Railways: Paris, France, 2001. [Google Scholar]
- Korea Rail Network Authority. KR C-08080. Analysis of Longitudinal Track-Bridge Interaction, Design Guidelines and Handbook; Korea Rail Network Authority: Seoul, Korea, 2017. (In Korean) [Google Scholar]
- Korea Rail Network Authority. KR C-14050. Continuous Welded Rail, Railway, Design Guidelines and Handbook; Korea Rail Network Authority: Seoul, Korea, 2016. (In Korean) [Google Scholar]
- Dassault Systèmes. Abaqus 2020 Analysis User‘s Manual; Dassault Systèmes: Vélizy-Villacoublay, France, 2020. [Google Scholar]
- Yun, K.M.; Park, B.H.; Bae, H.U.; Lim, N.H. Suggestion for Allowable Additional Compressive Stress Based on Track Conditions. J. Rail Rapid Transit. 2018, 235, 1309–1325. [Google Scholar] [CrossRef]
- Korean Railway Standards. KRS TR 0014-20R. In Rail Fastening System; Railway Industry Information Center: Seoul, Korea, 2020. (In Korean) [Google Scholar]
- Lim, N.H.; Han, S.Y.; Han, T.H.; Kang, Y.J. Parametric Study on Stability of Continuous Welded Rail Track-Ballast Resistance and Track Irregularity. Int. J. Steel Struct. 2008, 8, 171–181. [Google Scholar]
- Pita, A.; Teixeira, P.F.; Robuste, F. High speed and track deterioration: The role of vertical stiffness of the track. J. Rail Rapid Transit 2004, 218, 31–40. [Google Scholar] [CrossRef]
- Korea National Railway (KR). Track Maintenance Guideline; Korea National Railway: Seoul, Korea, 2020. (In Korean) [Google Scholar]
- Esveld Consulting Services. LONGSTAB Theoretical Manual - Computer Program for the Analysis of Track Stability and Longitudinal Forces. Available online: http://www.esveld.com/Download/SOFTWARE/LONGSTAB/LONGSTAB_theoretical_manual.pdf (accessed on 25 January 2021).
- International Union of Railway. UIC 720-R. Laying and Maintenance of CWR Track, 2nd ed.; UIC International Union of Railways: Paris, France, 2005. [Google Scholar]
- Khatibi, F.; Esmaeili, M.; Mohammadzadeh, S. Numerical investigation into the effect of ballast properties on buckling of continuously welded rail (CWR). J. Rail Rapid Transit 2020. [Google Scholar] [CrossRef]
- Consilvio, A.; Iorani, M.; Iovane, V.; Sciutto, M.; Sciutto, G. Real-time monitoring of the longitudinal strain of Continuous Welded Rail for safety improvement. J. Rail Rapid Transit 2020, 234, 1238–1252. [Google Scholar] [CrossRef]




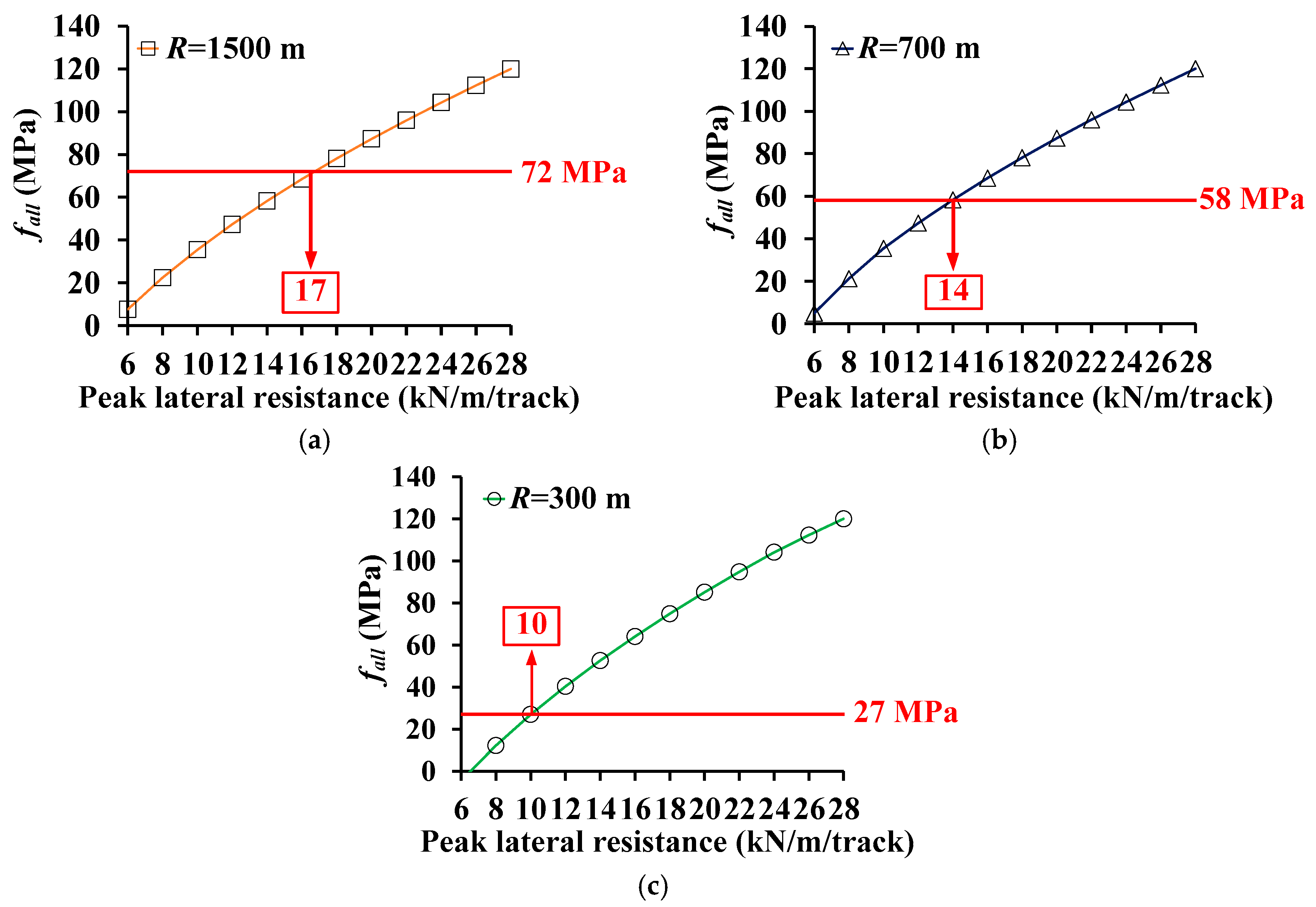



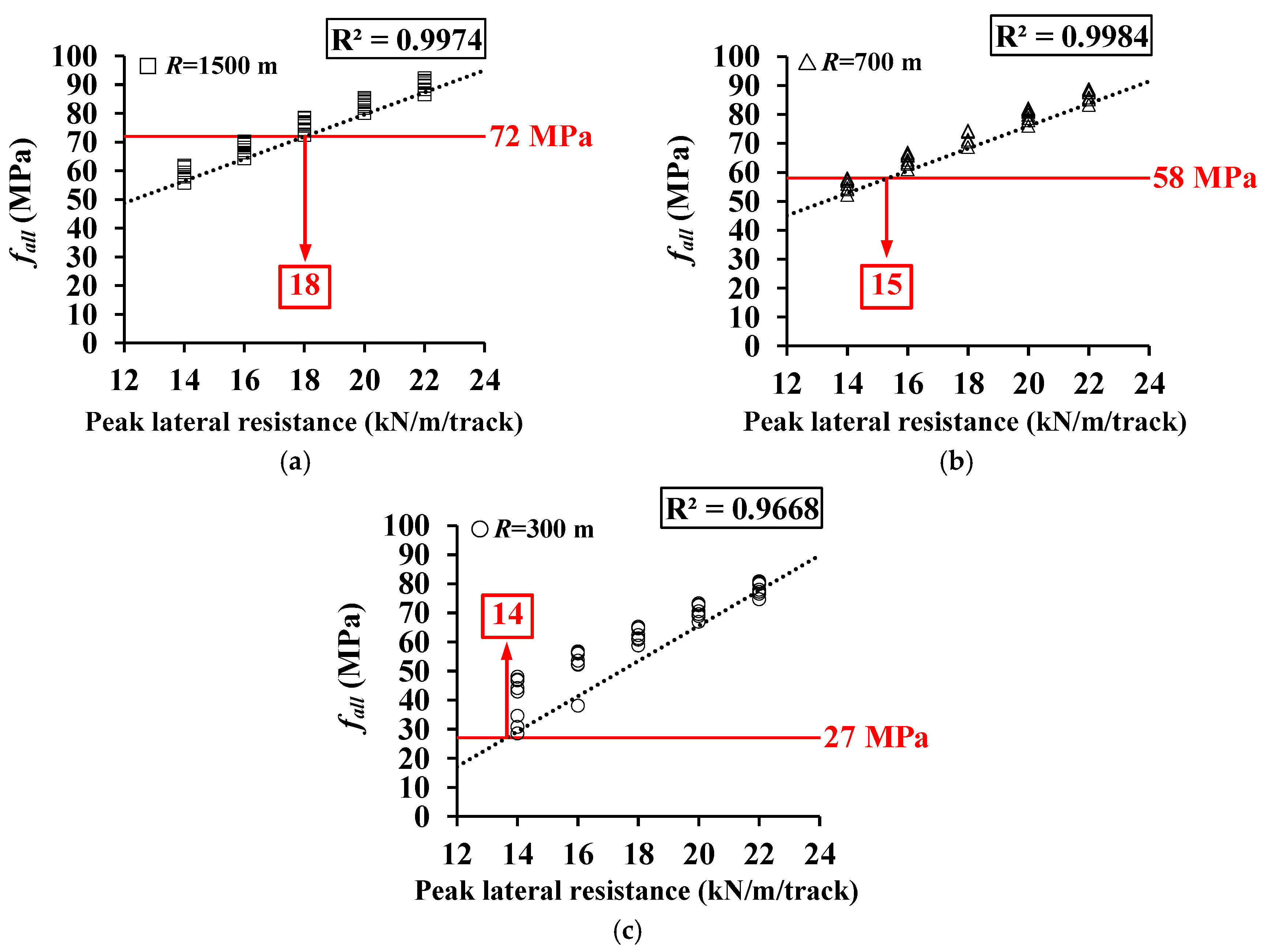
| Curve Radius, R (m) | Allowable Additional Stress (Compression, MPa) |
|---|---|
| R ≥ 1500 | 72 |
| R ≥ 700 | 58 |
| R ≥ 600 | 54 |
| R ≥ 300 | 27 |
| Stiffness | Value | References | Remark |
|---|---|---|---|
| Kx,f (N/m) | 1.4 × 107 | KRS TR 0014-20R [14] | Perfect elasto-plastic behavior with 7 kN of peak resistance |
| Ky,f (N/m) | 2.6 × 107 | Lim et al. [15] | Elastic behavior |
| Kz,f (N/m) | 8.0 × 107 | Pita et al. [16] | Elastic behavior |
| Rx,f,Ry,f, and Rz,f (N·m/rad) | 6.0 × 104 | Lim et al. [15] | Elastic behavior |
| Span Length (m) | D (m) | hw (mm) | tw (mm) | bf (mm) | tf (mm) | ||
|---|---|---|---|---|---|---|---|
| bf,u | bf,b | tf,u | tf,b | ||||
| 9 | 1.6 | 1170 | 10 | 250 | 250 | 30 | 30 |
| 15.2 | 1.8 | 1629 | 12 | 360 | 360 | 34 | 34 |
| 30 | 2.0 | 2548 | 12 | 480 | 560 | 38 | 40 |
| Span Length (m) | EA (kN) | EIy (kN·m2) | EIz (kN·m2) | GJ (kN·m2) |
|---|---|---|---|---|
| 9 | 1.15 × 107 | 2.76 × 106 | 7.38 × 106 | 3.50 × 105 |
| 15.2 | 1.87 × 107 | 8.42 × 106 | 1.52 × 107 | 8.04 × 105 |
| 30 | 3.04 × 107 | 3.51 × 107 | 3.08 × 107 | 2.38 × 106 |
| Parameter | Range | Remarks |
|---|---|---|
| Length of girder, LG (m) | 9, 15.2, and 30 | 3 cases |
| Curve radius, R (m) | 1500, 700, and 300 | 3 cases |
| Lateral disp. of the girder, eG | 0, LG/1500, and LG/1000 | 3 cases |
| Lateral resistance of girder-sleeper fastener, P.L.R. (kN/m/track) | 14–22 | 5 cases |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, H.-D.; Choi, S.; Moon, J. Lateral Resistance Requirement of Girder-Sleeper Fastener for CWR Track on an Open-Deck Steel Plate Girder Bridge. Appl. Sci. 2021, 11, 6681. https://doi.org/10.3390/app11156681
Lee H-D, Choi S, Moon J. Lateral Resistance Requirement of Girder-Sleeper Fastener for CWR Track on an Open-Deck Steel Plate Girder Bridge. Applied Sciences. 2021; 11(15):6681. https://doi.org/10.3390/app11156681
Chicago/Turabian StyleLee, Hyeoung-Deok, Sanghyun Choi, and Jiho Moon. 2021. "Lateral Resistance Requirement of Girder-Sleeper Fastener for CWR Track on an Open-Deck Steel Plate Girder Bridge" Applied Sciences 11, no. 15: 6681. https://doi.org/10.3390/app11156681
APA StyleLee, H.-D., Choi, S., & Moon, J. (2021). Lateral Resistance Requirement of Girder-Sleeper Fastener for CWR Track on an Open-Deck Steel Plate Girder Bridge. Applied Sciences, 11(15), 6681. https://doi.org/10.3390/app11156681







