Two-Dimensional Full-Waveform Joint Inversion of Surface Waves Using Phases and Z/H Ratios
Abstract
:1. Introduction
2. Calculation of 2D Rayleigh Wave Phase and Z/H-Ratio Kernel
2.1. D Full-Wave Sensitivity Kernels of the Traveltime Equation
2.2. D Full-Wave Sensitivity Kernels of the Z/H Ratio Equation
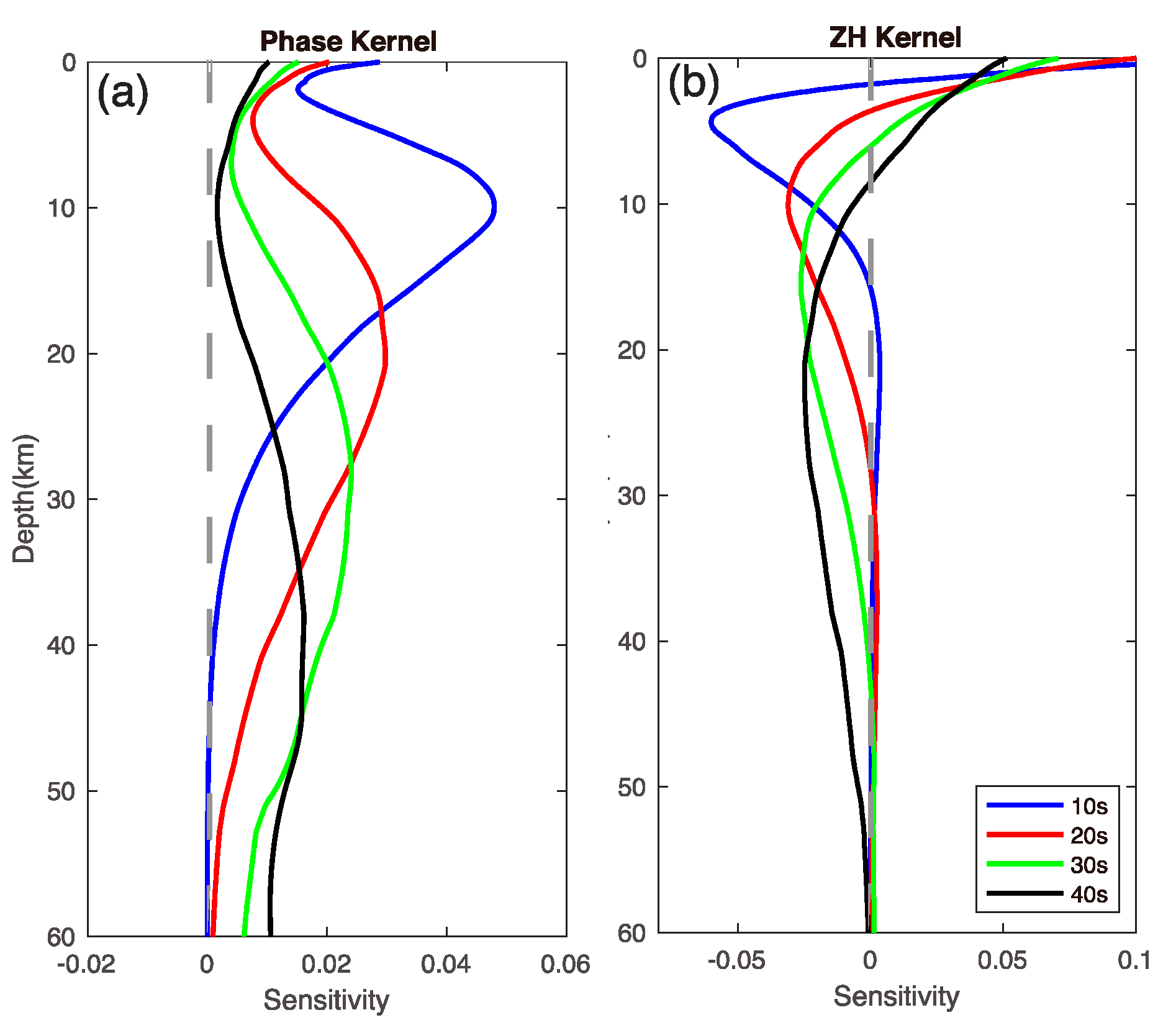
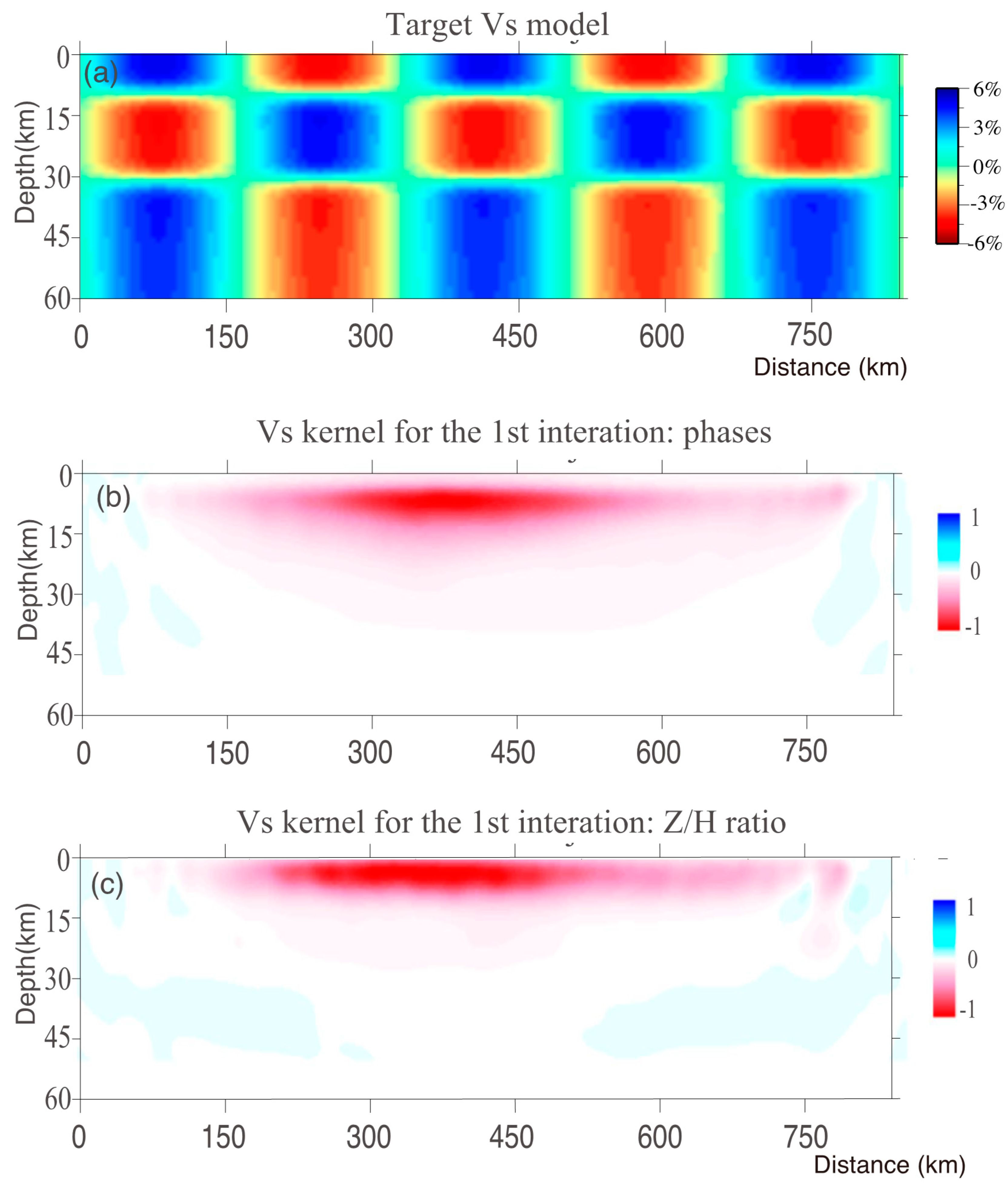
2.3. Sensitivity Calculation and Analysis
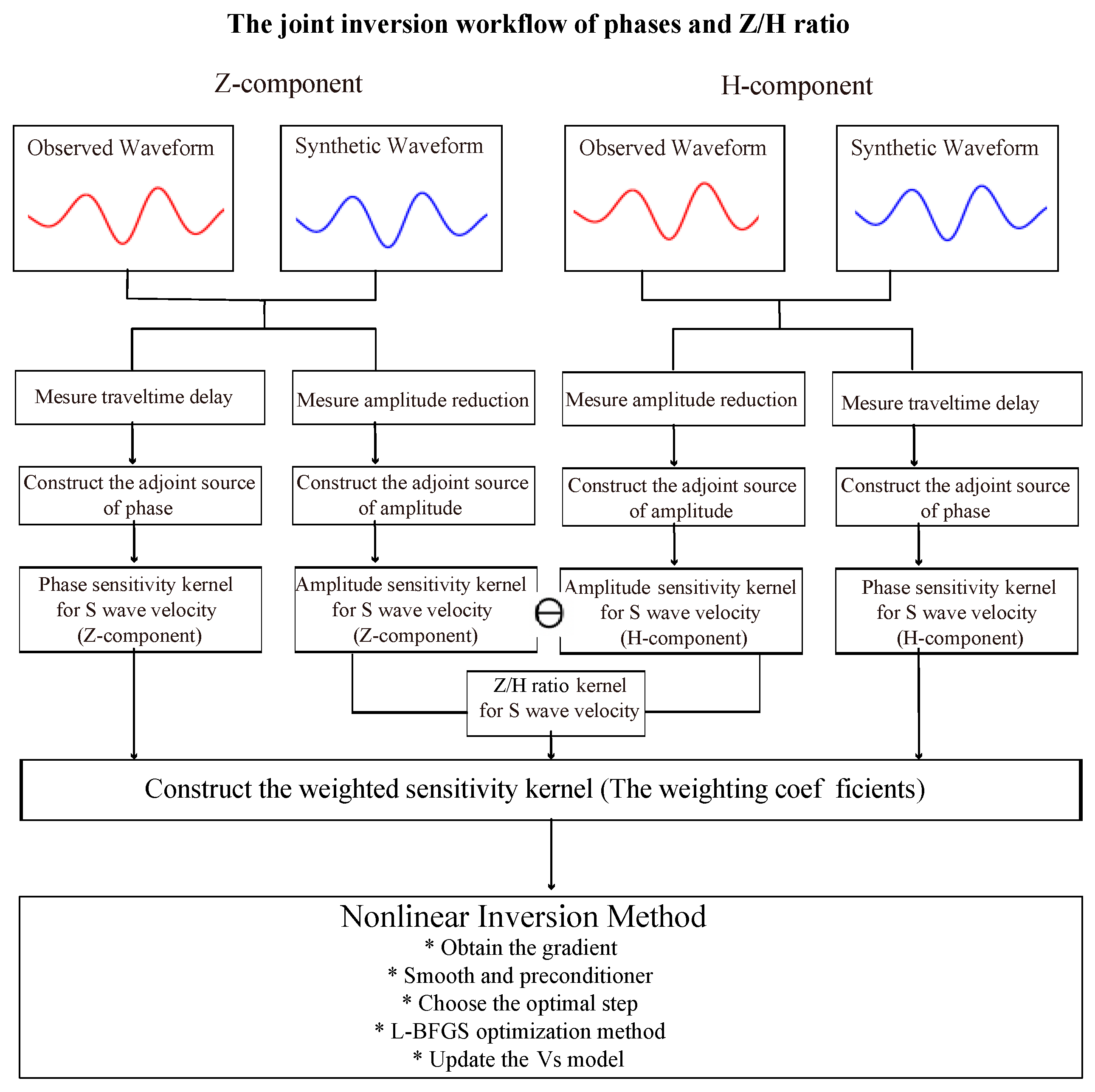
3. Joint Inversion of the Rayleigh Wave Phase and the Z/H Ratio
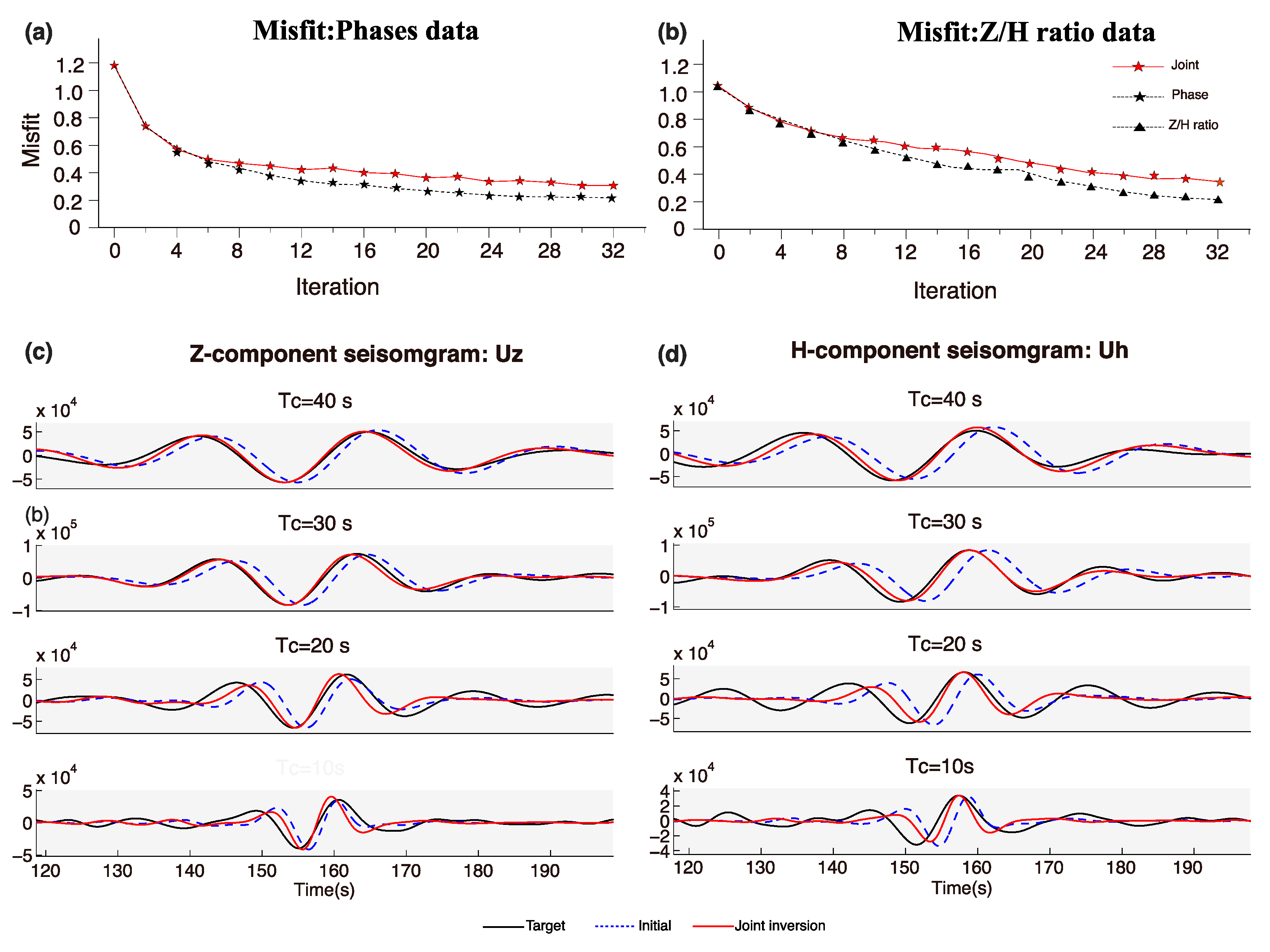
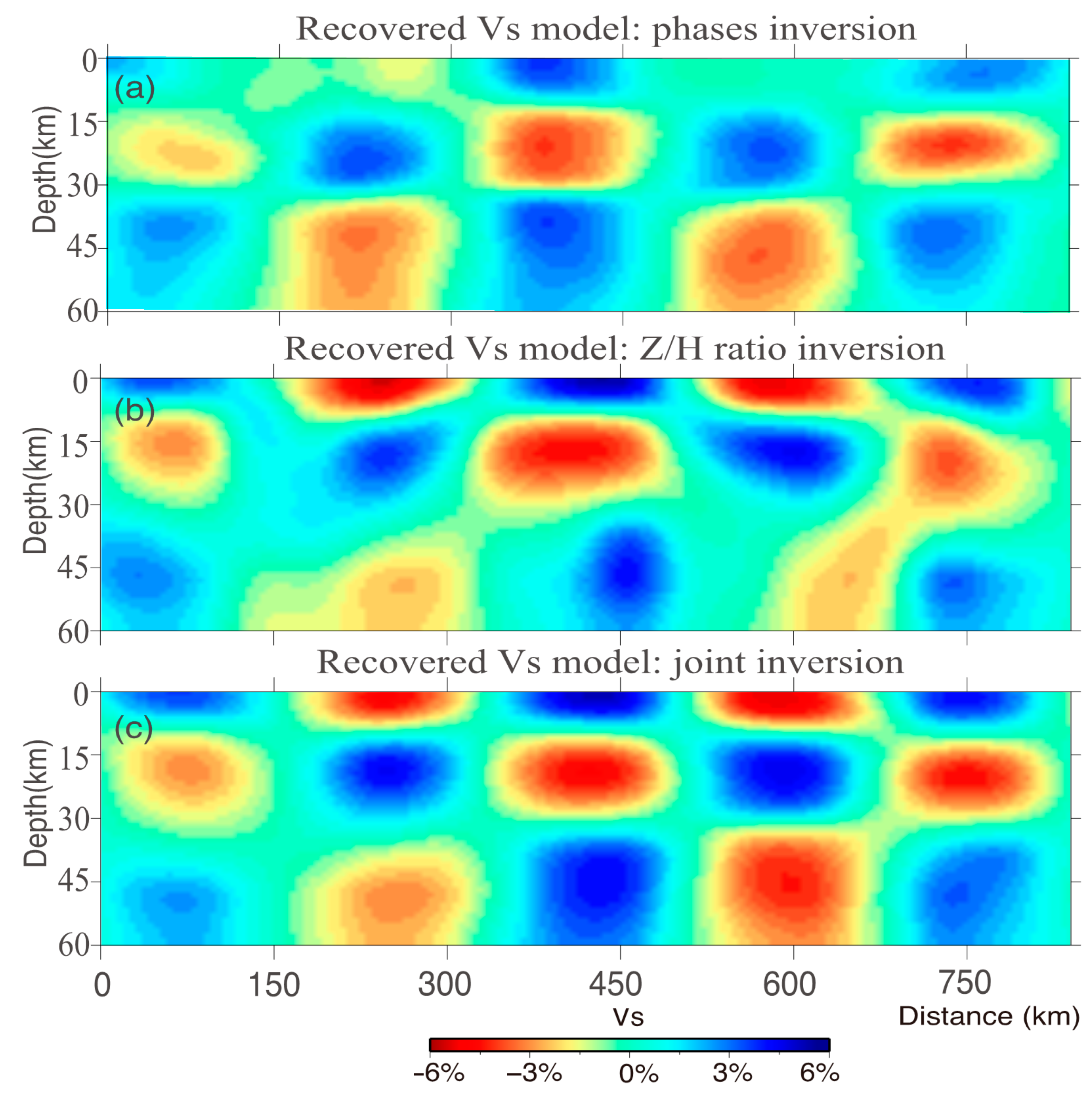
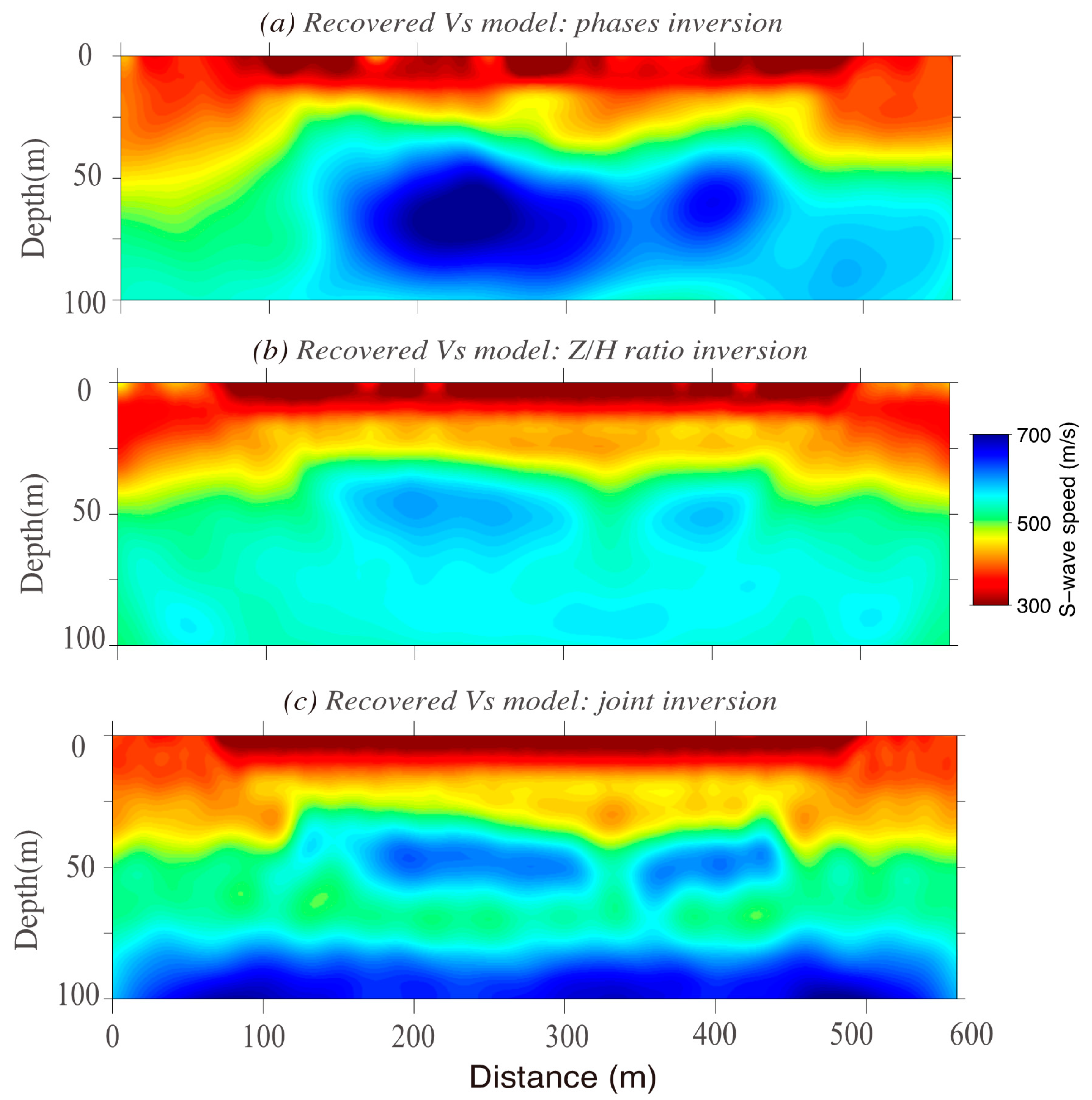
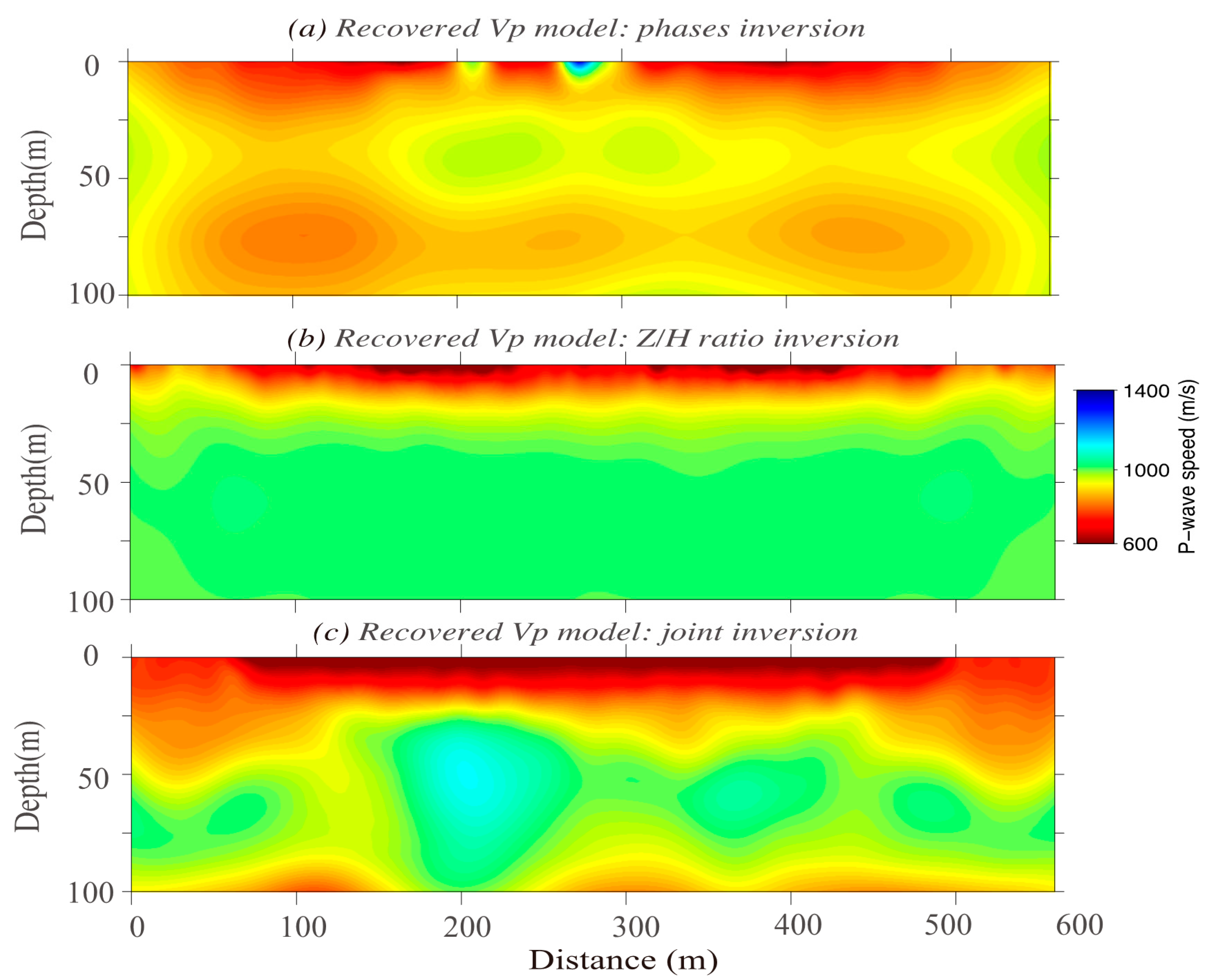
4. Inversion Experiments
4.1. Large-Scale Inversion Using Ambient Noise/Earthquake Surface Waves
4.2. Small-Scale Inversion Using Active Sources
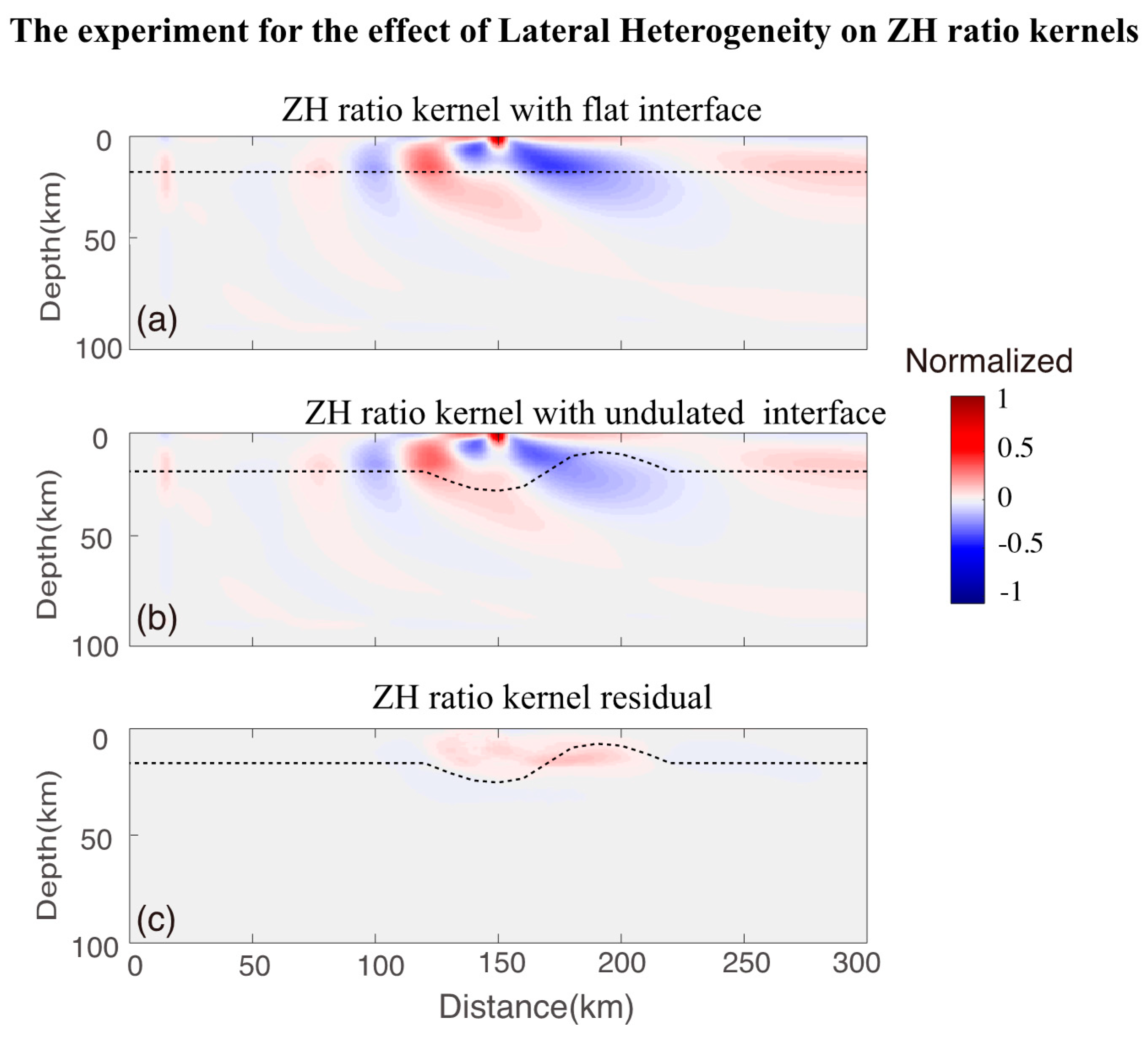
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Limited-Memory BFGS Algorithm
- (1)
- Evaluate
- (2)
- Set ;
- (3)
- If k > 0, compute pk from recursion, below;
- (4)
- Compute αk by line search and set
- (5)
- Evaluate
- (6)
- Set ;
- (7)
- Repeat (3–6), stopping immediately when
- (1)
- Set
- (2)
- Perform j times:
- (3)
- Set ;
- (4)
- Perform j times:
- (5)
- End with result ;
References
- Trampert, J.; Woodhouse, J.H. Global phase velocity maps of Love and Rayleigh waves between 40 and 150 seconds. Geophys. J. Int. 1995, 122, 675–690. [Google Scholar] [CrossRef] [Green Version]
- Simons, F.J.; Van Der Hilst, R.D.; Montagner, J.P.; Zielhuis, A. Multimode Rayleigh wave inversion for heterogeneity and azmuthal anisotropy of the Australian upper mantle. Geophys. J. Int. 2002, 151, 738–754. [Google Scholar] [CrossRef] [Green Version]
- Shapiro, N.M.; Ritzwoller, M.H. Monte-Carlo inversion for a global shear-velocity model of the crust and upper mantle. Geophys. J. Int. 2002, 151, 88–105. [Google Scholar] [CrossRef] [Green Version]
- Sabra, K.G.; Gerstoft, P.; Roux, P.; Kuperman, W.; Fehler, M.C. Surface wave tomography from microseisms in Southern California. Geophys. Res. Lett. 2005, 32, L14311. [Google Scholar] [CrossRef] [Green Version]
- Shapiro, N.M.; Campillo, M.; Stehly, L.; Ritzwoller, M.H. Highresolution surface-wave tomography from ambient seismic noise. Science 2005, 307, 1615–1618. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Ritzwoller, M.H.; Levshin, A.L.; Shapiro, N.M. Ambient noise Rayleigh wave tomography across Europe. Geophys. J. Int. 2007, 168, 259–274. [Google Scholar] [CrossRef] [Green Version]
- Lin, F.C.; Moschetti, M.P.; Ritzwoller, M.H. Surface wave tomography of the western United States from ambient seismic noise: Rayleigh and Love wave phase velocity maps. Geophys. J. Int. 2008, 173, 281–298. [Google Scholar] [CrossRef] [Green Version]
- Tanimoto, T.; Alvizuri, C. Inversion of the HZ ratio of microseisms for S-wave velocity in the crust. Geophys. J. Int. 2006, 165, 323–335. [Google Scholar] [CrossRef]
- Tanimoto, T.; Rivera, L. The ZH ratio method for long- period seismic data: Sensitivity kernels and observational techniques. Geophys. J. Int. 2008, 172, 187–198. [Google Scholar] [CrossRef] [Green Version]
- Chong, J.; Ni, S.; Zhao, L. Joint inversion of crustal structure with the Rayleigh wave phase velocity dispersion and the ZH ratio. Pure Appl. Geophys. 2015, 172, 2585–2600. [Google Scholar] [CrossRef]
- Komatitsch, D.; Tromp, J. Spectral-element simulations of global seismic wave propagation—I. Validation. Geophys. J. Int. 2002, 149, 390–412. [Google Scholar] [CrossRef]
- Komatitsch, D.; Tromp, J. Spectral-element simulations of global seismic wave propagation—II. Three-dimensional models, oceans, rotation and self-gravitation. Geophys. J. Int. 2002, 150, 303–318. [Google Scholar] [CrossRef]
- Bozdag, E.; Peter, D.; Lefebvre, M.; Komatitsch, D.; Tromp, J.; Hill, J.; Podhorszki, N.; Pugmire, D. Global adjoint tomography: First-generation model. Geophys. J. Int. 2016, 207, 1739–1766. [Google Scholar] [CrossRef]
- Chen, M.; Niu, F.; Liu, Q.; Tromp, J.; Zheng, X. Multi-parameter adjoint tomography of the crust and upper mantle beneath East Asia—Part I: Model construction and comparisons. J. Geophys. Res. 2015, 120, 1762–1786. [Google Scholar] [CrossRef] [Green Version]
- Fichtner, A.; Kennett, B.L.N.; Igel, H.; Bunge, H.-P. Full seismic waveform tomography for upper-mantle structure in the Australasian region using adjoint methods. Geophys. J. Int. 2009, 179, 1703–1725. [Google Scholar] [CrossRef] [Green Version]
- Liu, Q.; Gu, Y.J. Seismic imaging: From classical to adjoint tomography. Tectonophysics 2012, 566–567, 31–66. [Google Scholar] [CrossRef]
- Tape, C.; Liu, Q.; Maggi, A.; Tromp, J. Adjoint tomography of the southern California crust. Science 2009, 325, 988–992. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tape, C.; Liu, Q.; Maggi, A.; Tromp, J. Seismic tomography of the southern California crust based on spectral-element and adjoint methods. Geophys. J. Int. 2010, 180, 433–462. [Google Scholar] [CrossRef] [Green Version]
- Tromp, J.; Tape, C.; Liu, Q. Seismic tomography, adjoint methods, time reversal and banana-doughnut kernels. Geophys. J. Int. 2005, 160, 195–216. [Google Scholar] [CrossRef] [Green Version]
- Zhu, H.; Tromp, J. Mapping tectonic deformation in the crust and upper mantle beneath Europe and the North Atlantic Ocean. Science 2013, 341, 871–875. [Google Scholar] [CrossRef]
- Zhu, H.; Bozdağ, E.; Tromp, J. Seismic structure of the European upper mantle based on adjoint tomography. Geophys. J. Int. 2015, 201, 18–52. [Google Scholar] [CrossRef]
- Zhu, H.; Bozdağ, E.; Peter, D.; Tromp, J. Structure of the European upper mantle revealed by adjoint tomography. Nat. Geosci. 2012, 5, 493–498. [Google Scholar] [CrossRef]
- Chen, M.; Huang, H.; Yao, H.; van der Hilst, R.D.; Niu, F. Low wave speed zones in the crust beneath SE Tibet revealed by ambient noise adjoint tomograph. Geophys. Res. Lett. 2014, 41, 334–340. [Google Scholar] [CrossRef] [Green Version]
- Gao, H.; Shen, Y. Upper mantle structure of the Cascades from full-wave ambient noise tomography: Evidence for 3D mantle upwelling in the back-arc. Earth Planet. Sci. Lett. 2014, 390, 222–233. [Google Scholar] [CrossRef] [Green Version]
- Gao, H. Three-dimensional variations of the slab geometry correlate with earthquake distributions at the Cascadia subduction system. Nat. Commun. 2018, 9, 1204. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Savage, B.; Covellone, B.M.; Shen, Y. Wave speed structure of the eastern North American margin. Earth Planet. Sci. Lett. 2017, 459, 394–405. [Google Scholar] [CrossRef]
- Bao, X.Y.; Shen, Y. Full-waveform sensitivity kernels of component- differential traveltimes and ZH amplitude ratios for velocity and density tomography. J. Geophys. Res. Solid Earth 2018, 123, 4829–4840. [Google Scholar] [CrossRef]
- Chen, P.; Jordan, T.H.; Zhao, L. Full three-dimensional tomography: A comparison between the scattering-integral and adjoint-wavefield methods. Geophys. J. Int. 2007, 170, 175–181. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Shen, Y.; Zhao, L. Three-dimensional anisotropic seismic wave modelling in spherical coordinate by a collocated-grid finite-difference method. Geophys. J. Int. 2012, 188, 1359–1381. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Shen, Y. Cross-dependence of finite-frequency compressional waveforms to shear seismic wave speeds. Geophys. J. Int. 2008, 174, 941–948. [Google Scholar] [CrossRef] [Green Version]
- Zhao, L.; Jordan, T.H.; Olsen, K.B.; Chen, P. Fréchet kernels for imaging regional Earth structure based on three-dimensional reference models. Bull. Seismol. Soc. Am. 2005, 95, 2066–2080. [Google Scholar] [CrossRef]
- Zhang, C.; Yao, H.; Liu, Q.; Zhang, P.; Yuan, Y.O.; Feng, J.; Fang, L. Linear Array Ambient Noise Adjoint Tomography Reveals Intense Crust Mantle Interactions in North China Craton. J. Geophys. Res. Solid Earth 2018, 123, 368–383. [Google Scholar] [CrossRef]
- Tong, P.; Chen, C.; Komatitsch, D.; Basini, P.; Liu, Q. High-resolution seismic arra-y imaging based on a SEM-FK hybrid method. Geophys. J. Int. 2014, 197, 369–395. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Yao, H.; Tong, P.; Liu, Q.; Lei, T. Joint inversion of linear array ambient noise surface-wave and teleseismic body-wave data based on an adjoint-state method. Chin. J. Geophys. 2020, 63, 4065–4079. [Google Scholar]
- Romdhane, G.; Grandjean, G.; Brossier, R.; Rejiba, F.; Operto, S.; Virieux, J. Shallow-structure characterization by 2D elastic full-waveform inversion. Geophysics 2011, 76, R81–R93. [Google Scholar] [CrossRef] [Green Version]
- Nuber, A.; Manukyan, E.; Maurer, H. Enhancement of near-surface elastic full waveform inversion results in regions of low sensitivities. J. Appl. Geophys. 2015, 122, R192–R201. [Google Scholar] [CrossRef]
- Tran, K.; McVay, M.; Faraone, M.; Horhota, D. Sinkhole detection using 2D full seismic waveform tomography. Geophysics 2013, 78, R175–R183. [Google Scholar] [CrossRef]
- Groos, L. 2D Full Waveform Inversion of Shallow Seismic Rayleigh Waves. Ph.D. Thesis, Karlsruhe Institute of Technology, Karlsruhe, Germany, 2013. [Google Scholar]
- Forbriger, T.; Groos, L.; Schäfer, M. Line-source simulation for shallow-seismic data—Part 1: Theoretical background. Geophys. J. Int. 2014, 198, 1387–1404. [Google Scholar] [CrossRef] [Green Version]
- Schäfer, M.; Groos, L.; Forbriger, T.; Bohlen, T. Line-source simulation for shallow-seismic data. Part 2: Full-waveform inversion—A synthetic 2D case study. Geophys. J. Int. 2014, 198, 1405–1418. [Google Scholar] [CrossRef] [Green Version]
- Groos, L.; Schäfer, M.; Forbriger, T.; Bohlen, T. Application of a complete workflow for 2D elastic full-waveform inversion to recorded shallow-seismic Rayleigh waves. Geophysics 2017, 82, R109–R117. [Google Scholar] [CrossRef]
- Dahlen, F.; Baig, A. Fréchet kernels for body-wave amplitudes. Geophys. J. Int. 2002, 150, 440–466. [Google Scholar] [CrossRef] [Green Version]
- Liu, D.; Nocedal, J. On the limited memory BFGS method for large scale optimization. Math. Program. 1989, 45, 504–528. [Google Scholar] [CrossRef] [Green Version]
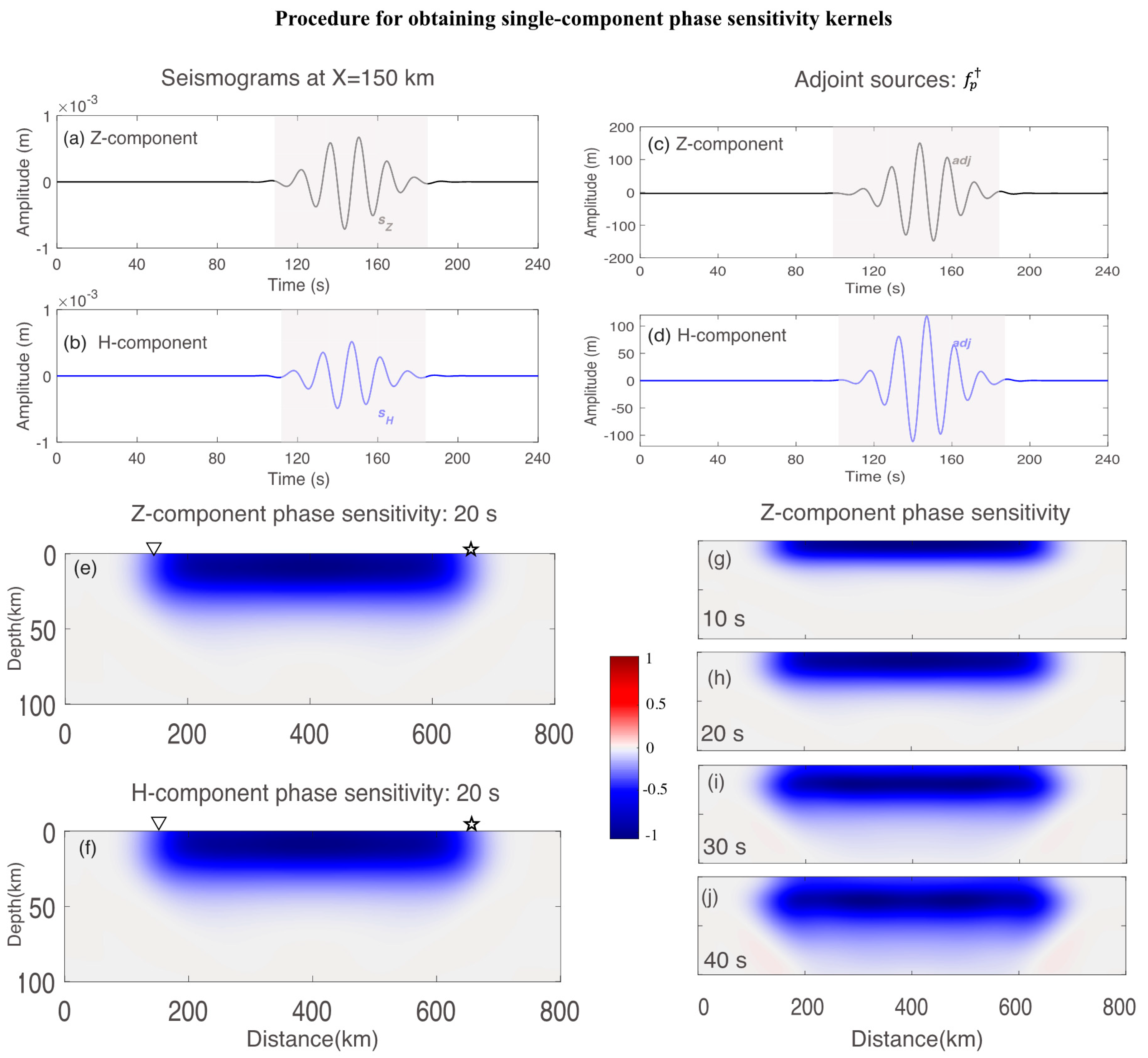



| Model Size (Nx × Nz) | x-Direction: 800 km; z-Direction: 100 km (300 × 40 Elements) |
|---|---|
| Material properties | Vp = 6000 m/s, vs. = 3500 m/s, ρ = 2800 g/m3 |
| Propagation time | 12,000 time steps; Time discretization: 0.02 s |
| Type of source-time function | Gaussian |
| Dominant frequency of source | 2 Hz |
| Source location | (650 km, 0 km) |
| Station location | (150 km, 0 km) |
| Type of Inversion | Phase Inversion | Z/H Ratio Inversion | Joint Inversion |
|---|---|---|---|
| Model size (Nx ∗ Nz) | x-direction: 600 m; z-direction: 100 m Nx = 100; Nz = 20 | ||
| Propagation time | 20,000 time steps; Time discretization: 0.0003 s | ||
| Number of processors for each source | 4 | 4 | 8 |
| Total number of CPUs/cores | 200 | 200 | 400 |
| Number of iterations | 46 | 54 | 38 |
| Time for inversion | 6.25 h | 6.72 h | 5.80 h |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Lei, T.; Wang, Y. Two-Dimensional Full-Waveform Joint Inversion of Surface Waves Using Phases and Z/H Ratios. Appl. Sci. 2021, 11, 6712. https://doi.org/10.3390/app11156712
Zhang C, Lei T, Wang Y. Two-Dimensional Full-Waveform Joint Inversion of Surface Waves Using Phases and Z/H Ratios. Applied Sciences. 2021; 11(15):6712. https://doi.org/10.3390/app11156712
Chicago/Turabian StyleZhang, Chao, Ting Lei, and Yi Wang. 2021. "Two-Dimensional Full-Waveform Joint Inversion of Surface Waves Using Phases and Z/H Ratios" Applied Sciences 11, no. 15: 6712. https://doi.org/10.3390/app11156712





