Investigation into the Influence of Division Pier on the Internal Flow and Pulsation in the Outlet Conduit of an Axial-Flow Pump
Abstract
:1. Introduction
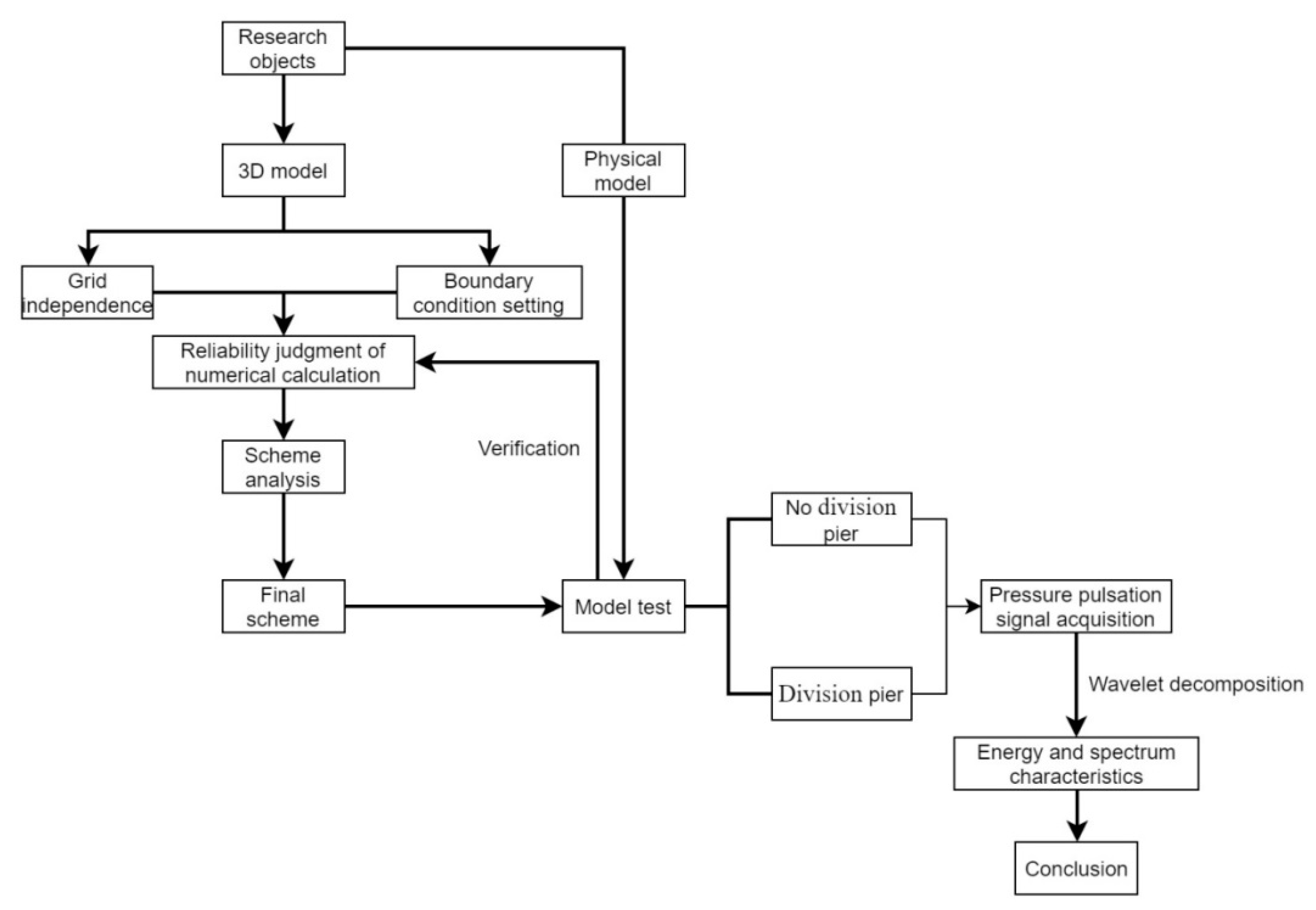
2. Numerical Simulation Method
2.1. Model Parameter
2.2. Grid Scheme and Boundary Conditions
2.2.1. Grid Scheme and Interface Setting
2.2.2. Boundary Conditions, Governing Equations and Turbulence Model
3. Test Equipment and Analysis Method
3.1. Test Equipment
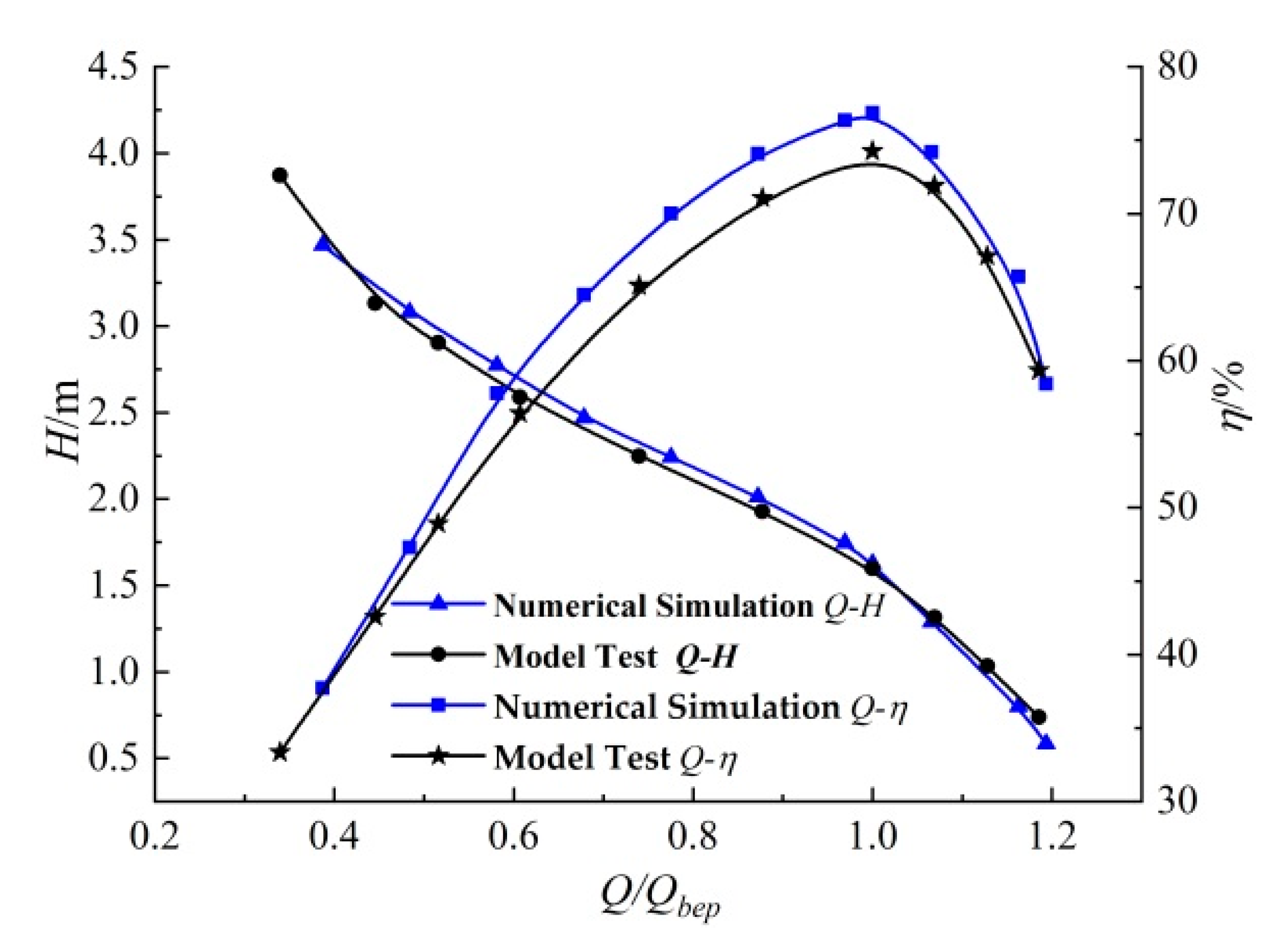
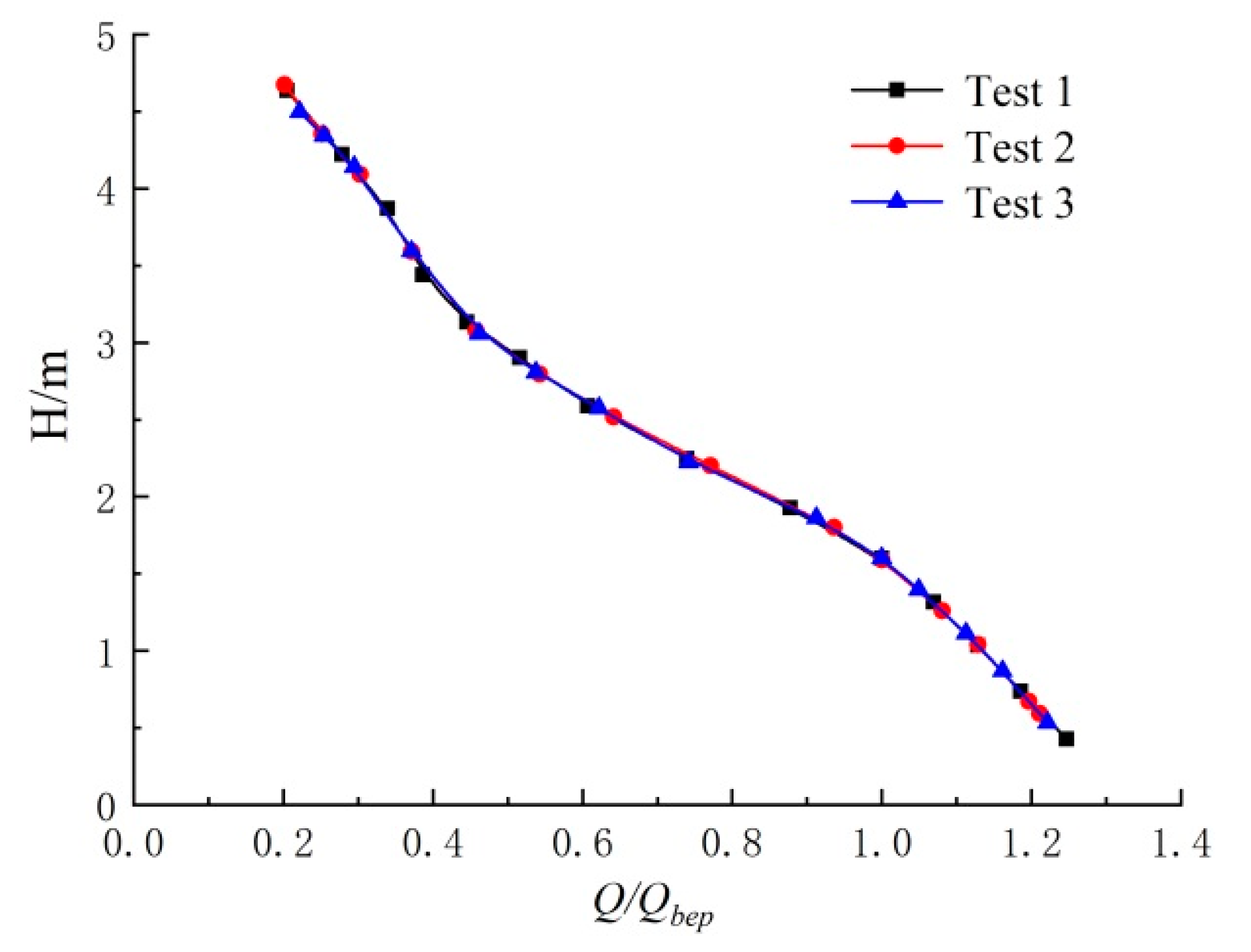
3.2. Total Uncertainty Analysis
3.3. Measurement and Analysis of Pressure Fluctuation
4. Results and Discussion
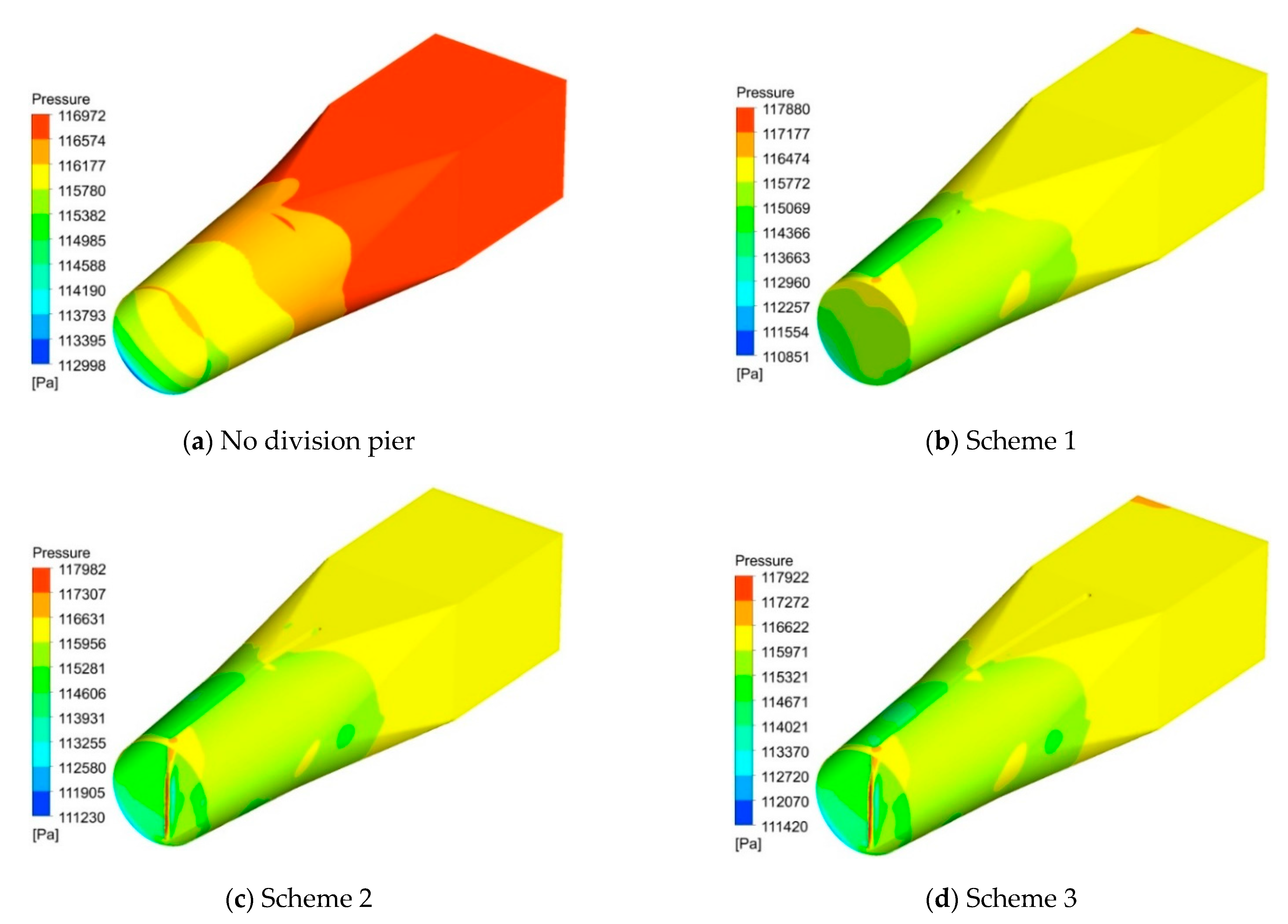
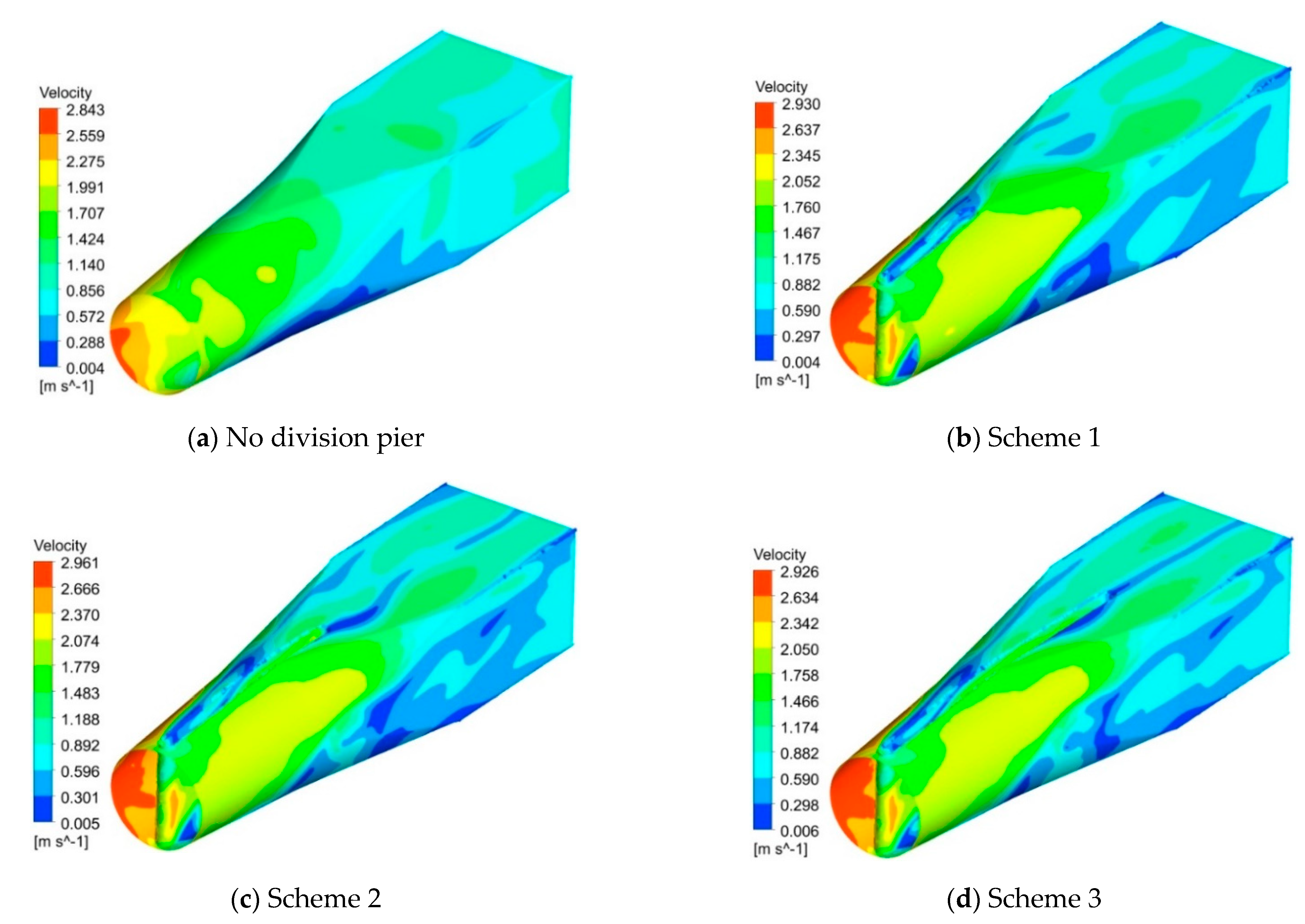
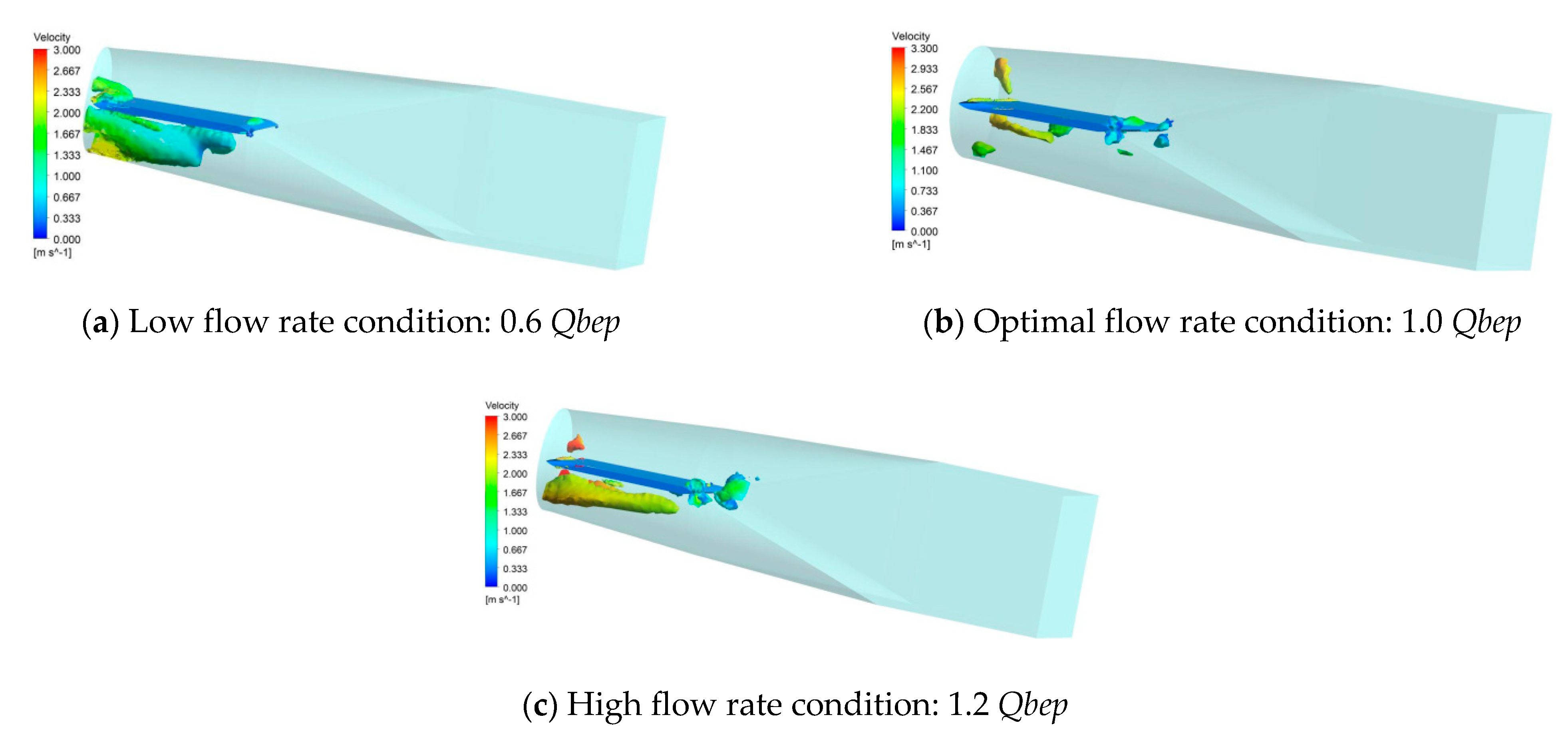
4.1. Flow Field Analysis of Straight Outlet Conduit
4.2. Analysis of Static Pressure and Velocity
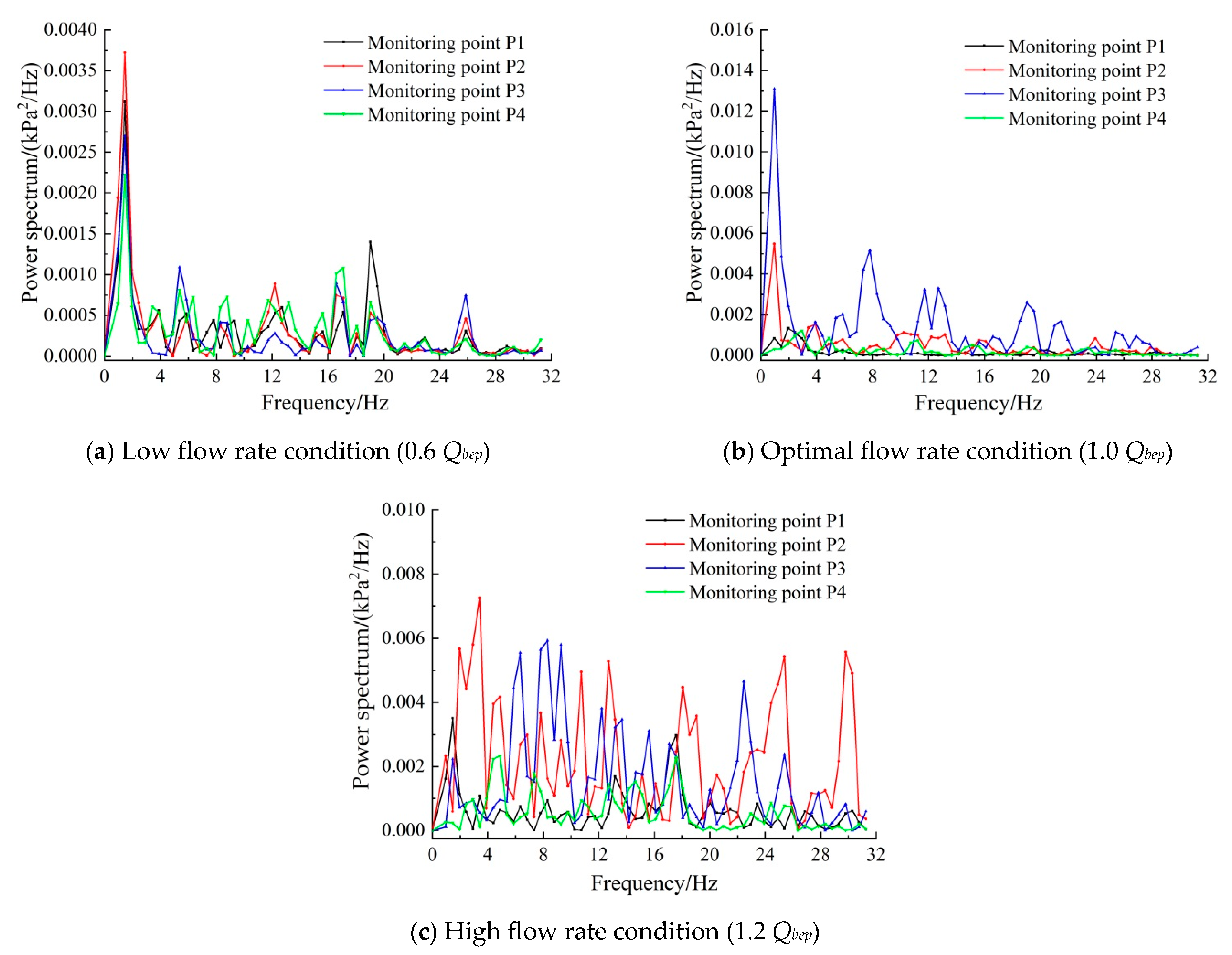
4.3. Analysis Results of Pressure Fluctuation Signal without Division Pier
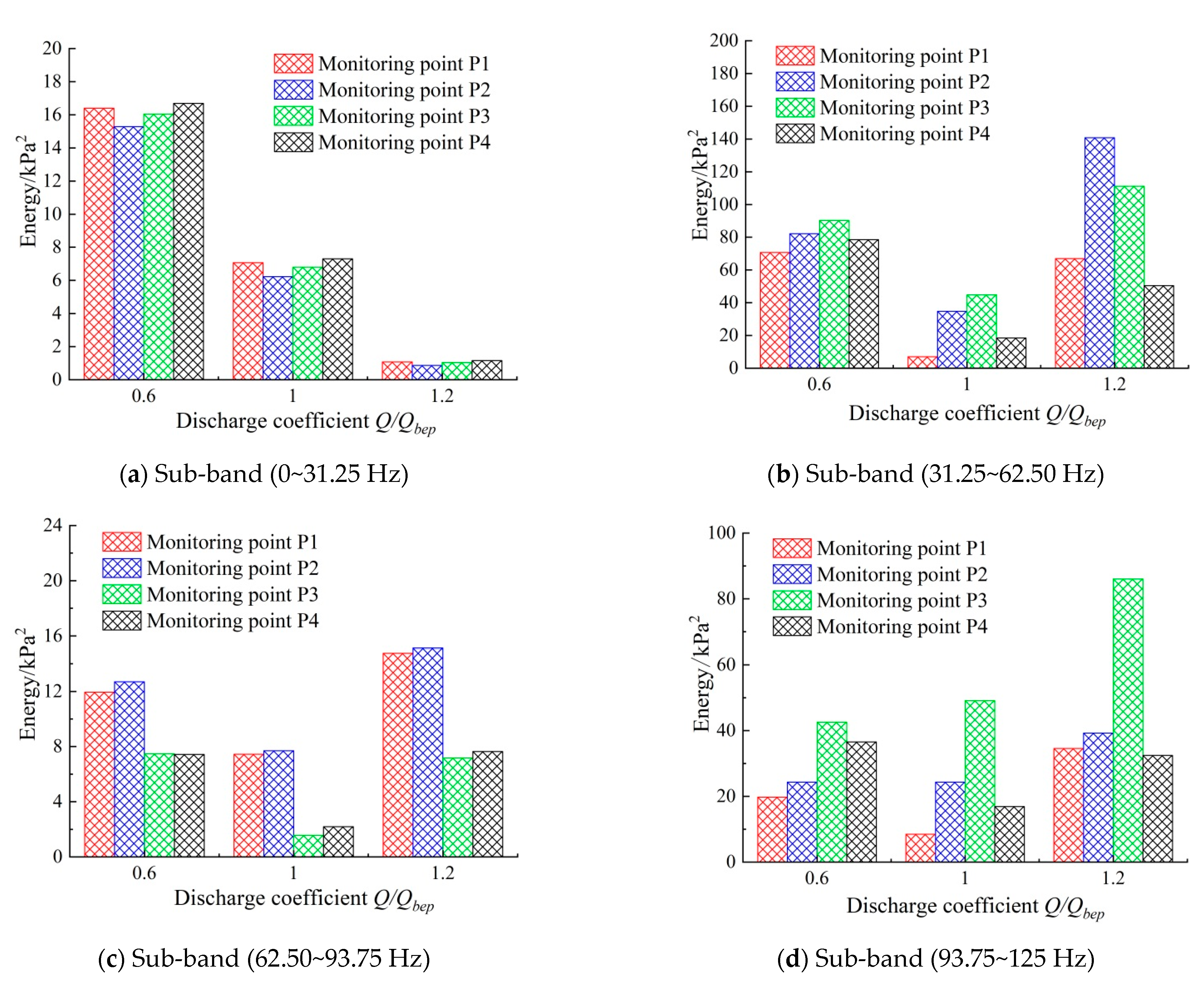
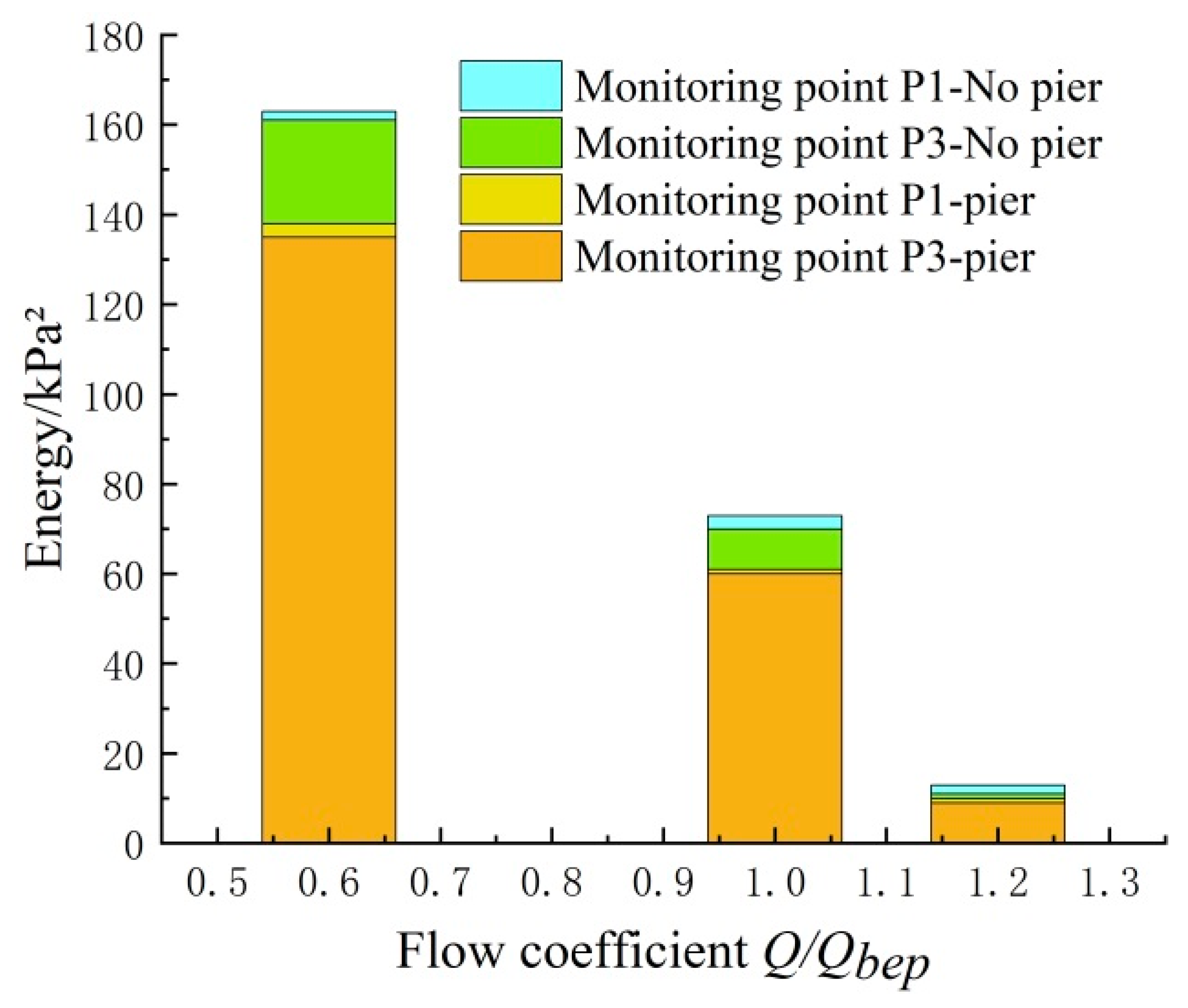
4.4. Analysis Results of Pressure Fluctuation with Division Pier
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Q | Flow rate |
| Qbep | Optimal flow rate |
| H | Head |
| D | Impeller diameter |
| η | Efficiency |
| Total system error of test | |
| f | Highest analysis frequency |
| fs | Sampling frequency of pressure fluctuation test |
| Eq | Systematic error of flow measurement |
| Total system uncertainty of the test bed | |
| Random uncertainty of the test bed | |
| Eh | Systematic error of head measurement |
| Em | Systematic error of torque measurement |
| En | System error of speed measurement |
| D | Wavelet packet |
References
- Zhang, Y.; Zhang, Z.; Zhang, J. Experimental Study on the Influence of Different Water Depth on Tidal Turbine Hydrodynamic Characteristics. Proc. CSEE 2020, 40, 6973–6982. [Google Scholar]
- Kan, K.; Chen, H.; Zheng, Y.; Zhou, D.; Binama, M.; Dai, J. Transient characteristics during power-off process in a shaft extension tubular pump by using a suitable numerical model. Renew. Energy 2021, 164, 109–121. [Google Scholar] [CrossRef]
- Kan, K.; Zheng, Y.; Chen, H.; Cheng, J.; Gao, J.; Yang, C. Study into the Improvement of Dynamic Stress Characteristics and Prototype Test of an Impeller Blade of an Axial-Flow Pump Based on Bidirectional Fluid–Structure Interaction. J. Appl. Sci. 2019, 9, 3601. [Google Scholar] [CrossRef] [Green Version]
- Liu, C. Analysis on technological innovation and development of axial flow pump system. Trans. Chin. Soc. Agric. Mach. 2015, 46, 49–59. [Google Scholar]
- Xie, L.; Wang, F.; He, C. Experimental study on hydrodynamic characteristics of 15 degree inclined axial flow pump device. Hydraul. Eng. 2019, 50, 798–805. [Google Scholar]
- Xu, L.; Yan, S.; Shi, W. Applicability of turbulence model for numerical calculation of hydraulic performance of siphon outlet channel. Hydro Sci. Eng. 2019, 42–49. [Google Scholar] [CrossRef]
- Yang, F.; Liu, C.; Tang, F. Analysis on hydraulic characteristics of outlet channel of pump device based on full channel simulation. Trans. Chin. Soc. Agric. Mach. 2014, 45, 83–89. [Google Scholar]
- Liang, J.; Lu, L.; Liu, R. The influence of middle pier on the hydraulic performance of outlet channel of large pumping station. Drain. Irrig. Mach. Eng. 2011, 29, 77–81. [Google Scholar]
- Duan, Y.; Zhou, R. Simulation analysis on temperature change effect of spillway tunnel lining during construction period of Xiaolangdi project. Hydroelectr. Eng. 2005, 49–54. [Google Scholar] [CrossRef]
- PI, J.; Qiu, C.; Yu, B. Test and Research on inlet and outlet channel type of large vertical axial flow pump station. Eng. J. Wuhan Univ. 1981, 55–64. [Google Scholar]
- Zhu, J.; He, Z.; Liu, D. Design and model test verification of bidirectional outlet channel of large axial flow pumping station. Eng. J. Wuhan Univ. 2005, 13–16. [Google Scholar] [CrossRef]
- Zhu, J.; He, Z.; Liu, D. Experimental study on two way inlet and outlet flow channel model. Pump Technol. 2005, 18–21. [Google Scholar]
- Kan, K.; Zixuan, Y.; Pin, L.; Yuan, Z.; Lian, S. Numerical Study of Turbulent Flow past a Rotating Axial-Flow Pump Based on a Level-set Immersed Boundary Method. Renew. Energy 2020, 168, 960–971. [Google Scholar] [CrossRef]
- Ramadhan, A.A. Investigation of the influence of various numbers of impeller blades on internal flow field analysis and the pressure pulsation of an axial pump based on transient flow behavior. Heat Transfer. 2020, 49. [Google Scholar] [CrossRef]
- Yu, I.; Yuhei, S.; Takao, N. Theoretical Analyses of the Number of Backflow Vortices on an Axial Pump or Compressor. Fluids Eng. 2020, 142. [Google Scholar] [CrossRef] [Green Version]
- Zhu, H.; Yuan, S. Influence of inlet flow field on the performance of siphon outlet passage. Trans. Chin. Soc. Agric. Mach. 2006, 193–196. [Google Scholar] [CrossRef]
- Yang, F.; Hu, W.; Liu, C. Numerical simulation and PIV test of flow field in straight pipe outlet passage of axial flow pump. Chin. J. Hydrodyn. 2019, 34, 795–802. [Google Scholar]
- Xu, L.; Xia, B.; Shi, W. The influence of the length of the middle pier on the hydraulic characteristics of the outlet channel of the inclined axial extension pump device. Trans. Chin. Soc. Agric. Eng. 2020, 36, 74–81. [Google Scholar]
- Chaoyue, W.; Fujun, W.; Yuan, T.; Dan, Z.; Lihua, X.; Chenglian, H.; Quanrong, Z.; Congbing, H. Investigation Into the Phenomenon of Flow Deviation in the S-Shaped Discharge Passage of a Slanted Axial-Flow Pumping System. Fluids Eng. 2020, 142. [Google Scholar] [CrossRef]
- Wangben, H.; Wangfu, J.; Xie, L. Study on the bias flow characteristics of outlet passage of inclined axial flow pump device. Water Conserv. 2021, 1–12. [Google Scholar] [CrossRef]
- Song, X.; Liu, C. Experimental investigation of floor-attached vortex effects on the pressure pulsation at the bottom of the axial flow pump sump. Renew. Energy 2020, 145, 2327–2336. [Google Scholar] [CrossRef]
- Wudong, L.; Zheng, Y.; Xue, H. Pressure fluctuation characteristics of axial extension tubular pump under multiple working conditions. Drain. Irrig. Mach. Eng. 2021, 39, 244–250. [Google Scholar]
- Zou, F.; Zou, D.; Rao, Z. Analysis of pressure fluctuation characteristics of sodium pump. Eng. Therm. Energy Power 2019, 34, 71–76. [Google Scholar]
- Jacob, S.L.K.; Madhu, R. An efficient interference mitigation approach for NavIC receivers using improved variational mode decomposition and wavelet packet decomposition. Trans. Emerg. Telecommun. Technol. 2021, 32. [Google Scholar] [CrossRef]
- Ni, D.; Zhang, N.; Gao, B.; Li, Z.; Yang, M. Dynamic measurements on unsteady pressure pulsations and flow distributions in a nuclear reactor coolant pump. Energy 2020, 198. [Google Scholar] [CrossRef]
- Sangho, C.; Jeonghwa, Y. Wavelet Packet Transform Modulus-Based Feature Detection of Stochastic Power Quality Disturbance Signals. Appl. Sci. 2021, 11, 2825. [Google Scholar] [CrossRef]
- Zi, D.; Wangfu, J.; Tao, R. Study on the influence of boundary layer grid scale on the calculation results of pumping station flow field. Hydraul. Eng. 2016, 47, 139–149. [Google Scholar]
- Li, J.; Wang, X.; Wang, W.; Wang, Y. Performance improvement of a high-speed aero-fuel centrifugal pump through active inlet injector. Proc. Inst. Mech. Eng. 2021, 235. [Google Scholar] [CrossRef]
- Desheng, Z.; Guangjian, Z.; Weidong, S.; Tongtong, L. Performance prediction and experimental verification of axial flow pump based on CFD. Appl. Mech. Mater. 2012, 1620. [Google Scholar] [CrossRef]
- Ramirez, R.; Avila, E.; Lopez, L.; Bula, A.; Forero, J.D. CFD characterization and optimization of the cavitation phenomenon in dredging centrifugal pumps. Alex. Eng. J. 2020, 59. [Google Scholar] [CrossRef]
- Shrifan, N.H.M.M.; Firdaus, A.M.; Ashidi, M.I.N. Maximal overlap discrete wavelet-packet transform aided microwave nondestructive testing. NDT E Int. 2021, 119. [Google Scholar] [CrossRef]
- Habbouche, H.; Benkedjouh, T.; Zerhouni, N. Intelligent prognostics of bearings based on bidirectional long short-term memory and wavelet packet decomposition. Int. J. Adv. Manuf. Technol. 2021, 114, 145–157. [Google Scholar] [CrossRef]
- Galletti, C.; Mariotti, A.; Siconolfi, L.; Mauri, R.; Brunazzi, E. Numerical investigation of flow regimes in T-shaped micromixers: Benchmark between finite volume and spectral element methods. Can. J. Chem. Eng. 2019, 97. [Google Scholar] [CrossRef]
- Jeong, J.; Mechanics, F. On the identification of a vortex. J. Fluid Mech. 1995, 285, 69–94. [Google Scholar] [CrossRef]
- Mariotti, A.; Galletti, C.; Salvetti, M.V.; Brunazzi, E. Unsteady Flow Regimes in a T-Shaped Micromixer: Mixing and Characteristic Frequencies. Ind. Eng. Chem. Res. 2019. [Google Scholar] [CrossRef]
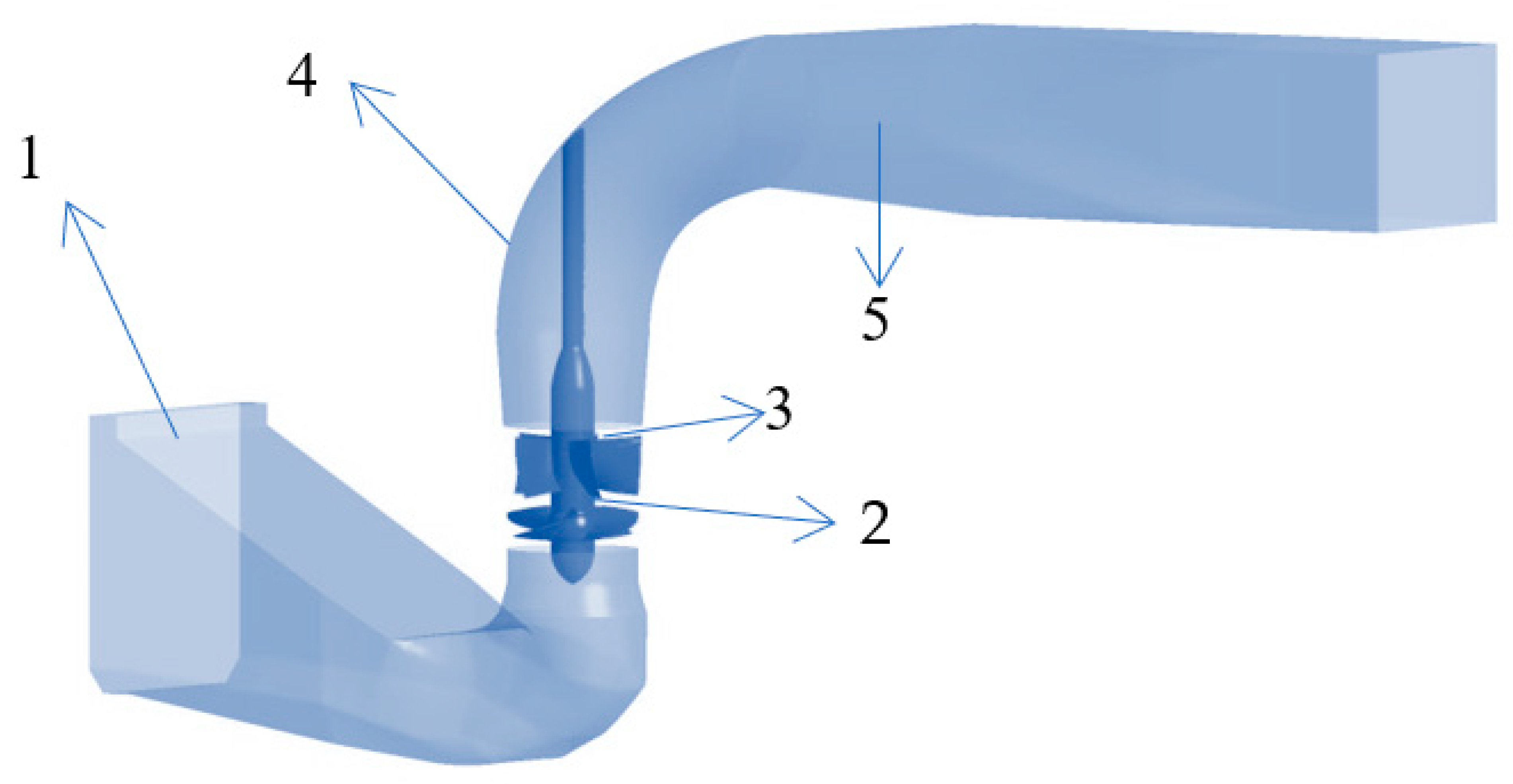






| Overcurrent Parts | Elbow Inlet Conduit | Impeller | Guide Vane | 90° Elbow | Straight Outlet Conduit |
|---|---|---|---|---|---|
| y+ | 268.083 | 90.244 | 71.627 | 249.616 | 193.776 |
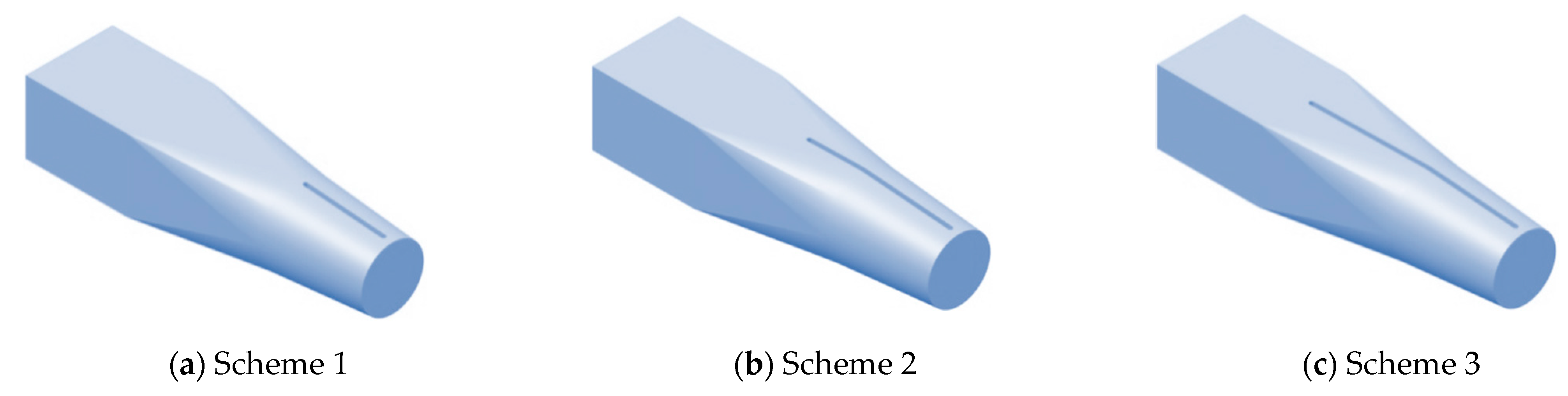
| Scheme | Head Loss (m) | Left (Q/Qbep) | Right (Q/Qbep) | Flow Distribution Ratio |
|---|---|---|---|---|
| 1 | 0.081 | 0.595 | 0.407 | 1.46 |
| 2 | 0.078 | 0.592 | 0.408 | 1.45 |
| 3 | 0.075 | 0.597 | 0.403 | 1.48 |
| Category | No Division Pier | With Division Pier | ||||||
|---|---|---|---|---|---|---|---|---|
| Monitoring Point P1 | Monitoring Point P3 | Monitoring Point P1 | Monitoring Point P3 | |||||
| Main Frequency/Hz | Power Spectrum/kPa2·Hz−1 | Main Frequency/Hz | Power Spectrum/kPa2·Hz−1 | Main Frequency/Hz | Power Spectrum/kPa2·Hz−1 | Main Frequency/Hz | Power Spectrum/kPa2·Hz−1 | |
| 0.6 Qbep | 1.46 | 0.0031 | 1.46 | 0.0027 | 1.95 | 0.0028 | 16.60 | 0.0022 |
| Qbep | 1.95 | 0.0013 | 0.98 | 0.0131 | 25.88 | 0.0012 | 0.98 | 0.0033 |
| 1.2 Qbep | 1.46 | 0.0035 | 8.30 | 0.0059 | 1.46 | 0.0026 | 2.44 | 0.0045 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, F.; Jiang, D.; Wang, T.; Chang, P.; Liu, C.; Liu, D. Investigation into the Influence of Division Pier on the Internal Flow and Pulsation in the Outlet Conduit of an Axial-Flow Pump. Appl. Sci. 2021, 11, 6774. https://doi.org/10.3390/app11156774
Yang F, Jiang D, Wang T, Chang P, Liu C, Liu D. Investigation into the Influence of Division Pier on the Internal Flow and Pulsation in the Outlet Conduit of an Axial-Flow Pump. Applied Sciences. 2021; 11(15):6774. https://doi.org/10.3390/app11156774
Chicago/Turabian StyleYang, Fan, Dongjin Jiang, Tieli Wang, Pengcheng Chang, Chao Liu, and Dongsheng Liu. 2021. "Investigation into the Influence of Division Pier on the Internal Flow and Pulsation in the Outlet Conduit of an Axial-Flow Pump" Applied Sciences 11, no. 15: 6774. https://doi.org/10.3390/app11156774
APA StyleYang, F., Jiang, D., Wang, T., Chang, P., Liu, C., & Liu, D. (2021). Investigation into the Influence of Division Pier on the Internal Flow and Pulsation in the Outlet Conduit of an Axial-Flow Pump. Applied Sciences, 11(15), 6774. https://doi.org/10.3390/app11156774







