Buckling Behavior of Thin-Walled Stainless-Steel Lining Wrapped in Water-Supply Pipe under Negative Pressure

Abstract

This paper presents a study about the buckling behavior of thin stainless-steel lining (SSL) for trenchless repair of urban water supply networks under negative pressure. The critical buckling pressure and displacement (p–δ) curves, temperature changing curves, hoop and axial strain of the lining monitoring section and the strain changes with system pressure (p–ε) of the lining under the action of different diameters, different lining wall thickness and different ventilation modes were obtained through five groups of full-scale tests. The variation principles of the post-buckling pressure and the reduction regularity of the flowing section of the lining were further investigated. By comparing different pipeline buckling models and introducing thin-shell theory, the buckling model of liner supported by existing pipe was established. The comparison between the test results and thin-shell theory indicates that one of the significances of the enhancement coefficient k value is to change the constraint condition of the aspect ratio, l/R, thus increasing the critical buckling pressure of the lining. Finally, an improved lining buckling prediction model (enhancement model) is presented. A previous test is used as a case study with the results showing that the enhanced model is able to predict critical buckling pressure and lobe-starting amount of the liner, which can provide guidance for trenchless restoration of the liner with thin-walled stainless steel.

1. Introduction

In recent years, the rehabilitation and construction area of the water supply network in China has significantly increased. Figure 1 shows that the government has invested more than 55 billion yuan in the water supply network market per year since 2011. Various types of materials, such as iron (including cast and spun), ductile iron (DI), steel, asbestos cement (AC), concrete, reinforced concrete (RC), polyvinyl chloride (PVC) and high-density polyethylene (HDPE), are often used in the construction of new water-supply pipes [1,2]. With the increase of pipeline operations, the probability of defects also increases significantly. There are several different modes and mechanisms for pipe failure, including internal and external corrosion [3], cracks [4], splits [2] and buckling [5]. Geometric defects of pipelines have also lead to deposition [6], leakage [7] and pipe explosion [8], which gradually reduces the hydraulic properties of the pipeline. Leakage and pipe burst accidents will reduce the pressure of pipe network system; increase the loss of water; pollute drinking water; and cause waste of resources, road damage, traffic disruption and other consequences [9]. Unfortunately, this often results in significant losses to people’s lives and property.

Water-supply networks are often installed in the underground space of urban built-up areas, thereby making it difficult to dig and repair broken pipes. Trenchless technology has been used for more than 25 years in China [10]. ISO 11298-1(2018) [11] provides seven methods for trenchless repair of water-supply pressure pipelines, namely lining with continuous pipes, lining with close-fit pipes, lining with cured-in-place pipes, lining with discrete pipes, lining with adhesive-backed hoses, lining with sprayed polymeric materials and lining with inserted hoses. However, the relevant theories and processes in design and construction are not perfected at present. Trenchless technology applied to water supply pressure defective pipelines includes the following categories: stainless-steel liner (SSL), folding of plastic liner, PVC liner and polymer liner [12].

Stainless steel has many desirable characteristics, including corrosion-resistant, long-lasting, tough, hygienic, adaptable and recyclable [13,14,15,16]. As early as the mid-1960s, Europe and the United States began to use stainless-steel pipes, gradually accounting for more than 85% of the water pipe market. Japan began to implement stainless-steel pipes around 1980 fully, and the market share gradually rose to 90%. East and Southeast Asia are the fastest growing regions for stainless-steel pipes, with an annual sales rate of stainless-steel pipes growing by 10%. At the beginning of the 21st century, the Chinese government made it mandatory to use plastic, aluminum–plastic composite water-supply pipes or stainless-steel and copper pipes as the materials of choice for water-supply pipelines. After 2017, many local governments, such as Beijing, Nanchang and Changsha, and the Pearl River Delta region, stipulated that stainless-steel pipes be used as water-supply pipes. Whether in China or other countries and regions, the application of stainless-steel liner repair technology to rehabilitate water-supply pipelines is in its infancy. Deng and Murakawa [17] presented a computational procedure for analyzing temperature field and residual stress in multi-pass welds in SUS304 stainless-steel pipe. Through laboratory tests, Wei Zhou et al. [18] studied the feasibility of using SSL to repair small pipe diameters. Shun Dong et al. [19] introduced a new type of SSL repair structure composed of multi-arch lining. The current SSL design in China is based on the CIPP (Cured In Place Pipe) lining design principle in ASTM F1216 [20]. According to the different degrees of damage of existing pipelines, two states are determined: the partially deteriorated state and the fully deteriorated state. Only the combination of external pressure and internal pressure is considered in the two states, while the consequences caused by negative pressure in the pressure pipeline are ignored. German Code ATV-M 127-2 [21] differentiates between three host pipe states: (1) State I for loose sewers without cracks; (2) State II for sewers with longitudinal cracks but a stable soil pipe system and (3) State III for cracked pipes with larger deformations and considerable risk for future collapse. The destructive of negative pressure is also not fully considered. There are, however, a number of test results showing that negative pressure will create a vacuum inside the liner. If the liner is not bond to the existing pipe as a whole, or the overall ring stiffness is insufficient, the two will eventually detach and cause the lining to buckle [18,22]. Therefore, negative pressures should also be considered the load factor in the operation of water-supply pipelines and should be fully considered in lining wall thickness.

This paper introduces several negative pressure simulation experiments whose purpose is to observe and evaluate the buckling resistance of the SSL. The method and effect of preventing buckling of SSL are studied by adding a limited amount of inner support rings. Finally, the evaluation, which focuses on SSL technology used for water supply and drainage pipeline repair, is given from the aspect of feasibility and applicability. Subsequently, suggestions to optimize the process are made.

2. Experimental Testing

The tests were carried out from 1 August 2020 to 30 September 2020. Fuzhou Water Engineering Co., LTD provided the test site. Through vacuum negative pressure tests, the stress and strain on the lining structure in the process were monitored, and the critical pressure, load–displacement curve and area relation of the de-caving part obtained.

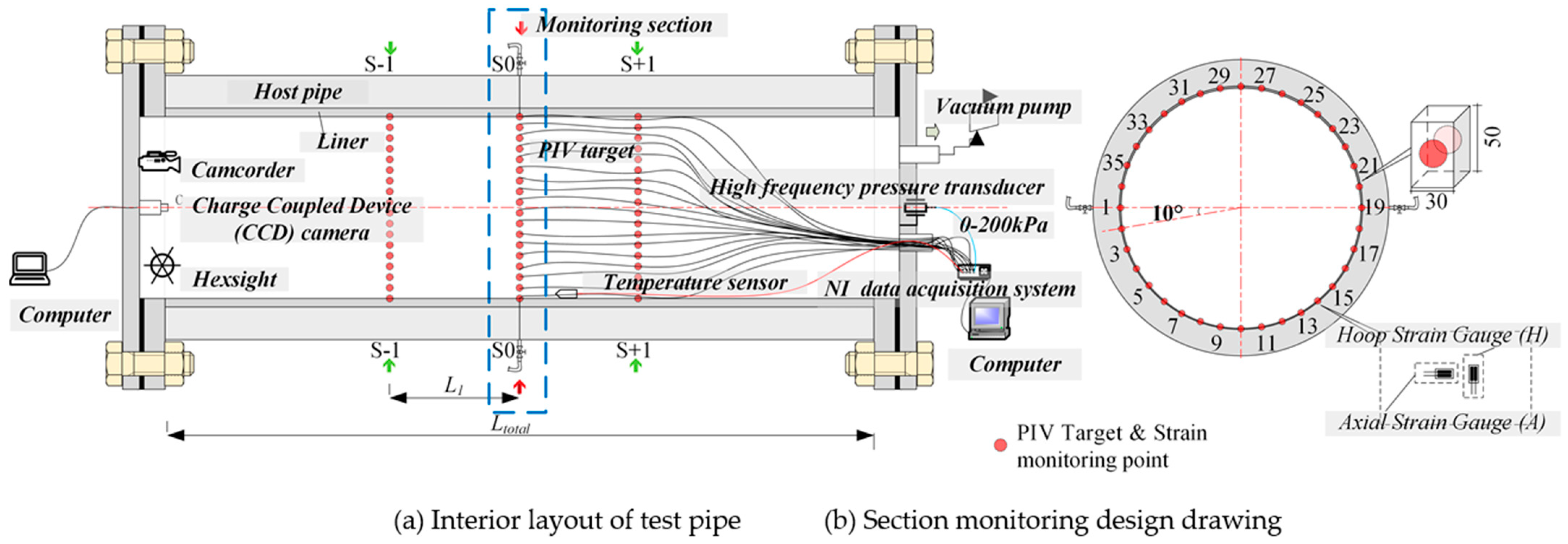
2.1. Experimental Setup

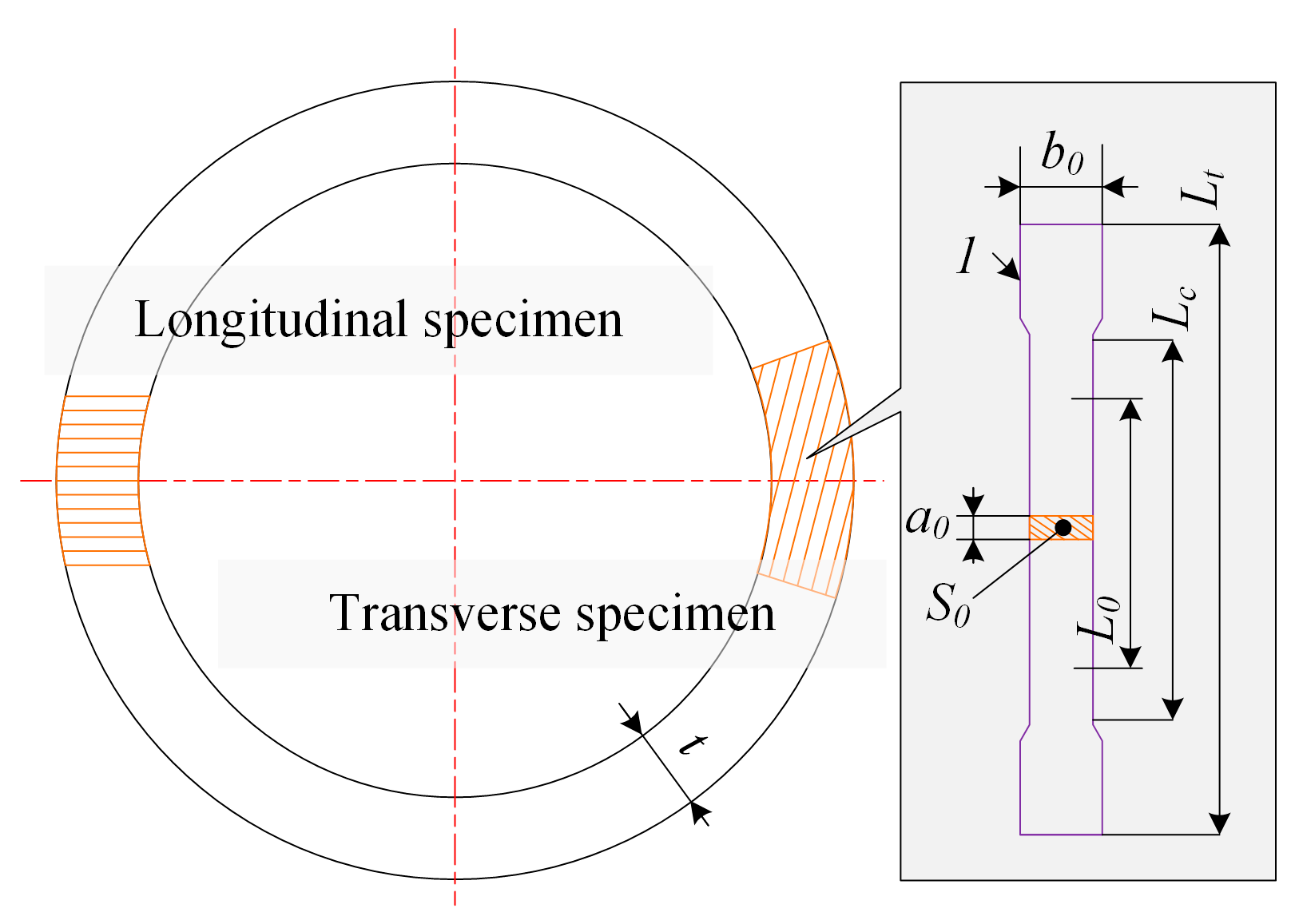
2.1.1. Basic Parameter Test

The basic performance parameters of the lining material are tested by the method in the national standard. The tensile strength is tested by the method recommended in GB/T 228.1 2010 [23], elastic modulus and Poisson’s ratio are determined by GB/T 22315 2008 [24], and sampling (Figure 2) is carried out in strict accordance with the provisions of GB/T 2975 2018 [25], respectively.

The results of each group of six specimens in the tensile test, elastic modulus and Poisson’s ratio test are as follows: (1) the yield strength of 304-stainless-steel plate is 258, 239, 246, 279, 247 and 276 MPa, respectively, and the average value is 257.5 MPa; (2) the tensile strength is 568, 579, 582, 563, 590 and 570 MPa, with an average value of 575 MPa; (3) the measured values of elastic modulus are 195, 188, 203, 185, 201 and 196 Gpa. The average value is 195 Gpa, and the measured Poisson’s ratio is 0.245, 0.25, 0, 0.244, 0.250, 0.252 and 0.241, with the mean of 0.247.

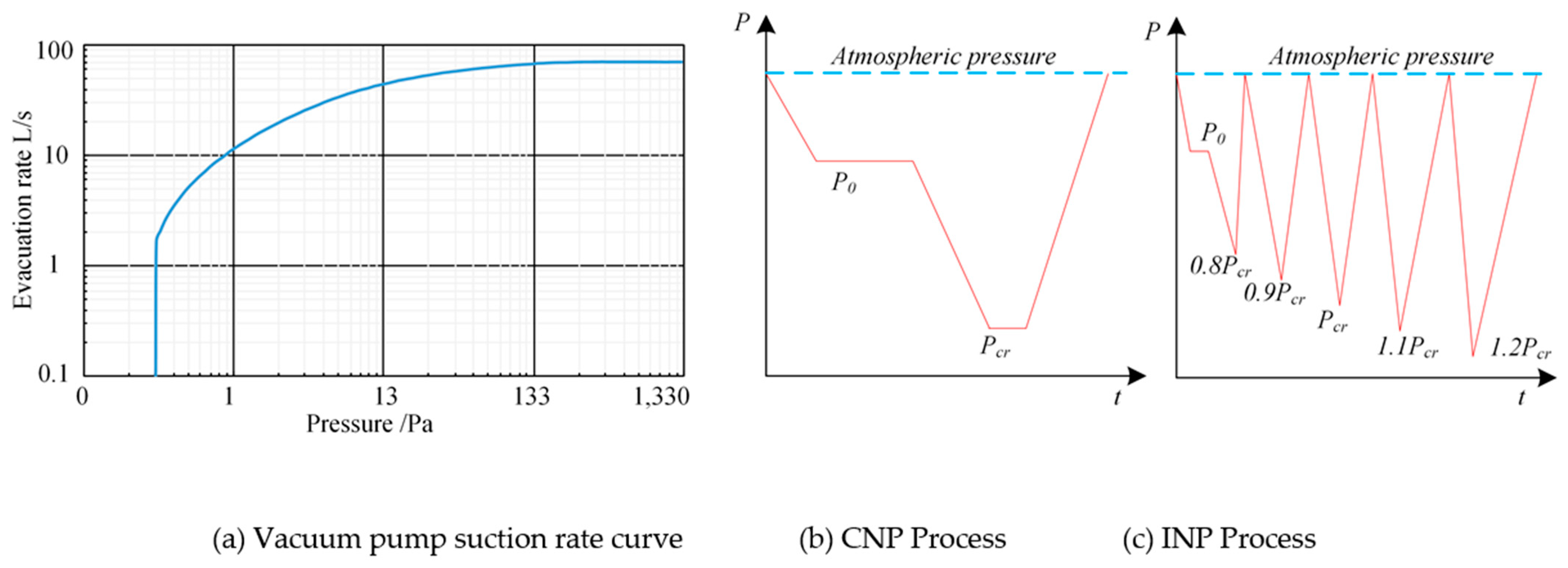
2.1.2. Negative Pressure Test

In order to investigate the influence of pipe diameter, wall thickness, loading mode and other factors on the lining’s anti-buckling ability under negative pressure, five groups of tests were designed (

Table 1. Measured geometric dimension of lined pipe specimens.

Specimen	D SSL (mm)	t (mm)	L (m)	OV (%)	g (%)
T1	800	1.79	5.0	0.91	1.64
T2	1000	1.79	7.5	1.34	0.61
T3	1200	2.17 *	8.0	0.90	0.63
T4	800	1.61	5.0	0.75	1.14
T5	800	1.79	5.0	1.56	2.00

* Due to material limitations on-site, the 1200 mm pipes have a wall thickness of 2.17 mm.

). The specimens were numbered T1–T5, respectively. In groups T1, T2 and T3, the host pipe diameter’s influence was considered, and the inner diameter was set as 800, 1000 and 1200 mm, respectively. In the tests of groups T1 and T4, the lining wall thickness was taken as a variable and set at 1.79 and 1.61 mm. T1 group was loaded with continuous air extraction, while T5 group immediately opened the inlet sealed with the host pipe after the vacuum degree was slightly lower than the measured value of T1, thus forming an instantaneous pressure difference. The specific loading process is described in the following section.

The host pipe is made of TPEP (Three layers Polyethylene Epoxy Resin) anticorrosive steel pipe. Before the test, diameter, initial deformation and local defects of the existing pipe were measured by a Laser Displacement Meter. SSL was rolled from a stainless-steel sheet, and the liner was welded into a thin barrel shell by argon arc welding technology, and the lap joint and interface seal of the ring was completed. It should be pointed out that the research shows that the port constraint effect can be ignored when the length to diameter ratio of the thin-walled cylinder exceeds 6 [26]. Thus, the host pipe length in this test was slightly larger than six-folds of the corresponding pipe diameter. After the lining was welded and placed for 24 h, the lining’s initial deformation was measured, and the initial ovality and annular gap were calculated as presented in Table 1.

In each group of tests, three monitoring sections were arranged at 500 mm from the middle to both sides of the pipe, and marked as S − 1, S0 and S + 1, respectively, from left to right. Every 10 degrees was marked for monitoring purposes. Strain changes in SSL during vacuum pumping were measured by sticking strain flowers. The strain gauge used was 120-5AA, with a sensitivity of 2.0 mv/V. Strain monitoring was only carried out at section S0, and two strain gauges were arranged at each measuring point to monitor transverse and longitudinal strains (Figure 3). Particle Image Velocimetry (PIV) technology was used to measure the deformation and displacement of the lining. The targets were made of wood blocks of 50 mm × 30 mm, and a unique pattern was pasted on the front surface to distinguish the monitoring targets. An ACA1920-155UM industrial camera produced in Basler Vision Technology Co., Ltd., Beijing, China was positioned in the middle of the flange cover at the left section with a resolution of 1369 × 1216, a pixel size of 5.86 μm × 5.86 μm, and a maximum frame rate of 155 fps. Simultaneity of multiple system measurements can be maintained by hardware/software triggers/system clocks. Due to the short buckling process under negative pressure, the image recording rate set in the system during the test was 40 frames per second. Two 400 W floodlights were arranged below the Charge Coupled Device (CCD) camera as the light source. A DJI OSMO Action Buff-Proof 4K HD camera was placed on the same side to record the whole test process. The negative pressure value of the internal cavity of the pipeline was obtained by the AIER high frequency absolute pressure sensor of 0–200 kPa, and its comprehensive accuracy was less than or equal to ±0.25% FS. The lining temperature change was monitored by a temperature sensor. The data monitored by the strain, pressure and temperature sensors were all collected by the NI system. The data collection cabinet was NI 9188 and NI 9189. The strain was collected by the NI 9237 input module with an accuracy up to ±100 ppm, and the pressure and temperature were collected by the NI 9203 input module with an accuracy of ±0.18%. All the collected data were converted into Excel data files by LabView 2019 software. The vacuum pump 2X-70 used in the test was manufactured by Shanghai Nanguang Vacuum Pump Factory, Shanghai, China; it has a pumping rate of 70 L/s and spindle speed of 450 r/min.

Because of the large sealed volume of the pipeline, a 2X-70 vacuum pump was adopted, and the curve of the suction speed changing with the pressure was shown in Figure 4a. The actual critical buckling load cannot be determined before the test, so when the vacuum reaches 10 kPa during the continuous pumping process (CNP Process), close the vacuum pump for 20 min to ensure reliable tightness of the test system. After that, the air was pumped at a constant rate until the lining flexed (Figure 4b). The critical buckling pressure of the continuous negative pressure was taken as the standard, multiplied by the corresponding coefficients (0.8, 0.9, 1.0, 1.1 and 1.2, respectively) to obtain a five-level vacuum degree (Figure 4c). It should be noted that, during the instantaneous negative pressure (INP) test, the instantaneous state was achieved by first reaching the preset test vacuum inside the main engine pipe and then immediately opening the inlet and closing the vacuum pump at the same time.

2.2. Experimental Result

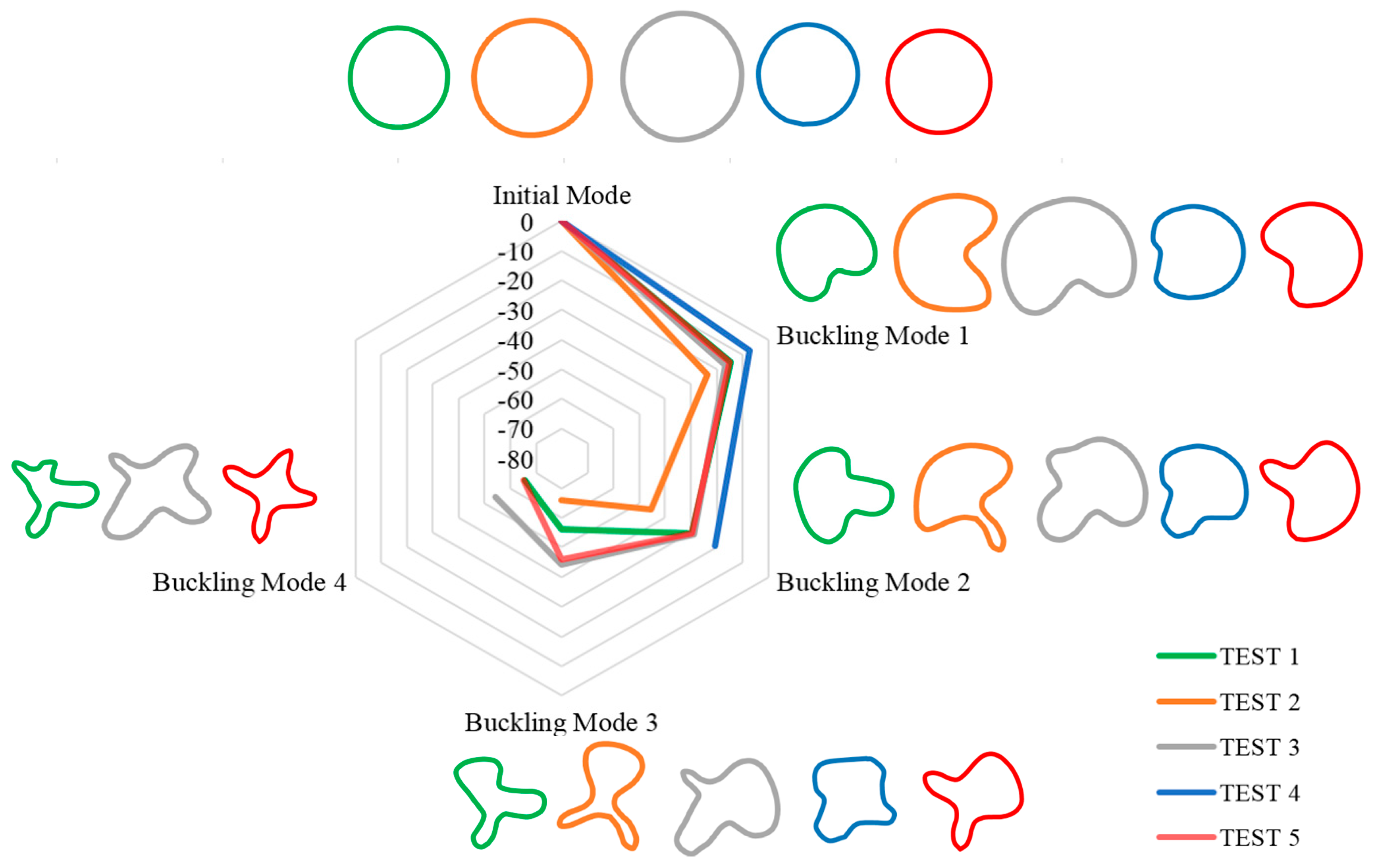
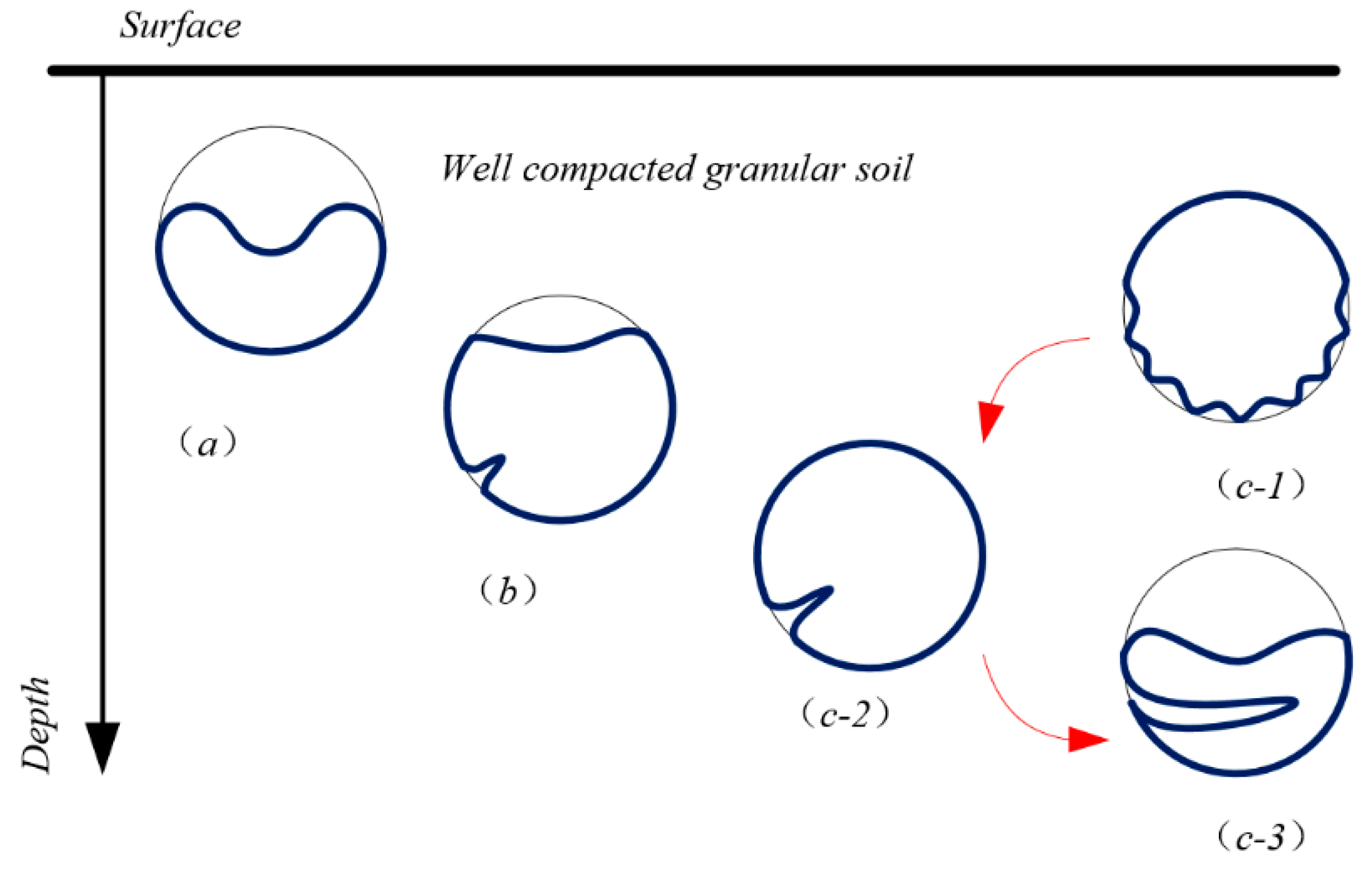
2.2.1. Visualization of Buckling Collapse

Figure 5 illustrates the buckling deformation of specimens T1 to T5, which were subjected to negative pressure. In the test process, the pipe, lining and flange cover plate acted like a sealed cavity. When the vacuum pump is operational, the system works on the surrounding air, resulting in the reduction of the pressure inside the system. It was apparent that the CCD camera field was covered in a cloud of white fog a few seconds before and after the lining buckled.

The critical buckling pressures of the tests were 55.12, 28.47, 34.44, 41.37 and 47.57 kPa, respectively. The temperature variation detected during the test are described in detail in Section 2.2.3. As shown in Figure 5, the lining of T1, T3 and T5 was compressed in four directions, resulting in four circumferential lobes. In addition, the test results show that the lining buckling occurs very quickly, and the lining has been slightly deformed before the critical buckling pressure was reached. It should be noted that, because the tests of groups T2 and T4 were carried out first, the tests of these two groups ended after the occurrence of only 3 and 2 lobes of the lining, in order to prevent excessive deformation of the lining, which made it impossible for the lining to move out of the existing pipeline.

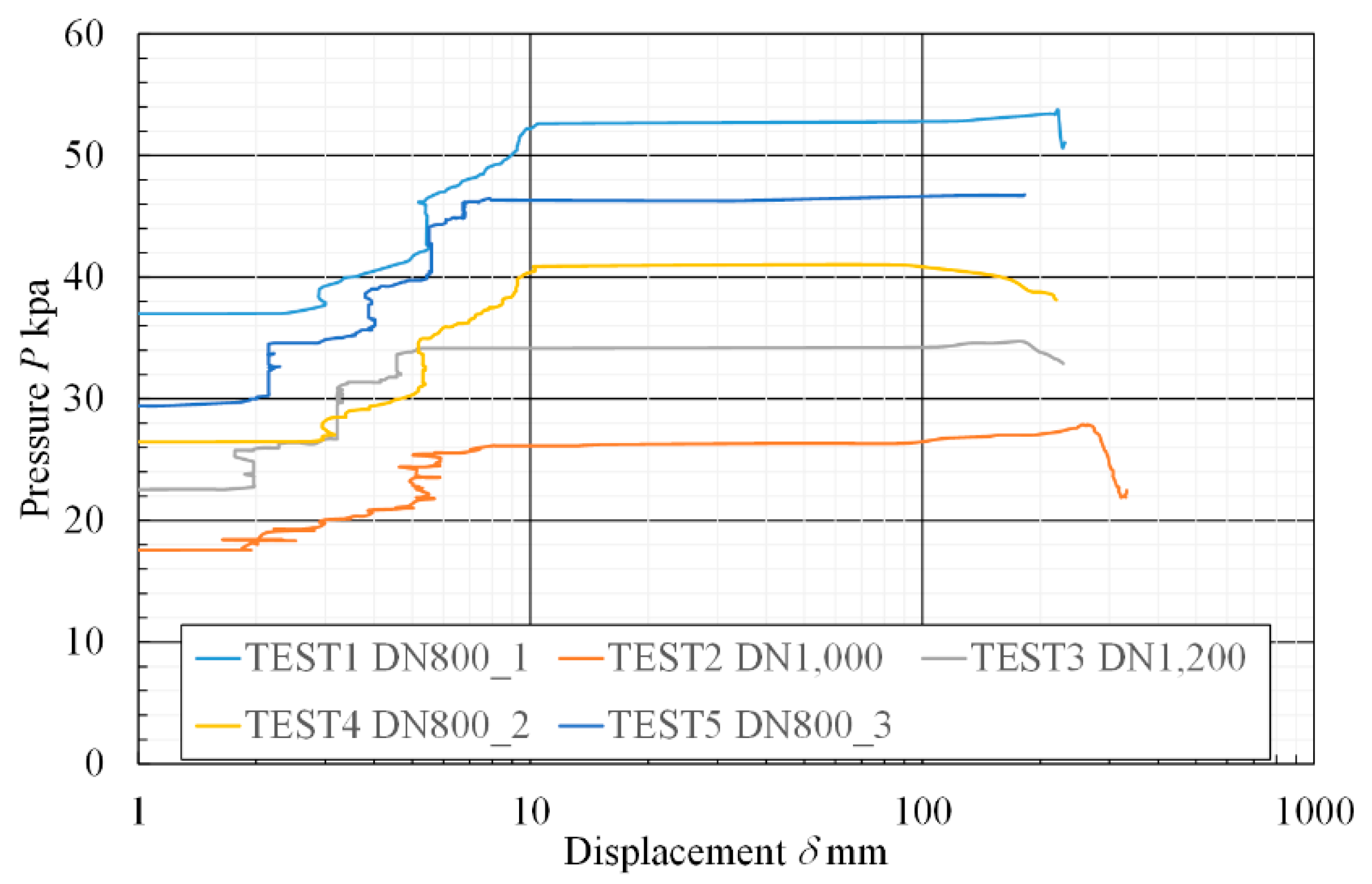
2.2.2. Critical Buckling Pressure

According to the test results in

Table 2. Test result (buckling pressure of different lobes and gradient, Gr).

Specimen Number	n = 1	Gr	n = 2	Gr	n = 3	Gr	n = 4	Gr
T1	55.12	0	52.44	−4.86%	54.45	+3.82%	68.84	+26.43%
T2	28.47	0	29.46	+3.49%	28.16	−4.42%	/	/
T3	34.44	0	53.59	+55.60%	47.70	−10.99%	47.84	−0.29%
T4	41.37	0	40.30	−2.58%	/	/	/	/
T5	47.57	0	52.87	+11.15%	54.02	+2.17%	54.38	+0.67%

, in T1 and T2, with the increase of lining diameter, the critical buckling pressure value presents a downward trend, and the data anomalies of T3 are explained in the foregoing contents. The test results of T1 and T4 show that, in thin-walled structures, the wall thickness has a significant impact on structural buckling, and the critical buckling pressure of the lining with a wall thickness of 1.61 mm decreases by nearly 25% compared with lining with a wall thickness of 1.79 mm. As for the influence of loading mode, the results concluded that the shorter the time for the pressure differentials to reach the threshold of critical buckling, the lower the critical buckling pressure of the lining structure. Compared with the T1 with continuous ventilation, the critical buckling pressure of the T5 decreased by 13.7%.

Figure 6 illustrates the curves of pressure–displacement in the logarithmic coordinates of several groups of tests, which all show the same law. The curve can be described as four stages during the extraction of the internal cavity. They stages are as follows: (1) the linear segment where the vacuum degree of the system increases and the displacement has minimal changes; (2) the nonlinear segment whose displacement increases with the increase of vacuum degree; (3) when the critical buckling pressure is reached, the pressure value remains constant and the displacement changes rapidly; and (4) with the increase of displacement, the system pressure begins to decrease, respectively. It can be found from the curve that, under the same wall thickness, the larger the pipe diameter, the more the liner reaches the third stage (T1 and T2). The displacements of the experimental groups (T1, T4) with the same pipe diameter and different wall thickness at the third stage were basically the same. In addition, instantaneous change of pressure differentials will also advance the lining into the third stage (T1 and T5).

After the first buckling value was observed, the post-buckling of the lining in several groups of tests was also observed in subsequent tests (Figure 7). The second column of each set of tests in Table 2 presents the increment of the system pressure at the time of each lobe generation compared to the previous buckling pressure. In groups T1, T2 and T4, the pressure values generated by several lobes were relatively close, with the mean values being 54.00, 28.70 and 40.84 kPa, respectively.

In group T3, the circumscribed length of the liner rolled by steel plate was 1436 mm, exceeding the DN1200 pipe by 236 mm, which made part of the liner overlap repeatedly. Thus, it showed two platforms in the peak value of buckling, with the mean values of 34.44 and 49.71 kPa, respectively. The post-buckling model results of group T5 show that, during the rapid “loading” process, the critical pressure values generated by several lobes were reduced. The critical pressure generated by the first lobe was 47.57 kPa, and the average pressure of the second to the fifth lobe was 53.76 kPa.

Through the data of PIV targets, the reduction regularity of lining area in several stages was obtained, and it is shown in Figure 8. Shahandeh and Showkati [27] presented the order of buckling state and cross-sectional area change of pipelines under external pressure. They concluded that the pipe presents uniform inward compression deformation at the elastic stage, and the multi-lobe plastic crushing phenomenon occurs only after the material enters the plastic stage. Compared with Shahandeh and Showkati’s model, the object studied in this paper is the lined pipe supported by existing pipes and the loading mode of negative pressure, thereby differing from the other models.

It can be seen from Figure 8 that the generation of buckling lobes seems random. However, the results found in Figure 5 show that all buckling are more likely to occur at the elliptical part of the lining. In general, under different buckling modes, the larger the diameter of liner with the same wall thickness, the greater the reduction of flowing section. For the same pipe diameter, the liner with thinner wall thickness has a relatively low reduction in the flowing section in this test. T1 and T5 tests revealed that the increasing method of vacuum had little influence on the reduction of the section, and finally the loss of the section came down to the same level in the fourth buckling mode.

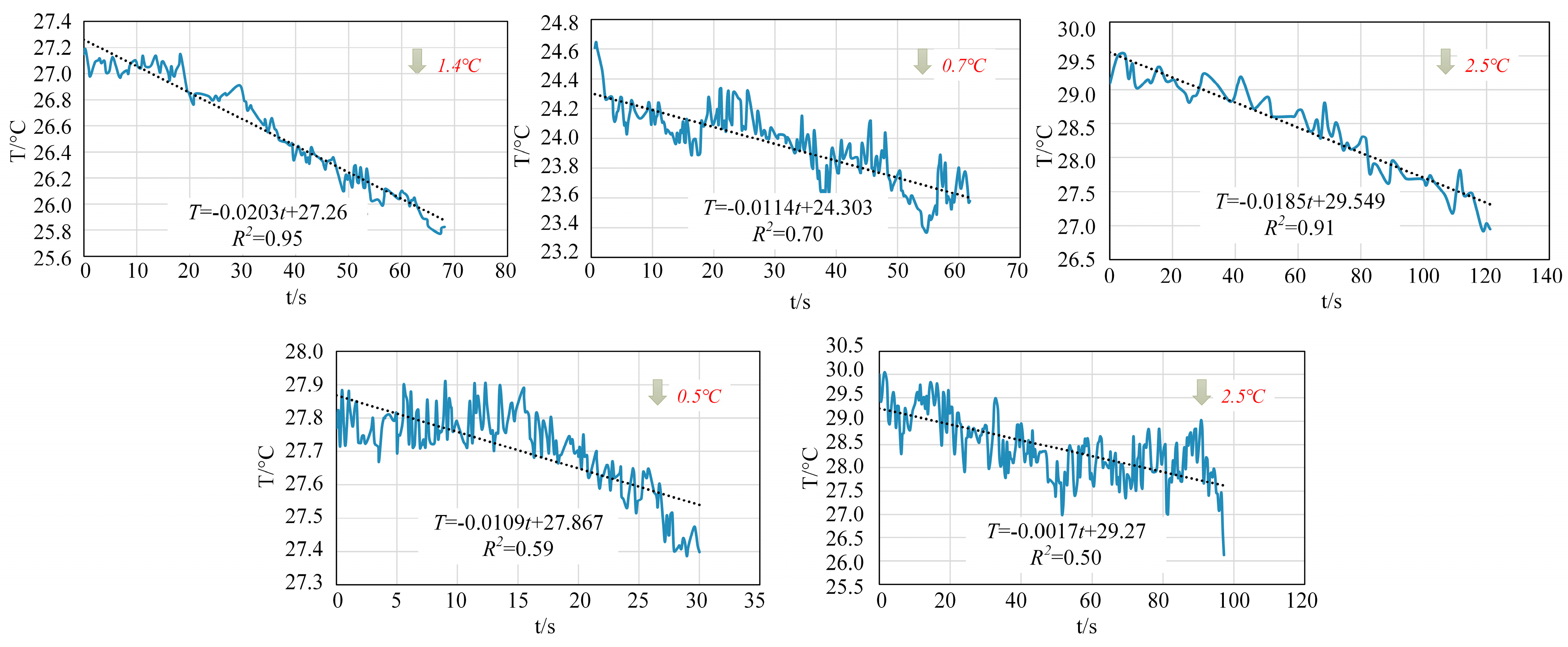
2.2.3. Temperature Variation

If the temperature changes when the lining is not limited by the outside and freely stretched, then the lining does not produce thermal stress; however, in the actual project of SSL repair, port is considered to have fixed end constraints due to welding. In the test, the end was also constrained by the fixed end; thus, the liner could not expand and contract freely when the temperature changed, and thermal stress was generated in the pipeline. The axial elastic modulus of SSL is sufficient, and the temperature change in a small range will also cause greater temperature stress. The temperature stress will make the welding part and the port connection part produce more significant local deformation or even damage, thus the thermal stress analysis of the lining is a necessary process. Figure 9 shows the temperature-change curve in the sealed cavity due to work done to the outside during the negative pressure test of groups T1–T5. During the test, the temperature decreased by 1.4, 0.7, 2.5, 0.5 and 2.5 °C, respectively.

$${\sigma }_z=\frac{p}{A}=a{E}_z\Delta T$$

(1)

Based on Equation (1), the change value of axial stress caused by temperature drop is 3.276, 1.638, 5.85, 1.17 and 5.85 MPa, respectively.

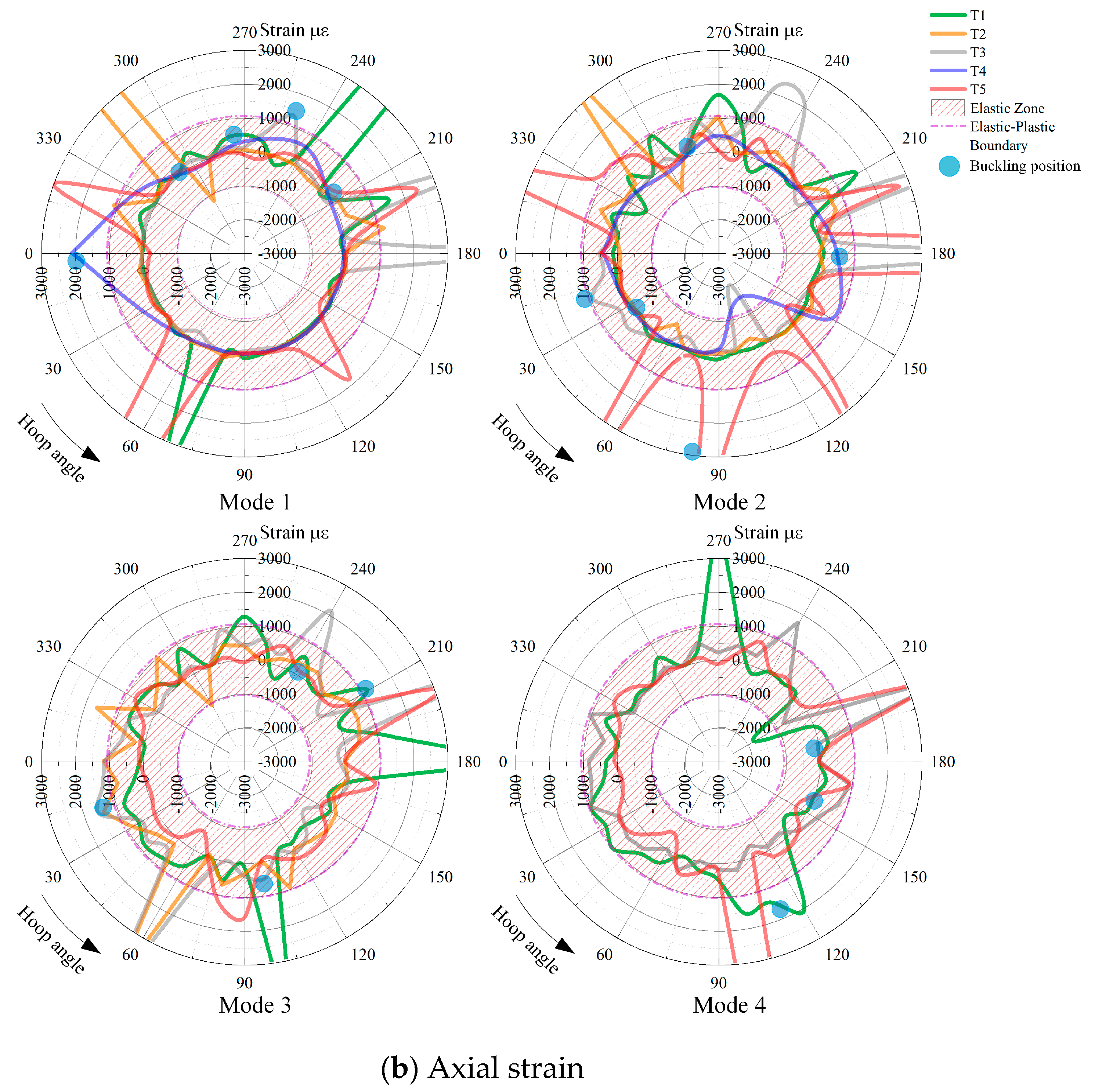
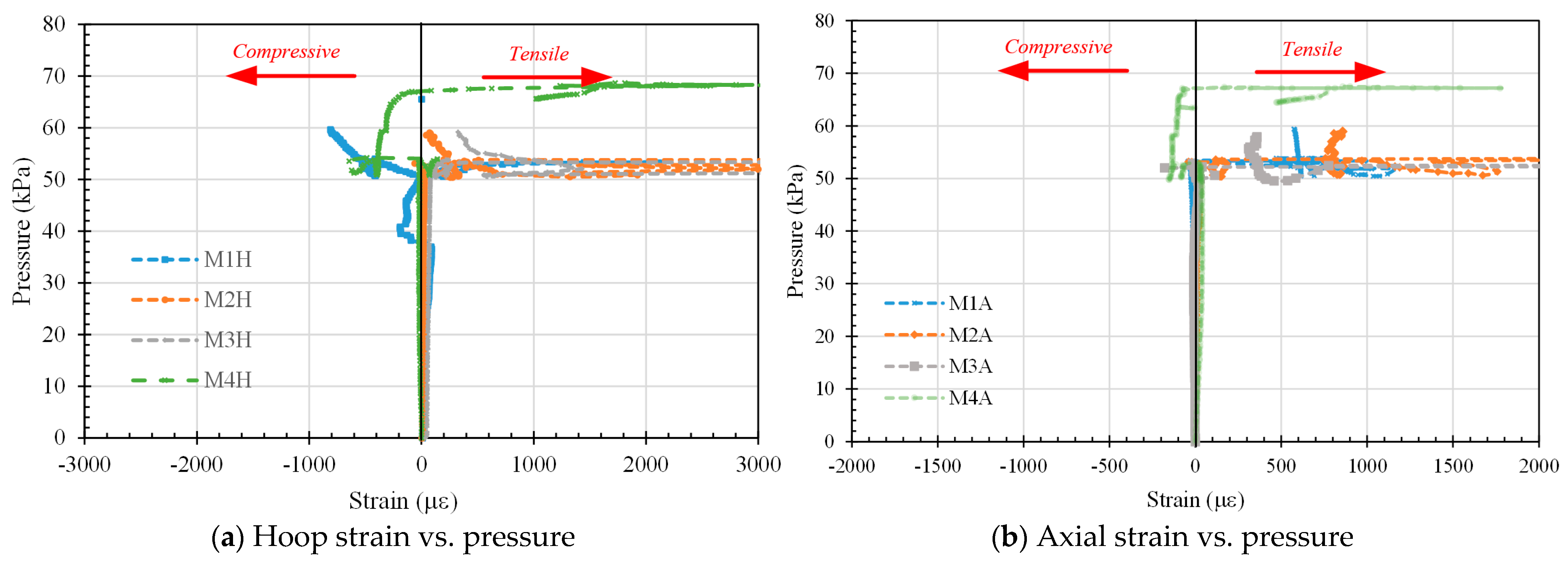
2.2.4. Hoop and Axial Strain

The gauge strain distributions in hoop and axial direction around the liner circumferences for the SSL specimens (T1–T5) are illustrated in Figure 10. Figure 11 shows the pressure–strain curves of the sample T1 under four different buckling modes. After buckling, both deformation and strain increase significantly, even if the pressure is less than the critical buckling pressure, which clearly indicates that the lining loses its structural stability after buckling. By analyzing the strain distribution, the mechanical behavior before and after buckling was also studied. Initially, the tensile strain develops uniformly around the lining. The annular strain was mostly strained before buckling. When buckling, the strain near the buckling position reaches a maximum (tension) or a minimum (compression). The annular strain distribution reveals the buckling position and buckling range of the lobe. After buckling, most strains relaxed when the vacuum was reduced, except the minimum strain near the buckling position.

According to the test results of lining mechanical properties in Section 2.1.1, the elastic limit strain of SSL was obtained as ε = 0.105%. Figure 10 shows the elastic strain area of the monitored cross-section during SSL buckling, and blue dots mark the location where the buckling occurred. According to the hoop and axial strain pattern of buckling mode 1, samples in groups T1, T2, T3 and T4 all enter plastic buckling state from elastic buckling. The hoop and axial strains corresponding to the buckling of T1, T3 and T4 groups exceeded the elastic limit range. However, only the axial strain exceeded the elastic limit when the T2 group’s buckling occurred. The buckling of group T5 occurred within the elastic limit, which was consistent with the video record of the experiment. When the initial buckling occurred and the vacuum degree was reduced, the retraction of the buckling part was observed. In Figure 11, whether in hoop or axial direction, with the increase of vacuum degree of the system under different modes, a large tensile stress occurs at the buckling position. When the critical pressure is reached, the tensile stress decreases. For M1H (Hoop Strain of Mode 1), SSL even eventually transforms from tensile stress to compressive stress. After producing three lobes, a fourth buckling lobe was produced at a higher pressure. The strain discipline recorded by the strain gauge at the position of the fourth lobe during the vacuum degree increase was as follows. Initially, the lining material reaches the limit of elastic strain (tensile strain). Subsequently, in the course of the three buckling lobes of the first platform, the lining material changes from tensile strain to compressive strain. Finally, as the vacuum continues to increase, the pressure state changes to the tensile state again, and buckling occurs in the second platform.

3. Analysis

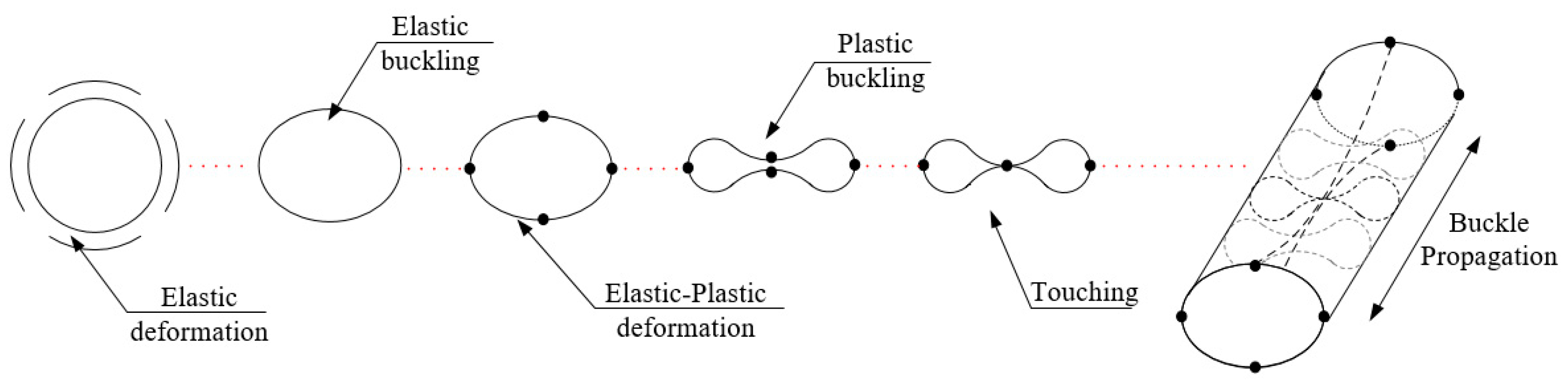
3.1. Classical Pipeline Buckling Model

The buckling of pipelines has been studied by many scholars, and some relatively mature theoretical results have been formed [27,28,29,30]. At present, the main buckling models of pipelines include buried pipeline buckling model and the Marine pipeline buckling model.

For buried pipes, P.S. Bulson [31] believes that if the pipe is buried in a shallow depth (i.e., H < R/2), when the static load is applied on the surface, the test shows that the collapse is usually caused by the collapse of the crown, as shown in Figure 12a. With the increase of buried depth, thin-walled pipes tend to buckle and lose stability at the invert, as shown in Figure 12c. At intermediate depths, the pipeline failure mode is the superposition of the two models, as shown in Figure 12b. As the surface pressure is increased, the thin wall of the pipeline around the lower part of the edge is buckled in the form of several elastic half-waves (Figure 12(c-1)), and then one of the buckles becomes larger (Figure 12(c-2)). This action causes the vertical diameter of the pipe to shrink, followed by an inward collapse of the crown, as shown in Figure 12(c-3).

For ocean pipelines, Shahandeh and Showkati [27] believe that the buckling of the pipeline is developed step by step in the process shown in Figure 13, from these states: elastic deformation, elastic buckling, elastic-plastic buckling deformation, plastic buckling, touch and buckle propagation along the pipeline, respectively.

For this test, the above two buckling models are not applicable because the test is a pipe-in-pipe structure and considering the changes of lining support conditions by external pipes. The following is a further discussion based on the comparison between free ring and thin-shell theory and experiments.

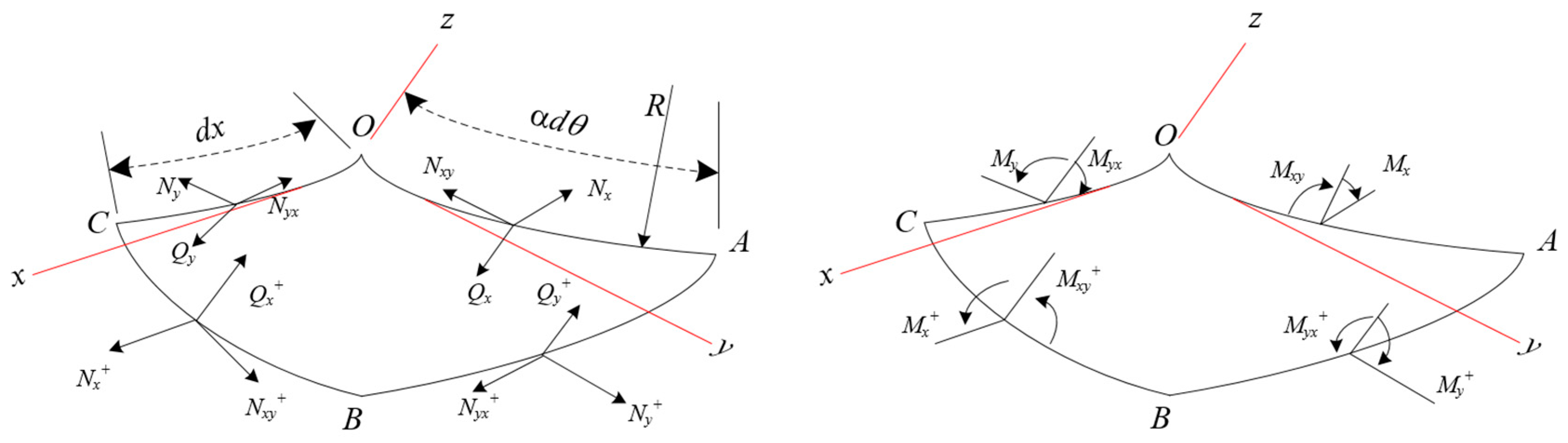
3.2. Free Ring and Thin-Shell Theory

The general condition of cylindrical shell deformation can be analyzed by the following model [32]:

The angular displacement of side BC and AB of volume element OABC for side OA and OC can be described by the following Equation. The rotation of side BC for side OA can be decomposed into three rotational components for the x, y and z axes, they are:

(1)

The relative angular displacement of side BC for side OA about the x-axis is as follows:

$$\frac{1}{R}\left(\frac{\partial v}{\partial x}+\frac{{\partial }^{2}w}{\partial x\partial \theta }\right)dx$$

(2)

(2)

The rotation of side BC about the y-axis of side OA is caused by the bending of the generatrix in the axial plane, and it is equal to the following:

$$-\frac{{\partial }^{2}w}{\partial x^2}dx$$

(3)

(3)

The rotation of side BC about the z-axis of side OA is caused by the bending of the generatrix in the tangent plane, and it equals the following:

$$\frac{{\partial }^{2}v}{\partial x^2}dx$$

(4)

Equations (2)–(4) give the three rotational components of side BC to side OA.

The rotation of side AB for side OC can be decomposed into three rotational components for the x-, y- and z-axis, they are as follows:

(1)

The relative angular displacement of side AB for side OC about the x axis is

$$d\theta +\left(\frac{\partial v}{R\partial \theta }+\frac{{\partial }^{2}w}{R\partial {\theta }^2}\right)d\theta$$

(5)

(2)

The rotation of side AB about the y-axis of side OC is caused by the bending of the generatrix in the axial plane, and it equals the following:

$$-\left(\frac{{\partial }^{2}w}{\partial \theta \partial x}+\frac{\partial v}{\partial x}\right)d\theta$$

(6)

(3)

The rotation of side AB about the z-axis of side OC is caused by the bending of the generatrix in the tangent plane, and it is equal to the following:

$$\left(\frac{{\partial }^{2}v}{\partial \theta \partial x}-\frac{\partial w}{\partial x}\right)d\theta$$

(7)

By projecting all forces depicted in Figure 14 on the x-, y- and z-axis, three equilibrium equations of volume element OABC can be obtained as follows:

$$R\frac{\partial N_x}{\partial x}+\frac{\partial N_{yx}}{\partial \theta }-N_y\left(\frac{{\partial }^{2}v}{\partial \theta \cdot \partial x}-\frac{\partial w}{\partial x}\right)-R{N}_{xy}\frac{{\partial }^{2}v}{\partial x^2}-R{Q}_x\frac{{\partial }^{2}w}{\partial x^2}-Q_y\left(\frac{{\partial }^{2}w}{\partial \theta \cdot \partial x}-\frac{\partial v}{\partial x}\right)=0$$

(8a)

$$\frac{\partial N_y}{\partial \theta }+R\frac{\partial N_{xy}}{\partial x}+R{N}_x\frac{{\partial }^{2}v}{\partial x^2}-Q_x\left(\frac{\partial v}{\partial x}+\frac{{\partial }^{2}w}{\partial x\cdot \partial \theta }\right)+N_y{}_x\left(\frac{{\partial }^{2}v}{\partial x\cdot \partial \theta }-\frac{{\partial }^{2}w}{\partial x\cdot \partial \theta }\right)-Q_y\left(1+\frac{\partial v}{R\cdot \partial \theta }+\frac{{\partial }^{2}w}{R\cdot \partial {\theta }^2}\right)=0$$

(8b)

$$R\frac{\partial Q_x}{\partial x}+\frac{\partial Q_y}{\partial \theta }+N_{xy}\left(\frac{\partial v}{\partial x}+\frac{{\partial }^{2}w}{\partial x\cdot \partial \theta }\right)+R{N}_x\frac{{\partial }^{2}w}{\partial x^2}+N_y\left(1+\frac{\partial v}{R\cdot \partial \theta }+\frac{{\partial }^{2}w}{R\cdot \partial {\theta }^2}\right)+N_{yx}\left(\frac{\partial v}{\partial x}+\frac{{\partial }^{2}w}{\partial x\cdot \partial \theta }\right)+pR=0$$

(8c)

For the three moment equations of x-, y- and z-axis, considering the slight displacement of side BC and side AB for side OA and side OC, respectively, it can be obtained as follows:

$$R\frac{\partial M_{xy}}{\partial x}-\frac{\partial M_y}{\partial \theta }-R{M}_x\frac{{\partial }^{2}v}{\partial x^2}-M_{yx}\left(\frac{{\partial }^{2}v}{\partial x\cdot \partial \theta }-\frac{\partial w}{\partial x}\right)+R{Q}_y=0$$

(9a)

$$\frac{\partial M_{yx}}{\partial \theta }+R\frac{\partial M_x}{\partial x}+R{M}_{xy}\frac{{\partial }^{2}v}{\partial x^2}-M_y\left(\frac{{\partial }^{2}v}{\partial x\cdot \partial \theta }-\frac{\partial w}{\partial x}\right)-R{Q}_x=0$$

(9b)

$$M_x\left(\frac{\partial v}{\partial x}+\frac{{\partial }^{2}w}{\partial x\cdot \partial \theta }\right)+R{M}_{xy}\frac{{\partial }^{2}w}{\partial x^2}+M_{yx}\left(1+\frac{\partial v}{R\cdot \partial \theta }+\frac{{\partial }^{2}w}{R\cdot \partial {\theta }^2}\right)-M_y\left(\frac{\partial v}{\partial x}+\frac{{\partial }^{2}w}{\partial x\cdot \partial \theta }\right)+R\left(N_{xy}-N_{yx}\right)=0$$

(9c)

The resultant force Nx, Ny and Nxy and torque Mx, My and Mxy in the above two equations can be represented by the three strain components ε₁, ε₂, γ, and the changes in curvature χ_x, χ_y, and χ_xy. Moreover, the variation of strain components and curvature can be represented by displacements u, v and w:

$${\epsilon }_1=\frac{\partial u}{\partial x}$$

(10a)

$${\epsilon }_2=\frac{\partial v}{R\partial \theta }-\frac{w}{a}$$

(10b)

$$\gamma =\frac{\partial u}{R\partial \theta }+\frac{\partial v}{\partial x}$$

(10c)

$${\chi }_x=\frac{{\partial }^{2}w}{\partial x^2}$$

(11a)

$${\chi }_y=\frac{1}{R^2}\left(\frac{\partial v}{\partial \theta }+\frac{{\partial }^{2}w}{\partial {\theta }^2}\right)$$

(11b)

$${\chi }_{xy}=\frac{1}{R}\left(\frac{\partial v}{\partial x}+\frac{{\partial }^{2}w}{\partial x\cdot \partial \theta }\right)$$

(11c)

When the ratio of length to the diameter of a cylinder is not large enough, the boundary conditions cannot be ignored. Assuming that all the resultant forces except N_y in Equation (8a–c) are small for the uniform transverse pressure, and the product of the derivatives of the displacements of u, v and w of these resultant forces can be omitted, the following equation can be obtained:

$$R\frac{\partial N_x}{\partial x}+\frac{\partial N_{yx}}{\partial \theta }-N_y\left(\frac{{\partial }^{2}v}{\partial \theta \cdot \partial x}-\frac{\partial w}{\partial x}\right)=0$$

(12a)

$$\frac{\partial N_y}{\partial \theta }+R\frac{\partial N_{xy}}{\partial x}-Q_y=0$$

(12b)

$$R\frac{\partial Q_x}{\partial x}+\frac{\partial Q_y}{\partial \theta }+N_y\left(1+\frac{\partial v}{R\cdot \partial \theta }+\frac{{\partial }^{2}w}{R\cdot \partial {\theta }^2}\right)+pR=0$$

(12c)

Assuming that the bending moment and the torque are very small, and omitting the product term of the derivatives of these torques and the derivatives of the displacements u, v and w, we get the following:

$$Q_x=\frac{\partial M_{yx}}{R\partial \theta }+\frac{\partial M_x}{\partial x}$$

(13a)

$$Q_y=\frac{\partial M_y}{R\partial \theta }-\frac{\partial M_{xy}}{\partial x}$$

(13b)

By substituting Equation (13a,b) into Equation (12a–c), respectively, then we get the following:

$$R\frac{\partial N_x}{\partial x}+\frac{\partial N_{yx}}{\partial \theta }-N_y\left(\frac{{\partial }^{2}v}{\partial \theta \cdot \partial x}-\frac{\partial w}{\partial x}\right)=0$$

(14a)

$$\frac{\partial N_y}{\partial \theta }+R\frac{\partial N_{xy}}{\partial x}-\frac{\partial M_y}{R\cdot \partial \theta }+\frac{\partial M_{xy}}{\partial x}=0$$

(14b)

$$R\frac{{\partial }^2{M}_{xy}}{\partial x\cdot \partial \theta }+R\frac{{\partial }^2{M}_x}{\partial x^2}+\frac{{\partial }^2{M}_y}{R\cdot \partial {\theta }^2}-\frac{{\partial }^2{M}_{xy}}{\partial x\cdot \partial \theta }+N_y\left(1+\frac{\partial v}{R\cdot \partial \theta }+\frac{{\partial }^{2}w}{R\cdot \partial {\theta }^2}\right)+pR=0$$

(14c)

The cylindrical shell remains circular under uniform distribution pressure and suffers uniform circumferential compression. Then we get the following:

$$v=0$$

(15a)

$$w=\frac{p{R}^2}{Et}$$

(15b)

$$N_x=0$$

(15c)

$$N_y=-pR$$

(15d)

$$M_x=M_y=M_{xy}=0$$

(15e)

In the discussion of shell buckling, only small deflections of equilibrium form leaving uniform compression are considered. Therefore, N_y in Equation (15d) is almost the same as -pR, which can be written as follows:

$$N_y=-pR+{N^{\prime }}_y$$

(15f)

where ${N^{\prime }}_y$ is a small change of resultant force -pR, which corresponds to the displacement u, v and w deviating from the cylindrical shape.

In addition, N_y·(1 + ε₁) and p·(1 + ε₁)·(1 + ε₂) are substituted for N_y and p when the elongation of the middle surface of the shell at buckling is included. Notice Equation (10a,b), and Equation (14) can be expressed in the following form:

$$R\frac{\partial N_x}{\partial x}+\frac{\partial N_{yx}}{\partial \theta }+pR\left(\frac{{\partial }^{2}v}{\partial \theta \cdot \partial x}-\frac{\partial w}{\partial x}\right)=0$$

(16a)

$$\frac{\partial N_y}{\partial \theta }+R\frac{\partial N_{xy}}{\partial x}-\frac{\partial M_y}{R\cdot \partial \theta }+\frac{\partial M_{xy}}{\partial x}=0$$

(16b)

$$R\frac{{\partial }^2{M}_{xy}}{\partial x\cdot \partial \theta }+R\frac{{\partial }^2{M}_x}{\partial x^2}+\frac{{\partial }^2{M}_y}{R\cdot \partial {\theta }^2}-\frac{{\partial }^2{M}_{xy}}{\partial x\cdot \partial \theta }+{N^{\prime }}_y-p\left(w+\frac{{\partial }^{2}w}{\partial {\theta }^2}\right)=0$$

(16c)

All the resultant force and the resultant torque can be expressed as the quantities related to u, v and w, combined with Equation (11) and the relation of thin-shell element:

$$\varphi =\frac{pR\left(1-{\mu }^2\right)}{Et}\mathrm{and}\alpha =\frac{t^2}{12R^2},$$

We get the following:

$$R^2\frac{{\partial }^{2}u}{\partial x}+\frac{1+v}{2}R\frac{{\partial }^{2}v}{\partial x\partial \theta }-vR\frac{\partial w}{\partial x}+R\varphi \left(\frac{{\partial }^{2}v}{\partial \theta \cdot \partial x}-\frac{\partial w}{\partial x}\right)+\frac{1-v}{2}\frac{{\partial }^{2}u}{\partial {\theta }^2}=0$$

(17a)

$$\frac{1+v}{2}R\frac{{\partial }^{2}u}{\partial x\cdot \partial \theta }+\frac{1-v}{2}{R}^2\frac{{\partial }^{2}v}{\partial x^2}-\frac{{\partial }^{2}v}{\partial {\theta }^2}-\frac{\partial w}{\partial \theta }+R\left[\frac{{\partial }^{2}v}{\partial {\theta }^2}+\frac{{\partial }^{3}w}{\partial {\theta }^3}+R^2\frac{{\partial }^{3}w}{\partial x^2\partial \theta }+R^2\left(1-v\right)\frac{{\partial }^{2}v}{\partial x^2}\right]=0$$

(17b)

$$Rv\frac{\partial u}{\partial x}+\frac{\partial v}{\partial \theta }-w-R\left[\frac{{\partial }^{3}v}{\partial {\theta }^3}+\left(2-v\right)R^2\frac{{\partial }^{3}v}{\partial x^2\partial \theta }+R^4\frac{{\partial }^{4}w}{\partial x^4}+\frac{{\partial }^{4}w}{\partial {\theta }^4}+2R^2\frac{{\partial }^{4}w}{\partial x^2\partial {\theta }^2}\right]=\varphi \left(w+\frac{{\partial }^{2}w}{\partial {\theta }^2}\right)$$

(17c)

Set the cylinder length as l, and take the following equation as the displacement when buckling:

$$u=A\sin n\theta \cdot \sin \frac{\pi x}{l}$$

(18a)

$$v=B\cos n\theta \cdot \cos \frac{\pi x}{l}$$

(18b)

$$w=C\sin n\theta \cdot \cos \frac{\pi x}{l}$$

(18c)

If we substitute Equation (18) into (17) and let λ = π·R/l, we obtain the following:

$$A\left(-{\lambda }^2-\frac{1-v}{2}{n}^2\right)+B\left(\frac{1+v}{2}n\lambda +n\lambda \varphi \right)+C\left(v+\varphi \right)\lambda =0$$

(19a)

$$A\left(\frac{1+v}{2}n\lambda \right)-B\left[\frac{1-v}{2}{\lambda }^2+n^2+n^2\alpha +\alpha \left(1-v\right){\lambda }^2\right]-C\left(n+\alpha n^3+\alpha n{\lambda }^3\right)=0$$

(19b)

$$A\left(v\lambda \right)-B\left(n+\alpha n^3+\left(2-v\right)\alpha n{\lambda }^2\right)-C\left[1+\alpha {\lambda }^4+\alpha n^4+2\alpha n^2{\lambda }^2+\varphi \left(1-n^2\right)\right]=0$$

(19c)

If A, B and C are equal to 0, the above equation can be satisfied, which corresponds to the circular equilibrium equation for the uniform compression of the shell. Only when the above equation gives non-zero solutions to A, B and C can there be A buckling equilibrium form, that is, the determinant of the Equation is zero.

The equation that determines the critical pressure is as follows:

$$\varphi \left(D+E\alpha +F\varphi \right)=G+H\alpha +K{\alpha }^2$$

(20)

In the absence of the magnitude of the critical pressure impact on the very small terms, substitute the expressions α, φ and λ into the equation:

$$\frac{\left(1-{\mu }^2\right)p_{cr}R}{Et}=\frac{1-{\mu }^2}{\left(n^2-1\right)\left(1+n^2{l}^2/{\pi }^2{R}^2\right)}+\frac{t^2}{12R^2}\left(n^2-1+\frac{2n^2-1-\mu }{1+n^2{l}^2/{\pi }^2{R}^2}\right)$$

(21)

When the cylinder is long enough, l/R is a large number, and the square of the denominator can be omitted.

$$p_{cr}=\frac{E{t}^3\left(n^2-1\right)}{12R^3\left(1-{\mu }^2\right)}$$

(22)

Equation (22) is the critical buckling pressure equation of thin-walled cylindrical shell.

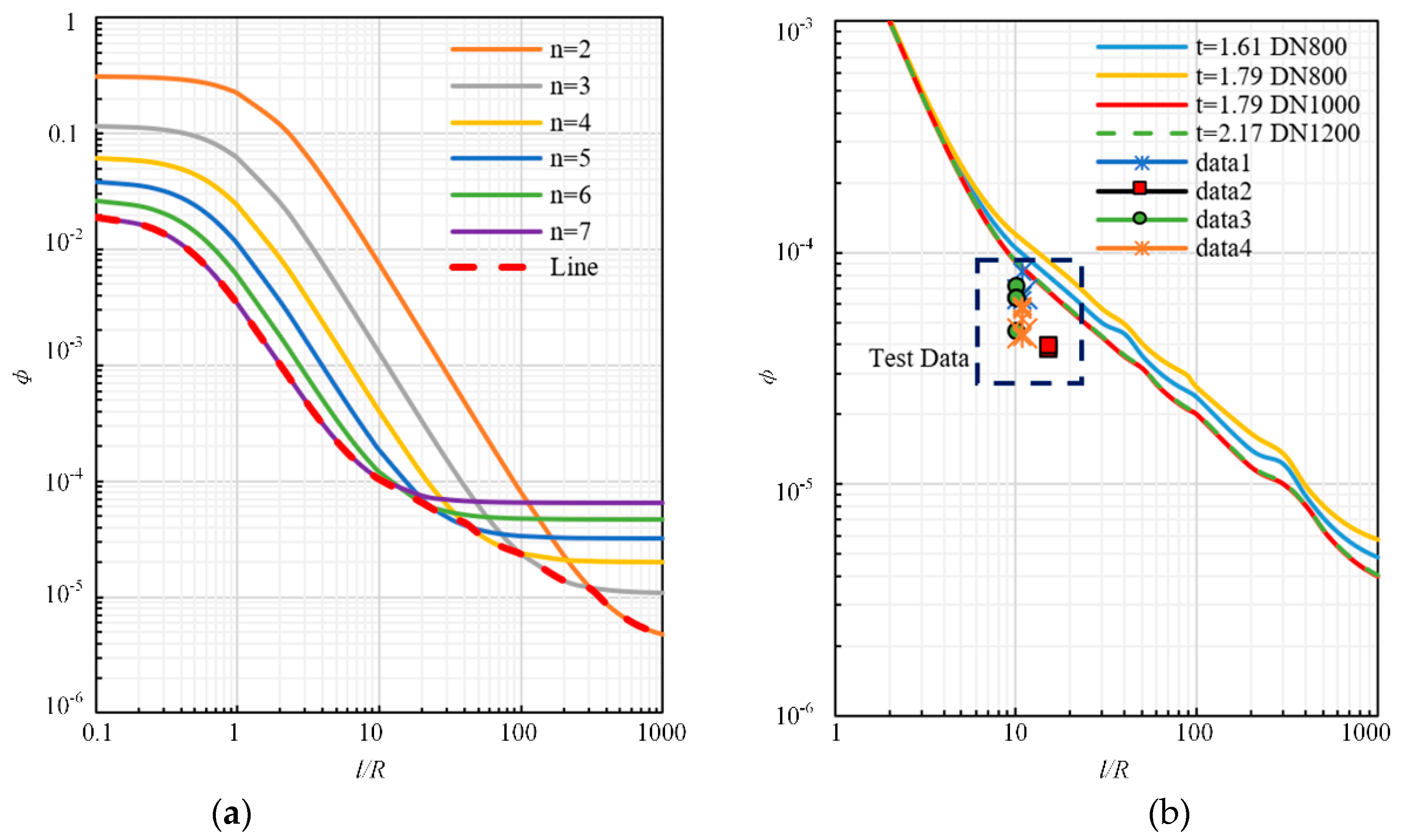
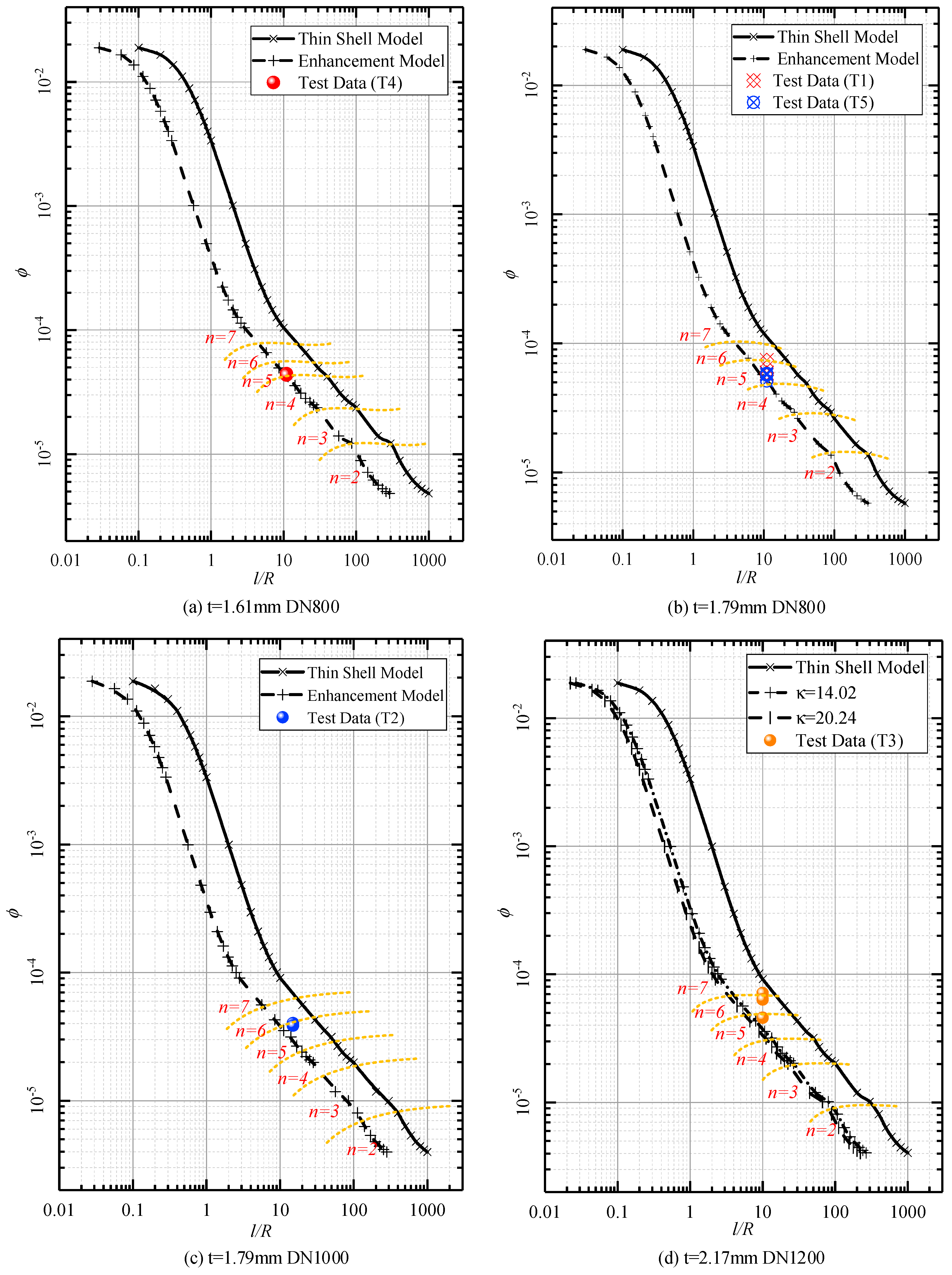
3.3. Comparison with Theoretical Predictions

The ratio l/R is used as the x-coordinate and the value φ as the y-coordinate. For each value of α, the part plotted by different value of n can be obtained. By substituting the performance parameters of the SSL (Elastic Modulus is 195 GPa; Poisson ration is 0.247; and t equals 1.61, 1.79 and 2.17 mm, respectively) into 22, the diagram shown in Figure 15 can be drawn. For the same value of α, we can finally get a line composed of the parts of the curve given for various values of n (see Figure 15a, red line). It shows that, for the cylindrical shell with short length, when the ratio l/R decreases, the critical load increases rapidly. For the long cylindrical thin shell, the critical buckling pressure is no longer related to the length but is equal to the cylinder’s value under the condition of infinite length.

The comparison between thin-shell theory and test results shows that the host pipe has a significant supporting effect on the lining. Based on Equation (22), the critical buckling pressure (p_cr0) of liner under ideal condition is calculated with the lobe number n equals 2. It then has the critical buckling pressure of this baseline, compared with the test results (p_test), the host pipe reinforcement coefficient k = p_test/p_cr0 is given, as shown in

Table 3. Enhancement coefficient k under different buckling modes.

No.	Theoretical Value of Free Ring Model/kPa	k1 Lobe 1	k2 Lobe 2	k3 Lobe 3	k4 Lobe 4	kaverage
Test 1	4.65	11.85	11.27	11.70	14.80	12.40
Test 2	2.26	12.57	13.01	12.43	NAN	12.67
Test 3	2.46	14.02	21.82	19.42	19.48	14.02/20.24
Test 4	3.39	12.22	11.90	NAN	NAN	12.06
Test 5	4.65	10.23	11.36	11.61	11.69	11.27

, and the test data is also plotted in Figure 15b.

It shows that, since to the thin-shell theory does not consider the reinforcement effect of HPs on lining, the result has a large deviation. In the data analysis, it is found that the enhancement effect of HPs can be divided into two parts: the first part is the raising of the threshold of lining lobes, and the second part shows the increase of critical buckling pressure for the lining. The l/R value is scaled to $\sqrt{k}$, and the thin-shell buckling Equation (21) is revised to Equation (23), which can be regarded as the lining buckling Equation considering the reinforcement effect of the existing pipeline.

$$p_{cr}=\frac{E{t}^3}{12R^3\left(1-{\mu }^2\right)}\left(n^2-1+\frac{2n^2-1-\mu }{1+n^2{l}^2/\kappa \cdot {\pi }^2{R}^2}\right)+\frac{Et}{\left(n^2-1\right)\left(1+n^2{l}^2/\kappa \cdot {\pi }^2{R}^2\right)R}$$

(23)

According to the curves and test data in Figure 16, Equation (23) can better predict the critical buckling pressure of the lining.

Figure 16 indicates that four lobes occur randomly in the lining when the vacuum degree of T4 group is between 33.4 and 48.5 kPa. However, five lobes occur randomly when the vacuum degree ranges from 46.5 to 70.0 kPa for T1 and T5, from 17.1 to 32.0 kPa for T2 and from 22.5 to 36.8 kPa for T3. Moreover, six lobes are easily generated between 36.8 and 54.8 kPa for T3. This further indicates that the thinner the wall thickness and the larger the pipe diameter, the lower the threshold for forming multiple lobes. Combined with the experimental results, Equation (23) is fully demonstrated.

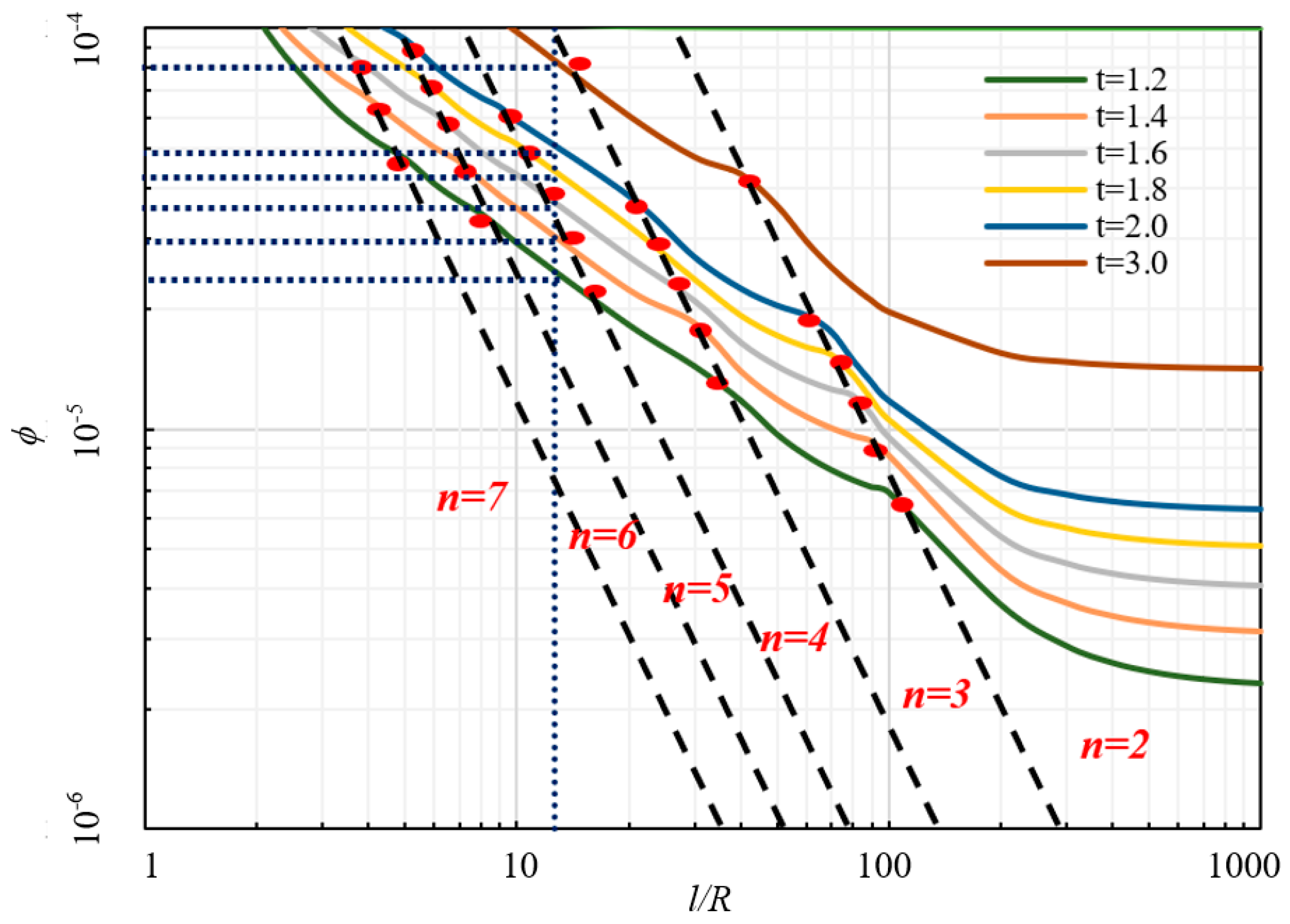
3.4. Design Procedures

Through an example analysis, this part introduces in detail the negative pressure design process by using SSL trenchless technology. It should be noted that one of the limitations of this article is that only the stability of the lining-water-supply pipeline system under negative pressure is considered. If the pipeline is buried in the ground, the soil pressure, hydrostatic pressure and traffic load on the pipeline must be considered comprehensively. Case parameters are as follows:

• Pipe diameter: DN800 mm; Pipe length: 10 m;
• Lining material model: stainless steel 304;
• Elastic Modulus: 195,000 MPa;
• Poisson ratio: 0.247;
• Thickness: 1.2 mm.

The design process is as follows:

(1)

Using the experimental results (Table 3), we take a relatively conservative value of 14.02 (The larger value of k_average in T1–T5);

(2)

Then, according to the actual lining material performance parameters, the curves under different lobe number n are calculated and drawn;

(3)

Obtaining the envelope curve of the buckling value φ and l/R ratio (See figure line ‘t = 1.2′ in Figure 17);

(4)

Taking the actual l/R ratio to determine the corresponding φ value and reverse calculating the critical buckling pressure;

(5)

If the calculated pressure does not meet the specified vacuum negative pressure value, several groups of large wall mass are used for the new drawing. In this case, several scenarios are considered (t = 1.2 mm, t = 1.4 mm, t = 1.6 mm, t = 1.8 mm, t = 2.0 mm and t = 3.0 mm);

(6)

So far, the ratio of l/R can be set as the actual value and plotted in the figure to obtain the corresponding value of φ. Applying the definition of φ, the critical buckling pressure can be derived reversely. The critical buckling values in this case are 14.33 kPa for t = 1.2 mm, 20.82 kPa for t = 1.4 mm, 28.86 kPa for t = 1.6 mm, 37.73 kPa for t = 1.8 mm, 50.70 kPa for t= 2.0 and 120.0 kPa for t= 3.0 mm, respectively;

(7)

Finally, t = 2.0 mm is taken as the repair wall thickness of the lining under the negative pressure of the water-supply pipeline (The standard requires it to withstand negative pressure of −0.05 MPa). Moreover, the lining generates four random lobes in this circumstance.

This case is based on an experiment carried out in 2013. The continuous negative pressure test shows that the 1.2 mm lining can withstand a vacuum of about 10 kPa, which is consistent with the results of the enhancement model in this paper. It should be noted that, due to the conservative enhancement coefficient value (compared with other values in Table 3), the buckling pressure is smaller than the actual pressure in the case of t =1.6 mm and t =1.80 mm. Moreover, this case further proves that, with the increase of lining wall thickness, the number of lobes becomes smaller and smaller, and the lobe formation becomes more and more difficult. Moreover, when t = 3.0 mm, the critical buckling pressure reached 0.120 MPa, which exceeded the vacuum degree range, indicating that, in this case, negative pressure is no longer a limiting factor for the lining with a wall thickness of 3.0 mm (considered negative pressure separately).

4. Summary and Conclusions

The buckling of stainless-steel liner encased in host pipe under continuous negative pressure (instantaneous negative pressure) was investigated experimentally in this paper. The buckling and post-buckling behavior of the liner pipe were expounded from the measurement of critical pressure, strain and displacement of liner. Finally, based on the thin-shell theory, an enhanced prediction model considering the support of existing pipelines was proposed, and an analytical solution was given. It should be noted that there will be more or less imperfections due to the installation of the on-site lining. Therefore, the research in this paper is carried out when the ovality is less than 1.6% and the annular gap is less than 2.0%. According to the research results of this paper, the following conclusions can be drawn:

(1)

When the pump and valve are switched on and off in the water supply network system, the inertia of the medium causes negative pressure and positive pressure, which can be considered as the local failure of the pipeline. The test equipment employed in this study is reliable and effective for the study of application of thin-wall stainless-steel trenchless repair technology to update the system stability of water-supply pipe network.

(2)

In the pre-buckling stage, the critical buckling pressure is closely related to the lining wall thickness and lining diameter. The smaller the lining wall thickness is, the smaller the critical buckling pressure is. Moreover, with the increase of pipe diameter, the critical buckling pressure of liner pipe with the same wall thickness tended to decrease.

(3)

The results show that the buckling behavior of the pipeline lining system is affected by the pressure change velocity. Under the condition of instantaneous negative pressure, it is easier to form lobes, but after the first lobe, the subsequent critical buckling pressure to form new lobes increases less than that of the continuous negative pressure test.

(4)

The buckling mode of inner liner under negative vacuum pressure is different from that of buried pipeline and deep-sea pipeline. The strain results indicate that with the increase of vacuum degree, the lining shows the elastic deformation of the full section, such as the elastic deformation of the lower end of the pipeline in Figure 12(c-1). After the material exceeds the elastic stage, the first lobe appears in the lining, and then the vacuum degree of the system decreases obviously. The system will reach a new equilibrium. With the increase of vacuum degree, new lobes will be formed. This process shows certain cyclic characteristics. The buckling position of several test liners is not the same, which is determined by the boundary constraints of the liners and host pipe.

(5)

One of the most important factors to consider in a water-supply pipeline is its ability to overflow. The critical buckling pressure of the subsequent lobes differs little from the critical buckling pressure of the first lobe. That is, as long as the buckling occurs, the subsequent lobes will be generated quickly. We believe that the overflow section in post-buckling is easier to reduce to the level of 50–60% of the original pipeline, which is unacceptable in the water supply network. Therefore, a reasonable design method should be applied to obtain the economic and reliable lining design’s wall thickness.

(6)

With the support of the existing pipe, the position where lining buckling produces greater tensile strain. The critical pressure of lining buckling deviates significantly from the theory of free ring. By comparing the two, the enhancement coefficient k, which ranges from 11.22 to 14.02, is obtained. The critical pressure calculation Equation given in the thin-shell theory can predict the number of buckling waves and critical buckling pressure, but it does not consider the supporting role of existing pipelines. The study shows that the enhancement coefficient k can be represented as the change of boundary conditions. By reducing the l/R ratio by $\sqrt{k}$ times, the improved enhanced model can predict the buckling value of the lining and the number of possible buckling lobes.

(7)

The enhanced prediction model can be used to design the inner wall thickness of the water-supply pipeline repaired by SSL. When the negative pressure is taken into account, the number of possible lobe formations decreases with the increase of lining wall thickness. If the lining thickness reaches a certain value, the required buckling pressure has exceeded the vacuum limit. In this case, negative pressure is not needed to be considered. However, considering the cost of the thin-walled stainless-steel lining, the reinforcement model can be applied to obtain the optimal wall thickness, thus making the lining design economical and safe.