Non-Slender n-Link Chain Driven by Single-Joint and Multi-Joint Muscle Actuators: Closed-Form Dynamic Equations and Joint Reaction Forces

Abstract

The author has derived the closed-form dynamic equations for a planar musculoskeletal chain composed of a generic number n of rigid links connected by ideal revolute joints. Single-joint and multi-joint muscles have been modeled as linear force actuators that can span from one joint to all the joints of the chain. The generic shape and size of each individual link of the chain accounts for different alignments among the center of mass of the link, the centers of rotation of the joints that articulate the link with its neighbors, and the points of application of the muscle forces and the possible contact external resistances acting on the link. The joint torque and the reaction force acting on each joint have been determined in closed-form by analytical quantification of the unique contribution of each individual kinematic and kinetic variable: (1) force of each single-joint or multi-joint muscle spanning or non-spanning the joint; (2) weight and contact external resistances acting on each individual link of the chain; (3) position, angular velocity, and angular acceleration of each individual link of the chain. The analytical results derived in this study can be applied to multilink musculoskeletal chains with deep/superficial and segmental/global muscles.

1. Introduction

The serial chain composed of rigid links connected by revolute joints is a reference model in robotics [1,2] and musculoskeletal biomechanics [3,4]. Closed-form dynamic equations (the dynamic equations that contain all the variables in explicit input-output form) have been derived for planar serial chains with a limited number (two or three) links, under additional simplifying assumptions related to both the passive and active elements of the chain [5,6,7,8]. Often, the links are modeled as slender rods, and each joint is assumed to be driven by an abstract torque actuator that produces a torque about the joint axis with no effect on the joint reaction force. As the number of links increases, the complexity of the closed-form equations becomes prohibitive [4] (p. 394), and computations are usually performed iteratively, for one link at a time [1,2,4]. The resulting Newton–Euler equations are not in closed form, as the motion of a single link is kinematically coupled to the motion of the other links, and the contribution of individual variables can no longer be discriminated [1,2,4,9].

The joints of a musculoskeletal chain are driven by muscles that can span multiple joints and induce axial (traction and compressive) and shear joint reaction forces [10,11,12,13]. Individual muscle actions, external forces acting on the chain, and inertial forces related to link movement can all contribute to joint torques and joint reaction forces [11,14,15]. Precise determination of the contribution that these unique components provide to the reaction forces acting on specific joint structures is one of the most crucial issues in musculoskeletal biomechanics [16,17,18].

The aim of this study is to derive the closed-form dynamic equations for a planar musculoskeletal chain, composed of a generic number n of rigid links of generic shape and size, and driven by single-joint and multi-joint muscle actuators that can span from one joint to all the joints of the chain. The specific goal is to determine the joint torque and the reaction force acting on each joint in closed-form by analytical quantification of the unique contribution of each relevant biomechanical parameter: (1) the force of each single-joint or multi-joint muscle spanning or non-spanning the joint; (2) the weight and contact external resistances acting on each individual link of the chain; (3) the position, angular velocity, and angular acceleration of each individual link of the chain.

The general closed-form equations derived in this study can be readily simplified to be applied to more basic chain models, for example, considering a limited number of links, replacing single and multi-joint joint muscle actuators with ideal torque actuators, and introducing simplifying assumptions on the link geometry and on the system of forces acting on each link. In particular, we will verify that the general closed-form equations can be reduced to the closed-form equations that have been reported for chains driven by ideal torque actuators and composed of two [4] or three [8] links modeled as slender rods, in absence of contact external resistances.

The analytical results derived in this study can be applied to multilink musculoskeletal chains with deep/superficial and segmental/global muscles.

2. Methods and Results

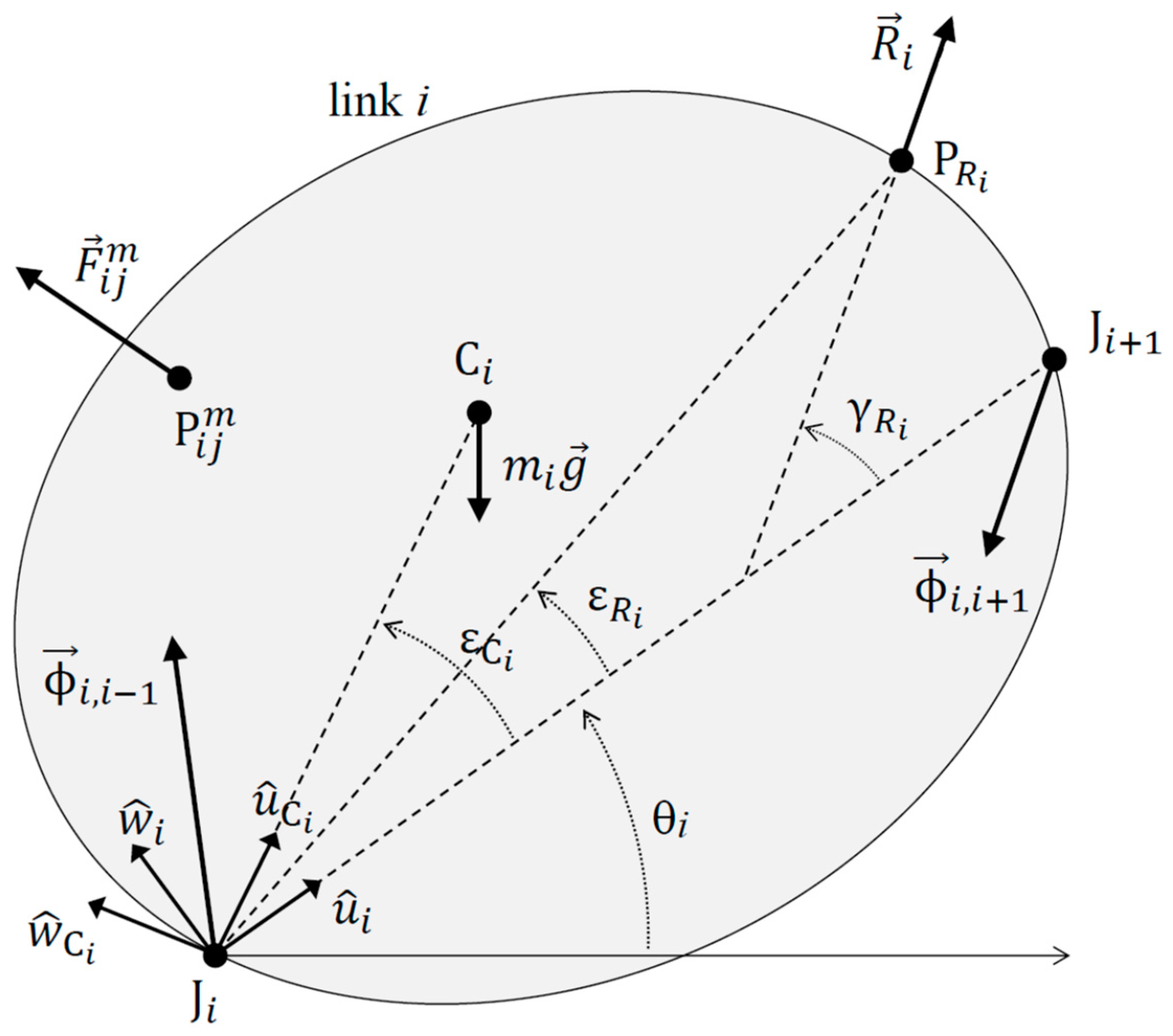
2.1. The Chain Model

We considered a planar musculoskeletal chain composed of a generic number n of rigid links connected by ideal revolute joints. Each link of the chain has a generic shape and size (Figure 1). Two adjacent links, link i − 1 and link i, articulate at joint i$\left(i=2,3,\dots ,n\right)$. The proximal link of the chain (link 1) is also articulated with a fixed base at joint 1, and the distal link (link n) only articulates with link n − 1 at joint n. The fixed base of the chain is referred to as “link 0”. The center of rotation of joint i is denoted by ${\mathrm{J}}_i$, and two points, ${\mathrm{J}}_0$ (distinct from ${\mathrm{J}}_1$) and ${\mathrm{J}}_{n+1}$ (distinct from ${\mathrm{J}}_n$), were arbitrarily selected within the base and link n, respectively. Single-joint and multi-joint muscles attached to the chain and base were modeled as linear force actuators that can span 1 to $n_{\mathrm{S}}$ joints $(n_{\mathrm{S}}\le n)$.

The following parameters are associated with each link i $\left(i=0,1,\dots ,n\right)$ of the chain (Figure 1): the distance $l_i=\left|{\mathrm{J}}_i{\mathrm{J}}_{i+1}\right|$ between ${\mathrm{J}}_i$ and ${\mathrm{J}}_{i+1}$, the unit vector ${\widehat{u}}_i$ of ${\mathrm{J}}_i{\mathrm{J}}_{i+1}$ $({\mathrm{J}}_i{\mathrm{J}}_{i+1}=l_i{\widehat{u}}_i)$, the angle ${\mathsf{\theta }}_i$ between ${\widehat{u}}_i$ and the horizontal X-axis (the counterclockwise direction of rotation is considered positive); the distance $l_{{\mathrm{C}}_i}=\left|{\mathrm{J}}_i{\mathrm{C}}_i\right|$ from ${\mathrm{J}}_i$ of the center of mass ${\mathrm{C}}_i$ of the link, the unit vector ${\widehat{u}}_{{\mathrm{C}}_i}$ of ${\mathrm{J}}_i{\mathrm{C}}_i$ (${\mathrm{J}}_i{\mathrm{C}}_i=l_{{\mathrm{C}}_i}{\widehat{u}}_{{\mathrm{C}}_i}$), the angle ${\mathsf{\epsilon }}_{{\mathrm{C}}_i}$ between ${\widehat{u}}_{{\mathrm{C}}_i}$ and ${\widehat{u}}_i$; the mass $m_i$, the moments of inertia $I_{{\mathrm{J}}_i}$ and $I_{{\mathrm{C}}_i}$ about ${\mathrm{J}}_i$ and ${\mathrm{C}}_i$; the accelerations ${\overrightarrow{a}}_{{\mathrm{J}}_i}$ and ${\overrightarrow{a}}_{{\mathrm{C}}_i}$ of ${\mathrm{J}}_i$ and ${\mathrm{C}}_i$; the angular velocity ${\overrightarrow{\mathsf{\omega }}}_i={\dot{\mathsf{\theta }}}_i\widehat{k}$ and acceleration ${\dot{\overrightarrow{\mathsf{\omega }}}}_i={\ddot{\mathsf{\theta }}}_i\widehat{k}$ ($\widehat{k}$ is the unit vector normal to the plane of the chain); and the unit vectors ${\widehat{w}}_i=\widehat{k}\times {\widehat{u}}_i$ and ${\widehat{w}}_{{\mathrm{C}}_i}=\widehat{k}\times {\widehat{u}}_{{\mathrm{C}}_i}$.

The external forces acting on each link i $\left(i=0,1,\dots ,n\right)$ are listed below (Figure 1):

• The weight $m_i\overrightarrow{g}$ of the link applied at ${\mathrm{C}}_i$.
• A contact external resistance ${\overrightarrow{R}}_i$ may act on a point ${\mathrm{P}}_{R_i}$ of the link at distance $l_{R_i}$ from ${\mathrm{J}}_i$ (${\mathsf{\epsilon }}_{R_i}$ is the angle between ${\mathrm{J}}_i{\mathrm{P}}_{R_i}$ and ${\widehat{u}}_i$, and ${\mathsf{\gamma }}_{R_i}$ the angle between ${\overrightarrow{R}}_i$ and ${\widehat{u}}_i$). The contact external force ${\overrightarrow{R}}_0$ acting on the base is typically the ground reaction force. The case of multiple contact external resistances acting on a link is examined in the discussion section.
• The sum of muscle forces ${\displaystyle \sum }_m{\overrightarrow{F}}_{ij}^m$ exerted on points ${\mathrm{P}}_{ij}^m$ of link i by the muscles joining link i to the other links j ($j=i\pm 1$ for single-joint muscles, $j=i\pm 2$ for two-joint muscles, etc.). The sum is extended over all muscles joining link i to link j.

The joint reaction force ${\overrightarrow{\mathsf{\varphi }}}_{i,i-1}$, exerted on link i by link i − 1, and ${\overrightarrow{\mathsf{\varphi }}}_{i,i+1}$, entered on link i by link i + 1. Only one joint reaction force acts on link 0 $({\overrightarrow{\mathsf{\varphi }}}_{01})$ and on link n $({\overrightarrow{\mathsf{\varphi }}}_{n,n-1})$. It is assumed that the line of action of ${\overrightarrow{\mathsf{\varphi }}}_{i,i-1}$ passes through ${\mathrm{J}}_i$ and that of ${\overrightarrow{\mathsf{\varphi }}}_{i,i+1}$ through ${\mathrm{J}}_{i+1}$. Biomechanically, the joint reaction force is the resultant of the bone-to-bone contact force and the forces developed by the tension of capsuloligamentous tissue.

The following relations hold: ${\overrightarrow{\mathsf{\varphi }}}_{i,i+1}=-{\overrightarrow{\mathsf{\varphi }}}_{i+1,i}$, ${\overrightarrow{F}}_{ij}^m=-{\overrightarrow{F}}_{ji}^m$, ${\dot{\mathsf{\theta }}}_0={\ddot{\mathsf{\theta }}}_0=0$, and ${\overrightarrow{a}}_{{\mathrm{J}}_0}={\overrightarrow{a}}_{{\mathrm{C}}_0}={\overrightarrow{a}}_{{\mathrm{J}}_1}=0$.

2.2. Force Equations and Joint Reaction Forces

The dynamic force equations of individual links i $\left(i=0,1,\dots ,n\right)$ are given by

$$\underset{\left(j\ge 0\right)}{\overset{i-1}{{\displaystyle \sum }_{j=i-n_{\mathrm{s}}}}}\left({\displaystyle \sum }_m{\overrightarrow{F}}_{ij}^m\right)+\underset{\left(j\le n\right)}{\overset{i+n_{\mathrm{s}}}{{\displaystyle \sum }_{j=i+1}}}\left({\displaystyle \sum }_m{\overrightarrow{F}}_{ij}^m\right)+m_i\overrightarrow{g}+{\overrightarrow{R}}_i+{\overrightarrow{\mathsf{\varphi }}}_{i,i-1}+{\overrightarrow{\mathsf{\varphi }}}_{i,i+1}=m_i{\overrightarrow{a}}_{{\mathrm{C}}_i}$$

(1)

where ${\overrightarrow{\mathsf{\varphi }}}_{-1,0}={\overrightarrow{\mathsf{\varphi }}}_{n,n+1}=0$ and the index j may only range between 0 and n. Adding together the last n − k equations $\left(i=k+1,k+2,\dots ,n\right)$ or the first k + 1 ones $\left(i=0,1,\dots ,k\right)$, and taking into account that ${\overrightarrow{F}}_{ij}^m=-{\overrightarrow{F}}_{ji}^m$ and ${\overrightarrow{\mathsf{\varphi }}}_{i,i+1}=-{\overrightarrow{\mathsf{\varphi }}}_{i+1,i}$, one can express the joint reaction forces ${\overrightarrow{\mathsf{\varphi }}}_{k,k+1}$ $\left(k=0,1,\dots ,n-1\right)$ in relation to the other parameters:

$${\overrightarrow{\mathsf{\varphi }}}_{k,k+1}={\displaystyle \sum }_{i=k+1}^n\left(m_i\overrightarrow{g}+{\overrightarrow{R}}_i\right)-{\displaystyle \sum }_{i=k+1}^n{m}_i{\overrightarrow{a}}_{{\mathrm{C}}_i}+{\displaystyle \sum }_{\begin{array}{c}{j}_2=k+1\\ \left(j_2\le n\right)\end{array}}^{k+n_{\mathrm{s}}}{\displaystyle \sum }_{\begin{array}{c}{j}_1=j_2-n_{\mathrm{s}}\\ \left(j_1\ge 0\right)\end{array}}^k\left({\displaystyle \sum }_m{\overrightarrow{F}}_{j_2{j}_1}^m\right)$$

(2)

$${\overrightarrow{\mathsf{\varphi }}}_{k,k+1}=-{\displaystyle \sum }_{i=0}^k\left(m_i\overrightarrow{g}+{\overrightarrow{R}}_i\right)+{\displaystyle \sum }_{i=0}^k{m}_i{\overrightarrow{a}}_{{\mathrm{C}}_i}+{\displaystyle \sum }_{\begin{array}{c}{j}_2=k+1\\ \left(j_2\le n\right)\end{array}}^{k+n_{\mathrm{s}}}{\displaystyle \sum }_{\begin{array}{c}{j}_1=j_2-n_{\mathrm{s}}\\ \left(j_1\ge 0\right)\end{array}}^k\left({\displaystyle \sum }_m{\overrightarrow{F}}_{j_2{j}_1}^m\right)$$

(3)

These two equations are equivalent, as it can be directly proved considering the force equation applied to the whole system of links, including link 0:

$${\displaystyle \sum }_{i=0}^n\left(m_i\overrightarrow{g}+{\overrightarrow{R}}_i\right)={\displaystyle \sum }_{i=0}^n{m}_i{\overrightarrow{a}}_{{\mathrm{C}}_i}$$

(4)

The accelerations ${\overrightarrow{a}}_{{\mathrm{C}}_i}\left(i=1,2,\dots ,n\right)$ can be expressed as a function of the angular velocity and acceleration of the individual links by applying recursively the equation the relates the accelerations of two arbitrary points of a rigid body:

$$\begin{gathered} {\overrightarrow{a}}_{{\mathrm{C}}_i}={\displaystyle \sum }_{j=0}^{i-1}\left({\overrightarrow{a}}_{{\mathrm{J}}_{j+1}}-{\overrightarrow{a}}_{{\mathrm{J}}_j}\right)+\left({\overrightarrow{a}}_{{\mathrm{C}}_i}-{\overrightarrow{a}}_{{\mathrm{J}}_i}\right)={\displaystyle \sum }_{j=0}^{i-1}({\ddot{\mathsf{\theta }}}_j\widehat{k}\times l_j{\widehat{u}}_j-{\dot{\mathsf{\theta }}}_j^2{l}_j{\widehat{u}}_j)+({\ddot{\mathsf{\theta }}}_i\widehat{k}\times l_{{\mathrm{C}}_i}{\widehat{u}}_{{\mathrm{C}}_i}-{\dot{\mathsf{\theta }}}_i^2{l}_{{\mathrm{C}}_i}{\widehat{u}}_{{\mathrm{C}}_i}) \\ ={\displaystyle \sum }_{j=0}^{i-1}({\ddot{\mathsf{\theta }}}_j{l}_j{\widehat{w}}_j-{\dot{\mathsf{\theta }}}_j^2{l}_j{\widehat{u}}_j)+({\ddot{\mathsf{\theta }}}_i{l}_{{\mathrm{C}}_i}{\widehat{w}}_{{\mathrm{C}}_i}-{\dot{\mathsf{\theta }}}_i^2{l}_{{\mathrm{C}}_i}{\widehat{u}}_{{\mathrm{C}}_i}) \end{gathered}$$

(5)

Equation (5) enables the closed-form determination of the inertial-term sum ${{\displaystyle \sum }}_{i=k+1}^n{m}_i{\overrightarrow{a}}_{{\mathrm{C}}_i}$ $\left(k=0,1,\dots ,n-1\right)$ in Equation (2)

$$\begin{array}{cc}\hfill {\displaystyle {\displaystyle \sum }_{i=k+1}^n}{m}_i{\overrightarrow{a}}_{{\mathrm{C}}_i}& ={\displaystyle {\displaystyle \sum }_{i=k+1}^n}{m}_i{\displaystyle {\displaystyle \sum }_{j=0}^{i-1}}({\ddot{\mathsf{\theta }}}_j{l}_j{\widehat{w}}_j-{\dot{\mathsf{\theta }}}_j^2{l}_j{\widehat{u}}_j)+{\displaystyle {\displaystyle \sum }_{i=k+1}^n}{m}_i({\ddot{\mathsf{\theta }}}_i{l}_{{\mathrm{C}}_i}{\widehat{w}}_{{\mathrm{C}}_i}-{\dot{\mathsf{\theta }}}_i^2{l}_{{\mathrm{C}}_i}{\widehat{u}}_{{\mathrm{C}}_i})\hfill \\ & =\left({\displaystyle {\displaystyle \sum }_{j=k+1}^n}{m}_j\right){\displaystyle {\displaystyle \sum }_{i=0}^k}({\ddot{\mathsf{\theta }}}_i{l}_i{\widehat{w}}_i-{\dot{\mathsf{\theta }}}_i^2{l}_i{\widehat{u}}_i)\\ & +(1-{\mathsf{\delta }}_{k,n-1}){\displaystyle {\displaystyle \sum }_{i=k+1}^{n-1}}\left[\left({\displaystyle {\displaystyle \sum }_{j=i+1}^n}{m}_j\right)({\ddot{\mathsf{\theta }}}_i{l}_i{\widehat{w}}_i-{\dot{\mathsf{\theta }}}_i^2{l}_i{\widehat{u}}_i)\right]+{\displaystyle {\displaystyle \sum }_{i=k+1}^n}{m}_i({\ddot{\mathsf{\theta }}}_i{l}_{{\mathrm{C}}_i}{\widehat{w}}_{{\mathrm{C}}_i}-{\dot{\mathsf{\theta }}}_i^2{l}_{{\mathrm{C}}_i}{\widehat{u}}_{{\mathrm{C}}_i})\end{array}$$

(6)

and the corresponding sum ${{\displaystyle \sum }}_{i=0}^k{m}_i{\overrightarrow{a}}_{{\mathrm{C}}_i}={{\displaystyle \sum }}_{i=1}^k{m}_i{\overrightarrow{a}}_{{\mathrm{C}}_i}$ $\left(k=1,2,\dots ,n\right)$ in Equation (3).

$$\begin{array}{cc}\hfill {\displaystyle {\displaystyle \sum }_{i=0}^k}{m}_i{\overrightarrow{a}}_{{\mathrm{C}}_i}& ={\displaystyle {\displaystyle \sum }_{i=1}^k}{m}_i{\displaystyle {\displaystyle \sum }_{j=0}^{i-1}}({\ddot{\mathsf{\theta }}}_j{l}_j{\widehat{w}}_j-{\dot{\mathsf{\theta }}}_j^2{l}_j{\widehat{u}}_j)+{\displaystyle {\displaystyle \sum }_{i=1}^k}{m}_i({\ddot{\mathsf{\theta }}}_i{l}_{{\mathrm{C}}_i}{\widehat{w}}_{{\mathrm{C}}_i}-{\dot{\mathsf{\theta }}}_i^2{l}_{{\mathrm{C}}_i}{\widehat{u}}_{{\mathrm{C}}_i})\hfill \\ & ={\displaystyle {\displaystyle \sum }_{i=0}^{k-1}}\left({\displaystyle {\displaystyle \sum }_{j=i+1}^k}{m}_j\right)({\ddot{\mathsf{\theta }}}_i{l}_i{\widehat{w}}_i-{\dot{\mathsf{\theta }}}_i^2{l}_i{\widehat{u}}_i)+{\displaystyle {\displaystyle \sum }_{i=1}^k}{m}_i({\ddot{\mathsf{\theta }}}_i{l}_{{\mathrm{C}}_i}{\widehat{w}}_{{\mathrm{C}}_i}-{\dot{\mathsf{\theta }}}_i^2{l}_{{\mathrm{C}}_i}{\widehat{u}}_{{\mathrm{C}}_i})\hfill \end{array}$$

(7)

With Equations (6) and (7), Equations (2) and (3) yield two equivalent closed-form expressions of the joint reaction forces ${\overrightarrow{\mathsf{\varphi }}}_{k,k+1}$ at the proximal joint 1 ($k=0$)

$$\begin{array}{cc}\hfill {\overrightarrow{\mathsf{\varphi }}}_{0,1}=-m_0\overrightarrow{g}-{\overrightarrow{R}}_0& +{\displaystyle {\displaystyle \sum }_{j=1}^{n_{\mathrm{s}}}}\left({\displaystyle {\displaystyle \sum }_m}{\overrightarrow{F}}_{j0}^m\right)\hfill \\ & ={\displaystyle {\displaystyle \sum }_{i=1}^n}(m_i\overrightarrow{g}+{\overrightarrow{R}}_i)+{\displaystyle {\displaystyle \sum }_{j=1}^{n_{\mathrm{s}}}}\left({\displaystyle {\displaystyle \sum }_m}{\overrightarrow{F}}_{j0}^m\right)-{\displaystyle {\displaystyle \sum }_{i=1}^{n-1}}\left[\left({\displaystyle {\displaystyle \sum }_{j=i+1}^n}{m}_j\right)({\ddot{\mathsf{\theta }}}_i{l}_i{\widehat{w}}_i-{\dot{\mathsf{\theta }}}_i^2{l}_i{\widehat{u}}_i)\right]\\ & -{\displaystyle {\displaystyle \sum }_{i=1}^n}{m}_i({\ddot{\mathsf{\theta }}}_i{l}_{{\mathrm{C}}_i}{\widehat{w}}_{{\mathrm{C}}_i}-{\dot{\mathsf{\theta }}}_i^2{l}_{{\mathrm{C}}_i}{\widehat{u}}_{{\mathrm{C}}_i})\end{array}$$

(8)

and at the other joints $2,3,\dots ,n$ $\left(k=1,2,\dots ,n-1\right)$.

$$\begin{gathered} {\overrightarrow{\mathsf{\varphi }}}_{k,k+1}={\displaystyle \sum }_{i=k+1}^n(m_i\overrightarrow{g}+{\overrightarrow{R}}_i)+{\displaystyle \sum }_{\begin{array}{c}{j}_2=k+1\\ \left(j_2\le n\right)\end{array}}^{k+n_s}{\displaystyle \sum }_{\begin{array}{c}{j}_1=j_2-n_s\\ \left(j_1\ge 0\right)\end{array}}^k\left({\displaystyle \sum }_m{\overrightarrow{F}}_{j_2{j}_1}^m\right)-\left({\displaystyle \sum }_{j=k+1}^n{m}_j\right){\displaystyle \sum }_{i=0}^k({\ddot{\mathsf{\theta }}}_i{l}_i{\widehat{w}}_i-{\dot{\mathsf{\theta }}}_i^2{l}_i{\widehat{u}}_i) \\ -\left(1-{\mathsf{\delta }}_{k,n-1}\right){\displaystyle \sum }_{i=k+1}^{n-1}\left[\left({\displaystyle \sum }_{j=i+1}^n{m}_j\right)({\ddot{\mathsf{\theta }}}_i{l}_i{\widehat{w}}_i-{\dot{\mathsf{\theta }}}_i^2{l}_i{\widehat{u}}_i)\right]-{\displaystyle \sum }_{i=k+1}^n{m}_i({\ddot{\mathsf{\theta }}}_i{l}_{{\mathrm{C}}_i}{\widehat{w}}_{{\mathrm{C}}_i}-{\dot{\mathsf{\theta }}}_i^2{l}_{{\mathrm{C}}_i}{\widehat{u}}_{{\mathrm{C}}_i}) \end{gathered}$$

(9)

$$\begin{array}{cc}\hfill {\overrightarrow{\mathsf{\varphi }}}_{k,k+1}& =-{\displaystyle {\displaystyle \sum }_{i=0}^k}(m_i\overrightarrow{g}+{\overrightarrow{R}}_i)+{\displaystyle \underset{\left(j_2\le n\right)}{\overset{k+n_s}{{\displaystyle \sum }_{j_2=k+1}}}}{\displaystyle {\displaystyle \sum }_{\begin{array}{c}{j}_1=j_2-n_s\\ \left(j_1\ge 0\right)\end{array}}^k}\left({\displaystyle {\displaystyle \sum }_m}{\overrightarrow{F}}_{j_2{j}_1}^m\right)+{\displaystyle {\displaystyle \sum }_{i=0}^{k-1}}\left({\displaystyle {\displaystyle \sum }_{j=i+1}^k}{m}_j\right)({\ddot{\mathsf{\theta }}}_i{l}_i{\widehat{w}}_i-{\dot{\mathsf{\theta }}}_i^2{l}_i{\widehat{u}}_i)\hfill \\ & +{\displaystyle {\displaystyle \sum }_{i=1}^k}{m}_i({\ddot{\mathsf{\theta }}}_i{l}_{{\mathrm{C}}_i}{\widehat{w}}_{{\mathrm{C}}_i}-{\dot{\mathsf{\theta }}}_i^2{l}_{{\mathrm{C}}_i}{\widehat{u}}_{{\mathrm{C}}_i})\end{array}$$

(10)

For the distal joint n ($k=n-1$) Equations (9) and (10) become

$$\begin{array}{cc}\hfill {\overrightarrow{\mathsf{\varphi }}}_{n-1,n}=m_n\overrightarrow{g}+& {\overrightarrow{R}}_n+{\displaystyle {\displaystyle \sum }_{j=n-n_{\mathrm{s}}}^{n-1}}\left({\displaystyle {\displaystyle \sum }_m}{\overrightarrow{F}}_{nj}^m\right)-m_n{\displaystyle {\displaystyle \sum }_{i=0}^{n-1}}({\ddot{\mathsf{\theta }}}_i{l}_i{\widehat{w}}_i-{\dot{\mathsf{\theta }}}_i^2{l}_i{\widehat{u}}_i)-m_n({\ddot{\mathsf{\theta }}}_n{l}_{{\mathrm{C}}_n}{\widehat{w}}_{{\mathrm{C}}_n}-{\dot{\mathsf{\theta }}}_n^2{l}_{{\mathrm{C}}_n}{\widehat{u}}_{{\mathrm{C}}_n})\hfill \\ & =-{\displaystyle {\displaystyle \sum }_{i=0}^{n-1}}(m_i\overrightarrow{g}+{\overrightarrow{R}}_i)+{\displaystyle {\displaystyle \sum }_{j=n-n_{\mathrm{s}}}^{n-1}}\left({\displaystyle {\displaystyle \sum }_m}{\overrightarrow{F}}_{nj}^m\right)+{\displaystyle {\displaystyle \sum }_{i=0}^{n-2}}\left({\displaystyle {\displaystyle \sum }_{j=i+1}^{n-1}}{m}_j\right)({\ddot{\mathsf{\theta }}}_i{l}_i{\widehat{w}}_i-{\dot{\mathsf{\theta }}}_i^2{l}_i{\widehat{u}}_i)\\ & +{\displaystyle {\displaystyle \sum }_{i=1}^{n-1}}{m}_i({\ddot{\mathsf{\theta }}}_i{l}_{{\mathrm{C}}_i}{\widehat{w}}_{{\mathrm{C}}_i}-{\dot{\mathsf{\theta }}}_i^2{l}_{{\mathrm{C}}_i}{\widehat{u}}_{{\mathrm{C}}_i})\end{array}$$

(11)

The joint reaction force ${\overrightarrow{\mathsf{\varphi }}}_{k,k+1}$ acting on the joint articulating link k and link k + 1 directly depends on the sum of the forces of all single-joint and multi-joint muscles spanning the joint, independently of their link attachments:

$${\overrightarrow{\mathrm{F}}}_{k,k+1}^{\mathrm{M}}={\displaystyle \sum }_{\begin{array}{c}{j}_2=k+1\\ \left(j_2\le n\right)\end{array}}^{k+n_s}{\displaystyle \sum }_{\begin{array}{c}{j}_1=j_2-n_s\\ \left(j_1\ge 0\right)\end{array}}^k\left({\displaystyle \sum }_m{\overrightarrow{F}}_{j_2{j}_1}^m\right)$$

(12)

2.3. Moment Equations and Muscle Torques

The dynamic moment equation of link n about ${\mathrm{J}}_n$ is given by

$$\begin{gathered} {\displaystyle \sum }_{j=n-n_{\mathrm{s}}}^{n-1}\left({\displaystyle \sum }_m{\mathrm{J}}_n{\mathrm{P}}_{nj}^m\times {\overrightarrow{F}}_{nj}^m\right)·\widehat{k}-m_{n}g{l}_{{\mathrm{C}}_n}\cos \left({\mathsf{\theta }}_n+{\mathsf{\epsilon }}_{{\mathrm{C}}_n}\right)+R_n{l}_{R_n}\sin \left({\mathsf{\gamma }}_{R_n}-{\mathsf{\epsilon }}_{R_n}\right) \\ =I_{{\mathrm{J}}_n}{\ddot{\mathsf{\theta }}}_n+{\mathrm{J}}_n{\mathrm{C}}_n\times m_n{\overrightarrow{a}}_{{\mathrm{J}}_n}·\widehat{k}=I_{{\mathrm{C}}_n}{\ddot{\mathsf{\theta }}}_n+{\mathrm{J}}_n{\mathrm{C}}_n\times m_n{\overrightarrow{a}}_{{\mathrm{C}}_n}·\widehat{k} \end{gathered}$$

where $I_{{\mathrm{J}}_n}=I_{{\mathrm{C}}_n}+m_n{l}_{{\mathrm{C}}_n}^2$ (Huygens–Steiner theorem). This equation, considering Equation (5) for ${\overrightarrow{a}}_{{\mathrm{C}}_n}$, becomes

$$\begin{array}{cc}\hfill {\displaystyle {\displaystyle \sum }_{j=n-n_{\mathrm{s}}}^{n-1}}({\displaystyle {\displaystyle \sum }_m}{\mathrm{J}}_n{\mathrm{P}}_{nj}^m& \times {\overrightarrow{F}}_{nj}^m)·\widehat{k}-m_{n}g{l}_{{\mathrm{C}}_n}\cos \left({\mathsf{\theta }}_n+{\mathsf{\epsilon }}_{{\mathrm{C}}_n}\right)+R_n{l}_{R_n}\sin \left({\mathsf{\gamma }}_{R_n}-{\mathsf{\epsilon }}_{R_n}\right)\hfill \\ & =I_{{\mathrm{J}}_n}{\ddot{\mathsf{\theta }}}_n+m_n{l}_{{\mathrm{C}}_n}{\displaystyle {\displaystyle \sum }_{i=1}^{n-1}}{l}_i[{\ddot{\mathsf{\theta }}}_i\cos \left({\mathsf{\theta }}_n+{\mathsf{\epsilon }}_{{\mathrm{C}}_n}-{\mathsf{\theta }}_i\right)+{\dot{\mathsf{\theta }}}_i^2\sin \left({\mathsf{\theta }}_n+{\mathsf{\epsilon }}_{{\mathrm{C}}_n}-{\mathsf{\theta }}_i\right)]\end{array}$$

(13)

For $k=1,2,\dots ,n-1$, the moment equation of link k about ${\mathrm{J}}_k$ includes the moment of the joint reaction force ${\overrightarrow{\mathsf{\varphi }}}_{k,k+1}$:

$$\begin{array}{ll}{\displaystyle \underset{\left(j\ge 0\right)}{\overset{k-1}{{\displaystyle \sum }_{j=k-n_{\mathrm{s}}}}}}({\displaystyle {\displaystyle \sum }_m}{\mathrm{J}}_k{\mathrm{P}}_{kj}^m& \times {\overrightarrow{F}}_{kj}^m)\cdot \widehat{k}+{\displaystyle {\displaystyle \sum }_{\begin{array}{c}j=k+1\\ \left(j\le n\right)\end{array}}^{k+n_{\mathrm{s}}}}\left({\displaystyle {\displaystyle \sum }_m}{\mathrm{J}}_k{\mathrm{P}}_{kj}^m\times {\overrightarrow{F}}_{kj}^m\right)\cdot \widehat{k}-m_{k}g{l}_{{\mathrm{C}}_k}\cos \left({\mathsf{\theta }}_k+{\mathsf{\epsilon }}_{{\mathrm{C}}_k}\right)+R_k{l}_{R_k}\sin \left({\mathsf{\gamma }}_{R_k}-{\mathsf{\epsilon }}_{R_k}\right)\\ & +{\mathrm{J}}_k{\mathrm{J}}_{k+1}\times {\overrightarrow{\mathsf{\varphi }}}_{k,k+1}\cdot \widehat{k}=I_{{\mathrm{C}}_k}{\ddot{\mathsf{\theta }}}_k+{\mathrm{J}}_k{\mathrm{C}}_k\times m_k{\overrightarrow{a}}_{{\mathrm{C}}_k}\cdot \widehat{k}\end{array}$$

Substitution of ${\overrightarrow{\mathsf{\varphi }}}_{k,k+1}$ with the right-hand side of Equation (2) or (3) gives Equations (14) and (15), respectively:

$$\begin{array}{cc}\hfill {\displaystyle \underset{\left(j\ge 0\right)}{\overset{k-1}{{\displaystyle \sum }_{j=k-n_{\mathrm{s}}}}}}({\displaystyle {\displaystyle \sum }_m}{\mathrm{J}}_k{\mathrm{P}}_{kj}^m& \times {\overrightarrow{F}}_{kj}^m)·\widehat{k}+{\displaystyle {\displaystyle \sum }_{\begin{array}{c}j=k+1\\ \left(j\le n\right)\end{array}}^{k+n_{\mathrm{s}}}}\left({\displaystyle {\displaystyle \sum }_m}{\mathrm{J}}_k{\mathrm{P}}_{kj}^m\times {\overrightarrow{F}}_{kj}^m\right)·\widehat{k}-m_{k}g{l}_{{\mathrm{C}}_k}\cos \left({\mathsf{\theta }}_k+{\mathsf{\epsilon }}_{{\mathrm{C}}_k}\right)+l_{R_k}{R}_k\sin \left({\mathsf{\gamma }}_{R_k}-{\mathsf{\epsilon }}_{R_k}\right)\hfill \\ & +{\mathrm{J}}_k{\mathrm{J}}_{k+1}\times {\displaystyle {\displaystyle \sum }_{i=k+1}^n}\left(m_i\overrightarrow{g}+{\overrightarrow{R}}_i-m_i{\overrightarrow{a}}_{{\mathrm{C}}_i}\right)·\widehat{k}+{\mathrm{J}}_k{\mathrm{J}}_{k+1}\times {\displaystyle \underset{\left(j_2\le n\right)}{\overset{k+n_{\mathrm{s}}}{{\displaystyle \sum }_{j_2=k+1}}}}{\displaystyle {\displaystyle \sum }_{\begin{array}{c}{j}_1=j_2-n_{\mathrm{s}}\\ \left(j_1\ge 0\right)\end{array}}^k}\left({\displaystyle {\displaystyle \sum }_m}{\overrightarrow{F}}_{j_2{j}_1}^m\right)·\widehat{k}\\ & =I_{{\mathrm{C}}_k}{\ddot{\mathsf{\theta }}}_k+{\mathrm{J}}_k{\mathrm{C}}_k\times m_k{\overrightarrow{a}}_{{\mathrm{C}}_k}·\widehat{k}\end{array}$$

(14)

$$\begin{array}{ll}{\displaystyle \underset{\left(j\ge 0\right)}{\overset{k-1}{{\displaystyle \sum }_{j=k-n_{\mathrm{s}}}}}}({\displaystyle {\displaystyle \sum }_m}{\mathrm{J}}_k{\mathrm{P}}_{kj}^m& \times {\overrightarrow{F}}_{kj}^m)·\widehat{k}+{\displaystyle {\displaystyle \sum }_{\begin{array}{c}j=k+1\\ \left(j\le n\right)\end{array}}^{k+n_{\mathrm{s}}}}\left({\displaystyle {\displaystyle \sum }_m}{\mathrm{J}}_k{\mathrm{P}}_{kj}^m\times {\overrightarrow{F}}_{kj}^m\right)·\widehat{k}-m_{k}g{l}_{{\mathrm{C}}_k}\cos \left({\mathsf{\theta }}_k+{\mathsf{\epsilon }}_{{\mathrm{C}}_k}\right)+l_{R_k}{R}_k\sin \left({\mathsf{\gamma }}_{R_k}-{\mathsf{\epsilon }}_{R_k}\right)\\ & -{\mathrm{J}}_k{\mathrm{J}}_{k+1}\times {\displaystyle {\displaystyle \sum }_{i=0}^k}(m_i\overrightarrow{g}+{\overrightarrow{R}}_i-m_i{\overrightarrow{a}}_{{\mathrm{C}}_i})·\widehat{k}+{\mathrm{J}}_k{\mathrm{J}}_{k+1}\times {\displaystyle \underset{\left(j_2\le n\right)}{\overset{k+n_{\mathrm{s}}}{{\displaystyle \sum }_{j_2=k+1}}}}{\displaystyle {\displaystyle \sum }_{\begin{array}{c}{j}_1=j_2-n_{\mathrm{s}}\\ \left(j_1\ge 0\right)\end{array}}^k}\left({\displaystyle {\displaystyle \sum }_m}{\overrightarrow{F}}_{j_2{j}_1}^m\right)·\widehat{k}\\ & =I_{{\mathrm{C}}_k}{\ddot{\mathsf{\theta }}}_k+{\mathrm{J}}_k{\mathrm{C}}_k\times m_k{\overrightarrow{a}}_{{\mathrm{C}}_k}·\widehat{k}\end{array}$$

(15)

To regroup the muscle force moments, the sum involving the muscle forces ${\overrightarrow{F}}_{j_2{j}_1}^m$ is split into three terms:

$$\begin{array}{cc}\hfill {\mathrm{J}}_k{\mathrm{J}}_{k+1}\times {\displaystyle \underset{\left(j_2\le n\right)}{\overset{k+n_{\mathrm{s}}}{{\displaystyle \sum }_{j_2=k+1}}}}& {\displaystyle \underset{\left(j_1\ge 0\right)}{\overset{k}{{\displaystyle \sum }_{j_1=j_2-n_{\mathrm{s}}}}}}\left({\displaystyle {\displaystyle \sum }_m}{\overrightarrow{F}}_{j_2{j}_1}^m\right)={\displaystyle \underset{\left(j_2\le n\right)}{\overset{k+n_{\mathrm{s}}}{{\displaystyle \sum }_{j_2=k+1}}}}{\displaystyle \underset{\left(j_1\ge 0\right)}{\overset{k}{{\displaystyle \sum }_{j_1=j_2-n_{\mathrm{s}}}}}}\left({\displaystyle {\displaystyle \sum }_m}{\mathrm{J}}_k{\mathrm{P}}_{j_2{j}_1}^m\times {\overrightarrow{F}}_{j_2{j}_1}^m\right)+{\displaystyle \underset{\left(j_2\le n\right)}{\overset{k+n_{\mathrm{S}}}{{\displaystyle \sum }_{j_2=k+1}}}}{\displaystyle {\displaystyle \sum }_{\begin{array}{c}{j}_1=j_2-n_{\mathrm{S}}\\ \left(j_1\ge 0\right)\end{array}}^k}\left({\displaystyle {\displaystyle \sum }_m}{\mathrm{P}}_{j_2{j}_1}^m{\mathrm{J}}_{k+1}\times {\overrightarrow{F}}_{j_2{j}_1}^m\right)\hfill \\ & ={\displaystyle \underset{\left(j_2\le n\right)}{\overset{k+n_{\mathrm{S}}}{{\displaystyle \sum }_{j_2=k+1}}}}\left({\displaystyle {\displaystyle \sum }_m}{\mathrm{J}}_k{\mathrm{P}}_{j_{2}k}^m\times {\overrightarrow{F}}_{j_{2}k}^m\right)+{\displaystyle \underset{\left(j_2\le n\right)}{\overset{k+n_{\mathrm{s}}-1}{{\displaystyle \sum }_{j_2=k+1}}}}{\displaystyle {\displaystyle \sum }_{\begin{array}{c}{j}_1=j_2-n_{\mathrm{s}}\\ \left(j_1\ge 0\right)\end{array}}^{k-1}}\left({\displaystyle {\displaystyle \sum }_m}{\mathrm{J}}_k{\mathrm{P}}_{j_2{j}_1}^m\times {\overrightarrow{F}}_{j_2{j}_1}^m\right)\\ & -{\displaystyle \underset{\left(j_2\le n\right)}{\overset{k+n_{\mathrm{s}}}{{\displaystyle \sum }_{j_2=k+1}}}}{\displaystyle {\displaystyle \sum }_{\begin{array}{c}{j}_1=j_2-n_{\mathrm{s}}\\ \left(j_1\ge 0\right)\end{array}}^k}\left({\displaystyle {\displaystyle \sum }_m}{\mathrm{J}}_{k+1}{\mathrm{P}}_{j_2{j}_1}^m\times {\overrightarrow{F}}_{j_2{j}_1}^m\right)\end{array}$$

The moments of all muscle forces in Equations (14) and (15) can then be rewritten as

$$\begin{array}{cc}\hfill {\displaystyle \underset{\left(j\ge 0\right)}{\overset{k-1}{{\displaystyle \sum }_{j=k-n_{\mathrm{s}}}}}}({\displaystyle {\displaystyle \sum }_m}{\mathrm{J}}_k{\mathrm{P}}_{kj}^m& \times {\overrightarrow{F}}_{kj}^m)\cdot \widehat{k}+{\displaystyle \underset{\left(j\le n\right)}{\overset{k+n_{\mathrm{s}}}{{\displaystyle \sum }_{j=k+1}}}}\left({\displaystyle {\displaystyle \sum }_m}{\mathrm{J}}_k{\mathrm{P}}_{kj}^m\times {\overrightarrow{F}}_{kj}^m\right)+{\mathrm{J}}_k{\mathrm{J}}_{k+1}\times {\displaystyle \underset{\left(j_2\le n\right)}{\overset{k+n_{\mathrm{s}}}{{\displaystyle \sum }_{j_2=k+1}}}}{\displaystyle {\displaystyle \sum }_{\begin{array}{c}{j}_1=j_2-n_{\mathrm{s}}\\ \left(j_1\ge 0\right)\end{array}}^k}\left({\displaystyle {\displaystyle \sum }_m}{\overrightarrow{F}}_{j_2{j}_1}^m\right)\hfill \\ & ={\displaystyle \underset{\left(j\ge 0\right)}{\overset{k-1}{{\displaystyle \sum }_{j=k-n_{\mathrm{s}}}}}}\left({\displaystyle {\displaystyle \sum }_m}{\mathrm{J}}_k{\mathrm{P}}_{kj}^m\times {\overrightarrow{F}}_{kj}^m\right)\cdot \widehat{k}-{\displaystyle \underset{\left(j\le n\right)}{\overset{k+n_{\mathrm{s}}}{{\displaystyle \sum }_{j=k+1}}}}\left({\displaystyle {\displaystyle \sum }_m}{\mathrm{J}}_k{\mathrm{P}}_{jk}^m\times {\overrightarrow{F}}_{jk}^m\right)+{\displaystyle {\displaystyle \sum }_{\begin{array}{c}{j}_2=k+1\\ \left(j_2\le n\right)\end{array}}^{k+n_{\mathrm{s}}}}\left({\displaystyle {\displaystyle \sum }_m}{\mathrm{J}}_k{\mathrm{P}}_{j_{2}k}^m\times {\overrightarrow{F}}_{j_{2}k}^m\right)\\ & +{\displaystyle \underset{\left(j_2\le n\right)}{\overset{k+n_{\mathrm{s}}-1}{{\displaystyle \sum }_{j_2=k+1}}}}{\displaystyle \underset{\left(j_1\ge 0\right)}{\overset{k-1}{{\displaystyle \sum }_{j_1=j_2-n_{\mathrm{s}}}}}}\left({\displaystyle {\displaystyle \sum }_m}{\mathrm{J}}_k{\mathrm{P}}_{j_2{j}_1}^m\times {\overrightarrow{F}}_{j_2{j}_1}^m\right)-{\displaystyle \underset{\left(j_2\le n\right)}{\overset{k+n_{\mathrm{s}}}{{\displaystyle \sum }_{j_2=k+1}}}}{\displaystyle {\displaystyle \sum }_{\begin{array}{c}{j}_1=j_2-n_{\mathrm{s}}\\ \left(j_1\ge 0\right)\end{array}}^k}\left({\displaystyle {\displaystyle \sum }_m}{\mathrm{J}}_{k+1}{\mathrm{P}}_{j_2{j}_1}^m\times {\overrightarrow{F}}_{j_2{j}_1}^m\right)\\ & ={\displaystyle \underset{\left(j_2\le n\right)}{\overset{k+n_{\mathrm{s}}-1}{{\displaystyle \sum }_{j_2=k}}}}{\displaystyle \underset{\left(j_1\ge 0\right)}{\overset{k-1}{{\displaystyle \sum }_{j_1=j_2-n_{\mathrm{s}}}}}}\left({\displaystyle {\displaystyle \sum }_m}{\mathrm{J}}_k{\mathrm{P}}_{j_2{j}_1}^m\times {\overrightarrow{F}}_{j_2{j}_1}^m\right)-{\displaystyle \underset{\left(j_2\le n\right)}{\overset{k+n_{\mathrm{s}}}{{\displaystyle \sum }_{j_2=k+1}}}}{\displaystyle {\displaystyle \sum }_{\begin{array}{c}{j}_1=j_2-n_{\mathrm{s}}\\ \left(j_1\ge 0\right)\end{array}}^k}\left({\displaystyle {\displaystyle \sum }_m}{\mathrm{J}}_{k+1}{\mathrm{P}}_{j_2{j}_1}^m\times {\overrightarrow{F}}_{j_2{j}_1}^m\right)\end{array}$$

(16)

The inertial factors ${\mathrm{J}}_k{\mathrm{C}}_k\times m_k{\overrightarrow{a}}_{{\mathrm{C}}_k}·\widehat{k}$, ${\mathrm{J}}_k{\mathrm{J}}_{k+1}\times {{\displaystyle \sum }}_{i=k+1}^n{m}_i{\overrightarrow{a}}_{{\mathrm{C}}_i}·\widehat{k}$, and ${\mathrm{J}}_k{\mathrm{J}}_{k+1}\times {{\displaystyle \sum }}_{i=0}^k{m}_i{\overrightarrow{a}}_{{\mathrm{C}}_i}·\widehat{k}$ (where ${\mathrm{J}}_k{\mathrm{C}}_k=l_{{\mathrm{C}}_k}{\widehat{u}}_{{\mathrm{C}}_k}$ and ${\mathrm{J}}_k{\mathrm{J}}_{k+1}=l_k{\widehat{u}}_k$) in Equations (14) and (15) are readily deduced from Equations (5)–(7), respectively $({\mathsf{\theta }}_0={\dot{\mathsf{\theta }}}_0={\ddot{\mathsf{\theta }}}_0=0)$:

$${\mathrm{J}}_k{\mathrm{C}}_k\times m_k{\overrightarrow{a}}_{{\mathrm{C}}_k}·\widehat{k}=m_k{l}_{{\mathrm{C}}_k}{\displaystyle \sum }_{i=0}^{k-1}{l}_i[{\ddot{\mathsf{\theta }}}_i\cos \left({\mathsf{\theta }}_k+{\mathsf{\epsilon }}_{{\mathrm{C}}_k}-{\mathsf{\theta }}_i\right)+{\dot{\mathsf{\theta }}}_i^2\sin \left({\mathsf{\theta }}_k+{\mathsf{\epsilon }}_{{\mathrm{C}}_k}-{\mathsf{\theta }}_i\right)]+m_k{l}_{{\mathrm{C}}_k}^2{\ddot{\mathsf{\theta }}}_k\left(k=1,\dots ,n\right)$$

(17)

$$\begin{array}{cc}\hfill {\mathrm{J}}_k{\mathrm{J}}_{k+i}\times {\displaystyle {\displaystyle \sum }_{i=k+1}^n}{m}_i& {\overrightarrow{a}}_{{\mathrm{C}}_i}·\widehat{k}\hfill \\ & =l_k\left({\displaystyle {\displaystyle \sum }_{j=k+1}^n}{m}_j\right){\displaystyle {\displaystyle \sum }_{i=0}^{k-1}}{l}_i[{\ddot{\mathsf{\theta }}}_i\cos \left({\mathsf{\theta }}_k-{\mathsf{\theta }}_i\right)+{\dot{\mathsf{\theta }}}_i^2\sin \left({\mathsf{\theta }}_k-{\mathsf{\theta }}_i\right)]+\left({\displaystyle {\displaystyle \sum }_{j=k+1}^n}{m}_j\right)l_k^2{\ddot{\mathsf{\theta }}}_k\\ & +\left(1-{\mathsf{\delta }}_{k,n-1}\right)l_k{\displaystyle {\displaystyle \sum }_{i=k+1}^{n-1}}\left({\displaystyle {\displaystyle \sum }_{j=i+1}^n}{m}_j\right)l_i[{\ddot{\mathsf{\theta }}}_i\cos \left({\mathsf{\theta }}_i-{\mathsf{\theta }}_k\right)-{\dot{\mathsf{\theta }}}_i^2\sin \left({\mathsf{\theta }}_i-{\mathsf{\theta }}_k\right)]\\ & +l_k{\displaystyle {\displaystyle \sum }_{i=k+1}^n}{m}_i{l}_{{\mathrm{C}}_i}[{\ddot{\mathsf{\theta }}}_i\cos \left({\mathsf{\theta }}_i+{\mathsf{\epsilon }}_{{\mathrm{C}}_i}-{\mathsf{\theta }}_k\right)-{\dot{\mathsf{\theta }}}_i^2\sin \left({\mathsf{\theta }}_i+{\mathsf{\epsilon }}_{{\mathrm{C}}_i}-{\mathsf{\theta }}_k\right)]\left(k=1,\dots ,n-1\right)\end{array}$$

(18)

$$\begin{array}{cc}\hfill {\mathrm{J}}_k{\mathrm{J}}_{k+i}\times {\displaystyle {\displaystyle \sum }_{i=0}^k}{m}_i{\overrightarrow{a}}_{{\mathrm{C}}_i}& ·\widehat{k}\hfill \\ & =l_k{\displaystyle {\displaystyle \sum }_{i=0}^{k-1}}\left({\displaystyle {\displaystyle \sum }_{j=i+1}^k}{m}_j\right)l_i[{\ddot{\mathsf{\theta }}}_i\cos \left({\mathsf{\theta }}_k-{\mathsf{\theta }}_i\right)+{\dot{\mathsf{\theta }}}_i^2\sin \left({\mathsf{\theta }}_k-{\mathsf{\theta }}_i\right)]\\ & +l_k{\displaystyle {\displaystyle \sum }_{i=1}^k}{m}_i{l}_{{\mathrm{C}}_i}[{\ddot{\mathsf{\theta }}}_i\cos \left({\mathsf{\theta }}_k-{\mathsf{\theta }}_i-{\mathsf{\epsilon }}_{{\mathrm{C}}_i}\right)+{\dot{\mathsf{\theta }}}_i^2\sin \left({\mathsf{\theta }}_k-{\mathsf{\theta }}_i-{\mathsf{\epsilon }}_{{\mathrm{C}}_i}\right)]\left(k=1,\dots ,n\right)\end{array}$$

(19)

Equations (14) and (15), considering Equations (16)−(19), result in the following two equivalent moment equations for the individual link k $\left(k=1,2,\dots ,n-1\right)$

$$\begin{array}{cc}\hfill {\displaystyle \underset{\left(j_2\le n\right)}{\overset{k+n_{\mathrm{s}}-1}{{\displaystyle \sum }_{j_2=k}}}}{\displaystyle \underset{\left(j_1\ge 0\right)}{\overset{k-1}{{\displaystyle \sum }_{j_1=j_2-n_{\mathrm{s}}}}}}& \left({\displaystyle {\displaystyle \sum }_m}{\mathrm{J}}_k{\mathrm{P}}_{j_2{j}_1}^m\times {\overrightarrow{F}}_{j_2{j}_1}^m\right)\cdot \widehat{k}-{\displaystyle \underset{\left(j_2\le n\right)}{\overset{k+n_{\mathrm{s}}}{{\displaystyle \sum }_{j_2=k+1}}}}{\displaystyle {\displaystyle \sum }_{\begin{array}{c}{j}_1=j_2-n_{\mathrm{s}}\\ \left(j_1\ge 0\right)\end{array}}^k}\left({\displaystyle {\displaystyle \sum }_m}{\mathrm{J}}_{k+1}{\mathrm{P}}_{j_2{j}_1}^m\times {\overrightarrow{F}}_{j_2{j}_1}^m\right)\cdot \widehat{k}-m_{k}g{l}_{{\mathrm{C}}_k}\cos \left({\mathsf{\theta }}_k+{\mathsf{\epsilon }}_{{\mathrm{C}}_k}\right)\hfill \\ & +R_k{l}_{R_k}\sin \left({\mathsf{\gamma }}_{R_k}-{\mathsf{\epsilon }}_{R_k}\right)+{\displaystyle {\displaystyle \sum }_{i=k+1}^n}[-m_{i}g{l}_k\cos {\mathsf{\theta }}_k+R_i{l}_k\sin \left({\mathsf{\gamma }}_{R_i}+{\mathsf{\theta }}_i-{\mathsf{\theta }}_k\right)]\\ & =m_k{l}_{{\mathrm{C}}_k}{\displaystyle {\displaystyle \sum }_{i=0}^{k-1}}{l}_i[{\ddot{\mathsf{\theta }}}_i\cos \left({\mathsf{\theta }}_k+{\mathsf{\epsilon }}_{{\mathrm{C}}_k}-{\mathsf{\theta }}_i\right)+{\dot{\mathsf{\theta }}}_i^2\sin \left({\mathsf{\theta }}_k+{\mathsf{\epsilon }}_{{\mathrm{C}}_k}-{\mathsf{\theta }}_i\right)]\\ & +l_k\left({\displaystyle {\displaystyle \sum }_{j=k+1}^n}{m}_j\right){\displaystyle {\displaystyle \sum }_{i=0}^{k-1}}{l}_i[{\ddot{\mathsf{\theta }}}_i\cos \left({\mathsf{\theta }}_k-{\mathsf{\theta }}_i\right)+{\dot{\mathsf{\theta }}}_i^2\sin \left({\mathsf{\theta }}_k-{\mathsf{\theta }}_i\right)]+\left(I_{{\mathrm{J}}_k}+{\displaystyle {\displaystyle \sum }_{j=k+1}^n}{m}_j\cdot l_k^2\right){\ddot{\mathsf{\theta }}}_k\\ & +\left(1-{\mathsf{\delta }}_{k,n-1}\right)l_k{\displaystyle {\displaystyle \sum }_{i=k+1}^{n-1}}\left({\displaystyle {\displaystyle \sum }_{j=i+1}^n}{m}_j\right)l_i[{\ddot{\mathsf{\theta }}}_i\cos \left({\mathsf{\theta }}_i-{\mathsf{\theta }}_k\right)-{\dot{\mathsf{\theta }}}_i^2\sin \left({\mathsf{\theta }}_i-{\mathsf{\theta }}_k\right)]\\ & +l_k{\displaystyle {\displaystyle \sum }_{i=k+1}^n}{m}_i{l}_{{\mathrm{C}}_i}[{\ddot{\mathsf{\theta }}}_i\cos \left({\mathsf{\theta }}_i+{\mathsf{\epsilon }}_{{\mathrm{C}}_i}-{\mathsf{\theta }}_k\right)-{\dot{\mathsf{\theta }}}_i^2\sin \left({\mathsf{\theta }}_i+{\mathsf{\epsilon }}_{{\mathrm{C}}_i}-{\mathsf{\theta }}_k\right)]\end{array}$$

(20)

$$\begin{array}{cc}\hfill {\displaystyle \underset{\left(j_2\le n\right)}{\overset{k+n_{\mathrm{s}}-1}{{\displaystyle \sum }_{j_2=k}}}}{\displaystyle \underset{\left(j_1\ge 0\right)}{\overset{k-1}{{\displaystyle \sum }_{j_1=j_2-n_{\mathrm{s}}}}}}& \left({\displaystyle {\displaystyle \sum }_m}{\mathrm{J}}_k{\mathrm{P}}_{j_2{j}_1}^m\times {\overrightarrow{F}}_{j_2{j}_1}^m\right)\cdot \widehat{k}-{\displaystyle \underset{\left(j_2\le n\right)}{\overset{k+n_{\mathrm{s}}}{{\displaystyle \sum }_{j_2=k+1}}}}{\displaystyle \underset{\left(j_1\ge 0\right)}{\overset{k}{{\displaystyle \sum }_{j_1=j_2-n_{\mathrm{s}}}}}}\left({\displaystyle {\displaystyle \sum }_m}{\mathrm{J}}_{k+1}{\mathrm{P}}_{j_2{j}_1}^m\times {\overrightarrow{F}}_{j_2{j}_1}^m\right)\cdot \widehat{k}-m_{k}g{l}_{{\mathrm{C}}_k}\cos \left({\mathsf{\theta }}_k+{\mathsf{\epsilon }}_{{\mathrm{C}}_k}\right)\hfill \\ & +R_k{l}_{R_k}\sin \left({\mathsf{\gamma }}_{R_k}-{\mathsf{\epsilon }}_{R_k}\right)+{\displaystyle {\displaystyle \sum }_{i=0}^k}\left[m_{i}g{l}_k\cos {\mathsf{\theta }}_k-R_i{l}_k\sin \left({\mathsf{\gamma }}_{R_i}+{\mathsf{\theta }}_i-{\mathsf{\theta }}_k\right)\right]\\ & =m_k{l}_{{\mathrm{C}}_k}{\displaystyle {\displaystyle \sum }_{i=0}^{k-1}}{l}_i[{\ddot{\mathsf{\theta }}}_i\cos \left({\mathsf{\theta }}_k+{\mathsf{\epsilon }}_{{\mathrm{C}}_k}-{\mathsf{\theta }}_i\right)+{\dot{\mathsf{\theta }}}_i^2\sin \left({\mathsf{\theta }}_k+{\mathsf{\epsilon }}_{{\mathrm{C}}_k}-{\mathsf{\theta }}_i\right)]\\ & -l_k{\displaystyle {\displaystyle \sum }_{i=0}^{k-1}}\left({\displaystyle {\displaystyle \sum }_{j=i+1}^k}{m}_j\right)l_i[{\ddot{\mathsf{\theta }}}_i\cos \left({\mathsf{\theta }}_k-{\mathsf{\theta }}_i\right)+{\dot{\mathsf{\theta }}}_i^2\sin \left({\mathsf{\theta }}_k-{\mathsf{\theta }}_i\right)]+I_{{\mathrm{J}}_k}{\ddot{\mathsf{\theta }}}_k\\ & -l_k{\displaystyle {\displaystyle \sum }_{i=1}^k}{m}_i{l}_{{\mathrm{C}}_i}[{\ddot{\mathsf{\theta }}}_i\cos \left({\mathsf{\theta }}_k-{\mathsf{\theta }}_i-{\mathsf{\epsilon }}_{{\mathrm{C}}_i}\right)+{\dot{\mathsf{\theta }}}_i^2\sin \left({\mathsf{\theta }}_k-{\mathsf{\theta }}_i-{\mathsf{\epsilon }}_{{\mathrm{C}}_i}\right)]\end{array}$$

(21)

The first term on the left-hand side of Equations (20) and (21) represents the moment ${\mathsf{\tau }}_k$ about ${\mathrm{J}}_k$ of the muscle forces exerted on the links distal to joint k by the single-joint and multi-joint muscles that span joint k

$${\mathsf{\tau }}_k={\displaystyle \sum }_{\begin{array}{c}{j}_2=k\\ \left(j_2\le n\right)\end{array}}^{k+n_{\mathrm{s}}-1}{\displaystyle \sum }_{\begin{array}{c}{j}_1=j_2-n_{\mathrm{s}}\\ \left(j_1\ge 0\right)\end{array}}^{k-1}\left({\displaystyle \sum }_m{\mathrm{J}}_k{\mathrm{P}}_{j_2{j}_1}^m\times {\overrightarrow{F}}_{j_2{j}_1}^m\right)·\widehat{k}$$

(22)

The second term, ${\mathsf{\tau }}_{k+1}$, has the same meaning but refers to joint k + 1.

The final step is the determination of the closed-form expression of each single torques ${\mathsf{\tau }}_k$ ($k=1,2,\dots ,n-1$), instead of the differences ${\mathsf{\tau }}_k-{\mathsf{\tau }}_{k+1}$. The distal torque ${\mathsf{\tau }}_n$ has already been determined by Equation (13). Adding together the moment Equation (20) or (21) with $k=k^{*},k^{*}+1,\dots ,n$ gives two equivalent expressions for ${\mathsf{\tau }}_{k^{*}}$

$$\begin{array}{cc}\hfill {\mathsf{\tau }}_{k^{*}}& ={\displaystyle \underset{\left(j_2\le n\right)}{\overset{k^{*}+n_{\mathrm{s}}-1}{{\displaystyle \sum }_{j_2=k^{*}}}}}{\displaystyle \underset{\left(j_1\ge 0\right)}{\overset{k^{*}-1}{{\displaystyle \sum }_{j_1=j_2-n_{\mathrm{s}}}}}}\left({\displaystyle {\displaystyle \sum }_m}{\mathrm{J}}_{k^{*}}{\mathrm{P}}_{j_2{j}_1}^m\times {\overrightarrow{F}}_{j_2{j}_1}^m\right)·\widehat{k}\hfill \\ & ={\displaystyle {\displaystyle \sum }_{k=k^{*}}^n}\left[m_{k}g{l}_{{\mathrm{C}}_k}\cos \left({\mathsf{\theta }}_k+{\mathsf{\epsilon }}_{{\mathrm{C}}_k}\right)-R_k{l}_{R_k}\sin \left({\mathsf{\gamma }}_{R_k}-{\mathsf{\epsilon }}_{R_k}\right)\right]\\ & +{\displaystyle {\displaystyle \sum }_{k=k^{*}}^{n-1}}{\displaystyle {\displaystyle \sum }_{i=k+1}^n}\left[m_{i}g{l}_k\cos {\mathsf{\theta }}_k-R_i{l}_k\sin \left({\mathsf{\gamma }}_{R_i}+{\mathsf{\theta }}_i-{\mathsf{\theta }}_k\right)\right]\\ & +{\displaystyle {\displaystyle \sum }_{k=k^{*}}^n}{m}_k{l}_{{\mathrm{C}}_k}{\displaystyle {\displaystyle \sum }_{i=0}^{k-1}}{l}_i[{\ddot{\mathsf{\theta }}}_i\cos \left({\mathsf{\theta }}_k+{\mathsf{\epsilon }}_{{\mathrm{C}}_k}-{\mathsf{\theta }}_i\right)+{\dot{\mathsf{\theta }}}_i^2\sin \left({\mathsf{\theta }}_k+{\mathsf{\epsilon }}_{{\mathrm{C}}_k}-{\mathsf{\theta }}_i\right)]\\ & +{\displaystyle {\displaystyle \sum }_{k=k^{*}}^{n-1}}{l}_k\left({\displaystyle {\displaystyle \sum }_{j=k+1}^n}{m}_j\right){\displaystyle {\displaystyle \sum }_{i=0}^{k-1}}{l}_i[{\ddot{\mathsf{\theta }}}_i\cos \left({\mathsf{\theta }}_k-{\mathsf{\theta }}_i\right)+{\dot{\mathsf{\theta }}}_i^2\sin \left({\mathsf{\theta }}_k-{\mathsf{\theta }}_i\right)]\\ & +{\displaystyle {\displaystyle \sum }_{k=k^{*}}^{n-1}}\left(I_{{\mathrm{J}}_k}+{\displaystyle {\displaystyle \sum }_{j=k+1}^n}{m}_j\cdot l_k^2\right){\ddot{\mathsf{\theta }}}_k+I_{{\mathrm{J}}_n}{\ddot{\mathsf{\theta }}}_n\\ & +{\displaystyle {\displaystyle \sum }_{k=k^{*}}^{n-1}}\left(1-{\mathsf{\delta }}_{k,n-1}\right)l_k{\displaystyle {\displaystyle \sum }_{i=k+1}^{n-1}}\left({\displaystyle {\displaystyle \sum }_{j=i+1}^n}{m}_j\right)l_i[{\ddot{\mathsf{\theta }}}_i\cos \left({\mathsf{\theta }}_i-{\mathsf{\theta }}_k\right)-{\dot{\mathsf{\theta }}}_i^2\sin \left({\mathsf{\theta }}_i-{\mathsf{\theta }}_k\right)]\\ & +{\displaystyle {\displaystyle \sum }_{k=k^{*}}^{n-1}}{l}_k{\displaystyle {\displaystyle \sum }_{i=k+1}^n}{m}_i{l}_{{\mathrm{C}}_i}[{\ddot{\mathsf{\theta }}}_i\cos \left({\mathsf{\theta }}_i+{\mathsf{\epsilon }}_{{\mathrm{C}}_i}-{\mathsf{\theta }}_k\right)-{\dot{\mathsf{\theta }}}_i^2\sin \left({\mathsf{\theta }}_i+{\mathsf{\epsilon }}_{{\mathrm{C}}_i}-{\mathsf{\theta }}_k\right)]\end{array}$$

(23)

$$\begin{array}{cc}\hfill {\mathsf{\tau }}_{k^{*}}& ={\displaystyle \underset{\left(j_2\le n\right)}{\overset{k^{*}+n_{\mathrm{s}}-1}{{\displaystyle \sum }_{j_2=k^{*}}}}}{\displaystyle {\displaystyle \sum }_{\begin{array}{c}{j}_1=j_2-n_{\mathrm{s}}\\ \left(j_1\ge 0\right)\end{array}}^{k^{*}-1}}\left({\displaystyle {\displaystyle \sum }_m}{\mathrm{J}}_{k*}{\mathrm{P}}_{j_2{j}_1}^m\times {\overrightarrow{F}}_{j_2{j}_1}^m\right)·\widehat{k}\hfill \\ & ={\displaystyle {\displaystyle \sum }_{k=k^{*}}^n}[m_{k}g{l}_{{\mathrm{C}}_k}\cos \left({\mathsf{\theta }}_k+{\mathsf{\epsilon }}_{{\mathrm{C}}_k}\right)-R_k{l}_{R_k}\sin \left({\mathsf{\gamma }}_{R_k}-{\mathsf{\epsilon }}_{R_k}\right)]\\ & -{\displaystyle {\displaystyle \sum }_{k=k^{*}}^{n-1}}{\displaystyle {\displaystyle \sum }_{i=0}^k}[m_{i}g{l}_k\cos {\mathsf{\theta }}_k-R_i{l}_k\sin \left({\mathsf{\gamma }}_{R_i}+{\mathsf{\theta }}_i-{\mathsf{\theta }}_k\right)]\\ & +{\displaystyle {\displaystyle \sum }_{k=k^{*}}^n}{m}_k{l}_{{\mathrm{C}}_k}{\displaystyle {\displaystyle \sum }_{i=0}^{k-1}}{l}_i[{\ddot{\mathsf{\theta }}}_i\cos \left({\mathsf{\theta }}_k+{\mathsf{\epsilon }}_{{\mathrm{C}}_k}-{\mathsf{\theta }}_i\right)+{\dot{\mathsf{\theta }}}_i^2\sin \left({\mathsf{\theta }}_k+{\mathsf{\epsilon }}_{{\mathrm{C}}_k}-{\mathsf{\theta }}_i\right)]\\ & -{\displaystyle {\displaystyle \sum }_{k=k^{*}}^{n-1}}{l}_k{\displaystyle {\displaystyle \sum }_{i=0}^{k-1}}\left({\displaystyle {\displaystyle \sum }_{j=i+1}^k}{m}_j\right)l_i[{\ddot{\mathsf{\theta }}}_i\cos \left({\mathsf{\theta }}_k-{\mathsf{\theta }}_i\right)+{\dot{\mathsf{\theta }}}_i^2\sin \left({\mathsf{\theta }}_k-{\mathsf{\theta }}_i\right)]+{\displaystyle {\displaystyle \sum }_{k=k*}^n}{I}_{{\mathrm{J}}_k}{\ddot{\mathsf{\theta }}}_k\\ & -{\displaystyle {\displaystyle \sum }_{k=k^{*}}^{n-1}}{l}_k{\displaystyle {\displaystyle \sum }_{i=1}^k}{m}_i{l}_{{\mathrm{C}}_i}[{\ddot{\mathsf{\theta }}}_i\cos \left({\mathsf{\theta }}_k-{\mathsf{\theta }}_i-{\mathsf{\epsilon }}_{{\mathrm{C}}_i}\right)+{\dot{\mathsf{\theta }}}_i^2\sin \left({\mathsf{\theta }}_k-{\mathsf{\theta }}_i-{\mathsf{\epsilon }}_{{\mathrm{C}}_i}\right)]\end{array}$$

(24)

In Appendix A, these equations are compared to the corresponding equations reported for chains driven by ideal torque actuators and composed of two or three links modeled as slender roads.

3. Discussion

We have derived the closed-form dynamic equations and joint reaction forces for a planar musculoskeletal chain, composed of a generic number n of rigid links of generic shape and size, and driven by single-joint and multi-joint muscle actuators that can span from one joint to all the joints of the chain. These closed-form analytical equations can be applied to multilink musculoskeletal chains with deep/superficial and segmental/global muscles.

Equations (8)–(11) highlight that the joint reaction force ${\overrightarrow{\mathsf{\varphi }}}_{k,k+1}$ exerted by link k + 1 on link k through joint k + 1 is determined by the forces ${\overrightarrow{F}}_{ij}^m$ of single-joint and multi-joint muscles spanning the joint ($i\le k$ and $j\ge k+1)$, with an additional one of the following two equivalent sets of data: (1) the angular velocity and acceleration of each individual link of the chain (link 1 to link n), and the weight and the contact external resistance acting on each link distal to the joint (link k + 1 to link n); (2) the angular velocity and acceleration of each link proximal to the joint (link 1 to link k), and the weight and contact external resistance acting on these links and the base (link 0 to link k). The choice of data set depends on the unknown contact external forces ${\overrightarrow{R}}_i$. For example, in many strengthening exercises executed lying down or sitting on a bench, the force acting on the base ${\overrightarrow{R}}_0$ is the only unknown contact external force, and the joint reaction forces can be determined using the first set of data (Equation (9)). In contrast, in the dynamic wall-squat exercise [19], the force exerted by the wall on the back is unknown, and the load acting on the lower-limb joints can be determined using the second set of data, provided that the ground reaction force ${\overrightarrow{R}}_0$ is determined by a force plate (Equation (10)). In both cases, the force of the muscles spanning the joint of interest should be properly estimated [20,21,22,23,24], which is beyond the scope of the study.

The reaction force ${\overrightarrow{\mathsf{\varphi }}}_{k,k+1}$ acting on joint k + 1 is indirectly affected by the force ${\overrightarrow{F}}_{ij}^m$ of muscles not spanning the joint ($i<j\le k$ or $k+1\le i<j$). The torque developed by ${\overrightarrow{F}}_{ij}^m$ yields inertial forces on links i and j, which propagate along the chain, contributing to the load acting on each joint (Equation (9)). This is, for example, the case in the effect of the soleus muscle force on the tibiofemoral joint during single-leg landing [25]. Nevertheless, the present study highlights that, in the static condition, a muscle force cannot affect the load acting on joints not spanned by the muscle.

Notably, with the use of the global reference frame, the link angular velocities ${\dot{\mathsf{\theta }}}_i$ occur in the closed-form dynamic equations only through the centripetal terms proportional to ${\dot{\mathsf{\theta }}}_i^2$, avoiding the Coriolis terms proportional to the products of link angular velocities in the local joint frames. This considerably simplifies the closed-form dynamic equations (Appendix A).

The limitations of this study are mainly related to the bidimensional nature of the adopted musculoskeletal chain model. In three dimensions, the mathematic formalism relative to the closed-form dynamic equations of the system becomes extremely complex [4]. An example of such 3D analysis has been recently presented for a six-link chain, with sagittal plane symmetry, to model the biomechanics of the barbell bench press exercise [26].

Another limitation stems from the assumption that only one contact external resistance acts on link i. In general, multiple contact external resistances can simultaneously act on an individual link of the chain. In two dimensions, the system of contact external resistances acting on a link constitutes a co-planar system of forces acting on a rigid body. This system can always be reduced to the resultant force $\overrightarrow{R}$ applied at a point of the central axis (if $\overrightarrow{R}\ne 0$), or to a force couple (if $\overrightarrow{R}=0$). The first case ($\overrightarrow{R}\ne 0$) was considered in this study. In the latter case ($\overrightarrow{R}=0$), the dynamic force equations and the joint reaction forces (Equations (9) and (10)) are not affected by the contact external resistances, while the torque of the equivalent force couple should simply be added to the moment Equations (20) and (21). The 2D reaction forces exerted on link i by link i − 1 constitute a co-planar system of forces acting on a rigid body as well. In general, the resultant ${\overrightarrow{\mathsf{\varphi }}}_{i,i-1}$ of these forces is non-zero in musculoskeletal joints. Therefore, this system of forces was reduced to the vector ${\overrightarrow{\mathsf{\varphi }}}_{i,i-1}$ applied at a point of the central axis. It was assumed that the line of action of this applied vector passes through ${\mathrm{J}}_i$. This implies that the moment of ${\overrightarrow{\mathsf{\varphi }}}_{i,i-1}$ about ${\mathrm{J}}_i$ is zero. In biomechanics, this assumption is often considered acceptable as long as the joint is not close to the extremes of its range of motion [27]. Furthermore, this assumption does not affect the force dynamic equations and the closed-form expression of the joint reaction forces (Equations (9) and (10)).

With these limitations, the analytical results derived in this paper can be applied to the study of the biomechanics of multilink musculoskeletal chains with deep/superficial and segmental/global muscles. One possible use is for modeling spinal dynamics during spine flexion, extension, and lateral flexion movements, where each vertebra is represented as a link. Another possible application that concerns chains with more than three links and deep/superficial multi-joint muscles is related to the flexion/extension movements of the fingers. The extrinsic flexor muscles of the fingers, the flexor digitorum superficialis and flexor digitorum profundus, cross more than three joints, from the elbow to the proximal interphalangeal joint, and from the wrist to the distal interphalangeal joint, respectively. Many natural lower limb movements, such as those occurring during walking, running, and jumping, involve sagittal-plane motion of the hip, knee, ankle, and metatarsophalangeal joints. The dynamics of these movements can be analyzed by Equations (1)–(24), as long as the toes (the basis of the chain) remain in contact with the ground.

It is important to point out that, in contrast to numerical computational models of human motion, the closed-form analytical model established in the present study clearly highlights the functional contribution to the joint forces and torques of each relevant biomechanical parameter (force of each single-joint or multi-joint muscle spanning or non-spanning the joint; weight and contact external resistances acting on each individual link of the chain; position, angular velocity, and angular acceleration of each individual link of the chain). Therefore, the effect of a change in any of these parameters can be readily assessed and understood. Ultimately, with our explicit analytical model, one can readily determine the outcome corresponding to any set of input values, either simulated or estimated experimentally by kinematic and electromyographic measurements and optimization techniques. This might also serve as a theoretical framework for the development of neurophysiological models for the study of neural control over joint movement and functional joint stability [28,29,30,31,32,33] in complex musculoskeletal chains.

4. Conclusions

This study presents a general approach for the closed-form solution to the dynamics of a planar musculoskeletal chain, composed of an arbitrary number n of rigid links of generic shape and size, and driven by single-joint and multi-joint muscle actuators. Specifically, Equations (8)–(13) and (20)–(24) constitute the closed-form expressions of the joint torque and the reaction force acting on each joint of the chain. These results can be applied to the study of the biomechanics of multilink musculoskeletal chains with deep/superficial and segmental/global muscles.