A Composite Metric Routing Approach for Energy-Efficient Shortest Path Planning on Natural Terrains
Abstract
:1. Introduction
- We propose a new greedy (Dijkstra-like) path planning algorithm for UGVs on irregular natural real-life terrains. The algorithm is based on a composite routing metric that combines the distance and energy consumption of the path.
- We consider the vehicle–soil contact Terramechanics in our algorithm, which involves the vehicle structure information and soil composition data. The algorithm also takes realistic soil and slope limitations, UGV power limitations and air humidity into account.
- Our numerical results indicate that the proposed composite metric performs better than the direct energy consumption metric in terms of reducing the overall constructed path distance, with a minimal increment in the energy consumption. Thus, our proposed approsach strikes a better balance between the path distance and energy consumption. Additionally, it is verified that the proposed greedy algorithm strongly outperforms the ACO implementation in terms of both the path distance and consumed energy, and algorithm running time.
- Our numerical running time results demonstrate that our algorithm is well-suited for sizable natural terrain graphs with thousands of nodes and tens of thousands of links.
2. Preliminaries
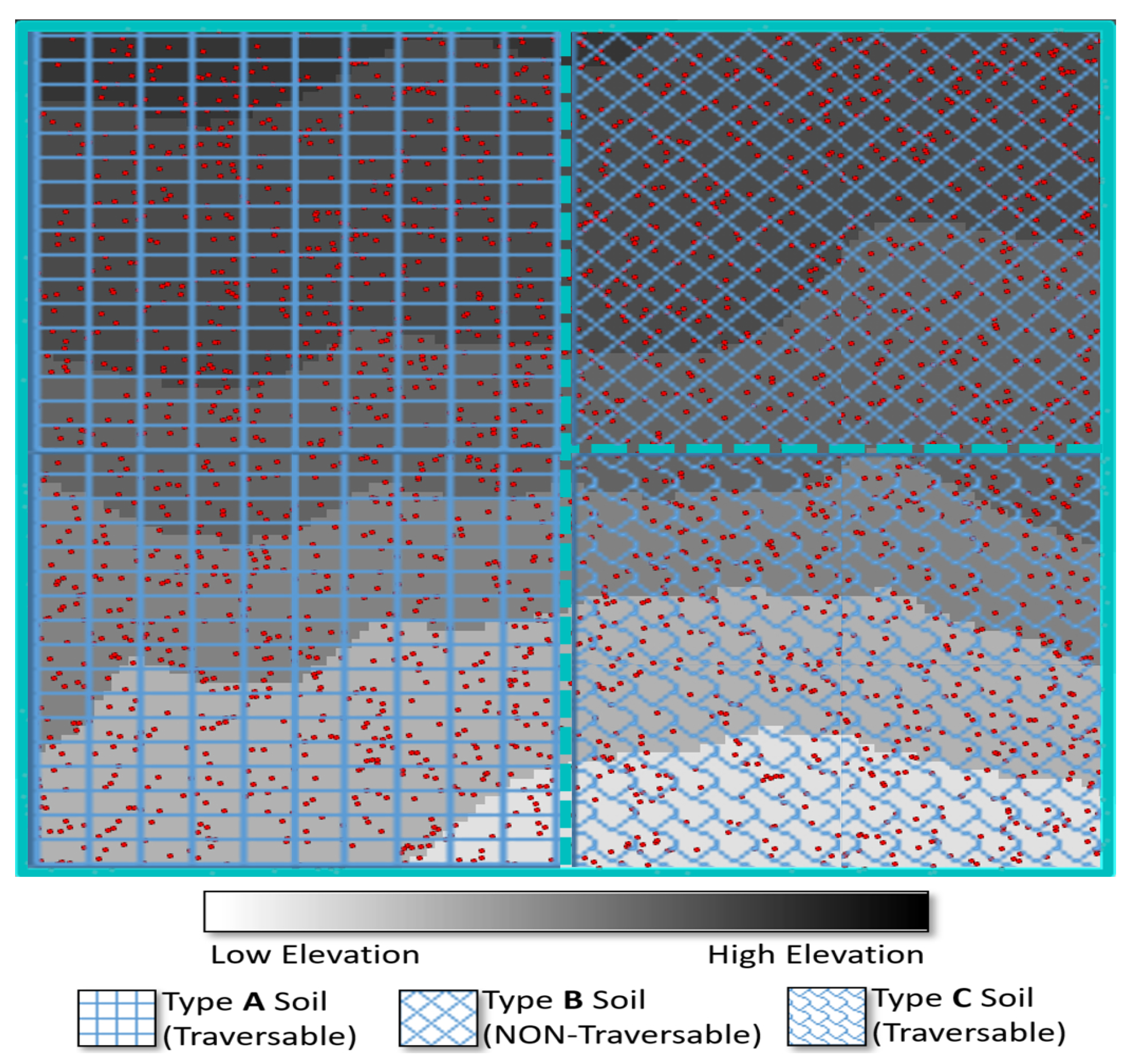
2.1. Soil Trafficability
2.2. Terrain Model Generation
2.3. Distance and Energy-Cost Calculations
3. Composite Metric Routing Approach
3.1. Composite Metric
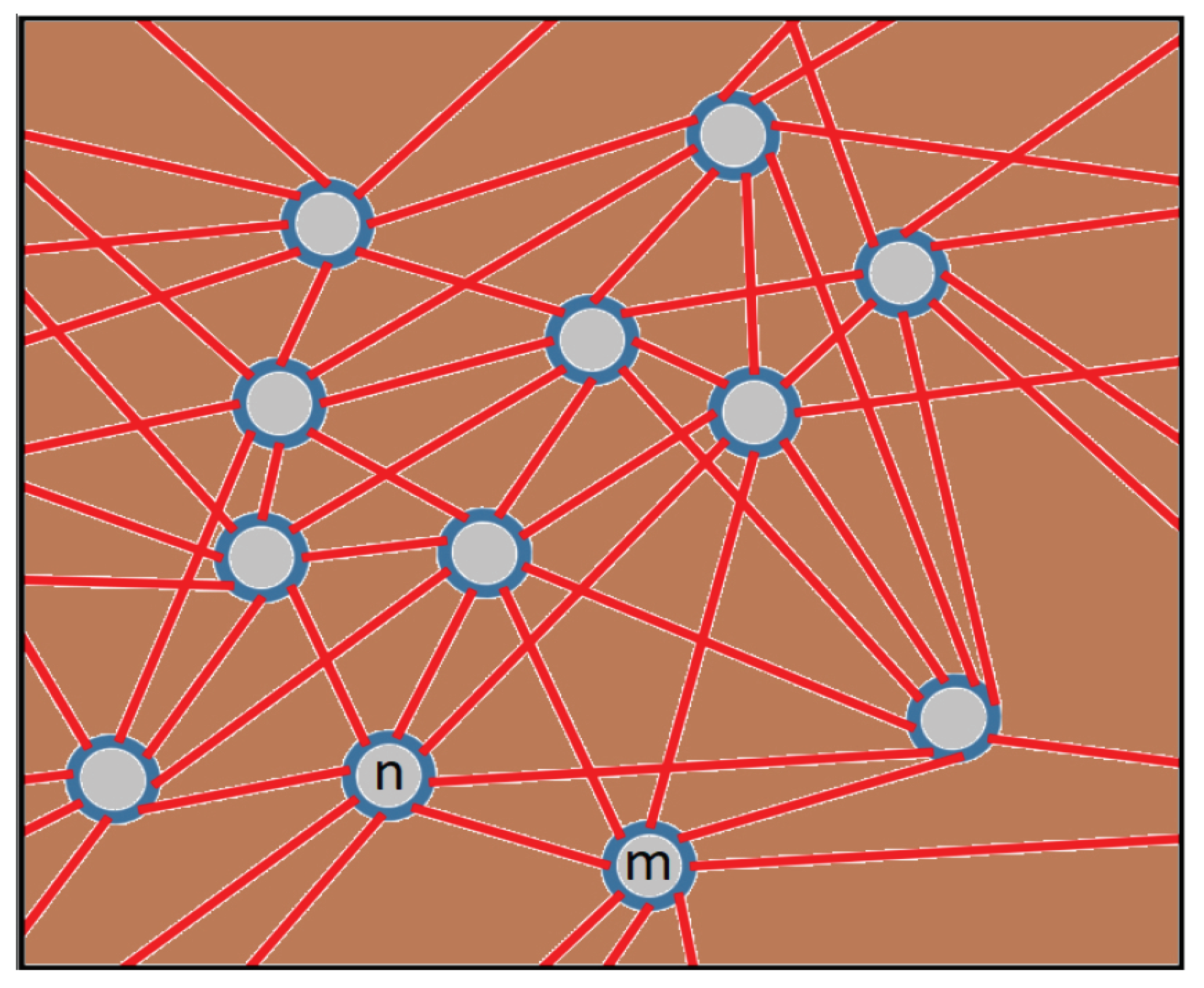
3.2. The Proposed Greedy Implementation
- Source and final (or finish) nodes of the required path, respectively;
- Distance of best path from the source node s to node n;
- energy cost of best path from the source node s to node n;
- Composite Metric of best path from the source node s to node n, i.e., ;
- P Set of nodes for which the best path from s is known;
- Predecessor of node n on the best path from the source node s.
| Algorithm 1:Composite Metric Greedy Implementation |
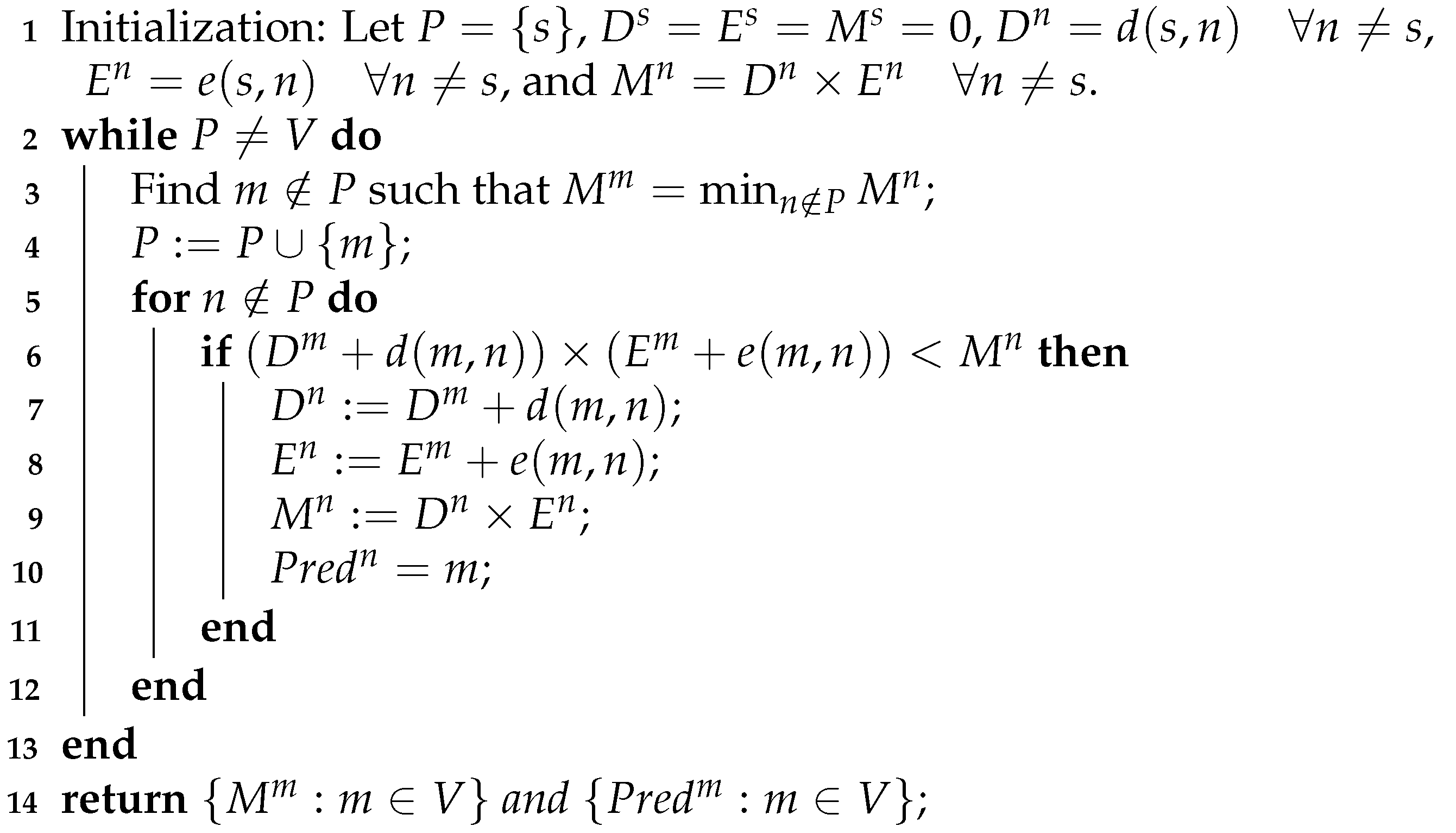 |
- the distance/length of the link;
- the angle of inclination of the link;
- the UGV itself; and
- the soil trafficability component (RCI), which depends on the weather humidity conditions.
4. Results and Discussion
4.1. Benchmarks for Comparison
4.2. Test Setup
4.3. Simulation Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Leighty, R.D. Terrain navigation concepts for autonomous vehicles. In Applications of Artificial Intelligence I; International Society for Optics and Photonics: Bellingham, WA, USA, 1984; Volume 485, pp. 120–125. [Google Scholar]
- Yaqoob, I.; Khan, L.U.; Kazmi, S.A.; Imran, M.; Guizani, N.; Hong, C.S. Autonomous driving cars in smart cities: Recent advances, requirements, and challenges. IEEE Netw. 2019, 34, 174–181. [Google Scholar] [CrossRef]
- Huang, H.; Savkin, A.V.; Ding, M.; Huang, C. Mobile robots in wireless sensor networks: A survey on tasks. Comput. Netw. 2019, 148, 1–19. [Google Scholar] [CrossRef]
- Bold, S.; Sosorbaram, B.; Lee, S.R. Implementation of autonomous unmanned aerial vehicle with moving-object detection and face recognition. In Information Science and Applications (ICISA) 2016; Springer: Berlin, Germany, 2016; pp. 361–370. [Google Scholar]
- Yan, C.; Xiang, X.; Wang, C. Towards real-time path planning through deep reinforcement learning for a uav in dynamic environments. J. Intell. Robot. Syst. 2020, 98, 297–309. [Google Scholar] [CrossRef]
- Ganganath, N.; Cheng, C.T.; Fernando, T.; Iu, H.H.; Tse, C.K. Shortest Path Planning for Energy-Constrained Mobile Platforms Navigating on Uneven Terrains. IEEE Trans. Ind. Inform. 2018, 14, 4264–4272. [Google Scholar] [CrossRef]
- Wu, C.; Dai, C.; Gong, X.; Liu, Y.J.; Wang, J.; Gu, X.; Wang, C.C. Energy-Efficient Coverage Path Planning for General Terrain Surfaces. IEEE Robot. Autom. Lett. 2019, 4, 2584–2591. [Google Scholar] [CrossRef]
- Comin, F.J.; Lewinger, W.A.; Saaj, C.M.; Matthews, M.C. Trafficability assessment of deformable terrain through hybrid wheel-leg sinkage detection. J. Field Robot. 2017, 34, 451–476. [Google Scholar] [CrossRef] [Green Version]
- Priddy, J.D.; Willoughby, W.E. Clarification of vehicle cone index with reference to mean maximum pressure. J. Terramech. 2006, 43, 85–96. [Google Scholar] [CrossRef]
- Kim, S.; Jin, H.; Seo, M.; Har, D. Optimal Path Planning of Automated Guided Vehicle using Dijkstra Algorithm under Dynamic Conditions. In Proceedings of the 2019 7th International Conference on Robot Intelligence Technology and Applications (RiTA), Daejeon, Korea, 1–3 November 2019; pp. 231–236. [Google Scholar]
- Wei, M.; Isler, V. Energy-efficient Path Planning for Ground Robots by and Combining Air and Ground Measurements. In Proceedings of the Conference on Robot Learning, Cambridge, MA, USA, 14–16 November 2020; pp. 766–775. [Google Scholar]
- Aksamentov, E.; Zakharov, K.; Tolopilo, D.; Usina, E. Approach to robotic mobile platform path planning upon analysis of aerial imaging data. In Proceedings of the 15th International Conference on Electromechanics and Robotics “Zavalishin’s Readings”; Springer: Berlin, Germany, 2020; pp. 93–103. [Google Scholar]
- Wallace, N.D.; Kong, H.; Hill, A.J.; Sukkarieh, S. Energy Aware Mission Planning for WMRs on Uneven Terrains. IFAC-PapersOnLine 2019, 52, 149–154. [Google Scholar] [CrossRef]
- Taghavifar, H.; Xu, B.; Taghavifar, L.; Qin, Y. Optimal Path-Planning of Nonholonomic Terrain Robots for Dynamic Obstacle Avoidance Using Single-Time Velocity Estimator and Reinforcement Learning Approach. IEEE Access 2019, 7, 159347–159356. [Google Scholar] [CrossRef]
- Xin, J.; Wei, L.; Wang, D.; Xuan, H. Receding horizon path planning of automated guided vehicles using a time-space network model. Optim. Control. Appl. Methods 2020, 41, 1889–1903. [Google Scholar] [CrossRef]
- Herrmann, T.; Wischnewski, A.; Hermansdorfer, L.; Betz, J.; Lienkamp, M. Real-Time Adaptive Velocity Optimization for Autonomous Electric Cars at the Limits of Handling. IEEE Trans. Intell. Veh. 2020. [Google Scholar] [CrossRef]
- Herrmann, T.; Passigato, F.; Betz, J.; Lienkamp, M. Minimum Race-Time Planning-Strategy for an Autonomous Electric Racecar. In Proceedings of the 2020 IEEE 23rd International Conference on Intelligent Transportation Systems (ITSC), Rhodes, Greece, 20–23 September 2020; pp. 1–6. [Google Scholar]
- Ebbesen, S.; Salazar, M.; Elbert, P.; Bussi, C.; Onder, C.H. Time-optimal control strategies for a hybrid electric race car. IEEE Trans. Control. Syst. Technol. 2017, 26, 233–247. [Google Scholar] [CrossRef]
- Hu, X.; Chen, L.; Tang, B.; Cao, D.; He, H. Dynamic path planning for autonomous driving on various roads with avoidance of static and moving obstacles. Mech. Syst. Signal Process. 2018, 100, 482–500. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, H.; Waslander, S.L.; Gong, J.; Xiong, G.; Yang, T.; Liu, K. Hybrid trajectory planning for autonomous driving in highly constrained environments. IEEE Access 2018, 6, 32800–32819. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, H.; Wang, K.; Zhang, C.; Yin, C.; Kang, X. Off-road path planning based on improved ant colony algorithm. Wirel. Pers. Commun. 2018, 102, 1705–1721. [Google Scholar] [CrossRef]
- Ganganath, N.; Cheng, C.T.; Tse, C.K. A constraint-aware heuristic path planner for finding energy-efficient paths on uneven terrains. IEEE Trans. Ind. Inform. 2015, 11, 601–611. [Google Scholar] [CrossRef] [Green Version]
- Saad, M.; Salameh, A.I.; Abdallah, S. Energy-efficient shortest path planning on uneven terrains: A composite routing metric approach. In Proceedings of the 2019 IEEE International Symposium on Signal Processing and Information Technology (ISSPIT), Ajman, United Arab Emirates, 10–12 December 2019; pp. 1–6. [Google Scholar]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant colony optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef] [Green Version]
- Winterkorn, H.F.; Fang, H.Y. Soil technology and engineering properties of soils. In Foundation Engineering Handbook; Springer: Berlin, Germany, 1991; pp. 88–143. [Google Scholar]
- Ciobotaru, T. Semi-empiric algorithm for assessment of the vehicle mobility. Leonardo Electron. J. Pract. Technol. 2009, 8, 19–30. [Google Scholar]
- Rowe, N.C.; Ross, R.S. Optimal grid-free path planning across arbitrarily contoured terrain with anisotropic friction and gravity effects. IEEE Trans. Robot. Autom. 1990, 6, 540–553. [Google Scholar] [CrossRef]
- Rula, A.A.; Nuttall, C.J., Jr. An Analysis of Ground Mobility Models (ANAMOB); Technical Report; Army Engineer Waterways Experiment Station Vicksburg Ms: Vicksburg, MS, USA, 1971. [Google Scholar]
- Sun, Z.; Reif, J.H. On finding energy-minimizing paths on terrains. IEEE Trans. Robot. 2005, 21, 102–114. [Google Scholar]
- Sobrinho, J.L. An algebraic theory of dynamic network routing. IEEE/ACM Trans. Netw. 2005, 13, 1160–1173. [Google Scholar] [CrossRef]
- Saad, M. Non-isotonic routing metrics solvable to optimality via shortest path. Comput. Netw. 2018, 145, 89–95. [Google Scholar] [CrossRef]


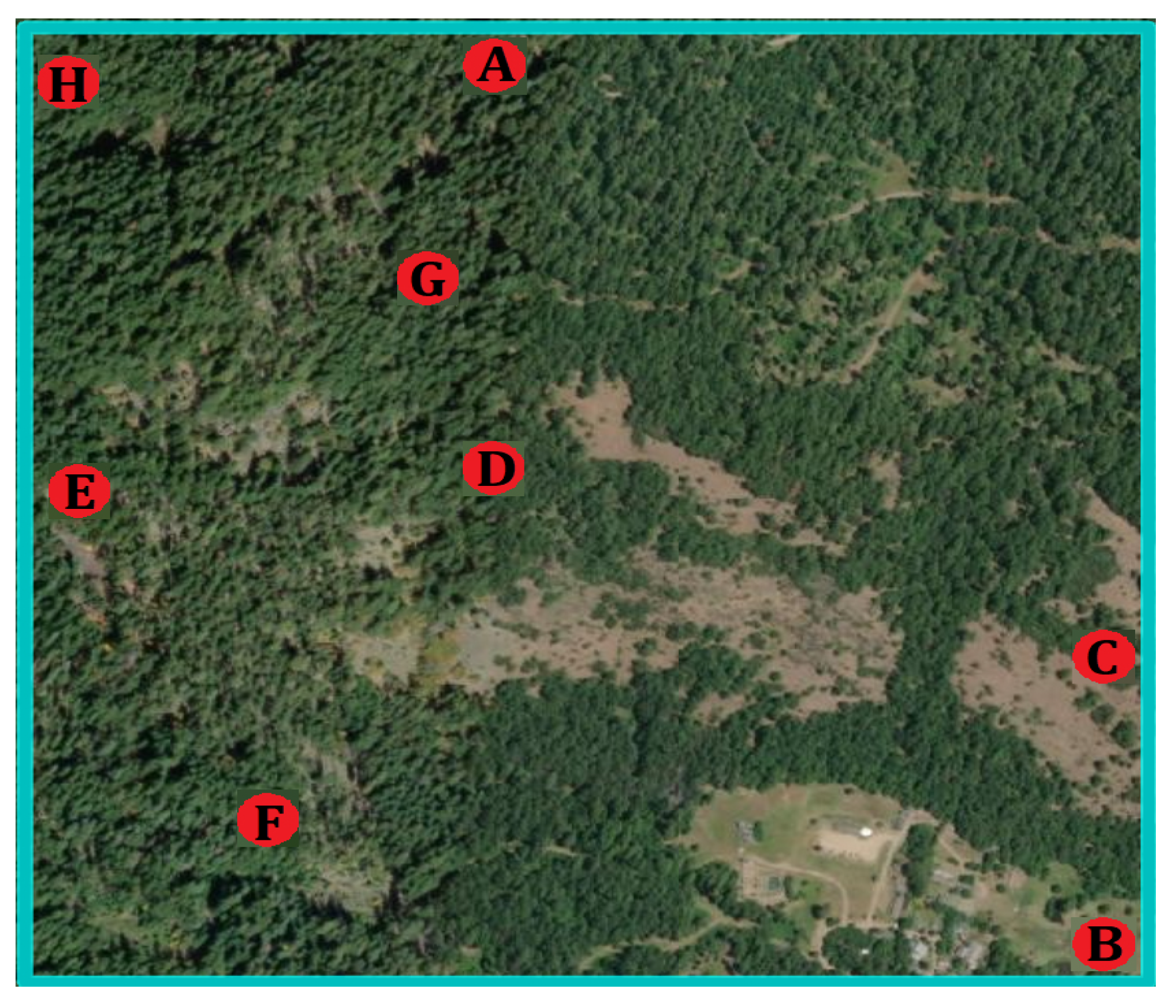

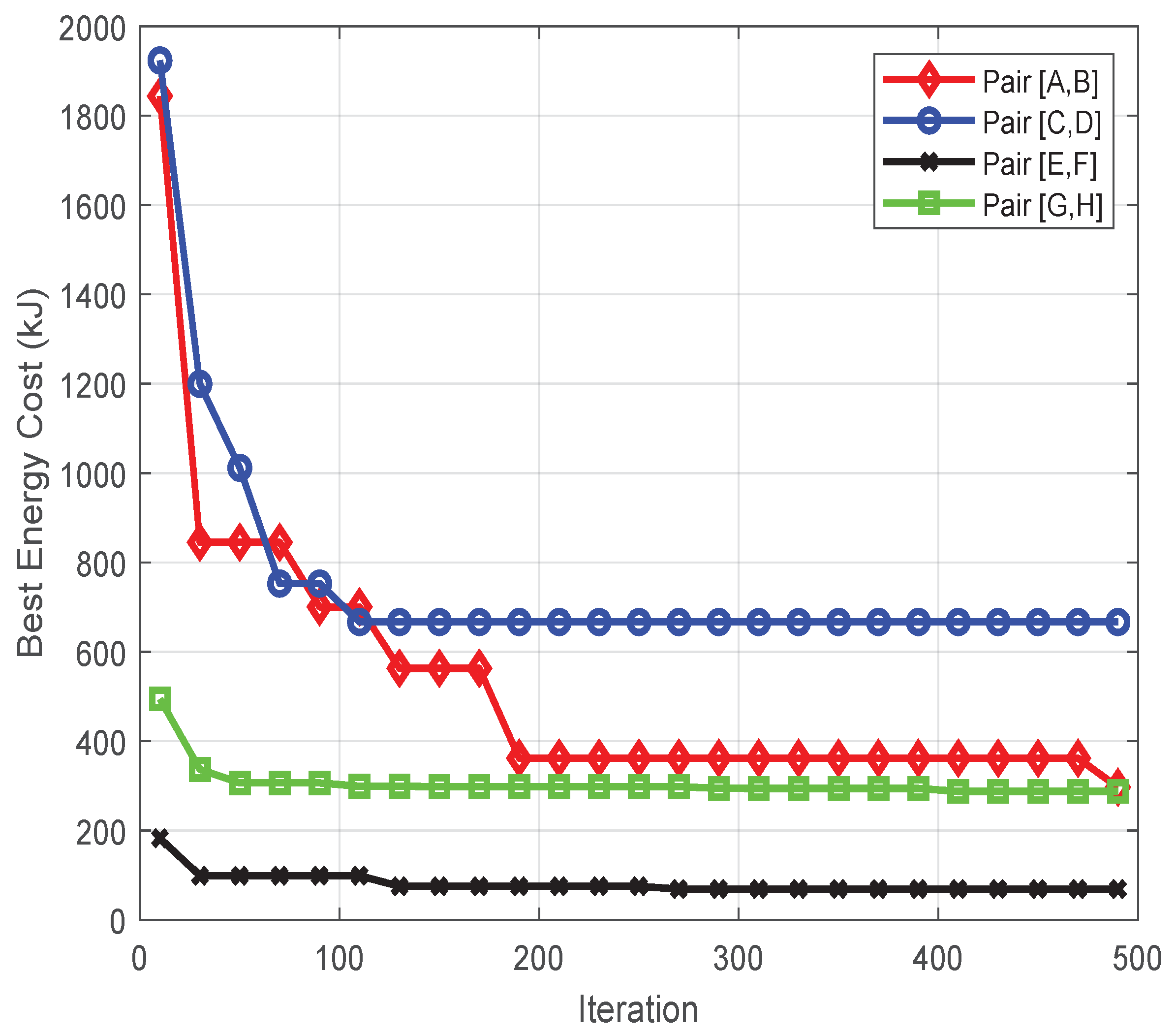
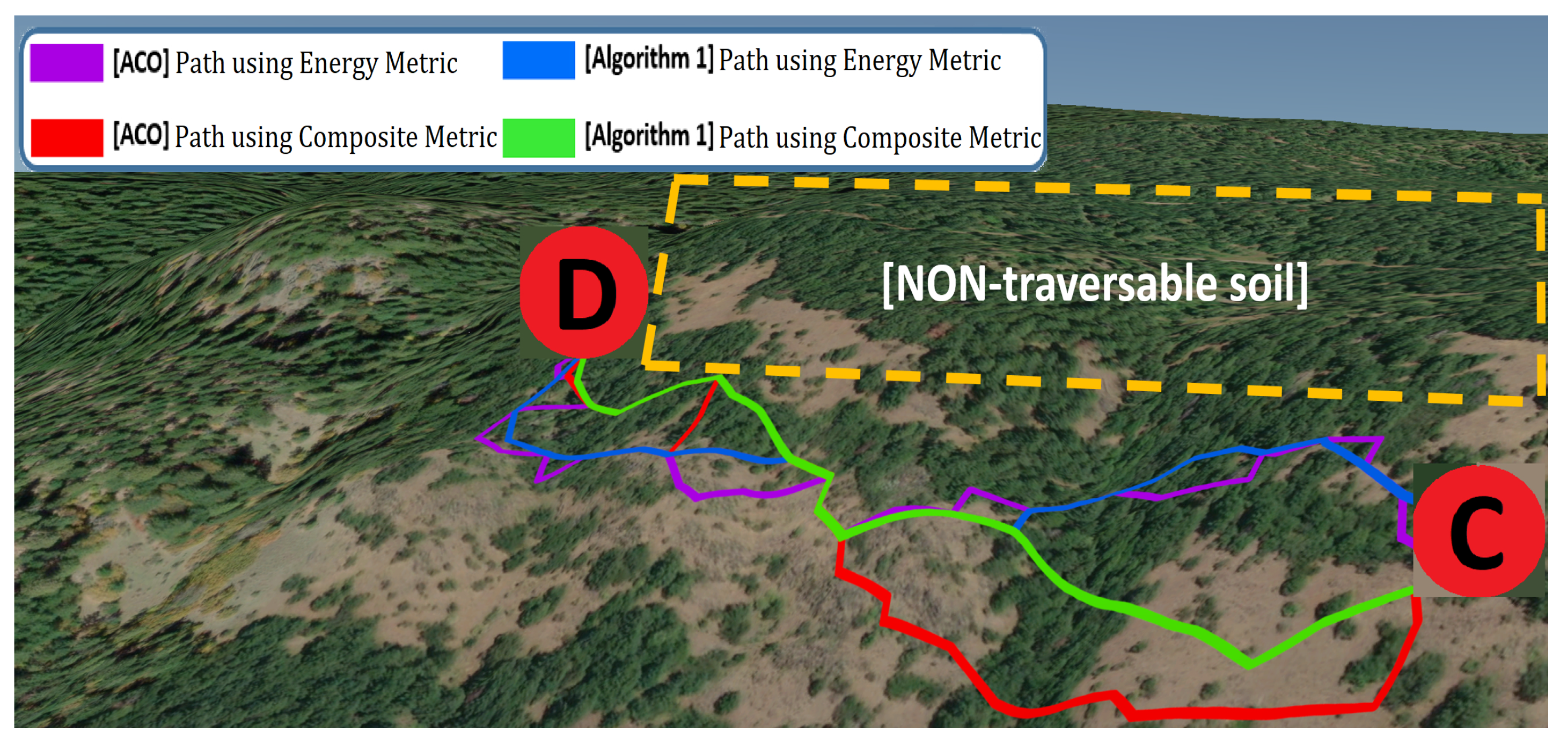
| Route Pair [s, f] | Path Length (m) and Energy (kJ) Resulting from [22] | Path Length (m) and Energy (kJ) Resulting from Algorithm 1 | Path Length Reduction (Due to Algorithm 1) | Additional Energy Cost (Due to Algorithm 1) | Elapsed Time for [22] | Elapsed Time for Algorithm 1 | ||
|---|---|---|---|---|---|---|---|---|
| (m) | (kJ) | (m) | (kJ) | (%) | (%) | (s) | (s) | |
| [A,B] | 1989.2 | 97.7 | 1828.9 | 98.5 | 8.06 | 0.80 | 3.35 | 3.42 |
| [C,D] | 1024.2 | 579.4 | 911 | 601.3 | 11.05 | 3.65 | 3.16 | 3.22 |
| [E,F] | 806.6 | 51 | 663.6 | 52.8 | 17.73 | 3.45 | 3.24 | 3.43 |
| [G,H] | 526.3 | 274 | 490.9 | 279.2 | 6.73 | 1.86 | 3.30 | 3.49 |
| Route Pair [s, f] | Path Length (m) and Energy (kJ) Resulting from ACO | Path Length Reduction (Due to Algorithm 1) | Energy-Cost Reduction (Due to Algorithm 1) | Elapsed Time for ACO | ||
|---|---|---|---|---|---|---|
| (m) | (kJ) | (%) | (%) | After 100 ite. (s) | After 500 ite. (s) | |
| [A,B] | 2388.3 | 296.8 | 23.38 | 66.81 | 58 230 | 230 |
| [C,D] | 1058.7 | 666.7 | 13.95 | 9.81 | 33 | 105 |
| [E,F] | 699.6 | 68.9 | 5.15 | 23.37 | 30 | 90 |
| [G,H] | 558.1 | 287.5 | 12.04 | 2.89 | 23 | 55 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saad, M.; Salameh, A.I.; Abdallah, S.; El-Moursy, A.; Cheng, C.-T. A Composite Metric Routing Approach for Energy-Efficient Shortest Path Planning on Natural Terrains. Appl. Sci. 2021, 11, 6939. https://doi.org/10.3390/app11156939
Saad M, Salameh AI, Abdallah S, El-Moursy A, Cheng C-T. A Composite Metric Routing Approach for Energy-Efficient Shortest Path Planning on Natural Terrains. Applied Sciences. 2021; 11(15):6939. https://doi.org/10.3390/app11156939
Chicago/Turabian StyleSaad, Mohamed, Ahmed I. Salameh, Saeed Abdallah, Ali El-Moursy, and Chi-Tsun Cheng. 2021. "A Composite Metric Routing Approach for Energy-Efficient Shortest Path Planning on Natural Terrains" Applied Sciences 11, no. 15: 6939. https://doi.org/10.3390/app11156939
APA StyleSaad, M., Salameh, A. I., Abdallah, S., El-Moursy, A., & Cheng, C. -T. (2021). A Composite Metric Routing Approach for Energy-Efficient Shortest Path Planning on Natural Terrains. Applied Sciences, 11(15), 6939. https://doi.org/10.3390/app11156939







