Calibration of GA Parameters for Layout Design Optimization Problems Using Design of Experiments

Abstract

In manufacturing-cell-formation research, a major concern is to make groups of machines into machine cells and parts into part families. Extensive work has been carried out in this area using various models and techniques. Regarding these ideas, in this paper, experiments with varying parameters of the popular metaheuristic algorithm known as the genetic algorithm have been carried out with a bi-criteria objective function: the minimization of intercell moves and cell load variation. The probability of crossover (A), probability of mutation (B), and balance weight factor (C) are considered parameters for this study. The data sets used in this paper are taken from benchmarked literature in this field. The results are promising regarding determining the optimal combination of the genetic parameters for the machine-cell-formation problems considered in this study.

1. Introduction

In general, facility-layout optimization problems are nonlinear, nonconvex, and multimodal in their nature. Facility-layout problems (FLP) can be divided according to types of manufacturing systems into four basic categories, which are product layout, process layout, static layout, and cellular layout [1]. Taking this classification into account, the proposed study addresses the cellular manufacturing problem. In the past, the main objective of a facility-layout problem was to minimize the material handling cost of the manufacturing system [2]. Presently, the main goal of the FLP is to improve manufacturing efficiency. In line with this, a number of authors suggested different objective functions for facility-layout problems, e.g., to maximize the throughput rate and minimize the conveyance time per trip [3] or minimize cycle times in order to increase productivity [4], and so forth.

An important issue in the design of cellular manufacturing systems (CMS) is the manufacturing-cell-formation problem (MCFP), which is based on group technology principles. Several taxonomies of the MCFP are reviewed in the literature, e.g., by Selim et al. [5], Bidanda et al. [6] and Modrak and Pandian [7]. The core of MCFP procedures is that machines are grouped into machine cells and parts into part families. In practical applications, it is not easy to arrange all parts and machines into autonomic cells, and therefore some operations have to be performed on separate machines. The cost of duplicating machines is often high, and therefore, related managerial decisions are usually trade-offs between economic and technological criteria [8,9,10]. During previous decades, numerous heuristic and metaheuristic methods and their variations were developed, tested and compared for this problem. The metaheuristics include the genetic algorithm (GA), simulated annealing, ant colony optimization, tabu search, scatter search, particle swarm optimization, GRASP and hybridized metaheuristics. There are several survey papers, such as by Herroelen et al. [11], Kolisch and Hartmann [12] and others, that present and compare the methods from various perspectives.

In this work, the focus is on application of GAs, and especially on finding out how the solutions of the cell-formation problem are influenced by a set of probability parameters of genetic operators, namely crossover and mutation, including balanced weight factors. In view of this, the presented work attempts to employ the Taguchi approach to find an optimal combination of parameters that impact the efficiency of the genetic algorithm and to explore whether the optimal combination of the genetic operators for the given type of MCFP can be influenced by the magnitude of the noise factors, which is represented by matrix size in our case.

2. A Brief Literature Review

In this section, a short review of the selected research on manufacturing cell formation will be given. John Holland, inspired by population genetics, introduced the concept of the GA in the 1970s. In 1975, the book [13] is published by him and his colleagues. The first GA-based approach for the cell-formation research area was proposed by Venugopal and Narendran [14]. It was a proposed mathematical model with a solution procedure based on a GA that can be purposely implemented in a cellular manufacturing environment. Joines and Houck [15] in their work applied a non-stationary penalty to solve CFP with a genetic algorithm. Gupta et al. [16] used a GA approach to solve the layout design problem with a predetermined number of manufacturing cells. Alsultan and Fedjki [17] utilized a GA approach to solve the machine-cell-part clustering problem in order to minimize total intercell and intracell moves. Gravel et al. [18] developed a GA with a double-loop, able to solve large-scale capacitated cell-formation problems with multiple routings. Moon and Gen [19] proposed a genetic algorithm to solve an integer programming model with consideration of alternative process plans and machine-duplication consideration. An adaptive genetic approach to solve the manufacturing-cell-formation problem in order to enhance the performance of the genetic search process was proposed by Mak et al. [20]. Zhao and Wu [21] evaluated the solutions of a multi-objective GA that applies minimizing costs due to intercell and intracell part flows, minimizing the total within-cell load variation and minimizing exceptional elements. They also incorporated in their research the multiple routes of parts. Arzi et al. [22] proposed a genetic algorithm with grouping efficiency and capacity requirements as objectives for large-scale systems design. Zolfaghari and Liang [23] tested and evaluated a genetic algorithm against simulated annealing and tabu search using binary cell-formation problems. Yasuda et al. [24] in their research proposed a method to solve the multi-objective CFP, partially adopting Falkenauer’s grouping genetic algorithm. It was also aimed at improving the efficiency of their algorithm with regards to initialization of the population, fitness valuation, and keeping the crossover operator from cloning. Other similar approaches were published with many innovative algorithms. For example, Farahani et al. [25] described ant colony optimization to solve machine–part cell-formation problems. Mohammad Mohammadi et al. [26] approached a layout problem in cellular manufacturing systems with alternative processing routings. Dmytryshyn et al. [27] suggested a novel modeling approach for solving the cell-formation problem. Kamalakannan et al. [28] developed a simulated annealing algorithm for solving CFP with ratio level data. Shashikumar et al. [29] determined the solution for CFP using a heuristics approach. Sharma et al. [30] had done research on an implementation model using AHP and ANP for CFP. Octavio et al. [31] developed metaheuristic algorithms to solve grouping problems. Mourtzis et al. [32] brought the idea of adaptive scheduling in cellular manufacturing systems. Firouzian et al. [33] developed an artificial immune system for part family clustering. Vitayasak et al. [34] proposed a GA-based layout design approach to solve robust machine layout design problems for systems subject to demand uncertainties and maintenance. Their innovative method includes an experimental design that was used to test the robust design approach with corrective, preventative, and combined maintenance regimes. Dolgui et al. [35] explored a reconfigurable manufacturing system that exhibited some crucial design and control characteristics for complex value-adding systems in highly dynamic scenarios. Such systems are designed at the outset for rapid change in the structure of machines, in order to quickly adjust production capacity and functionality within a part family in response to frequent market changes or intrinsic system changes. An interesting and very useful approach to the facility-layout design optimization was proposed by Bucki and Suchanek [36]. They proposed an effective tool for performance analysis of manufacturing systems from logistics viewpoint by using a mathematical simulation model.

It is worth mentioning other works that directly relate to the manufacturing cell-formation problem, such as the hybrid GA/branch and bound approach to solve the manufacturing-cell-formation problem using a graph partitioning formulation, which was proposed by Boulif and Atif [37]. Their effort has been made to take into account the natural constraints of real-life production systems. A typical CFP with the objective of minimizing the exceptional elements was explored by Mahdavi et al. [38]. Deljoo et al. [39] used a GA to solve the dynamic cell-formation problem. Based on their studies, they reconsidered the shortcomings related to machine relocation cost and machine purchasing cost and developed a model for dynamic CFP in order to resolve these two shortcomings. Arkat et al. [40] developed a multi-objective GA for CFP considering cellular layout and operations scheduling. Cell-formation problems related to scheduling problems with the objective to minimize makespan are available in references [41,42,43,44]. A new algorithm for CFP with alternative machines and multiple-operation-type machines was developed by Li [45]. Its purpose was to improve traditional group technology cell-formation methods by considering alternative machines and multiple-operation-type machines. Boulif [46] proposed a new graph-cut-based encoding representation in order to solve the CFP with the genetic algorithm. Obviously, there are other related works, since this domain attracts a large research interest.

3. Structure of Genetic Algorithm

In a GA, a high-quality candidate solution is represented by a collection of genes called chromosome. A chromosome’s potential is given by its fitness function. A population consists of a set of selected chromosomes, and the population is subjected to generations (or iterations). Finally, crossover and mutation operators are performed with defined probabilities to improve the solutions. A GA has several advantages over the traditional optimization methods. It may quickly arrive at a good solution set. As worse cases are eliminated, they will never affect the generated solution. GAs are one of the best methods to solve a problem about which little is known. This is because a genetic algorithm works by its own rules. This is a very useful strategy for a GA to solve highly complex problems in nature. In a GA, it is necessary for the problem solver to choose the appropriate coding method. If the solutions are coded in different combinations, then the GA will start its searching operation using its operators known as selection, crossover, and mutation, respectively. As is known, a suitable type of crossover technique for a particular problem can improve the GA’s performance [47]. All these methods are probabilistic in nature. The proper stopping criteria will be given as input for the GA to stop its searching process. This is done purely based on the experience of the problem-solver. Based on the stopping criteria, the GA will stop running and give the solution that it finds at that point of time. The solution of the problem has to be represented in the GA as a genome (or chromosome). The genetic algorithm then creates a population of solutions and applies genetic operators such as mutation, crossover, and selection to evolve the solutions in order to find the best one(s). The crucial aspects of using GAs are: the definition of the objective function, the definition and implementation of the genetic representation, the definition and implementation of the genetic operators [48].

GAs are frequently adopted to find out how to make the machine clusters form cells in accordance with the rules of production flow analysis. In cell formation, a GA works well and finds a good solution, as given in the abovementioned literature studies. It gives high-quality solutions even if the problem has a high level of complexity. There are few other traditional metaheuristics approaches that performing good searches in such a situation [49]. The following representation is used in a typical cell-formation problem solved using GA. This representation is popularly known as real coding (see Figure 1).

Depending on the number of cells to be accommodated in the layout, the number of genes on a chromosome increases. In the above example there are three cells and hence there are only 1, 2, and 3 values present in the chromosome of 8 genes (8 machines).

4. Mathematical Model of the Cell-Formation Problem

According to the review of the literature, the minimization of intercell flows and the total cell load variation can be considered the essential objectives in the manufacturing cell-formation research. Thus, the bi-objective fitness function used to evaluate the solution incorporates intercell flows and cell load variation. The mathematical model is given as:

Intercell flow fitness function:

$$\mathrm{Minimize}{f}_1={\displaystyle \sum }_i{\displaystyle \sum }_j{\displaystyle \sum }_k{a}_{ij}\left|X_{ik}-Y_{ik}\right|$$

(1)

Cell load variation fitness function:

Minimize

$$f_2={\displaystyle \sum }_i{\displaystyle \sum }_k{X}_{ik}{\displaystyle \sum }_j{\left({\mathit{\omega }}_{ij}-m_{ik}\right)}^2$$

(2)

Variable:

$$m_{\mathit{ik}}={\displaystyle \sum }_i{X}_{\mathit{ik}}\times Y_{\mathit{jk}}\times {\omega }_{\mathit{ij}}/{\displaystyle \sum }_i{X}_{\mathit{ik}}$$

(3)

Decision variables:

$${\omega }_{ij}=t_{ij};\mathrm{if}\mathrm{part}j\mathrm{is}\mathrm{processed}\mathrm{on}\mathrm{machine}i$$

(4)

0; otherwise

$$X_{ik}=1;\mathrm{if}\mathrm{machine}i\mathrm{is}\mathrm{in}\mathrm{cell}k$$

(5)

0; otherwise

$$Y_{jk}=1;\mathrm{if}\mathrm{part}j\mathrm{is}\mathrm{in}\mathrm{cell}k$$

(6)

0; otherwise

$$a_{ij}=1;\mathrm{if}\mathrm{part}j\mathrm{needs}\mathrm{to}\mathrm{be}\mathrm{processed}\mathrm{on}\mathrm{machine}i$$

(7)

0; otherwise

Constraints:

$${\displaystyle \sum }_k^c{X}_{ik}=1 \forall \in \left\{1,2,\dots ,m\right\}$$

(8)

$${\displaystyle \sum }_k^c{Y}_{jk}=1 \forall \in \left\{1,2,\dots ,p\right\}$$

(9)

$${\displaystyle \sum }{X}_{ik}\ge 1 \forall k \in \left\{1,2,\dots ,c\right\}$$

(10)

$${\displaystyle \sum }{Y}_{jk}\ge 1 \forall k \in \left\{1,2,\dots ,c\right\}$$

(11)

Bi-objective fitness function:

$$Z\left(t\right)=\alpha ·f_1+\left(1-\alpha \right)·f_2$$

(12)

The given model of cell-formation problem works with processing time. According to this model, we search to obtain the number of cells and the number of machines and parts within each cell. Equation (1) shows the calculation of the intercell flows, and Equation (2) shows the cell load variation. Equation (3) shows the average intercell processing time for the j-th part and k-th cell. Equation (4) shows the decision variables that assign the time t_ij of the i-th machine required to process the j-th part. Equations (5)–(7) are decision variables that state that x_ik, y_jk and a_jj are 0–1 binary numbers. Equations (8) and (9) ensure that each machine and part is attached to only one cell. Equations (10) and (11) ensures that, in each cell, there must be allocated at least one machine and one part, respectively. Equation (12) is the bi-objective fitness function for a non-binary cell-formation problem balanced by weight factor α.

A fitness function value is computed for each chromosome in the population, and the objective is to find a chromosome with the maximum fitness function value. Due to objective of minimizing both the total cell load variation and the exceptional elements, it is necessary to map it inversely and then maximize the result. Goldberg [50] suggested a mapping function given as:

$$F\left(t\right)=Z_{max}-Z\left(t\right)$$

(13)

The symbol F(t) stands for the fitness function of the t-th chromosome, and Z_max is the max[Z(t)] of all chromosomes (t). The advantage is that the worst chromosomes obtain a zero-fitness function value, so they are not going to be reproduced into the next generation.

The following procedure given by Zolfaghari and Liang [51] is used to assign parts into the machine cells:

$$P_{kj}=\left(\frac{f_{kj}}{f_k}\right)·\left(\frac{f_{kj}}{f_j}\right)·\left(\frac{T_{kj}}{T_j}\right)$$

(14)

where, P_kj is the membership index of the j-th part belonging to the k-th cell; f_kj is the number of machines in the k-th cell required by the j-th part; f_k is the total number of machines in the k-th cell; f_j is total number of machines required by the j-th part; T_kj is the processing time of the j-th part in the k-th cell; and T_j is the total processing time required by the j-th part.

5. Case Study on Layout Design Optimization

The procedure we decided to apply to analyzing the influence of genetic parameters on the final solution quality for reorganization of machines and parts into cells is an experimental design method developed by Genichi Taguchi. Here we established a P-diagram (see Figure 2) that identifies the inputs and outputs of the system together with control and noise factors.

The Taguchi experimental method consists of performing selected experiments to study the influence of several operating factors on output-parameter values. Taguchi separates the factors into two domains: control and noise factors. The difference between these two factor groups is that we cannot control them directly. The elimination of the noise factors is often impractical and impossible so the Taguchi method seeks to minimize the effect of noise, using optimal levels of important control factors based on the concept of robustness [52]. These three fundamental control factors are the probability of crossover (A), probability of mutation (B), and balance weight factor (C). The levels of each set of control factors are shown in

Table 1. Input signal factors and levels.

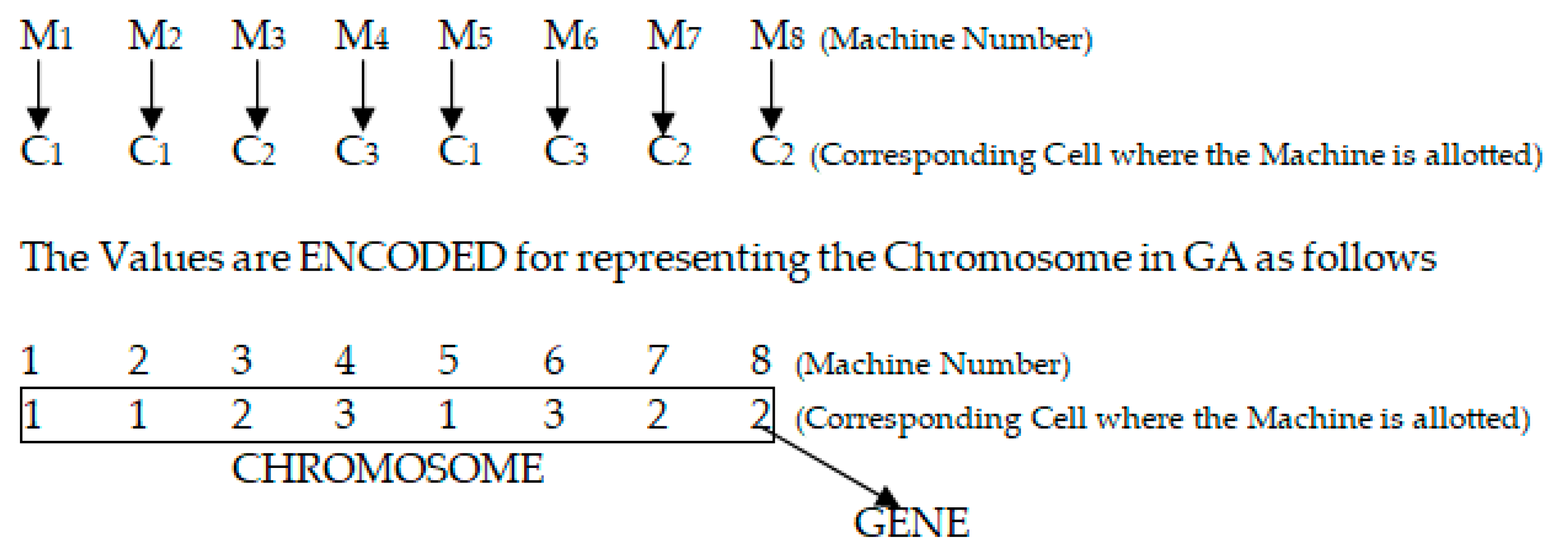
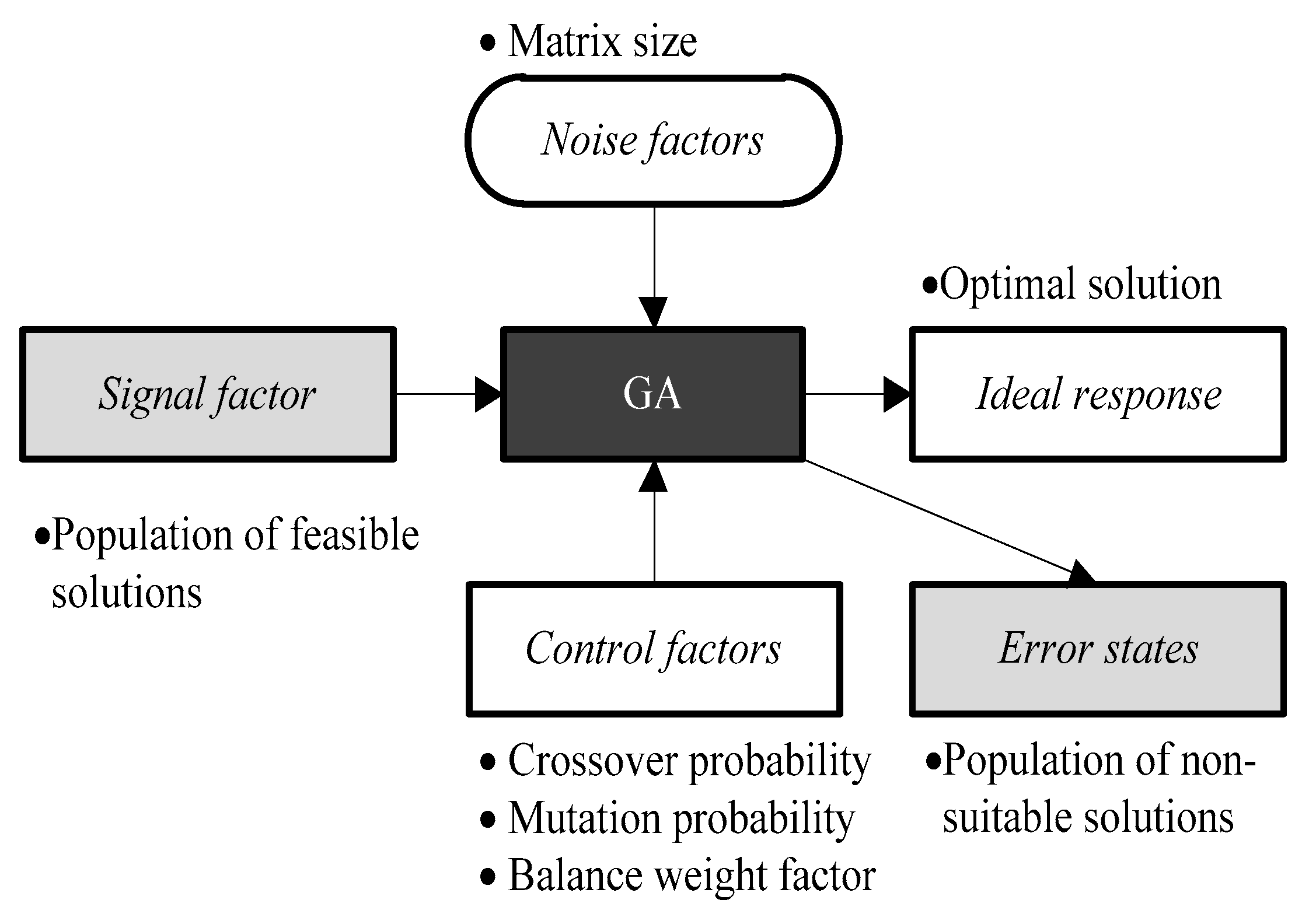
Control Factors	Description	Levels
		−	0	+
A	Probability of crossover (Pc)	0.3	0.6	0.8
B	Probability of mutation (Pm)	0.01	0.05	0.1
C	Balance weight factor (α)	0.4	0.6	0.8

.

Based on the principles of the genetic algorithm, these control-factor values are decided taking a reference from the optimization of control parameters for a genetic algorithms using an image registration problem [53]. In the evaluation of a final feasible solution, there also exist the so-called noise factors that have an impact on the results. These factors cause deviation in the search space size and the noise factors, such as the size of the machine-part matrix (D). The offered factors are composed of individual levels, wherein each level is completely independent. This particular case is under consideration with three levels of control and two levels of noise factors.

It is proposed to apply Taguchi quality concept for the assessment of the final solution, and, in this context, the L9 orthogonal array has been chosen. The results of the experiments are subsequently transformed into a signal-to-noise ratio. For reducing the variability of solutions around a target, the smaller-is-better S/N ratio (SNR) calculation is applied [54]:

$$SNR=-10\log [\frac{i}{n}{\displaystyle \sum }_{i=1}^n{Y}_i^2]$$

(15)

A signal-to-noise ratio is a measure of robustness that can be used to identify the control factor settings that minimize the effect of noise on the response. In the parameter design, there are two factors: the signal factor that can be controlled and the noise factor that is too expensive to control. In this research work, the signal factors are A, B, and C, wherein the noise factor is the exceptional element. Yi² is obtained from the mean sqare deviation (MSD) of signal factors and of exceptional elements. Here the ‘n’ represents the number of experiments that are performed using Taguchi’s experiment design.

Higher values of SNR will control the noise factors that lead to the minimization of the objective function. Since, in this research work, the objective is to minimize the combination of two functions, it is recommened from Taguchi’s SNR principle that the ‘smaller is better‘ is suitable for this approach.

The stopping criterion used to test algorithms was set at a number of generations [55], fixed to min 120. In order to conduct the experiment, we used a set of four instances and implemented the algorithms in PHP script. As a common performance measure, the number of exceptional elements (EE) has been used. The total set of experiments that were performed was obtained by combining the L9 array of the control factors. In order to obtain more objective results, we decided on two groups of size problems; the first of them consisted of 4 size problems (24 × 16, 24 × 40, 30 × 16, 30 × 40) as shown in

Table 2. Combination of factors and the resulting values of the trials of experiments (Group #1).

#	Factors		D	24 × 16	24 × 40	30 × 16	30 × 40	Results
	A	B	C	1	2	3	4	MSD	SNR
1	−	−	−	12	6	19	13	12.5	−22.49
2	−	0	0	15	5	21	5	11.5	−22.53
3	−	+	+	13	3	26	7	12.25	−23.54
4	0	−	0	11	0	12	4	6.75	−18.47
5	0	0	+	27	6	25	6	16	−25.52
6	0	+	−	11	0	9	4	6	−17.36
7	+	−	+	15	6	19	9	12.25	−22.45
8	+	0	−	12	3	17	7	9.75	−20.89
9	+	+	0	10	0	7	4	5.25	−16.15

, and the second one consisted of 19 size problems (see

Table 3. Combination of factors and resulting values of the trials of experiments (Group #2).

#	Factors		D	7 × 5	8 × 6	10 × 10	11 × 7	18 × 5	12 × 8	15 × 10	20 × 8	20 × 20	20 × 23	23 × 14	24 × 14	24 × 16	24 × 40	30 × 16	35 × 20	30 × 40	40 × 24	41 × 30	Results
	A	B	C	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	MSD	SNR
1	−	−	−	2	2	1	3	5	1	0	5	20	8	0	0	12	6	19	0	13	2	2	65.84	−18.19
2	−	0	0	2	2	0	3	5	1	0	9	17	4	0	0	15	5	21	0	5	0	3	60.74	−17.83
3	−	+	+	2	2	0	3	5	1	0	5	19	13	0	0	13	3	26	0	7	0	3	79.47	−19.00
4	0	−	0	2	2	0	3	5	1	0	12	24	10	0	0	11	0	12	0	4	0	3	60.68	−17.83
5	0	0	+	2	2	0	3	5	1	0	9	17	12	0	0	27	6	25	0	6	0	3	104.84	−20.21
6	0	+	−	2	2	0	3	5	1	0	27	32	14	0	0	11	0	9	0	4	0	3	116.79	−20.67
7	+	−	+	2	2	0	3	5	1	0	27	17	22	0	0	15	6	19	0	9	0	3	118.79	−20.75
8	+	0	−	2	2	0	3	5	1	0	9	19	8	0	0	12	3	17	0	7	0	3	55.21	−17.42
9	+	+	0	2	2	0	3	5	1	0	9	15	10	0	0	10	0	7	0	4	0	3	32.79	−15.16

).

The total number of experiments for the first group of size problems is 36 and for the second group of size problems is 171. The objective in this factorial experiment is to search values of the signal-to-noise ratio for “smaller-is-better”, which is computed for each set of experiments. After obtaining the results of Taguchi’s experiment design, EEs are transformed into S/N ratios. The results of the experiment for each series of experiments are presented in Table 2 and Table 3.

6. Conclusions

Based on Table 1 (input signal factors and levels), the crossover probability is considered in ascending order (lower to higher), which is mentioned in Table 2 and Table 3. The change in value for A occurs in every three rows; for B, the change in value occurs in every row in ascending order, and for factor C (1,2,3 then 2,3,1 then 3,1,2) as per the L9 orthogonal array representation. It happens incidentally that the last value (9th row) is better compared to other values, as far as this research concerned. The optimal level of the factors is the level with the highest SNR. Table 2 and Table 3 show that the optimal level has been obtained in the 9th row (refer to Table 2 and Table 3) where the value of factor A is 0.8, the value of factor B is 0.1, and the value of factor C is 0.6, mentioned as (+, +, 0) as per Table 1. The general view is that whenever the probability of crossover and/or mutation is increased, the number of searches in the solution space will also increase; thereby the chance of obtaining a better solution is increased. The Taguchi’s design of experiments based on this research work provides evidence to the above statement.

Building on this analysis the following conclusions and suggestions for further research have been made.

It can be stated that the Taguchi design of experiments method can be used as an effective tool to determine the optimal combination of the genetic operators for the given type of MCF problems, because two different experiments brought out that the optimal level of the factors A, B, and C are identical.

Due to the limited number of experimental groups, we can only anticipate that an optimal combination of the genetic operators for the given type of MCF problem is not influenced by the magnitude of the noise factors. Therefore, in our further research this dependence/independence relation will be investigated.

This work provides further evidence that the efficiency of a genetic algorithm is dependent on the mentioned control factors and their parameters. As a direction for future studies, it could be interesting to extend the parameters (for example, the probability of reproduction and the number of generations) and develop effective genetic algorithm incorporating advanced features. For more realistic models, it would be useful to consider several practical assumptions, such as machine-availability constraints or changeover times.