Determination of the Spatial Resolution in the Case of Imaging Magnetic Fields by Polarized Neutrons
Abstract
:1. Introduction
2. Some Mathematics on Spatial Resolution
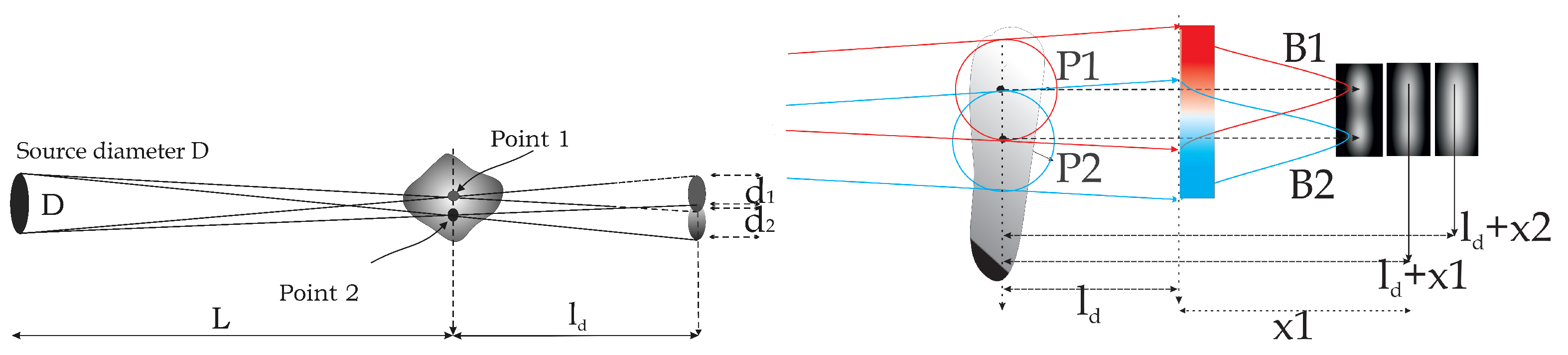
2.1. Spatial Resolution for Unpolarized Neutrons
2.2. Longitudinal Spatial Resolution of a Magnetic Field
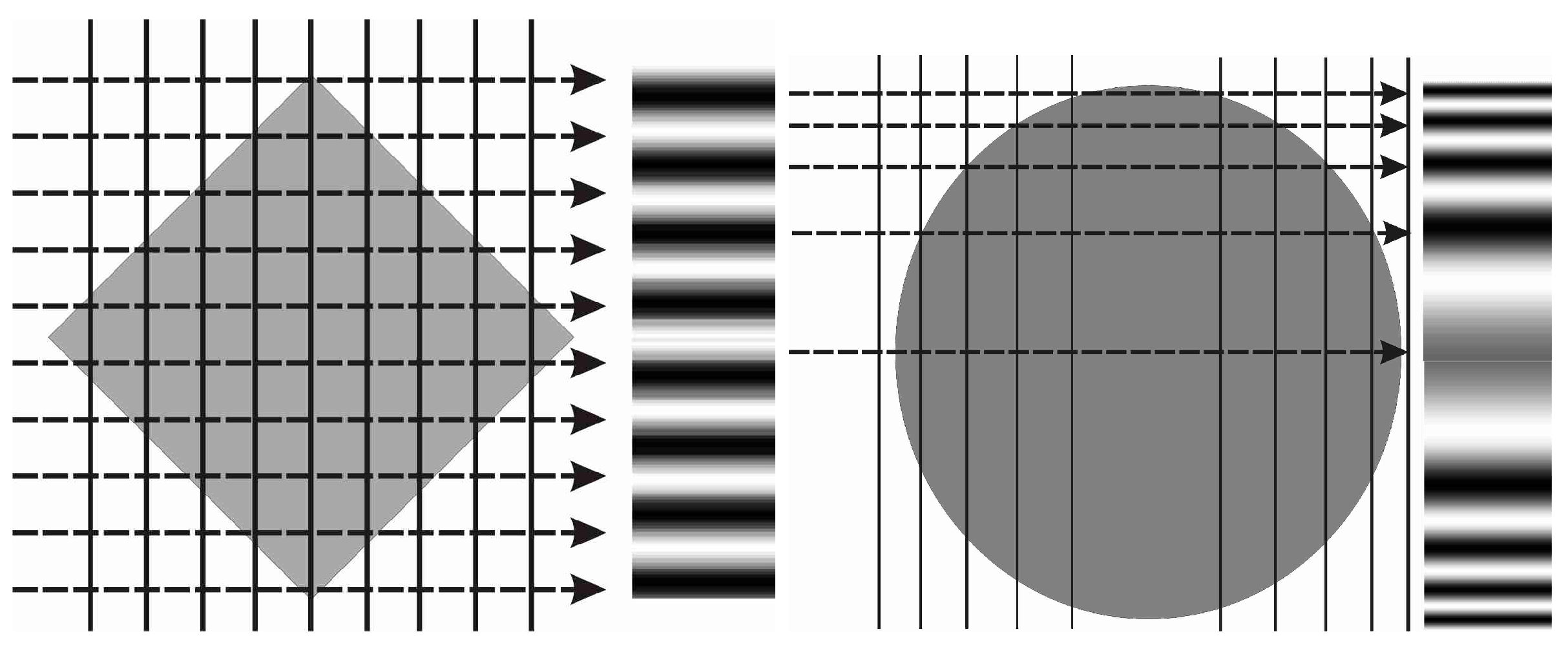
2.3. Lateral Spatial Resolution of a Magnetic Field
3. Experiments
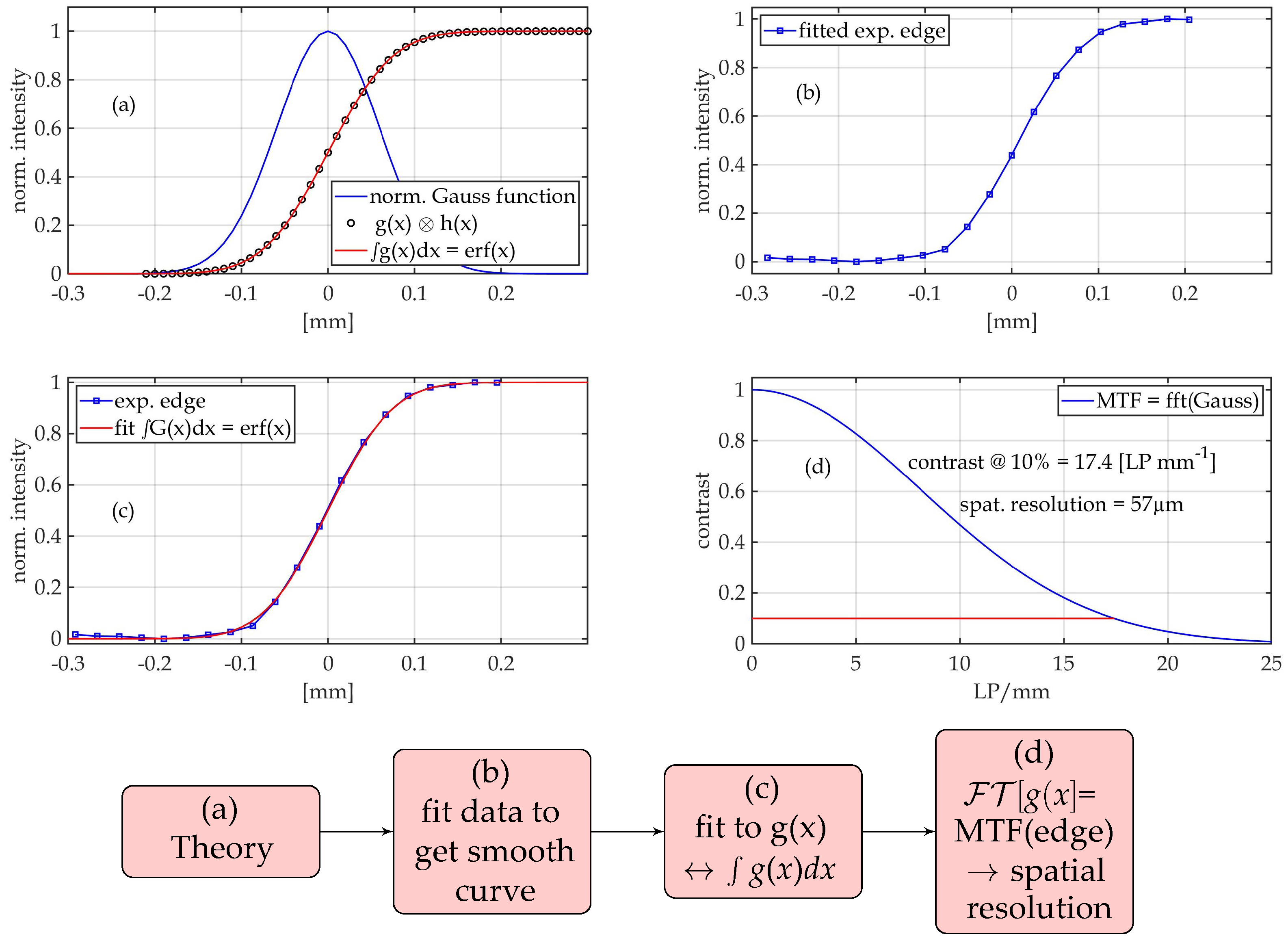
3.1. Determination of the Spatial Resolution for Unpolarized Neutrons
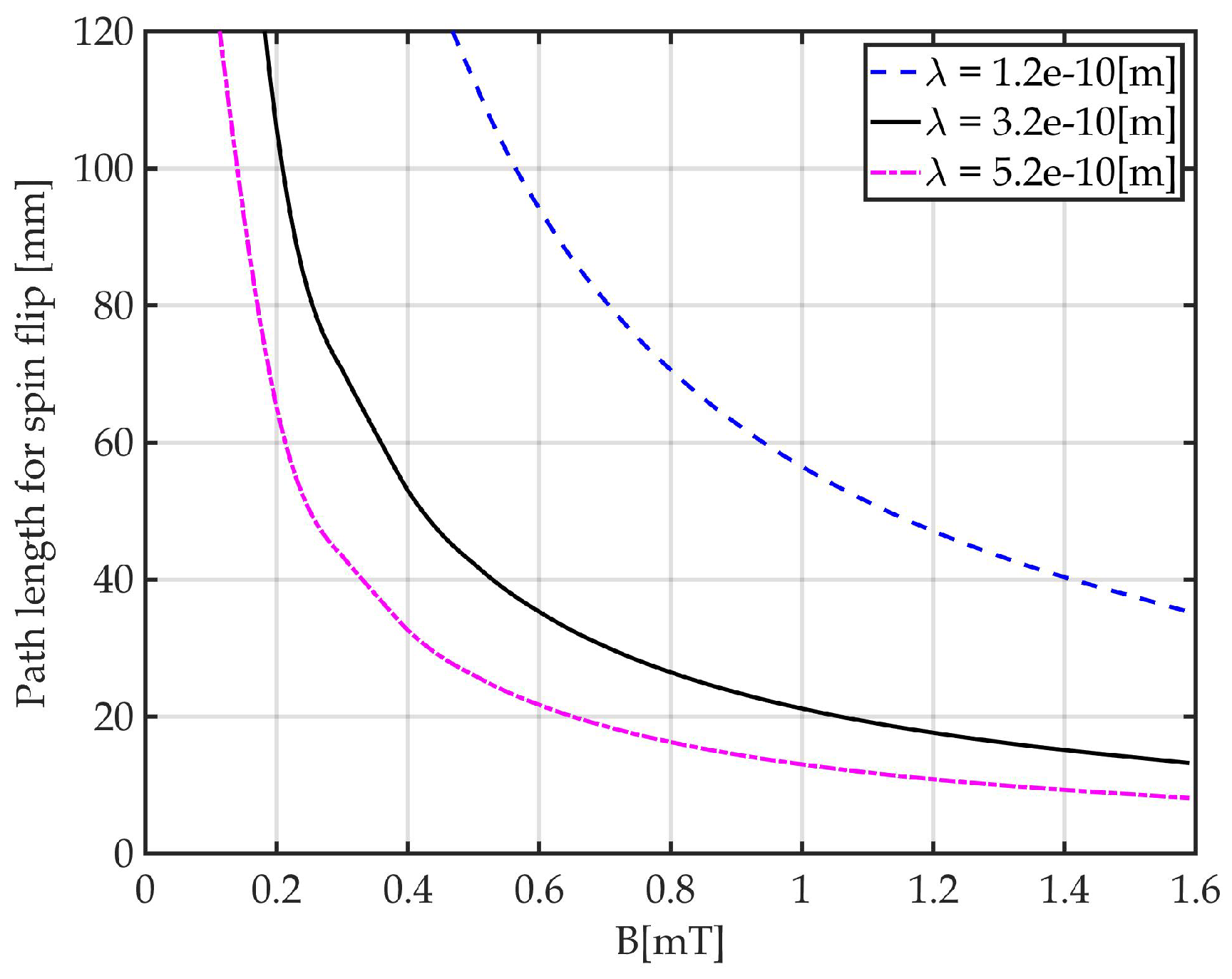
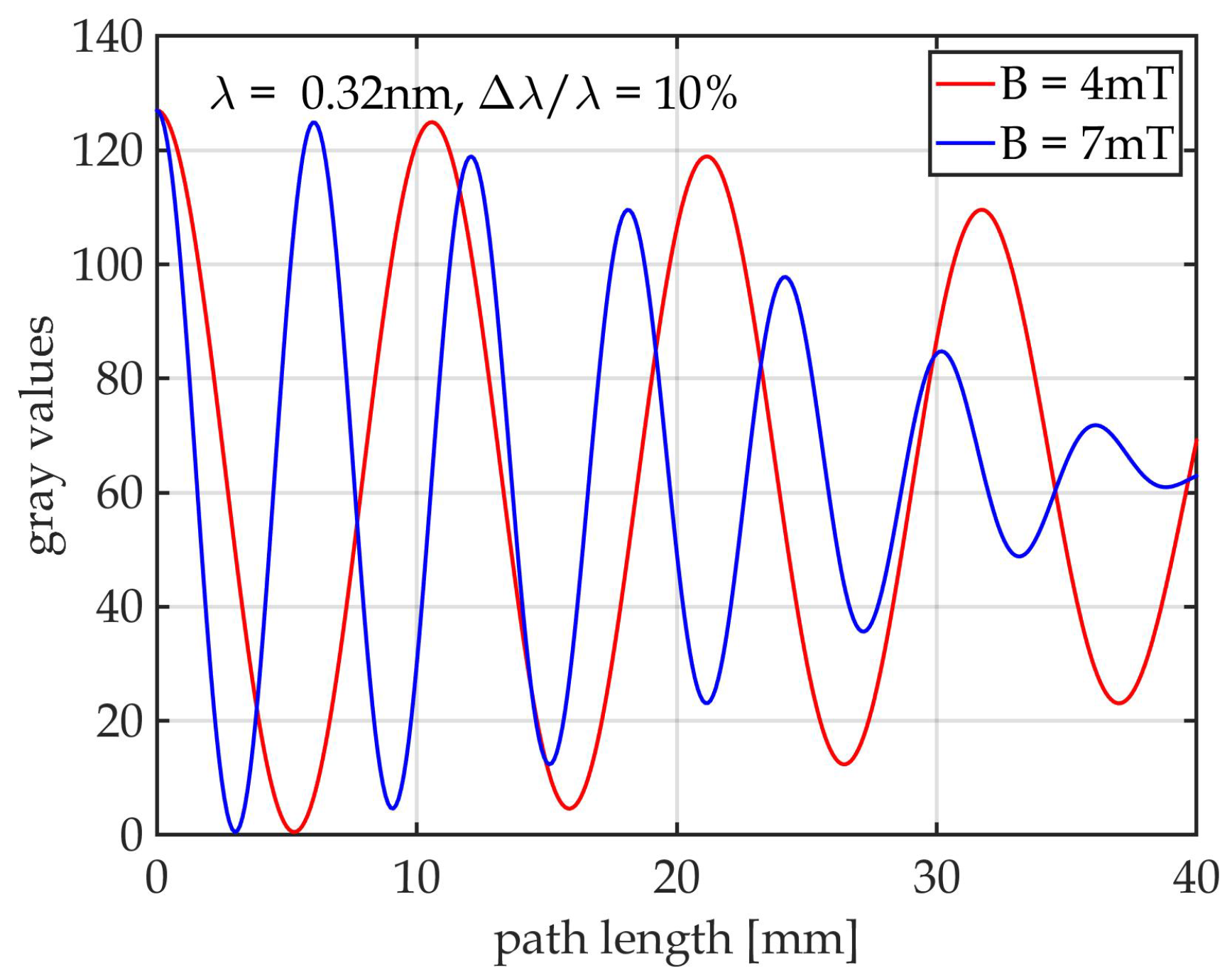
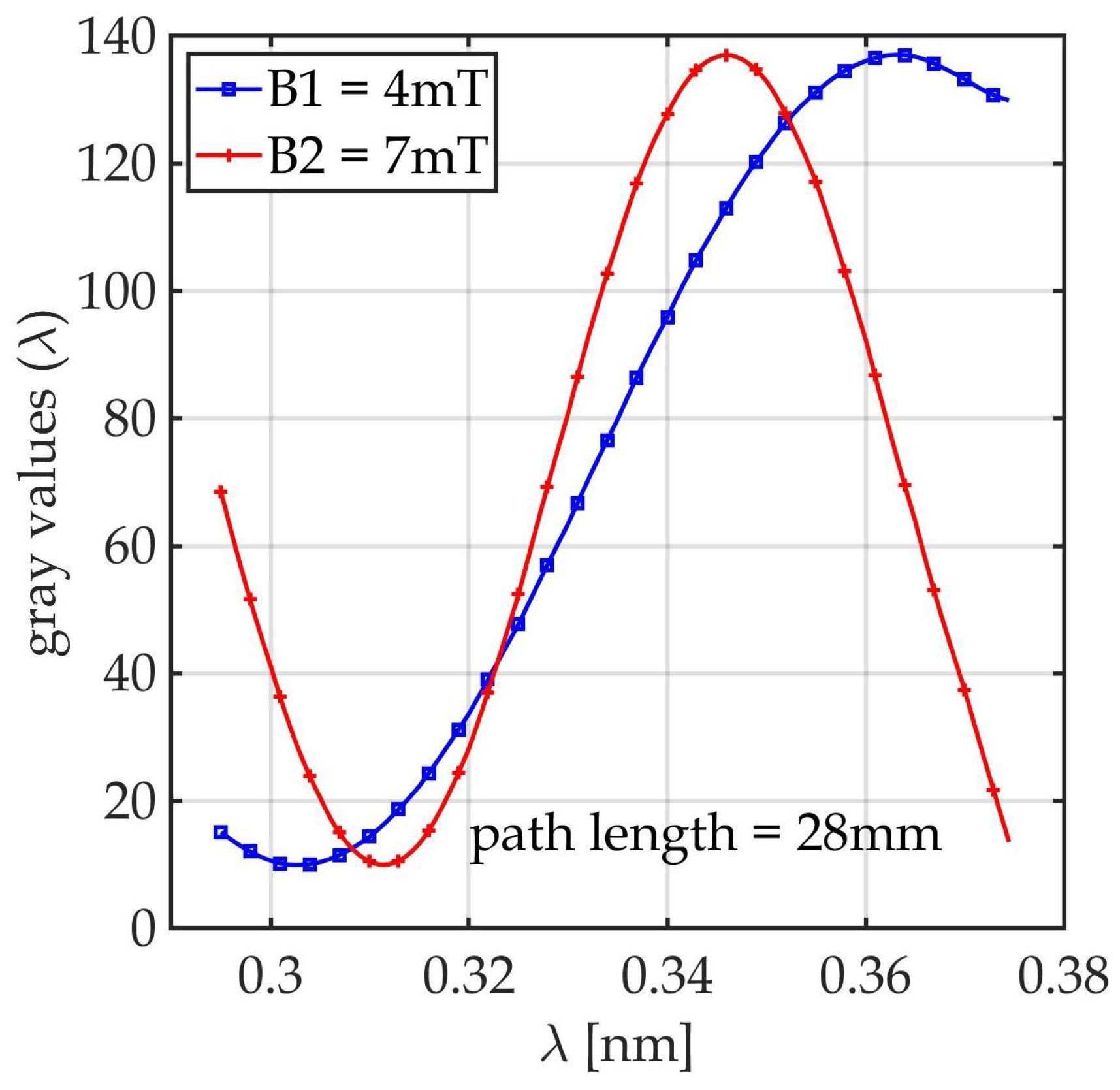
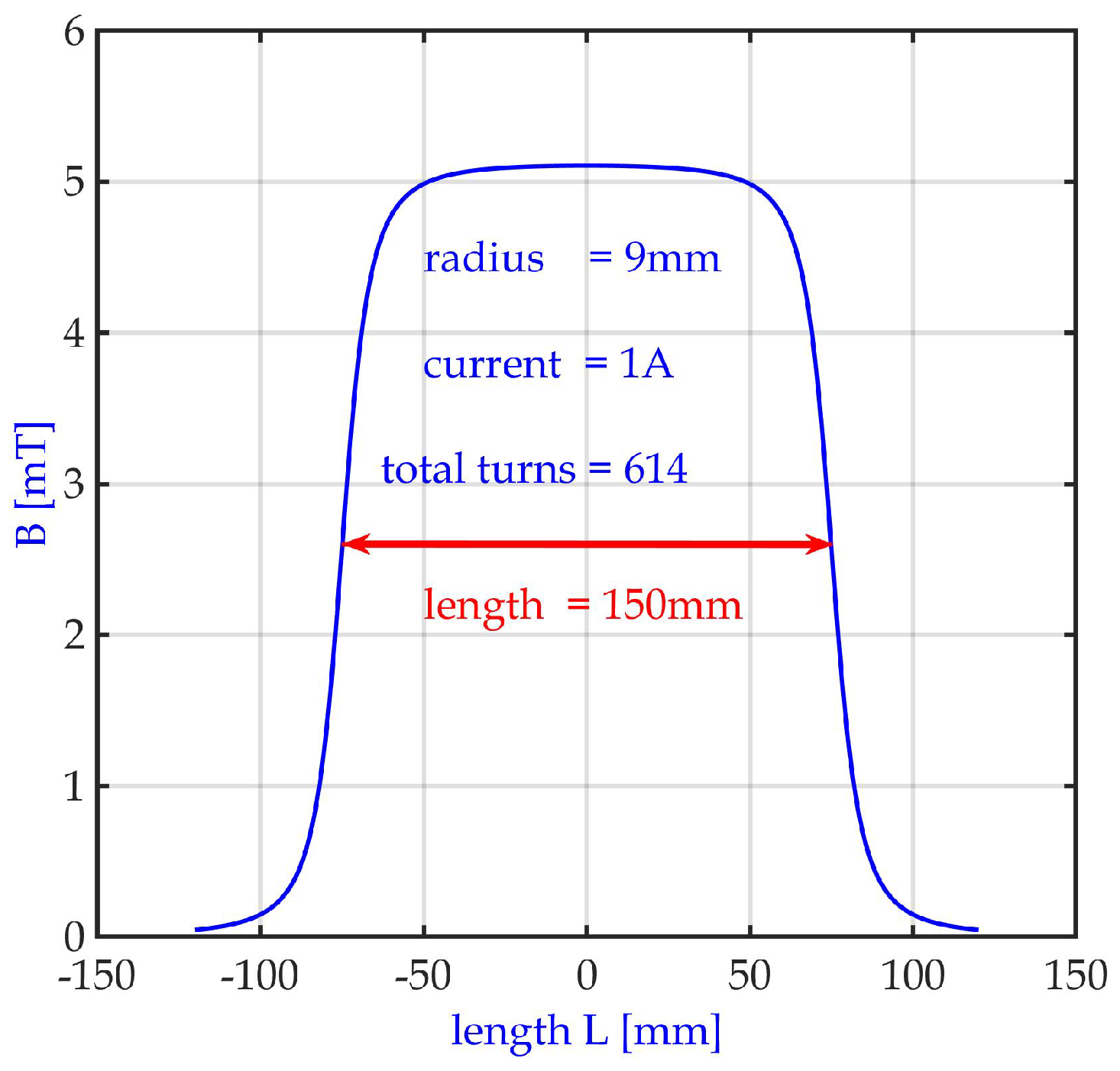
3.2. Longitudinal Magnetic Spatial Resolution
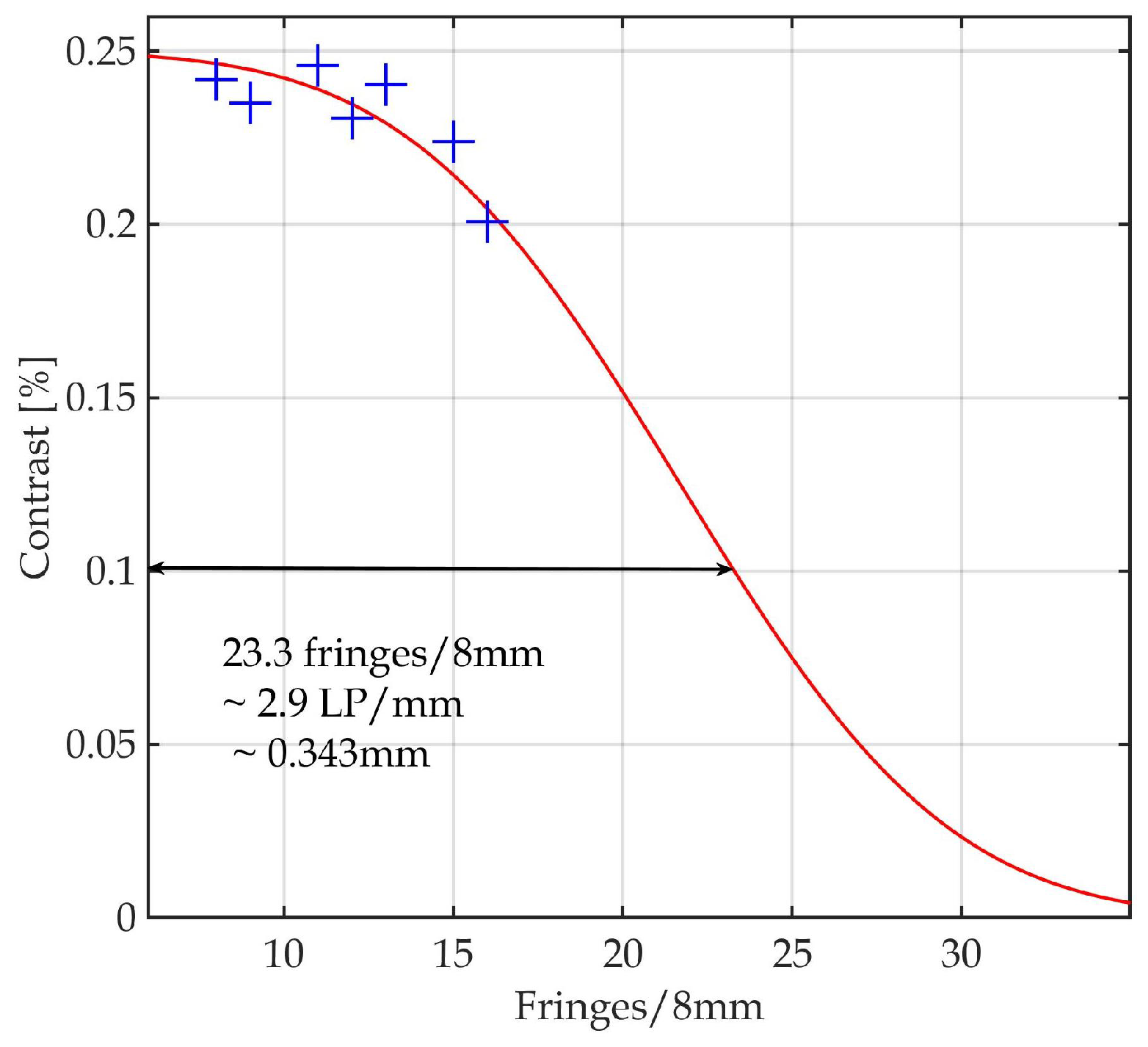
3.3. Lateral Magnetic Spatial Resolution
4. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References and Note
- Harms, A.A.; Zeilinger, A. A New Formulation of Total Unsharpness in Radiography. Phys. Med. Biol. 1977, 22, 70–80. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Harms, A.A.; Wyman, D.R. Mathematics and Physics of Neutron Radiography; D. Reidel Publishing Company: Dordrecht, The Netherlands, 1986. [Google Scholar]
- Brenizer, J.S. Nondestructive Testing Standards—Present and Future; Berger, H., Mordfin, L., Eds.; ASTM Publication Code Number (PCN) 04-011510-22; ASTM: West Conshohocken, PA, USA, 1992; p. 34. [Google Scholar]
- ASTM Standards: Designation: E 803–91 (Re-Approved 1996) Standard Test Method for Determining the L/D Ratio of Neutron Radiography Beams. Available online: https:astm.org/Standards/E803.htm (accessed on 16 July 2021).
- Smith, S.W. Digital Signal Processing; California Technical Publishing: San Diego, CA, USA, 1997–2011; Chapter 25; pp. 423–450. [Google Scholar]
- Buhr, E.; Günther-Kohfahl, S.; Neitzel, U. Accuracy of a simple method for deriving the presampled modulation transfer function of a digital radiographic system from an edge image. Med. Phys. 2003, 30, 2323–2331. [Google Scholar] [CrossRef] [PubMed]
- Samei, E.; Buhr, E.; Granfors, P.; Vandenbroucke, D.; Wang, X. Comparison of edge analysis techniques for the determination of the MTF of digital radiographic systems. Phys. Med. Biol. 2005, 50, 3613–3625. [Google Scholar] [CrossRef] [PubMed]
- Mori, I.; Machida, Y. Deriving the modulation transfer function of CT from extremely noisy edge profiles. Radiol. Phys. Technol. 2009, 2, 22–32. [Google Scholar] [CrossRef]
- Staude, A.; Goebbels, J. Determining the Spatial Resolution in Computed Tomography—Comparison of MTF and Line-Pair Structures. In Proceedings of the International Symposium on Digital Industrial Radiology and Computed Tomography, Berlin, Germany, 20–22 June 2011. [Google Scholar]
- Jakubek, J.; Holy, T.; Lehmann, E.; Pospisil, S.; Uher, J.; Vacik, J.; Vavrik, D. Neutron imaging with Medipix-2 chip and a coated sensor. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2006, 560, 143–147. [Google Scholar] [CrossRef]
- Baessler, S.; Gagarski, A.; Lychagin, E.; Mietke, A.; Muzychka, A.; Nesvizhevsky, V.; Pignol, G.; Strelkov, A.; Toperverg, B.; Zhernenkov, K. New methodical developments for GRANIT. Comptes Rendus Phys. 2011, 12, 729–754. [Google Scholar] [CrossRef]
- Lehmann, E.H.; Frei, G.; Kühne, G.; Boillat, P. The micro-setup for neutron imaging: A major step forward to improve the spatial resolution. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2007, 576, 389–396. [Google Scholar] [CrossRef]
- Tremsin, A.S.; Feller, W.B. The theory of compact and efficient circular-pore MCP neutron collimators. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2006, 556, 556–564. [Google Scholar] [CrossRef] [Green Version]
- Siegmund, O.H.; Vallerga, J.V.; Tremsin, A.S.; Mcphate, J.; Feller, B. High spatial resolution neutron sensing micro-channel plate detectors. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2007, 576, 178–182. [Google Scholar] [CrossRef]
- Williams, S.H.; Hilger, A.; Kardjilov, N.; Manke, I.; Strobl, M.; A Douissard, P.; Martin, T.; Riesemeier, H.; Banhart, J. Detection System for Microimaging with Neutrons. J. Instrum. 2012, 7, P02014. Available online: http://iopscience.iop.org/1748-0221/7/02/P02014 (accessed on 16 July 2021). [CrossRef] [Green Version]
- Parker, J.D.; Harada, M.; Hattori, K.; Iwaki, S.; Kabuki, S.; Kishimoto, Y.; Kubo, H.; Kurosawa, S.; Matsuoka, Y.; Miuchi, K.; et al. Spatial resolution of a μ PIC-based neutron imaging detector. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2013, 726, 155–161. [Google Scholar] [CrossRef] [Green Version]
- Trtik, P.; Hovind, J.; Grünzweig, C.; Bollhalder, A.; Thominet, V.; David, C.; Kaestner, A.; Lehmann, E.H. Improving the Spatial Resolution of Neutron Imaging at Paul Scherrer Institut—The Neutron Microscope Project. Phys. Procedia 2015, 69, 169–176. [Google Scholar] [CrossRef] [Green Version]
- Bingham, P.; Santos-Villalobos, H.; Lavrika, N.; Gregorb, J.; Bilheux, H. Magnified neutron radiography with coded sources. Phys. Procedia 2015, 69, 218–226. [Google Scholar] [CrossRef] [Green Version]
- Naganawa, N.; Awano, S.; Hino, M.; Hirose, M.; Hirota, K.; Kawahara, H.; Kitaguchi, M.; Mishima, K.; Nagae, T.; Shimizu, H.M.; et al. A neutron detector with spatial resolution of submicron using fine-grained nuclear emulsion. In Proceedings of the 8th International Topical Meeting on Neutron Radiography, ITMNR-8, Beijing, China, 4–8 September 2016. [Google Scholar]
- Hussey, D.S.; LaManna, J.M.; Baltic, E.; Jacobson, D.L. Neutron imaging detector with 2 μm spatial resolution based on event reconstruction of neutron capture in gadolinium oxysulfide scintillators. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2017, 866, 9–12. [Google Scholar] [CrossRef]
- Morgano, M.; Trtik, P.; Meyer, M.; Lehmann, E.H.; Hovind, J.; Strobl, M. Unlocking high spatial resolution in neutronimaging through an add-on fibre optics taper. Opt. Express 2018, 26, 1809–1816. [Google Scholar] [CrossRef]
- Cao, R.L.; Biegalski, S.R. The measurement of the presampled MTF of a high spatial resolution neutron imaging system. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2007, 582, 621–628. [Google Scholar] [CrossRef]
- Kuhls-Gilcrist, A.; Jain, A.; Bednarek, D.R.; Hoffmann, K.R.; Rudin, S. Accurate MTF measurement in digital radiography using noise response. Med. Phys. 2010, 37, 724–735. [Google Scholar] [CrossRef] [Green Version]
- Kaestner, A.P.; Kis, Z.; Radebe, M.J.; Mannes, D.; Hovind, J.; Grünzweig, C.; Kardjilov, N.; Lehmann, E.H. Samples to determine the resolution of neutron radiography and tomography. Phys. Procedia 2017, 88, 258–265. [Google Scholar] [CrossRef]
- Rueckel, J.; Stockmar, M.; Pfeiffer, F.; Herzen, J. Spatial resolution characterization of a X-ray microCT system. Appl. Radiat. Isot. 2014, 94, 230–234. [Google Scholar] [CrossRef]
- Trtik, P.; Lehmann, E.H. Progress in High-resolution Neutron Imaging at the Paul Scherrer Institut—The Neutron Microscope Project. J. Phys. Conf. Ser. 2016, 746, 012004. [Google Scholar] [CrossRef] [Green Version]
- Miller, S.R.; Marshall, M.S.J.; Wart, M.; Crha, J.; Trtik, P.; Nagarkar, V.V. High-Resolution Thermal Neutron Imaging With 10Boron/CsI:Tl Scintillator Screen. IEEE Trans. Nucl. Sci. 2020, 67, 1929–1933. [Google Scholar] [CrossRef]
- Hirota, K.; Ariga, T.; Hino, M.; Ichikawa, G.; Kawasaki, S.; Kitaguchi, M.; Mishima, K.; Muto, N.; Naganawa, N.; Shimizu, H.M. Neutron Imaging Using a Fine-Grained Nuclear Emulsion. Imaging 2021, 7, 4. [Google Scholar] [CrossRef]
- Kardjilov, N.; Manke, I.; Strobl, M.; Hilger, A.; Treimer, W.; Meissner, M.; Krist, T.; Banhart, J. Three-dimensional imaging of magnetic fields with polarized neutrons. Nat. Phys. 2008, 4, 399–403. [Google Scholar] [CrossRef] [Green Version]
- Gruenzweig, C.; David, C.; Bunk, O.; Dierolf, M.; Frei, G.; Kühne, G.; Schäfer, R.; Pofahl, S.; Rønnow, H.M.R.; Pfeiffer, F. Bulk magnetic domain structures visualized by neutron dark-field imaging. Appl. Phys. Lett. 2008, 93, 112504. [Google Scholar] [CrossRef] [Green Version]
- Manke, I.; Kardjilov, N.; Hilger, A.; Strobl, M.; Dawson, M.; Banhart, J. Polarized neutron imaging at the CONRAD instrument at Helmholtz Centre Berlin. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2009, 605, 26–29. [Google Scholar] [CrossRef]
- Manke, I.; Kardjilov, N.; Schäfer, R.; Hilger, A.; Strobl, M.; Dawson, M.; Grünzweig, C.; Behr, G.; Hentschel, M.; David, C.; et al. Three-dimensional imaging of magnetic domains. Nat. Commun. 2010, 1, 125. [Google Scholar] [CrossRef]
- Hilger, A. Charakterisierung Magnetischer Strukturen Durch Bildgebende Verfahren mit Kalten Neutronen. Ph.D. Thesis, Technical University Berlin, Berlin, Germany, 2010. [Google Scholar]
- Schulz, M.; Neubauer, A.; Masalovich, S.; Mühlbauer, M.; Calzada, E.; Schillinger, B.; Pfleiderer, C.; Böni, P. Towards a tomographic reconstruction of neutron depolarization data. J. Phys. Conf. Ser. 2010, 211, 012025. [Google Scholar] [CrossRef]
- Treimer, W.; Ebrahimi, O.; Karakas, N.; Seidel, S. PONTO—An instrument for imaging with polarized neutrons. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2011, 651, 53–56. [Google Scholar] [CrossRef]
- Treimer, W.; Ebrahimi, O.; Karakas, N.; Prozorov, R. Polarized neutron imaging and three-dimensional calculation of magnetic flux trapping in bulk of superconductors. Phys. Rev. B 2012, 85, 184522. [Google Scholar] [CrossRef] [Green Version]
- Treimer, W. Radiography and tomography with polarized neutrons. J. Magn. Magn. Mater. 2014, 350, 188–198. [Google Scholar] [CrossRef]
- Hilger, A.; Manke, I.; Kardjilov, N.; Osenberg, M.; Markötter, H.; Banhart, J. Tensorial neutron tomography of three dimensional magnetic vector fields in bulk materials. Nat. Commun. 2018, 9, 4023. [Google Scholar] [CrossRef] [Green Version]
- Sales, M.; Strobl, M.; Shinohara, T.; Tremsin, A.; Kuhn, L.T.; Lionheart, W.R.B.; Desai, N.M.; Dahl, A.B.; Schmidt, S. Three Dimensional Polarimetric Neutron Tomography of Magnetic Fields. Sci. Rep. 2018, 8, 2214. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Treimer, W. Neutron Radiography and Tomography. In Handbook of Advanced Non-Destructive Evaluation; Ida, N., Meyendorf, N., Eds.; Springer Nature Switzerland AG: Cham, Switzerland, 2019; Chapter 34; pp. 1217–1299. [Google Scholar]
- Treimer, W.; Seidel, S.O.; Ebrahimi, O. Neutron tomography using a crystal monochromator. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2010, 621, 502–505. [Google Scholar] [CrossRef]
- Treimer, W.; Strobl, M.; Hilger, A. Observation of edge refraction in ultra small angle neutron scattering. Phys. Lett. A 2002, 305, 87–92. [Google Scholar] [CrossRef]
- Strobl, M.; Treimer, W.; Kardjilov, N.; Hilger, A.; Zabler, S. On neutron phase contrast imaging. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2008, 266, 181–186. [Google Scholar] [CrossRef]
- Tremsin, A.; Lehmann, E.H.; Kardjilov, N.; Strobl, M.; Manke, I.; McPhate, J.; Vallerga, J.V.; Siegmund, O.H.W.; Feller, W.B. Refraction contrast imaging and edge effects in neutron radiography. J. Instrum. 2012, 7, C02047. [Google Scholar] [CrossRef]
- Strobl, M.; Treimer, W.; Walter, P.; Keil, S.; Manke, I. Magnetic field induced differential neutron phase contrast imaging. Appl. Phys. Lett. 2007, 91, 254104. [Google Scholar] [CrossRef]
- Treimer, W.; Strobl, M.; Hilger, A.; Seifert, C.; Feye-Treimer, U. Refraction as imaging signal for computerized (neutron) tomography. Appl. Phys. Lett. 2003, 83, 398–400. [Google Scholar] [CrossRef]
- Strobl, M.; Treimer, W.; Hilger, A. Small angle scattering signals for (neutron) computerized tomography. Appl. Phys. Lett. 2004, 85, 488–490. [Google Scholar] [CrossRef]
- Shannon, C.E. Communication in the Presence of Noise. Proc. IEEE 1998, 86, 447–457. [Google Scholar] [CrossRef]
- NIST Center for Neutron Research, CODATA Fundamental Constants. Available online: https://physics.nist.gov/cuu/Constants/ (accessed on 16 July 2021).
- Walcher, W. Praktikum der Physik; Teubner Studienbücher Physik: Stuttgart, Germany, 1985; p. 266. ISBN 3-519-43016-9. [Google Scholar]
- Treimer, W.; Ebrahimi, O.; Karakas, N. Observation of partial Meissner effect and flux pinning in superconducting lead containing non-superconducting parts. Appl. Phys. Lett. 2012, 101, 162603. [Google Scholar] [CrossRef]
- Köhler, R. Bestimmung der Modulationstransferfunktion für PONTO II im Falle Polarisierter Neutronen. (Determination of the Modulation Transfer Function of PONTO II in the Case of Polarized Neutrons). Bachelor’s Thesis, University of Applied Sciences Beuth Hochschule Berrlin, Department Mathematics-Physics-Chemistry, Berlin, Germany, 2013. [Google Scholar]
- Both Benders Were fabricated by ‘SwissNeutronics’, Neutron Optical Components, CH-5313 Klingnau. 2012.
- Hubert, A.; Schäfer, R. Magnetic Domains, The Analysis of Magnetic Microstructures; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Chatterji, T. (Ed.) Neutron Scattering from Magnetic Materials; Elsevier B. V.: Amsterdam, The Netherlands, 2006. [Google Scholar]




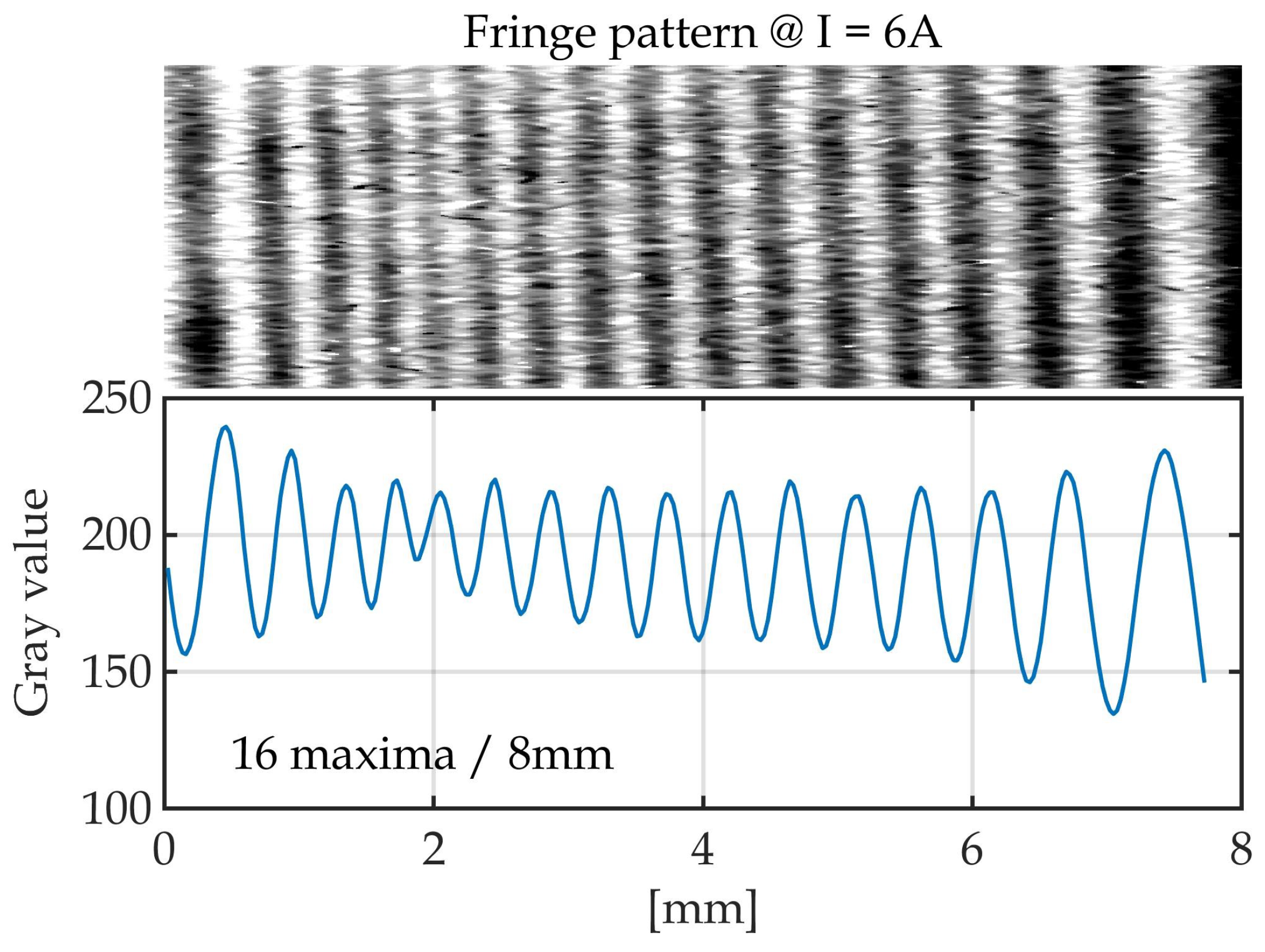


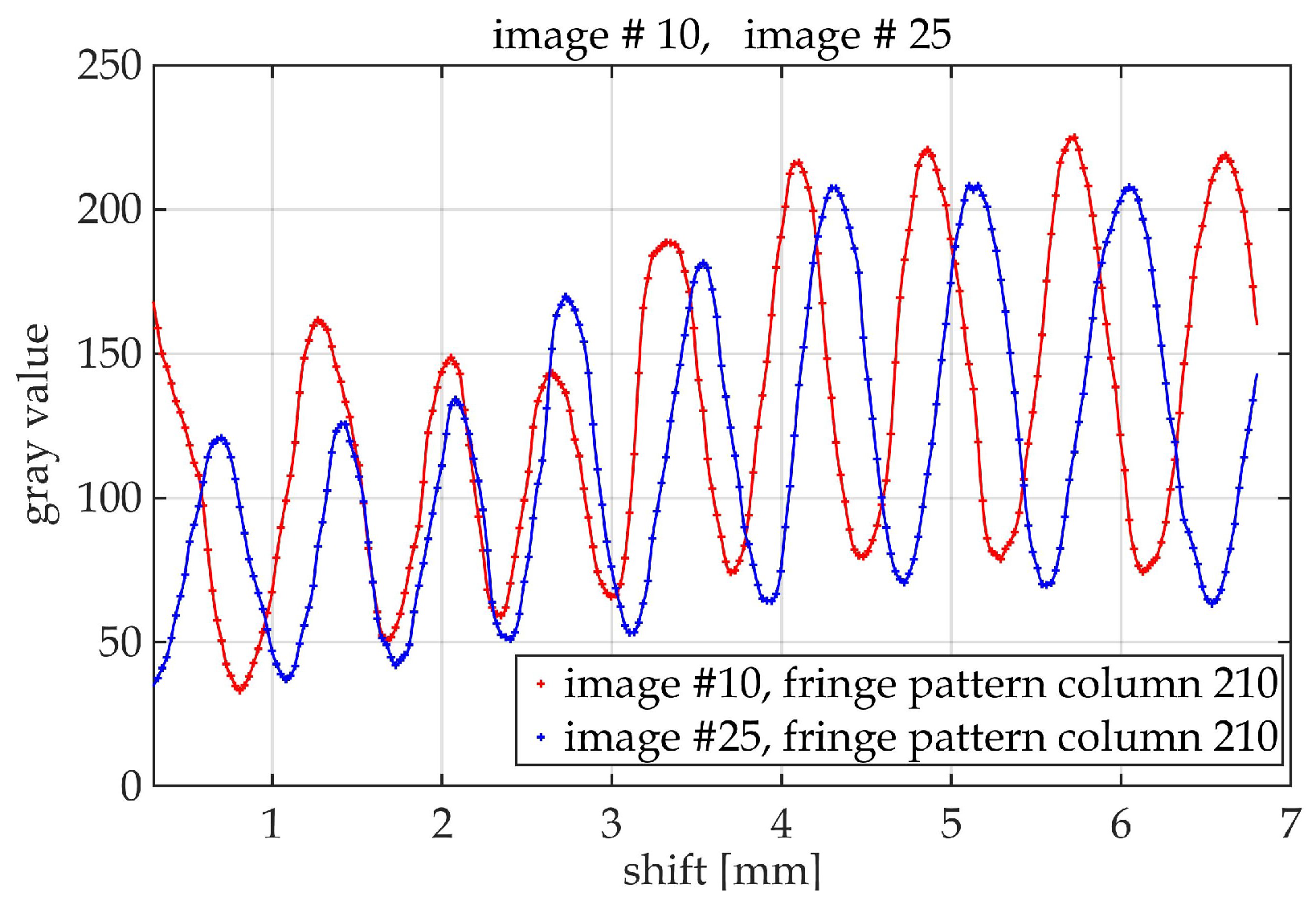
| Shift Nr. | Spin-Flip Distance | Standard Dev. |
|---|---|---|
| 0 | 396 | 87 |
| 10 | 381 | 51 |
| 25 | 381 | 46 |
| 30 | 380 | 48 |
| 50 | 415 | 73 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Treimer, W.; Köhler, R. Determination of the Spatial Resolution in the Case of Imaging Magnetic Fields by Polarized Neutrons. Appl. Sci. 2021, 11, 6973. https://doi.org/10.3390/app11156973
Treimer W, Köhler R. Determination of the Spatial Resolution in the Case of Imaging Magnetic Fields by Polarized Neutrons. Applied Sciences. 2021; 11(15):6973. https://doi.org/10.3390/app11156973
Chicago/Turabian StyleTreimer, Wolfgang, and Ralf Köhler. 2021. "Determination of the Spatial Resolution in the Case of Imaging Magnetic Fields by Polarized Neutrons" Applied Sciences 11, no. 15: 6973. https://doi.org/10.3390/app11156973





