Parametric Analysis of the Edge Capacitance of Uniform Slots and Application to Frequency-Variation Permittivity Sensors
Abstract
:1. Introduction
2. DB-DGS Microstrip Sensor and Sensitivity Analysis
3. Parametric Analysis
4. Validation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Muñoz-Enano, J.; Velez, P.; Gil, M.; Martin, F. Planar Microwave Resonant Sensors: A Review and Recent Developments. Appl. Sci. 2020, 10, 30. [Google Scholar] [CrossRef]
- Gennarelli, G.; Romeo, S.; Scarfi, M.R.; Soldovieri, F. A Microwave Resonant Sensor for Concentration Measurements of Liquid Solutions. IEEE Sens. J. 2013, 13, 1857–1864. [Google Scholar] [CrossRef]
- Jha, A.K.; Akhtar, M.J. A Generalized Rectangular Cavity Approach for Determination of Complex Permittivity of Materials. IEEE Trans. Instrum. Meas. 2014, 63, 2632–2641. [Google Scholar] [CrossRef]
- Wei, P.H.; Morey, B.; Dyson, T.; McMahon, N.; Hsu, Y.Y.; Gazman, S.; Klinker, L.; Ives, B.; Dowling, K.; Rafferty, C. A Conformal Sensor for Wireless Sweat Level Monitoring. In Proceedings of the 2013 IEEE Sensors (SENSORS2013), Baltimore, MD, USA, 3–6 November 2013; pp. 991–994. [Google Scholar]
- Rodgers, M.M.; Pai, V.M.; Conroy, R.S. Recent Advances in Wearable Sensors for Health Monitoring. IEEE Sens. J. 2015, 15, 3119–3126. [Google Scholar] [CrossRef]
- Galindo-Romera, G.; Herraiz-Martinez, F.J.; Gil, M.; Martinez-Martinez, J.J.; Segovia-Vargas, D. Submersible Printed Split-Ring Resonator-Based Sensor for Thin-Film Detection and Permittivity Characterization. IEEE Sens. J. 2016, 16, 3587–3596. [Google Scholar] [CrossRef]
- Grenier, K.; Dubuc, D.; Poleni, P.E.; Kumemura, M.; Toshiyoshi, H.; Fujii, T.; Fujita, H. Integrated Broadband Microwave and Microfluidic Sensor Dedicated to Bioengineering. IEEE Trans. Microw. Theory 2009, 57, 3246–3253. [Google Scholar] [CrossRef]
- Chretiennot, T.; Dubuc, D.; Grenier, K. A Microwave and Microfluidic Planar Resonator for Efficient and Accurate Complex Permittivity Characterization of Aqueous Solutions. IEEE Trans. Microw. Theory 2013, 61, 972–978. [Google Scholar] [CrossRef] [Green Version]
- Salim, A.; Kim, S.H.; Park, J.Y.; Lim, S. Microfluidic Biosensor Based on Microwave Substrate-Integrated Waveguide Cavity Resonator. J. Sens. 2018, 2018. [Google Scholar] [CrossRef] [Green Version]
- Zarifi, M.H.; Sadabadi, H.; Hejazi, S.H.; Daneshmand, M.; Sanati-Nezhad, A. Noncontact and Nonintrusive Microwave-Microfluidic Flow Sensor for Energy and Biomedical Engineering. Sci. Rep. 2018, 8. [Google Scholar] [CrossRef] [Green Version]
- Castillo-León, J.; Svendsen, W.E. Lab-on-a-Chip Devices and Micro-Total Analysis Systems; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar]
- Mandel, C.; Kubina, B.; Schussler, M.; Jakoby, R. Passive Chipless Wireless Sensor for Two-Dimensional Displacement Measurement. In Proceedings of the 41st European Microwave Conference (EuMC 2011), Manchester, UK, 10–13 October 2011; pp. 79–82. [Google Scholar]
- Vargas, M.P. Planar Metamaterial Based Microwave Sensor Arrays for Biomedical Analysis and Treatment; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Ebrahimi, A.; Withayachumnankul, W.; Al-Sarawi, S.; Abbott, D. High-Sensitivity Metamaterial-Inspired Sensor for Microfluidic Dielectric Characterization. IEEE Sens. J. 2014, 14, 1345–1351. [Google Scholar] [CrossRef] [Green Version]
- Schussler, M.; Mandel, C.; Puentes, M.; Jakoby, R. Metamaterial Inspired Microwave Sensors. IEEE Microw. Mag. 2012, 13, 57–68. [Google Scholar] [CrossRef]
- Boybay, M.S.; Ramahi, O.M. Material Characterization Using Complementary Split-Ring Resonators. IEEE Trans. Instrum. Meas. 2012, 61, 3039–3046. [Google Scholar] [CrossRef]
- Lee, C.S.; Yang, C.L. Complementary Split-Ring Resonators for Measuring Dielectric Constants and Loss Tangents. IEEE Microwave Wirel. Components Lett. 2014, 24, 563–565. [Google Scholar] [CrossRef]
- Yang, C.L.; Lee, C.S.; Chen, K.W.; Chen, K.Z. Noncontact Measurement of Complex Permittivity and Thickness by Using Planar Resonators. IEEE Trans. Microw. Theory 2016, 64, 247–257. [Google Scholar] [CrossRef]
- Withayachumnankul, W.; Jaruwongrungsee, K.; Tuantranont, A.; Fumeaux, C.; Abbott, D. Metamaterial-based microfluidic sensor for dielectric characterization. Sens. Actuators A Phys. 2013, 189, 233–237. [Google Scholar] [CrossRef] [Green Version]
- Salim, A.; Lim, S. Complementary Split-Ring Resonator-Loaded Microfluidic Ethanol Chemical Sensor. Sensors 2016, 16, 1802. [Google Scholar] [CrossRef] [Green Version]
- Su, L.J.; Mata-Contreras, J.; Velez, P.; Fernandez-Prieto, A.; Martin, F. Analytical Method to Estimate the Complex Permittivity of Oil Samples. Sensors 2018, 18, 984. [Google Scholar] [CrossRef] [Green Version]
- Abdolrazzaghi, M.; Zarifi, M.H.; Daneshmand, M. Sensitivity Enhancement of Split Ring Resonator based Liquid Sensors. In Proceedings of the 2016 IEEE Sensors, Orlando (SENSORS2016), Orlando, FL, USA, 10–13 October 2016. [Google Scholar]
- Abdolrazzaghi, M.; Zarifi, M.H.; Pedrycz, W.; Daneshmand, M. Robust Ultra-High Resolution Microwave Planar Sensor Using Fuzzy Neural Network Approach. IEEE Sens. J. 2017, 17, 323–332. [Google Scholar] [CrossRef]
- Zarifi, M.H.; Daneshmand, M. Monitoring Solid Particle Deposition in Lossy Medium Using Planar Resonator Sensor. IEEE Sens. J. 2017, 17, 7981–7989. [Google Scholar] [CrossRef]
- Zarifi, M.H.; Deif, S.; Abdolrazzaghi, M.; Chen, B.; Ramsawak, D.; Amyotte, M.; Vahabisani, N.; Hashisho, Z.; Chen, W.X.; Daneshmand, M. A Microwave Ring Resonator Sensor for Early Detection of Breaches in Pipeline Coatings. IEEE Trans. Ind. Electron. 2018, 65, 1626–1635. [Google Scholar] [CrossRef]
- Abdolrazzaghi, M.; Daneshmand, M.; Iyer, A.K. Strongly Enhanced Sensitivity in Planar Microwave Sensors Based on Metamaterial Coupling. IEEE Trans. Microw. Theory 2018, 66, 1843–1855. [Google Scholar] [CrossRef] [Green Version]
- Ebrahimi, A.; Scott, J.; Ghorbani, K. Ultrahigh-Sensitivity Microwave Sensor for Microfluidic Complex Permittivity Measurement. IEEE Trans. Microw. Theory 2019, 67, 4269–4277. [Google Scholar] [CrossRef]
- Horestani, A.K.; Naqui, J.; Shaterian, Z.; Abbott, D.; Fumeaux, C.; Martin, F. Two-dimensional alignment and displacement sensor based on movable broadside-coupled split ring resonators. Sens. Actuators A Phys. 2014, 210, 18–24. [Google Scholar] [CrossRef] [Green Version]
- Naqui, J.; Damm, C.; Wiens, A.; Jakoby, R.; Su, L.J.; Martin, F. Transmission Lines Loaded with Pairs of Magnetically Coupled Stepped Impedance Resonators (SIRs): Modeling and Application to Microwave Sensors. In Proceedings of the 2014 IEEE MTT-S International Microwave Symposium (IMS2014), Tampa, FL, USA, 1–6 June 2014. [Google Scholar]
- Su, L.J.; Naqui, J.; Mata-Contreras, J.; Martin, F. Modeling and Applications of Metamaterial Transmission Lines Loaded With Pairs of Coupled Complementary Split-Ring Resonators (CSRRs). IEEE Antenn. Wirel. Propag. Lett. 2016, 15, 154–157. [Google Scholar] [CrossRef] [Green Version]
- Su, L.J.; Naqui, J.; Mata, J.; Martin, F. Dual-Band Epsilon-Negative (ENG) Transmission Line Metamaterials based on Microstrip Lines Loaded with Pairs of Coupled Complementary Split Ring Resonators (CSRRs): Modeling, Analysis and Applications. In Proceedings of the 9th International Congress on Advanced Electromagnetic Materials in Microwaves and Optics (Metamaterials 2015), Oxford, UK, 7–12 September 2015; pp. 298–300. [Google Scholar]
- Su, L.J.; Naqui, J.; Mata-Contreras, J.; Velez, P.; Martin, F. Transmission line metamaterials based on pairs of coupled split ring resonators (SRRs) and complementary split ring resonators (CSRR): A comparison to the light of the lumped element equivalent circuits. In Proceedings of the International Conference on Electromagnetics in Advanced Applications (ICEAA), Torino, Italy, 7–11 September 2015. [Google Scholar]
- Naqui, J.; Damm, C.; Wiens, A.; Jakoby, R.; Su, L.J.; Mata-Contreras, J.; Martin, F. Transmission Lines Loaded With Pairs of Stepped Impedance Resonators: Modeling and Application to Differential Permittivity Measurements. IEEE Trans. Microw. Theory 2016, 64, 3864–3877. [Google Scholar] [CrossRef] [Green Version]
- Su, L.J.; Mata-Contreras, J.; Velez, P.; Martin, F. Splitter/Combiner Microstrip Sections Loaded With Pairs of Complementary Split Ring Resonators (CSRRs): Modeling and Optimization for Differential Sensing Applications. IEEE Trans. Microw. Theory 2016, 64, 4362–4370. [Google Scholar] [CrossRef]
- Velez, P.; Su, L.J.; Grenier, K.; Mata-Contreras, J.; Dubuc, D.; Martin, F. Microwave Microfluidic Sensor Based on a Microstrip Splitter/Combiner Configuration and Split Ring Resonators (SRRs) for Dielectric Characterization of Liquids. IEEE Sens. J. 2017, 17, 6589–6598. [Google Scholar] [CrossRef] [Green Version]
- Ebrahimi, A.; Scott, J.; Ghorbani, K. Differential Sensors Using Microstrip Lines Loaded With Two Split-Ring Resonators. IEEE Sens. J. 2018, 18, 5786–5793. [Google Scholar] [CrossRef]
- Damm, C.; Schussler, M.; Puentes, M.; Maune, H.; Maasch, M.; Jakoby, R. Artificial Transmission Lines for High Sensitive Microwave Sensors. In Proceedings of the 2009 IEEE Sensors (SENSORS2009), Christchurch, New Zealand, 25–28 October 2009; pp. 755–758. [Google Scholar]
- Ferrandez-Pastor, F.J.; Garcia-Chamizo, J.M.; Nieto-Hidalgo, M. Electromagnetic Differential Measuring Method: Application in Microstrip Sensors Developing. Sensors 2017, 17, 1650. [Google Scholar] [CrossRef] [Green Version]
- Muñoz-Enano, J.; Velez, P.; Barba, M.G.; Martin, F. An Analytical Method to Implement High-Sensitivity Transmission Line Differential Sensors for Dielectric Constant Measurements. IEEE Sens. J. 2020, 20, 178–184. [Google Scholar] [CrossRef]
- Gil, M.; Velez, P.; Aznar-Ballesta, F.; Muñoz-Enano, J.; Martin, F. Differential Sensor Based on Electroinductive Wave Transmission Lines for Dielectric Constant Measurements and Defect Detection. IEEE Trans. Antenn. Propag. 2020, 68, 1876–1886. [Google Scholar] [CrossRef]
- Muñoz-Enano, J.; Velez, P.; Barba, M.G.; Mata-Contreras, J.; Martin, F. Differential-Mode to Common-Mode Conversion Detector Based on Rat-Race Hybrid Couplers: Analysis and Application to Differential Sensors and Comparators. IEEE Trans. Microw. Theory 2020, 68, 1312–1325. [Google Scholar] [CrossRef]
- Muñoz-Enano, J.; Velez, P.; Su, L.J.; Gil-Barba, M.; Martin, F. A Reflective-Mode Phase-Variation Displacement Sensor. IEEE Access 2020, 8, 189565–189575. [Google Scholar] [CrossRef]
- Casacuberta, P.; Muñoz-Enano, J.; Velez, P.; Su, L.J.; Gil, M.; Martin, F. Highly Sensitive Reflective-Mode Defect Detectors and Dielectric Constant Sensors Based on Open-Ended Stepped-Impedance Transmission Lines. Sensors 2020, 20, 6236. [Google Scholar] [CrossRef] [PubMed]
- Coromina, J.; Muñoz-Enano, J.; Vélez, P.; Ebrahimi, A.; Scott, J.; Ghorbani, K.; Martín, F. Capacitively-Loaded Slow-Wave Transmission Lines for Sensitivity Improvement in Phase-Variation Permittivity Sensors. In Proceedings of the 2020 50th European Microwave Conference (EuMC), Utrecht, The Netherlands, 12–14 January 2021; pp. 491–494. [Google Scholar]
- Muñoz-Enano, J.; Vélez, P.; Su, L.; Gil, M.; Casacuberta, P.; Martín, F. On the Sensitivity of Reflective-Mode Phase-Variation Sensors Based on Open-Ended Stepped-Impedance Transmission Lines: Theoretical Analysis and Experimental Validation. IEEE Trans. Microw. Theory Tech. 2021, 69, 308–324. [Google Scholar] [CrossRef]
- Su, L.J.; Muñoz-Enano, J.; Velez, P.; Orta, P.C.; Gil, M.; Martin, F. Highly Sensitive Phase Variation Sensors Based on Step-Impedance Coplanar Waveguide (CPW) Transmission Lines. IEEE Sens. J. 2021, 21, 2864–2872. [Google Scholar] [CrossRef]
- Su, L.J.; Muñoz-Enano, J.; Velez, P.; Casacuberta, P.; Gil, M.; Martin, F. Phase-Variation Microwave Sensor for Permittivity Measurements Based on a High-Impedance Half-Wavelength Transmission Line. IEEE Sens. J. 2021, 21, 10647–10656. [Google Scholar] [CrossRef]
- Su, L.J.; Muñoz-Enano, J.; Velez, P.; Gil-Barba, M.; Casacuberta, P.; Martin, F. Highly Sensitive Reflective-Mode Phase-Variation Permittivity Sensor Based on a Coplanar Waveguide Terminated With an Open Complementary Split Ring Resonator (OCSRR). IEEE Access 2021, 9, 27928–27944. [Google Scholar] [CrossRef]
- Muñoz-Enano, J.; Coromina, J.; Velez, P.; Su, L.J.; Gil, M.; Casacuberta, P.; Martin, F. Planar Phase-Variation Microwave Sensors for Material Characterization: A Review and Comparison of Various Approaches. Sensors 2021, 21, 1542. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Coromina, J.; Muñoz-Enano, J.; Velez, P.; Scott, J.; Ghorbani, K.; Martin, F. Highly Sensitive Phase-Variation Dielectric Constant Sensor Based on a Capacitively-Loaded Slow-Wave Transmission Line. IEEE Trans. Circuits I 2021, 68, 2787–2799. [Google Scholar] [CrossRef]
- Naqui, J.; Duran-Sindreu, M.; Martin, F. Novel Sensors Based on the Symmetry Properties of Split Ring Resonators (SRRs). Sensors 2011, 11, 7545–7553. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Naqui, J.; Durán-Sindreu, M.; Martín, F. On the symmetry properties of coplanar waveguides loaded with symmetric resonators: Analysis and potential applications. In Proceedings of the 2012 IEEE/MTT-S International Microwave Symposium Digest (MTT2012), Montreal, QC, Canada, 17–22 June 2012; pp. 1–3. [Google Scholar]
- Naqui, J.; Duran-Sindreu, M.; Martin, F. Alignment and Position Sensors Based on Split Ring Resonators. Sensors 2012, 12, 11790–11797. [Google Scholar] [CrossRef] [Green Version]
- Naqui, J.; Martin, F. Transmission Lines Loaded With Bisymmetric Resonators and Their Application to Angular Displacement and Velocity Sensors. IEEE Trans. Microw. Theory 2013, 61, 4700–4713. [Google Scholar] [CrossRef]
- Horestani, A.K.; Fumeaux, C.; Al-Sarawi, S.F.; Abbott, D. Displacement Sensor Based on Diamond-Shaped Tapered Split Ring Resonator. IEEE Sens. J. 2013, 13. [Google Scholar] [CrossRef]
- Horestani, A.K.; Abbott, D.; Fumeaux, C. Rotation Sensor Based on Horn-Shaped Split Ring Resonator. IEEE Sens. J. 2013, 13, 3014–3015. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Withayachumnankul, W.; Al-Sarawi, S.F.; Abbott, D. Metamaterial-Inspired Rotation Sensor with Wide Dynamic Range. IEEE Sens. J. 2014, 14, 2609–2614. [Google Scholar] [CrossRef] [Green Version]
- Horestani, A.K.; Naqui, J.; Abbott, D.; Fumeaux, C.; Martin, F. Two-dimensional displacement and alignment sensor based on reflection coefficients of open microstrip lines loaded with split ring resonators. Electron. Lett. 2014, 50, 620–622. [Google Scholar] [CrossRef] [Green Version]
- Naqui, J.; Martin, F. Angular Displacement and Velocity Sensors Based on Electric-LC (ELC) Loaded Microstrip Lines. IEEE Sens. J. 2014, 14, 939–940. [Google Scholar] [CrossRef] [Green Version]
- Naqui, J.; Coromina, J.; Karami-Horestani, A.; Fumeaux, C.; Martin, F. Angular Displacement and Velocity Sensors Based on Coplanar Waveguides (CPWs) Loaded with S-Shaped Split Ring Resonators (S-SRR). Sensors 2015, 15, 9628–9650. [Google Scholar] [CrossRef] [Green Version]
- Velez, P.; Muñoz-Enano, J.; Ebrahimi, A.; Herrojo, C.; Paredes, F.; Scott, J.; Ghorbani, K.; Martin, F. Single-Frequency Amplitude-Modulation Sensor for Dielectric Characterization of Solids and Microfluidics. IEEE Sens. J. 2021, 21, 12189–12201. [Google Scholar] [CrossRef]
- Shi, D.Y.; Guo, J.H.; Chen, L.; Xia, C.C.; Yu, Z.F.; Ai, Y.; Li, C.M.; Kang, Y.J.; Wang, Z.M. Differential microfluidic sensor on printed circuit board for biological cells analysis. Electrophoresis 2015, 36, 1854–1858. [Google Scholar] [CrossRef] [PubMed]
- Velez, P.; Grenier, K.; Mata-Contreras, J.; Dubuc, D.; Martin, F. Highly-Sensitive Microwave Sensors Based on Open Complementary Split Ring Resonators (OCSRRs) for Dielectric Characterization and Solute Concentration Measurement in Liquids. IEEE Access 2018, 6, 48324–48338. [Google Scholar] [CrossRef]
- Vélez, P.; Muñoz-Enano, J.; Grenier, K.; Mata-Contreras, J.; Dubuc, D.; Martín, F. Split Ring Resonator-Based Microwave Fluidic Sensors for Electrolyte Concentration Measurements. IEEE Sens. J. 2019, 19, 2562–2569. [Google Scholar] [CrossRef]
- Velez, P.; Muñoz-Enano, J.; Gil, M.; Mata-Contreras, J.; Martin, F. Differential Microfluidic Sensors Based on Dumbbell-Shaped Defect Ground Structures in Microstrip Technology: Analysis, Optimization, and Applications. Sensors 2019, 19, 31889. [Google Scholar] [CrossRef] [Green Version]
- Muñoz-Enano, J.; Vélez, P.; Gil, M.; Mata-Contreras, J.; Martín, F. Microwave Comparator based on Defect Ground Structures. In Proceedings of the 2019 European Microwave Conference in Central Europe (EuMCE), Prague, Czech Republic, 13–15 May 2019; pp. 244–247. [Google Scholar]
- Vélez, P.; Muñoz-Enano, J.; Martín, F. Electrolyte Concentration Measurements in DI Water with 0.125 g/L Resolution by means of CSRR-Based Structures. In Proceedings of the 2019 49th European Microwave Conference (EuMC), Paris, France, 1–3 October 2019; pp. 340–343. [Google Scholar]
- Muñoz-Enano, J.; Vélez, P.; Gil, M.; Mata-Contreras, J.; Grenier, K.; Dubuc, D.; Martín, F. Microstrip Lines Loaded with Metamaterial-Inspired Resonators for Microwave Sensors/Comparators with Optimized Sensitivity. In Proceedings of the 2019 49th European Microwave Conference (EuMC), Paris, France, 1–3 October 2019; pp. 754–757. [Google Scholar]
- Muñoz-Enano, J.; Velez, P.; Gil, M.; Martin, F. Microfluidic reflective-mode differential sensor based on open split ring resonators (OSRRs). Int. J. Microw. Wirel. Technol. 2020, 12, 588–597. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Scott, J.; Ghorbani, K. Transmission Lines Terminated With LC Resonators for Differential Permittivity Sensing. IEEE Microw. Wirel. Compon. Lett. 2018, 28, 1149–1151. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Scott, J.; Ghorbani, K. Microwave reflective biosensor for glucose level detection in aqueous solutions. Sens. Actuators A Phys. 2020, 301, 1662. [Google Scholar] [CrossRef]
- Velez, P.; Muñoz-Enano, J.; Martin, F. Differential Sensing Based on Quasi-Microstrip Mode to Slot-Mode Conversion. IEEE IEEE Microw. Wirel. Compon. Lett. 2019, 29, 690–692. [Google Scholar] [CrossRef]
- Naqui, J. Symmetry Properties in Transmission Lines Loaded with Electrically Small Resonators Circuit Modeling and Applications; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar]
- Martín, F. Artificial Transmission Lines for RF and Microwave Applications; John Wiley: Hoboken, NJ, USA, 2015. [Google Scholar]
- Marques, R.; Martin, F.; Sorolla, M. Metamaterials with Negative Parameters: Theory, Design, and Microwave Applications; Wiley-Interscience: Hoboken, NJ, USA; Lightning Source UK Ltd.: Milton Keynes, UK, 2013. [Google Scholar]
- Duran-Sindreu, M.; Naqui, J.; Paredes, F.; Bonache, J.; Martin, F. Electrically Small Resonators for Planar Metamaterial, Microwave Circuit and Antenna Design: A Comparative Analysis. Appl. Sci. 2012, 2, 375–395. [Google Scholar] [CrossRef] [Green Version]
- Makimoto, M.; Yamashita, S. Compact bandpass filters using stepped impedance resonators. Proc. IEEE 1979, 67, 16–19. [Google Scholar] [CrossRef]
- Naqui, J.; Duran-Sindreu, M.; Bonache, J.; Martin, F. Implementation of shunt-connected series resonators through stepped-impedance shunt stubs: Analysis and limitations. IET Microw. Antennas Propag. 2011, 5, 1336–1342. [Google Scholar] [CrossRef]
- Naqui, J.; Martín, F. Mechanically Reconfigurable Microstrip Lines Loaded with Stepped Impedance Resonators and Potential Applications. Int. J. Antennas Propag. 2014, 2014, 1–8. [Google Scholar] [CrossRef]
- Pendry, J.B.; Holden, A.J.; Robbins, D.J.; Stewart, W.J. Magnetism from conductors and enhanced nonlinear phenomena. IEEE Trans. Microw. Theory 1999, 47, 2075–2084. [Google Scholar] [CrossRef] [Green Version]
- Martel, J.; Marques, R.; Falcone, F.; Baena, J.D.; Medina, F.; Martin, F.; Sorolla, M. A new LC series element for compact bandpass filter design. IEEE Microw. Wirel. Compon. Lett. 2004, 14, 210–212. [Google Scholar] [CrossRef]
- Baena, J.D.; Marques, R.; Medina, F.; Martel, J. Artificial magnetic metamaterial design by using spiral resonators. Phys. Rev. B 2004, 69, 4402. [Google Scholar] [CrossRef]
- Schurig, D.; Mock, J.J.; Smith, D.R. Electric-field-coupled resonators for negative permittivity metamaterials. Appl. Phys. Lett. 2006, 88, 6681. [Google Scholar] [CrossRef] [Green Version]
- Ahn, D.; Park, J.S.; Kim, C.S.; Kim, J.; Qian, Y.X.; Itoh, T. A design of the low-pass filter using the novel microstrip defected ground structure. IEEE Trans. Microw. Theory 2001, 49, 86–93. [Google Scholar] [CrossRef]
- Safwat, A.M.E.; Podevin, F.; Ferrari, P.; Vilcot, A. Tunable bandstop defected ground structure resonator using reconfigurable dumbbell-shaped coplanar waveguide. IEEE Trans Microw. Theory 2006, 54, 3559–3564. [Google Scholar] [CrossRef]
- Falcone, F.; Lopetegi, T.; Baena, J.D.; Marques, R.; Martin, F.; Sorolla, M. Effective negative-ε stopband microstrip lines based on complementary split ring resonators. IEEE Microw. Wirel. Compon. Lett. 2004, 14, 280–282. [Google Scholar] [CrossRef]
- Velez, A.; Aznar, F.; Bonache, J.; Velazquez-Ahumada, M.C.; Martel, J.; Martin, F. Open Complementary Split Ring Resonators (OCSRRs) and Their Application to Wideband CPW Band Pass Filters. IEEE Microw. Wirel. Compon. Lett. 2009, 19, 197–199. [Google Scholar] [CrossRef]
- Naqui, J.; Duran-Sindreu, M.; Martin, F. Differential and Single-Ended Microstrip Lines Loaded with Slotted Magnetic-LC Resonators. Int. J. Antenn. Propag. 2013, 2013. [Google Scholar] [CrossRef]
- Muñoz-Enano, J.; Velez, P.; Herrojo, C.; Gil, M.; Martin, F. On the Sensitivity of Microwave Sensors based on Slot Resonators and Frequency Variation. In Proceedings of the 2019 International Conference on Electromagnetics in Advanced Applications (ICEAA), Granada, Spain, 9–13 September 2019; pp. 112–115. [Google Scholar]
- Drake, E.; Medina, F.; Horno, M. Quick computation of [C] and [L] matrices of generalized multiconductor coplanar waveguide transmission lines. IEEE Trans. Microw. Theory Tech. 1994, 42, 2328–2335. [Google Scholar] [CrossRef]
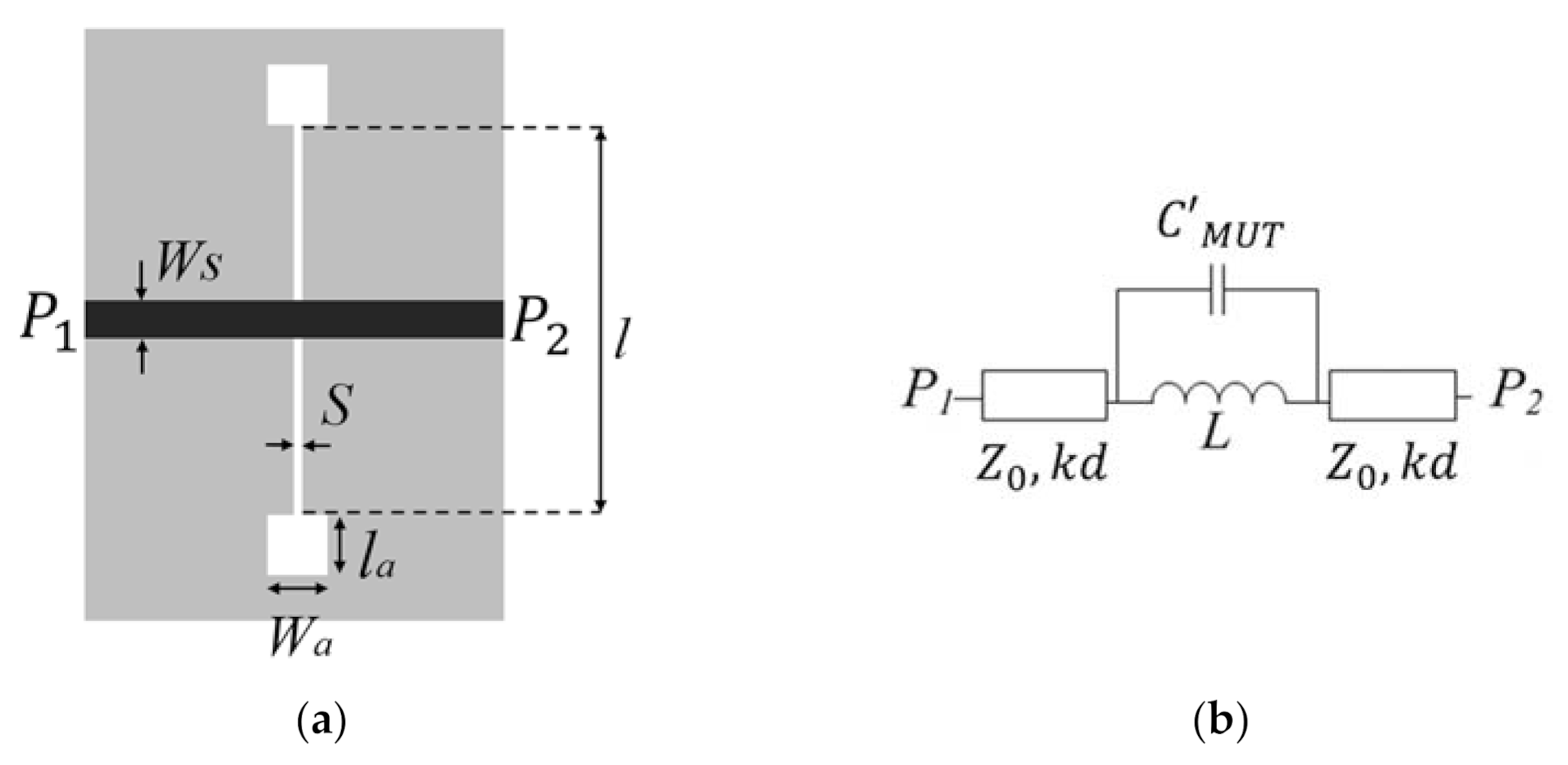
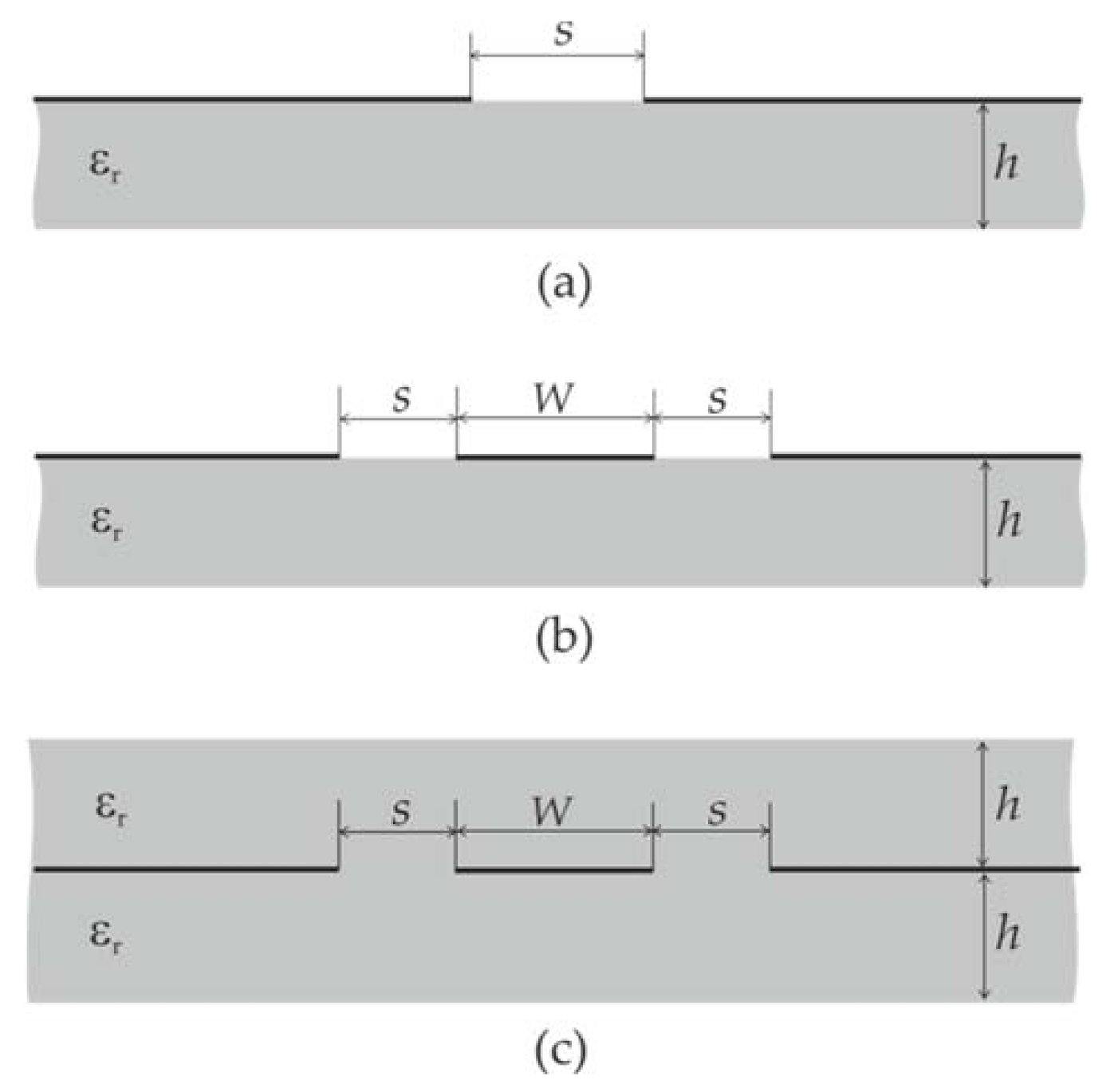

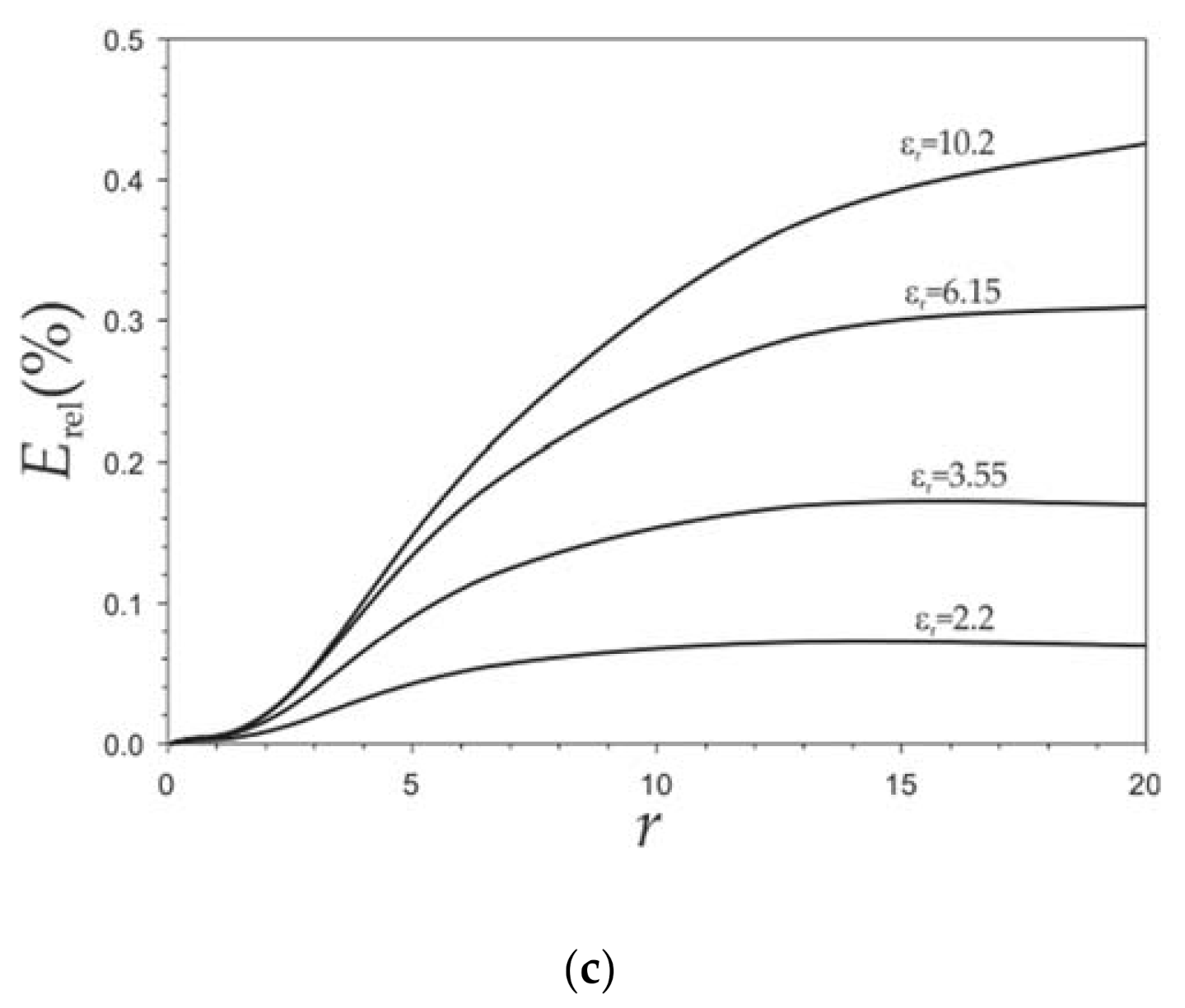


| Sensor | f0,air (GHz) | Ws (mm) | εr | h (mm) | S (mm) | l (mm) | Wa (mm) | la (mm) |
|---|---|---|---|---|---|---|---|---|
| A | 3.204 | 3.91 | 2.20 | 1.270 | 0.300 | 21 | 3.7 | 3.7 |
| B | 3.226 | 0.562 | 3.55 | 0.254 | 0.300 | 20 | 3.5 | 3.5 |
| C | 3.22 | 1.13 | 3.55 | 0.508 | 0.600 | 21.6 | 3.5 | 3.5 |
| D | 3.24 | 0.368 | 6.15 | 0.254 | 0.200 | 20 | 2.3 | 2.3 |
| E | 3.28 | 1.184 | 10.2 | 1.270 | 0.200 | 13.5 | 1.7 | 1.7 |
| F | 3.29 | 1.184 | 10.2 | 1.270 | 0.300 | 15 | 1.6 | 1.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muñoz-Enano, J.; Martel, J.; Vélez, P.; Medina, F.; Su, L.; Martín, F. Parametric Analysis of the Edge Capacitance of Uniform Slots and Application to Frequency-Variation Permittivity Sensors. Appl. Sci. 2021, 11, 7000. https://doi.org/10.3390/app11157000
Muñoz-Enano J, Martel J, Vélez P, Medina F, Su L, Martín F. Parametric Analysis of the Edge Capacitance of Uniform Slots and Application to Frequency-Variation Permittivity Sensors. Applied Sciences. 2021; 11(15):7000. https://doi.org/10.3390/app11157000
Chicago/Turabian StyleMuñoz-Enano, Jonathan, Jesús Martel, Paris Vélez, Francisco Medina, Lijuan Su, and Ferran Martín. 2021. "Parametric Analysis of the Edge Capacitance of Uniform Slots and Application to Frequency-Variation Permittivity Sensors" Applied Sciences 11, no. 15: 7000. https://doi.org/10.3390/app11157000
APA StyleMuñoz-Enano, J., Martel, J., Vélez, P., Medina, F., Su, L., & Martín, F. (2021). Parametric Analysis of the Edge Capacitance of Uniform Slots and Application to Frequency-Variation Permittivity Sensors. Applied Sciences, 11(15), 7000. https://doi.org/10.3390/app11157000










