Probability Characteristics, Area Reduction, and Wind Directionality Effects of Extreme Pressure Coefficients of High-Rise Buildings
Abstract
:1. Introduction
2. Experiment Setup and Data Analysis
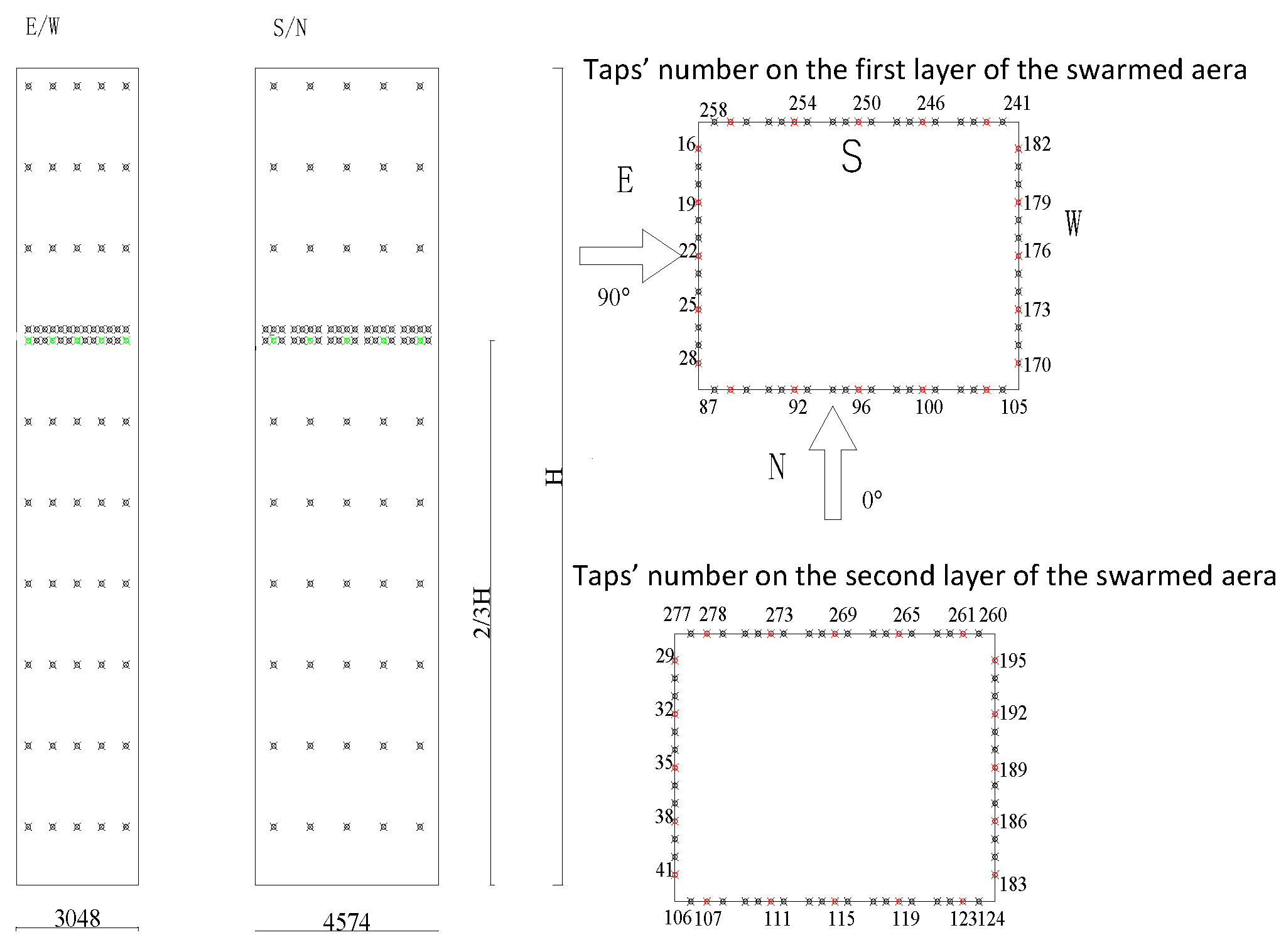
2.1. Wind Tunnel Test Setup
2.2. Data Analysis
3. Results and Discussion
3.1. Probability Characteristics of Extreme Pressure Coefficients
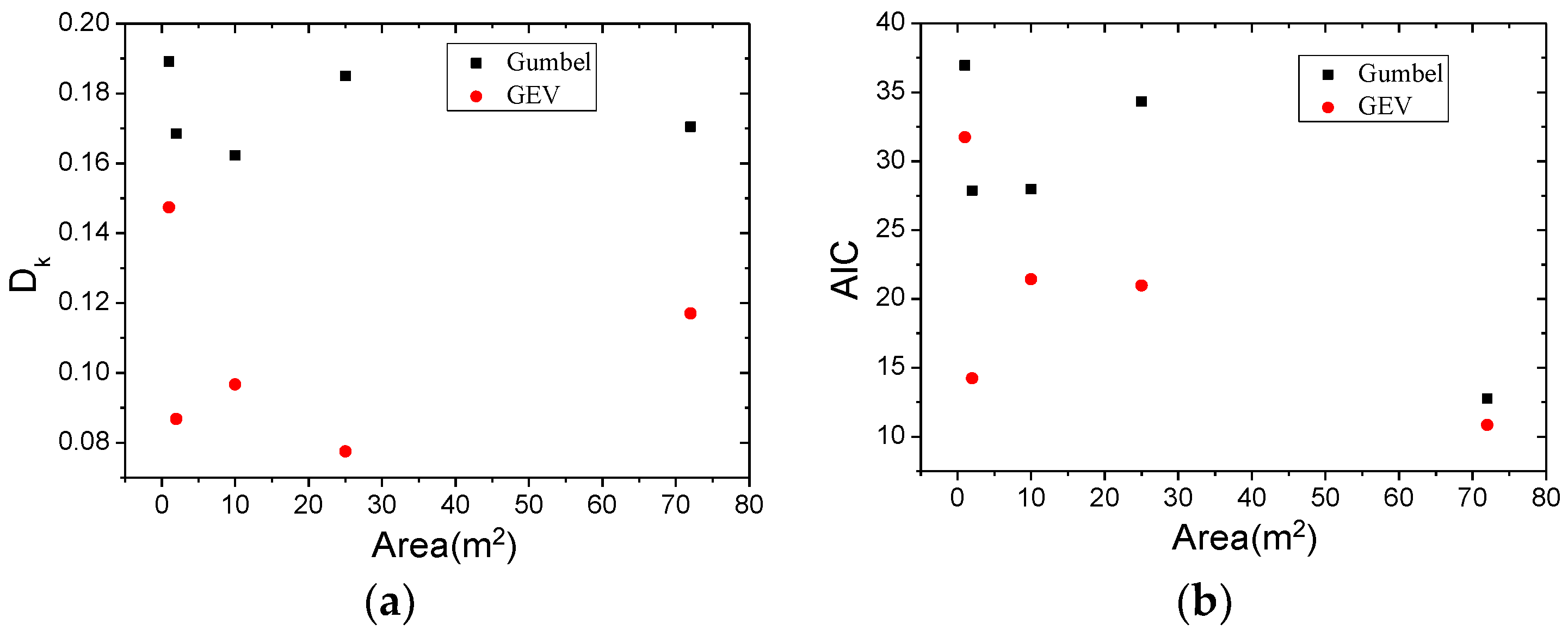
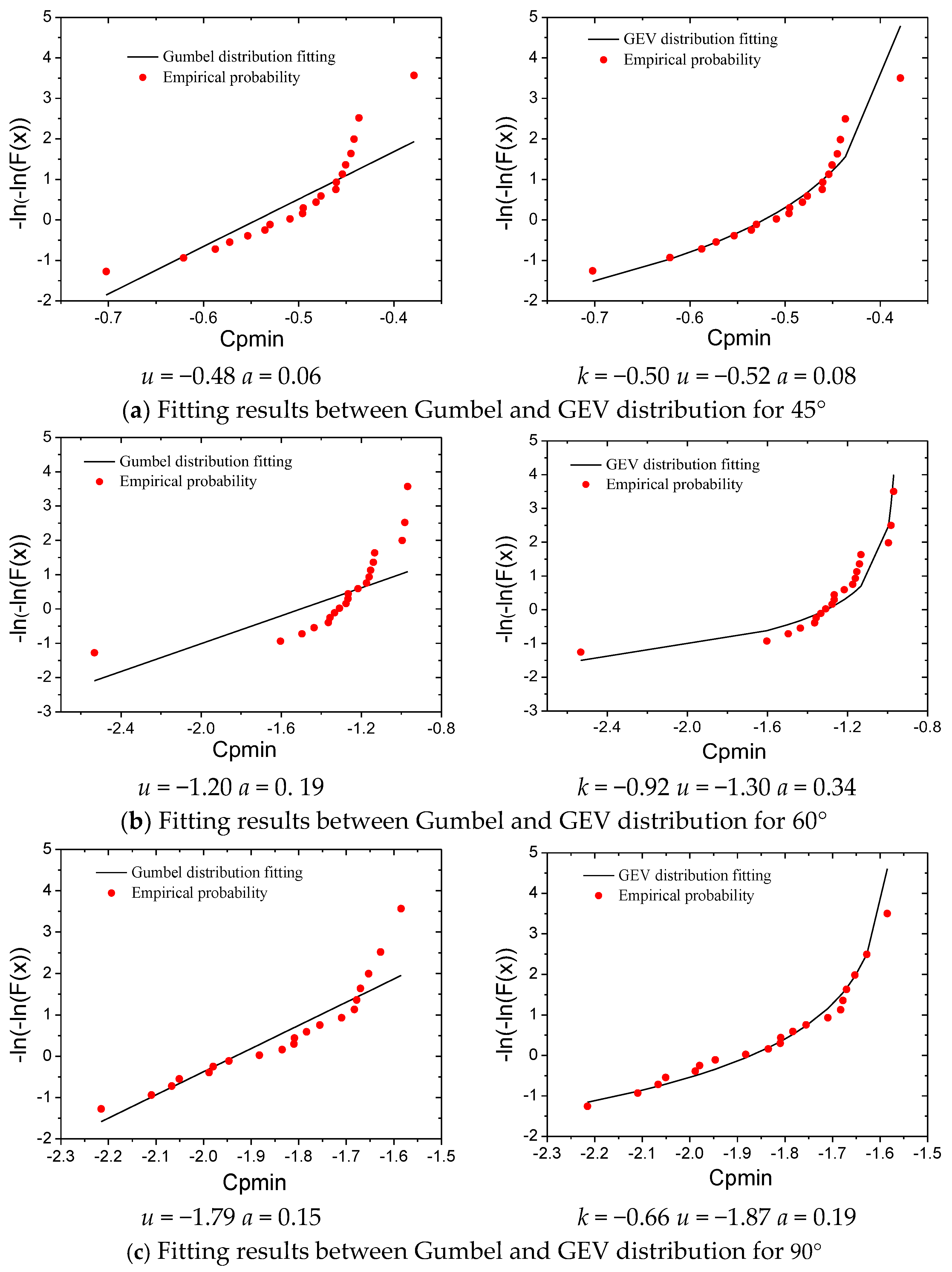
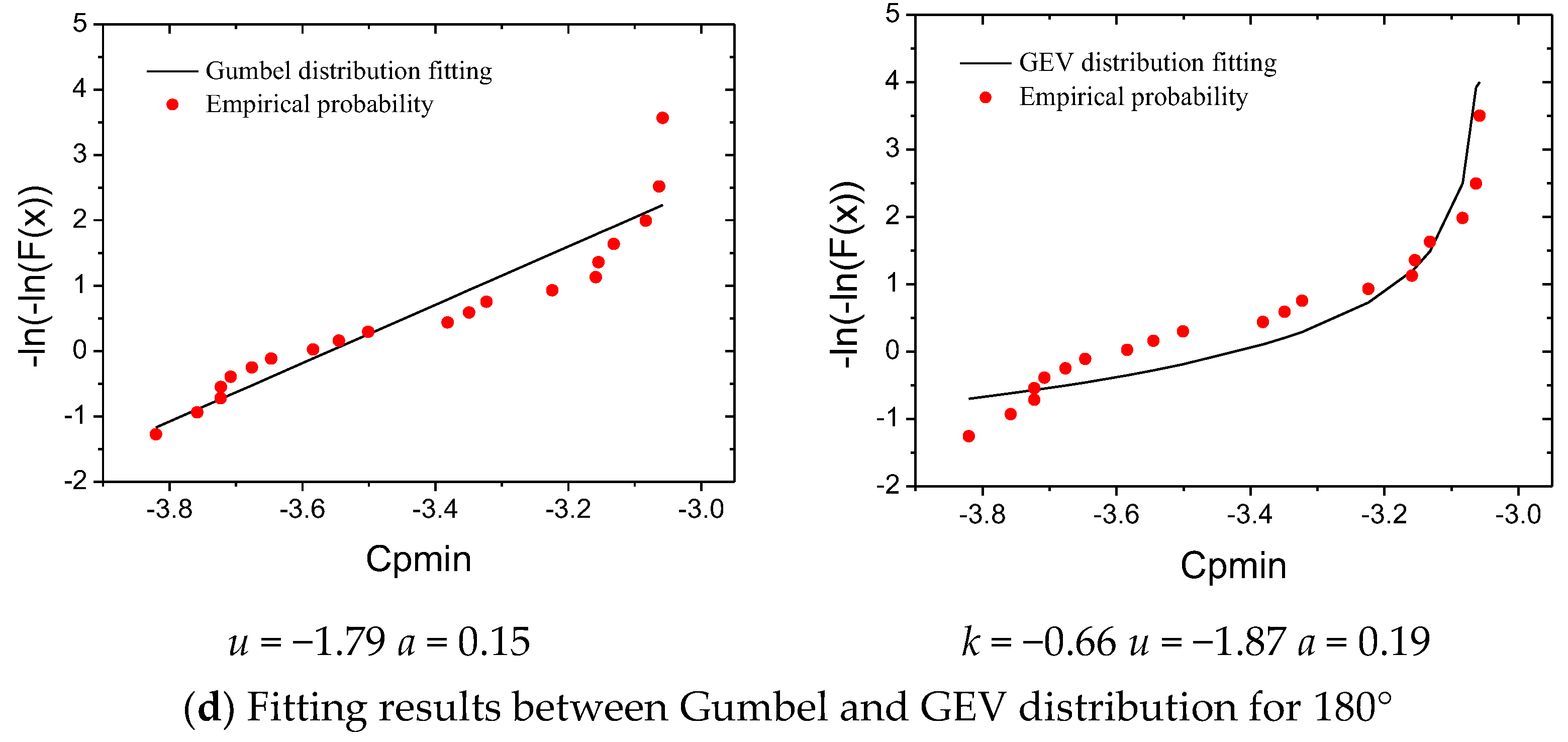
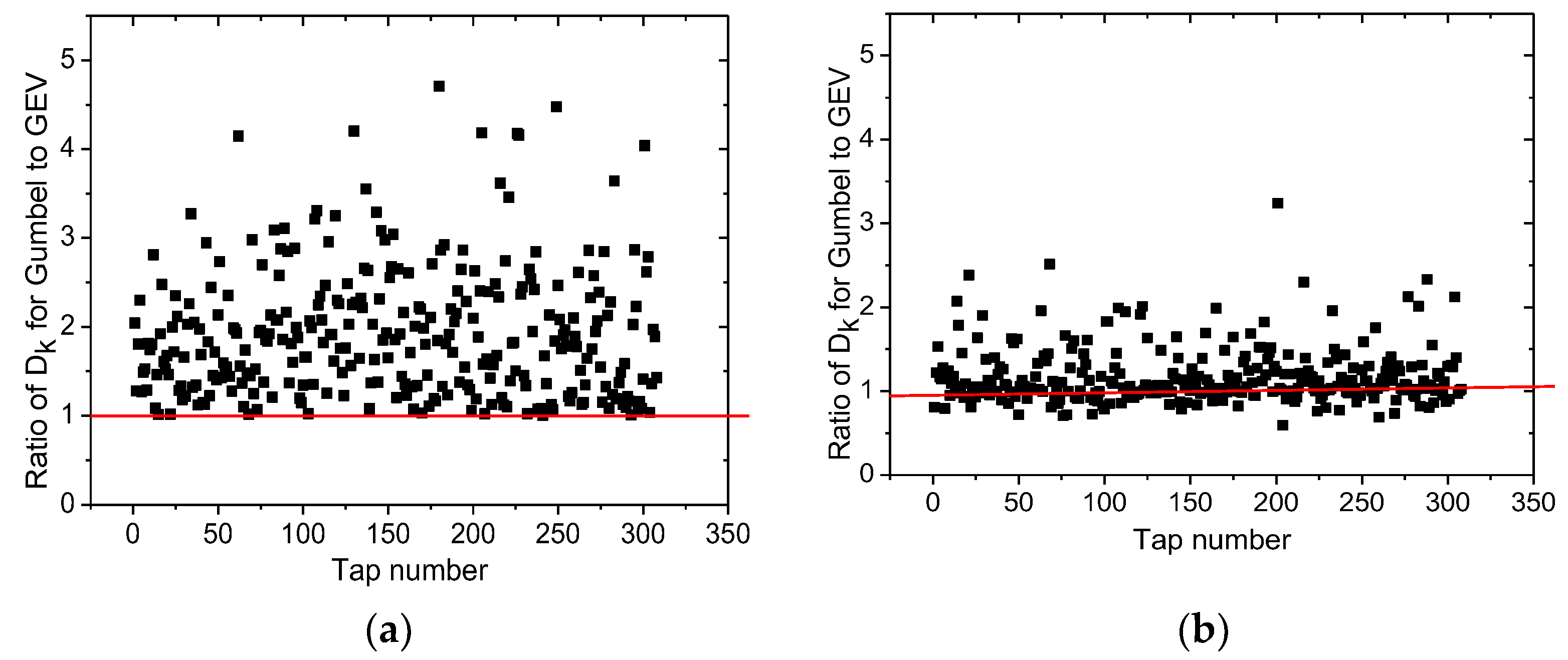
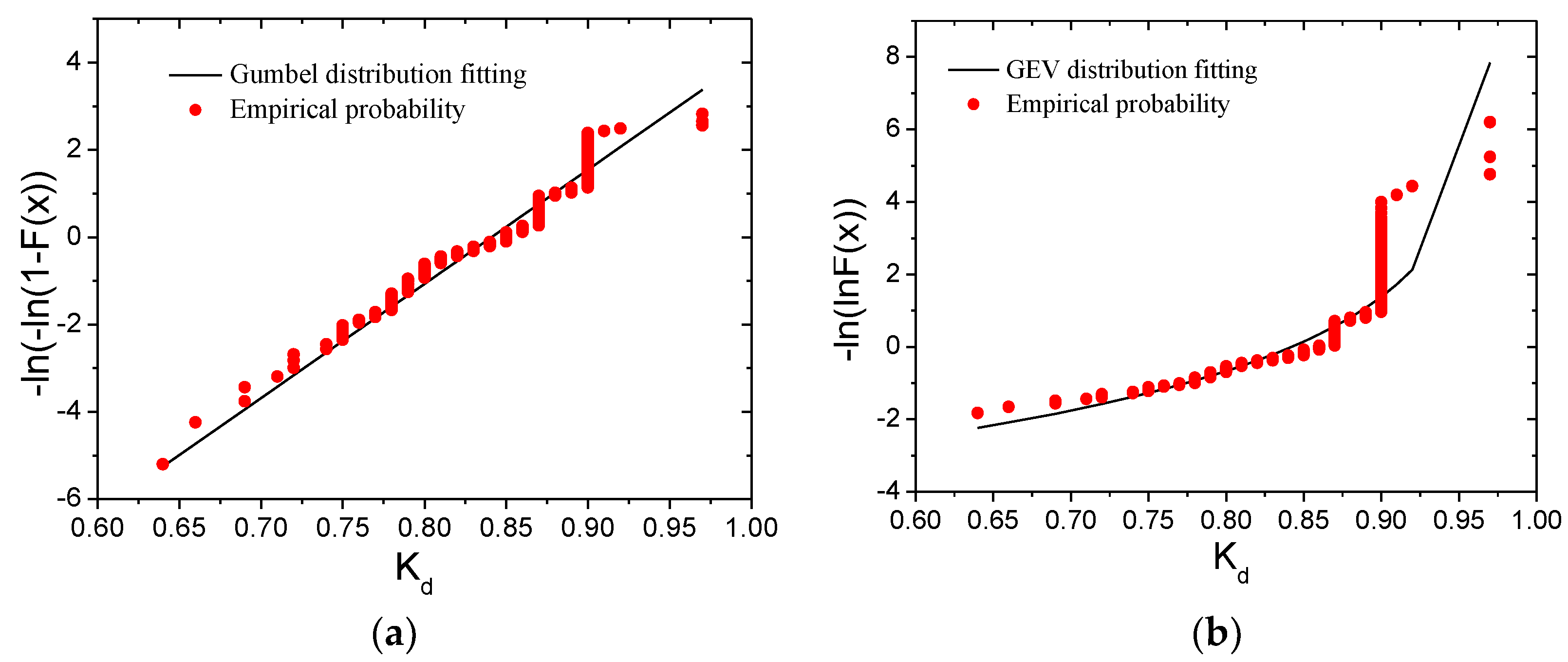
3.1.1. Extreme Value Distribution Type
3.1.2. Probability Distribution Modelling of Extreme Pressure Coefficient
3.1.3. Comparison of Extreme Pressure Coefficients with Current Specifications
3.2. Area Reduction of Extreme Pressure Coefficient
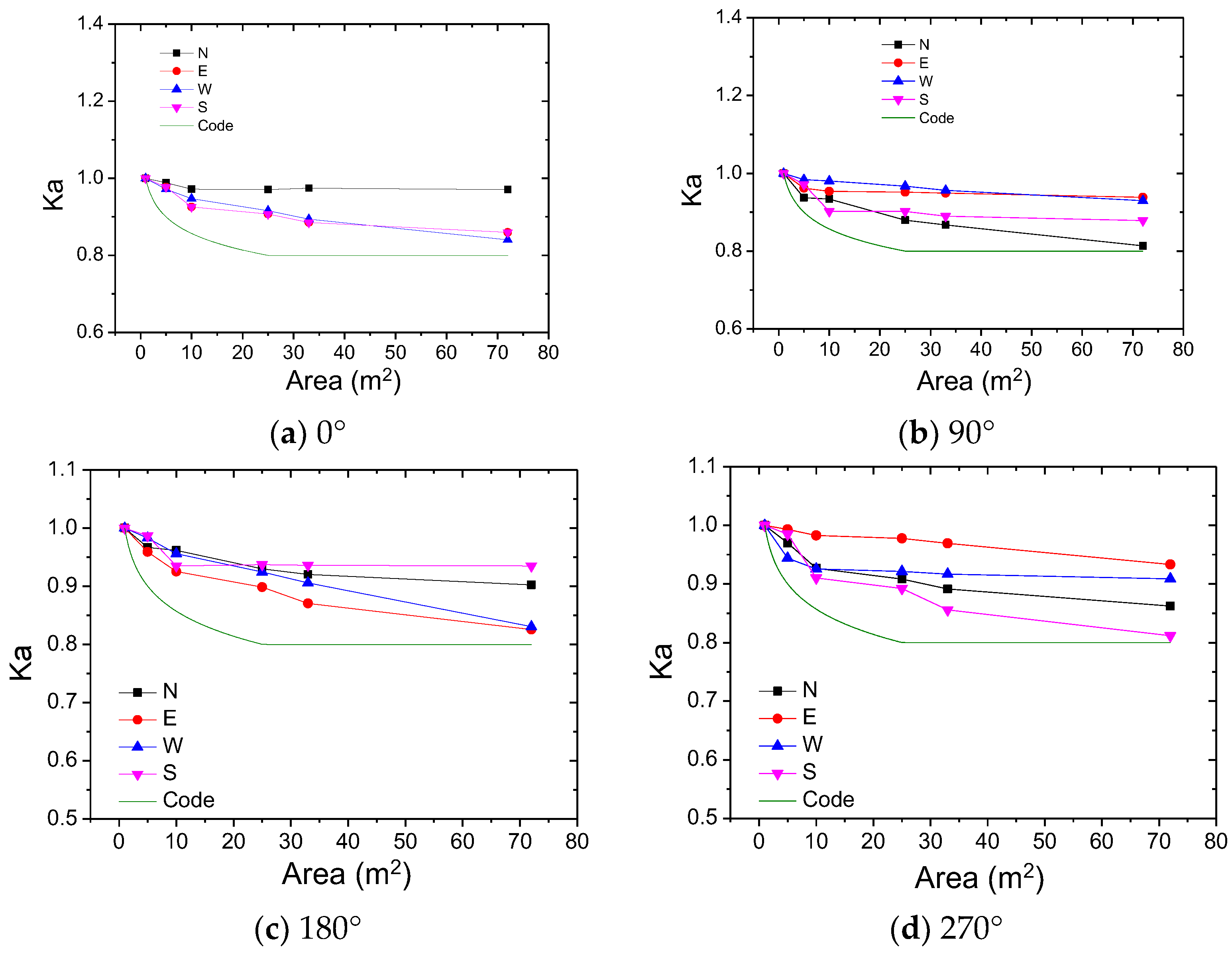
3.2.1. Extreme Pressure Coefficient for Different Area Sizes under Different Wind Angles
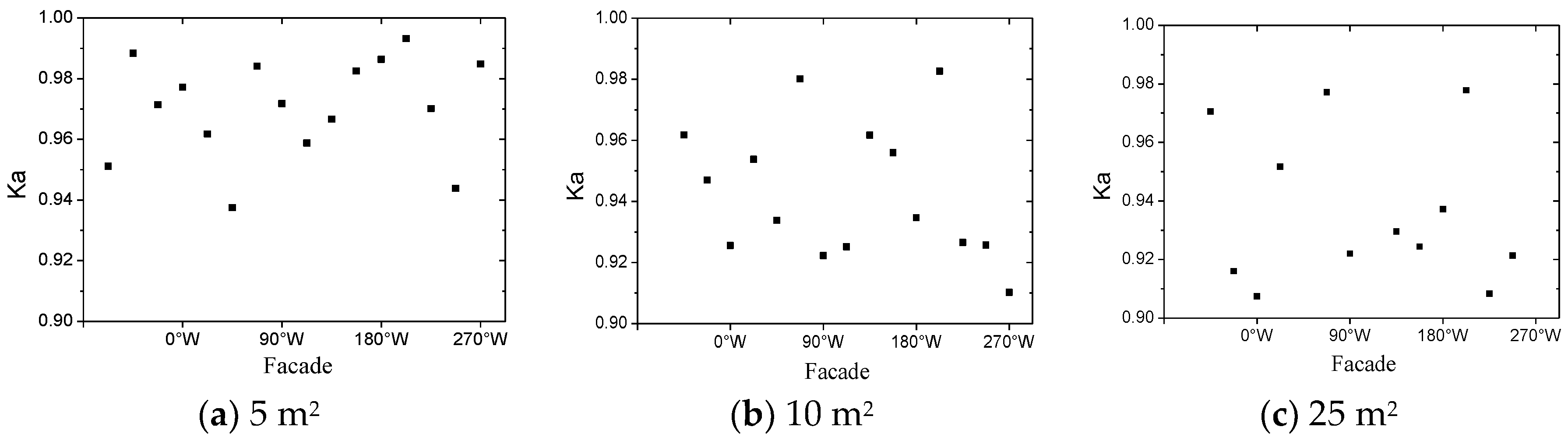
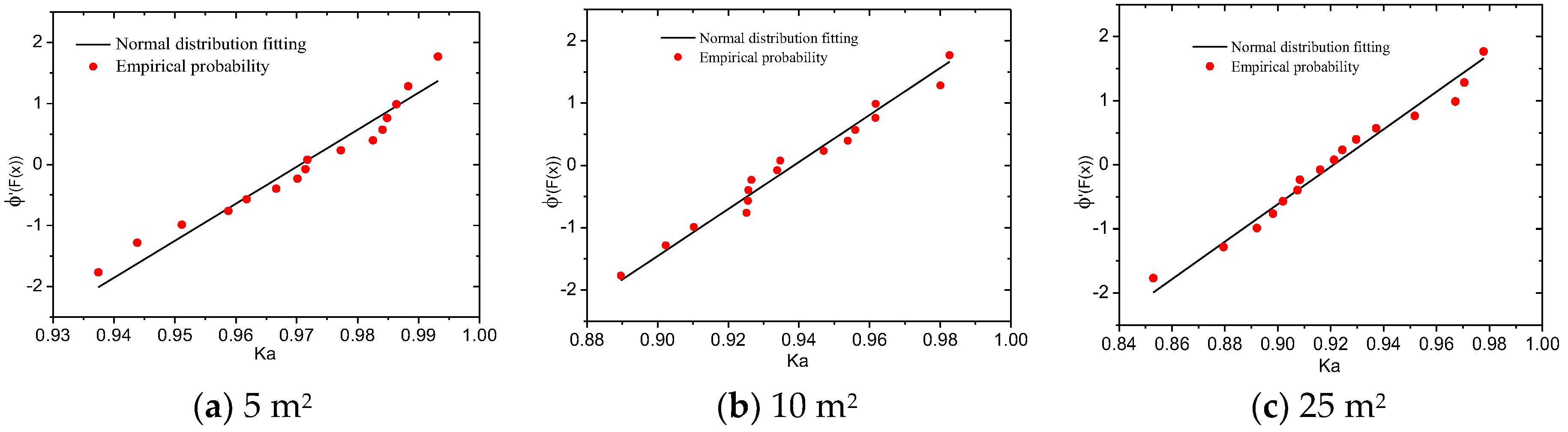
3.2.2. Area Reduction Factor of Extreme Pressure Coefficient
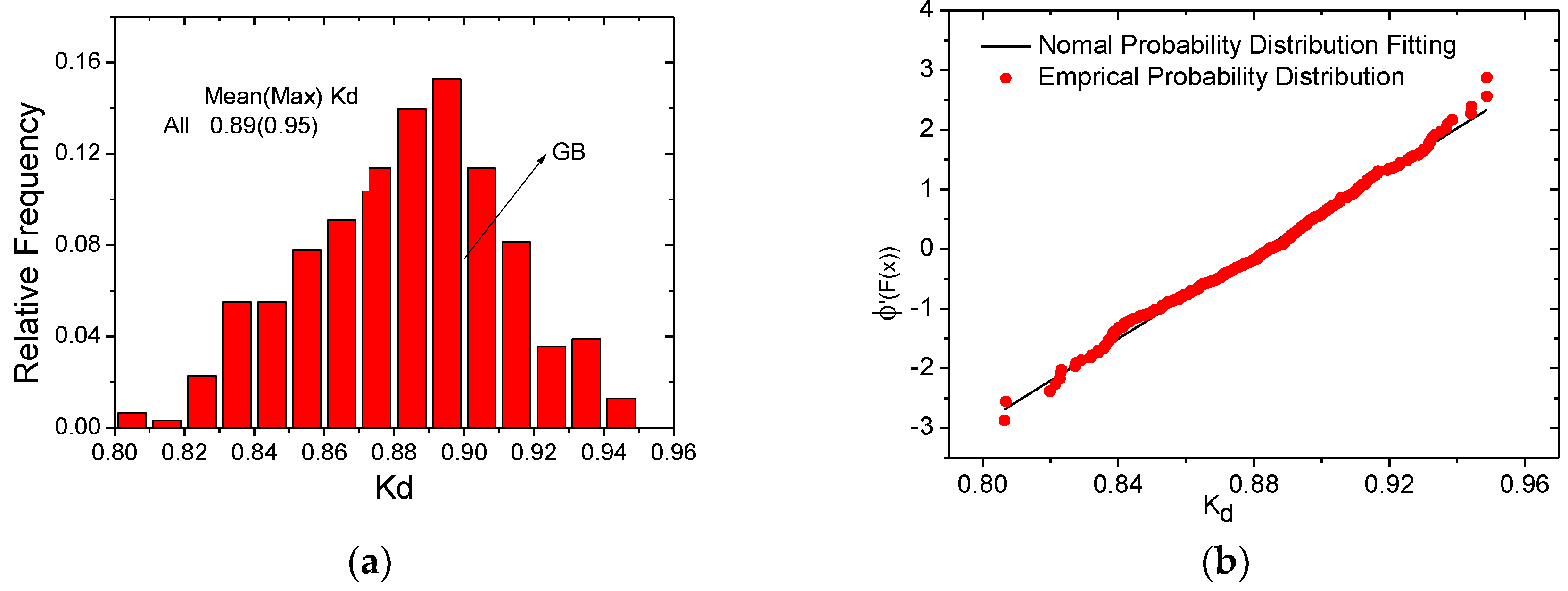
3.3. Wind Directionality Effects of Extreme Wind Loads
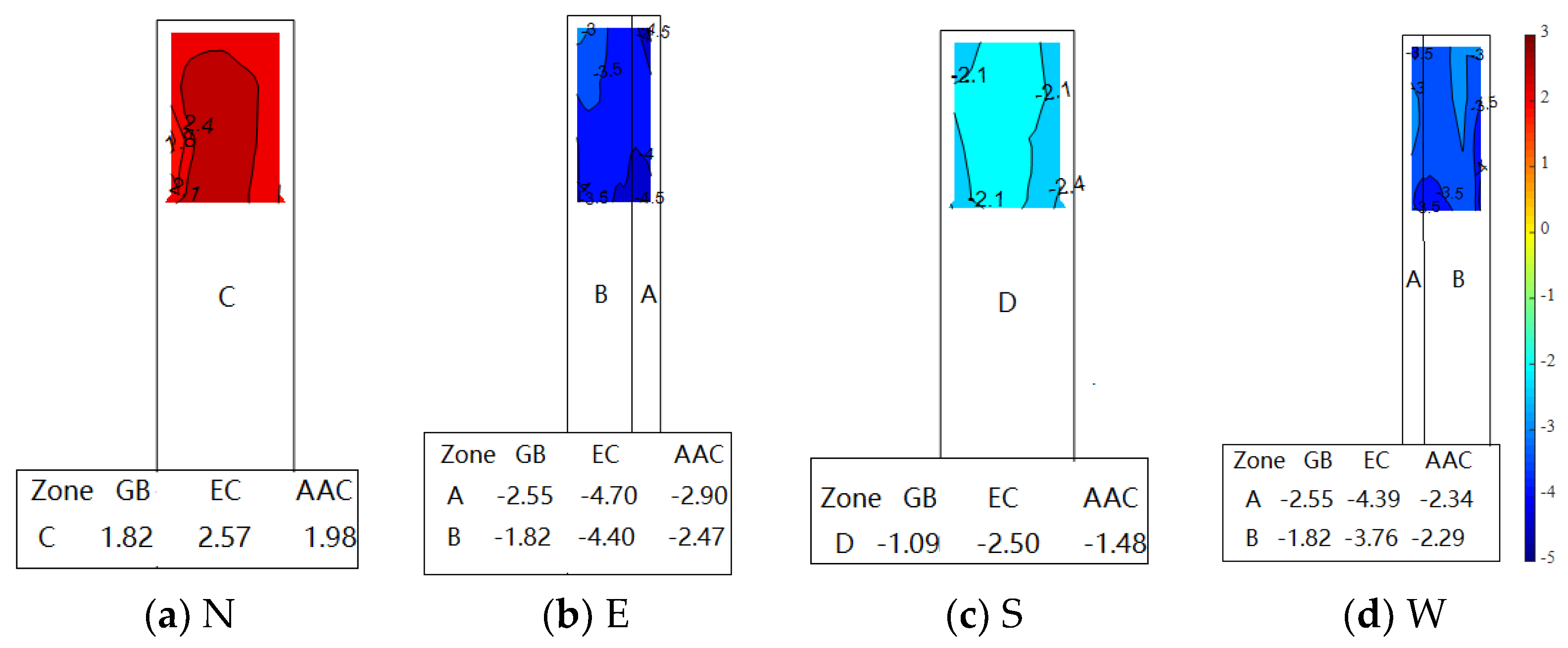
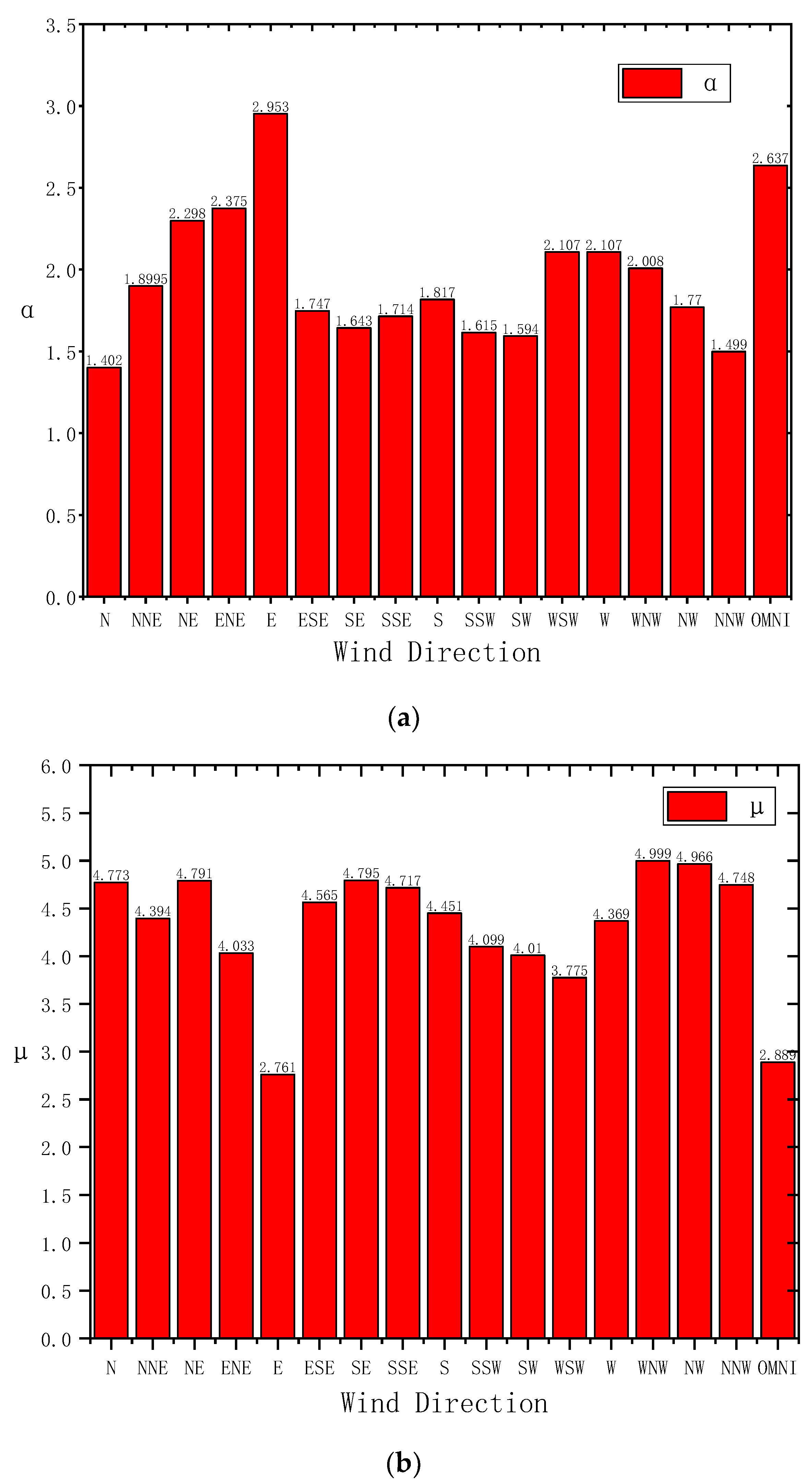
3.3.1. Wind Directionality of Known Building Orientation
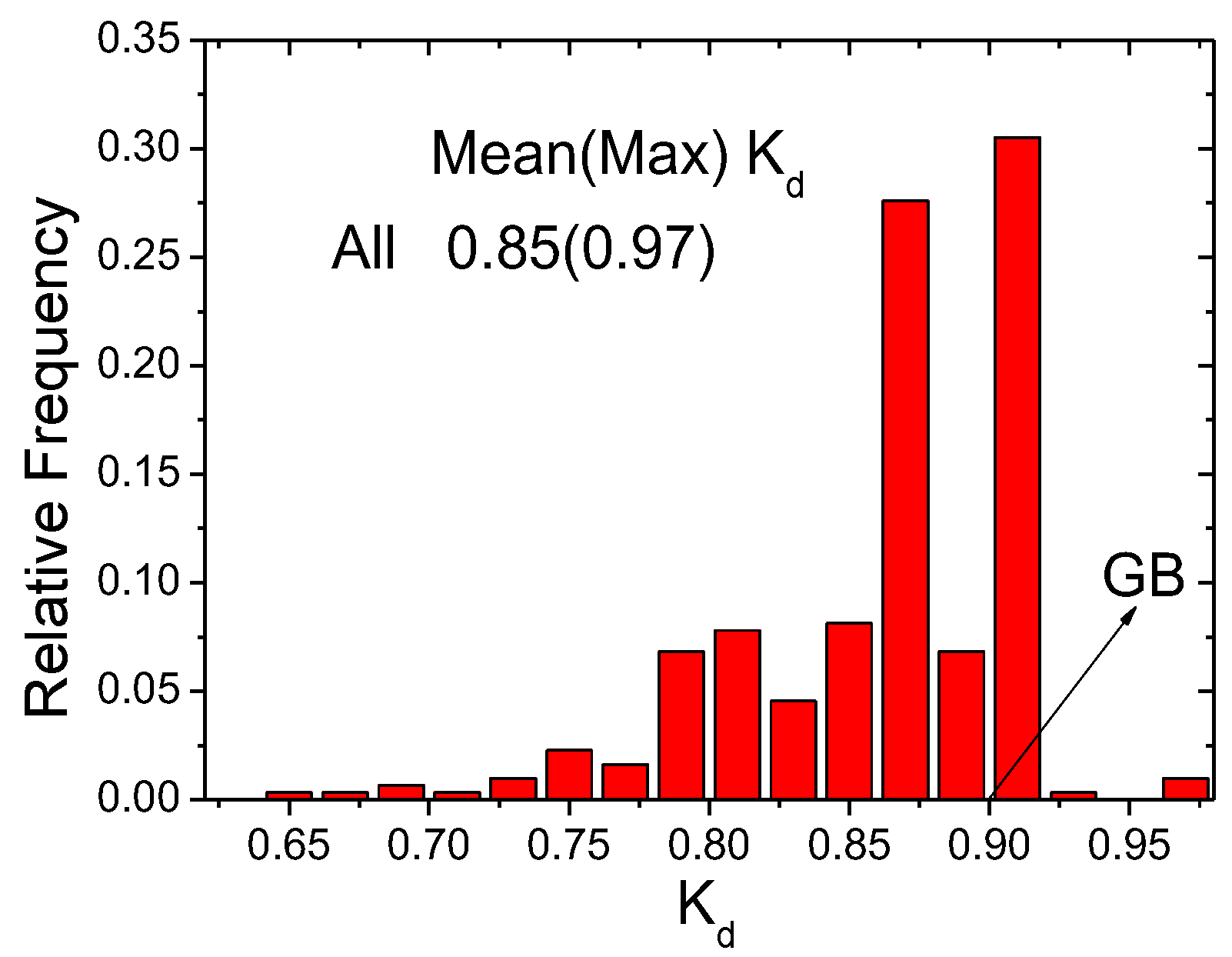
3.3.2. Wind Directionality with Unknown Building Orientation
4. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, Q.; Li, X.; He, Y.; Yi, J. Observation of wind fields over different terrains and wind effects on a super-tall building during a severe typhoon and verification of wind tunnel predictions. J. Wind Eng. Ind. Aerodyn. 2017, 162, 73–84. [Google Scholar] [CrossRef]
- Sun, X.; Liu, H.; Su, N.; Wu, Y. Investigation on wind tunnel tests of the Kilometer skyscraper. Eng. Struct. 2017, 148, 340–356. [Google Scholar] [CrossRef]
- Park, S.; Yeo, D. Second-Order Effects on Wind-Induced Structural Behavior of High-Rise Steel Buildings. J. Struct. Eng. 2018, 144, 04017209. [Google Scholar] [CrossRef] [Green Version]
- Rizzo, F. Investigation of the Time Dependence of Wind-Induced Aeroelastic Response on a Scale Model of a High-Rise Building. Appl. Sci. 2021, 11, 3315. [Google Scholar] [CrossRef]
- Cook, N.J.; Mayne, J.R. A novel working approach to the assessment of wind loads for equivalent static design. J. Wind Eng. Ind. Aerodyn. 1979, 4, 149–164. [Google Scholar] [CrossRef]
- Cook, N.J.; Mayne, J.R. A refined working approach to the assessment of wind loads for equivalent static design. J. Wind Eng. Ind. Aerodyn. 1980, 6, 125–137. [Google Scholar] [CrossRef]
- Peterka, J. Selection of local peak pressure coefficients for wind tunnel studies of buildings. J. Wind Eng. Ind. Aerodyn. 1983, 13, 477–488. [Google Scholar] [CrossRef]
- Holmes, J.D.; Cochran, L.S. Probability distributions of extreme pressure coefficients. J. Wind Eng. Ind. Aerodyn. 2003, 91, 893–901. [Google Scholar] [CrossRef]
- Chen, X.Z.; Huang, G.Q. Estimation of probabilistic extreme wind load effects: Combination of aerodynamic and wind climate data. J. Eng. Mech. 2010, 136, 747–760. [Google Scholar] [CrossRef]
- Quan, Y.; Wang, F.; Gu, M. A method for estimation of extreme values of wind pressure on buildings based on the generalized extreme-value theory. Math. Probl. Eng. 2014, 2014, 926253. [Google Scholar] [CrossRef] [Green Version]
- Wu, D. Study on Effect Uncertainty and Wind-Resistance Design of Long-Span Roofs. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, July 2012. (In Chinese). [Google Scholar]
- Rizzo, F.; Huang, M. Peak value estimation for wind-induced lateral accelerations in a high-rise building. Struct. Infrastruct. Eng. 2021, 1–17. [Google Scholar] [CrossRef]
- Kopp, G.A.; Morrison, M.J. Component and Cladding Wind Loads for Low-Slope Roofs on Low-Rise Buildings. J. Struct. Eng. 2018, 144, 04018019. [Google Scholar] [CrossRef] [Green Version]
- ASCE. Wind Loads. Minimum Design Loads for Buildings and Other Structures; ASCE Standard Series; ASCE: Reston, VA, USA, 2010; Volume ASCE/SEI 7-10, pp. 241–258. [Google Scholar]
- Lawson, T. The design of cladding. Build. Environ. 1976, 11, 37–38. [Google Scholar] [CrossRef]
- Holmes, J.D. Equivalent time averaging in wind engineering. J. Wind Eng. Ind. Aerodyn. 1997, 72, 411–419. [Google Scholar] [CrossRef]
- GB50009. Load Code for the Design of Building Structure; Ministry of Housing and Urban-Rural Construction of the People’s Republic of China: Beijing, China, 2012.
- Isyumov, N.; Ho, E.; Case, P. Influence of wind directionality on wind loads and responses. J. Wind Eng. Ind. Aerodyn. 2014, 133, 169–180. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, X. Assessing probabilistic wind load effects via a multivariate extreme wind speed model: A unified framework to consider directionality and uncertainty. J. Wind Eng. Ind. Aerodyn. 2015, 147, 30–42. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Tian, X.; Tee, K.F.; Li, Q.-S.; Li, Y.-G. Aerodynamic treatments for reduction of wind loads on high-rise buildings. J. Wind Eng. Ind. Aerodyn. 2018, 172, 107–115. [Google Scholar] [CrossRef]
- Cao, J.; Tamura, Y.; Yoshida, A. Wind pressures on multi-level flat roofs of medium-rise buildings. J. Wind Eng. Ind. Aerodyn. 2012, 103, 1–15. [Google Scholar] [CrossRef]
- Mo, H.; Hong, H.; Fan, F. Estimating the extreme wind speed for regions in China using surface wind observations and reanalysis data. J. Wind Eng. Ind. Aerodyn. 2015, 143, 19–33. [Google Scholar] [CrossRef]
- Yang, Y.X.; Ge, Y.J.; Xiang, H.F. Statistical analysis of wind speed based on the joint distribution of wind speed and wind direction. Struct. Eng. 2002, 3, 29–36. (In Chinese) [Google Scholar]
- Laboy-Rodríguez, S.T.; Gurley, K.R.; Masters, F.J. Revisiting the directionality factor in ASCE 7. J. Wind Eng. Ind. Aerodyn. 2014, 133, 225–233. [Google Scholar] [CrossRef]







| Type of Distribution | Form | Condition |
|---|---|---|
| Extreme value Type I distribution: Gumbel distribution | ||
| Extreme value Type Ⅱ distribution: Frechet distribution | ||
| Extreme value Type Ⅲ distribution: Weibull distribution | ||
| Extreme Probability Distribution | Extreme Value Type I Distribution | Extreme Value Type II Distribution | Extreme Value Type III Distribution |
|---|---|---|---|
| Minimum | 0 | 0 | 100% |
| Maximum | 7% | 55% | 38% |
| Measuring Taps Number | 16 | 19 | 22 | 87 | 106 | 110 | 177 | 197 | 256 | 279 |
|---|---|---|---|---|---|---|---|---|---|---|
| Kd | 0.79 | 0.88 | 0.84 | 0.88 | 0.9 | 0.78 | 0.86 | 0.8 | 0.82 | 0.90 |
| Direction (g) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Kd (g) | 0.90 | 0.92 | 0.95 | 0.81 | 0.88 | 0.87 | 0.85 | 0.90 |
| Direction (g) | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| Kd (g) | 0.90 | 0.83 | 0.71 | 0.89 | 0.80 | 0.80 | 0.90 | 0.97 |
| Tap Number | 16 | 19 | 22 | 87 | 106 | 110 | 177 | 197 | 256 | 279 |
|---|---|---|---|---|---|---|---|---|---|---|
| Kd | 0.90 | 0.89 | 0.91 | 0.88 | 0.89 | 0.86 | 0.89 | 0.93 | 0.89 | 0.86 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Xiao, F.; Zou, Y.; Li, S.; Yang, S.; Feng, C.; Chen, Y. Probability Characteristics, Area Reduction, and Wind Directionality Effects of Extreme Pressure Coefficients of High-Rise Buildings. Appl. Sci. 2021, 11, 7121. https://doi.org/10.3390/app11157121
Li S, Xiao F, Zou Y, Li S, Yang S, Feng C, Chen Y. Probability Characteristics, Area Reduction, and Wind Directionality Effects of Extreme Pressure Coefficients of High-Rise Buildings. Applied Sciences. 2021; 11(15):7121. https://doi.org/10.3390/app11157121
Chicago/Turabian StyleLi, Shouke, Feipeng Xiao, Yunfeng Zou, Shouying Li, Shucheng Yang, Chao Feng, and Yuankun Chen. 2021. "Probability Characteristics, Area Reduction, and Wind Directionality Effects of Extreme Pressure Coefficients of High-Rise Buildings" Applied Sciences 11, no. 15: 7121. https://doi.org/10.3390/app11157121
APA StyleLi, S., Xiao, F., Zou, Y., Li, S., Yang, S., Feng, C., & Chen, Y. (2021). Probability Characteristics, Area Reduction, and Wind Directionality Effects of Extreme Pressure Coefficients of High-Rise Buildings. Applied Sciences, 11(15), 7121. https://doi.org/10.3390/app11157121






