Geotechnical Design Practices and Soil–Structure Interaction Effects of an Integral Bridge System: A Review
Abstract
:1. Introduction
2. Terminologies and Definitions of Integral Bridges
3. Geotechnical Guidelines and Practices for the Design of Integral Bridges
3.1. USA Practices
3.1.1. AASHTO LRFD Bridge Design Specification
- Calculations of when the movement is more than zero but less than the movement required to fully mobilise passive and/or active pressure; however, some USA states use linear interpolation to estimate the mobilised earth pressure for such cases;
- The abutment displacement is taken as the displacement at the top of the abutment regardless of whether the mode of movement is rotational, translational or a combination of both;
- The values of fully mobilised displacements are based on a study conducted by Clough and Duncan [30] under monotonic loading. However, the abutment–soil interaction in integral bridges involves cyclic loading, which almost certainly differs from the monotonic loading case.
3.1.2. Practices in USA States
3.2. UK Practice
- the characteristic thermal movement of the end of the deck is less than or equal to 40 mm;
- the skew angle does not exceed 30°.
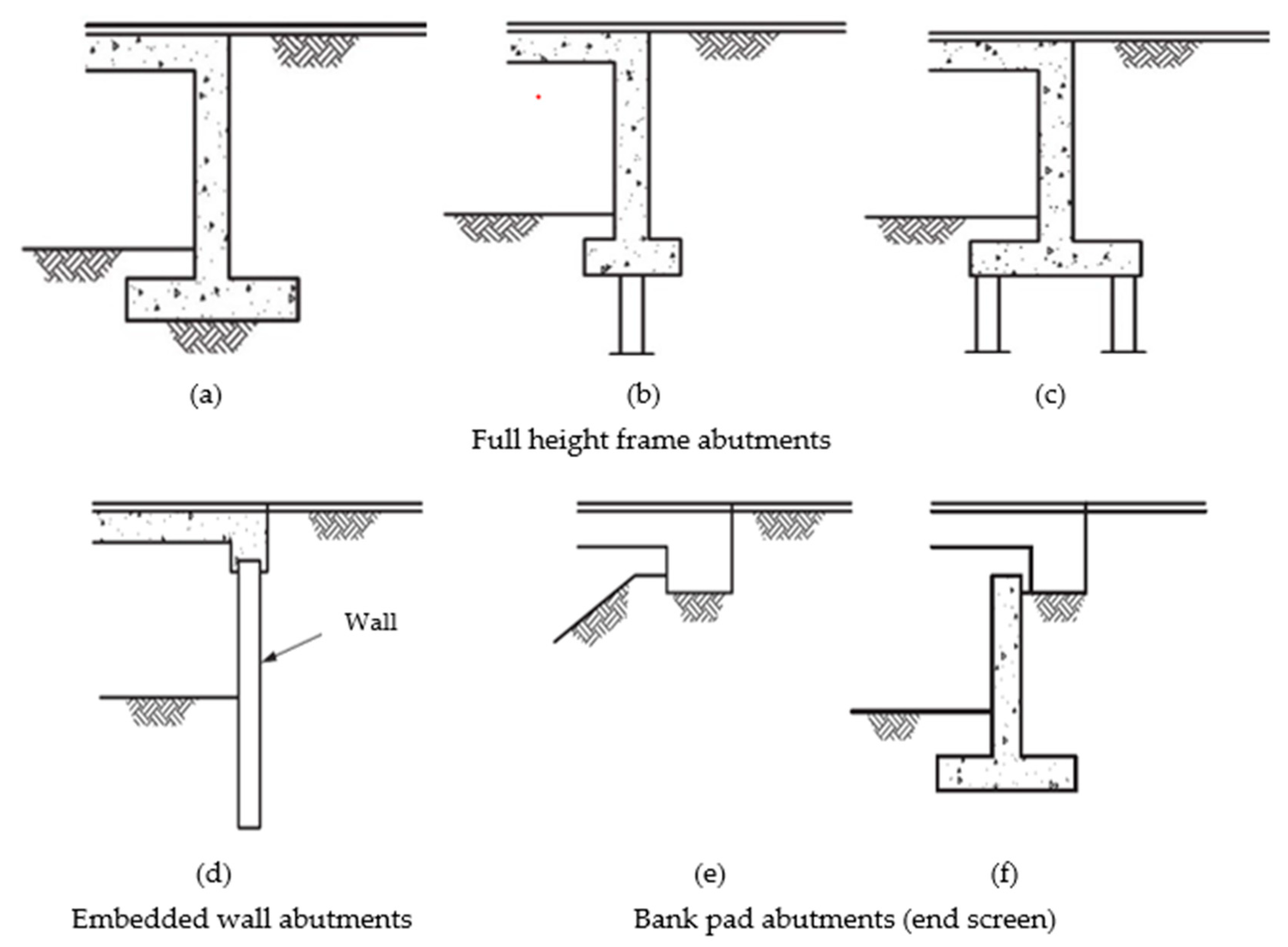
- abutments on spread footings (e.g., full height frame abutments as shown in Figure 1a);
- end screen abutments;
- abutments seated on pile caps with more than one row of piles, provided that the sway at pile cap level is sufficiently small for at-rest earth pressure to be considered at pile cap level.
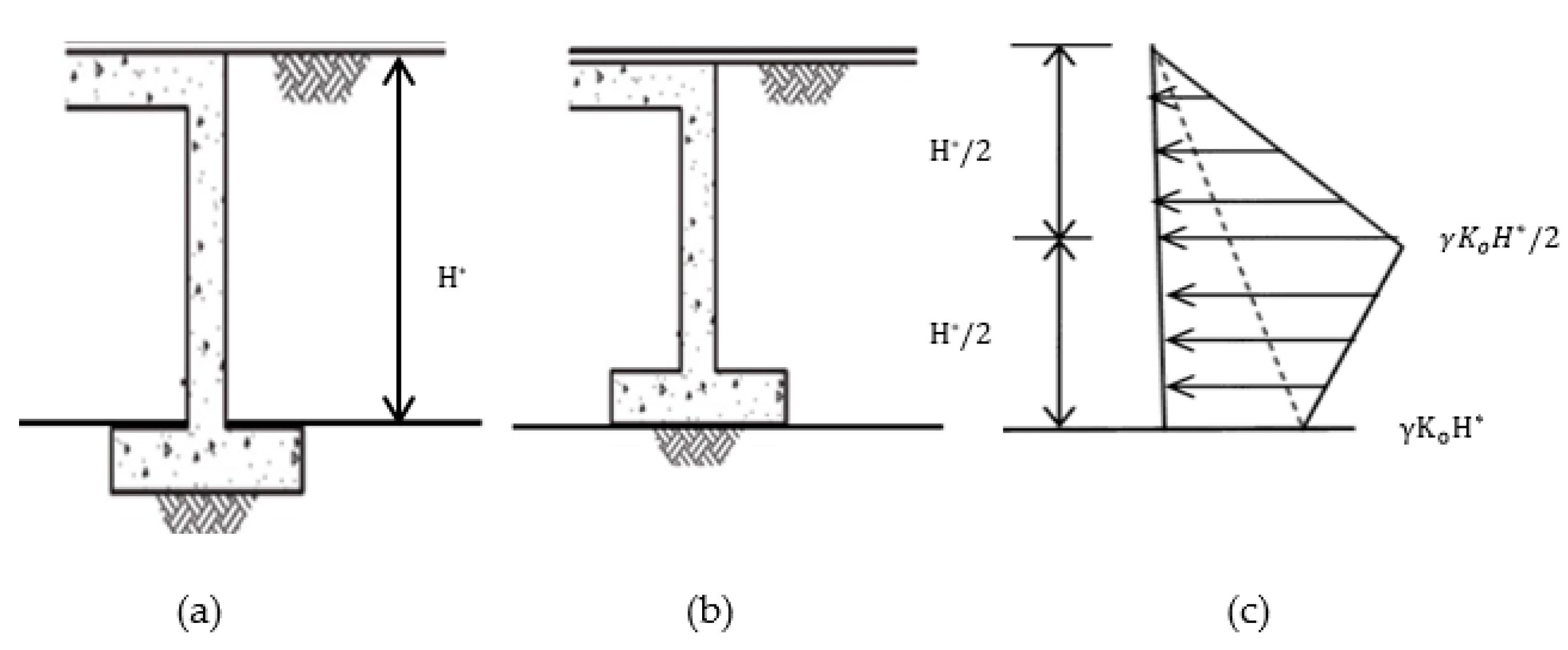
Limit Equilibrium Approach
- C depends on Young’s modulus of the subgrade, E;
- C is 20 for foundations on flexible soils (E ≤ 100 MPa);
- C is 66 for foundations on rock or soils (E ≥ 1000 MPa), and C may be calculated by linear interpolation for values of E between 100 and 1000 MPa.
3.3. Australian and New Zealand Practices
- Design Manual for Roads and Bridges, Design of Integral bridges BA 42/96 [45];
3.4. Canadian Practices
3.5. Japanese Practices
3.6. Swedish Practices
- (for unfavourable earth pressure conditions, such as forces from temperature changes)
- (for favourable earth pressure, such as forces from braking vehicle)
- at-rest pressure
- passive earth pressure
- H = abutment height
- δ = horizontal abutment displacement towards the embankment.
3.7. Swiss Practices
3.8. Finnish Practices
3.9. Comments on Geotechnical Guidelines and Practices for the Design of Integral Bridges under Thermal Loading
3.9.1. SSI Analysis
3.9.1.1. SSI Analysis Based on PD 6694-1
- the nonlinear response of the backfill to deck expansion and contraction;
- the effect of cyclic movement of an abutment on soil properties, which may be based on 120 cycles with a magnitude of characteristic thermal movement ();
- variation of soil properties at different depths and at different strains;
- the degree of compaction of soil;
- the superimposed thermal effects of daily and seasonal temperature changes;
- the rotational and axial stiffness of the deck;
- horizontal soil arching between piles;
- in certain conditions, minimum earth pressure can be more vulnerable than maximum earth pressure. Therefore, the pressure envelope design covering all the possible conditions of expansion and contraction is needed. This should incorporate the possible combinations of minimum earth pressures with maximum expansion and maximum earth pressures with minimum expansion.
- is the designed horizontal spring stiffness per square meter;
- is the design elastic modulus of the soil;
- is the height of the end screen or wall; and
- is the width of the abutment.
3.9.1.2. Comments on SSI Research Studies and Current Published Guidelines
3.9.2. Proposed Strategies to Minimise the Effects of SSI
- No isolation;
- Partial isolation;
- Full isolation.
4. Conclusions
- The nomenclatures on integral bridges in the design guidelines are not standardised across different jurisdictions. For example, AASHTO [5] defines an integral bridge as an IAB and does not further sub classify the integral bridges. In European countries, integral bridges are commonly defined as either fully integral bridges or semi-integral bridges based on the structural connection between the bridge deck and abutment, though these are analogous to the definitions of IABs and SIABs, respectively. A portal frame bridge (PFB) in Japan and end screen bridge in Sweden are other prominent examples of disparate terminologies of the integral bridges in different countries. There are also disagreements on the definitions and types of abutments in different states of the USA. In this review, we have attempted to unify some of the nomenclatures. An integral bridge is defined in this paper as a bridge structure where the bridge deck is without any joints for expansion or contraction of the deck and may be further sub-categorised as an integral abutment bridge (IAB) or a semi-integral abutment bridge (SIAB) depending on the connection between deck and abutment.
- The design method and the design lateral earth pressure distribution behind the abutment (whether SSI is needed or not) are defined with respect to the type of abutments, length, and skew angle limit of integral bridges. In addition, the design practices of integral bridges, including threshold limits on the bridge length and skew angle, and types of abutments, vary across the literature. Knowledge gaps still exist in understanding the effects of different type and geometry of abutment, length and skewness of bridge, type of backfill and SSI. Filling the knowledge gaps is necessary to extend the application and improve the performance of integral bridges.
- The factors considered and the equations used to calculate the earth pressure distribution behind the integral and semi-integral abutment (see Table A1 in Appendix A) in the USA vary from state to state. Some states are still using the traditional Rankine and Coulomb active and passive earth pressure theories derived for retaining structures under monotonic loading cases. In addition, the designed abutment displacement is considered as the displacement at the top, irrespective of the mode of displacement and flexibility of the abutment. Moreover, the displacement of the abutment is cyclic in nature, and the abutment displacement also depends on the nonlinear response of the backfill.
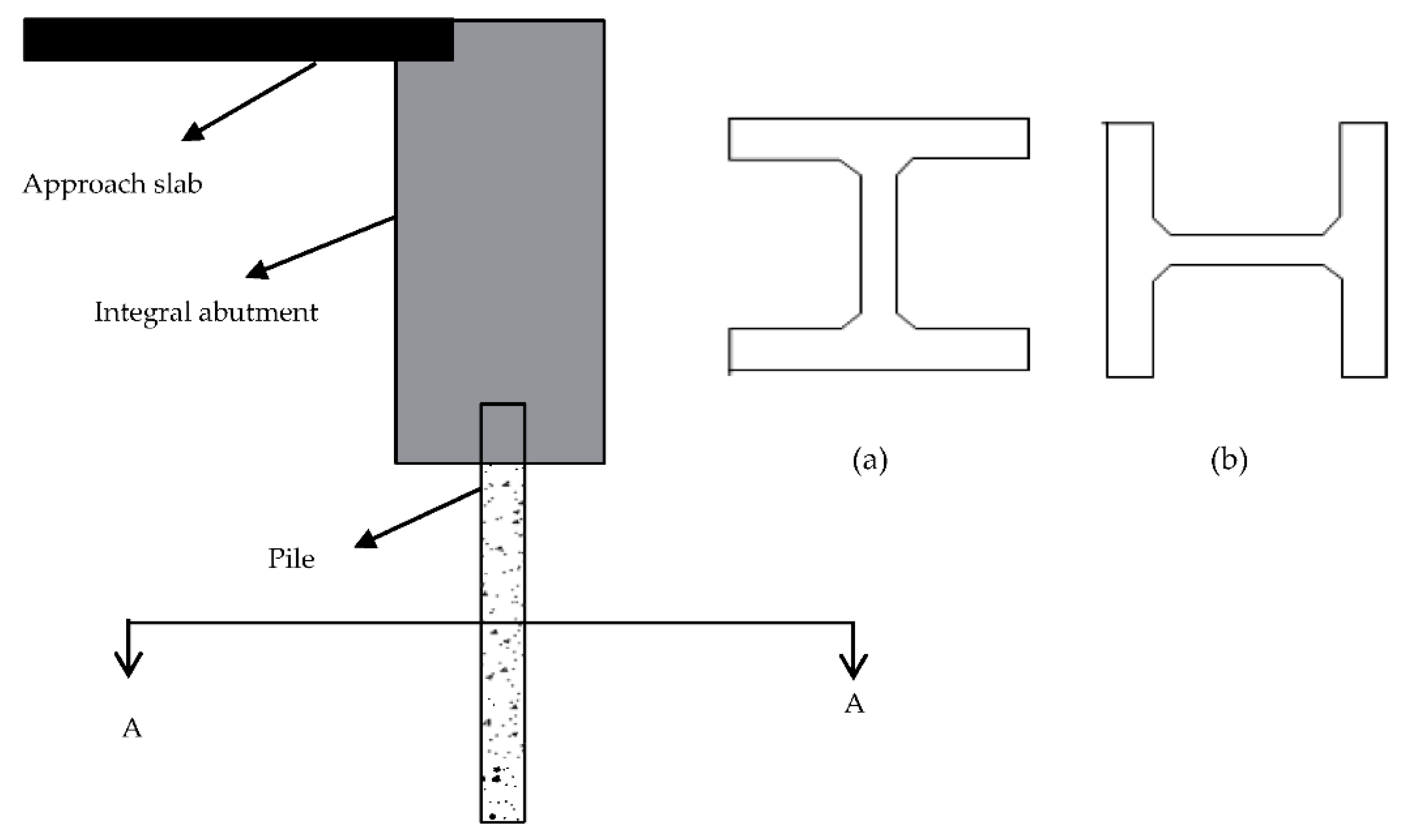
- Most of the design practices lack comprehensive design guidelines on pile foundation for the integral bridges. The types of abutment foundation, restriction on the abutment foundation, and design of the abutment foundation (such as the orientation of the pile, type of pile and embedded length of the pile) have resulted in conflicting practices in some cases. In addition, the transferred effects from the abutment and abutment–soil interaction could have different effects on the pile foundation. Abutment–soil interactions and pile–soil interactions should be investigated in a holistic manner in the design of integral bridges.
- Measures to reduce adverse SSI effects and the consideration of the SSI in the design of integral bridges are required. Both have been recommended in principle and to a different extent in the design standards. Some standards have advised 3D analysis of the integral bridge system incorporating the SSI (e.g., PD 6694-1 [25] and Massachusetts LRFD Bridge Manual-Part I [40]). However, there is very little information on the 3D coupled analysis of the integral bridge structure and soil. Appropriate guidelines to identify the governing soil parameters and changes in soil behavior during cyclic abutment displacement are needed to develop the numerical soil model to study the SSI mechanism in integral bridges. The numerical studies should be combined with scaled model laboratory experiments and field monitoring of actual integral bridges to gain critical insights into the SSI effects (e.g., as recommended in PD 6694-1 [25]).
- Seasonal and diurnal temperature cycles cause dissimilar period and amplitude variations in the displacements of the bridge structure. In addition, the superimposed thermal effect (daily and seasonal temperature changes) can have different effects on integral bridges compared to the daily or seasonal thermal changes only. However, design guidelines (such as PD 6694-1 [25] and AASHTO [5]) mainly focus on the effects of the seasonal cycles. In addition, some studies found that the shape of the earth pressure distribution behind the integral abutments depends on the magnitude of the abutment displacement [17]. Some standards (e.g., PD 6694-1 [25]; Massachusetts LRFD Bridge Manual-Part I [40]; Utah Bridge Design Manual [37]) further recommend that the magnitude of lateral pressure should be considered as a function of abutment displacement. These indicate the importance of considering the superimposed effects of seasonal and diurnal temperature cycles in postulating the earth pressure and establishing the bending moment distribution on the integral and semi-integral abutment, abutment foundation, and development of the settlement trough at the bridge approach.
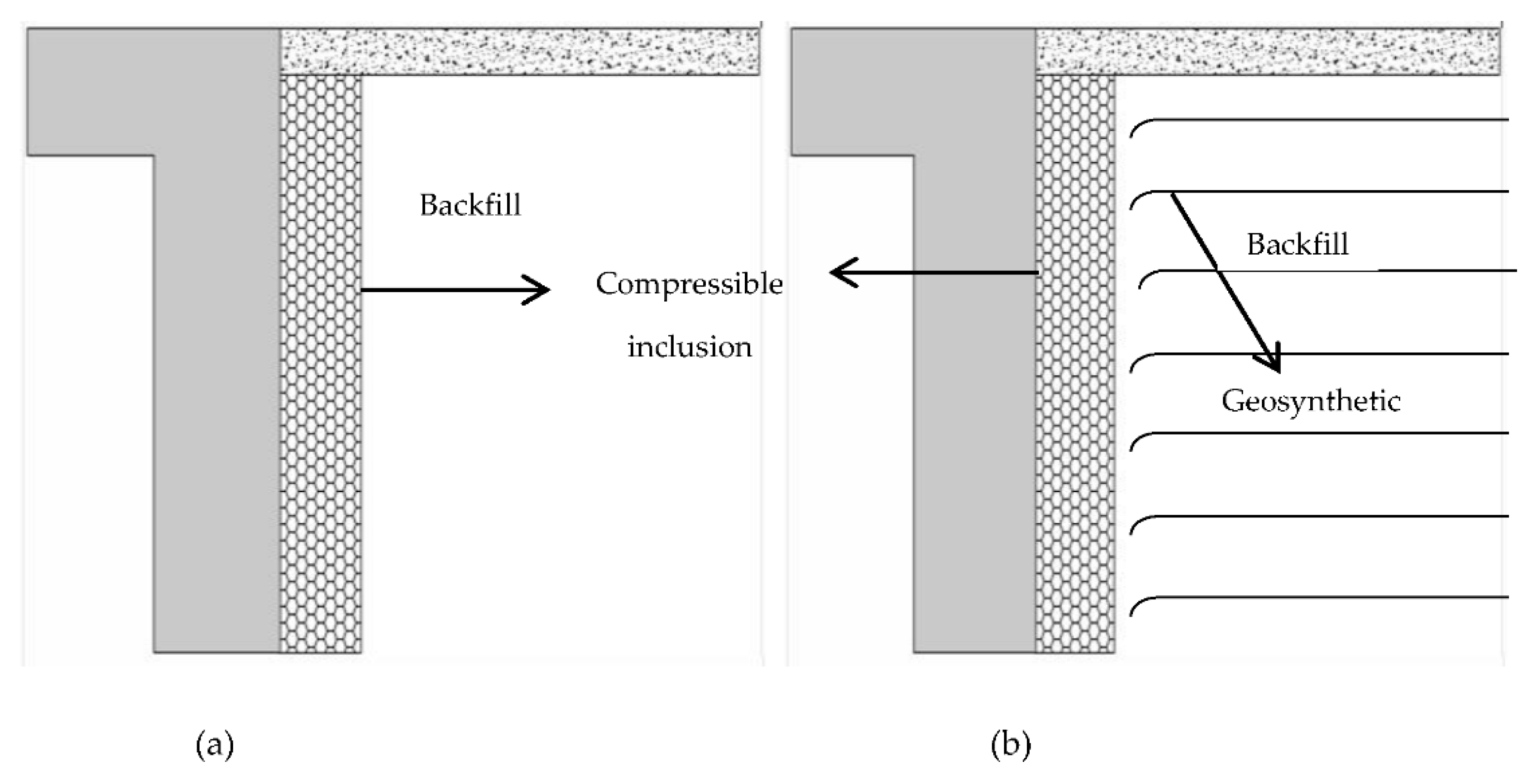
- The review suggests that the principle of isolation being applied to mitigate SSI effects needs more detailed study. Abutment–backfill separation with the use of compressible inclusion and reinforced backfill (MSE wall) are just two more common approaches to mitigate the soil flow, soil slumping, soil settlement and stress ratcheting effects on integral bridges. Other self-stable backfill systems, e.g., soil-cement column wall [10] and EPS geofoam embankment [15], are potential solutions as well. However, most of these suggestions are derived from the lab experiments and finite element analysis, and no explicit design guidelines for such approaches are yet available. In contrast, Alberta and Manitoba strictly avoided the use of foam material behind the integral abutment, as they can be compressed in the long term, which could develop unequal movements at the bridge abutments. Therefore, most appropriate solutions to minimise the earth pressure behind the abutment need to be explored and discussed in the design guidelines to increase the applicability of the integral bridges, and to substitute the integral bridges as an option for longer traditional bridges.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| States | Types of Integral Abutments | Limiting Design Criteria | Geotechnical Design Considerations/Practices | Mitigation Measures with Respect to Geotechnical Requirements |
|---|---|---|---|---|
| Colorado [41] | Integral abutments and semi-integral abutments |
|
|
|
| Alaska [31] | Semi-integral abutments |
|
|
|
| Ohio [36] | Integral abutments and semi-integral abutments |
|
|
|
| Idaho [32] | Integral abutments |
|
|
|
| Maine [35] | Full integral abutments and semi-integral abutments |
|
|
|
| Massachusetts [40] | Integral and semi-integral abutments |
|
|
|
| North Dakota [33] | Integral abutments |
|
|
|
| Pennsylvania [42] | Integral and semi-integral abutment |
|
|
|
| New Hampshire [43] | Integral abutments and Semi-integral abutments |
|
| |
| Oregon [39] | Integral abutments and semi-integral abutments |
|
|
|
| Virginia [34] | Full integral abutment and semi-integral abutment |
|
|
|
| Utah [37] | Integral abutments and semi-integral abutments |
|
|
|
| Illinios [91] | Integral abutments and semi-integral abutments |
|
|
|
| Minnesota [92] | Integral and semi-integral abutments |
|
|
|
| Nevada [93] | Integral abutments; (a) diaphragm-with-footing-abutment, which is semi-integral abutments as described in other practices. (b) diaphragm-with-pile-abutment, which is integral abutments (full integral abutments) as described in other practices. |
|
|
|
| New Jersey [39] | Integral abutments and semi-integral abutments |
|
|
|
Appendix B. Earth Pressure Distribution on Integral and Semi-Integral Abutment
Appendix B.1. Idaho
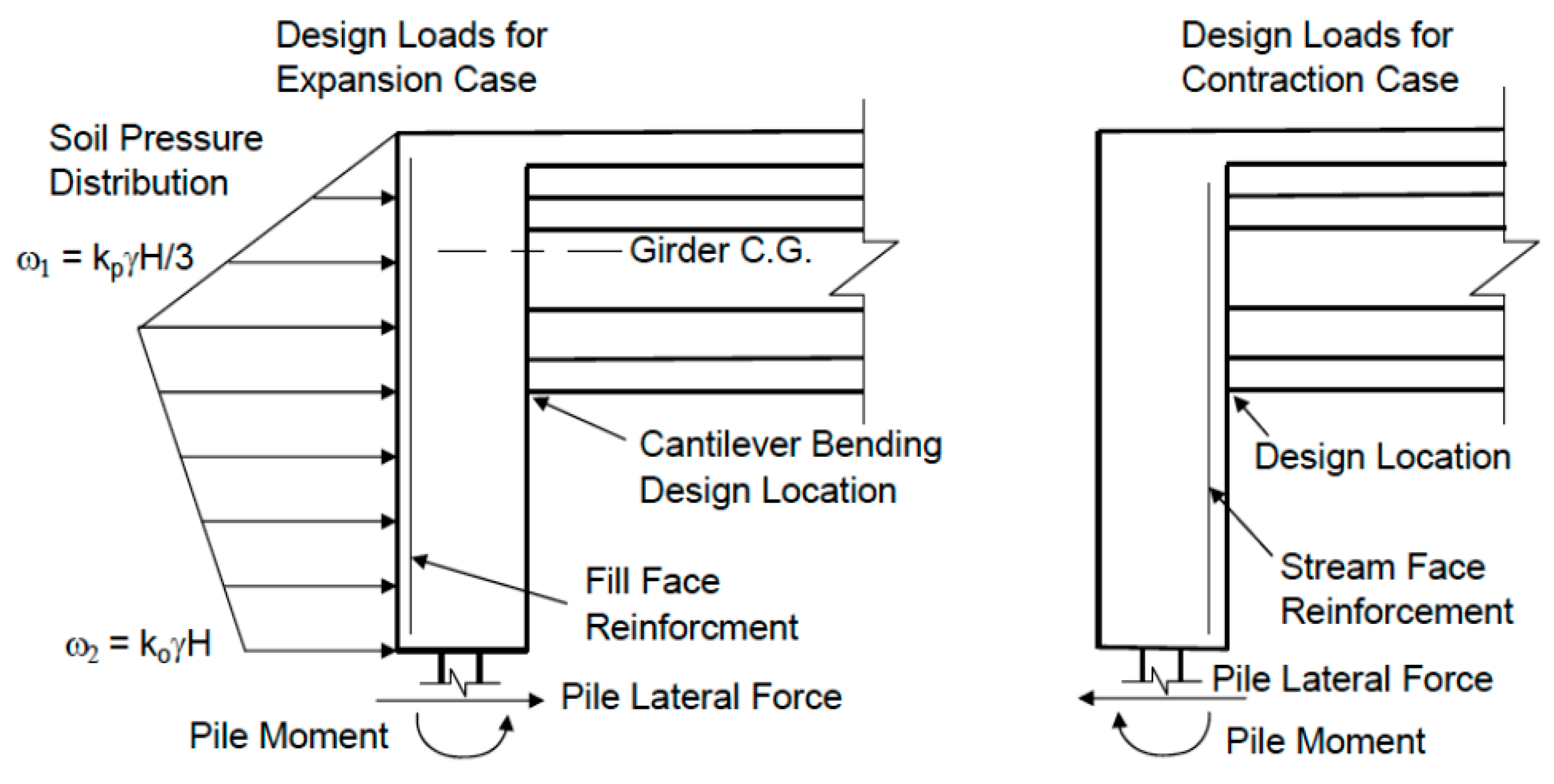
Appendix B.2. Minnesota
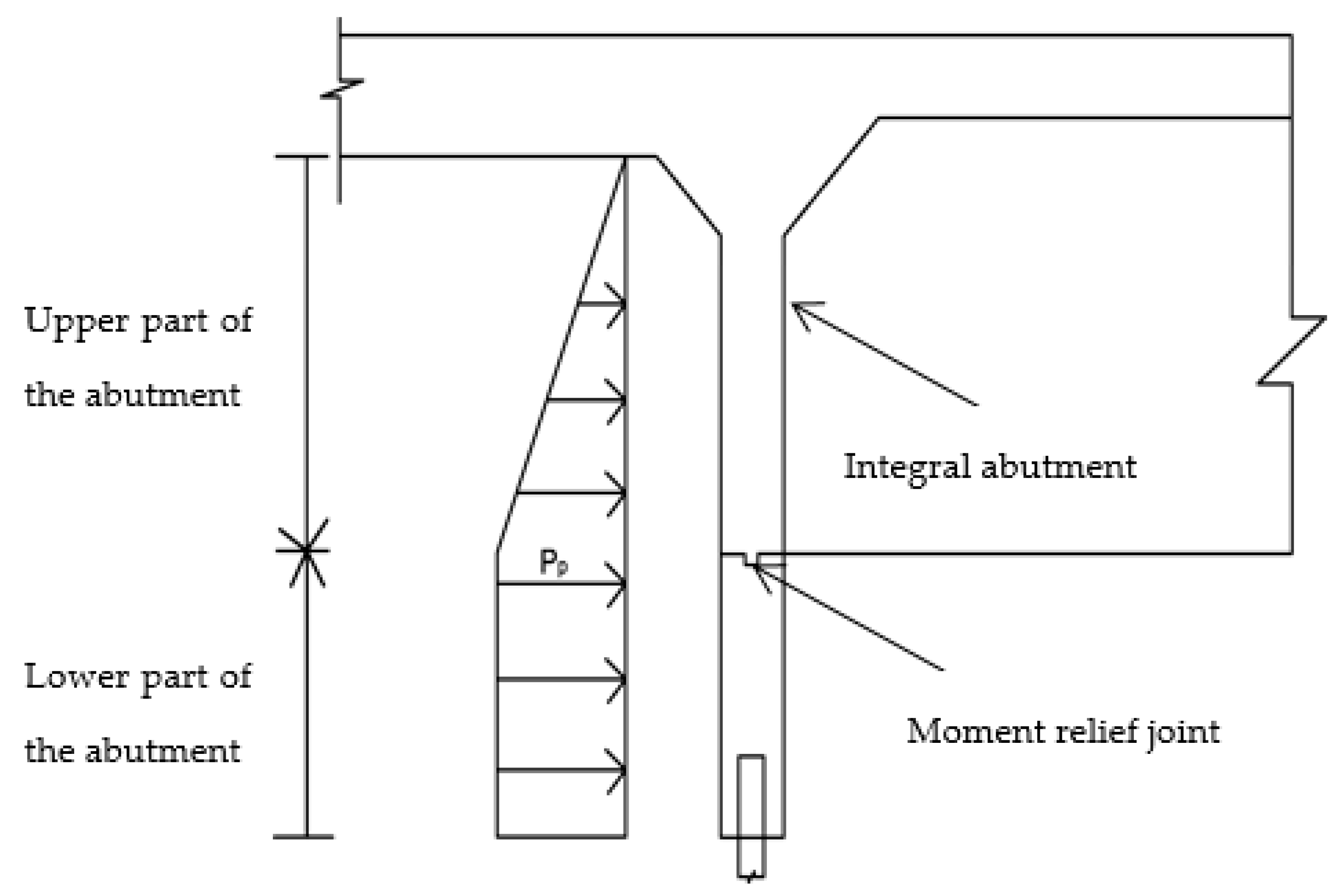
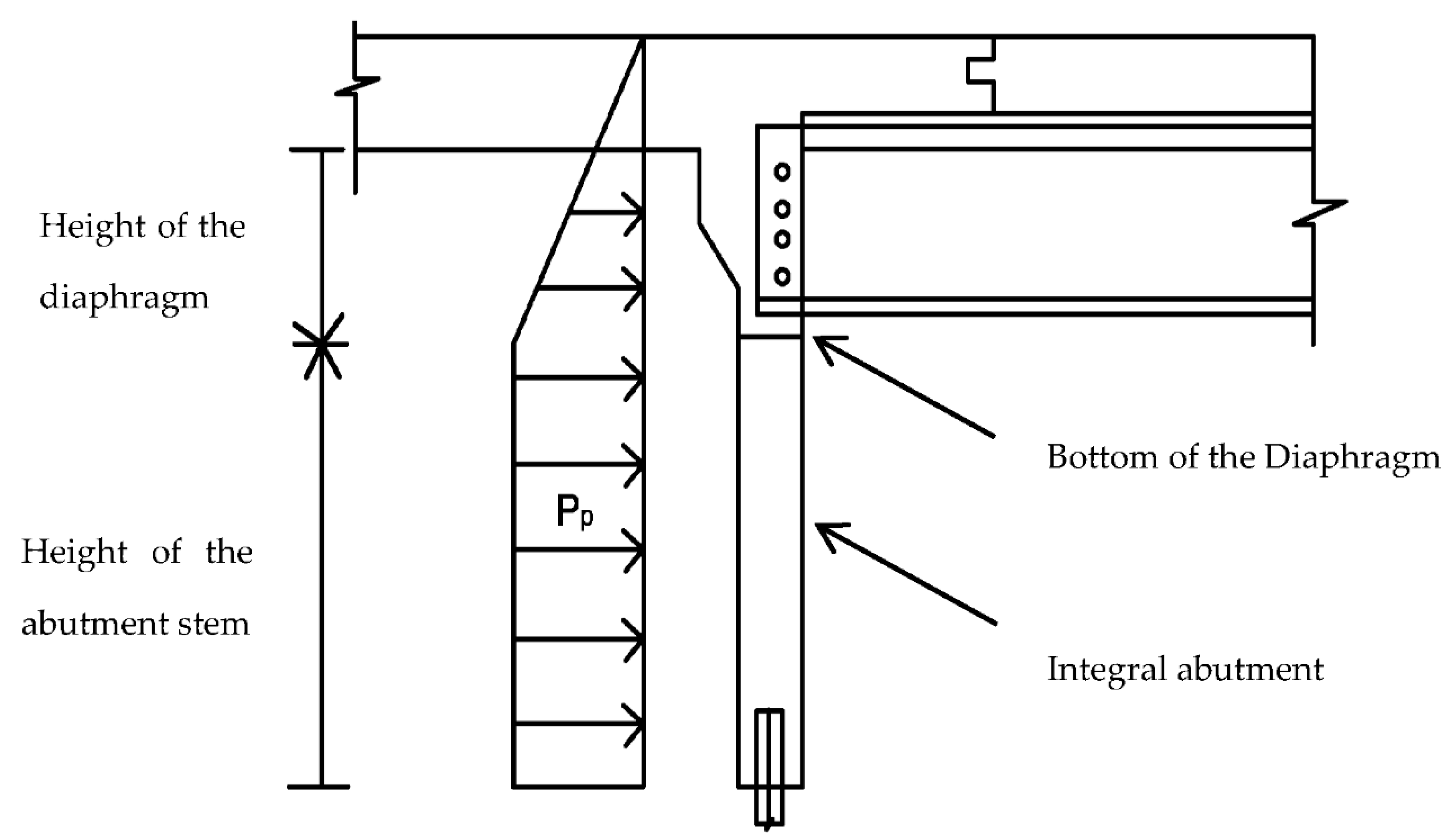
Appendix B.3. New Hampshire
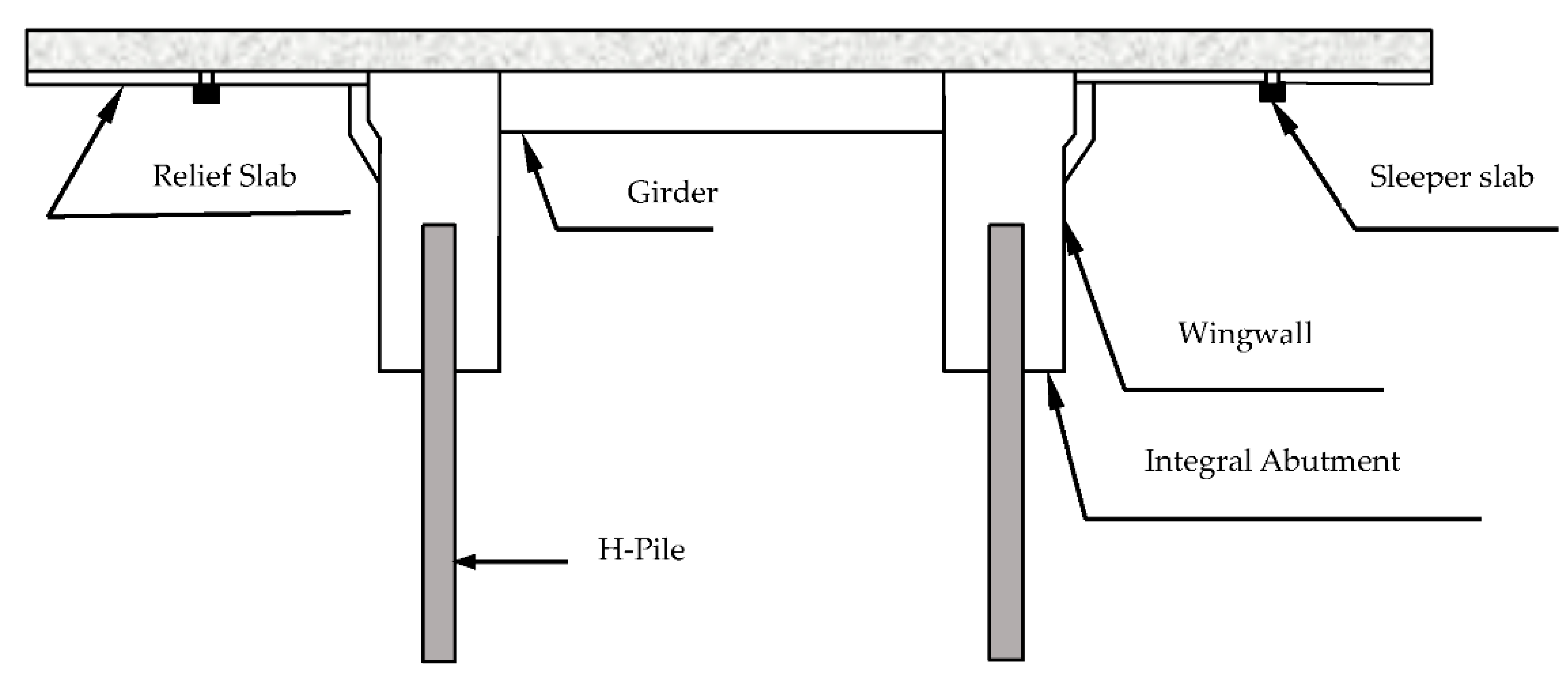
Appendix C. Sleeper Slab
Appendix D. Skew Angle
References
- Biddle, A.; Iles, D.; Yandzio, E. Integral Steel Bridges: Design Guidance; SCI-Pub--163, Steel; Construction Institute: Ascot, UK, 1997. [Google Scholar]
- Wasserman, E.P.; Walker, J.H. Integral abutments for steel bridges. In Highway Structures Design Handbook; American Iron and Steel Institute: Washington, DC, USA, 1996; Volume II. [Google Scholar]
- White, H. Integral Abutment Bridges: Comparison of Current Practice between European Countries and the United States of America; Transportation Research and Development Bureau, New York State Department of Transportation: New York, NY, USA, 2007.
- Burke, J.R.M.P. Integral and Semi-Integral Bridges; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Hassiotis, S.; Roman, E. A survey of current issues on the use of integral abutment bridges. Bridge Struct. 2005, 1, 81–101. [Google Scholar] [CrossRef]
- Tabatabai, H.; Magbool, H.; Bahumdain, A.; Fu, C. Criteria and Practices of Various States for the Design of Jointless and Integral Abutment Bridges. In Third International Workshop on Jointless Bridges; UWM Digital Commons: Seattle, DC, USA, 2017. [Google Scholar]
- Sandberg, J.; Magnino, L.; Nowak, P.; Wiechecki, M.; Thusyanthan, I. The Integral Bridge Design Concept for the Third Runway at Heathrow, UK; Thomas Telford Ltd.: London, UK, 2020; Volume 173, pp. 112–120. [Google Scholar]
- Al-Qarawi, A.; Leo, C.; Liyanapathirana, D. Effects of Wall Movements on Performance of Integral Abutment Bridges. Int. J. Geomech. 2020, 20, 1–14. [Google Scholar] [CrossRef]
- Bloodworth, A.; Xu, M.; Banks, J.; Clayton, C. Predicting the Earth Pressure on Integral Bridge Abutments. J. Bridge Eng. 2012, 17, 371–381. [Google Scholar] [CrossRef]
- Fartaria, C. Soil-Structure Interaction in Integral Abutment Bridges; Instituto Superior Téchnico, Universidade Téchinca de Lisboa: Lisbon, Portugal, 2012. [Google Scholar]
- Shamsabadi, A.; Rollins, K.M.; Kapuskar, M. Nonlinear soil–abutment–bridge structure interaction for seismic performance-based design. J. Geotech. Geoenviron. Eng. 2007, 133, 707–720. [Google Scholar] [CrossRef]
- England, G.L.; Tsang, N.C.; Bush, D.I. Integral Bridges: A Fundamental Approach to the Time–Temperature Loading Problem; Thomas Telford Ltd.: London, UK, 2000. [Google Scholar]
- England, G. A thermal displacement compensation unit for integral bridges. Pat. Bridge Struct. 2005, 2605437, A1. [Google Scholar]
- Springman, S.; Norrish, A.; Ng, C. Cyclic Loading of Sand behind Integral Bridge Abutments; TRL Report 146; Transport Research Laboratory: London, UK, 1996. [Google Scholar]
- Horvath, J.S. Integral-Abutment Bridges: Problems and Innovative Solutions Using EPS Geofoam and Other Geosynthetics; CE/GE-00-2; Manhattan College: Bronx, NY, USA, 2000. [Google Scholar]
- Horvath, J.S. Lateral pressure reduction on earth-retaining structures using geofoams: Correcting some misunderstandings. In Proceedings of the Earth Retention Conference, Earth Retention Conference (ER), Bellevue, WA, USA, 1–4 August 2010; pp. 862–869. [Google Scholar]
- Huang, F.; Shan, Y.; Chen, G.; Lin, Y.; Tabatabai, H.; Briseghella, B. Experiment on Interaction of Abutment, Steel H-Pile and Soil in Integral Abutment Jonitless Bridges (IAJBs) under Low-Cycle Pseudo-Static Displacement Loads. Appl. Sci. 2020, 10, 1358. [Google Scholar] [CrossRef] [Green Version]
- Huang, J.; Shield, C.K.; French, C.E. Parametric study of concrete integral abutment bridges. J. Bridge Eng. 2008, 13, 511–526. [Google Scholar] [CrossRef]
- Mitoulis, S.A. Challenges and opportunities for the application of integral abutment bridges in earthquake-prone areas: A review. Soil Dyn. Earthq. Eng. 2020, 135, 106183. [Google Scholar] [CrossRef]
- Razmi, J.; McCabe, M. Analytical and Computational Modeling of Integral Abutment Bridges Foundation Movement due to Seasonal Temperature Variations. Int. J. Geomech. 2020, 20, 04019189. [Google Scholar] [CrossRef]
- Karalar, M.; Dicleli, M. Effect of thermal induced flexural strain cycles on the low cycle fatigue performance of integral bridge steel H-piles. Eng. Struct. 2016, 124, 388–404. [Google Scholar] [CrossRef]
- Philip, B.E. IAB: An Exploratory Study on Integral Abutment Bridges. Int. J. Sci. Res. Dev. 2017, 5, 312–316. [Google Scholar]
- AASHTO. LRFD Bridge. Design Specifications, 9th ed.; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2020. [Google Scholar]
- White, H.; Pétursson, H.; Collin, P. Integral abutment bridges: The European way. Pract. Period. Struct. Des. Constr. 2010, 15, 201–208. [Google Scholar] [CrossRef]
- PD 6694-1:2011+A1:2020. Recommendations for the Design of Structures Subject to Traffic Loading to BS EN 1997-1:2004+A1:2013; BSI (British Standard International): London, UK, 2020. [Google Scholar]
- Jaky, J. The coefficient of earth pressure at rest. J. Soc. Hung. Archit. Eng. 1944, 7, 355–358. [Google Scholar]
- Mayne, P.W.; Kulhawy, F. K-OCR Relationships in Soil; Elsevier Science: Amsterdam, The Netherlands, 1982; Volume 20, p. A2. [Google Scholar]
- Terzaghi, K.; Peck, R.B.; Mesri, G. Soil Mechanics in Engineering Practice, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1996. [Google Scholar]
- US Navy. Foundations and Earth Structures Design Manual 7.2; Department of the Navy, Naval Facilities Engineering Command: Alexandria, VA, USA, 1982. [Google Scholar]
- Clough, G.W.; Duncan, J.M. Chapter 6-Earth Pressures. In Foundation Engineering Handbook, 2nd ed.; Fang, H.Y., Ed.; Chapman and Hall: New York, NY, USA, 1991; pp. 223–235. [Google Scholar]
- Alaska Department of Transportation. Bridge. Design Manual 2017; Alaska Department of Transportation: Juneau, AK, USA, 2017.
- Idaho Department of Transportation. Bridge. Design Manual 2017; Idaho Department of Transportation: Boise, ID, USA, 2019.
- North Dakota Department of Transportation. North. Dakota Bridge. Design Manual 2013; North Dakota Department of Transportation: Bismarck, ND, USA, 2013.
- Virginia Department of Transportation. Manual of the Structure and Bridge. Division 2020; Virginia Department of Transportation: Richmond, VA, USA, 2020.
- Maine Department of Transportations. Bridge. Design Manual 2018; Maine Department of Transportation: Augusta, ME, USA, 2018.
- Ohio Department of Transportation. Manual of the Structure and Bridge. Division 2020; Ohio Department of Transportation: Columbus, OH, USA, 2020.
- Utah Department of Transportation. Utah Bridge. Design Manual 2017; Utah Department of Transportation: Salt Lake City, UT, USA, 2017.
- Oregon Department of Transportation. Oregon Bridge. Design Manual 2016; Oregon Department of Transportation: Salem, OR, USA, 2019.
- New Jersey Department of Transportation. New Jersey Bridge. Design Manual 2016; Highway Division, New Jersey Department of Transportation: Bordentown, NJ, USA, 2016.
- Massachusetts Department of Transportations. LRFD Bridge. Design Manual—Part. I 2020; Massachusetts Department of Transportation: Boston, MA, USA, 2020.
- Colorado Department of Transportation. Bridge. Design Manual 2020; Colorado Department of Transportation: Denver, CO, USA, 2020.
- Pennsylvania Department of Transportation. Pennsylvania Bridge. Design Manual, Part 4 2019; Pennsylvania Department of Transportation: Harrisburg, PA, USA, 2019.
- New Hampshire Department of Transportation. New Hampshire Bridge. Design Manual 2019; New Hampshire Department of Transportation: Concord, NH, USA, 2019.
- British Standards Institution. BS 8110-1:1997 Structural Use of Concrete. Code of Practice for Design and Construction; BSI: London, UK, 1997. [Google Scholar]
- HA (Highways Agency). BA 42/96 Design Manual for Roads and Bridges; The Design of Integral Bridges: London, UK, 2003; Volume 1.
- Clayton, C.R.I.; Xu, M.; Bloodworth, A. A laboratory study of the development of earth pressure behind integral bridge abutments. Géotechnique 2006, 56, 561–571. [Google Scholar] [CrossRef] [Green Version]
- Tapper, L.; Lehane, B. Lateral Stress Development on Integral Bridge Abutments, Developments in Mechanics and Structures of Materials; CRC Press/Balkema: Boca Raton, FL, USA, 2005; pp. 1069–1075. [Google Scholar]
- Xu, M.; Clayton, C.R.I.; Bloodworth, A.G. The earth pressure behind full-height frame integral abutments supporting granular fill. Can. Geotech. J. 2007, 44, 284. [Google Scholar] [CrossRef]
- Standards Australia. Concrete Structures Standard, AS 3600–2009; Standards Australia: Sydney, NSW, Australia, 2009. [Google Scholar]
- Standards Australia. Australian Bridge Design Code, AS 5100–2017; Standards Australia: Sydney, NSW, Australia, 2017. [Google Scholar]
- Roads and Traffic Authority. Bridge. Policy Circular BPC 2007/05: Design of Integral Bridges; RTA: Sydney, NSW, Australia, 2007.
- PD 6694-1. Recommendations for the Design of Structures Subject to Traffic Loading to BS EN 1997-1:2004+A1; BSI (British Standard International): London, UK, 2011. [Google Scholar]
- New Zealand Transport Agency. Bridge. Manual, 3rd ed.; SP/M/022; NZ Transport Agency: Wellington, New Zealand, 2013.
- Al-Ani, M.; Murashev, A.; Palermo, A.; Andisheh, K.; Wood, J.; Goodall, D.; Lloyd, N. Criteria and guidance for the design of integral bridges. In Proceedings of the Institution of Civil. Engineers—Bridge. Engineering; Thomas Telford Ltd.: London, UK, 2018; Volume 171, pp. 143–154. [Google Scholar] [CrossRef]
- Lan, C. On the Performance of Super-Long Integral Abutment Bridges: Parametric Analyses and Design Optimization; University of Trento: Trento, Italy, 2012. [Google Scholar]
- Technical Standards Branch. Bridge. Design Structures Design Criteria 2018, Version 8.1; Alberta Transportation: Valleyview, AB, Canada, 2018.
- Ministry of Transportation. Provincial Highways Management Division, Highway Standards Branch, Structural Manual 2016; Ministry of Transportation: Toronto, ON, Canada, 2016.
- Iwasaki, N.; Tenma, S.; Kurita, A. Portal frame bridges in Japan: State of the art report. Struct. Eng. Int. 2011, 21, 290–296. [Google Scholar] [CrossRef]
- Nishida, H.; Miyata, H.; Kimura, S.; Kohno, T.; Nanazawa, T.; Nakatani, S. Design and construction guideline of integral abutment bridges for Japanese highways. In Proceedings of the 28th US-Japan Bridge Engineering Workshop, Tsukuba, Japan, 22–23 October 2009; PWRI: Tsukuba, Japan, 2012. [Google Scholar]
- Akiyama, H.; Kajikawa, Y. Fundamentally Structural Characteristics of Integral Bridges. Ph.D. Thesis, Graduate School of Natural Science and Technology Kanazawa University, Kanazawa City, Japan, 2008. [Google Scholar]
- Design Guidelines Part. II; NEXCO Companies: Kanazawa City, Japan, 2006.
- Public Works Research Centre and Nippon Steel Corporation. Guidelines for Planning of Steel Integral Bridges (Draft); Nippon Steel Corporation: Tokyo, Japan, 2004. [Google Scholar]
- Kerokoski, O.; Pétursson, H. Integral bridge abutment-approach embankment interaction. In IABSE Symposium on Large Structures and Infrastructures for Environmentally Constrained and Urbanized Areas; International Association for Bridge and Structural Engineering: Zürich, Switzerland, 2010; pp. 462–463. [Google Scholar]
- Vägverket, B. Bridge. Code of Practice; Publication number 2004:56; Swedish Road Administration: Borlänge, Sweden, 2004. [Google Scholar]
- Kovac, B. Structural Response of Circular Concrete Filled Tube Piers in Integral Bridges; Universitat Politècnica de Catalunya: Barcelona, Spain, 2010. [Google Scholar]
- Kaufmann, W.; Alvarez, M. Swiss federal roads office guidelines for integral bridges. Struct. Eng. Int. 2011, 21, 189–194. [Google Scholar] [CrossRef]
- Bundesamt für Strassen ASTRA. Richtlinie für Konstruktive Einzelheiten von Brücken; Kapitel 3; Bundesamt für Strassen ASTRA: Bern, Sweden, 2010.
- Kerokoski, O. Soil-Structure Interaction of Long Jointless Bridges with Integral Abutments; Tampere University of Technology: Tampere, Finland, 2006. [Google Scholar]
- Arsoy, S.; Barker, R.M.; Duncan, J.M. The Behavior of Integral Abutment Bridges; VTRC 00-CR03; Virginia Transportation Research Council: Charlottesville, VA, USA, 1999.
- Kim, W.; Laman, J.A. Integral abutment bridge response under thermal loading. Eng. Struct. 2010, 32, 1495–1508. [Google Scholar] [CrossRef]
- Paul, M.D.; Laman, J.A.; Linzell, D.G. Thermally Induced Superstructure Stress in Prestressed Girder Integral Abutment Bridges. Ph.D. Thesis, Pennsylvania State University, State College, PA, USA, 2003; pp. 287–297. [Google Scholar]
- Zhu, Z.; Davidson, M.T.; Harik, I.E.; Sun, L.; Sandefur, K. Effect of superstructure temperature changes on intermediate pier foundation stresses in integral abutment bridges. J. Bridge Eng. 2015, 20, 04014058. [Google Scholar] [CrossRef]
- Wood, J.; Murashev, A.; Palermo, A.; Al-Ani, M.; Andisheh, K.; Goodall, D. Criteria and Guidance for the Design of Integral Bridges in New Zealand; 047844530X; New Zealand Transport Agency: Wellington, New Zealand, 2015.
- Hambly, E.G.; Burland, J.B. Bridge. Foundations and Substructures; The Stationary Office: London, UK, 2015. [Google Scholar]
- O’Brien, E.J.; Keogh, D.; O’Connor, A.; Lehane, B. Bridge. Deck Analysis, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2015; ISBN 139781482227246. [Google Scholar]
- Seed, H.; Idriss, I.M. Soil Moduli and Damping Factors for Dynamic Response Analyses; Report no. EERC 70-10; University of California: Auckland, CA, USA, 1970. [Google Scholar]
- Hamadouche, M.A. Effect of plastic volumetric strains on shakedown of hardening granular soils. Mech. Res. Commun. 2020, 103, 103473. [Google Scholar] [CrossRef]
- Jia, P.-F.; Kong, L.-W. Modeling of ratcheting accumulation of secondary deformation due to stress-controlled high-cyclic loading in granular soils. J. Cent. South Univ. 2015, 22, 2306–2315. [Google Scholar] [CrossRef]
- Barker, R.M.; Duncan, J.M.; Rojiani, K.B.; Ooi, P.S.; Tan, C.; Kim, S. Manuals for the Design of Bridge Foundations: Shallow Foundations, Driven Piles, Retaining Walls and Abutments, Drilled Shafts, Estimating Tolerable Movements, and Load Factor Design Specifications and Commentary; Transportation Research Board: Washington, DC, USA, 1991. [Google Scholar]
- Burke, J.R.; Martin, P. Design of integral concrete bridges. Am. Concr. Inst. 1993, 15, 37–42. [Google Scholar]
- Chen, Y.F. Important considerations, guidelines, and practical details of integral bridges. J. Eng. Technol. 1997, 14, 16–19. [Google Scholar]
- Helmut, E. Geotechnical aspects of the mass-highway guidelines for integral abutment Bridges. In Design of Integral Abutment Bridges, BSCE/ASCE Geotechnical and Structural Groups Seminar; Bentley College: Waltham, MA, USA, 1999; pp. 207–224. [Google Scholar]
- Dicleli, M. A rational design approach for prestressed-concrete-girder integral bridges. Eng. Struct. 2000, 22, 230–245. [Google Scholar] [CrossRef]
- Al-Qarawi, A. A Study on the Fundamental Behaviour of Soil-Structure Interaction and Mitigating Effects of EPS Geofoam Inclusions in Integral Abutment Bridges. Ph.D. Thesis, Western Sydney University, Sydney, NSW, Australia, 2020. [Google Scholar]
- Athanasopoulos-Zekkos, A.; Lamote, K.; Athanasopoulos, G. Use of EPS geofoam compressible inclusions for reducing the earthquake effects on yielding earth retaining structures. Soil Dyn. Earthq. Eng. 2012, 41, 59–71. [Google Scholar] [CrossRef]
- Mitoulis, S.A.; Palaiochorinou, A.; Georgiadis, I.; Argyroudis, S. Extending the application of integral frame abutment bridges in earthquake-prone areas by using novel isolators of recycled materials. Earthq. Eng. Struct. Dyn. 2016, 45, 2283–2301. [Google Scholar] [CrossRef] [Green Version]
- Horvath, J.S. Integral-Abutment Bridges: A Complex Soil-Structure Interaction Challenge. In Geotechnical Engineering for Transportation Projects; Geotechnical Special Publication: Los Angeles, CA, USA, 2004; pp. 460–467. [Google Scholar] [CrossRef]
- Reeves, J.; Filz, G. Earth Force Reduction by a Synthetic Compressible Inclusion; Department of Civil Eng., Virginia Tech, Geotech Systems Corp.: Blacksburg, VA, USA, 2000. [Google Scholar]
- Reid, R.A.; Soupir, S.P.; Schaefer, V.R. Mitigation of void development under bridge approach slabs using rubber tire chips. In Recycled Materials in Geotechnical Applications; ASCE: Reston, VI, USA, 1998; pp. 37–50. [Google Scholar]
- AASHTO. LRFD Bridge. Design Specifications, 7th ed.; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2014. [Google Scholar]
- Illinios Department of Transportation. Bridge. Design Manual 2019; Illinios Department of Transportation: Springfield, IL, USA, 2019.
- Minnesota Department of Transportation. Minnesota Bridge. Design Manual 2016; Highway Division, Minnesota Department of Transportation: St. Paul, MN, USA, 2016.
- Nevada Department of Transportation. Nevada Bridge. Design Manual 2009; Highway Division, Nevada Department of Transportation: Carson City, NV, USA, 2009.
- AASHTO. LRFD Bridge. Design Specifications, 4th ed.; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2007. [Google Scholar]
- AASHTO. Standard Specifications for Highway Bridges, 17th ed.; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2002. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sigdel, L.D.; Al-Qarawi, A.; Leo, C.J.; Liyanapathirana, S.; Hu, P. Geotechnical Design Practices and Soil–Structure Interaction Effects of an Integral Bridge System: A Review. Appl. Sci. 2021, 11, 7131. https://doi.org/10.3390/app11157131
Sigdel LD, Al-Qarawi A, Leo CJ, Liyanapathirana S, Hu P. Geotechnical Design Practices and Soil–Structure Interaction Effects of an Integral Bridge System: A Review. Applied Sciences. 2021; 11(15):7131. https://doi.org/10.3390/app11157131
Chicago/Turabian StyleSigdel, Lila Dhar, Ahmed Al-Qarawi, Chin Jian Leo, Samanthika Liyanapathirana, and Pan Hu. 2021. "Geotechnical Design Practices and Soil–Structure Interaction Effects of an Integral Bridge System: A Review" Applied Sciences 11, no. 15: 7131. https://doi.org/10.3390/app11157131
APA StyleSigdel, L. D., Al-Qarawi, A., Leo, C. J., Liyanapathirana, S., & Hu, P. (2021). Geotechnical Design Practices and Soil–Structure Interaction Effects of an Integral Bridge System: A Review. Applied Sciences, 11(15), 7131. https://doi.org/10.3390/app11157131







