Property Analysis of Slag Composite Concrete Using a Kinetic–Thermodynamic Hydration Model

Abstract

Slag is increasingly unitized for the production of sustainable concrete. This paper presents a procedure with which to analyze the property development of slag composite concrete. Experimental studies of the hydration heat and compressive strength development and simulation studies using a kinetic hydration model and a thermodynamic model were performed. First, we performed an experimental study of the isothermal hydration heat of cement–slag blends. Based on the results of the experimental study on cumulative hydration heat, the reaction degree of slag was determined. We found that the reaction degree of slag decreased as the slag content increased. Second, the reaction degree of slag and cement were used as the input parameters for the Gibbs energy minimization (GEM) thermodynamic equilibrium model. Moreover, the phase assemblage of hydrating cement–slag was determined. The trends of calcium silicate hydrate (CSH) are similar to those of strength. Based on the CSH content, the strength of hardening cement–slag blends was determined. In addition, the calcium hydroxide (CH) content resulting from the thermodynamic model shows good agreement with the experimental results. In summary, the integrated kinetic–thermodynamic model is useful for analyzing the properties of cement–slag blends.

1. Introduction

Granulated blast furnace slag is a by-product of steel and iron manufacture and can be used as a mineral admixture for producing sustainable concrete. Slag composite concrete shows various advantages, such as good workability, high late-stage strength, good resistance to chloride penetration, and good appearance [1,2]. In addition, slag composite concrete is a sustainable alternative because it has lower CO₂ emissions and the cost of materials is lower than plain concrete [2,3,4].

Numerous experimental and theoretical studies have been carried out to investigate the reaction degree, hydration heat, and strength of slag composite concrete.

First, regarding experimental studies, Erdogan and Koçak [5] found that the compressive strength of slag composite concrete has a strong linear relationship with hydration heat at the same age. Lumley et al. [6] and Iyoda et al. [7] found that as the replacement percentage increases and the water/binder ratio decreases, the reaction degree of slag decreases. Liu et al. [8] found that slag cement has a positive effect on late-stage strength and workability and a negative effect on the capillary absorption and salt scaling of ultra-high-performance concrete. Castellano et al. [9] found that 40% slag composite concrete showed a strength crossover, while 80% slag composite concrete did not show a strength crossover. Kim et al. [10] found that 30% is the optimal replacement percentage of slag for producing high early-strength concrete.

Second, regarding theoretical modeling, Bougara et al. [11] evaluated the compressive strength of slag composite concrete using a statistical model of the slag replacement ratio, curing temperature, water/binder ratio, and bound water content. Kandiri et al. [12] evaluated the compressive strength of slag composite concrete using artificial neural networks. Wan et al. [13] performed a second-degree regression of the 3, 7, 14, and 28-day strength of cement–slag–fly ash ternary composite. Tan et al. [14] proposed a kinetic hydration model to determine the hydrating layer thickness of slag particles. Xie et al. [15] developed a kinetic hydration model for slag geopolymer and found that the slag reaction consists of a process of phase boundary reaction and a process of diffusion. Fernández et al. [16] constructed a thermodynamic model of cement–slag blends and evaluated the hydration product assemblage. Schöler et al. [17] analyzed the hydration products of cement–slag–fly ash–limestone quaternary blends and found the optimal combination for strength. Han et al. [18] analyzed the hydration kinetics of cement–slag composite considering the influence of the slag replacement percentage and curing temperature. Gruyaert et al. [19] analyzed the reaction extent of cement, slag, and total binder in binary blends based on the experimental study results of hydration heat, combined water, and backscattered electron image analysis.

Based on our investigations, we found that previous models in this field have several weak points. First, the models of Bougara et al. [11], Kandiri et al. [12], and Wan et al. [13] are statistical models that are difficult to generalize to different mixing proportions and various curing conditions. Second, the models of Tan et al. [14] and Xie et al. [15] are used for alkali-activated slag concrete. It is difficult to simulate the hydration of cement–slag binary composite concrete in these models. Third, the models of Fernández et al. [16] and Schöler et al. [17] are useful for evaluating the phase assemblages of hydration products, however, the reaction degrees of slag in the works of Fernández et al. [16] and Schöler et al. [17] were derived from experimental measurements, which require a large amount of time and money. In other words, if a kinetic model could be used to calculate the reaction extent of slag in binary blends of cement–slag, the use of time- and cost-consuming experimental measurements can be eliminated. Fourth, the studies of Han et al. [18] and Gruyaert et al. [19] do not analyze the interactions between individual reactions of cement and slag. The coefficients of the kinetic models in the studies of Han et al. [18] and Gruyaert et al. [19] change as the mixtures change.

To overcome the weaknesses of previous models, this paper details a procedure to analyze the property development of slag composite concrete. We performed experimental and simulation studies on the hydration heat and strength of cement–slag blends. Based on the results of the experimental study of the hydration heat of binary blends of cement–slag, the reaction degree of slag was determined. The coefficients of the hydration model were constant for various mixtures. Moreover, the reaction extent of slag and cement were used as the input parameters of a Gibbs energy minimization (GEM) thermodynamic equilibrium model and the contents of CSH were determined. The strength of hardening cement–slag blends was determined using a linear equation of the CSH contents.

The structure of this paper is as follows: Section 1 presents the introduction; Section 2 and Section 3 show a hydration-based property evaluation model and the experimental verification of the proposed model, respectively; Section 4 presents a discussion; and Section 5 contains the conclusion.

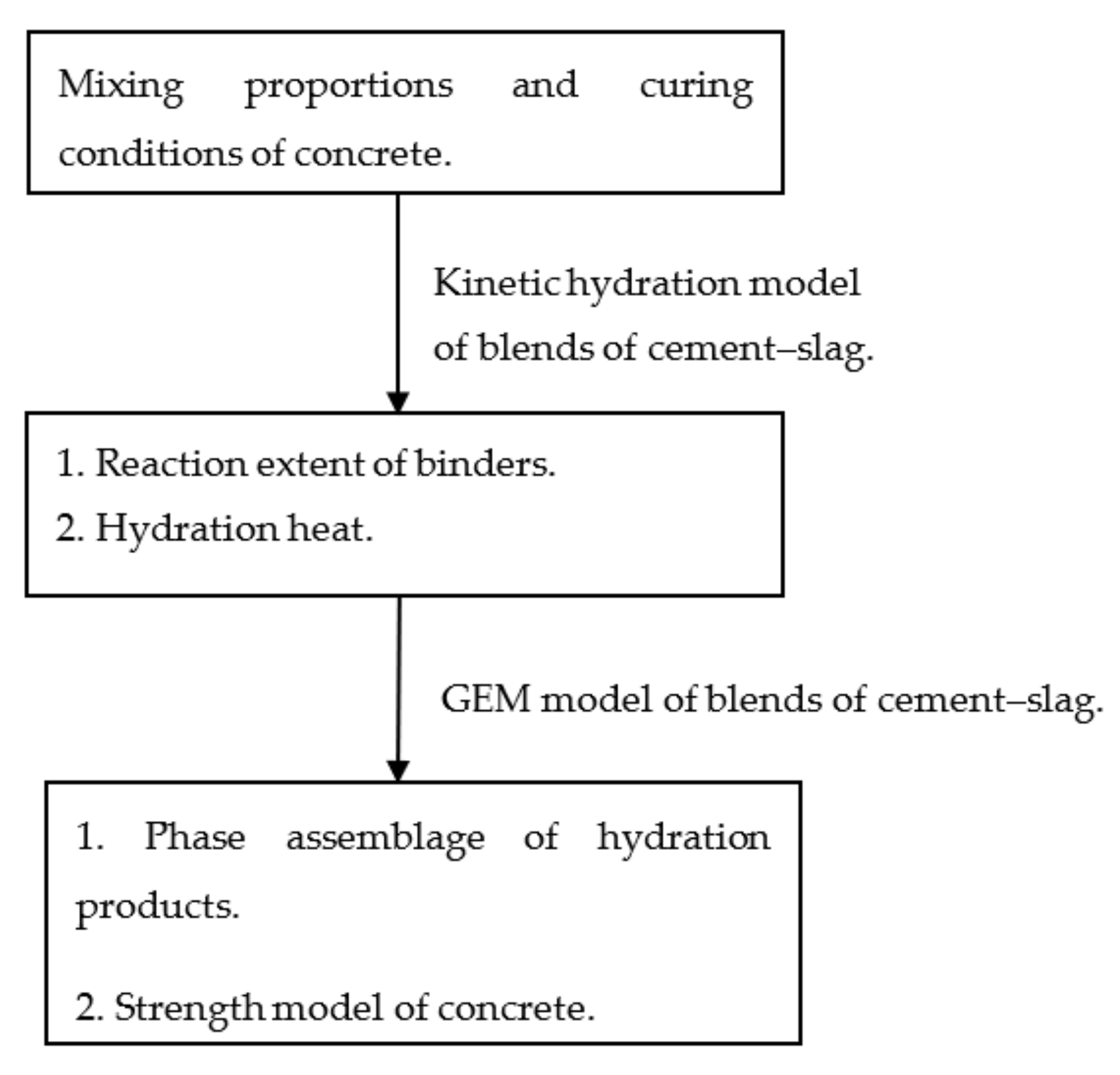
2. Hydration-Based Property Evaluation Model of Binary Blends of Cement–Slag

2.1. Cement Hydration Model

Our previous studies [20,21] utilized a kinetic model that mimics the hydration process for Portland cement. The material composition, such as the cement composition and the concrete mixtures, and the curing conditions, such as the curing temperature, are considered in this kinetic model. The model considers the kinetic process of cement hydration as a period of initial dormancy, a process of phase-boundary reaction, and a process of diffusion. The degree of hydration of the clinker composition ${\alpha }_i$ (i = 1, 2, 3, and 4 denote the mineral composition of cement, such as C₃S, C₂S, C₃A, and C₄AF, respectively) can be calculated based on the numerical integration method in the time domain as ${\alpha }_i={\displaystyle {\int }_0^t\left(\frac{d{\alpha }_i}{dt}\right)}dt$, where $\frac{d{\alpha }_i}{dt}$ is the rate of cement hydration. The equation for the rate of cement hydration $\frac{d{\alpha }_i}{dt}$ is simplified as follows:

$$\frac{d{\alpha }_i}{dt}=f(B,C,De,k{r}_i)*{\lambda }_1*{\lambda }_2,$$

(1)

$$\alpha =\frac{{\displaystyle \sum _{i=1}^{i=4}{\alpha }_i{m}_i}}{{\displaystyle \sum _{i=1}^{i=4}{m}_i}},$$

(2)

where $B$ and $C$ denote the rate-determining coefficients in the period of initial dormancy, $De$ and $k{r}_i$ are the reaction parameters in diffusion-controlled periods and phase boundary-controlled periods, respectively, and ${\lambda }_1$ and ${\lambda }_2$ consider the capillary water withdrawal during the hydration process. The withdrawal of capillary water can lower the rate of hydration. ${\lambda }_1$ covers the capillary water withdrawal because of the development of microstructure, while ${\lambda }_2$ covers the capillary water withdrawal because of the consumption of capillary water (${\lambda }_2=\frac{W_{cap}}{W_0}$, where $W_{cap}$ and $W_0$ are the mass of capillary water and the mass of mixed water in concrete mixtures, respectively). For $m_i$, i = 1, 2, 3, and 4 denote the mass fractions of the mineral composition of cement, such as C₃S, C₂S, C₃A, and C₄AF, respectively. $\alpha$ is the reaction degree of Portland cement. For concrete with a normal strength, the withdrawal of capillary water is less obvious, while for high-strength concrete at the late age of hydration, the withdrawal of capillary water is significant. Due to the consideration of capillary water withdrawal, the kinetic model is valid for both concrete with normal strength and concrete with high strength. The degree of hydration of Portland cement can be determined based on the individual hydration degree of the clinker component.

2.2. Reaction Model of Slag in Cement–Slag Composite

Slag can be used as a mineral admixture to replace partial cement. Based on the experimental results for the isothermal hydration heat of binary blends of cement–slag, Maekawa et al. [22] found that the reaction of slag has a similar kinetic process to that of cement. On the other hand, slag is a cementitious material that has both hydraulicity and pozzolanicity [23]. The reaction of slag can be activated by calcium hydroxide (CH). In hydrating cement–slag blends, CH is produced by the hydration of cement and CH is consumed by the reaction of slag. Considering the kinetic process of the slag reaction and the cementitious material property of slag, the reaction equation for slag in binary blends can be written as ${\alpha }_{SG}={\displaystyle {\int }_0^t\left(\frac{d{\alpha }_{SG}}{dt}\right)}dt$, where ${\alpha }_{SG}$ is the extent of the reaction of slag. The differential equation of the reaction rate of slag in the binary blends is shown as follows:

$$\begin{array}{l}\frac{d{\alpha }_{SG}}{dt}=\frac{CH(t)}{P}*{\lambda }_2*f_{SG}(B_{SG},C_{SG},D{e}_{SG0},k{r}_{SG})\\ =\frac{CH(t)}{P}*{\lambda }_2*\frac{3{\rho }_w}{v_{SG}{r}_{SG0}{\rho }_{SG}}\frac{1}{\frac{1}{\frac{B_{SG}}{{({\alpha }_{SG})}^{1.5}}+C_{SG}*{({\alpha }_{SG})}^3}-\frac{r_{SG0}^{}}{D_{eSG0}*\ln (\frac{1}{{\alpha }_{SG}})}+\frac{r_{SG0}^{}}{D_{eSG0}*\ln (\frac{1}{{\alpha }_{SG}})}{(1-{\alpha }_{SG})}^{\frac{-1}{3}}+\frac{1}{k_{rSG}}{(1-{\alpha }_{SG})}^{\frac{-2}{3}}}\end{array}$$

(3)

where ${\alpha }_{SG}$ is the extent of the reaction of slag; $\frac{d{\alpha }_{SG}}{dt}$ is the rate of the reaction of slag; $B_{SG}$ and $C_{SG}$ are the reaction parameters of slag in a period of dormancy; $D{e}_{SG0}$ is the initial value of the reaction parameter of slag in a diffusion-controlled period; $k{r}_{SG}$ is the reaction parameter of slag in a period of phase boundary control; ${\rho }_w$ and ${\rho }_{SG}$ are the mean densities of water and slag, respectively; $v_{SG}$ is the mass of consumed CH when one gram of slag reacts ($v_{SG}=0.25-0.1\frac{P}{P+C_0}$, where $C_0$ and $P$ denote the mass of cement and slag in the concrete mixtures, respectively); $r_{SG0}$ is the particle radius of slag; and $CH(t)$ is the mass of CH in the hydrating blends.

In Equation (3), the item $\frac{CH(t)}{P}$ considers the dependence of the reaction of slag on the available CH content in hydrating cement–slag blends. The item ${\lambda }_2$ (${\lambda }_2=\frac{W_{cap}}{W_0}$) considers the dependence of the slag reaction on the available capillary water content in hydrating blends of cement–slag. In summary, Equation (3) considers the hydraulicity of slag using item ${\lambda }_2$ and considers the pozzolanicity of slag using item $\frac{CH(t)}{P}$. In addition, the item $D_{eSG0}*\ln (\frac{1}{{\alpha }_{SG}})$ considers the densification of hydration products and the decrease in the accessibility of reactants during the diffusion control process [24].

2.3. Interactions between Individual Reactions of Cement and Slag

For a binary composite of cement–slag, individual reactions of cement and slag coexist and show interactions. This study uses the capillary water content and CH content in the hydrating system to consider the interactions between the individual reactions of cement and slag. The content of capillary water in the hydrating composite system can be determined as follows:

$$W_{cap}=W_0-0.4*C_0*\alpha -0.45*{\alpha }_{SG}*P,$$

(4)

where $0.4*C_0*\alpha$ and $0.45*{\alpha }_{SG}*P$ are the mass of consumed capillary water from the hydration of cement and the reaction of slag, respectively.

For hydrating a cement–slag binary composite, the mass of CH can be calculated as follows:

$$CH(t)=C{H}_{CE}*C_0*\alpha -v_{SG}*{\alpha }_{SG}*P,$$

(5)

where $C{H}_{CE}$ means the mass of CH produced for 1 g of hydrated cement. $C{H}_{CE}*C_0*\alpha$ is the mass of CH produced by the hydration of cement. $v_{SG}*{\alpha }_{SG}*P$ is the mass of CH consumed by the reaction of slag.

2.4. Hydration Heat

For hydrating a binary composite system, the slag reaction and cement hydration contribute to the hydration heat. The total released heat equals the sum of the individual reactions of binders as follows:

$$Q=C_0*H_C*\alpha +P*H_{SG}*{\alpha }_{SG},$$

(6)

where $H_C$ and $H_{SG}$ denote the specific heat generation from cement hydration and the slag reaction, respectively. $H_C$ can be determined based on the cement’s mineral composition [22]. The value of the specific heat generation of slag reaction $H_{SG}$ was proposed as 630 J/g [25,26]. The terms $C_0*H_C*\alpha$ and $P*H_{SG}*{\alpha }_{SG}$ consider the release of heat from the cement hydration and the slag reaction, respectively.

As shown in Equation (6), cumulative hydration heat can be used as an indirect method to determine the extent of the reaction of slag. Moreover, the coefficients of the reaction model of slag can be determined based on the calibration of the results of the experimental study of hydration heat. In addition, because the proposed model covers the interactions between individual reactions of slag and cement, the coefficients of the slag reaction model and the cement hydration model are constants for various mixtures with different slag replacement percentages and water/binder ratios.

2.5. Summary of the Proposed Model

The Gibbs energy minimization program (GEM-Selektor) is widely used for analyzing the phase assemblage, pore solution composition, and durability of cement-based materials [16,17,27]. The strength development of hydrating binary cement–slag closely relates to the phase assemblage of the hydration products [16,17,27].

This paper proposes an integrated kinetic–thermodynamic model of binary blends of cement–slag. As shown in Figure 1, the reaction extent of slag can be determined based on the results of the experimental study of the hydration heat of binary blends of cement–slag. Moreover, the reaction extent of slag and cement are used as the input parameters of a Gibbs energy minimization (GEM) thermodynamic equilibrium model. The contents of the hydration products are determined. Moreover, strength development is evaluated using the contents of the products of hydration.

3. Experimental Studies and Modeling

3.1. Materials and Methods

Portland cement (type I) and blast furnace slag were used to prepare the paste specimen.

Table 1. Chemical composition of cement and slag.

	CaO	SiO2	Al2O3	Fe2O3	MgO	SO3	Na2O	TiO2	Loss on Ignition
Cement	64.7	21.1	5.77	3.14	0.89	1.61	0.25	0.22	2.32
Slag	34.63	35.85	9.79	0.46	13.84	3.45	0.35	0.62	1.01

shows the chemical composition of cement and slag. The SiO₂ content in slag is much higher than that in cement, which favors the production of secondary calcium silicate hydrate and contributes to the strength development.

Table 2. Physical properties of the binder components.

	Fineness (cm2/g)	Specific Gravity
Cement	3300	3.15
Slag	4500	2.90

shows the physical properties of cement and slag.

Table 3. Specimens and tests.

Slag Replacement Percentages	Water/Binder Ratio	Curing Temperature	Isothermal Calorimetry Tests	Strength Tests
0	0.5	20 °C	From mixing time to 7 days	3, 7, 14, 28, and 90 days
30%
50%

shows the specimens and test stages. The water/binder ratio of the specimens was 0.5. The slag replacement percentages were 0%, 30%, and 50%.

The hydration heat and the compressive strength of the paste specimen were measured. The curing temperature of the specimens was 20 °C. The hydration heat was measured using isothermal calorimetry from the time of mixing to 7 days. The strengths were measured from the early stages (three days) to the late stage of 90 days. Cubic specimens (50 ∗ 50 ∗ 50 mm³) were used for strength testing. Sealed curing was used for the specimens in the compressive strength test.

3.2. Experimental Results

Figure 2a shows the experimental results of the rate of heat of hydration. The rate of hydration heat was normalized by the mass of the binder. First, for plain paste, the rate of hydration showed three peaks. The first peak occurred at the starting time, which was due to the rapid dissolution of C₃A. The second peak occurred at about 12 h, which was due to the hydration of C₃S of cement. The third peak occurred at about 17 h, which was due to the renewed dissolution of the aluminum of cement. After 3 days, the rate of hydration heat was low because diffusion became the controlling process of hydration. Second, as the replacement percentage of slag increased from 0% to 30% and 50%, the rate of hydration heat decreased. This was due to the dilution effect of slag addition. For specimens with 30% and 50% slag, the time corresponding to the second peak (C₃S peak) was similar to that of plain concrete. Meanwhile, the third peak was much higher and sharper than the second peak. This was due to the aluminum phase in slag being much higher than that in cement. Third, Figure 2b shows the hydration heat normalized by the mass of cement. From mixing to the time of 9 h, the three curves of plain, 30% slag, and 50% slag merged together. This means that the slag reaction did not start at an early stage. In other words, in the early stage, the slag reaction was in the dormant period. After this stage, the difference in hydration heat between the control specimen and the slag-blended specimen was the result of the slag reaction.

Figure 3 shows the strength development. At 3, 7, and 14 days, as the slag replacement percentage increased, the compressive strength of the concrete was reduced. This was due to the dilution effect of slag. Meanwhile, after curing for 28 days, the compressive strength of the slag composite specimen was higher than that of the plain specimen due to the reaction of the slag. In other words, strength crossover phenomena occurred between the slag-blended specimens and the plain specimens.

3.3. Modeling

3.3.1. Kinetic Model

Equation (6) shows that the hydration heat of blends of cement–slag is dependent on the individual reactions of cement and slag. The Portland cement hydration model can determine the heat release from cement hydration. Thus, using the experimental results for cumulative heat, the reaction coefficients of the reaction model of slag were determined and are shown in

Table 4. Reaction coefficients of the reaction model of slag.

${\mathit{B}}_{\mathit{S}\mathit{G}}$ (cm/h)	${\mathit{C}}_{\mathit{S}\mathit{G}}$ (cm/h)	${\mathit{k}}_{\mathit{r}\mathit{S}\mathit{G}}$ (cm/h)	${\mathit{D}}_{\mathit{e}\mathit{S}\mathit{G}0}$ (cm2/h)
8.93 × 10−9	0.10	1.0 × 10−5	1.86 × 10−11

. Figure 4 shows the results of the analysis of the heat of hydration. As a very early age (from mixing to about 5 h), the increase in the cumulative hydration heat was slow because the hydration of the binder was in a period of initial dormancy. From 5 h to about 20 h, the increase in the cumulative hydration heat became quicker because the phase boundary reaction was the controlling process of hydration. After 20 h, the increase in the cumulative hydration heat became much slower because diffusion was the controlling process of hydration. Moreover, as the slag replacement percentage increased, the cumulative heat of the hydration decreased. This was because slag has a much slower reaction rate than cement.

Figure 5 shows a parameter study of cement–slag blends. Figure 5a shows that as the slag replacement percentage increased, the hydration degree of cement increased. This was because of the increase in the capillary water concentration from the dilution effect of slag. Figure 5b shows that as the slag replacement percentage increased, the reaction degree of slag decreased. This was due to the weakening of the alkali activation effect of CH for higher volumes of slag. Moreover, the slag reaction degree was much lower than the hydration degree of cement. Figure 5c,d shows the components of hydration heat—i.e., the total hydration heat, the heat from Portland cement hydration, and the heat from the slag chemical reaction. For a 50% slag composite paste at the age of 7 days, about 68% of the heat was from cement hydration. In other words, although the mass fraction of cement was the same as that of slag, the hydration heat from cement hydration was much higher than that from the slag reaction.

Figure 5b shows the extent of the slag reaction at an early age (from the time of mixing to 7 days). The proposed model can evaluate the reaction degree of slag at various stages, such as at early and late stages. Iyoda et al. [7] measured the reaction extent of slag over a longer term using selective dissolution methods. The water/binder ratio of the specimen was 0.5, and the slag replacement percentages were 42% and 67%, respectively. The curing temperature was 20 °C. The reaction extent of slag was measured from 3 to 91 days. As shown in Figure 6a,b, the analysis of the reaction extent of slag over a longer term shows agreement with the results of this experiment. In other words, the proposed model is valid for various stages, such as early and late stages. Moreover, as the hydration model considers the interactions between the individual reactions of cement and slag, the coefficients of the reaction model do not change as the mixtures of the specimens change.

3.3.2. Thermodynamic Equilibrium Model

GEM-Selektor can be used to analyze the phase assemblage of hydrating products. When using GEM-Selektor, the compound composition of the cement and slag, curing temperatures, and reaction degree of the cement and slag are necessary input parameters. The phase assemblage is one of the output results of GEM-Selektor. GEM-Selektor, which incorporates the thermodynamic database of cement, is used to evaluate the equilibrium reaction of hydrating cement–slag blends [16,17].

Figure 7a–c shows the results of the phase assemblage from GEM-Selektor. First, for plain paste, as the hydration time increased, the contents of the compositions of clinkers deceased. In the early age, the consumption of C₃S was quick, while at the late age, the reaction rate of C₃S was slow because diffusion was the dominant process in late-stage hydration. In this study, CSHQ was assumed to be the major type of calcium silicate hydrate (CSH). The mass of CSH is much higher than that of other hydration products, such as CH and ettringite. In addition, the content of capillary water decreased as the hydration proceeded. At later stages, the content of capillary water reached a plateau and a decrease in capillary water was not obvious. Second, for 30% and 50% slag paste, at early stages, the consumption of slag was quick, while at late stages, the reaction rate of slag was slow because diffusion was the control process in the late-stage reactions. With the increase in the slag replacement ratios, the calcium hydroxide content decreased. This was due to the dilution effect and the chemical reaction of slag. With the increase in the slag replacement ratios, the content of hydrotalcite increased. This was because slag has a higher MgO content than cement, which favors the formation of hydrotalcite. At the late stages, 30% slag paste had a higher CSH content than plain paste. This was because slag has a higher content of SiO₂ than cement.

Cho [28] measured the calcium hydroxide content of hydrating blends of cement–slag using thermogravimetric analysis. The water/binder ratio of the paste specimens was 0.5; the slag replacement percentages were 0%, 30%, and 50%; and the curing temperature of paste specimens was 20 °C. CH was measured from 3 days to 90 days. Figure 8 shows the analysis of GEM-Selektor, which is generally in agreement with Cho’s experiments. For plain specimens, the CH content initially showed a rapid increase, exhibited a slow increase, then finally reached a plateau. For 50% slag paste, at the early stages, the CH content showed an increase because the hydration of cement was the dominant process, while in later stages, the CH content showed a decrease because the chemical reaction of slag became the dominant process. Compared with the plain specimen, the 50% slag specimen showed a much lower CH content. This was because of the consumption of CH from the slag reaction and the reduction in the cement content.

Figure 9a shows the GEM-Selektor calculation results for combined water. For plain paste, at the early stages, the combined water content increased rapidly, while in later stages of curing, an increment in combined water was not obvious. Meanwhile, for blended paste in later stages of curing, the increment in combined water was more obvious than in plain paste. This was because of the reaction of slag in late stages. Moreover, with the increase in the slag replacement percentage, the content of combined water decreased. At later stages, 30% slag paste had a similar combined water content to that of plain paste, while 50% slag paste had a lower combined water content than that of plain paste. Figure 9b shows that for specimens with different mixtures and different ages, the strength of concrete was linearly dependent on the combined water content. The combined water-based strength model is shown as follows:

$$\mathrm{Strength}=1.9473*\mathrm{combined} \mathrm{water}-10.22$$

(7)

Figure 9c shows that as the slag content increased, the starting time of the strength decreased. The trend of the starting time of the compressive strength showed a similarity to the final results. Slag composite concrete has a higher setting time than plain concrete. However, Figure 9c does not reflect the strength crossover phenomenon. The coefficient of determination of the combined water-based strength model is 0.82.

Figure 10a shows the calculation results for CSH. In the early stages, slag-blended specimens had a lower CSH content, while at late stages, the composite specimens had a higher CSH content than the plain specimens. We can see that the trend in the CSH development is similar to that of compressive strength. Figure 10b shows that for specimens with different mixtures and different ages, the strength of concrete was linearly dependent on the CSH content.

$$\mathrm{Strength}=0.9303*\mathrm{CSH}-8.52$$

(8)

Figure 10c shows that as the slag content increased, the starting time of the strength decreased. Figure 10c reflects the strength crossover phenomenon. As the slag content increased, the time of the strength crossover was extended. The coefficient of determination of the CSH-based strength model was 0.87—much higher than that of the combined water-based strength model. Thus, compared with the combined water content, the CSH content was more suitable for the evaluation of the strength of cement–slag blends.

4. Discussion

Compared with previous studies, the main innovations of this paper are as follows:

First, using the results of the experimental study of the isothermal heat of hydration, we determined the reaction degree of slag. There are many experimental techniques for measuring the reaction extent of slag, such as the method of selective dissolution, the back-scattered electrons (BSE) image analysis method, and nuclear magnetic resonance testing [29,30,31]. These experimental methods are direct methods that directly demonstrate the reaction extent of slag. In contrast, isothermal hydration heat must be measured using the indirect method because the reactions of cement and slag are coupled together. The proposed model can separate the slag reaction from the hydration of Portland cement. Slag reactions are decoupled from the hydration of Portland cement. The contribution of slag to the hydration heat can be quantitatively determined. The results from using the indirect method in this study show agreement with the results of the direct method used in [7].

Second, the reaction degree of slag is an essential input parameter for GEM-Selektor. The proposed kinetic hydration model can determine the reaction degree of slag, which can be used as an input parameter for GEM-Selektor. The purpose of this study was not to replace GEM-Selektor but to provide convenient input parameters for GEM-Selektor. Moreover, because the coefficients of the proposed kinetic hydration model are constant for various mixtures, one set of experimental data on hydration heat is sufficient to determine the coefficients [32]. In other words, by using the proposed kinetic hydration model, the high time- and cost-consumption of other methods for the measurement of the reaction extent of slag can be eliminated.

Third, the theoretical implication of the work is that the proposed kinetic–thermodynamic hydration model can predict the phase assemblage and strength development of cement–slag composite. Moreover, because concrete’s durability properties are closely related to phase assemblage, the proposed model has potential application in predicting the durability properties of concrete. In addition, the main practical implication of the work is the material design and construction management of slag composite concrete. Based on the proposed model, concrete manufacturers can select the suitable slag replacement percentages, and the construction managers can confirm the stages of the removal of formwork from concrete structures.

5. Conclusions

This study demonstrates a procedure for analyzing the development of properties in slag composite concrete.

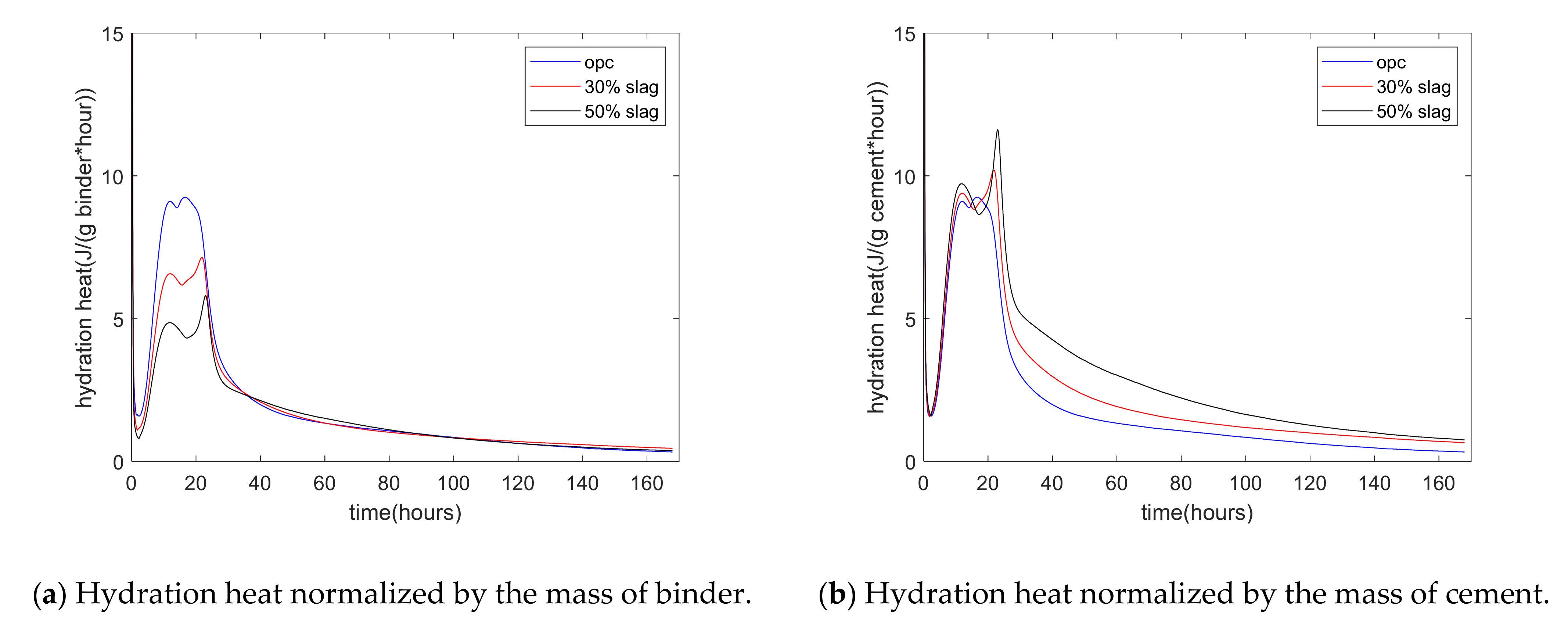
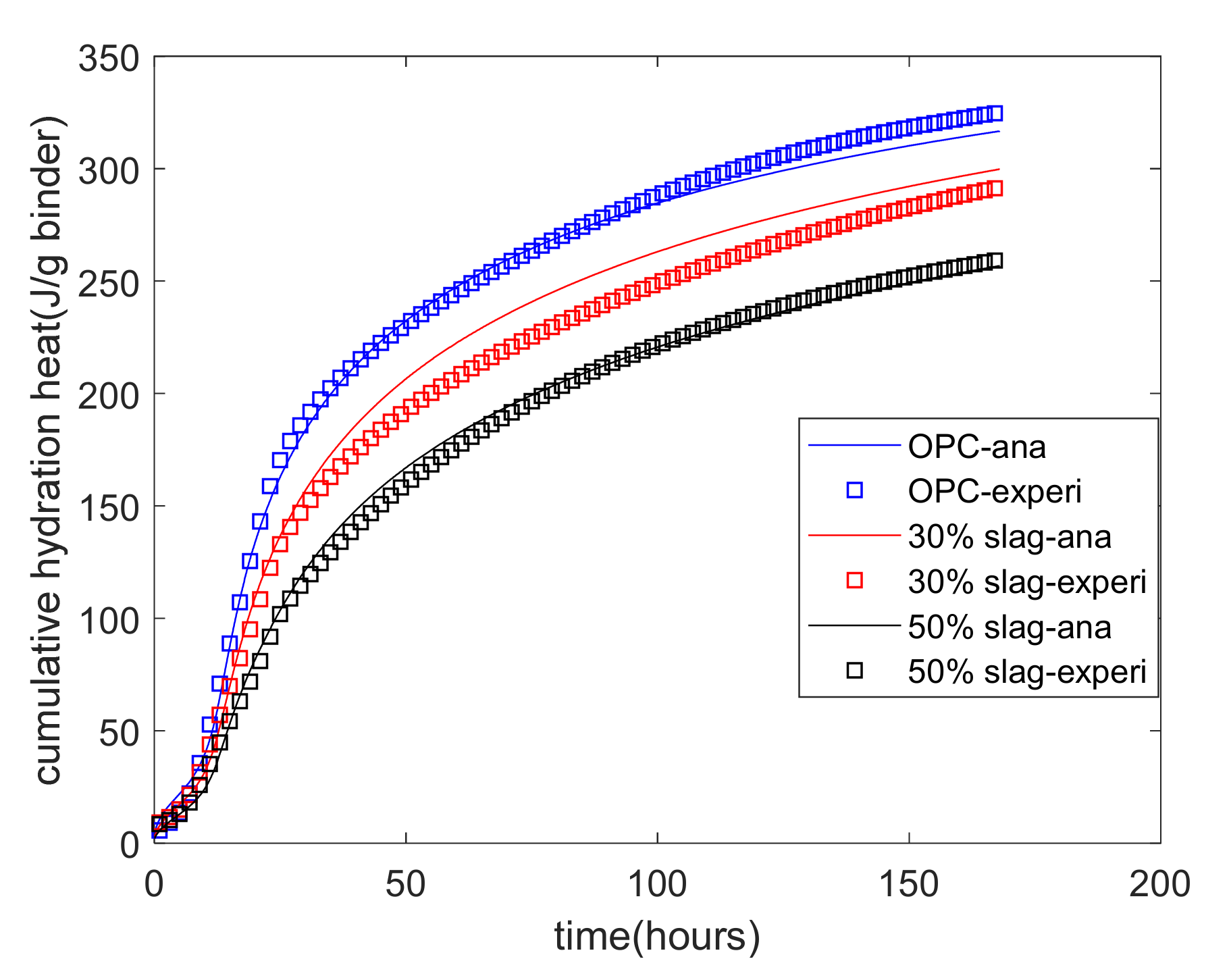
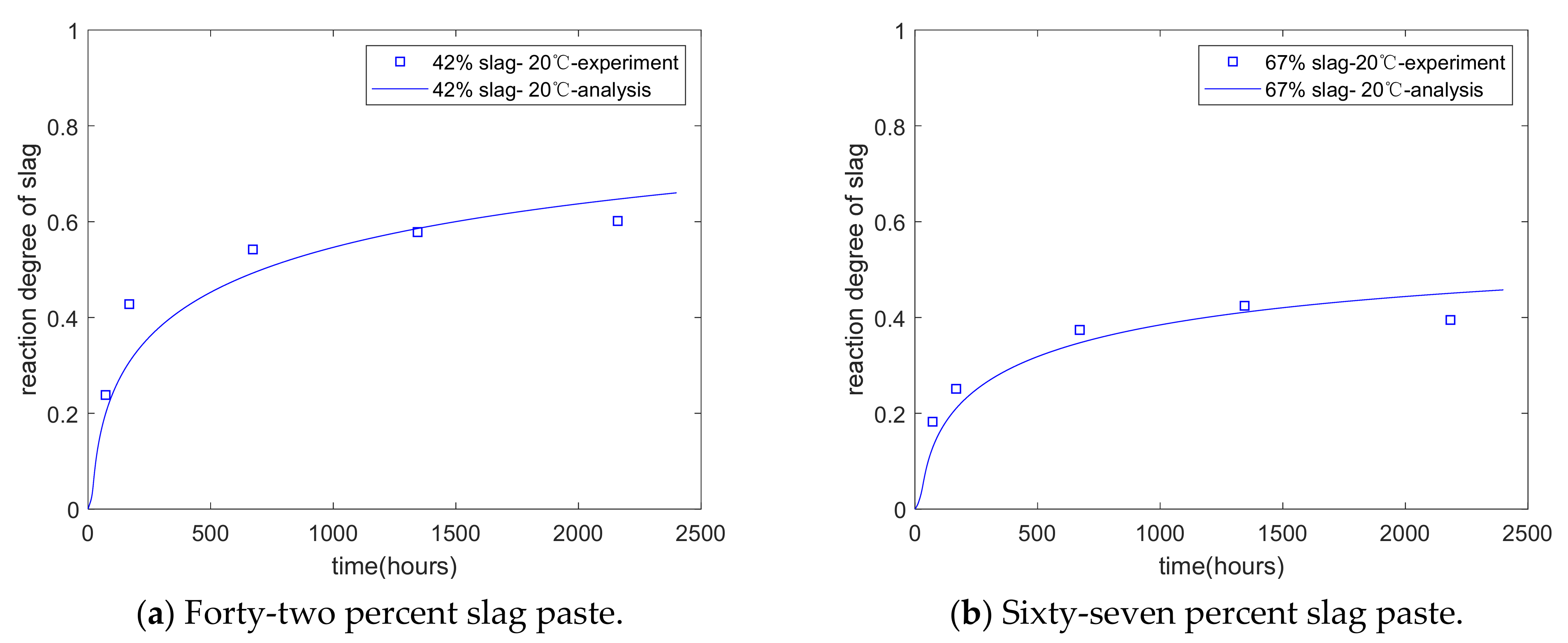
• First, we performed an experimental study on the isothermal hydration heat of blends of cement–slag. As the replacement percentages of slag increased from 0% to 30% and 50%, the rate of hydration heat decreased. For specimens with 30% and 50% slag, the third peak for the dissolution of aluminum was much higher and sharper than the second peak. Moreover, using the experimental results for the isothermal heat of hydration, we determined the reaction extent of slag. The analysis found that, as the replacement percentage of slag increased, the reaction extent of the slag was reduced. In addition, because the proposed model covers the interactions between the individual reactions of slag and cement, the coefficients of the slag reaction model and the cement hydration model are constant for various mixtures.
• Second, during the isothermal calorimetry test, both cement hydration and slag reaction contribute to heat release. Because the proposed kinetic hydration model can separate the slag reaction from cement hydration, the contribution of the slag reaction on heat release can be determined. Moreover, the reaction degree of slag can be calculated. Thus, based on the use of the kinetic hydration model, the isothermal calorimetry test can be used as an indirect method for determining the reaction degree of slag.
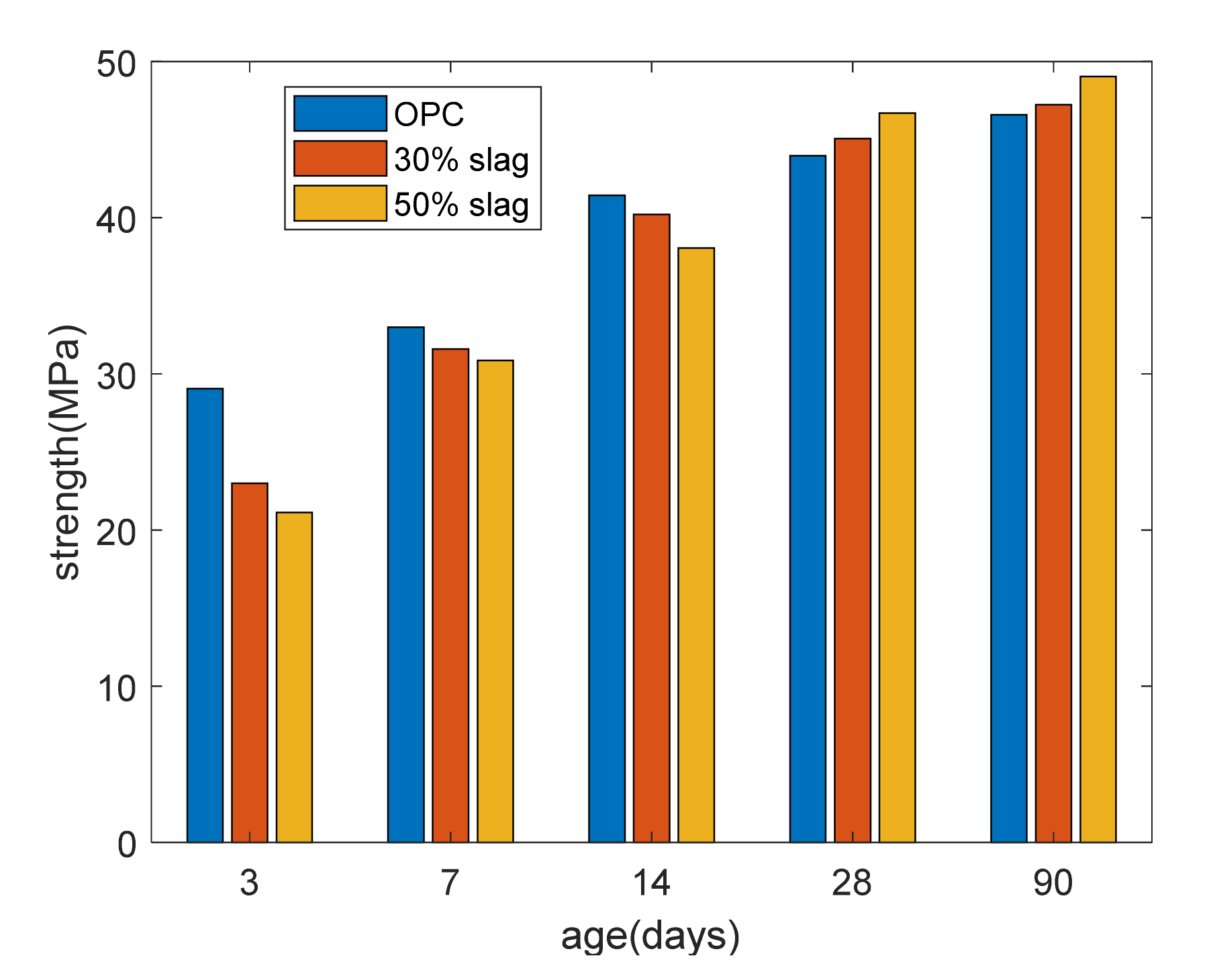
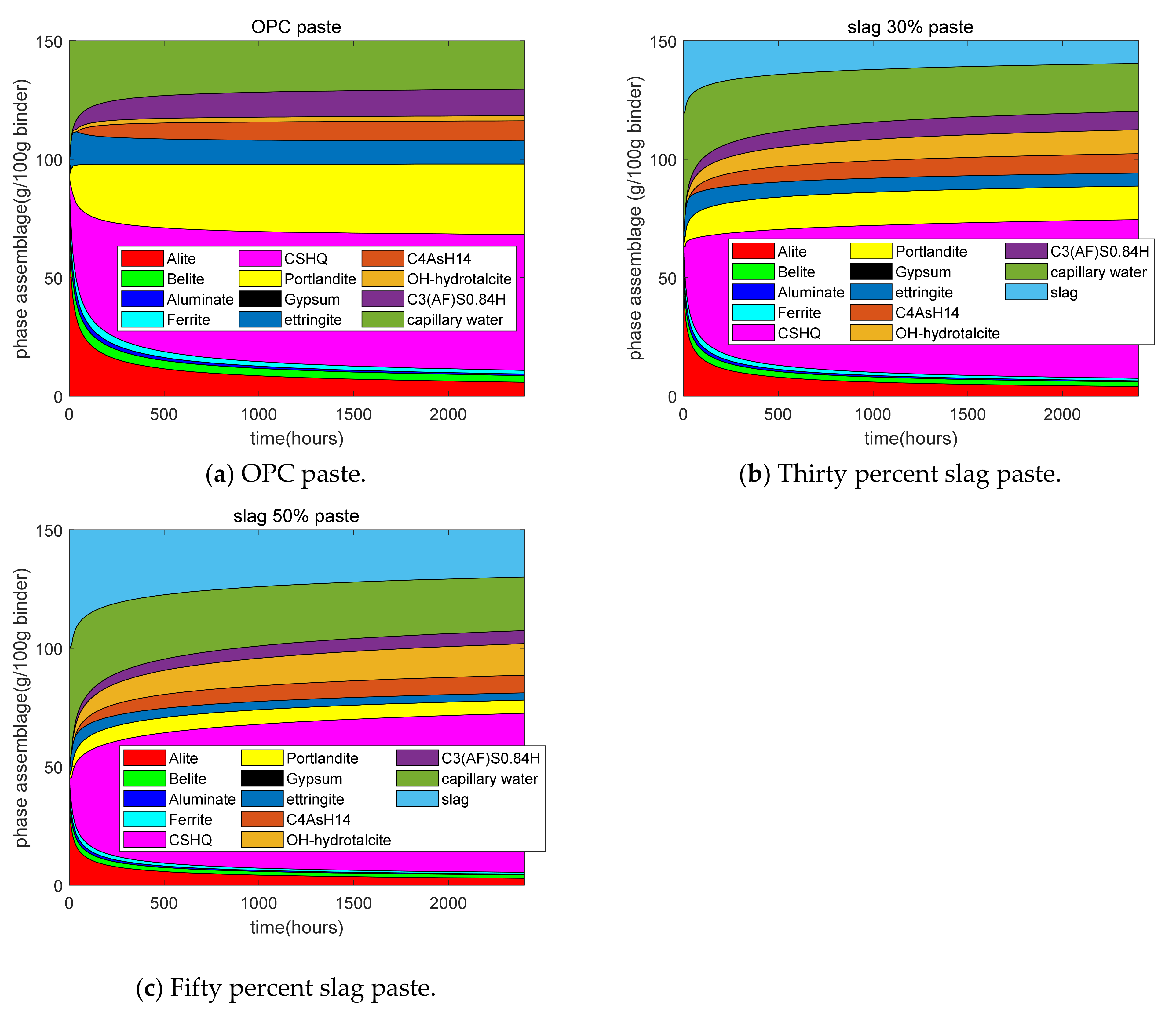
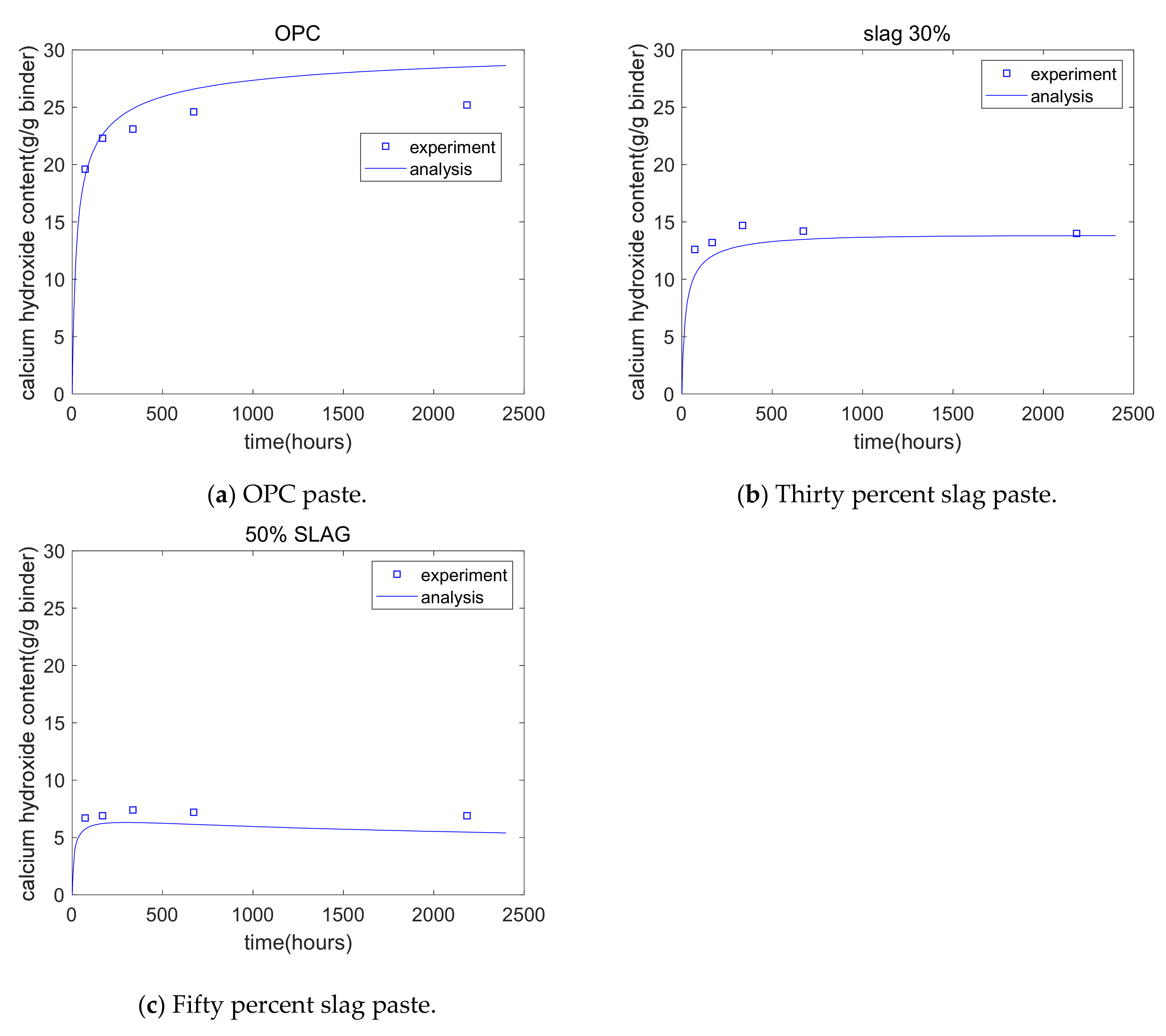
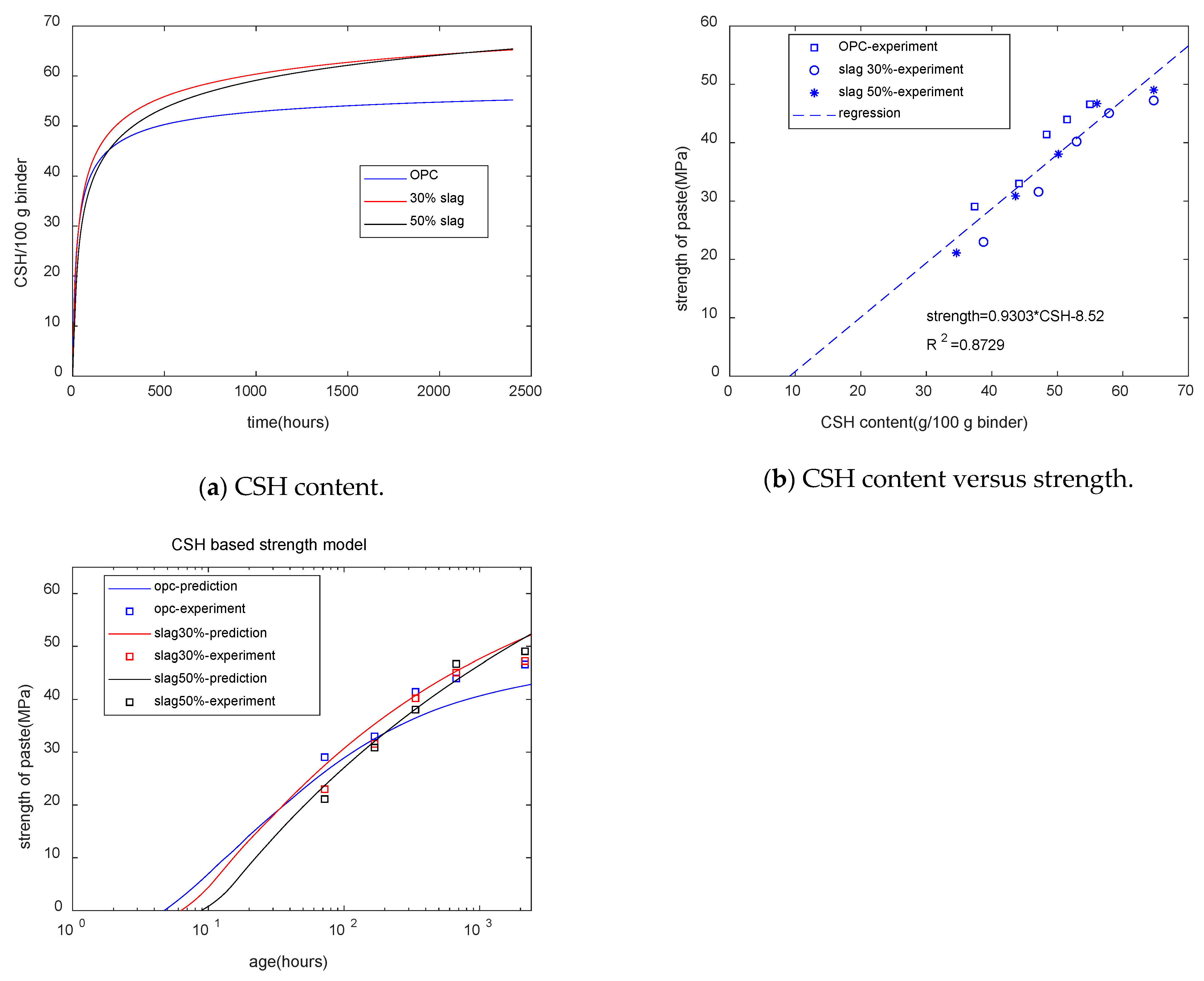
• Third, the reaction extents of slag and cement were used as input parameters for the thermodynamic equilibrium model, and the phase assemblage of the hydration of cement–slag was determined. Using the experimental results for strength and the analysis results of GEM-Selektor, we found that the strength of paste is linearly dependent on the combined water content or CSH content. The coefficients of determination for the combined water-based strength model and the CSH-based strength model were 0.82 and 0.87, respectively. The combined water-based strength model cannot reflect the strength crossover between plain paste and blended paste, while the CSH-based strength model can reflect the strength crossover. The CSH-based strength model showed that as the slag content increased, the time of the strength crossover grew longer. Compared with the combined water content, the CSH content is more suitable for the evaluation of the strength of cement–slag blends.
• Fourth, the specific contributions of this study are summarized as follows: (1) we proposed a kinetic hydration model to evaluate the reaction extent of slag and cement based on an isothermal calorimetry test, (2) we used the calculation results of the kinetic hydration model as input data for a thermodynamic model and evaluated the phase assemblage of hydrating cement–slag composite, and (3) we evaluated the strength development of hardening concrete using phase assemblage of composite concrete.

In summary, the evolution of the phase assemblage (chemical compositions) of cement–slag blends can be calculated based on the integrated kinetic–thermodynamic model. Moreover, the development of the compressive strength (mechanical property) of composite concrete can be evaluated using a phase assemblage, such as CSH content or combined water content. Thus, the proposed model is useful for analyzing the chemical and mechanical properties of cement–slag blends.