Theoretical and Experimental Study of Optimization of Polarization Spectroscopy for the D2 Closed Transition Line of 87Rb Atoms
Abstract
:1. Introduction
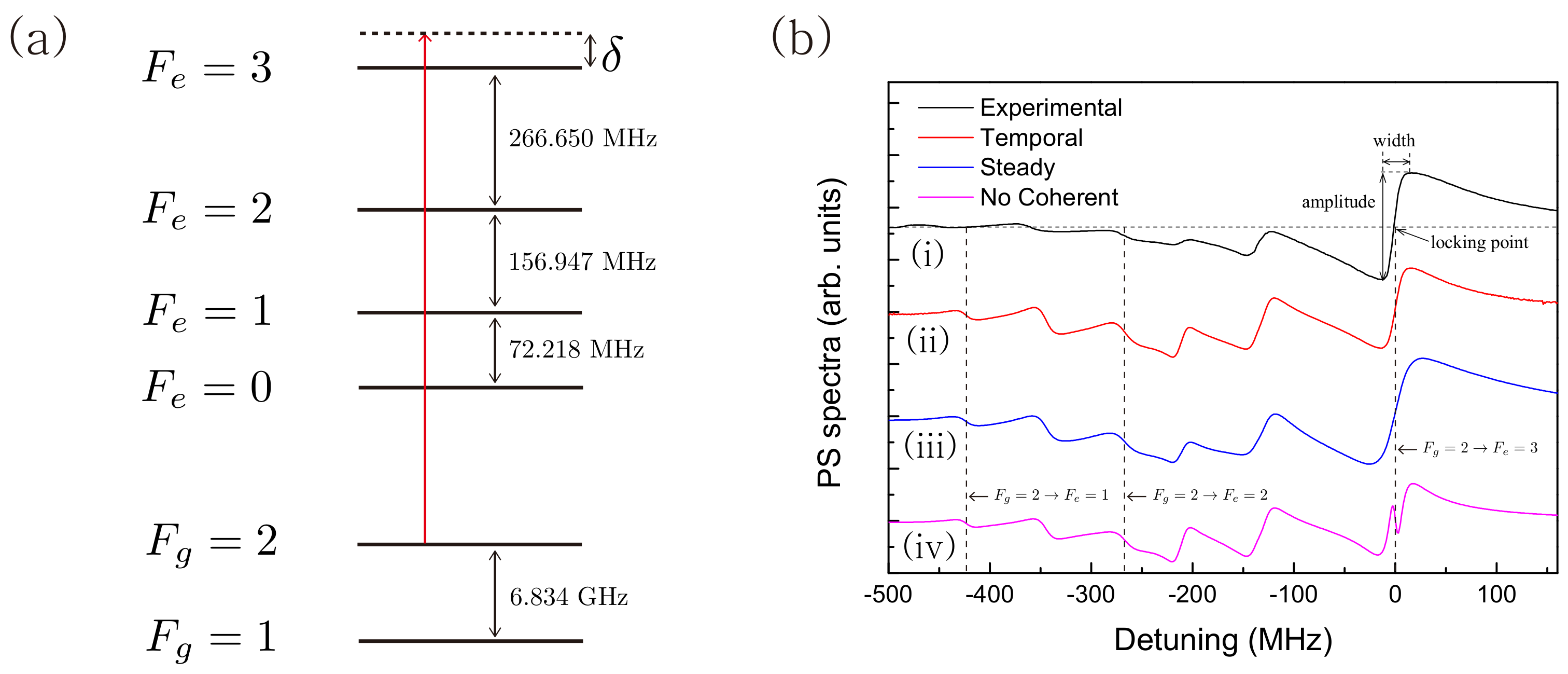
2. Experimental Setup
3. Theory
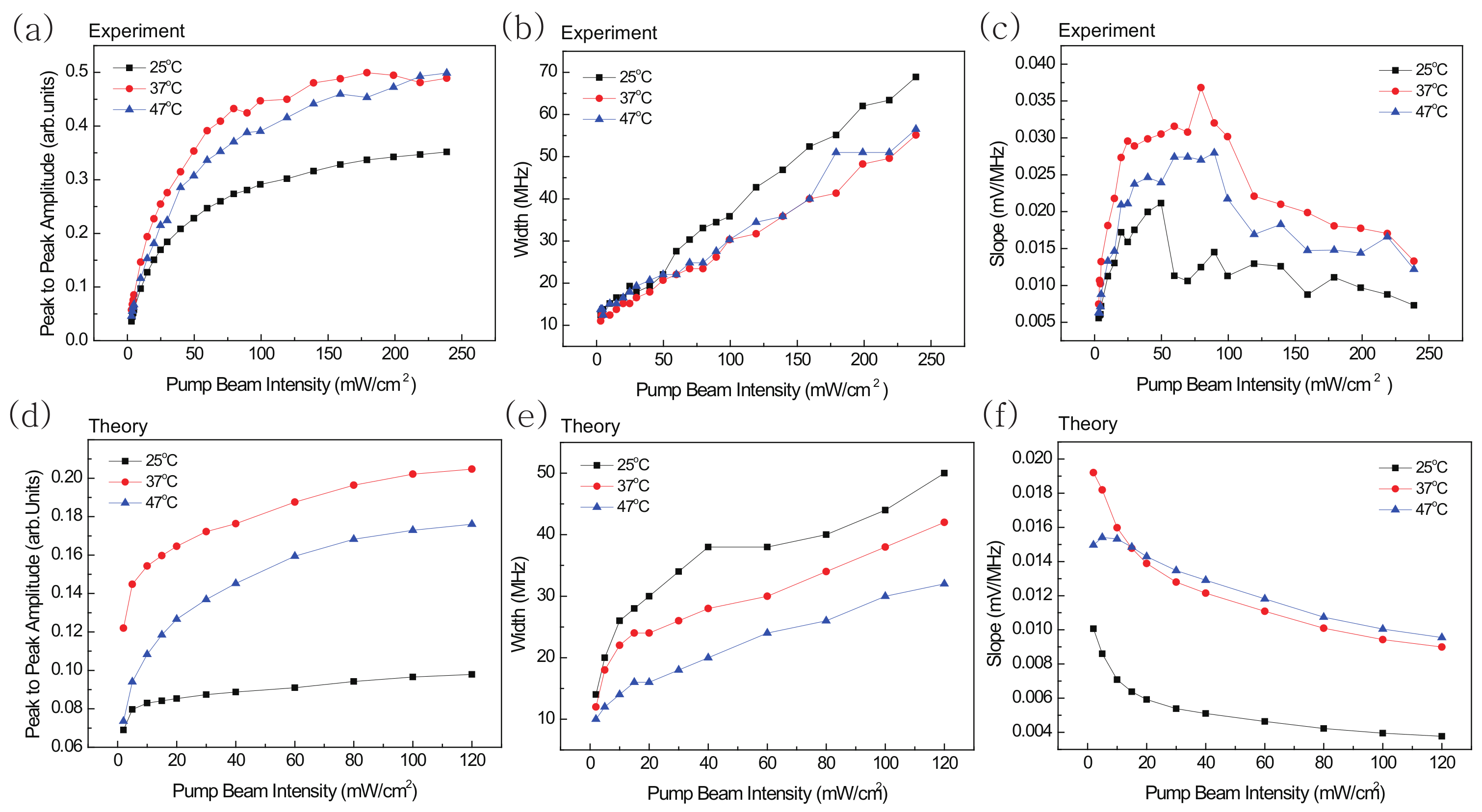
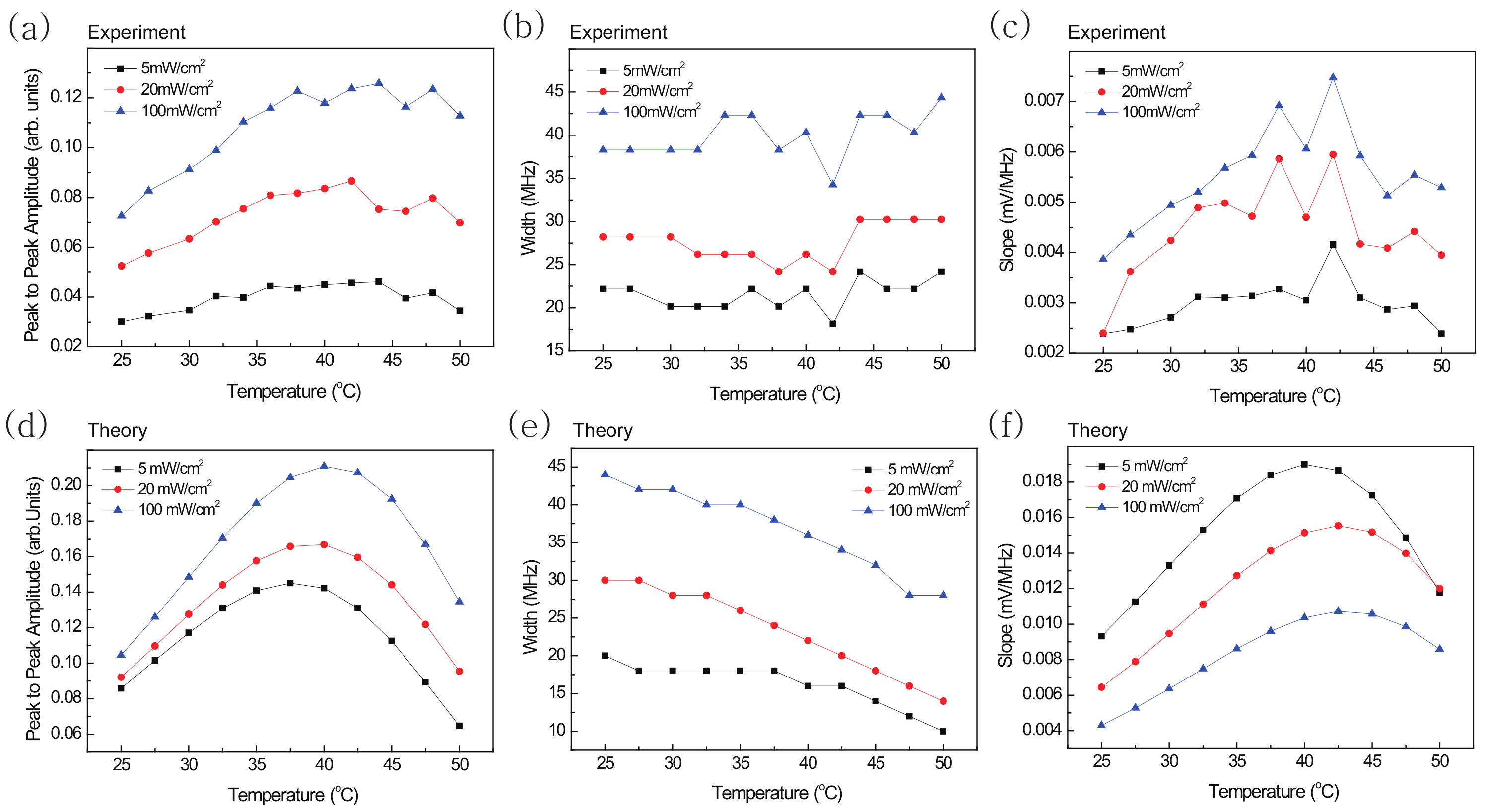
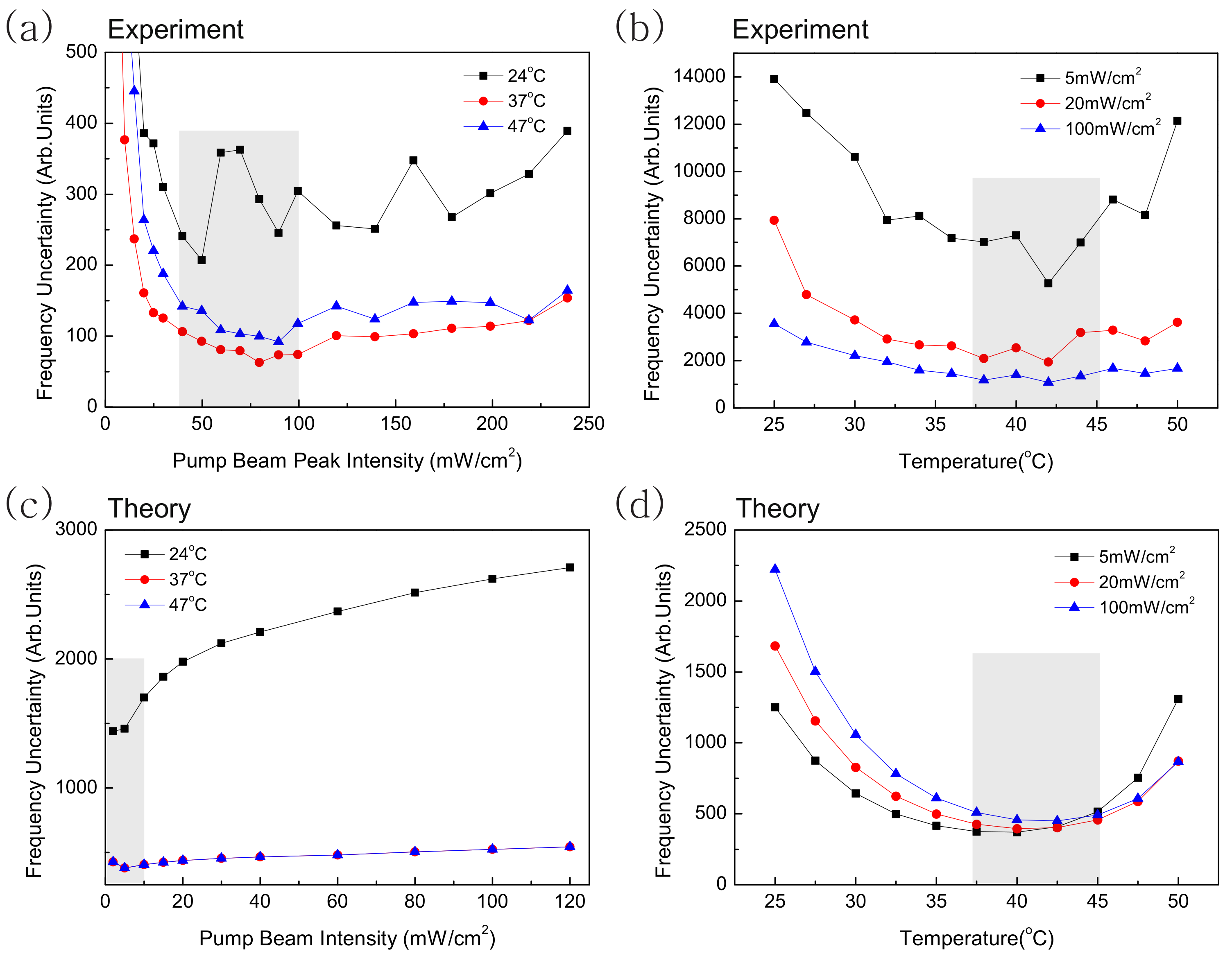
4. Results and Discussions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Demtröder, W. Laser Spectroscopy; Springer: Berlin, Germany, 1998. [Google Scholar]
- Moon, G.; Noh, H.R. Analytic solutions for the saturated absorption spectra. J. Opt. Soc. Am. B 2008, 25, 701–711. [Google Scholar] [CrossRef]
- Moon, G.; Noh, H.R. A comparison of the dependence of saturated absorption signals on pump beam diameter and intensity. J. Opt. Soc. Am. B 2008, 25, 2101–2106. [Google Scholar] [CrossRef]
- Moon, G.; Noh, H.R. Observation of nonstationary effects in saturation spectroscopy. Opt. Commun. 2008, 281, 294–298. [Google Scholar] [CrossRef]
- Wieman, C.; Hänsch, T.W. Doppler-Free Laser Polarization Spectroscopy. Phys. Rev. Lett. 1976, 36, 1170. [Google Scholar] [CrossRef]
- Do, H.D.; Moon, G.; Noh, H.R. Polarization spectroscopy of rubidium atoms: Theory and experiment. Phys. Rev. A 2008, 77, 032513. [Google Scholar] [CrossRef]
- Jeong, T.; Won, J.Y.; Noh, H.R. Line shapes in polarization spectroscopy for the rubidium D1 line in an external magnetic field. Opt. Commun. 2013, 292, 106–110. [Google Scholar] [CrossRef]
- Corwin, K.L.; Lu, Z.; Hand, C.F.; Epstein, R.J.; Wieman, C.E. Frequency-stabilized diode laser with the Zeeman shift in an atomic vapor. Appl. Opt. 1998, 37, 3295–3298. [Google Scholar] [CrossRef]
- Millett-Sikking, A.; Hughes, I.G.; Tierney, P.; Cornish, S.L. DAVLL lineshapes in atomic rubidium. J. Phys. B At. Mol. Opt. Phys. 2007, 40, 187. [Google Scholar] [CrossRef]
- Shim, U.; Kim, J.A.; Jhe, W. Saturated absorption spectroscopy in the presence of a longitudinal magnetic field. J. Korean Phys. Soc. 1999, 35, 222–225. [Google Scholar]
- Wasik, G.; Gawlik, W.; Zachorowski, J.; Zawadzki, W. Laser frequency stabilization by Doppler-free magnetic dichroism. Appl. Phys. B 2002, 75, 613–619. [Google Scholar] [CrossRef]
- Choi, G.W.; Noh, H.R. Line shapes in sub-Doppler DAVLL in the 87Rb-D2 line. Opt. Commun. 2016, 367, 312–315. [Google Scholar] [CrossRef]
- Choi, G.W.; Noh, H.R. Sub-Doppler DAVLL spectra of the D1 line of rubidium: A theoretical and experimental study. J. Phys. B At. Mol. Opt. Phys. 2015, 48, 115008. [Google Scholar] [CrossRef]
- McCarron, D.J.; King, S.A.; Cornish, S.L. Modulation transfer spectroscopy in atomic rubidium. Meas. Sci. Technol. 2008, 19, 105601. [Google Scholar] [CrossRef]
- Noh, H.R.; Park, S.E. Modulation transfer spectroscopy for two-level atoms at high laser intensity. Opt. Commun. 2015, 336, 173–176. [Google Scholar] [CrossRef]
- Park, S.E.; Noh, H.R. Modulation transfer spectroscopy mediated by spontaneous emission. Opt. Express 2013, 21, 14066–14073. [Google Scholar] [CrossRef] [PubMed]
- Nakanishi, S.; Ariki, H.; Itoh, H.; Kondo, K. Frequency-modulation spectroscopy of rubidium atoms with an AlGaAs diode laser. Opt. Lett. 1987, 12, 864–866. [Google Scholar] [CrossRef]
- Supplee, J.M.; Whittaker, E.A.; Lenth, W. Theoretical description of frequency modulation and wavelength modulation spectroscopy. Appl. Opt. 1994, 33, 6294–6302. [Google Scholar] [CrossRef] [PubMed]
- Bjorklund, G.C.; Levenson, M.D.; Lenth, W.; Ortiz, C. Frequency modulation (FM) spectroscopy. Appl. Phys. B 1983, 32, 145–152. [Google Scholar] [CrossRef]
- Sun, J.-F.; Yin, S.-Q.; Xu, Z.; Hong, T.; Wang, Y.-Z. Optimization of polarization spectroscopy for rubidium D lines. Chin. Phys. B. 2013, 22, 024207. [Google Scholar] [CrossRef]
- Lee, S.L.; Lee, S.B.; Park, S.E.; Hong, H.G.; Heo, M.S.; Seo, S.W.; Jeong, J.Y.; Kwon, T.Y.; Moon, G. Compact modulation transfer spectroscopy module for highly stable laser frequency. Opt. Lasers Eng. 2021, 146, 106698. [Google Scholar] [CrossRef]
- Hu, Z.K.; Sun, B.L.; Duan, X.C.; Zhou, M.K.; Chen, L.L.; Zhan, S.; Zhang, Q.Z.; Luo, J. Demonstration of an ultrahigh-sensitivity atom-interferometry absolute gravimeter. Phys. Rev. A 2013, 88, 043610. [Google Scholar] [CrossRef]
- Bidel, Y.; Zahzam, N.; Blanchard, C.; Bonnin, A.; Cadoret, M.; Bresson, A.; Rouxel, D.; Lequentrec-Lalancette, M.F. Absolute marine gravimetry with matter-wave interferometry. Nat. Commun. 2018, 9, 627. [Google Scholar] [CrossRef]
- Ménoret, V.; Vermeulen, P.; Moigne, N.L.; Bonvalot, S.; Bouyer, P.; Landragin, A.; Desruelle, B. Gravity measurements below 10−9 g with a transportable absolute quantum gravimeter. Sci. Rep. 2018, 8, 12300. [Google Scholar] [CrossRef]
- Luo, Y.; Yan, S.; Jia, A.; Wei, C.; Li, Z.; Wang, E.; Yang, J. Revisiting the laser frequency locking method using acousto-optic frequency modulation transfer spectroscopy. Chin. Opt. Lett. 2016, 14, 121401. [Google Scholar]
- Harris, M.L.; Adams, C.S.; Cornish, S.L.; McLeod, I.C.; Tarleton, E.; Hughes, I.G. Polarization spectroscopy in rubidium and cesium. Phys. Rev. A 2006, 73, 062509. [Google Scholar] [CrossRef] [Green Version]
- Jeong, T.; Noh, H.R. Polarization Spectroscopy for the 85Rb D1 Line in a Strong Pump Field. J. Korean Phys. Soc. 2013, 63, 896–899. [Google Scholar] [CrossRef]
- Do, H.D.; Heo, M.S.; Moon, G.; Noh, H.R.; Jhe, W. Analytic calculation of the lineshapes in polarization spectroscopy of rubidium. Opt. Commun. 2008, 281, 4042–4047. [Google Scholar] [CrossRef]
- Noh, H.R. Line shape in polarization spectroscopy for the Jg = 0 → Je = 1 transition: An analytical study. J. Opt. Soc. Am. B 2016, 33, 1523–1528. [Google Scholar] [CrossRef]
- Moon, G.; Yang, S.C.; Kim, J.T.; Noh, H.R. Polarization rotation spectral profiles for the D2 line of 87Rb atoms: Theory and experiment. J. Phys. B At. Mol. Opt. Phys. 2019, 52, 225004. [Google Scholar] [CrossRef]
- Seo, M.J.; Won, J.Y.; Noh, H.R. Variation in the Polarization State of Arbitrarily Polarized Light via a Circular Anisotropic Atomic Medium. J. Korean Phys. Soc. 2011, 59, 253–256. [Google Scholar] [CrossRef]
- Sagle, J.; Namiotka, R.K.; Huennekens, J. Measurement and modelling of intensity dependent absorption and transit relaxation on the cesium D1 line. J. Phys. B At. Mol. Opt. Phys. 1996, 29, 2629. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeong, J.; Lee, S.; Hwang, S.; Baek, J.; Noh, H.-R.; Moon, G. Theoretical and Experimental Study of Optimization of Polarization Spectroscopy for the D2 Closed Transition Line of 87Rb Atoms. Appl. Sci. 2021, 11, 7219. https://doi.org/10.3390/app11167219
Jeong J, Lee S, Hwang S, Baek J, Noh H-R, Moon G. Theoretical and Experimental Study of Optimization of Polarization Spectroscopy for the D2 Closed Transition Line of 87Rb Atoms. Applied Sciences. 2021; 11(16):7219. https://doi.org/10.3390/app11167219
Chicago/Turabian StyleJeong, Jeongyoun, Sanglok Lee, Sungi Hwang, Jaeuk Baek, Heung-Ryoul Noh, and Geol Moon. 2021. "Theoretical and Experimental Study of Optimization of Polarization Spectroscopy for the D2 Closed Transition Line of 87Rb Atoms" Applied Sciences 11, no. 16: 7219. https://doi.org/10.3390/app11167219
APA StyleJeong, J., Lee, S., Hwang, S., Baek, J., Noh, H.-R., & Moon, G. (2021). Theoretical and Experimental Study of Optimization of Polarization Spectroscopy for the D2 Closed Transition Line of 87Rb Atoms. Applied Sciences, 11(16), 7219. https://doi.org/10.3390/app11167219





