Abstract
Unmanned Aerial Vehicles (UAVs) are abundantly becoming a part of society, which is a trend that is expected to grow even further. The quadrotor is one of the drone technologies that is applicable in many sectors and in both military and civilian activities, with some applications requiring autonomous flight. However, stability, path planning, and control remain significant challenges in autonomous quadrotor flights. Traditional control algorithms, such as proportional-integral-derivative (PID), have deficiencies, especially in tuning. Recently, machine learning has received great attention in flying UAVs to desired positions autonomously. In this work, we configure the quadrotor to fly autonomously by using agents (the machine learning schemes being used to fly the quadrotor autonomously) to learn about the virtual physical environment. The quadrotor will fly from an initial to a desired position. When the agent brings the quadrotor closer to the desired position, it is rewarded; otherwise, it is punished. Two reinforcement learning models, Q-learning and SARSA, and a deep learning deep Q-network network are used as agents. The simulation is conducted by integrating the robot operating system (ROS) and Gazebo, which allowed for the implementation of the learning algorithms and the physical environment, respectively. The result has shown that the Deep Q-network network with Adadelta optimizer is the best setting to fly the quadrotor from the initial to desired position.
1. Introduction
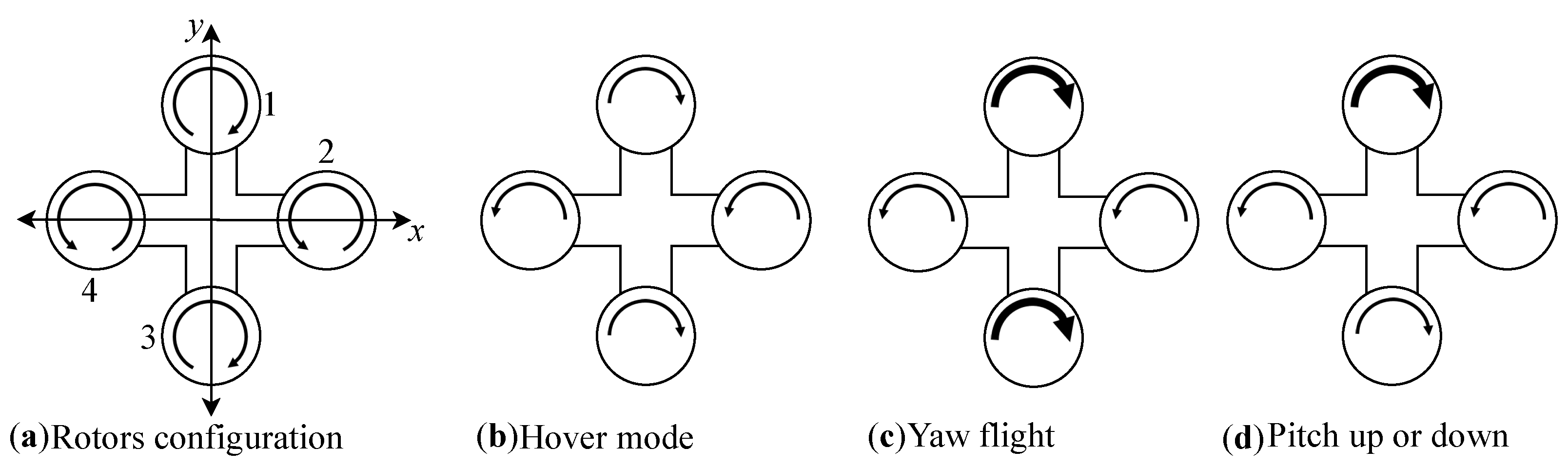
In recent times, drone or unmanned aerial vehicle (UAV) technology has advanced significantly, and it can be applied not only in the military sector but also in civilian areas, such as in search and rescue (SAR) and package shipment, due to its high mobility and large overload maneuver [1]. Many researchers worldwide are now working to address issues related to UAVs. Herein, we focus on the application, performance, and implementation of machine learning algorithms for controlling UAVs. Even though there are several types of UAVs, such as fixed wings, quadrotors, blimps, helicopters, and ducted fan [2], due to its small size, low inertia, maneuverability, and cheap price, the quadrotor had become an industry favorite [3]. There are several applications of the quadrotor in industries such as film, agriculture, delivery, infrastructure inspection, etc. [3,4]. A quadrotor or quadcopter (henceforth, the terms UAV, drone, quadcopter, and quadrotor are used interchangeably) is a type of UAV with four rotors designed in a cross configuration with two pairs of opposite rotors rotating in the clockwise direction, whereas the other rotor pair rotates in a counter-clockwise direction to balance the torque [5]. Figure 1 shows the famous arrangements of the rotors of a quadcopter for flight mode.
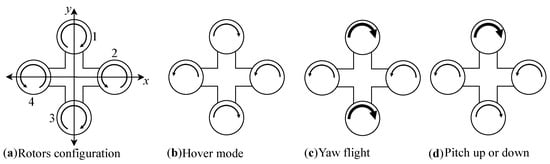
Figure 1.
Configuration of rotors in quadcopter.
Configuration “A” shows how the rotors of the drone work when rotors 1 and 3 rotate in the clockwise direction, and rotors 2 and 4 rotate in the same counter-clockwise direction. Configuration “B” depicts the drone in hovering mode. In this case, all rotors have the same torques. Configuration “C” shows how the drone performs a yaw flight, where the strength torques of rotors 1 and 3 exceed those of rotors 2 and 4, or the strength torques of rotors 2 and 4 exceed those of rotors 1 and 3. Both scenarios are dependent on the direction of the drone flight with reference to the Z-axis. Configuration “D” represents the pitch up and pitch down. Here, one rotor has greater torque strength than the rest of the rotors. The rotor that can produce greater torque strength depends on the movements, which provides better flexibility.
Traditionally, a closed-loop proportional integral derivative (PID) controller is used to fly the quadrotor from the initial to the desired position. The PID controller flies the UAV by tuning values such as . However, tuning these values is a challenging and cumbersome task. In contrast, recent reinforcement learning-based controllers have shown a more promising way than the conventional method to fly a quadrotor accurately [6,7].
In this paper, to study this phenomenon further, we integrated learning algorithms with a simulation environment and tested their performance under different conditions, optimization, and reward functions. We use the robot operating system (ROS) framework [8], together with Gazebo [9], for simulation, and OpenAI Gym to load the agents (machine learning algorithms) [10]. The drones will be flown from the initial to the desired position autonomously via one of the agents. The agent flying the quadrotor will take one step from the initial to the desired position. Then, for the remaining distance, if the current distance is closer than the previous, the agent will be rewarded; otherwise, it will be punished. This process allows the agent to learn its physical environment.
Q-learning and State–action–reward–state–action (SARSA) reinforcement learning as well as Deep Q-network (DQN) deep learning agents are selected as agents. Since the DQN algorithm can be optimized to improve the performance, Adadelta [11], RMSProp [12], Stochastic Gradient Descent (SGD) [13], and ADAM [14] optimizers are used in this work. On the other hand, two reward functions are used to evaluate the actions taken by an agent, Euclidean distance and mean square error (MSE) of distance. For agents, handling even the simplest task is difficult. Hence, we choose to conduct our simulation using data-position (X, Y, and Z) to specify initial and desired positions. Our work shows that autonomous flight, without the involvement of other additional sensors such as light detection and ranging (LiDAR) or vision, is possible, which saves the power of the UAV and reduces the cost. In addition, we have shown that the learning process is highly dependent on the optimizer and reward function, rather than the learning steps.
The rest of this paper is organized as follows: in Section 2, issues related to this work are discussed. In Section 3, preliminary concepts are presented, while in Section 4, the agents used in this work are explained. The simulation environment and performance evaluation are in Section 5 and Section 6, respectively. Finally, a conclusion to our work is given in Section 7.
2. Related Work
Although machine learning-based autonomous flights have been the main focus of current researchers, conventional UAV control algorithms are still in play. In this section, a literature review from both directions is presented. Thus far, the most widely used algorithms for UAV control are traditional control concepts, which do not involve any type of intelligence. Numerous techniques and algorithms can be used in UAV control systems. Among them are the proportional integral derivative (PID), linear quadratic regulators (LQR), sliding mode control (SMC), model predictive control (MPC), integrator backstepping, adaptive control, robust control, optimal control, and feedback control [15]. PID is the most widely used controller with a feedback mechanism and is an industry favorite [16]. The PID controller has achieved better performances for controlling pitch angles, etc. [17]. Generally, the PID controller has been successfully applied in the quadcopter, although with several limitations.
Batikan et al. [18] proposed a technique with the application of a self-tuning fuzzy PID in real-time trajectory tracking of UAVs. The work focused on stabilizing the altitude and trajectory. Meanwhile, Eresen et al. [19] presented the vision for the detection of obstacles. The work demonstrated flying autonomously in urban areas while avoiding obstacles. Goodarzi et al. [20] proposed a full six degree of freedom dynamic model of a quadrotor. The controller was developed to avoid singularities of the minimal altitude representation. Lwin et al. [21] proposed a method that combines a Kalman filter for separating true signal from noise and a PID controller to calculate the error. For the stability of the flight control system, the UAV was adjusted by the PID parameters. Salih et al. [22] presented a new method for autonomous flight control for a quadrotor with a model vertical take-off and landing (VTOL).
The work by Zang et al. [23] focused on controlling the UAV height during drone operation. The algorithm in this work uses active disturbance rejection control (ADRC) and Kalman filtering to process controlling the height as well as to enable autonomous flight of the UAV. The authors of [24], Siti et al., use a hierarchical strategy to improve the PID controller to dive the UAV in a predetermined trajectory using only system orientation. First, a reference model (RM) is used to synthesize the PID in the inner loop, and then genetic algorithm is applied to optimize the outer loop. In [25], Hermans et al. proposed a solution to control the UAV in a geofencing application, which is a virtual boundary of a specific geographical area. An explicit reference governor (ERG) that first stabilizes the UAV and then uses the Lyapunov theory to control the UAV is presented in this paper.
Nevertheless, the PID has several limitations, such as complicated and challenging tuning. Furthermore, the PID or classic controller still lacks complete handling and solving the control problem of an autonomous flight of the quadrotor. Due to the strides made in artificial intelligence, specifically machine learning, researchers both in academia and industry are now turning their attention to this matter to solve autonomous flight control in UAVs. Supervised learning is one of the most used methods in attempting UAV control, but the training dataset has been problematic in this regard. Hence, the focus has now been shifted to reinforcement learning (RL), which is also the case in our work. Reinforcement learning entails learning what to do and how the agent resolves some challenges by taking actions in the environment such that the agent maximizes reward [26]. The reinforcement learning algorithm can reduce learning times and increase stability [27]. Currently, deep RL is a powerful approach for controlling complex systems and situations [28].
W Koch et al. [5] used reinforcement learning to improve the accuracy and precision of altitude control of UAVs to replace classic control algorithms, such as the PID. Zhao et al. [29] presented their research on the use of RL to learn a path while avoiding obstacles. At first, the Q-learning algorithm was used to allow UAVs to learn the environment, and then the adaptive and random exploration (ARE) approach was used to accomplish both task navigation and obstacle avoidance. Kim et al. [30,31] proposed a path planning and obstacle avoiding strategy for UAVs through RL. The Q-learning and deep double dueling deep Q-network (DD-DQN) [32] learning algorithms are used to navigate the simulation environment. On the other hand, Cheng et al. [33] presented a method focused on enemy avoidance based on an RL, where a UAV is expected to avoid another UAV coming its way. The authors have shown that the learned policy achieved a higher possibility of reaching the goal compared with the random and fixed-rule policies. Kahn et al. [34] argued that even RL can be unsafe for the robot during training. The aim of the research was to develop an algorithm that takes uncertainty into consideration. On the other hand, Hwangbo et al. [35] proposed a method to control the quadrotor actuators via the RL technique. The drone was able to produce accurate responses, achieving high stability even under poor conditions.
The impact of reinforcement learning on UAV control and path planning has been demonstrated in several dimensions. However, more research output is expected to further verify and solidify the usage of RL in UAV operation than that of conventional PID techniques. Furthermore, researchers focus on the single machine learning technique with a single reward function for improving and testing autonomous flight in UAVs. Our goal is to demonstrate the difference between the widely used machine learning agents for autonomous UAV flight under multiple reward conditions and optimization functions.
3. Preliminaries
Three popular toolkits have been used in our research, namely (i) ROS, (ii) Gazebo simulator, and OpenAI Gym. First, ROS is used to determine the speed, direction, and destination of the drone. The parameters are then used to produce actions that are sent to the Gazebo simulator to visualize the movement of the drone. Following this, ROS uses the reinforcement learning algorithms available in OpenAI Gym to determine the next action. In this section, a brief introduction to these three toolkits is provided.
3.1. ROS
ROS is an open-source and flexible middleware framework for writing robot software [8]. Despite including an operating system in its name, this toolkit is not one. It is more similar to a motherboard where chips and other modules are mounted on, to create a computer. The ROS is a framework that allows developers to collaborate on developing software and firmware for robots. However, it provides services such as a hardware abstraction layer, low-level device control, sending a message in-process, and packet management, which are characteristics of a typical operating system.
Enabling robots to complete a simple task, which could easily be handled by humans, involves several components and complex systems. However, several components written by different people can be assembled using ROS bottom-up architecture, so as to contribute to the collaborative development of the robotic software.
3.2. Gazebo Simulator
Unlike typical software, which is limited to the virtual world, the software for robots and UAVs takes action in the physical world. Hence, visualizing the steps taken and the decisions made by the robots is part of the experiment. For this, we employed the Gazebo Simulator, which is an open-source 3D robotics simulator, to see the simulation and action [9].
In addition to being open-source, there are several advantages to using Gazebo. It has a range of robots that are highly accurate, efficient, and have great visualization. Furthermore, the integration with ROS is simple, and testing as well as training it with AI algorithms in realistic scenarios is possible. A comparison of robotic simulation tools is available in [36].
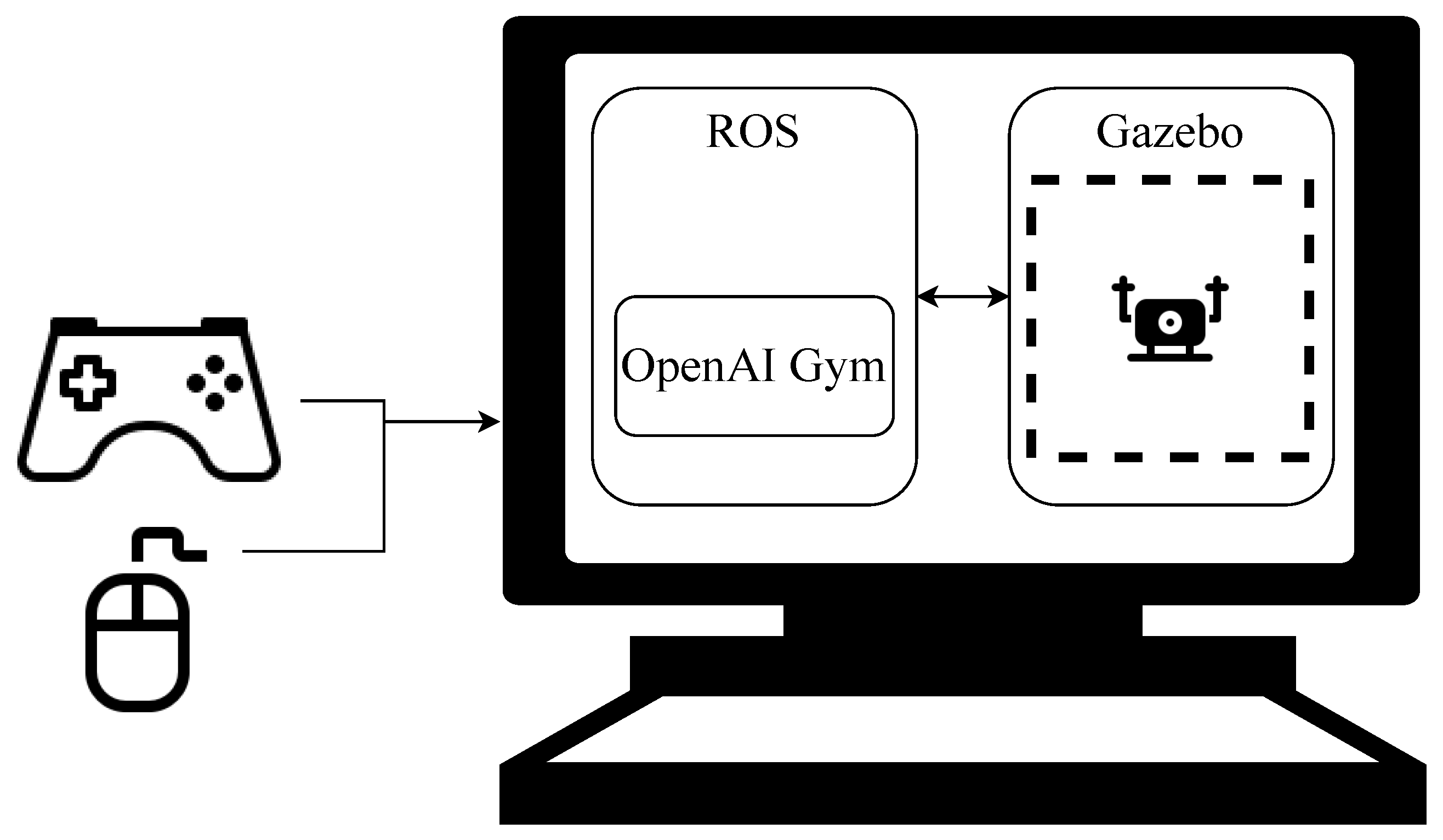
Drone model: In this work, a drone model, which has been developed by the Technical University of Munich (TUM), is used, which represents most off-the-shelf quadrotors on the market. This package is based on TU Darmstadt ROS PKG and the simulator Ardrone. The simulator can simulate AR.Drone 1.0 and 2.0. This simulator can connect to sticks and other devices, and Figure 2 from [37] shows how a joystick or a mouse can be used to control the drone in the simulator.
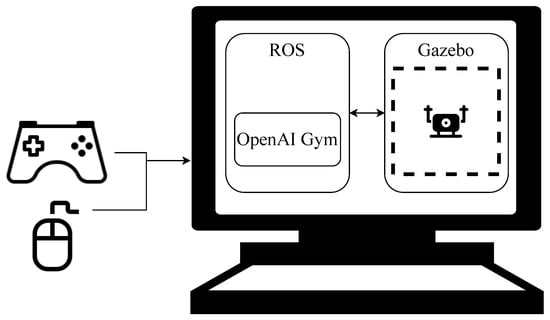
Figure 2.
Simulation configuration.
The TUM drone simulator has been forked by Shanghai Jiao Tong University for development to test the SLAM algorithm with different sensors such as inertial measurement unit (IMU), range finder, and laser range. This simulator will work on Ubuntu 16.04 and 18.4 and Gazebo 7.
3.3. OpenAI Gym
To develop and compare multiple reinforcement learning algorithms, we use the Python-based gym toolkit [10]. All three learning agents used here are from this toolkit. The goal of this work is to enhance productivity in the AI sector by providing an easy-to-set and flexible environment.
4. Agents
In this section, we discuss three popular reinforcement learning algorithms, which are to be used by the agent/learner, the quadrotor in our case. Whenever the agent chooses the best action or policy, it will receive a reward or point. However, the agent will be left with its current state and reward instead of using the information from the environment for future feedback. Usually, to optimize its reward, the agent is forced to decide between choosing a new action to enter a new state or an old action to be in a known state, which is referred to as “exploration versus exploitation trade-off”. The agent then considers whether the environment is known or unknown and takes the next action [38]. Table 1 summarizes all three agents used in this study.

Table 1.
Type of agent algorithm.
4.1. Q-Learning
Q-learning is a special case of a temporal difference (TD) learning process, where an agent iteratively takes all actions in all states to obtain the optimal reward. In Q-learning, the next action is taken such that the state will maximize the reward. The goal of this learning process is to find the optimal estimation of the optimal state-action value function Q* in the case of an unknown model [38]. The Q-learning algorithm samples a new state s and takes a new action a, which are used to update the policy value according to the following equation:
The aim is to find the optimal policy Q*, which can be represented as follows:
4.2. SARSA
SARSA is another reinforcement learning algorithm used to train an agent in an unknown environment. The name is derived from the quintuples s, a, r, s, a that are used to update the Q function, which is given as follows [39]:
SARSA not only depends on the reward to be obtained from the current state and action, but it also takes the state and action it will be in.
4.3. DQN
The Deep Q network (DQN) is one of the popular algorithms in reinforcement learning, also called deep reinforcement learning (DRL). As the name suggests, DQN is a combination of Q-learning with the neural network (NN) and many-layered or deep NN specialization for a spatial processing array of data [26]. This means that the DQN is a multi-layered neural network for a given state ‘s’ that outputs a vector of actions value , where is the trainable weights of the network parameter. Since is approximately [40], the target function used in the DQN is written as:
The DQN model was coded by using the Keras and Tensorflow backend framework. We used three hidden layers. The layer of the parameters is shown in Table 2.

Table 2.
Layer purpose.
4.4. Optimizers
All the algorithms examined in this work are variants of first-order optimization. However, it is impossible to pick the best one among them provided that the performance depends on the problem environment and dataset.
4.4.1. SGD
One of the most usual methods is SGD, which is used to train a neural network. SGD uses a small collection of data (mini-batch) in comparison to BGD, which uses the entire set of data (batch) [13].
4.4.2. RMSProp
SGD requires many steps, which makes it slower in comparison. Interestingly, RMSProp targets resolving the diminishing learning rate of Adagrad. In RMSProp, the learning is adjusted automatically by using a moving average of the squared gradient [12].
4.4.3. Adadelta
Similarly, an extension of Adagrad is Adadelta, and it accumulates a fixed size past gradient rather than all past squared gradients. At any given time t, the running average depends only on the previous average and the current gradient [11].
4.4.4. ADAM
Instead of a single gradient, Adam adapts multiple gradients, along with an adaptive learning rate according to the magnitude of the gradient [14].
4.5. Reward Computation
In this study, agents are rewarded based on the distance measures between the initial and desired position. Two reward functions are used in our work. First, a simple Euclidean distance is used as a reward function to compare the three agents. Then the agent that showed a better performance is examined with a mean square error computed using training and predicted distance data.
The Euclidean distance is the ordinary straight-line distance between two points in Euclidean space [41]. In this case, we use three-dimensional Euclidean space as shown in Equation (5):
where , p is the position the UAV is at the step, q is the desired position, and N is the number of steps taken from the initial to desired position. We assume that at least one step is taken from the initial point towards the desired position. The reward points are given in Table 3.

Table 3.
Rewards condition.
To compute the MSE [42] using Equation (6), we used the data obtained during a training session that resulted in the fastest path from the initial to desired position. After each step, the MSE is calculated and compared to the MSE computed from the previous step to generate the reward. The MSE-based reward points are also shown in Table 3.
where is the Euclidean distance at step i, whereas is the distance after step i during training for the fastest path. The agent uses the Euclidean function to shorten the distance between the UAV and destination, whereas the MSE is used to find the fastest path.
5. Environment
Here, the simulation environment is discussed. The first subsection entails the experiment setup and general overview of the system, while the next subsection presents the building of the drone environment in the experiment, including an action command for the drone, collection of the data sensor, and reward function.
5.1. Experimental Setup
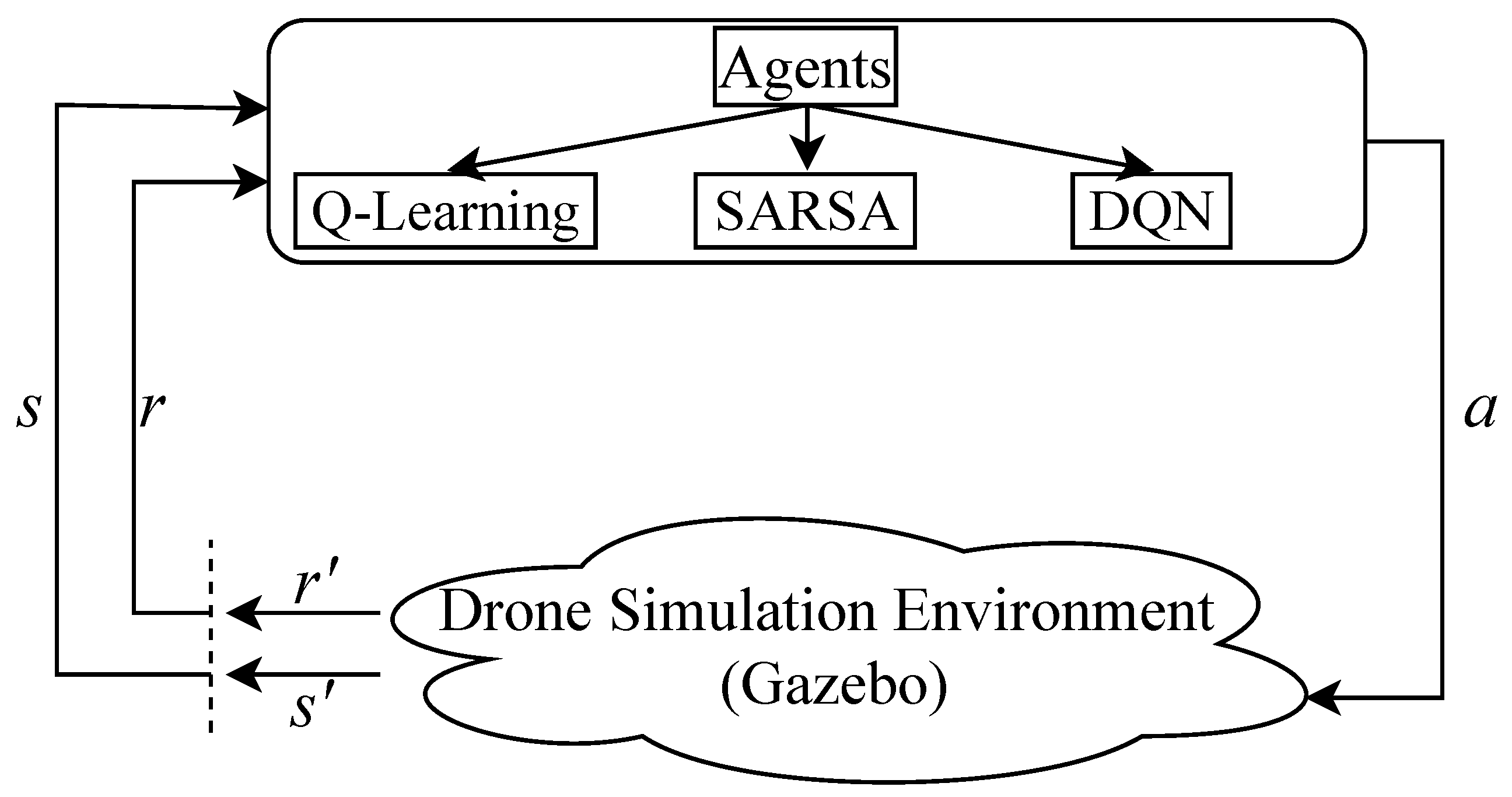
For visualization, interface, and its highly dynamic physics engine, Gazebo is chosen. The first step is to start it. Then the ROS is used to control the drone. Here, OpenAI Gym, which provides the learning agents, is implemented inside the ROS to control the drone. The drone simulator in Gazebo creates the environment and sends several data sensors to give feedback to the agent, and the agent must send actions (Figure 3).
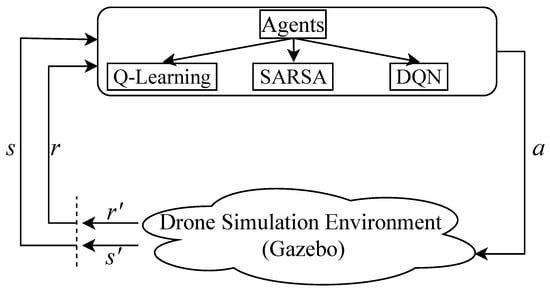
Figure 3.
State, reward, agent, and environment interaction.
First, the drone is trained with a certain number of episodes. The training is expected to move the drone from one location to a predetermined desired destination. Data from the drone simulator contain the positions X, Y, and Z that will be sent to the ROS, and the reinforcement learning algorithm was trained in controlling the drone to fly directly to the desired position. The agent will send one of the ten commands (actions) in Table 4.

Table 4.
Velocity commands.
The final goal is to fly the drone autonomously. In the training process of the drone, reinforcement learning algorithms are used, which involves several parts, agents, and environments.
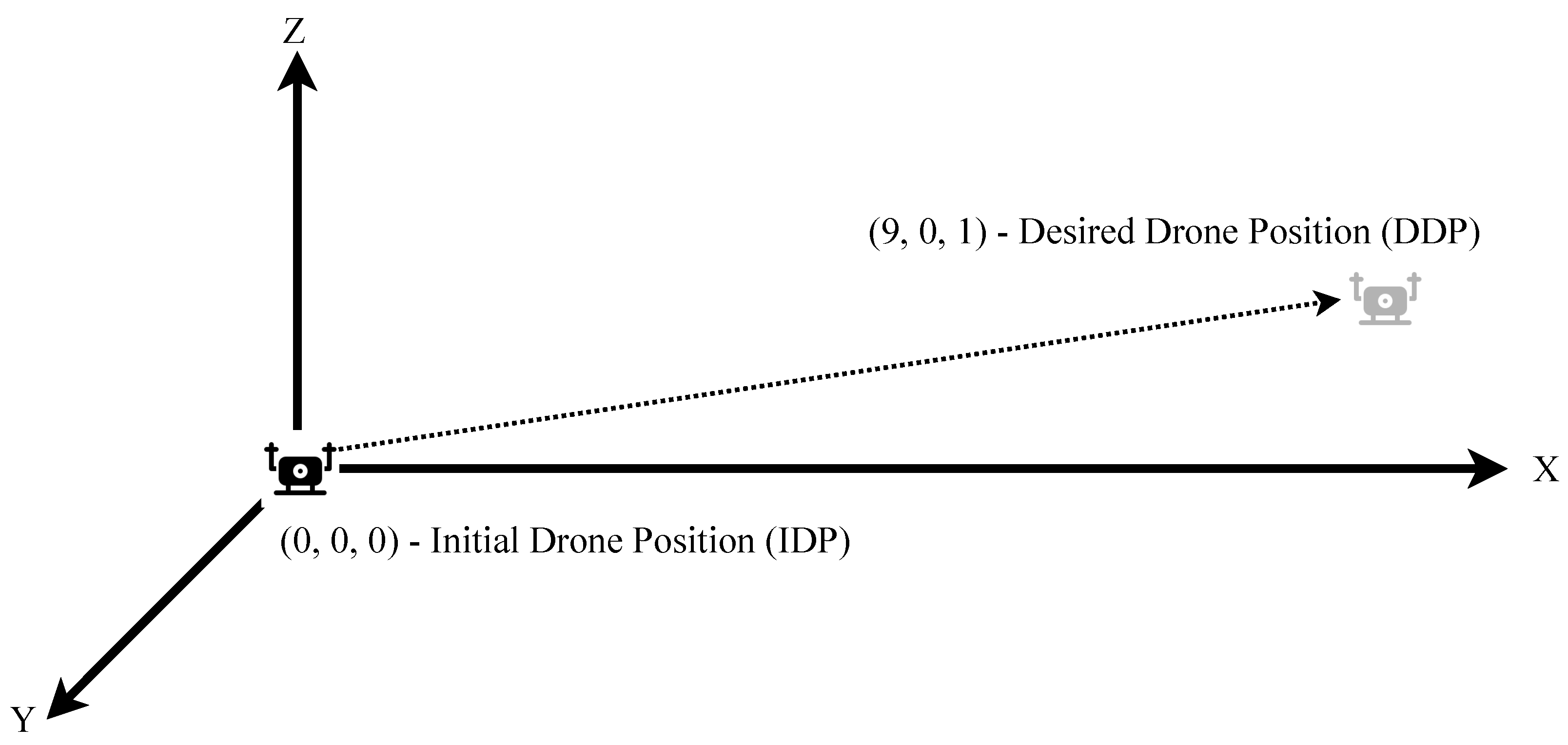
The first condition from the drone is on the floor, Initial Drone Position (IDP), where the coordinated ground truth is X = 0.0, Y = 0.0, Z = 0.0, as shown in Figure 4. The goal is then to move it to the Desired Drone Position (DDP), such as X = 9.0, Y = 0.0, Z = 1.0 (Figure 4).
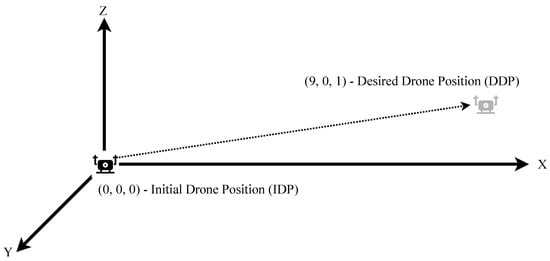
Figure 4.
Drone movement from initial to the desired position.
The training starts with the agent sending the take-off command. The drone environment must take off with an altitude of 1 m from the floor and send a message to the agent, “take-off success.” Then every 0.3 s, the agent sends action and receives a reward feed point as feedback from the environment.
The training session is divided into episodes, each containing 100 steps to arrive from the initial to the desired location. The agent accumulates each reward it receives per step and calculates the average reward at the end of the episode, which it then uses to learn and adopt.
5.2. Drone Environment
One of the main parts of reinforcement learning is a physical environment, and this environment has been developed for the AR drone. Following the OpenAI decisions, the environment only provides the abstraction, not the agent. This means that the environment is independent of the agent, which resides in the ROS.
Directed by the OpenAI Gym rule, the environment must contain registration, steps, and rewards. This will make sure that the interaction between the simulation and OpenAI is smooth. The following tasks are executed to achieve this [10].
- 1
- Registration: registers the training environment in the gym as an available one.
- 2
- Init: in this stage, several parameters such as take-off and landing commands, as well as training parameters such as the value of the speed, desired position, running steps (new command sending time, 0.3 s), the maximum inclination of the drone, and the maximum altitude of the drone, are set. Simulation stabilization is also done at this stage.
- 3
- Reset: this task allows one to reset simulation, pause/resume simulation, reset the robot to initial conditions, and take observation of the state of the drone.
- 4
- Step: for a given action selected by the reinforcement learning algorithm, the quadrotor performs corresponding movements after determining the velocity values as shown in Table 4. The speed value in our simulation is 1 m/s.
- 5
- Observe data: is a function block to obtain data from the drone sensor and also data about position and IMU.
- 6
- Process data: based on the data from the environment and IMU, a reward function is used to compute the progress of the quadrotor to the desired position, such that the quadrotor is given a reward or penalized. Then, the next action will be sent to the drone. Roll, pitch, and altitude movements are also penalized or rewarded.
6. Evaluation
In this section, we first explain the parameters used for the simulation and follow with the result obtained from the experiment.
Since our goal is to understand the behavior of the learning algorithms in flying the drones autonomously, most of the ROS and Gazebo parameters are kept to default settings. The three most influential parameters for our simulation are:
- 1
- Learning Rate (): when set to 0, robots will not learn; the ideal value is always greater than 0.
- 2
- Discount Factor (): setting it to 0 means that agents consider only the current reward; the best value is to arrange it in such a way that the rewards will increase to a higher value for the long-term.
- 3
- Exploration Constant (): is used to randomize decisions; setting it to a number approaching 1 (such as 0.9) will make 90% of the actions stochastic.
A summary of these and other parameters is shown in Table 5. The simulation is run from 500 to 1000 episodes, each of which is 100 steps. At the end of each episode, the drone will start again in the initial condition and receive feedback and the called observation. In every episode, the drone tries to take a maximum number of steps, learning every step to obtain a high reward point. There are one initial and three desired positions (Table 6).

Table 5.
Simulation hyperparameters.

Table 6.
Initial and desired positions.
Result and Discussion
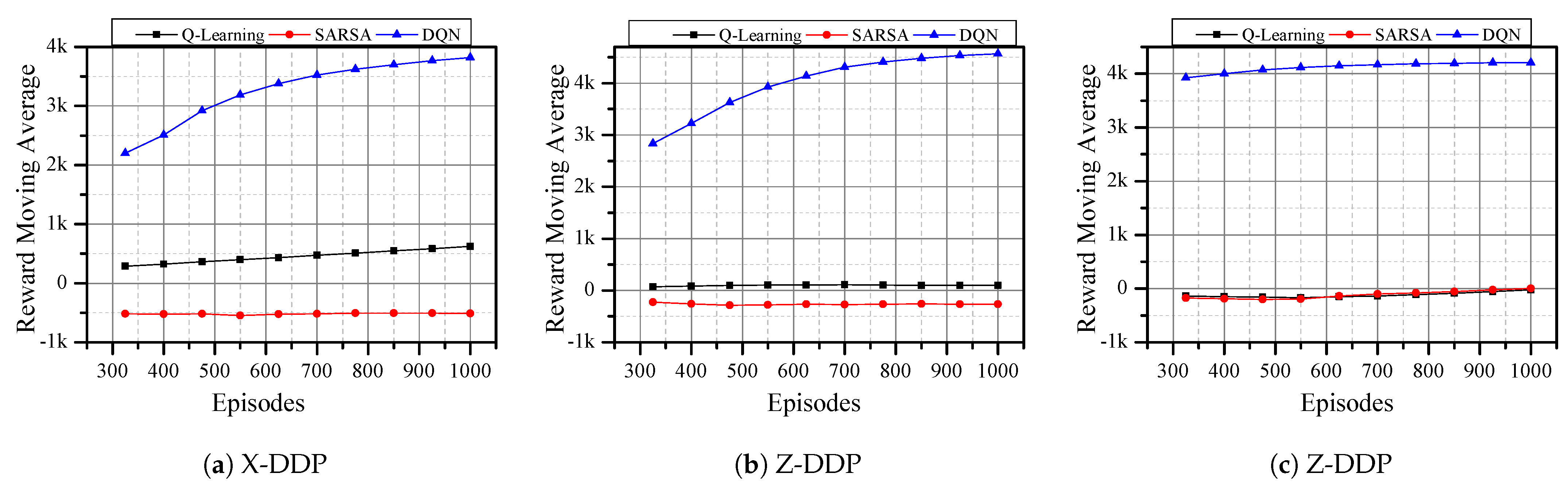
Here, we discuss the results obtained from all three learning algorithms discussed above. For DQN, we use the RMSProp optimizer [12]. Figure 5 shows the moving average of the rewards that the agent received after completing an episode. The Euclidean distance reward function is used during this run. All three learning algorithms gained rewards as the number of episodes increased, in all directions.
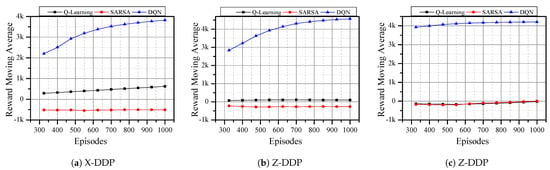
Figure 5.
Learning algorithms with 100 steps/episode for a total of 1000 episodes using the Euclidean distance reward
function.
However, DQN showed significant improvement and had no negative moving average reward in any direction. Compared to SARSA, Q-learning has better performance in X-DDP and Y-DDP (Figure 5a,b, respectively). Nevertheless, both algorithms have a negative reward in Z-DDP (Figure 5c). This indicates that DQN has no problem in flying horizontally or vertically, while SARSA and Q-learning are able to fly horizontally but not vertically. As can be seen from the results, the change in reward after the 500th episode is small. Hence, the rest of the evaluations are tested for 500 episodes only, whereas the reward function remains the Euclidean distance.
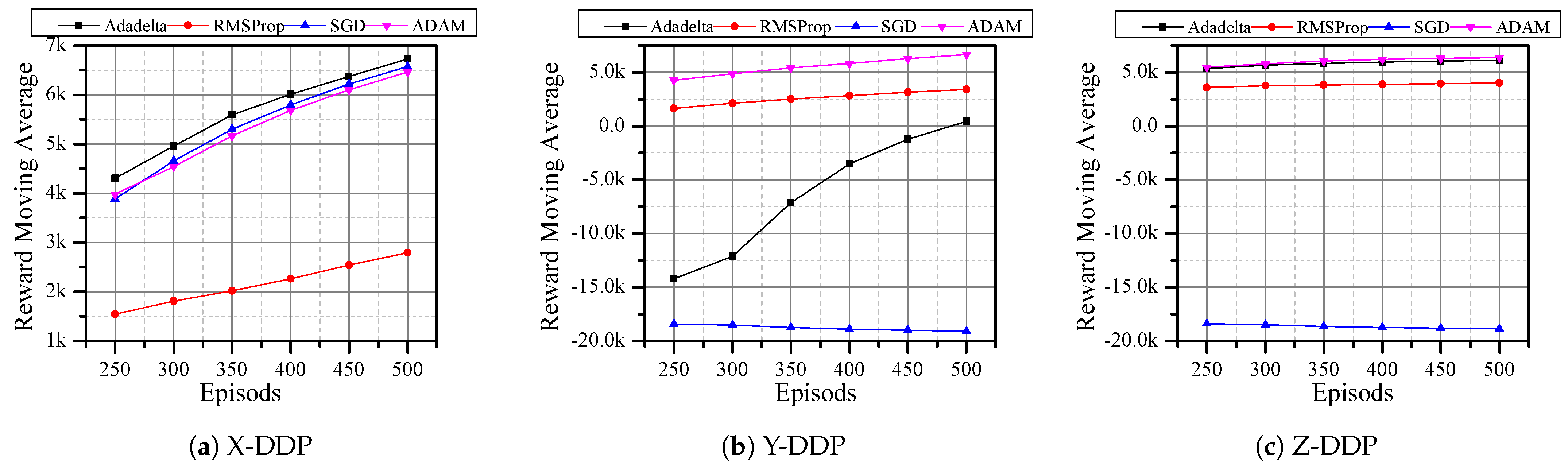
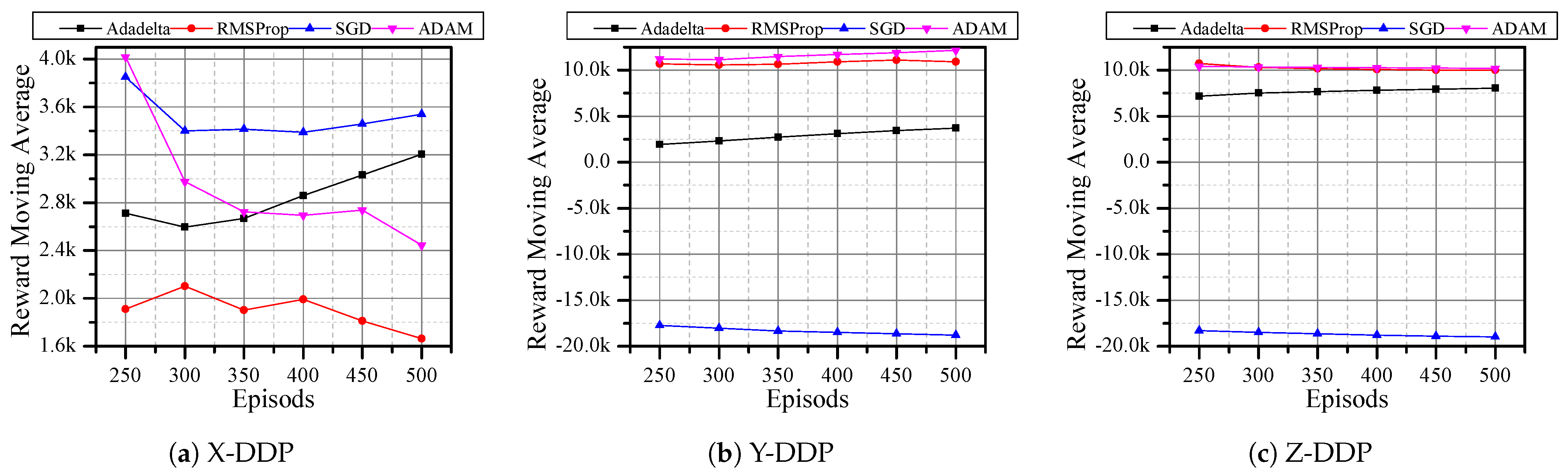
Since DQN with RMSProp optimizer has better rewards, we analyzed the performance of DQN under other optimizers such as Adadelta [11], SGD [13], and ADAM [14]. Here, the agent is expected to reach the desired position in only 500 steps. In X-DDP and Z-DDP, the Adadelta optimizer has a better reward (Figure 6a,c). Even though the SGD optimizer showed a good reward in X-DDP, the result in Figure 6b,c shows that SGD has a negative reward. When the agent uses the RMSProp optimizer, it never outperforms other optimizers in any of the directions, whereas the agent shows good performance with the ADAM optimizer in all directions (Figure 6). In Figure 5, there are six results that obtained negative rewards; by dropping Q-learning and SARSA and adopting other optimizers, we reduced that number to three (Figure 6). Then, we replaced the reward function with MSE, which further reduced the negative reward results to two (Figure 7). Although all optimizers show a good sign in flying the quadrotor autonomously, Adam and Adadelta are the best optimizers in both horizontal and vertical desired positions. In addition, we can see from Figure 6 and Figure 7 that the agent is always improving towards a positive reward when with the Adadelta optimizer. This shows the significant role that the optimizers and the reward functions play in flying the drone autonomously.
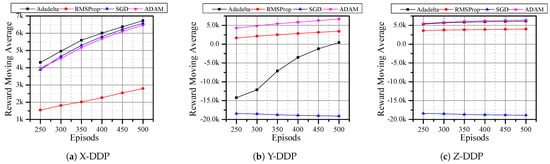
Figure 6.
DQN and different optimizers with 100 steps/episode for a total of 500 episodes using the Euclidean distance
reward function.
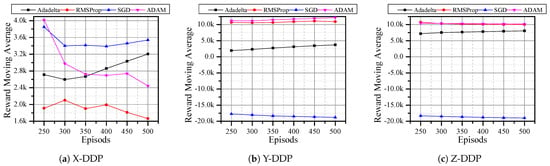
Figure 7.
DQN and different optimizers with 100 steps/episode for a total of 500 episodes using MSE reward function.
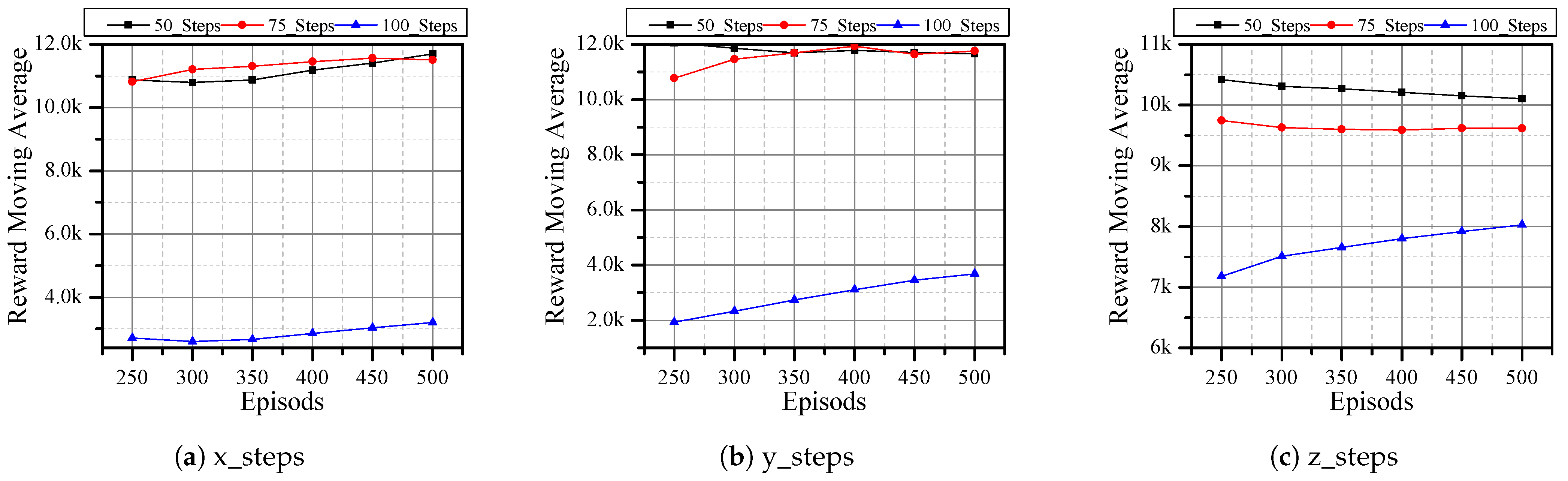
Therefore, using the Adadelta optimizer and MSE reward function, we evaluated the performance of the DQN agent under different steps, that is, the maximum number of steps an agent can take between the initial and desired position. The results in Figure 8 indicate that by limiting the number of steps, the reward increases, which means that the agent performs better. This is due to the fact that the agent is not taking unnecessary actions that might lead to negative rewards. However, reducing the number of steps just to improve reward does not result in better performance, as there are small differences between 50 and 75 steps. In addition, realistic scenarios are not as simple as the simulation cases which can be reached in a few steps.
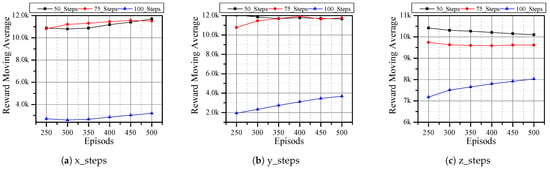
Figure 8.
DQN and Adadelta optimizer with steps/episode varying for a total of 500 episodes using MSE reward function.
The results obtained in this evaluation showed that learning algorithms can be used to fly drones autonomously. In addition to the learning algorithms, the choice of reward function and optimizer also impacts the performance of autonomous drone flight. Overall, the DQN agent using either the Adadelta or ADAM optimizer and applying the MSE reward function with the number of steps set to 50 shows the best performance in our assessment. In the future, we plan to add more obstacles, use multiple reward functions, and select different learning schemes depending on the next step, such as up, down, or horizontal. We hope that this will reveal more interesting characteristics of the learning schemes.
7. Conclusions
Autonomously flying UAVs can no longer continue to use traditional controllers such as PID due to tuning, stability, and flexibility issues. However, new reinforcement and deep learning methods are currently showing better control and movement strategies in autonomous UAV flights.
In this work, the simulation and performance evaluation of learning algorithms such as Q-learning, SARSA, and DQN was presented. These algorithms have been evaluated under a combination of positions (X, Y, and Z direction desired positions), optimizers (RMSProp, Adadelta, SGD, and ADAM), and reward functions (Euclidean distance and its MSE). From the evaluation, DQN with the Adadelta optimizer using MSE has shown the best performance in flying drones from the initial to the desired position.
In the future, we plan to investigate the performance of other deep network and neural network learning algorithms under environments that involve obstacles and complicated destinations and to introduce a complex reward function that is more suitable for the autonomous UAV flight.
Author Contributions
Conceptualization, methodology, validation, and writing—original draft preparation, Y.Z.J. and Y.W.N.; supervision, project administration, funding acquisition, B.K. and M.A.; software, resources, visualization, M.T.R.K. and R.P.; writing—review and editing, validation, S.H.A.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Bisa Research Grant of Keimyung University in 2020 (No. 20200195).
Institutional Review Board Statement
Not Applicable.
Informed Consent Statement
Not Applicable.
Data Availability Statement
The data used in the experimental evaluation of this study are available within this article.
Conflicts of Interest
The authors declare no conflict of interest regarding the publication of this manuscript.
References
- Zhang, Y.; Zu, W.; Gao, Y.; Chang, H. Research on autonomous maneuvering decision of UCAV based on deep reinforcement learning. In Proceedings of the 2018 Chinese Control and Decision Conference (CCDC), Shenyang, China, 9–11 June 2018; pp. 230–235. [Google Scholar]
- Valavanis, K.P.; Vachtsevanos, G.J. Handbook of Unmanned Aerial Vehicles; Springer: Berlin/Heidelberg, Germany, 2015; Volume 1. [Google Scholar]
- Lippitt, C.D.; Zhang, S. The impact of small unmanned airborne platforms on passive optical remote sensing: A conceptual perspective. Int. J. Remote Sens. 2018, 39, 4852–4868. [Google Scholar] [CrossRef]
- Alwateer, M.; Loke, S.W.; Zuchowicz, A. Drone services: Issues in drones for location-based services from human-drone interaction to information processing. J. Locat. Based Serv. 2019, 13, 94–127. [Google Scholar] [CrossRef]
- Koch, W.; Mancuso, R.; West, R.; Bestavros, A. Reinforcement Learning for UAV Attitude Control. ACM Trans. Cyber-Phys. Syst. 2019, 3, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Pham, H.X.; La, H.M.; Feil-Seifer, D.; Nguyen, L.V. Autonomous UAV Navigation Using Reinforcement Learning. arXiv 2018, arXiv:1801.05086. [Google Scholar]
- Bou-Ammar, H.; Voos, H.; Ertel, W. Controller design for quadrotor UAVs using reinforcement learning. In Proceedings of the 2010 IEEE International Conference on Control Applications, Yokohama, Japan, 8–10 September 2010; pp. 2130–2135. [Google Scholar] [CrossRef] [Green Version]
- Quigley, M.; Conley, K.; Gerkey, B.; Faust, J.; Foote, T.; Leibs, J.; Wheeler, R.; Ng, A.Y. ROS: An open-source Robot Operating System. In Proceedings of the ICRAWorkshop on Open Source Software, Kobe, Japan, 12–17 May 2009; Volume 3, p. 5. [Google Scholar]
- Koenig, N.; Howard, A. Design and use paradigms for gazebo, an open-source multi-robot simulator. In Proceedings of the 2004 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) (IEEE Cat. No. 04CH37566), Sendai, Japan, 28 September–2 October 2004; Volume 3, pp. 2149–2154. [Google Scholar]
- Brockman, G.; Cheung, V.; Pettersson, L.; Schneider, J.; Schulman, J.; Tang, J.; Zaremba, W. Openai gym. arXiv 2016, arXiv:1606.01540. [Google Scholar]
- Zeiler, M.D. Adadelta: An adaptive learning rate method. arXiv 2012, arXiv:1212.5701. [Google Scholar]
- Tieleman, T.; Hinton, G. Divide the Gradient by a Running Average of Its Recent Magnitude. Coursera: Neural Networks for Machine Learning. Technical Report. 2017. Available online: https://www.scirp.org/(S(czeh2tfqyw2orz553k1w0r45))/reference/ReferencesPapers.aspx?ReferenceID=1911091 (accessed on 5 August 2021).
- Zhang, C.; Liao, Q.; Rakhlin, A.; Miranda, B.; Golowich, N.; Poggio, T. Theory of deep learning IIb: Optimization properties of SGD. arXiv 2018, arXiv:1801.02254. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Kim, J.; Gadsden, S.A.; Wilkerson, S.A. A comprehensive survey of control strategies for autonomous quadrotors. Can. J. Electr. Comput. Eng. 2019, 43, 3–16. [Google Scholar]
- Lee, K.; Kim, H.; Park, J.; Choi, Y. Hovering control of a quadrotor. In Proceedings of the ICCAS 2012—2012 12th International Conference on Control, Automation and Systems, Jeju Island, Korea, 17–21 October 2012; pp. 162–167. [Google Scholar]
- Zulu, A.; John, S. A Review of Control Algorithms for Autonomous Quadrotors. Open J. Appl. Sci. 2014, 04, 547–556. [Google Scholar] [CrossRef] [Green Version]
- Demir, B.E.; Bayir, R.; Duran, F. Real-time trajectory tracking of an unmanned aerial vehicle using a self-tuning fuzzy proportional integral derivative controller. Int. J. Micro Air Veh. 2016, 8, 252–268. [Google Scholar] [CrossRef] [Green Version]
- Eresen, A.; İmamoğlu, N.; Önder Efe, M. Autonomous quadrotor flight with vision-based obstacle avoidance in virtual environment. Expert Syst. Appl. 2012, 39, 894–905. [Google Scholar] [CrossRef]
- Goodarzi, F.; Lee, D.; Lee, T. Geometric nonlinear PID control of a quadrotor UAV on SE(3). In Proceedings of the 2013 European Control Conference (ECC), Zurich, Switzerland, 17–19 July 2013; pp. 3845–3850. [Google Scholar] [CrossRef] [Green Version]
- Lwin, N.; Tun, H.M. Implementation Of Flight Control System Based On Kalman And PID Controller For UAV. Int. J. Sci. Technol. Res. 2014, 3, 309–312. [Google Scholar]
- Salih, A.L.; Moghavvemi, M.; Mohamed, H.A.; Gaeid, K.S. Flight PID controller design for a UAV quadrotor. Sci. Res. Essays 2010, 5, 3660–3667. [Google Scholar]
- Zang, Z.; Ma, Z.; Wang, Y.; Ji, F.; Nie, H.; Li, W. The Design of Height Control System of Fully Autonomous UAV Based on ADRC-PID Algorithm. J. Phys. Conf. Ser. 2020, 1650, 032136. [Google Scholar] [CrossRef]
- Siti, I.; Mjahed, M.; Ayad, H.; El Kari, A. New trajectory tracking approach for a quadcopter using genetic algorithm and reference model methods. Appl. Sci. 2019, 9, 1780. [Google Scholar] [CrossRef] [Green Version]
- Hermand, E.; Nguyen, T.W.; Hosseinzadeh, M.; Garone, E. Constrained control of UAVs in geofencing applications. In Proceedings of the 2018 26th Mediterranean Conference on Control and Automation (MED), Zadar, Croatia, 19–22 June 2018; pp. 217–222. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction, 2nd ed.; The MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Xia, W.; Li, H.; Li, B. A Control Strategy of Autonomous Vehicles Based on Deep Reinforcement Learning. In Proceedings of the 2016 9th International Symposium on Computational Intelligence and Design (ISCID), Hangzhou, China, 10–11 December 2016; Volume 2, pp. 198–201. [Google Scholar] [CrossRef]
- Tuyen, L.P.; Layek, A.; Vien, N.A.; Chung, T. Deep reinforcement learning algorithms for steering an underactuated ship. In Proceedings of the 2017 IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems (MFI), Daegu, Korea, 16–18 November 2017; pp. 602–607. [Google Scholar] [CrossRef] [Green Version]
- Yijing, Z.; Zheng, Z.; Xiaoyi, Z.; Yang, L. Q learning algorithm based UAV path learning and obstacle avoidence approach. In Proceedings of the 2017 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017; pp. 3397–3402. [Google Scholar] [CrossRef]
- Kim, J.; Shin, S.; Wu, J.; Kim, S.D.; Kim, C.G. Obstacle Avoidance Path Planning for UAV Using Reinforcement Learning Under Simulated Environment. In Proceedings of the IASER 3rd International Conference on Electronics, Electrical Engineering, Computer Science, Okinawa, Japan, 14–18 July 2017; pp. 34–36. [Google Scholar]
- Shin, S.Y.; Kang, Y.W.; Kim, Y.G. Obstacle avoidance drone by deep reinforcement learning and its racing with human pilot. Appl. Sci. 2019, 9, 5571. [Google Scholar] [CrossRef] [Green Version]
- Van Hasselt, H.; Guez, A.; Silver, D. Deep reinforcement learning with double q-learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; Volume 30. [Google Scholar]
- Cheng, Q.; Wang, X.; Yang, J.; Shen, L. Automated Enemy Avoidance of Unmanned Aerial Vehicles Based on Reinforcement Learning. Appl. Sci. 2019, 9, 669. [Google Scholar] [CrossRef] [Green Version]
- Kahn, G.; Villaflor, A.; Pong, V.; Abbeel, P.; Levine, S. Uncertainty-Aware Reinforcement Learning for Collision Avoidance. arXiv 2017, arXiv:cs.LG/1702.01182. [Google Scholar]
- Hwangbo, J.; Sa, I.; Siegwart, R.; Hutter, M. Control of a Quadrotor With Reinforcement Learning. IEEE Robot. Autom. Lett. 2017, 2, 2096–2103. [Google Scholar] [CrossRef] [Green Version]
- Giuliani, M.; Assaf, T.; Giannaccini, M.E. Towards Autonomous Robotic Systems. In Proceedings of the 19th Annual Conference, TAROS 2018, Bristol, UK, 25–27 July 2018; Springer: Berlin/Heidelberg, Germany, 2018; Volume 10965. [Google Scholar]
- Hongrong, H.; Jürgen, S. Tum_Simulator-ROS Wiki. Available online: http://wiki.ros.org/tum_simulator (accessed on 5 August 2021).
- Mohri, M.; Rostamizadeh, A.; Talwalkar, A. Foundations of Machine Learning; The MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Suh, J.; Tanaka, T. SARSA (0) reinforcement learning over fully homomorphic encryption. arXiv 2020, arXiv:2002.00506. [Google Scholar]
- Nair, A.; Srinivasan, P.; Blackwell, S.; Alcicek, C.; Fearon, R.; De Maria, A.; Panneershelvam, V.; Suleyman, M.; Beattie, C.; Petersen, S.; et al. Massively parallel methods for deep reinforcement learning. arXiv 2015, arXiv:1507.04296. [Google Scholar]
- Danielsson, P.E. Euclidean distance mapping. Comput. Graph. Image Process. 1980, 14, 227–248. [Google Scholar] [CrossRef] [Green Version]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).