Joint Optimization Method of Spare Parts Stocks and Level of Repair Analysis Considering the Multiple Failure Modes
Abstract
:1. Introduction
2. System Description
2.1. Two-Indenture Fleet System Description
- (1)
- In a given fleet system, the deterioration process of each homogenous component is independent and uniform, which indicates that each component randomly degenerates according to the same law over time.
- (2)
- The subcomponent will be replaced to repair system, if the corresponding component fails. Therefore, when a component should be maintained, each subcomponent at the same echelon level should be decided moved, discard, or repaired.
- (3)
- It takes little time on replacing a defective LRU, and the replacement belongs to operational availability. Therefore, compared with the supply and operational availability, we should focus on the former one (supply availability).
- (4)
- Discarding the LRU implies that its SRUs are discarded as well.
- (5)
- For each component at each location, an (s − 1, s) continuous review inventory control policy (one for one replenishment) is used. That is, the replenishing and ordering strategy for one missing component is adopted to keep the stock at the level of s.Because each component has multiple failure modes, and each mode has a different failure mechanism and failure rate, the system has different degrees of influence and consequences [14]. Two assumptions of multiple failure modes of components are added in this study:
- (6)
- The failure modes of the component appear randomly.
- (7)
- Minor fault mode could be repaired on base location; serious fault mode should be sent to the depot location for repair.
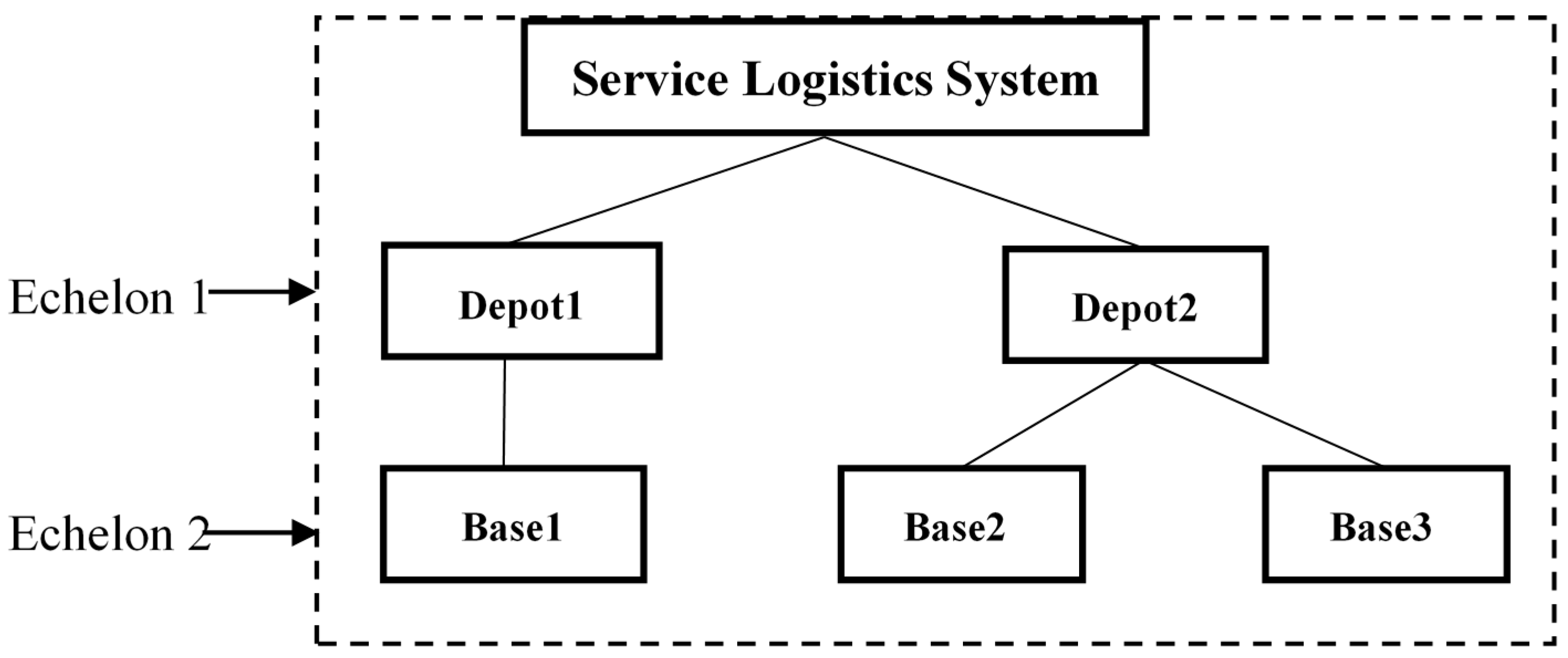
2.2. Two-Echelon Service Logistics System Description
- (1)
- Each maintenance location has a set of resources, including spare parts, maintenance workers, maintenance equipment, and tools. The maintenance capability is proportional to the resources available for maintenance.
- (2)
- The discard decision is only considered in the Depot.
- (3)
- A failed (sub)component may not be shipped to a lower echelon level. When a failed component with echelon level should be repaired, the corresponding subcomponent must be maintained at echelon level , rather than a lower level.
- (4)
- There are no lateral transshipments between locations at the same echelon level or emergency shipments from locations at a higher echelon level; functioning spare parts are only supplied from one specific location at the next higher echelon level.
3. Two-Echelon Two-Indenture System Modelling
3.1. Mathematical Model of LORA
- (1)
- Analyze the maintenance decision of failure components based on failure mode: move, repair, discard;
- (2)
- Analyze the level of repair decision-making;
- (3)
- Determine the maintenance resources needed to implement the maintenance decision.
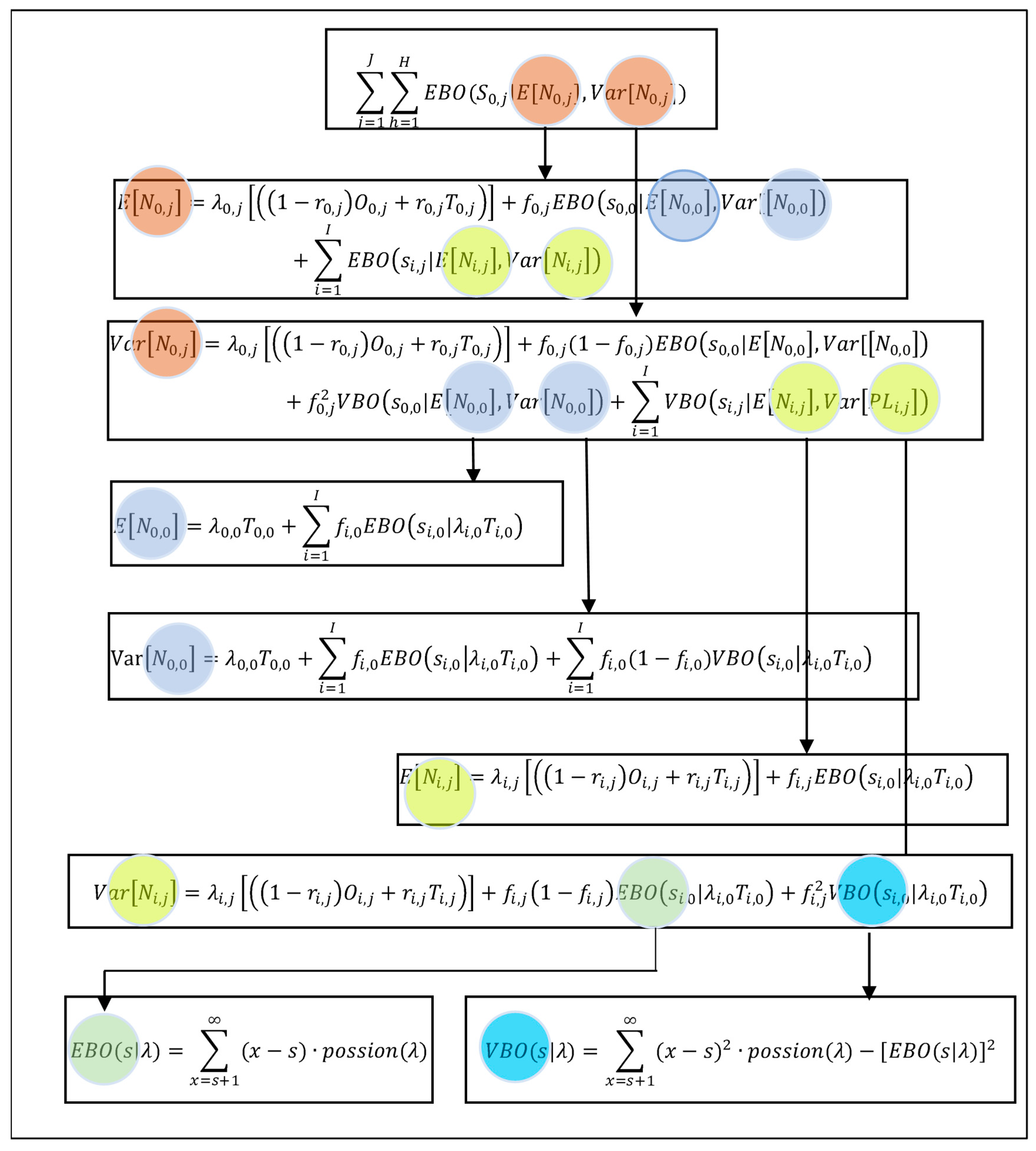
3.2. Mathematical Model of Spare Parts Stock
3.3. Mathematical Model of Joint Optimization
3.4. Mathematical Model Solution
4. Numerical Experiment
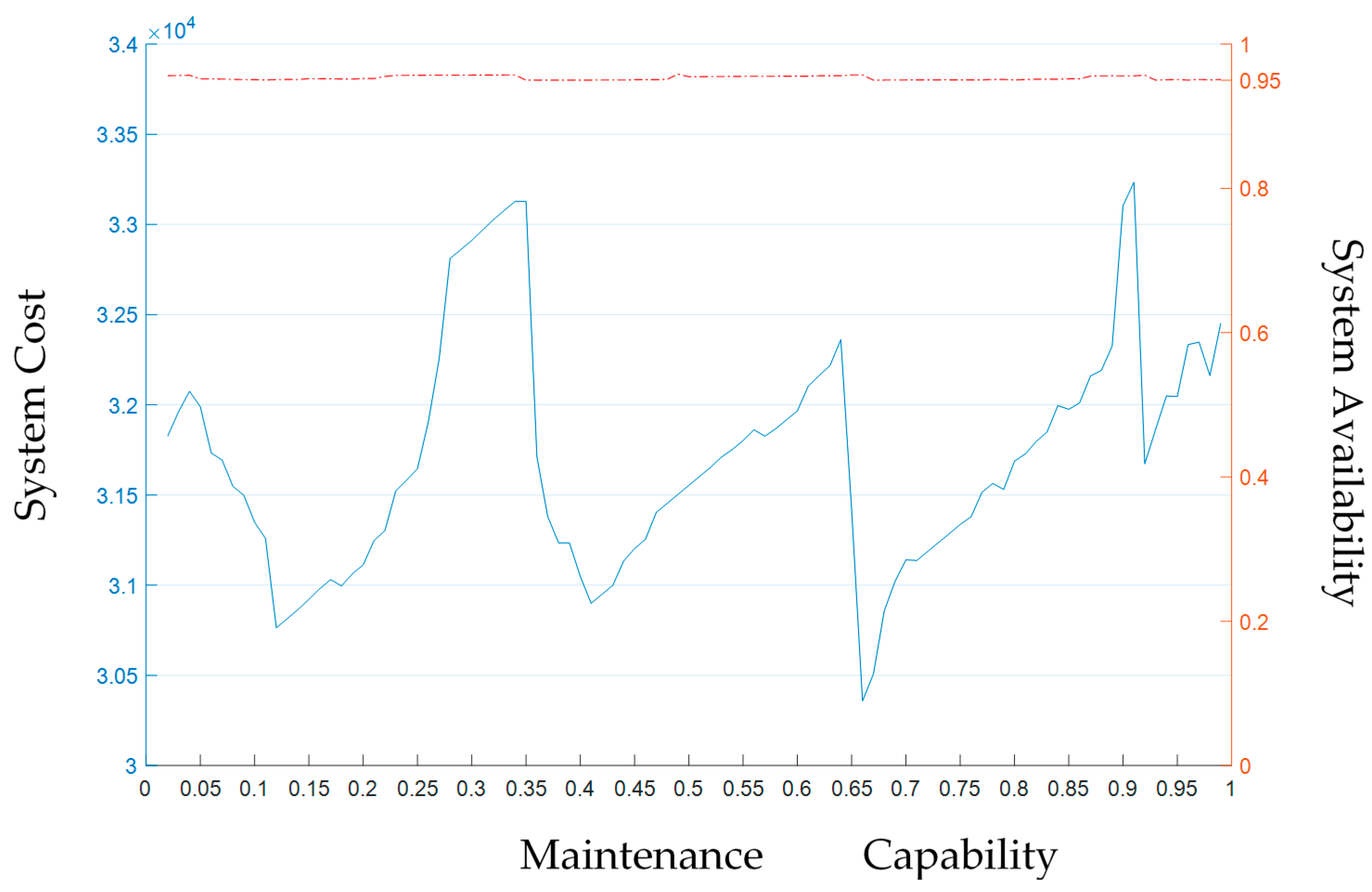
4.1. Analysis of the Influence of Maintenance Capability on Service Logistics Cost
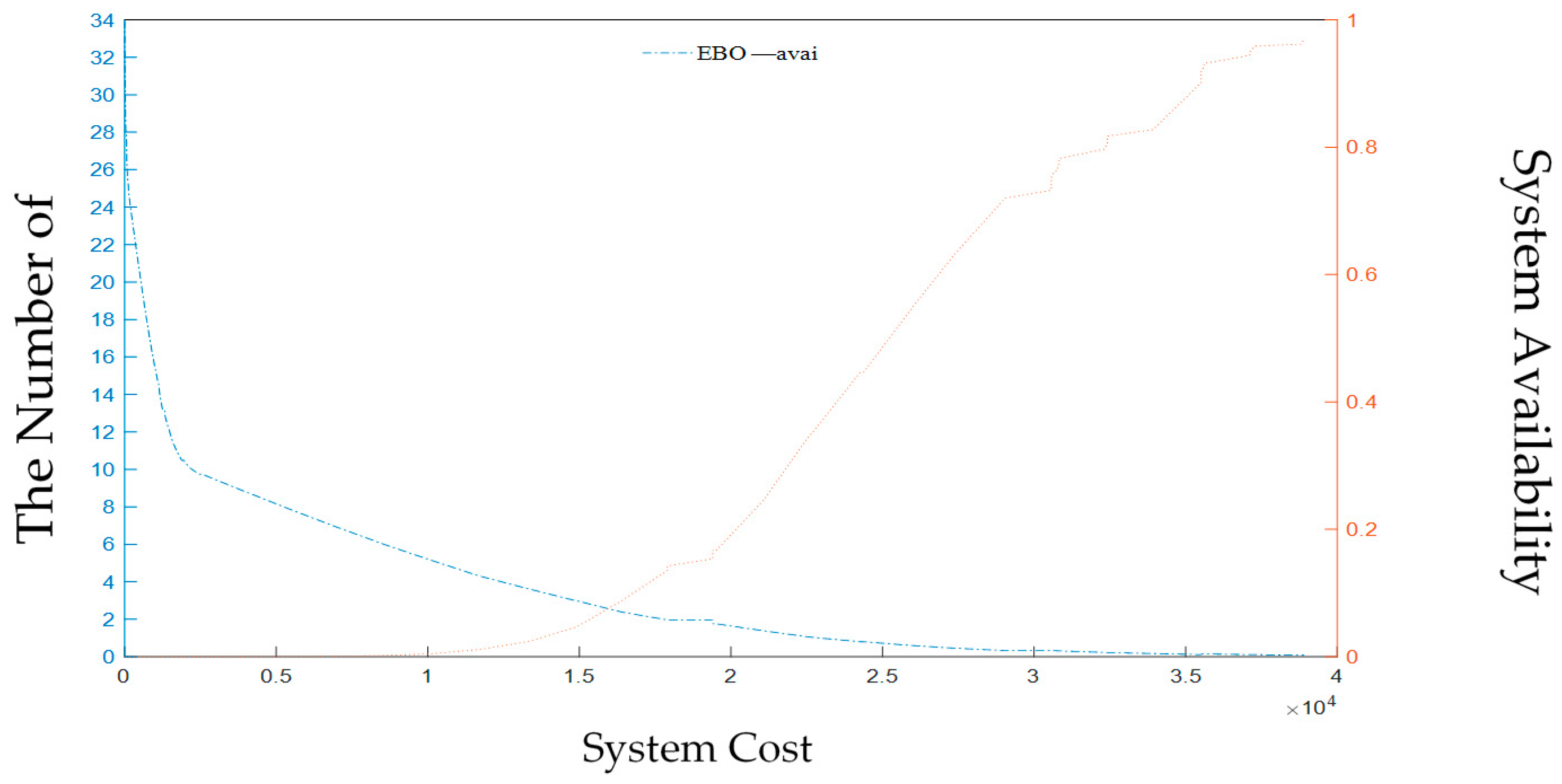
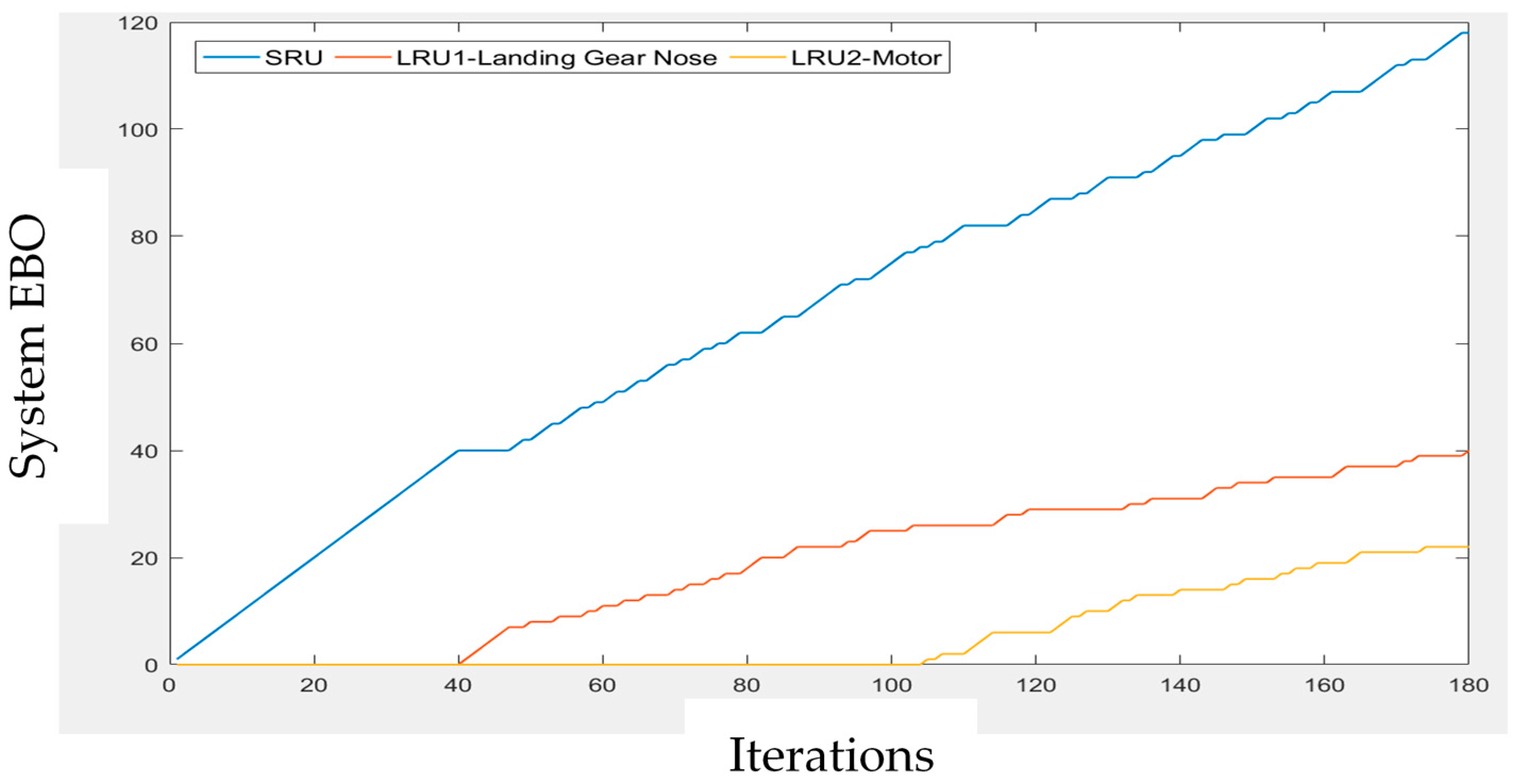
4.2. Spare Parts Inventory Analysis of Fleet System
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Duran, O.; Rojas, S.; Duran, P. Measuring the Impact of Maintenance Postponement on Overall Performance in a Chilean Crushing Plant. IEEE Lat. Am. Trans. 2018, 16, 1951–1958. [Google Scholar] [CrossRef]
- Kristjanpoller, F.; Viveros, P.; Zio, E.; Rodrigo, P.; Oscar, A. Equivalent availability index for the performance measurement of haul truck fleets. Eksploat. Niezawodn. Maint. Reliab. 2020, 22, 583–591. [Google Scholar] [CrossRef]
- Li, J.L.; Teng, K.N.; Xia, F.; Sun, Y. Fleet maintenance scheduling based on availability. Pract. Underst. Math. 2017, 47, 154–163. [Google Scholar]
- Li, J.L.; Teng, K.N.; Xu, J.H.; Xia, F.; Li, J.Y. Research on combat readiness of military aircraft group. Mod. Def. Technol. 2017, 45, 147–154. [Google Scholar]
- Institute for Defense Analyses. GEIA-STD-0007: Level of Repair Analysis; US Department of Defense: Washington, DC, USA, 2019.
- Zhou, L.; Peng, Y.W.; Li, Q.; Ruan, M. Research on general model of task oriented spare parts support evaluation. Syst. Eng. Electron. Technol. 2017, 39, 2046–2051. [Google Scholar]
- Xue, T.; Feng, Y.W.; Xue, X.F. Research on joint optimization model of equipment repair level and spare parts inventory. Mech. Sci. Technol. 2015, 34, 963–968. [Google Scholar]
- Barros, L.L. The optimization of repair decisions using life-cycle cost parameters. IMA J. Math. Appl. Bus. Ind. 1998, 9, 403–413. [Google Scholar] [CrossRef]
- Barros, L.L.; Riley, M. A combinatorial approach to level of repair analysis. Eur. J. Oper. Res. 2001, 129, 242–251. [Google Scholar] [CrossRef]
- Basten, R.J.; Van der Heijden, M.C.; Schutten, J.M. A minimum cost flow model for level of repair analysis. Int. J. Prod. Econ. 2011, 133, 233–242. [Google Scholar] [CrossRef] [Green Version]
- Basten, R.J.; van der Heijden, M.C.; Schutten, J.M. Practical extensions to a minimum cost flow model for level of repair analysis. Eur. J. Oper. Res. 2011, 211, 333–342. [Google Scholar] [CrossRef]
- Basten, R.J.; Schutten, J.M.J.; Van Der Heijden, M.C. An efficient model formulation for level of repair analysis. Ann. Oper. Res. 2009, 172, 119–142. [Google Scholar] [CrossRef] [Green Version]
- Brick, E.S.; Uchoa, E. A facility location and installation or resources model for level of repair analysis. Eur. J. Oper. Res. 2009, 192, 479–486. [Google Scholar] [CrossRef]
- Zuo, F.J.; Le, Y.; Mi, J.; Liu, Z.; Huang, H.-Z. Reliability analysis of gear transmission with considering failure correlation. Eksploat. Niezawodn. Maint. Reliab. 2015, 17, 617–623. [Google Scholar] [CrossRef]
- McNamara, D.; Cunningham, A.; Jenkinson, I.; Wang, J. Application of the Monte Carlo Method to Marine System Maintenance Studies considering Failure Modes and Spare Part Stock Control. J. Mar. Eng. Technol. 2014, 13, 37–58. [Google Scholar]
- Qiu, Q.; Cui, L.; Gao, H. Availability and maintenance modelling for systems subject to multiple failure modes. Comput. Ind. Eng. 2017, 108, 192–198. [Google Scholar] [CrossRef]
- Wang, Y.H.; Deng, C.; Hu, X.H.; Gao, J.; Hu, C.J. Preventive maintenance scheduling for complex mechanical device based on multiple failure modes. Comput. Integr. Manuf. Syst. 2015, 21, 2504–2514. [Google Scholar]
- Alfredsson, P. Optimization of multi-echelon repairable component inventory systems with simultaneous location of repair facilities. Eur. J. Oper. Res. 1997, 99, 584–595. [Google Scholar] [CrossRef]
- Basten, R.J.; Van der Heijden, M.C.; Schutten, J.M. Joint optimization of level of repair analysis and spare parts stocks. Eur. J. Oper. Res. 2012, 223, 474–483. [Google Scholar] [CrossRef] [Green Version]
- Basten, R.J.; Van der Heijden, M.C.; Schutten, J.M.; Kutanoglu, E. An Approximate Approach for the Joint Problem of Level of Repair Analysis and Spare Parts Stocking. Ann. Oper. Res. 2015, 224, 121–145. [Google Scholar] [CrossRef] [Green Version]
- Chefi, T.; Al-Alawin, A.; Ghiani, G.; Manni, E. Approximation Neighborhood Evaluation for the Design of the Logistics Support of Complex Engineering Systems. RAIRO Rech. Oper. 2017, 51, 1–16. [Google Scholar]
- Xue, W.K.; Xiao, B.P.; Li, D.D.; Ma, L. Joint optimization of LORA and spares inventory with fuzzy parameters. In Proceedings of the 2016 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Bali, Indonesia, 4–7 December 2016; pp. 1640–1645. [Google Scholar]
- Guo, L.H.; Fan, J.J.; Wen, M.L.; Kang, R. Joint optimization of LORA and spares stocks considering corrective maintenance time. J. Syst. Eng. Electron. 2015, 26, 85–95. [Google Scholar] [CrossRef]
- Liu, W.M.; Liu, K.L.; Deng, T.H. Modelling analysis and improvement of an integrated chance constrained model for level of repair analysis and spare parts supply control. Int. J. Prod. Res. 2020, 58, 3090–3109. [Google Scholar] [CrossRef]
- Cavalieri, S.; Garetti, M.; Macchi, M.; Pinto, R. A decision-making framework for managing maintenance spare parts. Prod. Plan. Control 2008, 19, 379–396. [Google Scholar] [CrossRef]
- Sherbrooke, C.C. Optimal Inventory Modelling of Systems. Multi-Echelon Techniques, 2nd ed.; Kluwer: Dordrecht, The Netherlands, 2005; pp. 101–125. [Google Scholar]
- Muckstadt, J.A. Analysis and Algorithms for Service Parts Supply Chains; Springer: New York, NY, USA, 2010. [Google Scholar]
- Feng, Y.W.; Lu, C.; Xue, X.F.; Liu, Y. Research on multi echelon inventory allocation of civil aircraft spare parts considering maintenance ratio. J. Northwest Univ. Technol. 2018, 36, 582–589. [Google Scholar]
- Puig JE, P.; Basten, R. Defining line replaceable units. Eur. J. Oper. Res. 2015, 247, 310–320. [Google Scholar] [CrossRef] [Green Version]
- Costantino, F.; Giulio, D.G. Multi-echelon, Multi-indenture Spare Parts Inventory Control Subject to System Availability and Budget Constraints. Reliab. Eng. Syst. Saf. 2013, 119, 95–101. [Google Scholar] [CrossRef]
- Muckstadt, J.A. A Model for a Multi-Item, Multi-Echelon, Multi-Indenture Inventory System. Manag. Sci. 1973, 20, 472–481. [Google Scholar] [CrossRef]
- Patriarca, R.; Costantino, F.; Di Gravio, G. Inventory model for a multi-echelon system with unidirectional lateral transshipment. Expert Syst. Appl. 2016, 65, 372–382. [Google Scholar] [CrossRef]
- Pascual, R.; Santelices, G.; Lüer-Villagra, A.; MacCawley, A. Optimal repairable spare-parts procurement policy under total business volume discount environment. Reliab. Eng. Syst. Saf. 2017, 159, 276–282. [Google Scholar] [CrossRef]
- Li, Y.F.; Huang, H.Z.; Mi, J.; Peng, W.; Han, X. Reliability analysis of multi-state systems with common cause failures based on Bayesian network and fuzzy probability. Ann. Oper. Res. 2019. [Google Scholar] [CrossRef]
- Li, Y.F.; Liu, Y.; Huang, T.; Peng, W.; Han, X. Reliability assessment for systems suffering common cause failure based on Bayesian networks and proportional hazards model. Qual. Reliab. Eng. Int. 2020, 36, 2509–2520. [Google Scholar] [CrossRef]


| Variable Name | Implication | |
|---|---|---|
| Input Variables | Component number, LRU: ; SRU: | |
| LRU family number, | ||
| Location number, Depot: ; Base: | ||
| Subsystem number, | ||
| Yearly demand means value of component at location | ||
| Conditioned failure rate of a SRU on the parent LRU | ||
| Repairing probability of component at location | ||
| Repairing time of component at location | ||
| Order and ship time of component from the Base to the location | ||
| Price of component | ||
| The number of components in the system | ||
| Intermediate Variables | Quantity of component in repair at location | |
| Decision Variables | Maintenance policy d of component at location | |
| Allocation of Maintenance resources at location | ||
| Level of inventory of component at location | ||
| Components | Inventory Lever | |||
|---|---|---|---|---|
| Depot | Base1 | Base2 | Base3 | |
| 4 | 9 | 17 | 15 | |
| 4 | 3 | 5 | 4 | |
| 2 | 1 | 2 | 2 | |
| 3 | 1 | 2 | 2 | |
| 4 | 2 | 5 | 3 | |
| 2 | 5 | 8 | 6 | |
| 2 | 2 | 3 | 3 | |
| 3 | 3 | 5 | 5 | |
| 3 | 3 | 5 | 5 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, R.; Chen, G.; Wu, J.; Zhou, W.; Huang, Z. Joint Optimization Method of Spare Parts Stocks and Level of Repair Analysis Considering the Multiple Failure Modes. Appl. Sci. 2021, 11, 7254. https://doi.org/10.3390/app11167254
Wang R, Chen G, Wu J, Zhou W, Huang Z. Joint Optimization Method of Spare Parts Stocks and Level of Repair Analysis Considering the Multiple Failure Modes. Applied Sciences. 2021; 11(16):7254. https://doi.org/10.3390/app11167254
Chicago/Turabian StyleWang, Ruiqi, Guangyu Chen, Jie Wu, Wei Zhou, and Zheng Huang. 2021. "Joint Optimization Method of Spare Parts Stocks and Level of Repair Analysis Considering the Multiple Failure Modes" Applied Sciences 11, no. 16: 7254. https://doi.org/10.3390/app11167254
APA StyleWang, R., Chen, G., Wu, J., Zhou, W., & Huang, Z. (2021). Joint Optimization Method of Spare Parts Stocks and Level of Repair Analysis Considering the Multiple Failure Modes. Applied Sciences, 11(16), 7254. https://doi.org/10.3390/app11167254






