Study of the Optimal Waveforms for Non-Destructive Spectral Analysis of Aqueous Solutions by Means of Audible Sound and Optimization Algorithms
Abstract
:1. Introduction
2. Materials and Methods
- MLS signal: a signal generated by MATLAB, taking into account that the maximum length is 30 s. The amplitude is 60% of the full scale (FS);
- White noise: a signal generated by Audacity, with an amplitude of 60% of the FS;
- A set of chirp signals generated by Audacity, with a duration of 1 s each, from 150 Hz to 15 kHz;
- Square pulses with a period of 250 ms and 50% of duty cycle.
3. Algorithm for Clustering Problem
3.1. From Genetic Algorithm to Grouping Genetic Algorithm
3.2. The Fitness Function: The Extreme Learning Machine
3.3. Metaheuristic GGA+ELM Algorithm Application for Spectral Analysis
4. Results and Discussion
4.1. Acoustic Response Spectrum
4.2. Feature Extraction
- Maximum number of generations = 50 generations;
- Training data size = 80%;
- Testing data size = 20%;
- Population size = 50 individuals;
- Mutation probability = 0.1;
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bonacucina, G.; Cespi, M.; Mencarelli, G.; Casettari, L.; Palmieri, G.F. The Use of Acoustic Spectroscopy in the Characterisation of Ternary Phase Diagrams. Int. J. Pharm. 2013, 441, 603–610. [Google Scholar] [CrossRef]
- Bonacucina, G.; Perinelli, D.R.; Cespi, M.; Casettari, L.; Cossi, R.; Blasi, P.; Palmieri, G.F. Acoustic Spectroscopy: A Powerful Analytical Method for The Pharmaceutical Field? Int. J. Pharm. 2016, 503, 174–195. [Google Scholar] [CrossRef] [PubMed]
- Dukhin, A.S.; Goetz, P.J. Ultrasound for Characterizing Colloids. In ACS Symposium Series; American Chemical Society: Washington, DC, USA, 1999, 2004; pp. 91–120. [Google Scholar]
- Povey, M.J. Ultrasonic Techniques for Fluids Characterization; Elsevier: Amsterdam, The Netherlands, 1997. [Google Scholar]
- Contreras, N.I.; Fairley, P.; McClements, D.J.; Povey, M.J. Analysis of The Sugar Content of Fruit Juices and Drinks Using Ultrasonic Velocity Measurements. Int. J. Food Sci. Technol. 1992, 27, 515–529. [Google Scholar] [CrossRef]
- Dzida, M.; Zorebski, E.; Zorębski, M.; Żarska, M.; Geppert-Rybczyńska, M.; Chorążewski, M.; Cibulka, I. Speed of Sound and Ultrasound Absorption in Ionic Liquids. Chem. Rev. 2017, 117, 3883–3929. [Google Scholar] [CrossRef] [Green Version]
- Santos, J.; Ferreira, A.; Santos, M.; Vasco, J.; Cardoso, M.; Ramalho, A. Versatile Low Cost Device for Measuring The Sound Speed in Liquids. In Proceedings of the Meetings on Acoustics ICU, Bruges, Belgium, 3–6 September 2019. [Google Scholar]
- Dukhin, A.S.; Goetz, P.J. Acoustic and Electroacoustic Spectroscopy for Characterizing Concentrated Dispersions and Emulsions. Adv. Colloid Interface Sci. 2001, 92, 73–132. [Google Scholar] [CrossRef]
- Habrioux, M.; Nasri, D.; Daridon, J.L. Measurement of Speed of Sound, Density Compressibility and Viscosity in Liquid Methyl Laurate and Ethyl Laurate up to 200 MPa by Using Acoustic Wave Sensors. J. Chem. Thermodyn. 2018, 120, 1–12. [Google Scholar] [CrossRef]
- Javed, M.A.; Baumhögger, E.; Vrabec, J. Thermodynamic Speed of Sound Data for Liquid and Supercritical Alcohols. J. Chem. Eng. Data 2019, 64, 1035–1044. [Google Scholar] [CrossRef] [Green Version]
- Holmes, M.J.; Parker, N.G.; Povey, M.J.W. Temperature Dependence of Bulk Viscosity in Water Using Acoustic Spectroscopy. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2011; Volume 269, No. 1; p. 012011. [Google Scholar]
- Hoche, S.; Hussein, M.A.; Becker, T. Density, Ultrasound Velocity, Acoustic Impedance, Reflection and Absorption Coefficient Determination of Liquids via Multiple Reflection Method. Ultrasonics 2015, 57, 65–71. [Google Scholar] [CrossRef]
- Pal, B.; Roy, S. Probing Aqueous Electrolytes with Fourier Spectrum Pulse-Echo Technique. J. Mol. Liq. 2019, 291, 111302. [Google Scholar] [CrossRef] [Green Version]
- Pal, B. Fourier Spectrum Pulse-Echo for Acoustic Characterization. J. Nondestruct. Eval. 2018, 37, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Povey, M.J. Ultrasound Particle Sizing: A Review. Particuology 2013, 11, 135–147. [Google Scholar] [CrossRef]
- Silva, C.A.; Saraiva, S.V.; Bonetti, D.; Higuti, R.T.; Cunha, R.L.; Pereira, L.O.; Fileti, A.M. Application of Acoustic Models for Polydisperse Emulsion Characterization using Ultrasonic Spectroscopy in The Long Wavelength Regime. Colloids Surf. A Physicochem. Eng. Asp. 2020, 602, 125062. [Google Scholar] [CrossRef]
- Vos, B.; Crowley, S.V.; O’Sullivan, J.; Evans-Hurson, R.; McSweeney, S.; Krüse, J.; O’mahony, J.A. New Insights into the Mechanism of Rehydration of Milk Protein Concentrate Powders Determined by Broadband Acoustic Resonance Dissolution Spectroscopy (BARDS). Food Hydrocoll. 2016, 61, 933–945. [Google Scholar] [CrossRef] [Green Version]
- Yan, J.; Wright, W.M.; O’Mahony, J.A.; Roos, Y.; Cuijpers, E.; van Ruth, S.M. A Sound Approach: Exploring a Rapid and Non-Destructive Ultrasonic Pulse Echo System for Vegetable Oils Characterization. Food Res. Int. 2019, 125, 108552. [Google Scholar] [CrossRef]
- Buckin, V. High-Resolution Ultrasonic Spectroscopy. J. Sens. Sens. Syst. 2018, 7, 207–217. [Google Scholar] [CrossRef]
- Page, J.H. Ultrasonic Spectroscopy of Complex Media. Nano Optics and Atomics: Transport of Light and Matter Waves. In Proceedings of the International School of Physics “Enrico Fermi”, Course CLXXIII, Varenna, Italy, 23 June–3 July 2011; pp. 115–131. [Google Scholar]
- Buckin, V.; Altas, M.C. Ultrasonic Monitoring of Biocatalysis in Solutions and Complex Dispersions. Catalysts 2017, 7, 336. [Google Scholar] [CrossRef] [Green Version]
- Murdoch, N.; Chide, B.; Lasue, J.; Cadu, A.; Sournac, A.; Bassas-Portús, M.; Mimoun, D. Laser-Induced Breakdown Spectroscopy Acoustic Testing of the Mars 2020 Microphone. Planet. Space Sci. 2019, 165, 260–271. [Google Scholar] [CrossRef] [Green Version]
- Chide, B.; Maurice, S.; Murdoch, N.; Lasue, J.; Bousquet, B.; Jacob, X.; Wiens, R.C. Listening to Laser Sparks: A Link between Laser-Induced Breakdown Spectroscopy, Acoustic Measurements and Crater Morphology. Spectrochim. Acta Part B At. Spectrosc. 2019, 153, 50–60. [Google Scholar] [CrossRef] [Green Version]
- Jahanshahi, A.; Sabzi, H.Z.; Lau, C.; Wong, D. GPU-NEST: Characterizing Energy Efficiency of Multi-GPU Inference Servers. IEEE Comput. Archit. Lett. 2020, 19, 139–142. [Google Scholar] [CrossRef]
- Jahanshahi, A. Tinycnn: A Tiny Modular CNN Accelerator for Embedded FPGA. arXiv 2019, arXiv:1911.06777. [Google Scholar]
- Wu, C.; Shao, S.; Tunc, C.; Hariri, S. Video Anomaly Detection Using Pre-Trained Deep Convolutional Neural Nets and Context Mining. In Proceedings of the 2020 IEEE/ACS 17th International Conference on Computer Systems and Applications (AICCSA), Antalya, Turkey, 2–5 November 2020; pp. 1–8. [Google Scholar]
- Khan, S.; Rahmani, H.; Shah, S.A.A.; Bennamoun, M.A. Guide to Convolutional Neural Networks for Computer Vision. Synth. Lect. Comput. Vis. 2018, 8, 1–207. [Google Scholar] [CrossRef]
- Luo, X.J.; Oyedele, L.O.; Ajayi, A.O.; Akinade, O.O.; Owolabi, H.A.; Ahmed, A. Feature Extraction and Genetic Algorithm Enhanced Adaptive Deep Neural Network for Energy Consumption Prediction in Buildings. Renew. Sustain. Energy Rev. 2020, 131, 109980. [Google Scholar] [CrossRef]
- Tran, D.H.; Luong, D.L.; Chou, J.S. Nature-Inspired Metaheuristic Ensemble Model for Forecasting Energy Consumption in Residential Buildings. Energy 2020, 191, 116552. [Google Scholar] [CrossRef]
- Roshani, M.; Phan, G.T.; Ali, P.J.M.; Roshani, G.H.; Hanus, R.; Duong, T.; Kalmoun, E.M. Evaluation of Flow Pattern Recognition and Void Fraction Measurement in Two Phase Flow Independent of Oil Pipeline’s Scale Layer Thickness. Alex. Eng. J. 2021, 60, 1955–1966. [Google Scholar] [CrossRef]
- Nabavi, M.; Elveny, M.; Danshina, S.D.; Behroyan, I.; Babanezhad, M. Velocity prediction of Cu/Water Nanofluid Convective Flow in a Circular Tube: Learning CFD data by Differential Evolution Algorithm Based Fuzzy Inference System (DEFIS). Int. Commun. Heat Mass Transf. 2021, 126, 105373. [Google Scholar] [CrossRef]
- Roshani, M.; Sattari, M.A.; Ali, P.J.M.; Roshani, G.H.; Nazemi, B.; Corniani, E.; Nazemi, E. Application of GMDH Neural Network Technique to Improve Measuring Precision of a Simplified Photon Attenuation based Two-Phase Flowmeter. Flow Meas. Instrum. 2020, 75, 101804. [Google Scholar] [CrossRef]
- Hong, T.; Pinson, P.; Wang, Y.; Weron, R.; Yang, D.; Zareipour, H. Energy Forecasting: A review and Outlook. IEEE Open Access J. Power Energy 2020. [Google Scholar] [CrossRef]
- Runge, J.; Zmeureanu, R. Forecasting Energy Use in Buildings Using Artificial Neural Networks: A Review. Energies 2019, 12, 3254. [Google Scholar] [CrossRef] [Green Version]
- Mason, K.; Duggan, J.; Howley, E. Forecasting Energy Demand, Wind Generation and Carbon Dioxide Emissions in Ireland using Evolutionary Neural Networks. Energy 2018, 155, 705–720. [Google Scholar] [CrossRef]
- Arabi, M.; Dehshiri, A.M.; Shokrgozar, M. Modeling Transportation Supply and Demand Forecasting using Artificial Intelligence Parameters (Bayesian model). J. Appl. Eng. Sci. 2018, 16, 43–49. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Chen, X.; Yu, J. A Hybrid Energy Feature Extraction Approach for Ship-Radiated Noise based on CEEMDAN Combined with Energy Difference and Energy Entropy. Processes 2019, 7, 69. [Google Scholar] [CrossRef] [Green Version]
- García Díaz, P.; Martínez Rojas, J.A.; Utrilla Manso, M.; Monasterio Expósito, L. Analysis of Water, Ethanol, and Fructose Mixtures using Nondestructive Resonant Spectroscopy of Mechanical Vibrations and a Grouping Genetic Algorithm. Sensors 2018, 18, 2695. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Praat: Doing Phonetics by Computer. Available online: http://www.praat.org/ (accessed on 1 June 2021).
- Audacity ® | Free, Open Source, Cross-Platform Audio Software. Available online: https://www.audacityteam.org (accessed on 1 June 2021).
- MATLAB for Artificial Intelligence. Available online: https://www.mathworks.com/ (accessed on 1 June 2021).
- García-Díaz, P.; Sánchez-Berriel, I.; Martínez-Rojas, J.A.; Diez-Pascual, A.M. Unsupervised Feature Selection Algorithm for Multiclass Cancer Classification of Gene Expression RNA-Seq Data. Genomics 2020, 112, 1916–1925. [Google Scholar] [CrossRef] [PubMed]
- De Lit, P.; Falkenauer, E.; Delchambre, A. Grouping Genetic Algorithms: An Efficient Method to Solve the Cell Formation Problem. Math. Comput. Simul. 2000, 51, 257–271. [Google Scholar] [CrossRef]
- Falkenauer, E. The Grouping Genetic Algorithms: Widening the Scope of the GAs. Belg. J. Oper. Research. Stat. Comput. Sci. 1993, 33, 79–102. [Google Scholar]
- Falkenauer, E. Genetic Algorithms for Grouping Problems; Wiley: New York, NY, USA, 1998. [Google Scholar]
- James, T.L.; Brown, E.C.; Keeling, K.B. A Hybrid Grouping Genetic Algorithm for the Cell Formation Problem. Comput. Oper. Res. 2007, 34, 2059–2079. [Google Scholar] [CrossRef]
- Brown, E.C.; Sumichrast, R.T. Evaluating Performance Advantages of Grouping Genetic Algorithms. Eng. Appl. Artif. Intell. 2005, 18, 1–12. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhu, Q.Y. Extreme Learning Machine: Theory and Applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Huang, G.B.; Chen, L. Convex Incremental Extreme Learning Machine. Neurocomputing 2007, 70, 3056–3062. [Google Scholar] [CrossRef]
- Huang, G.B.; Chen, L. Enhanced Random Search Based Incremental Extreme Learning Machine. Neurocomputing 2008, 71, 3460–3468. [Google Scholar] [CrossRef]
- Huang, G.B.; Xiaojian, H.; Zhou, D. Optimization Method based Extreme Learning Machine for Classification. Neurocomputing 2010, 74, 155–163. [Google Scholar] [CrossRef]
- Huang, G.B.; Wang, D.H.; Lan, Y. Extreme Learning Machines: A Survey. Int. J. Mach. Learn. Cybern. 2011, 2, 107–122. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhou, H.; Ding, X.; Zhang, R. Extreme Learning Machine for Regression and Multiclass Classification. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2012, 42, 513–529. [Google Scholar] [CrossRef] [Green Version]
- Luo, X.; Chang, X.; Ban, X. Regression and Classification using Extreme Learning Machine based on L1-Norm and L2-Norm. Neurocomputing 2016, 174, 179–186. [Google Scholar] [CrossRef]
- Cornejo-Bueno, L.; Nieto-Borge, J.C.; García-Díaz, P.; Rodríguez, G.; Salcedo-Sanz, S. Significant Wave Height and Energy Flux Prediction for Marine Energy Applications: A Grouping Genetic Algorithm—Extreme Learning Machine Approach. Renew. Energy 2016, 97, 380–389. [Google Scholar] [CrossRef]
- Duan, L.; Bao, M.; Miao, J.; Xu, Y.; Chen, J. Classification Based on Multilayer Extreme Learning Machine for Motor Imagery Task form EEG signals. Procedia Comput. Sci. 2016, 88, 176–184. [Google Scholar] [CrossRef] [Green Version]
- Kohavi, R.l.; Jonh, G.H. Wrappers for Features Subset Selection. Artif. Intell. 1997, 97, 273–324. [Google Scholar] [CrossRef] [Green Version]
- Yao, X.; Liu, Y.; Lin, G. Evolutionary Programming Made Faster. IEEE Trans. Evol. Comput. 1999, 3, 82–102. [Google Scholar]
- Quiroz-Castellanos, M.; Cruz-Reyes, L.; Torres-Jimenez, J.; Gómez S., C.; Fraire Huacuja, H.J.; Alvim, A.C.F. A Grouping Genetic Algorithm with Controlled Gene Transmission for The Bin Packing Problem. Comput. Oper. Res. 2015, 55, 52–64. [Google Scholar] [CrossRef]
- Wicker, D.; Rizki, M.M.; Tamburino, L.A. The Multi-Tiered Tournament Selection for Evolutionary Neural Network Synthesis, Symposium on Combinations of Evolutionary Computation and Neural Networks. IEEE 2000, 207–215. [Google Scholar]
- Xie, H.; Zhang, M.; Andreae, P.; Johnson, M. An Analysis of Multi-Sampled Issue and No-Replacement Tournament Selection. In Proceedings of the 10th annual conference on Genetic and evolutionary computation, Atlanta, GA, USA, July 2008; pp. 1323–1330. [Google Scholar]

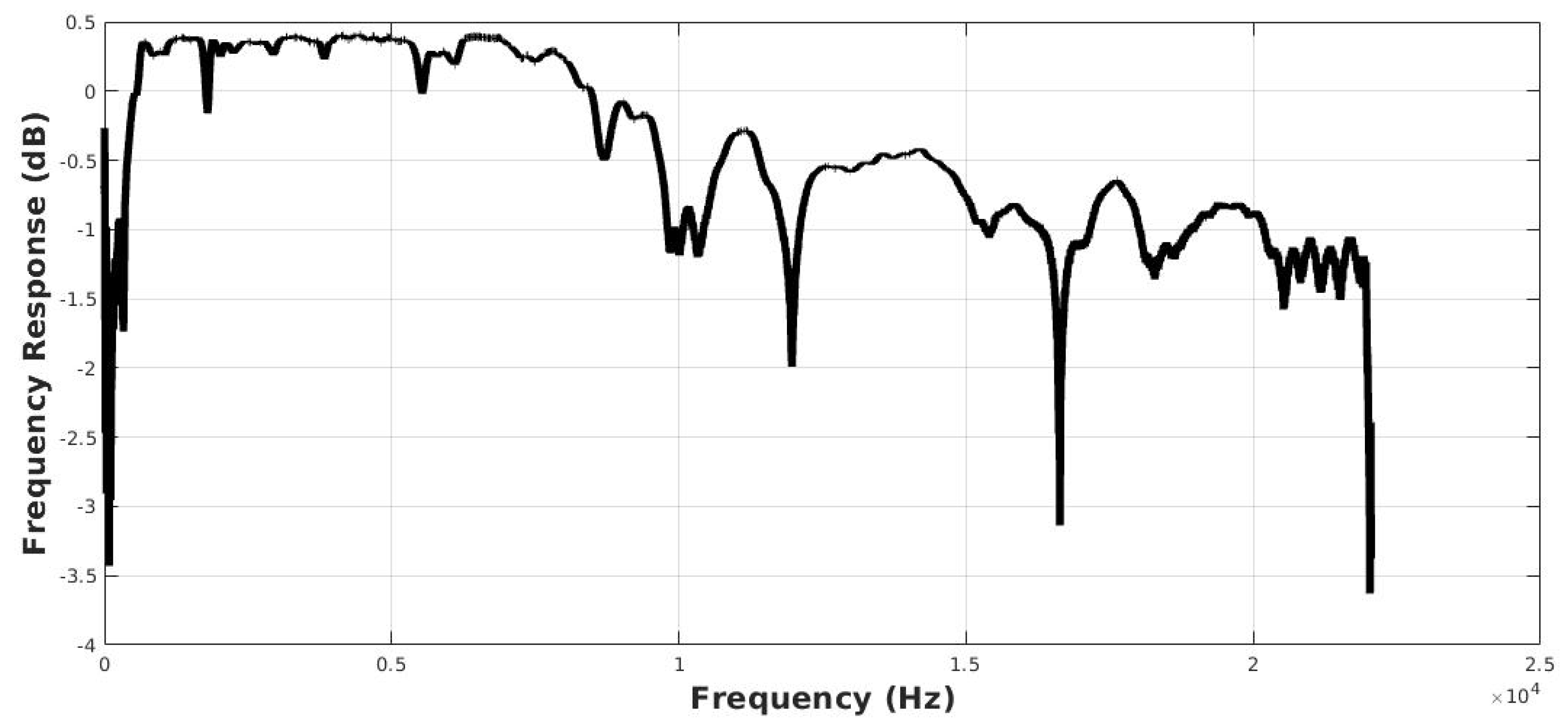
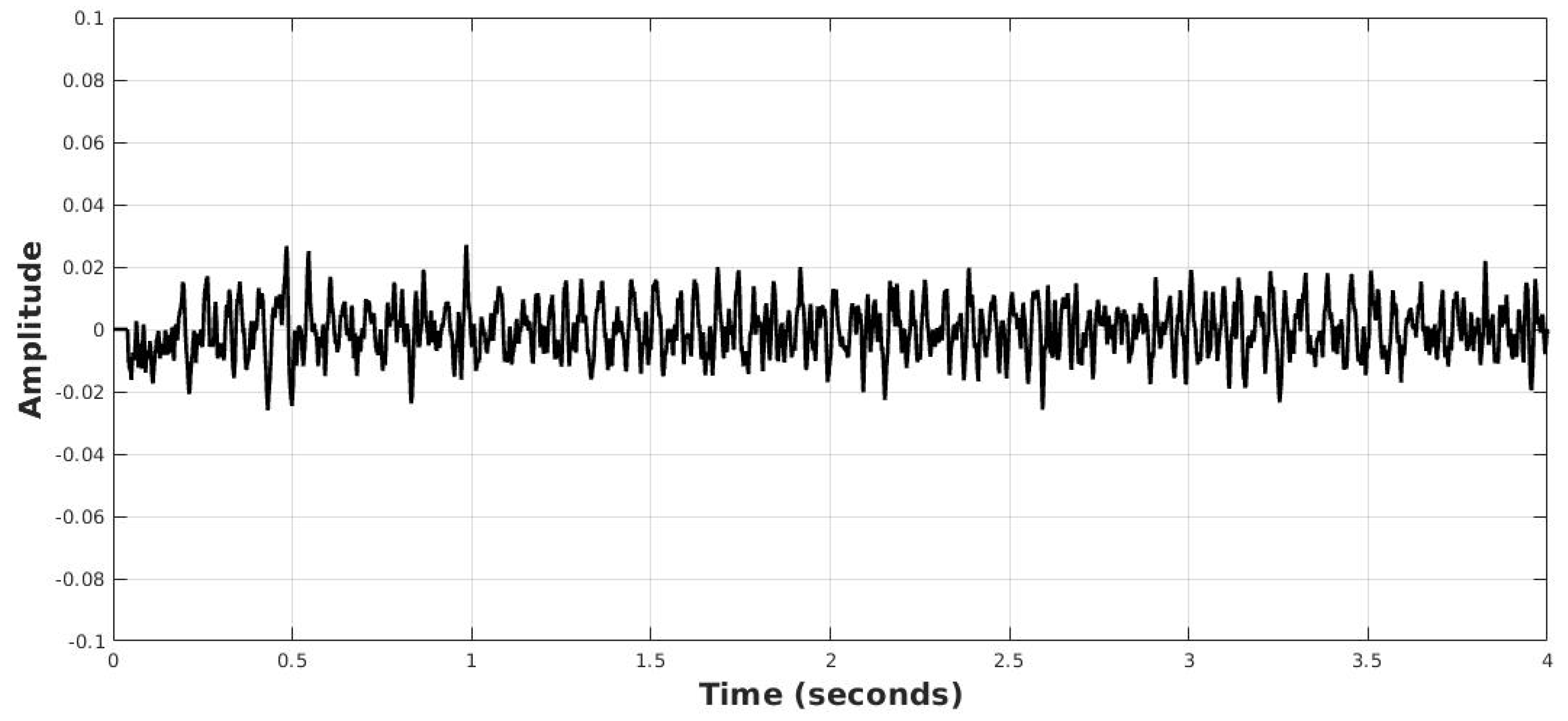
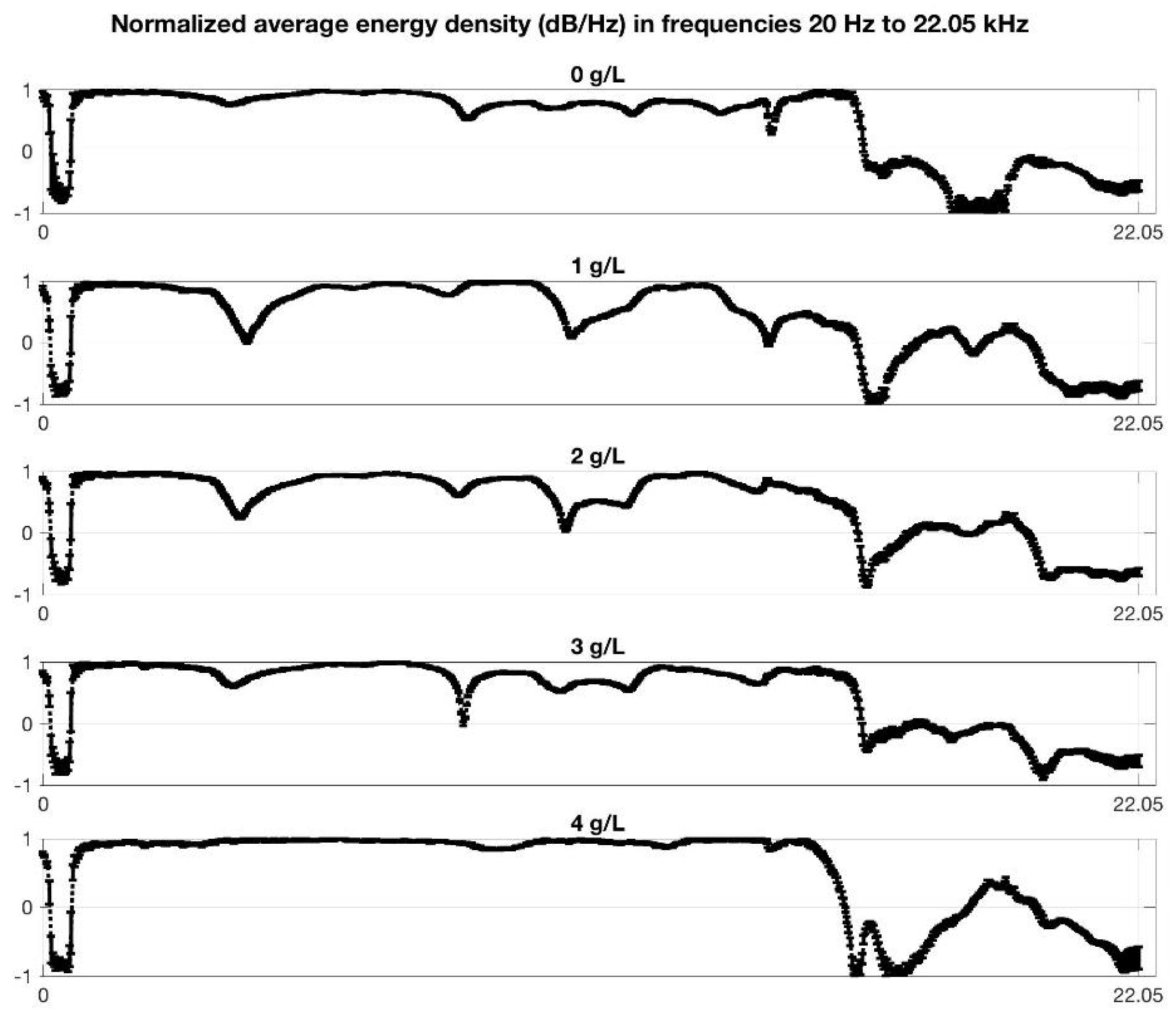
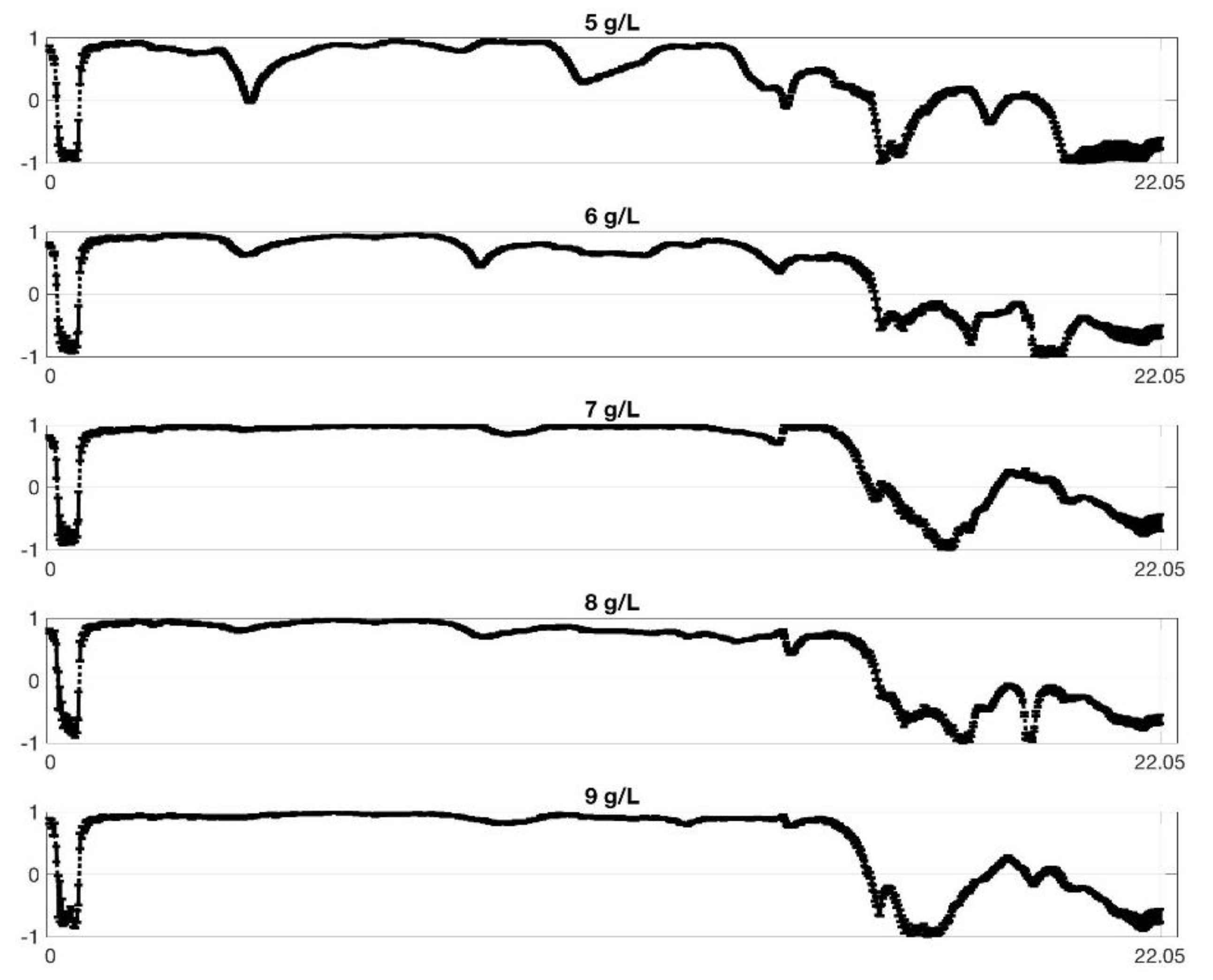

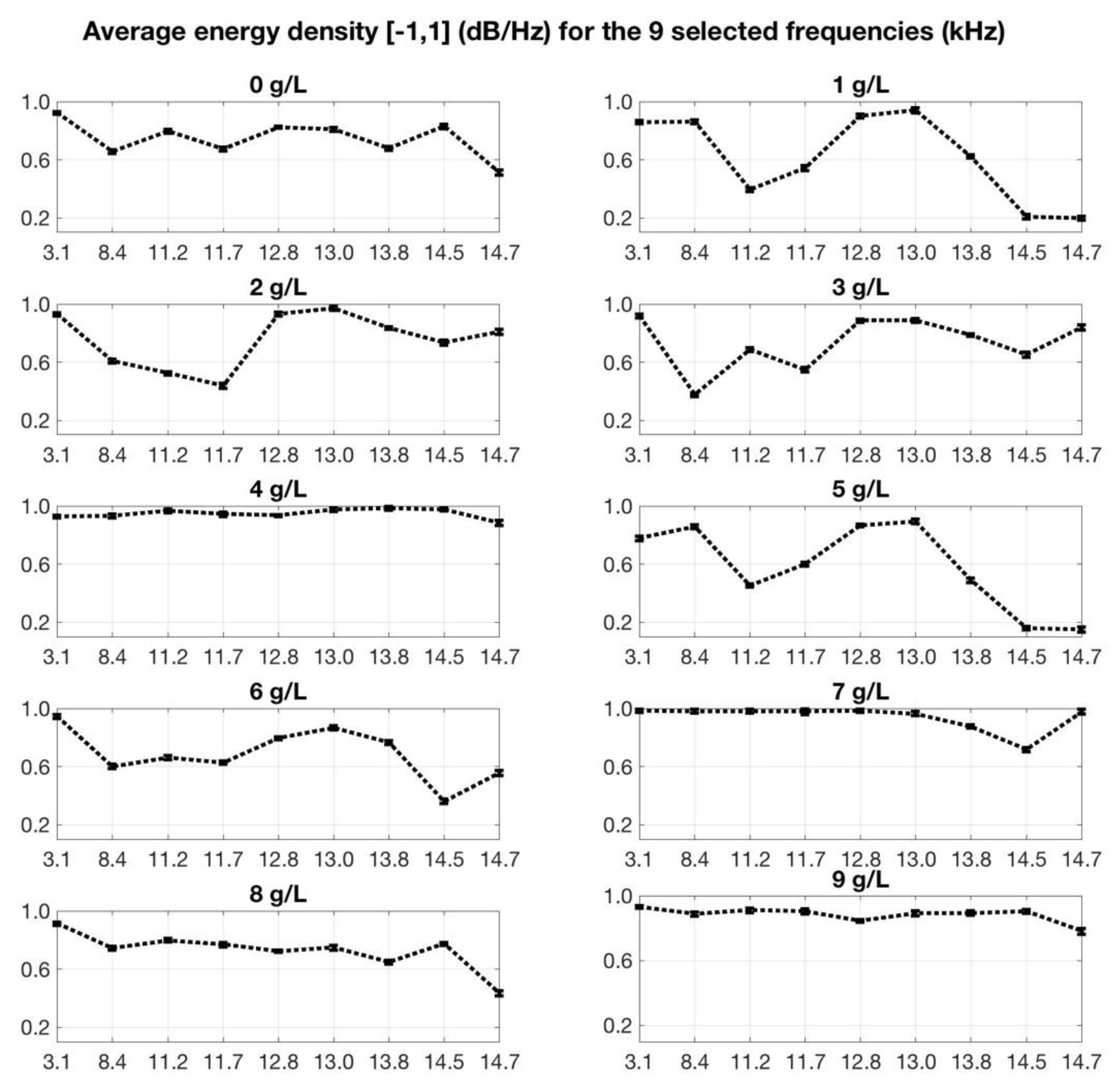

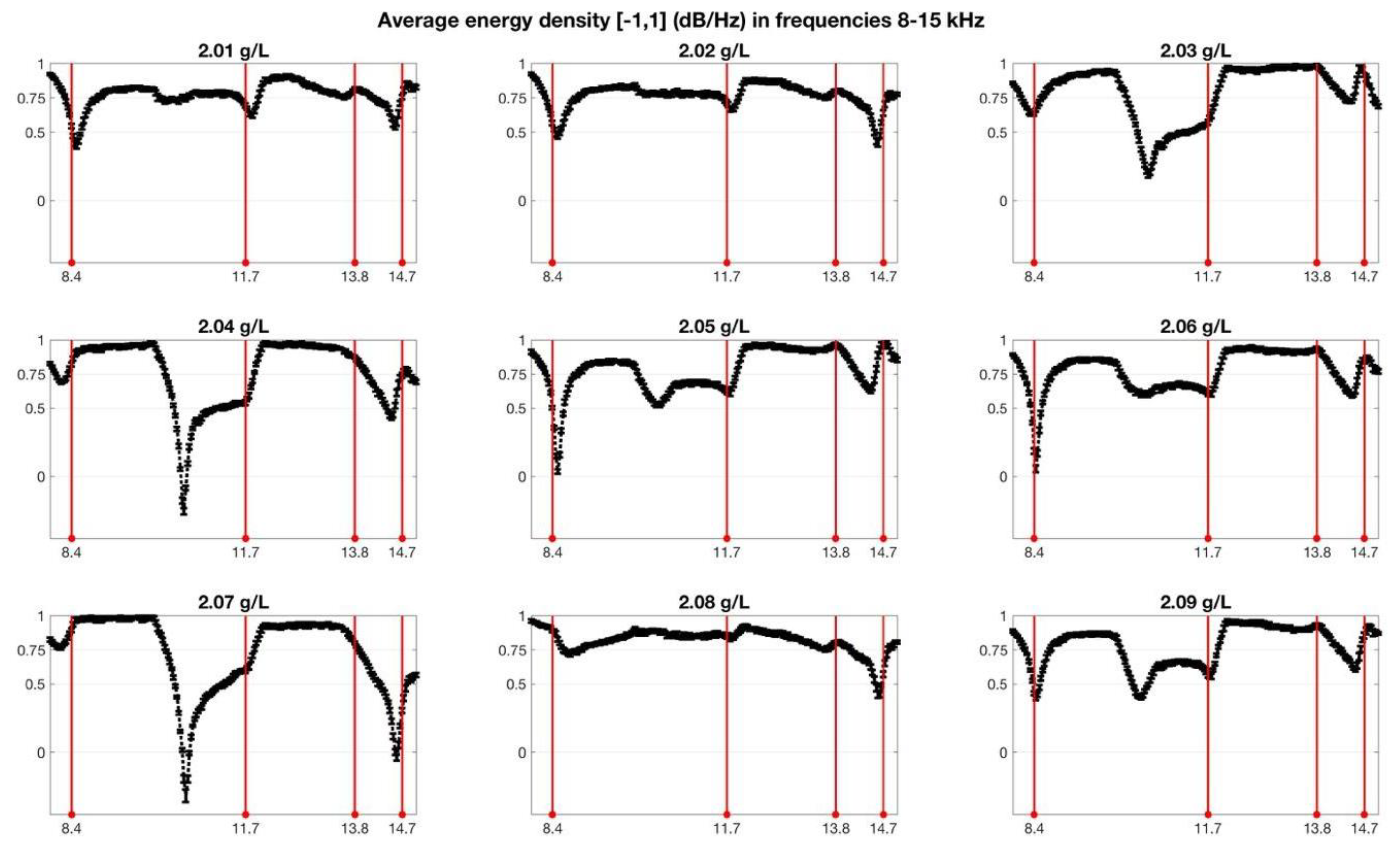

| Fructose Concentration (g/L) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| Number of samples | 13 | 13 | 13 | 13 | 13 | 13 | 13 | 13 | 13 | 13 |
| Total samples | 130 | |||||||||
| Fructose Concentration (g/L) | 2.1 | 2.2 | 2.3 | 2.4 | 2.5 | 2.6 | 2.7 | 2.8 | 2.9 |
|---|---|---|---|---|---|---|---|---|---|
| Number of samples | 13 | 13 | 13 | 13 | 13 | 13 | 13 | 13 | 13 |
| Total samples | 117 | ||||||||
| Fructose Concentration (g/L) | 2.01 | 2.02 | 2.03 | 2.04 | 2.05 | 2.06 | 2.07 | 2.08 | 2.09 |
|---|---|---|---|---|---|---|---|---|---|
| Number of samples | 13 | 13 | 13 | 13 | 13 | 13 | 13 | 13 | 13 |
| Total samples | 117 | ||||||||
| Frequencies (kHz) | Classifier 1 | Classifier 2 |
|---|---|---|
| f1 | 8.4 | 3.1 |
| f2 | 11.7 | 11.2 |
| f3 | 13.8 | 12.8 |
| f4 | 14.7 | 13.0 |
| f5 | - | 14.5 |
| Classifier | 0–9 g/L (±1 g/L) | 2.0–3.0 g/L (±0.1 g/L) | 2.00–2.10 g/L (±0.01 g/L) | |||
|---|---|---|---|---|---|---|
| Average Accuracy | Standard Deviation | Average Accuracy | Standard Deviation | Average Accuracy | Standard Deviation | |
| 1 | 99.71 | 0.0126 | 90.32 | 0.0704 | 98.65 | 0.0272 |
| 2 | 97.60 | 0.0415 | 85.89 | 0.0727 | 80.78 | 0.0824 |
| Combined classifier | 99.82 | 0.0123 | 98.98 | 0.0266 | 98.65 | 0.0272 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
García Díaz, P.; Utrilla Manso, M.; Alpuente Hermosilla, J.; Martínez Rojas, J.A. Study of the Optimal Waveforms for Non-Destructive Spectral Analysis of Aqueous Solutions by Means of Audible Sound and Optimization Algorithms. Appl. Sci. 2021, 11, 7301. https://doi.org/10.3390/app11167301
García Díaz P, Utrilla Manso M, Alpuente Hermosilla J, Martínez Rojas JA. Study of the Optimal Waveforms for Non-Destructive Spectral Analysis of Aqueous Solutions by Means of Audible Sound and Optimization Algorithms. Applied Sciences. 2021; 11(16):7301. https://doi.org/10.3390/app11167301
Chicago/Turabian StyleGarcía Díaz, Pilar, Manuel Utrilla Manso, Jesús Alpuente Hermosilla, and Juan A. Martínez Rojas. 2021. "Study of the Optimal Waveforms for Non-Destructive Spectral Analysis of Aqueous Solutions by Means of Audible Sound and Optimization Algorithms" Applied Sciences 11, no. 16: 7301. https://doi.org/10.3390/app11167301
APA StyleGarcía Díaz, P., Utrilla Manso, M., Alpuente Hermosilla, J., & Martínez Rojas, J. A. (2021). Study of the Optimal Waveforms for Non-Destructive Spectral Analysis of Aqueous Solutions by Means of Audible Sound and Optimization Algorithms. Applied Sciences, 11(16), 7301. https://doi.org/10.3390/app11167301







