Neutron-Induced Nuclear Cross-Sections Study for Plasma Facing Materials via Machine Learning: Molybdenum Isotopes
Abstract
:1. Introduction
2. Materials and Methods
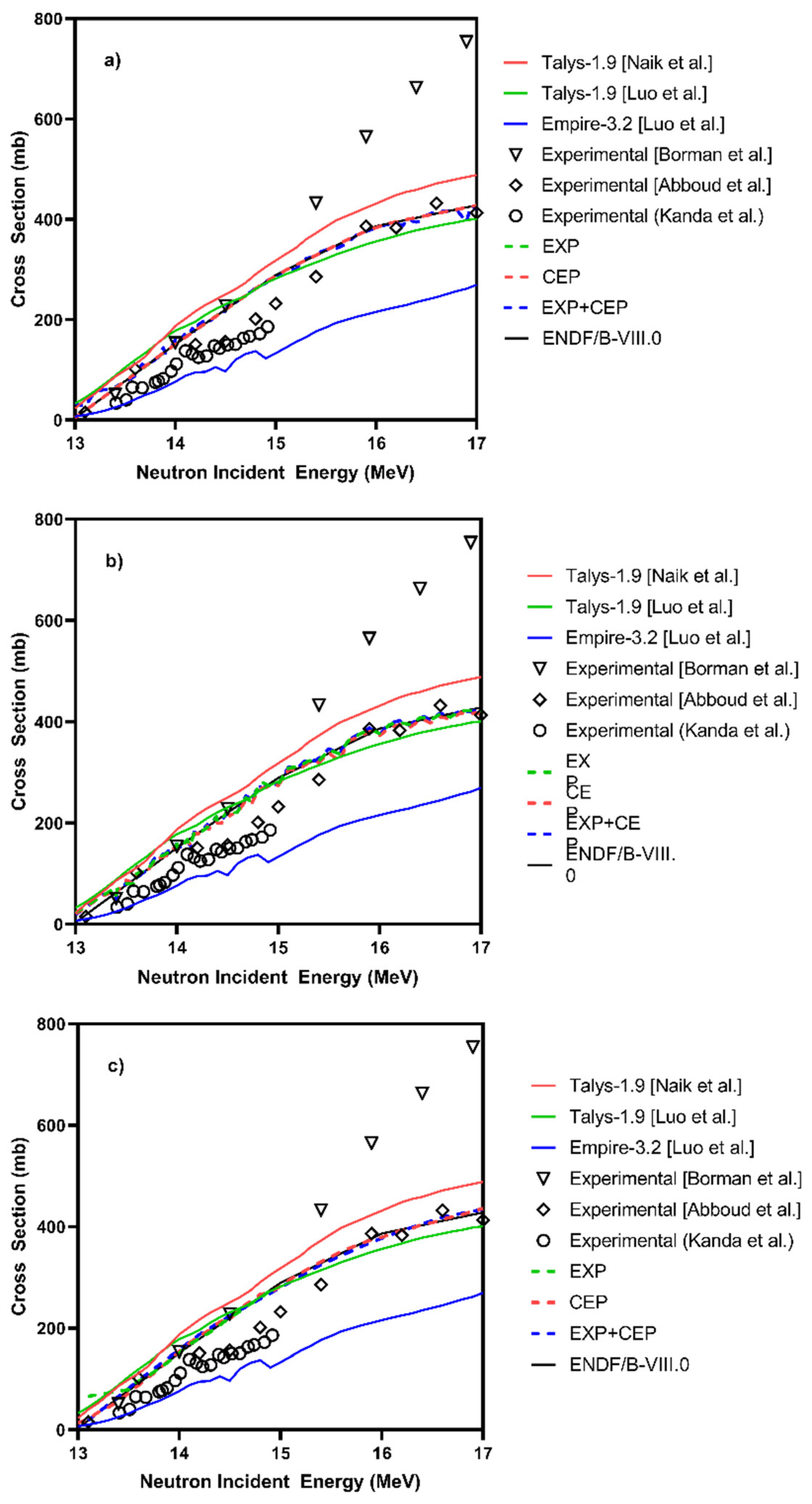
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Algorithms | Input Data | RMSE | |
|---|---|---|---|
| GPR | TALYS 1.9 [19] | 1.7712 | 0.99 |
| TALYS 1.9 [3] | 1.8748 | 0.99 | |
| EMPIRE 3.2 [3] | 1.6036 | 0.99 | |
| TALYS 1.9 [3,19] | 2.3065 | 0.99 | |
| TALYS 1.9 + EMPIRE 3.2 [3,19] | 2.6242 | 0.99 | |
| TALYS 1.9 + EMPIRE 3.2 [3] | 1.7649 | 0.99 | |
| TALYS 1.9 + TALYS 1.9 + EMPIRE 3.2 [3,19] | 2.4981 | 0.99 | |
| RF | TALYS 1.9 [19] | 11.739 | 0.99 |
| TALYS 1.9 [3] | 11.072 | 0.99 | |
| EMPIRE 3.2 [3] | 12.113 | 0.99 | |
| TALYS 1.9 [3,19] | 10.423 | 0.99 | |
| TALYS 1.9 + EMPIRE 3.2 [3,19] | 6.7575 | 0.99 | |
| TALYS 1.9 + EMPIRE 3.2 [3] | 11.253 | 0.99 | |
| TALYS 1.9 + TALYS 1.9 + EMPIRE 3.2 [3,19] | 6.6829 | 0.99 | |
| SVM | TALYS 1.9 [19] | 6.4485 | 0.99 |
| TALYS 1.9 [3] | 7.5603 | 0.99 | |
| EMPIRE 3.2 [3] | 4.3977 | 0.99 | |
| TALYS 1.9 [3,19] | 2.7543 | 0.99 | |
| TALYS 1.9 + EMPIRE 3.2 [3,19] | 4.5357 | 0.99 | |
| TALYS 1.9 + EMPIRE 3.2 [3] | 1.8763 | 0.99 | |
| TALYS 1.9 + TALYS 1.9 + EMPIRE 3.2 [3,19] | 4.2918 | 0.99 |
| Algorithms | Input Data | RMSE | |
|---|---|---|---|
| GPR | Borman et al. [17] | 18.996 | 0.98 |
| Abboud et al. [18] | 2.7569 | 0.99 | |
| Kanda et al. [20] | 0.88192 | 0.99 | |
| RF | Borman et al. [17] | 7.0876 | 0.99 |
| Abboud et al. [18] | 10.64 | 0.99 | |
| Kanda et al. [20] | 6.5792 | 0.99 | |
| Borman et al. + Abboud et al. [17,18] | 8.4342 | 0.99 | |
| Borman et al. + Kanda et al. [17,20] | 7.1418 | 0.99 | |
| Abboud et al. + Kanda et al. [18,20] | 10.872 | 0.99 | |
| Borman et al. + Abboud et al. + Kanda et al. [17,18,20] | 10.598 | 0.99 | |
| SVM | Borman et al. [17] | 38.494 | 0.92 |
| Abboud et al. [18] | 126.95 | 0.07 | |
| Kanda et al. [20] | 1.1155 | 0.99 |
| Algorithms | Input Data | RMSE | |
|---|---|---|---|
| GPR | TALYS 1.9 + Borman et al. [17,19] | 79.079 | 0.61 |
| TALYS 1.9 + Borman et al. [3,17] | 70.147 | 0.69 | |
| EMPIRE 3.2 + Borman et al. [3,17] | 24.114 | 0.96 | |
| TALYS 1.9 + Borman et al. [3,17,19] | 82.77 | 0.57 | |
| TALYS 1.9 + EMPIRE 3.2 + Borman et al. [3,17,19] | 60.895 | 0.77 | |
| TALYS 1.9 + EMPIRE 3.2 + Borman et al. [3,17] | 62.863 | 0.75 | |
| TALYS 1.9 + TALYS 1.9 + EMPIRE 3.2 + Borman et al. [3,17,19] | 68.467 | 0.71 | |
| TALYS 1.9 + Abboud et al. [18,19] | 4.9163 | 0.99 | |
| TALYS 1.9 + Abboud et al. [3,18] | 7.1168 | 0.99 | |
| EMPIRE 3.2 + Abboud et al. [3,18] | 2.2094 | 0.99 | |
| TALYS 1.9 + Abboud et al. [3,18,19] | 5.0829 | 0.99 | |
| TALYS 1.9 + EMPIRE 3.2 + Abboud et al. [3,18,19] | 4.938 | 0.99 | |
| TALYS 1.9 + EMPIRE 3.2 + Abboud et al. [3,18] | 9.1249 | 0.99 | |
| TALYS 1.9 + TALYS 1.9 + EMPIRE 3.2 + Abboud et al. [3,18,19] | 4.2338 | 0.99 | |
| TALYS 1.9 + Kanda et al. [19,20] | 88.581 | 0.51 | |
| TALYS 1.9 + Kanda et al. [3,20] | 86.902 | 0.53 | |
| EMPIRE 3.2 + Kanda et al. [3,20] | 89.188 | 0.50 | |
| TALYS 1.9 + Kanda et al. [3,19,20] | 86.423 | 0.53 | |
| TALYS 1.9 + EMPIRE 3.2 + Kanda et al. [3,19,20] | 88.112 | 0.51 | |
| TALYS 1.9 + EMPIRE 3.2 + Kanda et al. [3,20] | 86.835 | 0.53 | |
| TALYS 1.9 + TALYS 1.9 + EMPIRE 3.2 + Kanda et al. [3,19,20] | 86.697 | 0.53 | |
| RF | TALYS 1.9 + Borman et al. [17,19] | 6.6887 | 0.99 |
| TALYS 1.9 + Borman et al. [3,17] | 6.8452 | 0.99 | |
| EMPIRE 3.2 + Borman et al. [3,17] | 7.6775 | 0.99 | |
| TALYS 1.9 + Borman et al. [3,17,19] | 12.598 | 0.99 | |
| TALYS 1.9 + EMPIRE 3.2 + Borman et al. [3,17,19] | 9.9778 | 0.99 | |
| TALYS 1.9 + EMPIRE 3.2 + Borman et al. [3,17] | 7.886 | 0.99 | |
| TALYS 1.9 + TALYS 1.9 + EMPIRE 3.2 + Borman et al. [3,17,19] | 8.3505 | 0.99 | |
| TALYS 1.9 + Abboud et al. [18,19] | 6.9508 | 0.99 | |
| TALYS 1.9 + Abboud et al. [3,18] | 9.8844 | 0.99 | |
| EMPIRE 3.2 + Abboud et al. [3,18] | 6.8545 | 0.99 | |
| TALYS 1.9 + Abboud et al. [3,18,19] | 12.626 | 0.99 | |
| TALYS 1.9 + EMPIRE 3.2 + Abboud et al. [3,18,19] | 6.7171 | 0.99 | |
| TALYS 1.9 + EMPIRE 3.2 + Abboud et al. [3,18] | 10.747 | 0.99 | |
| TALYS 1.9 + TALYS 1.9 + EMPIRE 3.2 + Abboud et al. [3,18,19] | 6.75 | 0.99 | |
| TALYS 1.9 + Kanda et al. [19,20] | 11.376 | 0.99 | |
| TALYS 1.9 + Kanda et al. [3,20] | 6.6964 | 0.99 | |
| EMPIRE 3.2 + Kanda et al. [3,20] | 8.2924 | 0.99 | |
| TALYS 1.9 + Kanda et al. [3,19,20] | 7.4009 | 0.99 | |
| TALYS 1.9 + EMPIRE 3.2 + Kanda et al. [3,19,20] | 10.413 | 0.99 | |
| TALYS 1.9 + EMPIRE 3.2 + Kanda et al. [3,20] | 6.6962 | 0.99 | |
| TALYS 1.9 + TALYS 1.9 + EMPIRE 3.2 + Kanda et al. [3,19,20] | 13.099 | 0.99 | |
| SVM | TALYS 1.9 + Borman et al. [17,19] | 133.6 | −0.12 |
| TALYS 1.9 + Borman et al. [3,17] | 133.6 | −0.12 | |
| EMPIRE 3.2 + Borman et al. [3,17] | 133.6 | −0.12 | |
| TALYS 1.9 + Borman et al. [3,17,19] | 133.6 | −0.12 | |
| TALYS 1.9 + EMPIRE 3.2 + Borman et al. [3,17,19] | 133.6 | −0.12 | |
| TALYS 1.9 + EMPIRE 3.2 + Borman et al. [3,17] | 133.6 | −0.12 | |
| TALYS 1.9 + TALYS 1.9 + EMPIRE 3.2 + Borman et al. [3,17,19] | 133.6 | −0.12 | |
| TALYS 1.9 + Abboud et al. [18,19] | 7.1575 | 0.99 | |
| TALYS 1.9 + Abboud et al. [3,18] | 8.6507 | 0.99 | |
| EMPIRE 3.2 + Abboud et al. [3,18] | 31.192 | 0.95 | |
| TALYS 1.9 + Abboud et al. [3,18,19] | 5.8921 | 0.99 | |
| TALYS 1.9 + EMPIRE 3.2 + Abboud et al. [3,18,19] | 27.998 | 0.96 | |
| TALYS 1.9 + EMPIRE 3.2 + Abboud et al. [3,18] | 5.9724 | 0.99 | |
| TALYS 1.9 + TALYS 1.9 + EMPIRE 3.2 + Abboud et al. [3,18,19] | 11.044 | 0.99 | |
| TALYS 1.9 + Kanda et al. [19,20] | 138.43 | −0.2 | |
| TALYS 1.9 + Kanda et al. [3,20] | 138.43 | −0.2 | |
| EMPIRE 3.2 + Kanda et al. [3,20] | 138.43 | −0.2 | |
| TALYS 1.9 + Kanda et al. [3,19,20] | 138.43 | −0.2 | |
| TALYS 1.9 + EMPIRE 3.2 + Kanda et al. [3,19,20] | 138.43 | −0.2 | |
| TALYS 1.9 + EMPIRE 3.2 + Kanda et al. [3,20] | 138.43 | −0.2 | |
| TALYS 1.9 + TALYS 1.9 + EMPIRE 3.2 + Kanda et al. [3,19,20] | 138.43 | −0.2 |
References
- Rubel, M.J.; Bailescu, V.; Coad, J.P.; Hirai, T.; Likonen, J.; Linke, J.; Lungu, C.P.; Matthews, G.F.; Pedrick, L.; Riccardo, V.; et al. Beryllium plasma-facing components for the ITER-Like wall project at JET. J. Phys. Conf. Ser. 2008, 100, 062028. [Google Scholar] [CrossRef]
- Mehta, M.; Singh, N.L.; Makwana, R.; Mukherjee, S.; Vansola, V.; Sheela, Y.S.; Khirwadkar, S.; Abhangi, M.; Vala, S.; Suryanarayana, S.V.; et al. Neutron induced reaction cross-section for the plasma facing fusion reactor material—Tungsten isotopes. In Proceedings of the 2018 19th International Scientific Conference on Electric Power Engineering (EPE), Brno, Czech Republic, 16–18 May 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Luo, J.; Jiang, L. Cross-Sections for n,2n, (n,α, (n,p), {(n,d), and (n,t) Reactions on Molybdenum Isotopes in the Neutron Energy Range of 13 to 15 MeV. Chin. Phys. C 2020, 44, 114002. [Google Scholar] [CrossRef]
- Otuka, N.; Dupont, E.; Semkova, V.; Pritychenko, B.; Blokhin, A.I.; Aikawa, M.; Babykina, S.; Bossant, M.; Chen, G.; Dunaeva, S.; et al. Towards a more complete and accurate experimental nuclear reaction data library (EXFOR): International collaboration between Nuclear Reaction Data Centres (NRDC). Nucl. Data Sheets 2014. [Google Scholar] [CrossRef] [Green Version]
- Betak, E. Recommendations for pre-equilibrium calculations. Meas. Calc. Eval. Phot. Prod. Data 1999, 31, 134–138. [Google Scholar]
- Weisskopf, V.F.; Ewing, D.H. On the yield of nuclear reactions with heavy elements. Phys. Rev. 1940, 57, 472–485. [Google Scholar] [CrossRef]
- Bitam, T.; Belgaid, M. Newly developed semi-empirical formulas of nuclear excitation functions for (n,α) reactions at the energy range 12 ≤ En ≤ 20 MeV and mass number range 30 ≤ A ≤ 128. Nucl. Phys. A 2019, 991, 121614. [Google Scholar] [CrossRef]
- Yiğit, M. A Review of (n,p) and (n,α) nuclear cross sections on palladium nuclei using different level density models and empirical formulas. Appl. Radiat. Isot. 2018, 140, 355–362. [Google Scholar] [CrossRef] [PubMed]
- Yiğit, M. Analysis of cross sections of (n,t) nuclear reaction using different empirical formulae and level density models. Appl. Radiat. Isot. 2018, 139, 151–158. [Google Scholar] [CrossRef] [PubMed]
- Yiğit, M.; Bostan, S.N. Study on cross section calculations for (n,p) nuclear reactions of cadmium isotopes. Appl. Radiat. Isot. 2019, 154. [Google Scholar] [CrossRef] [PubMed]
- Neudecker, D.; Grosskopf, M.; Herman, M.; Haeck, W.; Grechanuk, P.; Vander Wiel, S.; Rising, M.E.; Kahler, A.C.; Sly, N.; Talou, P. Enhancing nuclear data validation analysis by using machine learning. Nucl. Data Sheets 2020, 167, 36–60. [Google Scholar] [CrossRef]
- Iwamoto, H. Generation of nuclear data using gaussian process regression. J. Nucl. Sci. Technol. 2020, 57, 932–938. [Google Scholar] [CrossRef]
- Zhang, Y.; Ling, C. A strategy to apply machine learning to small datasets in materials science. NPJ Comput. Mater. 2018, 4, 28–33. [Google Scholar] [CrossRef] [Green Version]
- Herman, M.; Capote, R.; Carlson, B.V.; Obložinský, P.; Sin, M.; Trkov, A.; Wienke, H.; Zerkin, V. EMPIRE: Nuclear reaction model code system for data evaluation. Nucl. Data Sheets 2007, 108, 2655–2715. [Google Scholar] [CrossRef]
- Koning, A.J.; Rochman, D. Modern nuclear data evaluation with the TALYS code system. Nucl. Data Sheets 2012, 113, 2841–2934. [Google Scholar] [CrossRef]
- Brown, D.A.; Chadwick, M.B.; Capote, R.; Kahler, A.C.; Trkov, A.; Herman, M.W.; Sonzogni, A.A.; Danon, Y.; Carlson, A.D.; Dunn, M.; et al. ENDF/B-VIII.0: The 8th Major Release of the Nuclear Reaction Data Library with CIELO-Project Cross Sections, New Standards and Thermal Scattering Data. Nucl. Data Sheets 2018, 148, 1–142. [Google Scholar] [CrossRef]
- Bormann, M.; Feddersen, H.-K.; Hölscher, H.-H.; Scobel, W.; Wagener, H. (N, 2n) Anregungsfunktionen Für54Fe,70Ge,74Se,85Rb,8688Sr,89Y,92Mo,204Hg Im Neutronenenergiebereich 13–18 MeV. Z. Für Phys. A At. Nucl. 1976, 277, 203–210. [Google Scholar] [CrossRef]
- Abboud, A.; Decowski, P.; Grochulski, W.; Marcinkowski, A.; Piotrowski, J.; Siwek, K.; Wilhelmi, Z. Isomeric Cross-Section Ratios and Total Cross Sections for the 74se(n, 2n)73g, Mse, 90zr(n, 2n)89g, Mzr and 92mo(n, 2n)91g, Mmo Reactions. Nucl. Phys. A 1969, 139, 42–56. [Google Scholar] [CrossRef]
- Naik, H.; Kim, G.; Kim, K.; Nadeem, M.; Sahid, M. Production Cross-Sections of Mo-Isotopes Induced by Fast Neutrons Based on the 9Be(p, n) Reaction. Eur. Phys. J. Plus 2020, 135. [Google Scholar] [CrossRef]
- Kanda, Y. The excitation functions and isomer ratios for neutron-induced reactions on 92Mo and 90Zr. Nucl. Physics Sect. A 1972, 185, 177–195. [Google Scholar] [CrossRef]
- Bishnoi, S.; Singh, S.; Ravinder, R.; Bauchy, M.; Gosvami, N.N.; Kodamana, H.; Krishnan, N.M.A. Predicting young’s modulus of oxide glasses with sparse datasets using machine learning. J. Non. Cryst. Solids 2019, 524, 119643. [Google Scholar] [CrossRef] [Green Version]
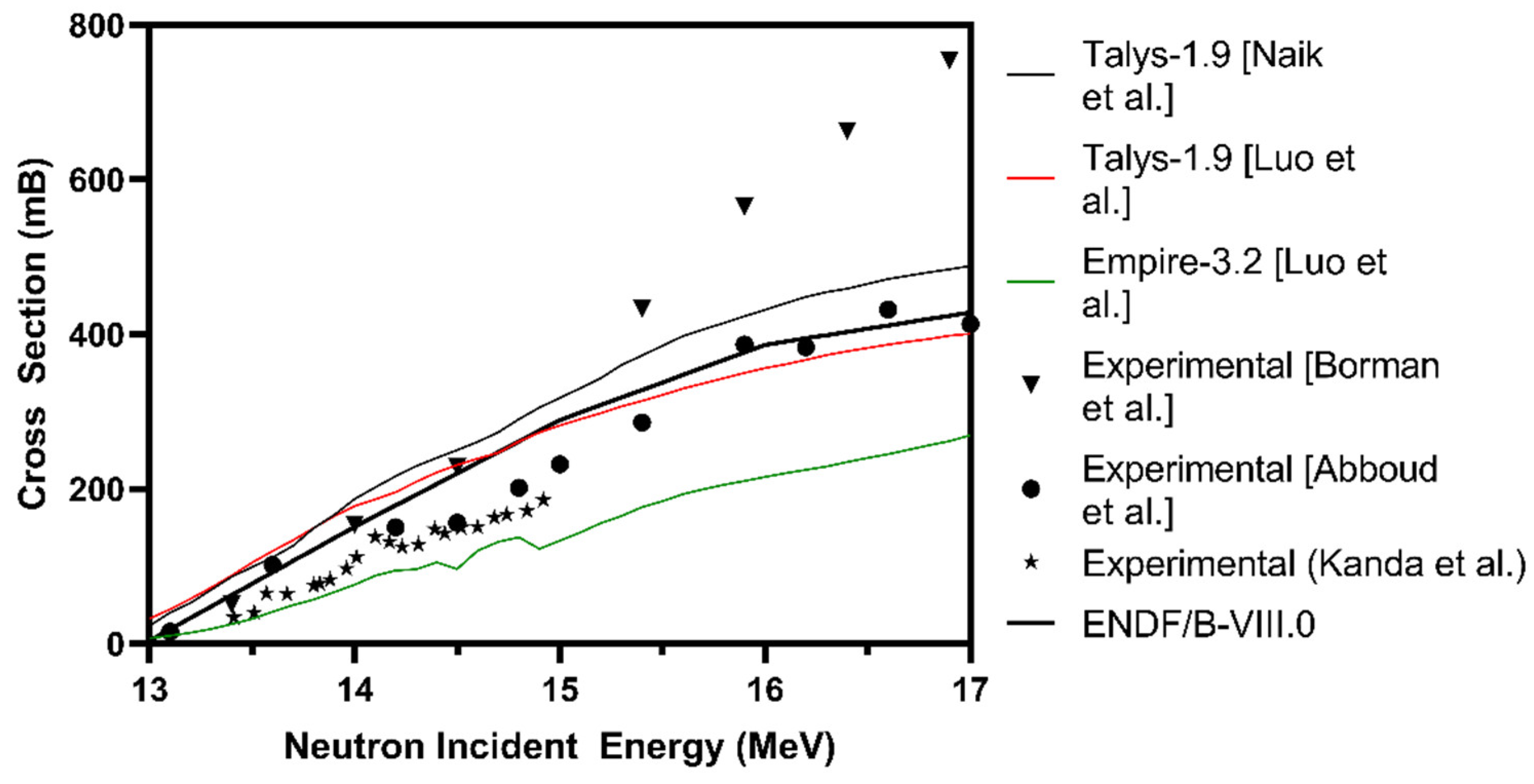
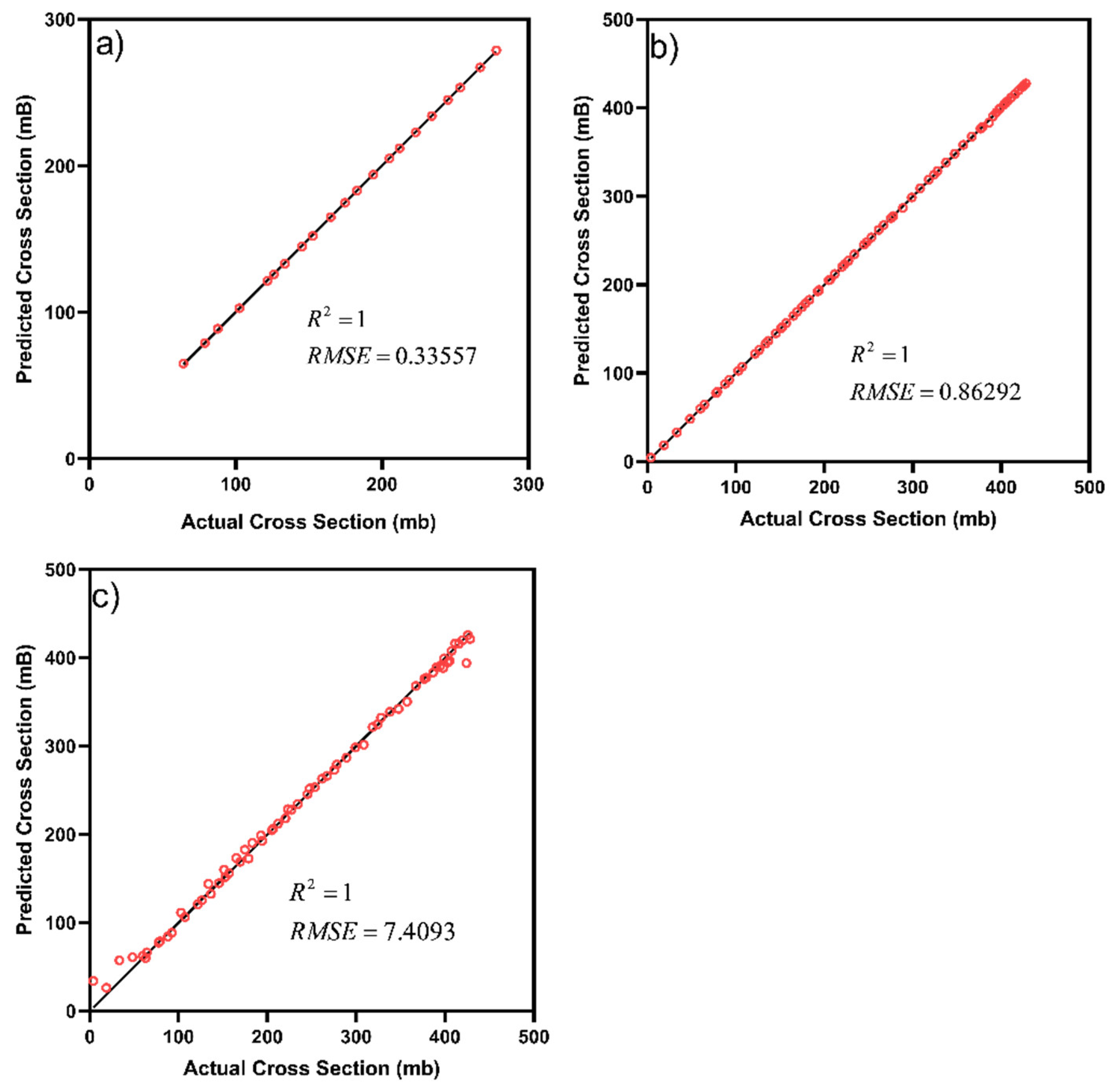
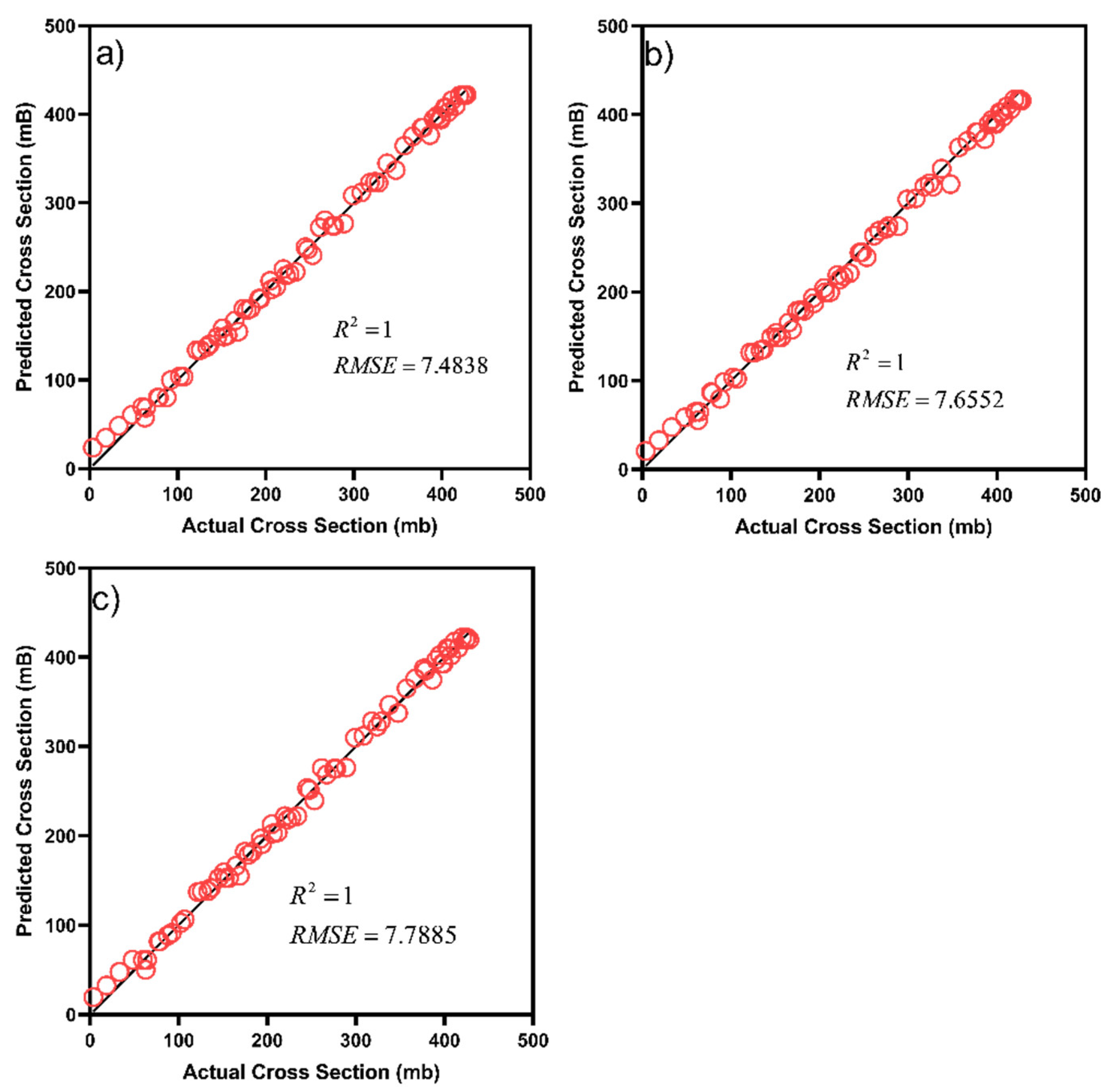
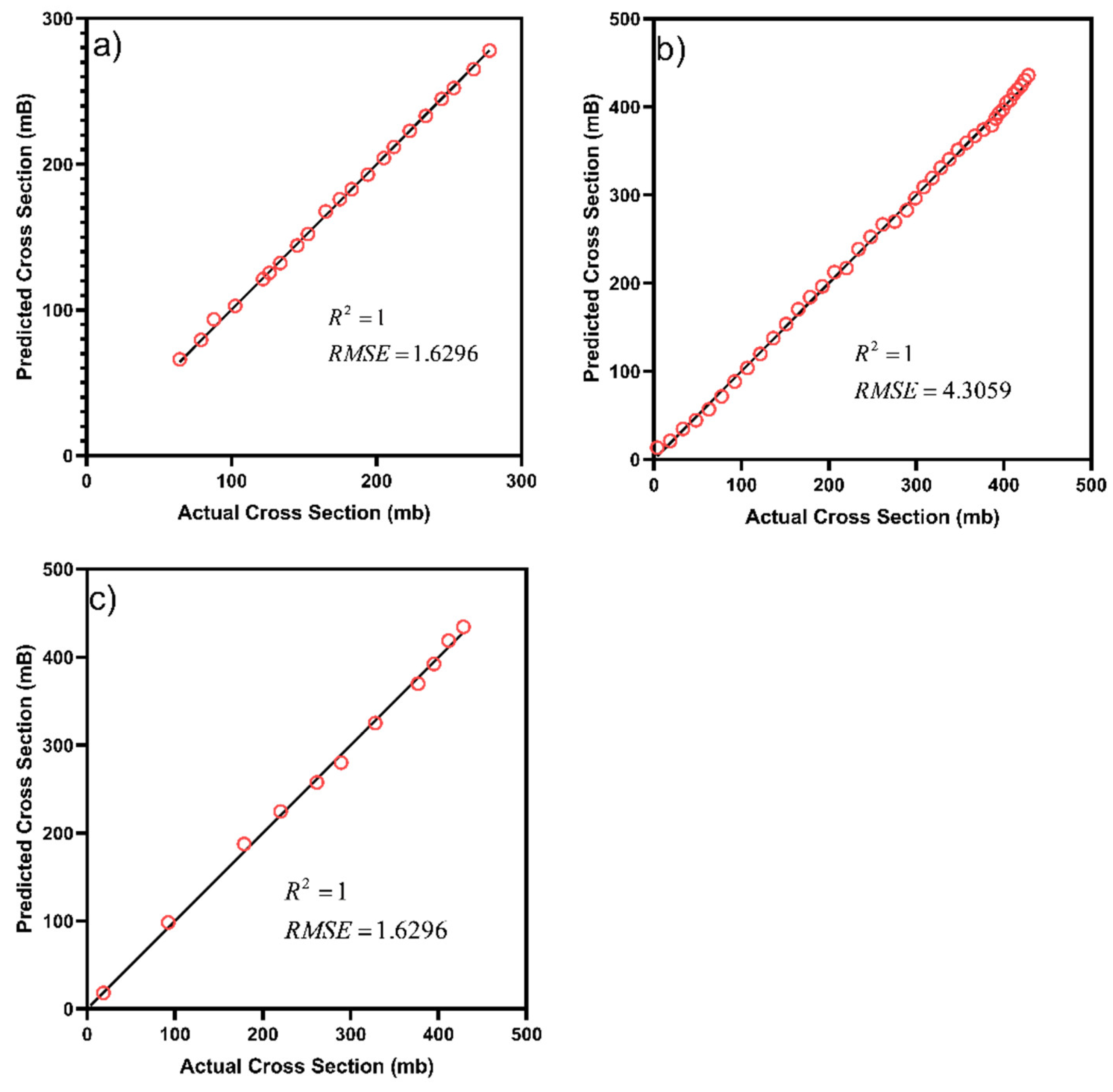
| Variable | Variable Name | No of Data Points | Variable Type |
|---|---|---|---|
| X1 | Incident Energy () | 41 | Input |
| X2 | EMPIRE 3.2 output () [3] | 41 | Input |
| X3 | TALYS 1.9 output () [3,19] | 82 | Input |
| X4 | Borman et al. [17] | 7 | Input |
| X5 | Abboud et al. [18] | 11 | Input |
| X6 | Kanda et al. [20] | 21 | Input |
| Y1 | ENDF/B-VIII.0 library () [16] | 41 | Output |
| Algorithms | Input | Hyperparameters |
|---|---|---|
| GPR | EXP | Linear basis function, isotropic rational quadratic, 39.2269 kernal scale, σ = 0.00010974 |
| EXP + CEP | Radial basis function, non-isotropic matern 3/2, 114.1658 kernal scale, σ = 1246.4488 | |
| CEP | Radial basis function, non-isotropic matern 3/2, 249.3891 kernal scale, σ = 3.477 | |
| RF | EXP | Bagged tree, 3 leaves, 10 learners and 2 predictors |
| EXP + CEP | Bagged tree, 2 leaves, 172 learners and 4 predictors | |
| CEP | Bagged tree, 1 leaf, 13 learners and 4 predictors | |
| SVM | EXP | Quadratic kernel funcion, 992.923 box constraints, ε = 1.1308 |
| EXP + CEP | Linear kernel function, 0.01304 box constraints, ε = 1.5412 | |
| CEP | Cubic kernel function, 150.2836 box constraints, ε = 5.6412 |
| Algorithms | Input | RMSE (mB) | |
|---|---|---|---|
| GPR | EXP | 1 | 0.33557 |
| EXP + CEP | 1 | 7.4093 | |
| CEP | 1 | 0.86292 | |
| RF | EXP | 1 | 7.4838 |
| EXP + CEP | 1 | 7.7885 | |
| CEP | 1 | 7.6552 | |
| SVM | EXP | 1 | 1.6296 |
| EXP + CEP | 1 | 5.9236 | |
| CEP | 1 | 4.3059 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hamid, M.A.B.; Beh, H.G.; Oluwatobi, Y.A.; Chew, X.Y.; Ayub, S. Neutron-Induced Nuclear Cross-Sections Study for Plasma Facing Materials via Machine Learning: Molybdenum Isotopes. Appl. Sci. 2021, 11, 7359. https://doi.org/10.3390/app11167359
Hamid MAB, Beh HG, Oluwatobi YA, Chew XY, Ayub S. Neutron-Induced Nuclear Cross-Sections Study for Plasma Facing Materials via Machine Learning: Molybdenum Isotopes. Applied Sciences. 2021; 11(16):7359. https://doi.org/10.3390/app11167359
Chicago/Turabian StyleHamid, Mohamad Amin Bin, Hoe Guan Beh, Yusuff Afeez Oluwatobi, Xiao Yan Chew, and Saba Ayub. 2021. "Neutron-Induced Nuclear Cross-Sections Study for Plasma Facing Materials via Machine Learning: Molybdenum Isotopes" Applied Sciences 11, no. 16: 7359. https://doi.org/10.3390/app11167359
APA StyleHamid, M. A. B., Beh, H. G., Oluwatobi, Y. A., Chew, X. Y., & Ayub, S. (2021). Neutron-Induced Nuclear Cross-Sections Study for Plasma Facing Materials via Machine Learning: Molybdenum Isotopes. Applied Sciences, 11(16), 7359. https://doi.org/10.3390/app11167359






