Evaluation of the Erosion Characteristics for a Marine Pump Using 3D RANS Simulations
Abstract
:1. Introduction
2. Computational Model
2.1. Governing Equations
2.2. Erosion Model
2.3. Cavitation Model
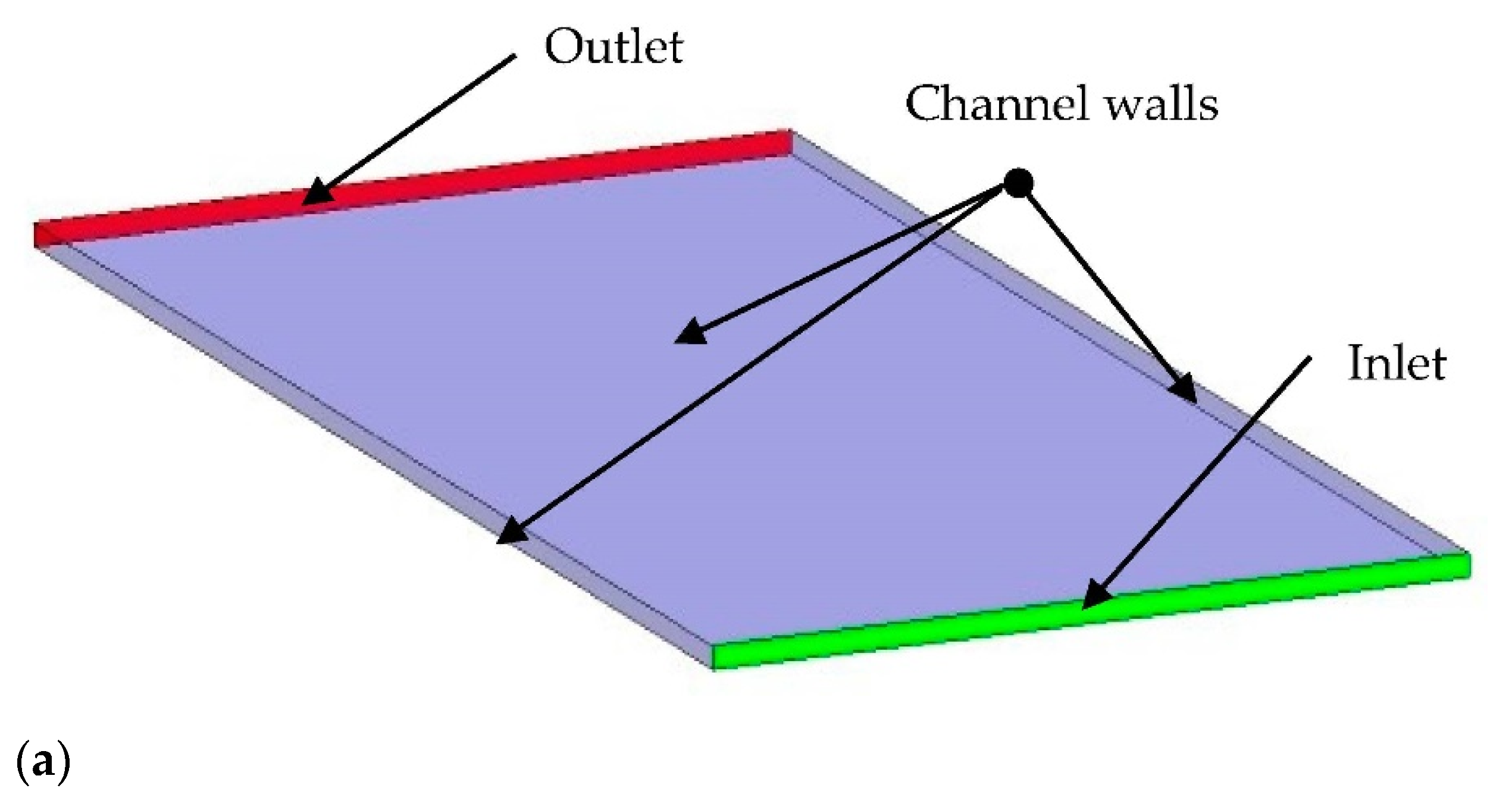
2.4. Computational Domain and Boundary Conditions
2.5. Mesh Generation
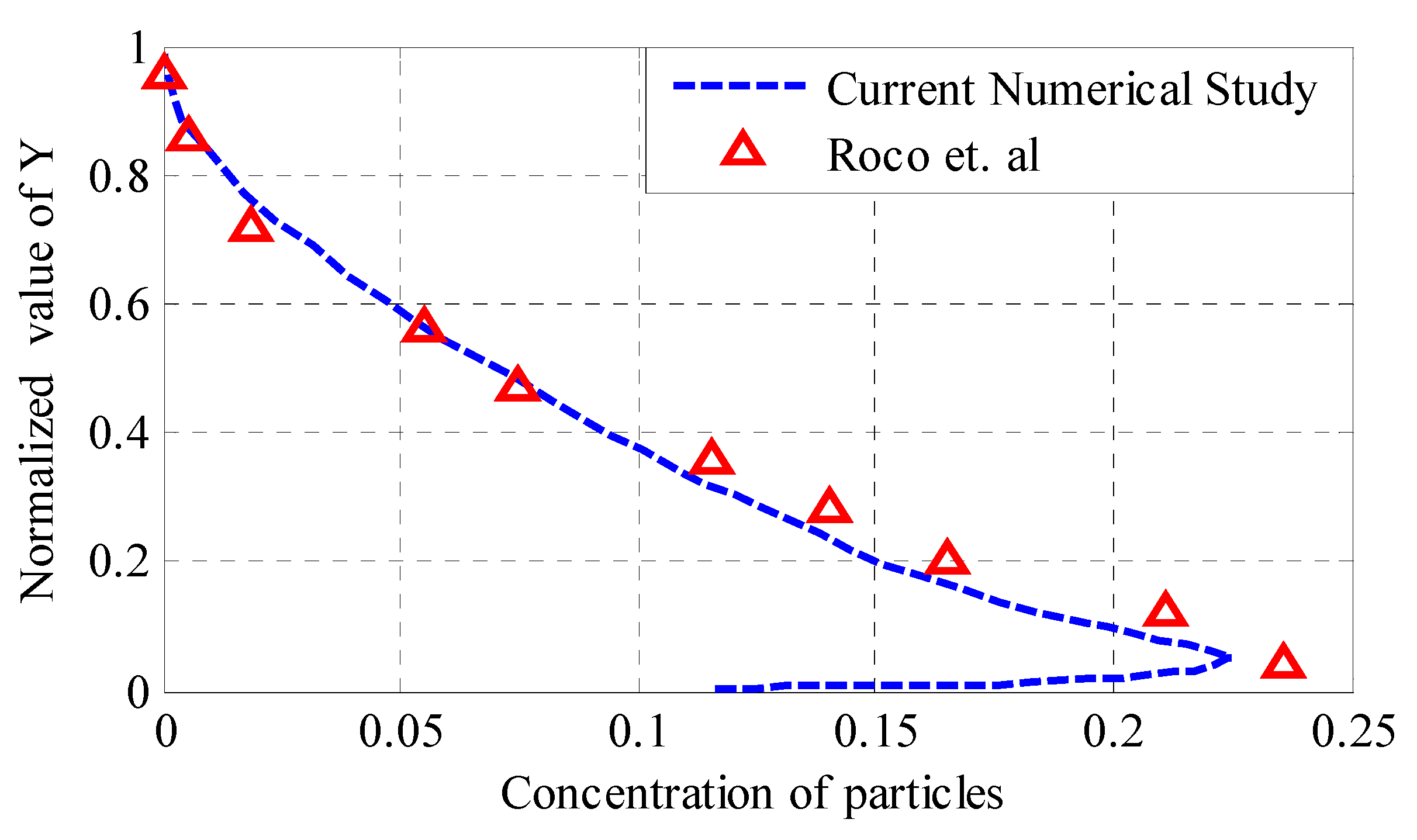
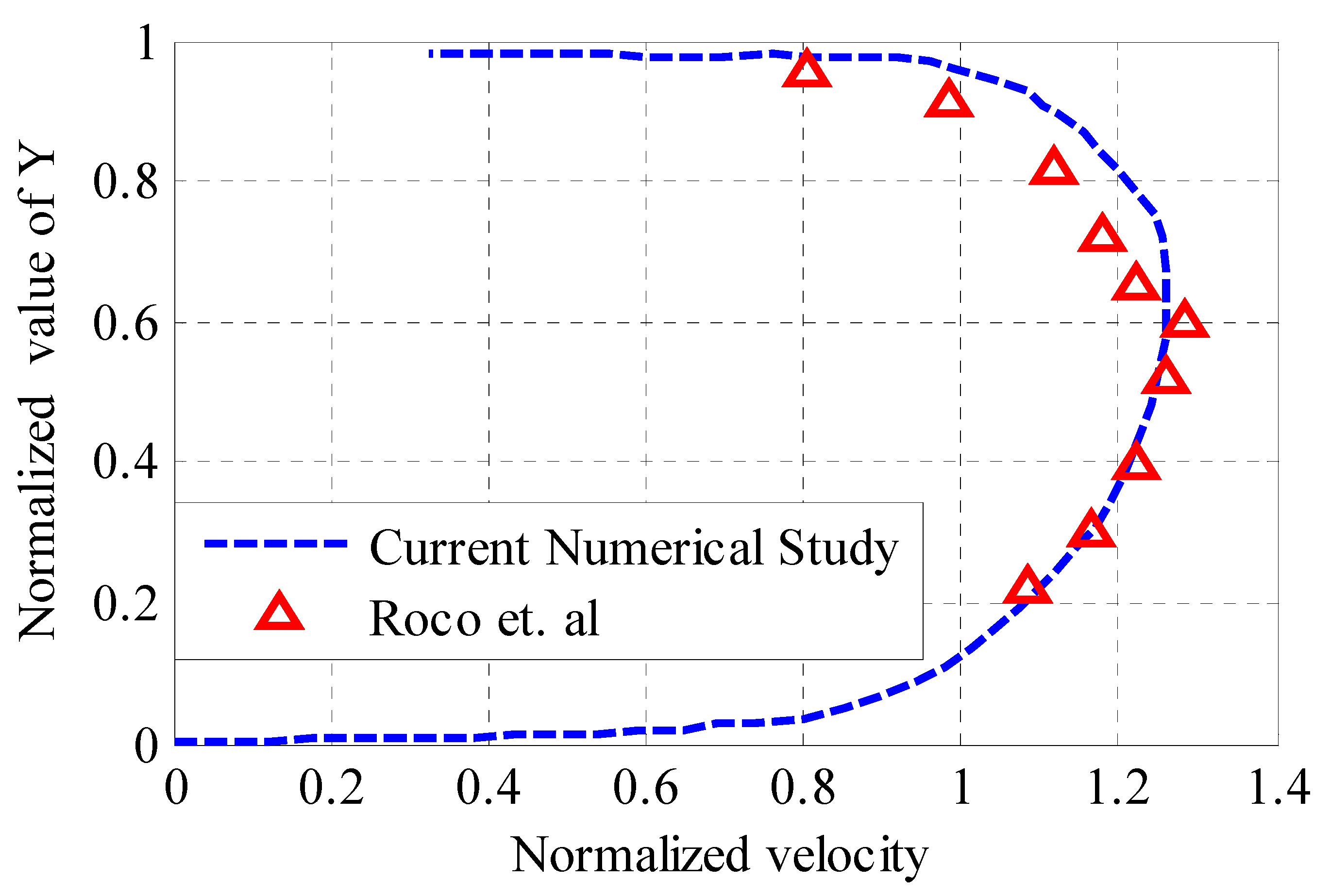
3. Validation of the Numerical Model
4. Results
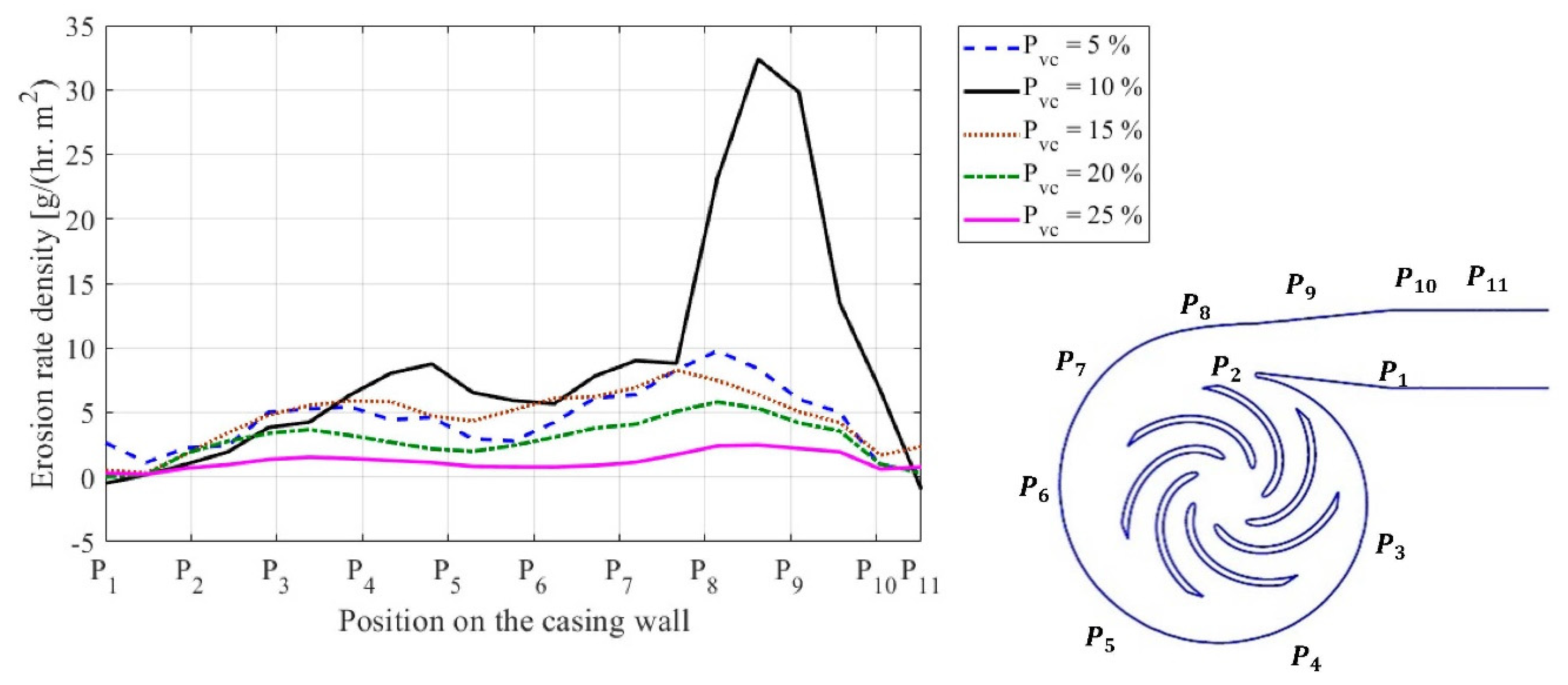
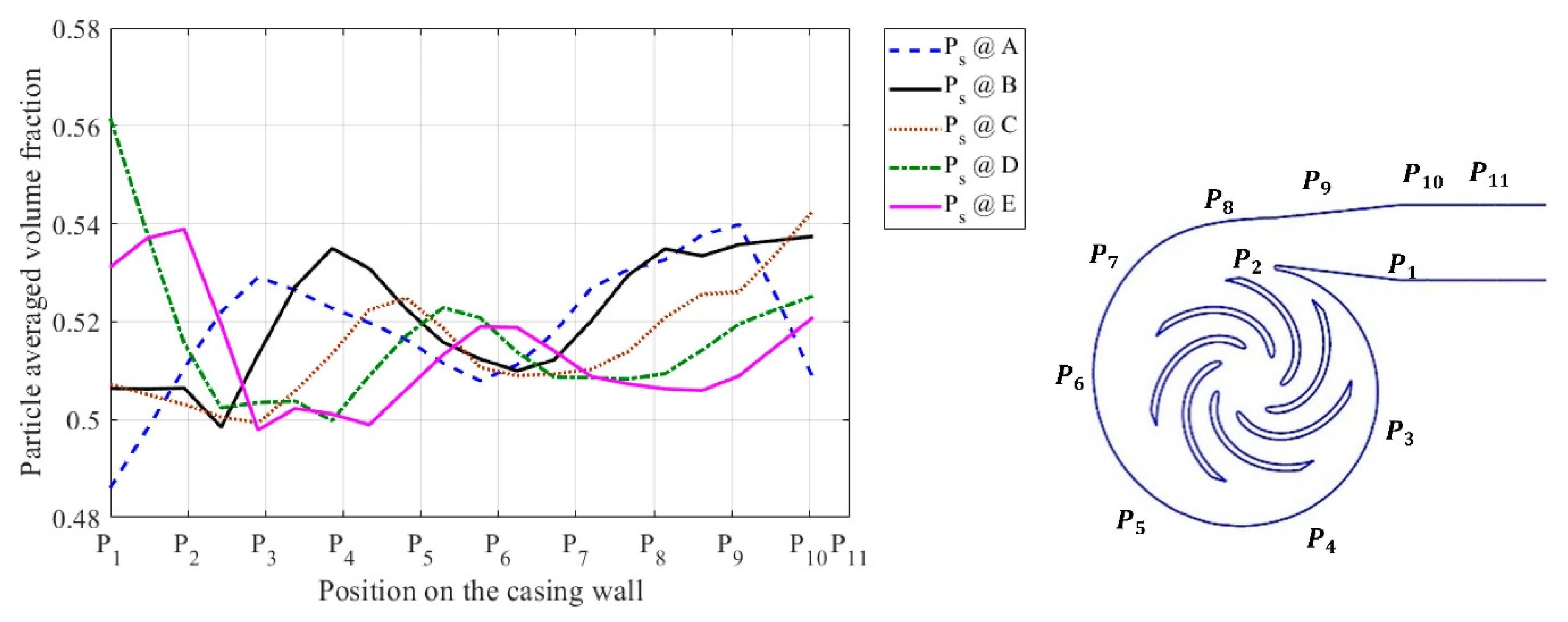
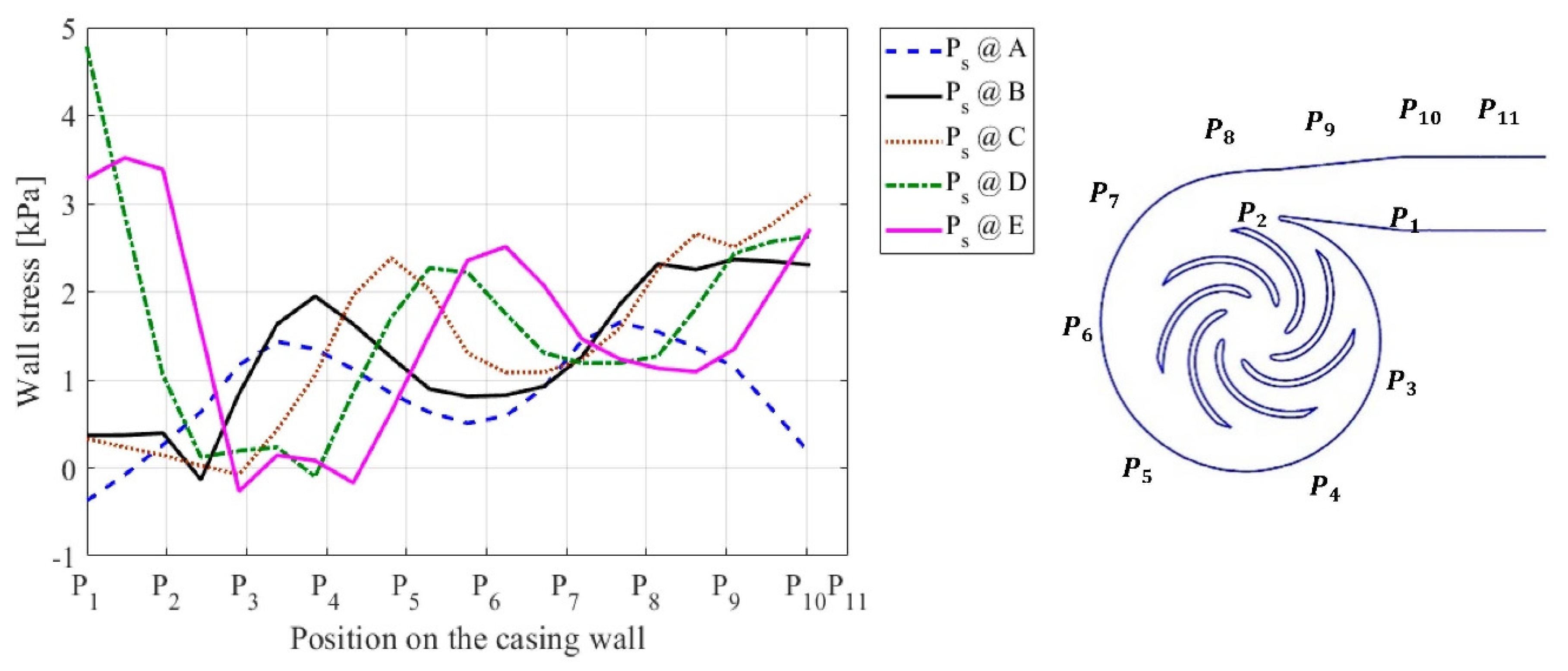
4.1. Effect of the Concentration of Solid Particles
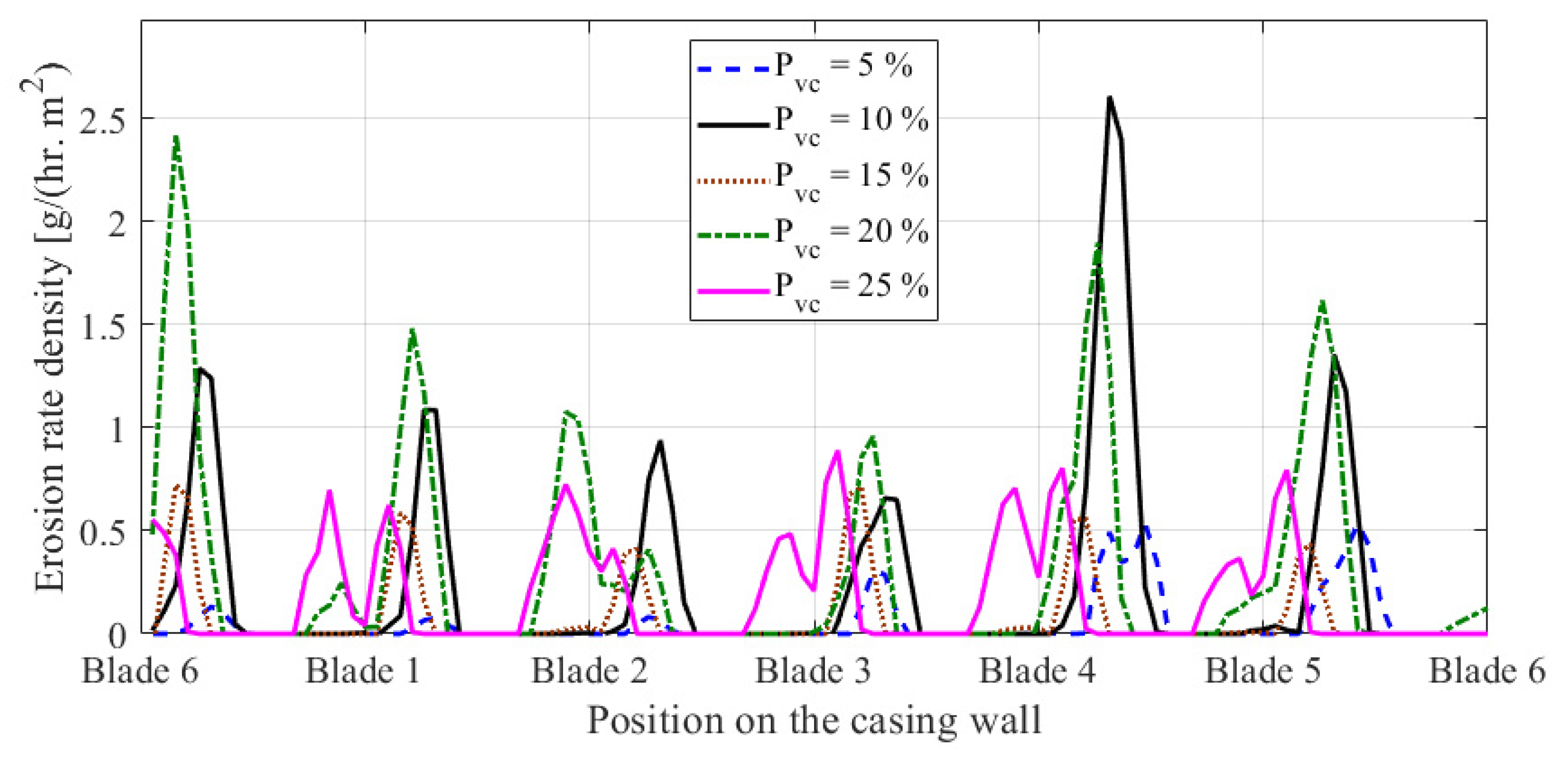
4.2. Effect of Particle Size
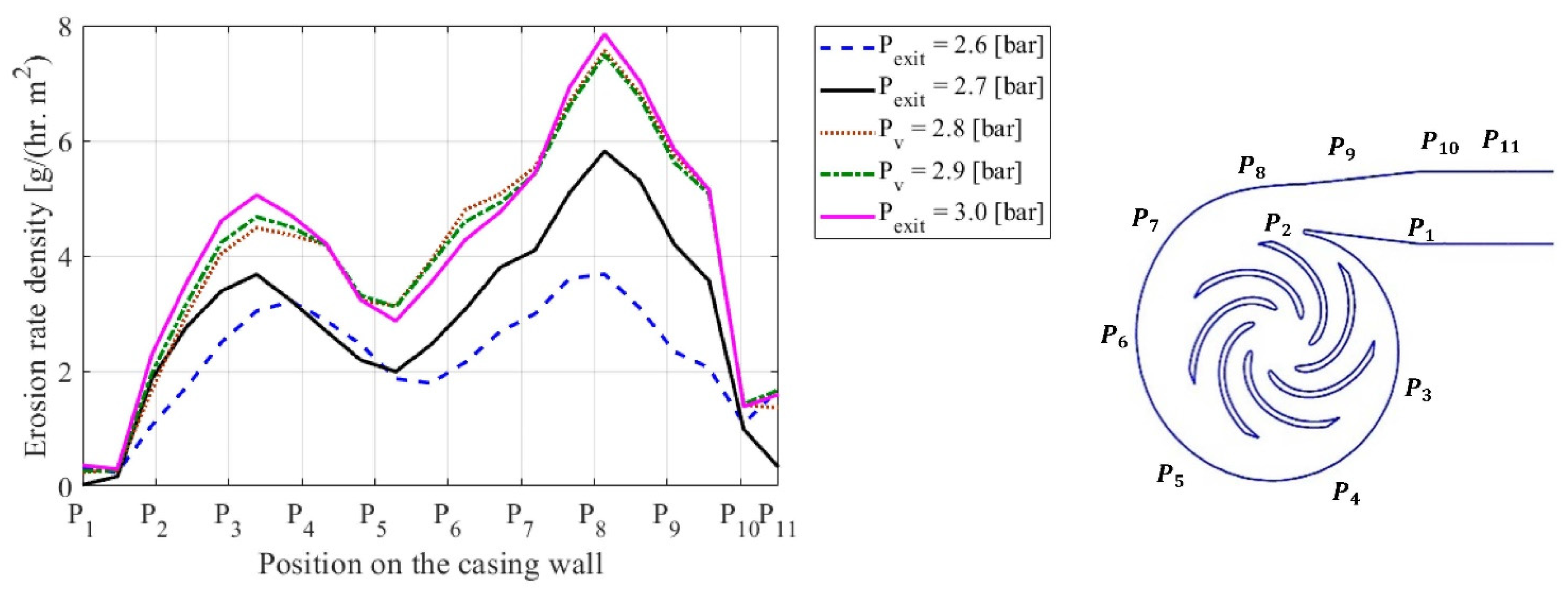
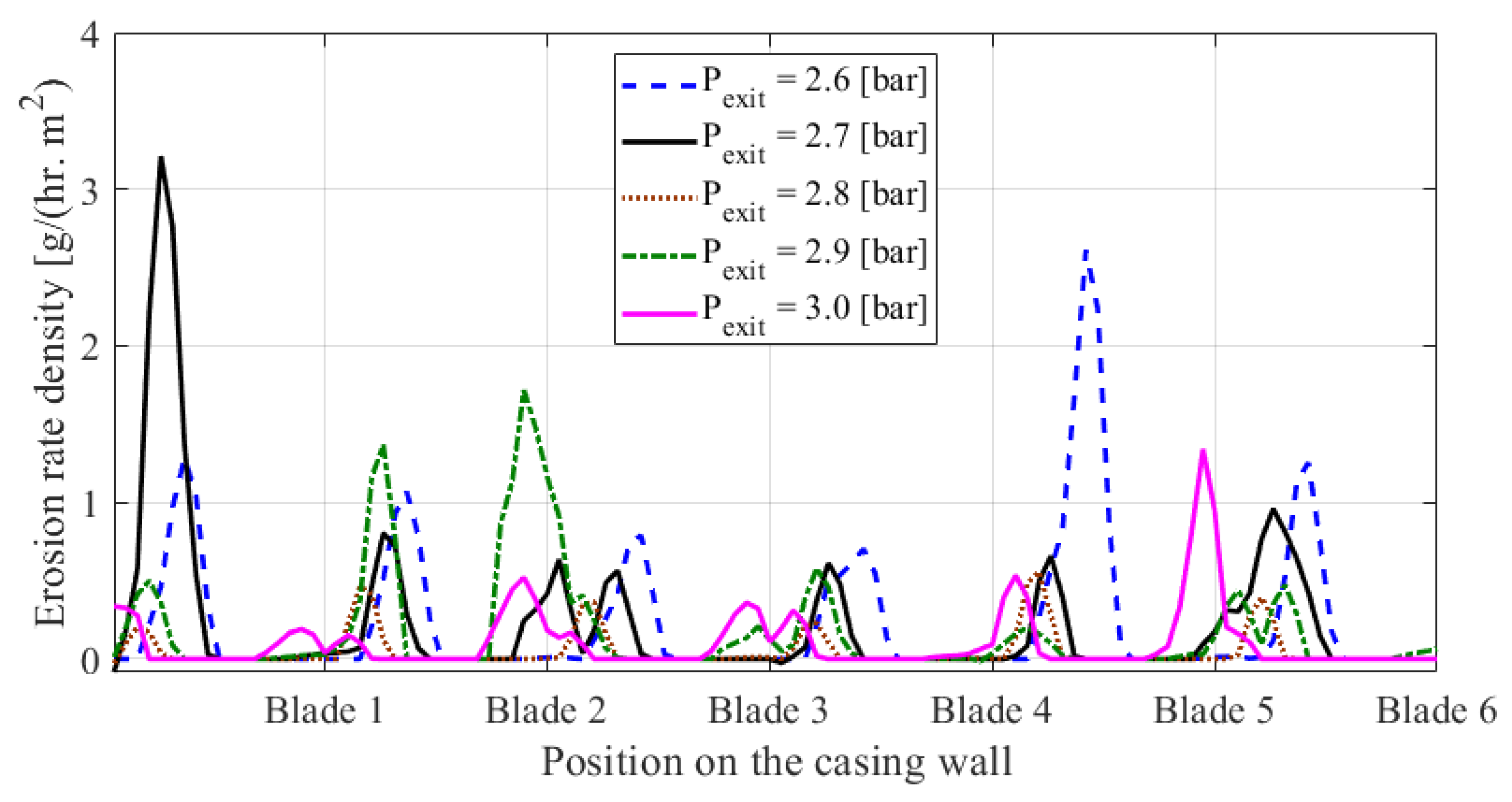
4.3. Effect of the Exit Pressure Head Conditions on Erosion Rates
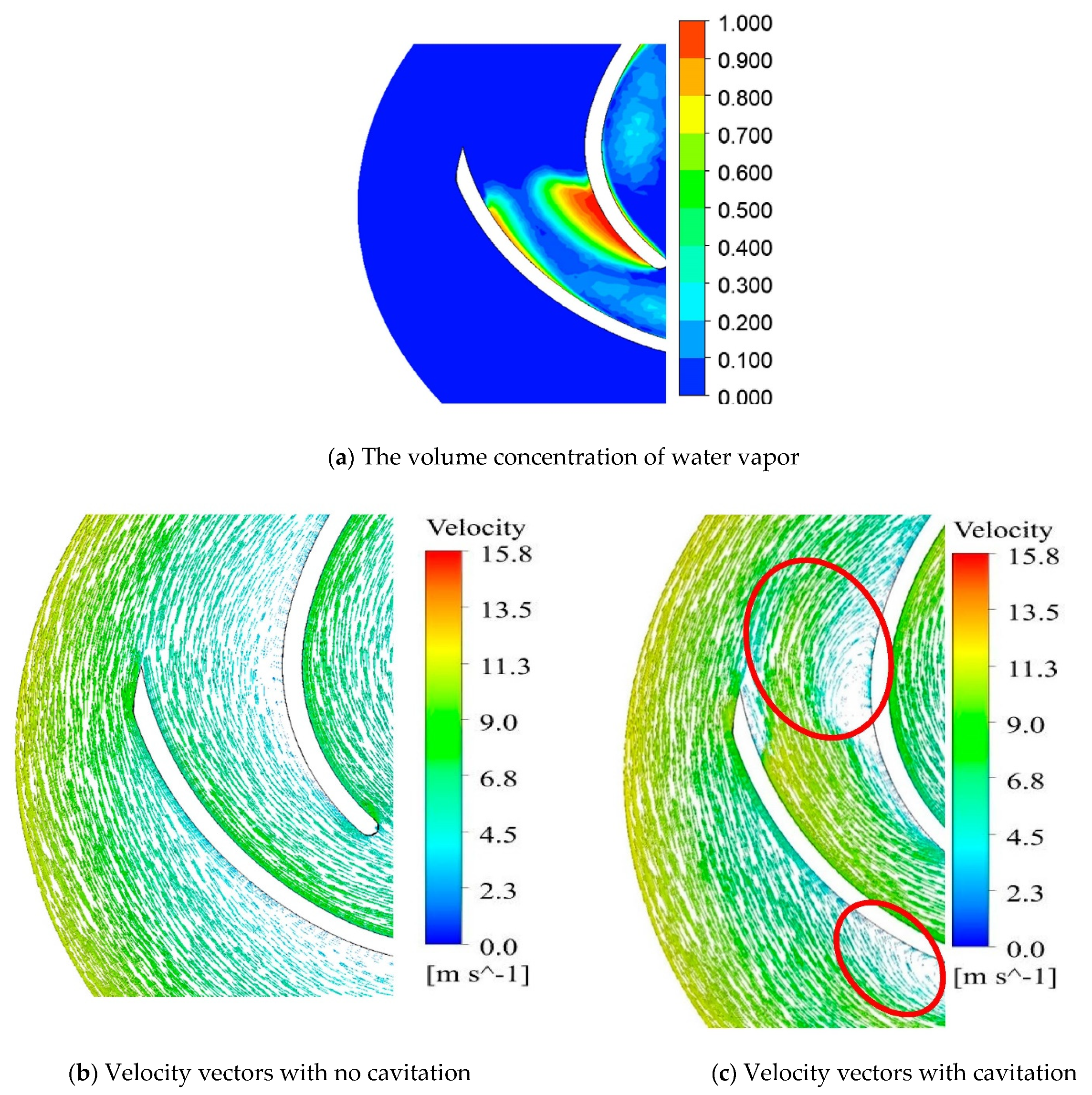
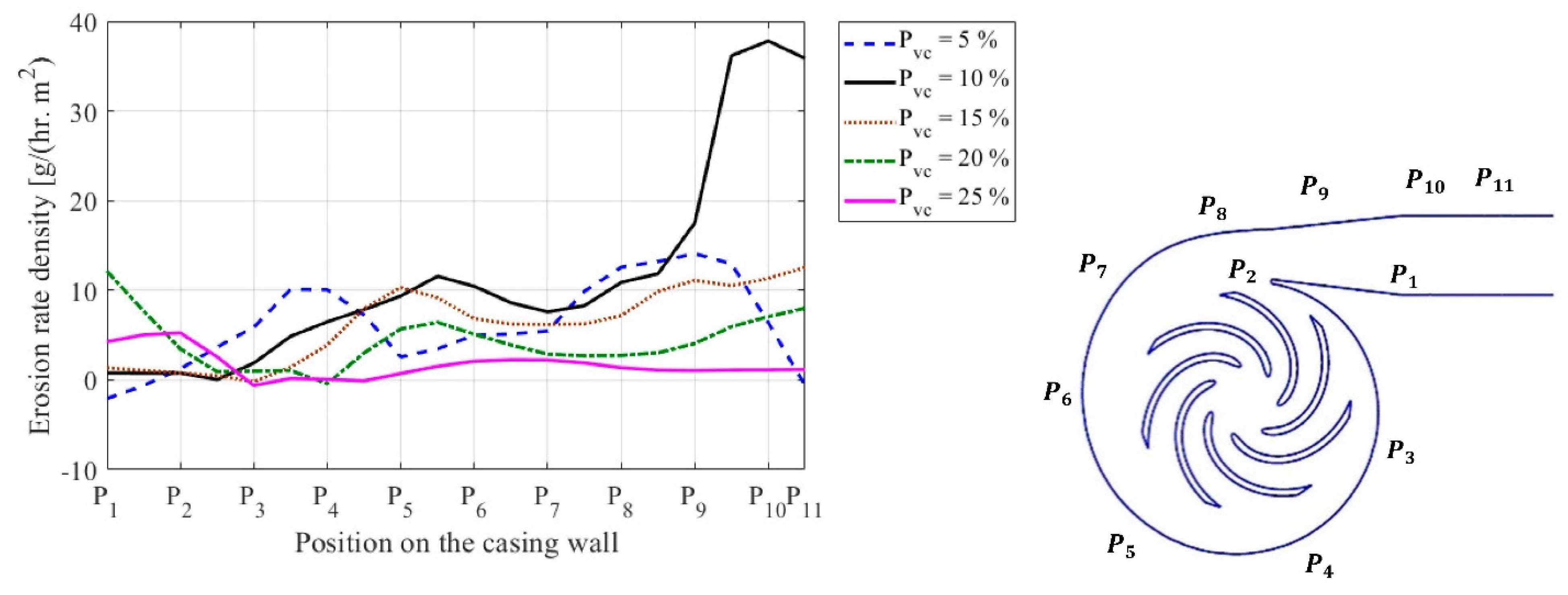
4.4. Effect of Cavitation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wilson, K.C. Principles of Particulate Slurry Flow. In Slurry Transport Using Centrifugal Pumps, 3rd ed.; Springer: New York, NY, USA, 2006; pp. 83–101. [Google Scholar]
- Wilson, K.C. Centrifugal Pumps. In Slurry Transport Using Centrifugal Pumps, 3rd ed.; Springer: New York, NY, USA, 2006; pp. 190–226. [Google Scholar]
- Wilson, G. The Effects of Slurries on Centrifugal Pump Performance. In Fourth International Pump User Symposium; 1987; pp. 19–26. Available online: http://turbolab.tamu.edu/proc/pumpproc/P4/P419-25.pdf (accessed on 15 February 2021).
- Roco, M.C.; Cader, T. Numerical Method to Predict Wear Distribution in Slurry Pipelines. In Advances in Pipe; Protection, G., Thorns, J.J., Eds.; BHRA Fluid Engineering: Cranfield, UK, 1988; pp. 53–85. [Google Scholar]
- Roco, J.; Nair, M.C.; Addie, P.; Dennis, G.R. Erosion of concentrated slurry in turbulent flow. ASME FED 1984, 13, 69–77. [Google Scholar]
- Minemura, T.; Uchiyama, K. Calculation of the Three-Dimensional Behavior of Spherical Solid Particles Entrained in a Radial-Flow Impeller Pump. Proc. Int. Mech. Eng. 1990, 204, 159–166. [Google Scholar]
- Roco, C.; Addie, G.R. Analytical Model and Experimental studies on Slurry flow and erosion in pump casings. Slurry Transp. 1983, 8, 263–275. [Google Scholar]
- Roco, R.J.; Addie, M.C.; Visintainer, G.R. Study of Casing Performances in Centrifugal Slurry Pumps. Part. Sci. Technol. 1985, 3, 65–88. [Google Scholar] [CrossRef]
- Pagalthivarthi, K.V.; Ravi, M.R.; Gupta, P.K.; Tyagi, V. CFD Prediction of Erosion Wear in Centrifugal Slurry Pumps for Dilute Slurry Flows. J. Comput. Multiph. Flows 2011, 3, 225–245. [Google Scholar] [CrossRef] [Green Version]
- Zhong, Y.; Minemura, K. Measurement of erosion due to particle impingement and numerical prediction of wear in pump casing. Wear 1996, 199, 36–44. [Google Scholar] [CrossRef]
- Addie, J.R.; Pagalthivarthi, G.R.; Kadambi, K.V. PIV and Finite Element Comparisons of Particles Inside a Slurry Pump Casing. In Proceedings of the International Conference on Hydrotransport 16, Santiago, Chile, 26–28 April 2004; pp. 547–559. [Google Scholar]
- Charoenngam, G.R.; Subramanian, P.; Kadambi, A.; Addie, J.R. Investigations of Slurry Flow in a Centrifugal Pump Using Particle Image Velocimetry. In Proceedings of the 4th International conference on multiphase flow, New Orleans, LA, USA, 27 May–1 June 2001. [Google Scholar]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method; Pearson Education: London, UK, 2007. [Google Scholar]
- Pagalthivarthi, K.V.; Gupta, P.K.; Tyagi, V.; Ravi, M.R. CFD Predictions of Dense Slurry Flow in Centrifugal Pump Casings. World Acad. Sci. Eng. Technol. Int. J. Mech. Aerospace, Ind. Mechatron. Manuf. Eng. 2011, 5, 538–550. Available online: https://www.waset.org/Publications/cfd-predictions-of-dense-slurry-flow-in-centrifugal-pump-casings/3699?p=2 (accessed on 14 March 2017).
- Brown, G. Use of CFD to Predict and Reduce Erosion in an Industrial Slurry Piping System. Available online: http://www.cfd.com.au/cfd_conf06/PDFs/073Bro.pdf (accessed on 11 March 2017).
- Saeed, M.; Berrouk, A.S.; Siddiqui, M.S.; Awais, A.A. Effect of printed circuit heat exchanger’s different designs on the performance of supercritical carbon dioxide Brayton cycle. Appl. Therm. Eng. 2020, 179, 115758. [Google Scholar] [CrossRef]
- Saeed, M.; Alawadi, K.; Kim, S.C. Performance of Supercritical CO2 Power Cycle and Its Turbomachinery with the Printed Circuit Heat Exchanger with Straight and Zigzag Channels. Energies 2020, 14, 62. [Google Scholar] [CrossRef]
- Salim, M.S.; Saeed, M.; Kim, M.-H. Performance Analysis of the Supercritical Carbon Dioxide Re-compression Brayton Cycle. Appl. Sci. 2020, 10, 1129. [Google Scholar] [CrossRef] [Green Version]
- Menter, F.R.; Eloret, S. Zonal two equation kappa-omega turbulence models for aerodynamic flows. In Proceedings of the 23rd Fluid Dynamics, Plasmadynamics, and Lasers Conference, Orlando, FL, USA, 6–9 July 1993. [Google Scholar]
- Siddiqui, M.S.; Latif, S.T.M.; Saeed, M.; Rahman, M.; Badar, A.W.; Hasan, S.M. Reduced order model of offshore wind turbine wake by proper orthogonal decomposition. Int. J. Heat Fluid Flow 2020, 82, 108554. [Google Scholar] [CrossRef]
- Saeed, M.; Berrouk, A.S.; Siddiqui, M.S.; Awais, A.A. Numerical investigation of thermal and hydraulic characteristics of sCO2-water printed circuit heat exchangers with zigzag channels. Energy Convers. Manag. 2020, 224, 113375. [Google Scholar] [CrossRef]
- Ha, S.T.; Ngo, L.C.; Saeed, M.; Jeon, B.J.; Choi, H. A comparative study between partitioned and monolithic methods for the problems with 3D fluid-structure interaction of blood vessels. J. Mech. Sci. Technol. 2017, 31, 281–287. [Google Scholar] [CrossRef]
- Saeed, M.; Awais, A.A.; Berrouk, A.S. CFD aided design and analysis of a precooler with zigzag channels for supercritical CO2 power cycle. Energy Convers. Manag. 2021, 236, 114029. [Google Scholar] [CrossRef]
- Saeed, M.; Berrouk, A.S.; AlShehhi, M.S.; AlWahedi, Y.F. Numerical investigation of the thermohydraulic characteristics of microchannel heat sinks using supercritical CO2 as a coolant. J. Supercrit. Fluids 2021, 176, 105306. [Google Scholar] [CrossRef]
- Awais, A.A.; Saeed, M.; Kim, M.-H. Performance enhancement in minichannel heat sinks using supercritical carbon dioxide (sCO2) as a coolant. Int. J. Heat Mass Transf. 2021, 177, 121539. [Google Scholar] [CrossRef]
- Cai, X.; Gu, R.; Pan, P.; Zhu, J. Unsteady aerodynamics simulation of a full-scale horizontal axis wind turbine using CFD methodology. Energy Convers. Manag. 2016, 112, 146–156. [Google Scholar] [CrossRef]
- Sayed, M.A.; Kandil, H.; Shaltot, A. Aerodynamic analysis of different wind-turbine-blade profiles using finite-volume method. Energy Convers. Manag. 2012, 64, 541–550. [Google Scholar] [CrossRef]
- Sørensen, N.N.; Michelsen, J.A.; Schreck, S. Navier-Stokes predictions of the NREL phase VI rotor in the NASA Ames 80 ft × 120 ft wind tunnel. Wind. Energy 2002, 5, 151–169. [Google Scholar] [CrossRef]
- Saeed, M.; Kim, M.-H. Thermal and hydraulic performance of SCO2 PCHE with different fin configurations. Appl. Therm. Eng. 2017, 127, 975–985. [Google Scholar] [CrossRef]
- Saeed, M.; Kim, M.-H. Airborne wind turbine shell behavior prediction under various wind conditions using strongly coupled fluid structure interaction formulation. Energy Convers. Manag. 2016, 120, 217–228. [Google Scholar] [CrossRef]
- Saeed, M.; Kim, M.-H. Aerodynamic performance analysis of an airborne wind turbine system with NREL Phase IV rotor. Energy Convers. Manag. 2017, 134, 278–289. [Google Scholar] [CrossRef]
- Van Bussel, G.J.W. The science of making more torque from wind: Diffuser experiments and theory revisited. J. Phys. Conf. Ser. 2007, 75, 012010. [Google Scholar] [CrossRef]
- Hansen, M.O.L.; Sørensen, N.N.; Flay, R.G.J. Effect of Placing a Diffuser around a Wind Turbine. Wind. Energy 2000, 3, 207–213. [Google Scholar] [CrossRef]
- Hutchings, I. Mechanical and metallurgical aspects of the erosion of metals. In Proceedings of the International Conference on Corrosion-Erosion of Coal Conversion System Materials, Berkeley, CA, USA, 24–26 January 1979; pp. 393–427. [Google Scholar]
- Finnie, I. Some observations on the erosion of ductile metals. Wear 1972, 19, 81–90. [Google Scholar] [CrossRef]
- Franc, J.P. The Rayleigh-Plesset equation: A simple and powerful tool to understand various aspects of cavitation. In Fluid Dynamics of Cavitation and Cavitating Turbopumps; Springer: Berlin/Heidelberg, Germany, 2007; pp. 1–41. [Google Scholar]
- ANSYS CFX. CFX-Pre User’s Guide Release 16.0; Ansys Inc.: Canonsburg, PA, USA, 2015. [Google Scholar]
- Siddiqui, M.S.; Khalid, M.H.; Zahoor, R.; Butt, F.S.; Saeed, M.; Badar, A.W. A numerical investigation to analyze effect of turbulence and ground clearance on the performance of a roof top vertical-axis wind turbine. Renew. Energy 2021, 164, 978–989. [Google Scholar] [CrossRef]


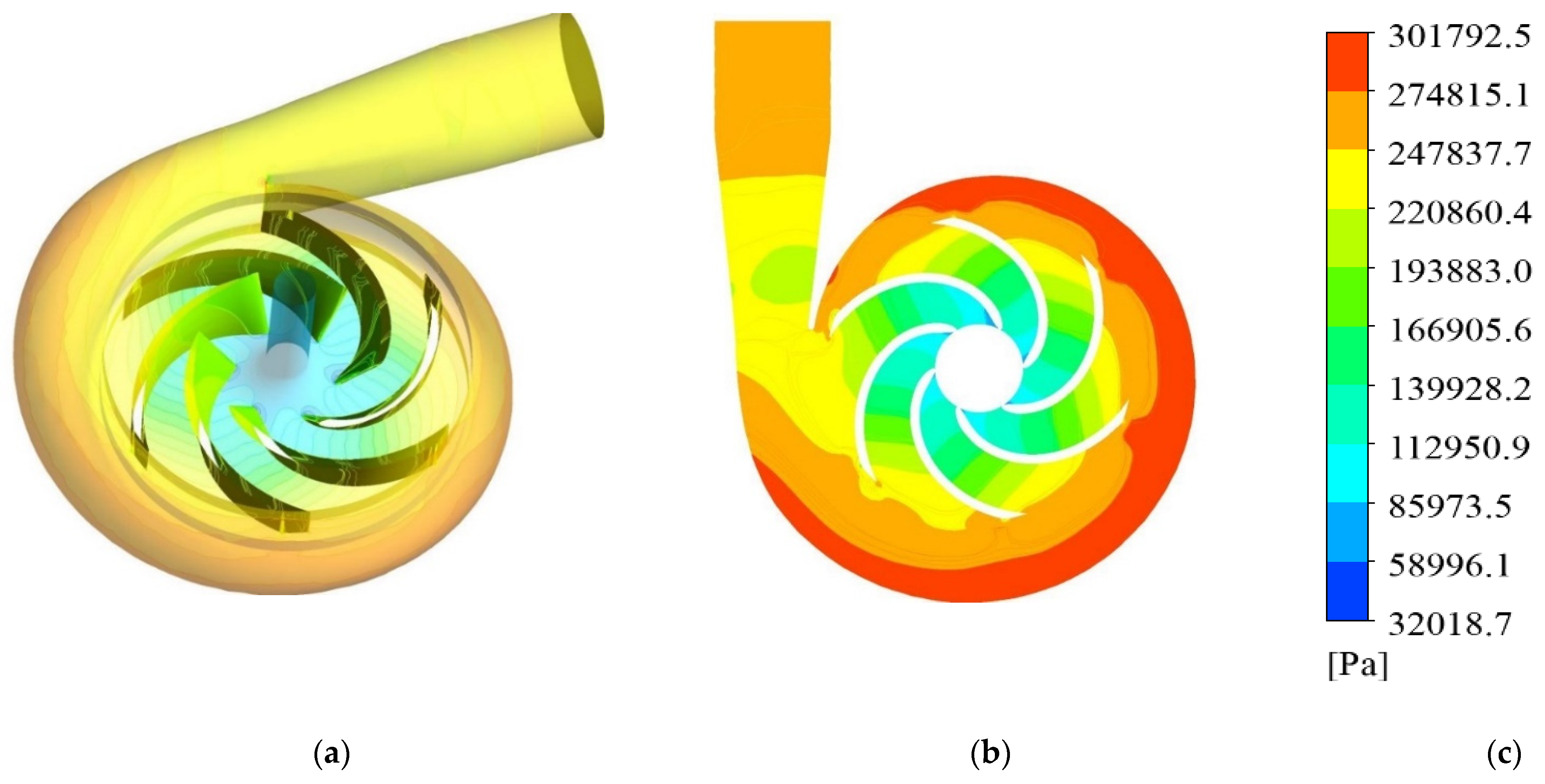

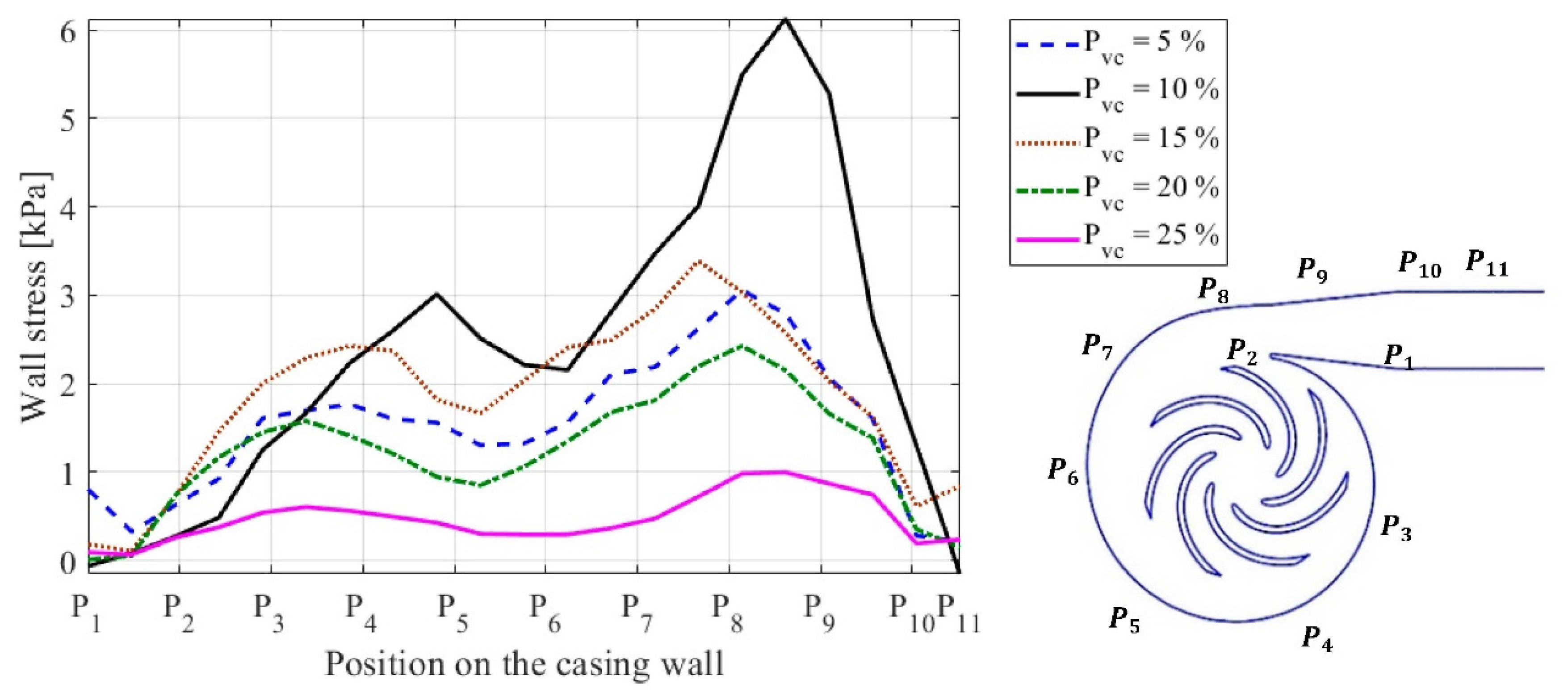
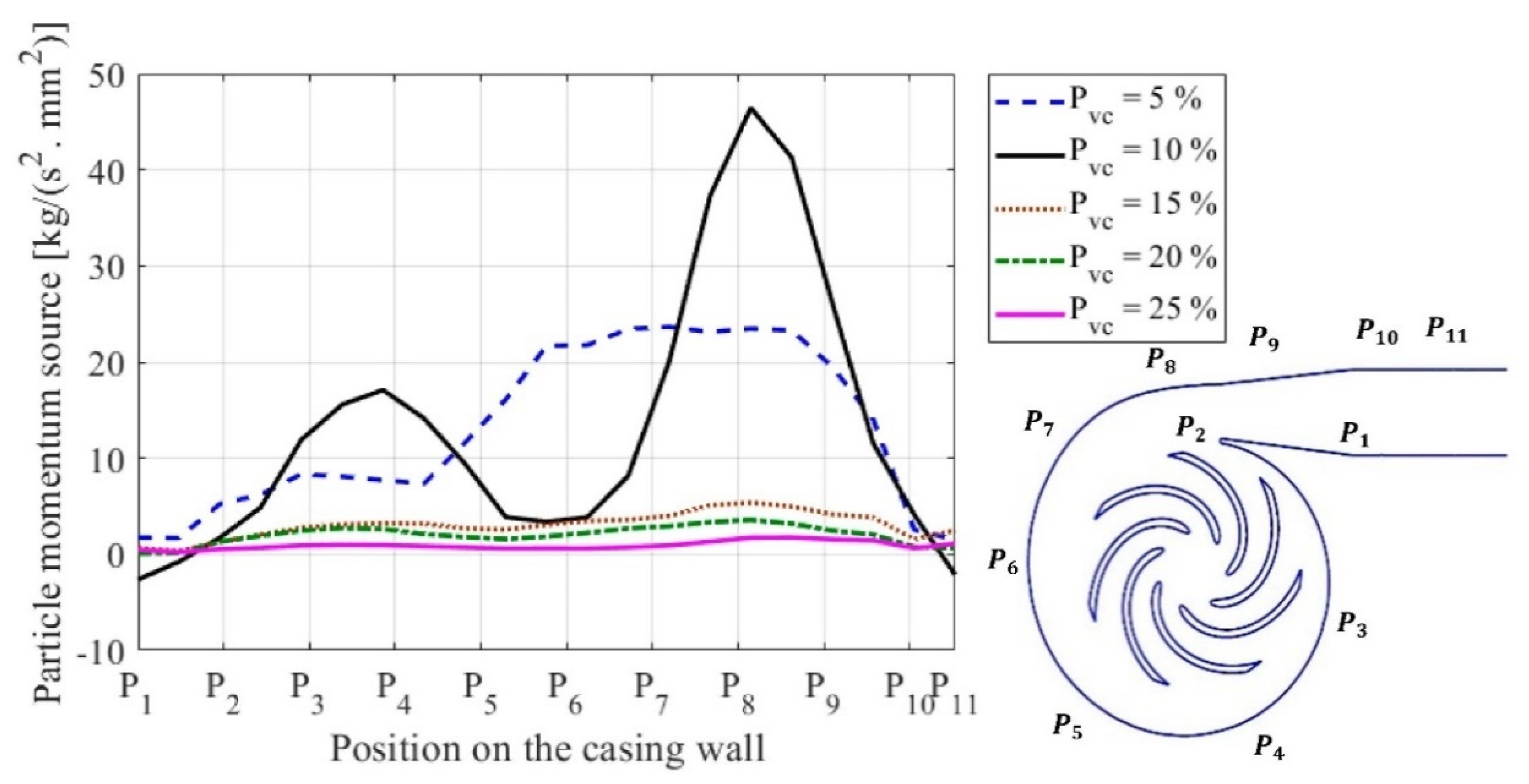
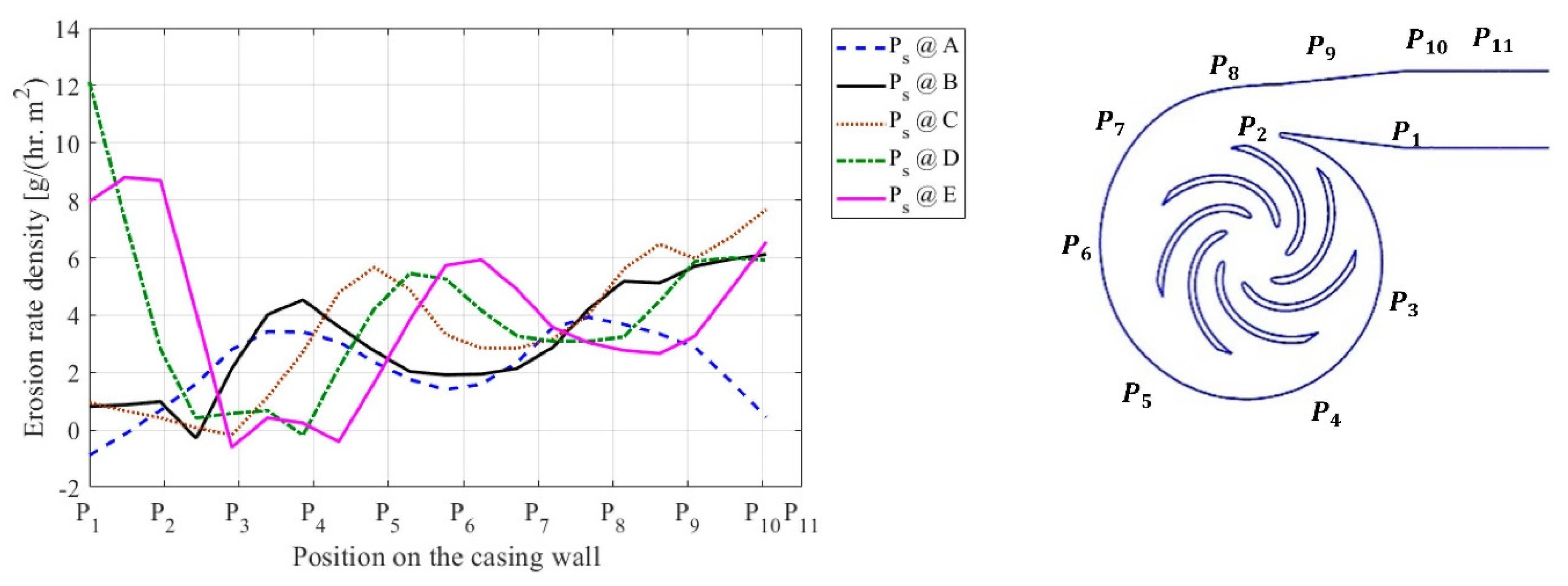
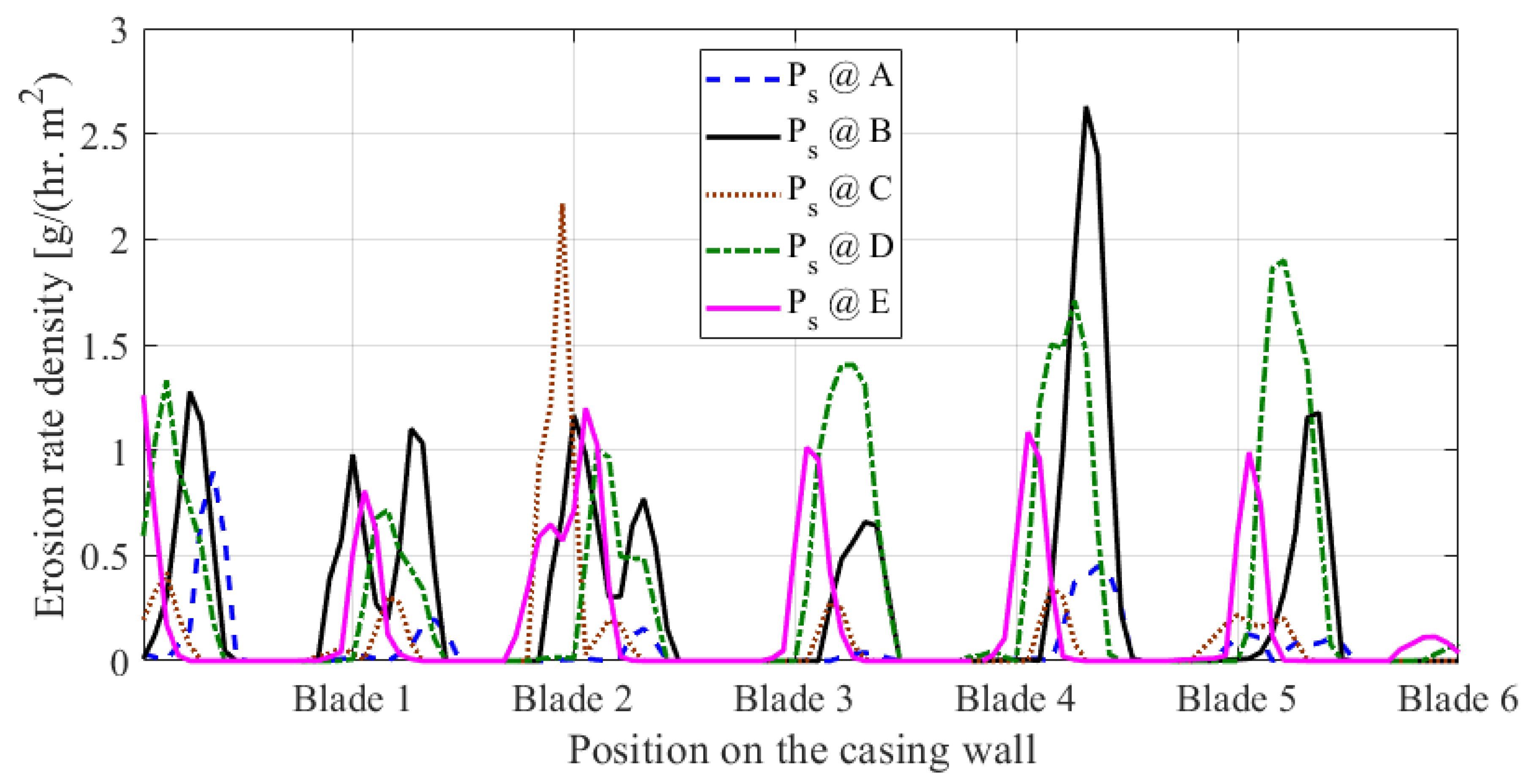
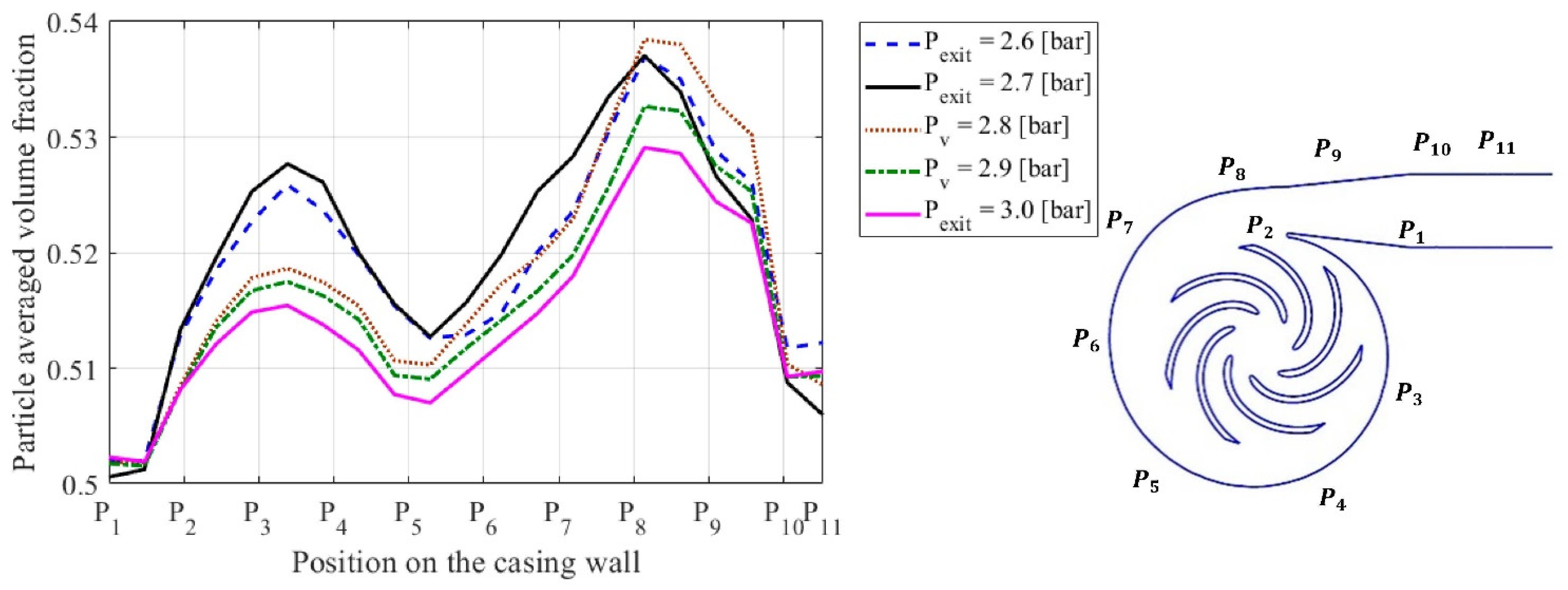
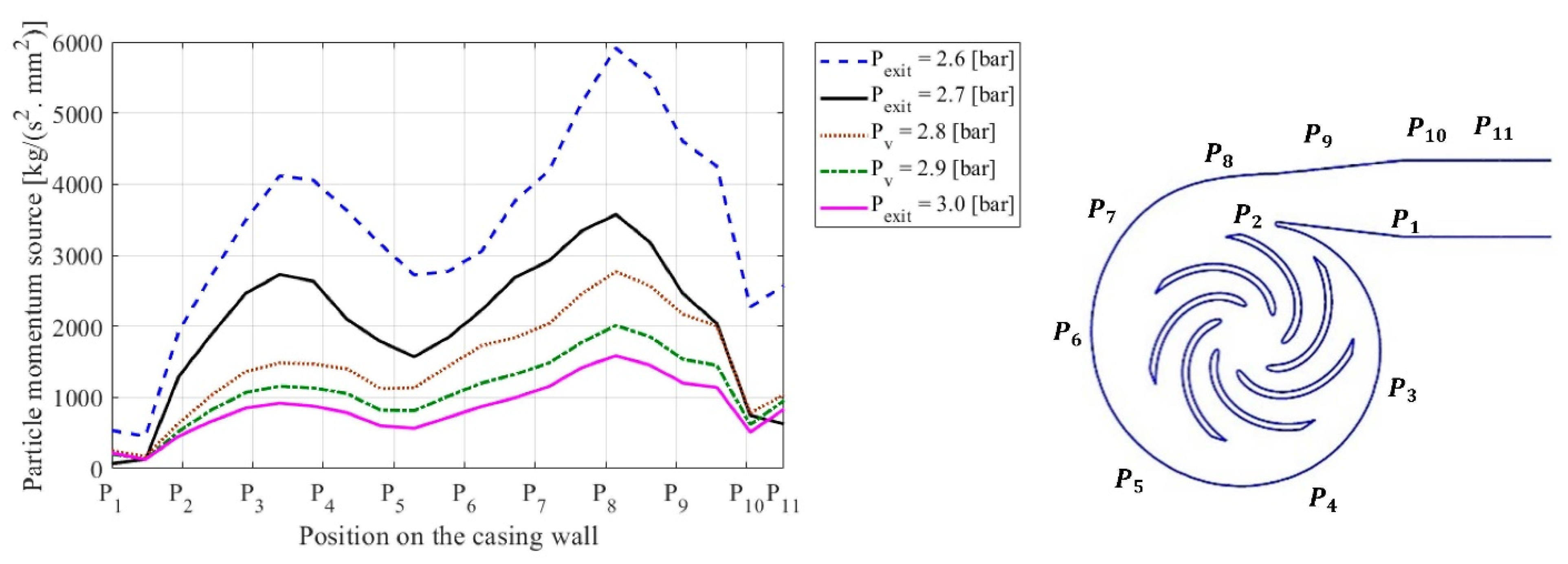
| Simulations | Exit Pressure | Particle Concentration | Particle Distribution [m] | |||||
|---|---|---|---|---|---|---|---|---|
| Min | Min | Max | Ave | Std. Dev. | ||||
| 1 | 2.6, 2.7, 2.8, 2.9, 3.0 | With cavitation and without cavitation | 5%, 7.5%, 10%, 12.5%, 15%, 20%, 25% | Ps → A | 50 | 250 | 150 | 120 |
| Ps → B | 100 | 500 | 300 | 120 | ||||
| Ps → C | 150 | 750 | 450 | 120 | ||||
| Ps → D | 200 | 1000 | 600 | 120 | ||||
| Ps → E | 250 | 1250 | 750 | 120 | ||||
| Rotating Domain (Impeller) | Stationary Domain (Casing) | Number of Nodes | Memory Allocate [MB] | Computation Time for Ten Iterations | Computed Pump Power [kW] | ||||
|---|---|---|---|---|---|---|---|---|---|
| Mesh | Division along with the Blade Height | Divisions in the O-Grid Region | Divisions in the Tip Clearance Region | Divisions in the Inlet Domain | Element Size in the Stationary Domain | ||||
| M1 | 35 | 10 | 5 | 15 | 0.003 | 1,025,341 | 11,325 | 57 | 11.2 |
| M2 | 45 | 20 | 7 | 20 | 0.002 | 1,523,452 | 18,256 | 97 | 10.7 |
| M3 | 60 | 30 | 11 | 25 | 0.0015 | 2,742,863 | 35,261 | 195 | 9.26 |
| M4 | 70 | 40 | 15 | 30 | 0.001 | 3,929,536 | 47,325 | 310 | 9.19 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alawadhi, K.; Alzuwayer, B.; Alrahmani, M.; Murad, A. Evaluation of the Erosion Characteristics for a Marine Pump Using 3D RANS Simulations. Appl. Sci. 2021, 11, 7364. https://doi.org/10.3390/app11167364
Alawadhi K, Alzuwayer B, Alrahmani M, Murad A. Evaluation of the Erosion Characteristics for a Marine Pump Using 3D RANS Simulations. Applied Sciences. 2021; 11(16):7364. https://doi.org/10.3390/app11167364
Chicago/Turabian StyleAlawadhi, Khaled, Bashar Alzuwayer, Mosab Alrahmani, and Ahmed Murad. 2021. "Evaluation of the Erosion Characteristics for a Marine Pump Using 3D RANS Simulations" Applied Sciences 11, no. 16: 7364. https://doi.org/10.3390/app11167364
APA StyleAlawadhi, K., Alzuwayer, B., Alrahmani, M., & Murad, A. (2021). Evaluation of the Erosion Characteristics for a Marine Pump Using 3D RANS Simulations. Applied Sciences, 11(16), 7364. https://doi.org/10.3390/app11167364





