A Multi-Objective Hybrid Genetic Algorithm for Sizing and Siting of Renewable Distributed Generation

Abstract

Renewable generation has been addressed in several aspects but it still represents a new paradigm for the expansion of the electricity supply. This paper aims to propose a new model for the sizing and siting problem of distributed generation (DG), based on renewable sources and considering three main aspects: technical, from the distribution utility viewpoint; economical, from the DG owner’s viewpoint, and environmental, from a sustainability perspective. A multi-objective Genetic Algorithm and the Maximin metric are implemented to obtain optimal Pareto sets; also, three decision criteria, considering the concept of preference, are applied to select a final solution from Pareto sets. Case-studies are carried out in medium voltage systems: the 69-bus distribution test system, known from literature, and a 918-bus Brazilian distribution system. Diversity of alternatives in the obtained Pareto sets testify algorithm effectiveness in searching for solutions to the distributed generation sizing and siting problem, in order to ensure power loss reductions, investment return, and environmental benefits. The proposed methodology contributes to the discussions and perspectives among electricity utilities, DG owners, society, and regulators regarding planning and decision making tools.

1. Introduction

Electrical power systems have been characterized by a centralized production, in which generation location is usually far from load centers, therefore requiring extensive and expensive transmission and distribution networks [1]. Currently, new opportunities provided by technological advances in reduced scale energy generation (on-site power generation) and regulatory changes have made possible the growth of the DG concept [2], leading to new challenges on power systems planning and operation due to the increased complexity of the systems resulting from DG insertions.

DG plants intrinsically bring some advantages to the electricity sector, such as load relief, reduction of technical losses, diversification of energy sources, stimulation of new technologies and a higher local equalization between energy offering and demand [3]. In addition, the DG concept represents new investment perspectives to the electricity market, foments the creation of new companies and originates new jobs and careers; furthermore, its growing represents a step to transform a passive customer into an active one.

Nonetheless, Distribution Companies (DisCo) have faced many challenges due to DG penetration, such as bidirectional power flows, rising of short-circuit levels, overvoltages, and overcurrents, islanding operation, and an increase in the operating scenarios caused by intermittence of some primary energy sources, e.g., sun, wind, and water [4]. As a result, the academic community has shown interest in these topics, dealing with them through diverse approaches, such as technical (from planning and operation viewpoint), economic, environmental, normative, and technological.

Therefore, many aspects can be considered in DG planning strategies. For example, concerning DG sizing, it is difficult to define an efficient modularization of a DG power plant, because every strategy is highly dependent on the DG concept adopted, like the ones described in [2,4,5,6,7]. Another aspect corresponds to DG siting, which can be done by selecting a bus in a specific network or among different networks. Also, DG benefits (single objective of interest) or benefit-sets can be used as criteria to DG siting/sizing planning and the target of the benefit DisCo, DG owners or final customers. Finally, network technical constraints associated to the system operation, as well as local regulations, especially about whom is the decision-maker, can also be fundamental issues.

Several works in the technical literature address studies regarding DG planning in distribution networks by different methods and with different objectives. Firstly, Genetic Algorithms (GA) and Particle Swarm Optimization (PSO) have been prominent in DG studies. In ref. [8], a methodology based on fuzzy-GA to improve voltage stability margin and net income is presented. In ref. [9], a hybrid GA with PSO is applied to reduce energy losses and voltage variation and improve a voltage stability index. Similarly, in ref. [10] a hybrid GA with a technique for order preference by similarity to the ideal solution to reduce energy losses and improve voltage profile is proposed. In ref. [11], a multi-objective GA to reduce DisCo costs is presented, and finally, in ref. [12], a multi-objective PSO to increase DG owner net income and to reduce DisCo costs is also proposed.

Other methods have also been applied to deal with the referred problem. In ref. [13], an artificial bee colony algorithm is used to minimize active energy losses. Moreover, ant colony optimization to minimize DG owner’s cost and energy active losses is proposed in [14,15], respectively. In ref. [16], the authors present an ant colony optimization to reduce DG owner cost, and a cuckoo search algorithm is applied to reduce energy losses in [17].

Combinations of analytical methods and evolutionary algorithms have also been proposed for DG planning. For example, the Branch-and-bound method is applied in [18] to reduce distribution expansion costs. Differential evolution is used in [19] to solve the DG planning problem in order to increase net income. Dynamic programming in [20] is applied for DG allocation in such a way as to increase the DisCo benefits. Additionally, the teaching–learning-based optimization algorithm is proposed in [21] to reduce energy losses and improve voltage profile and voltage stability. A hybrid evolutionary algorithm with game theory to maximize DG owner net income and reduce energy losses; voltage variation stability index and energy cost is presented in [22]. Pareto frontier differential evolution to reduce energy losses and voltage variation and to improve voltage stability is proposed in [23]. Finally, mixed-integer linear programming via CPLEX to increase the DG owner’s net income and reduce DisCo cost is considered in [24].

As a contribution to this line of research, a multi-objective analysis for the DG sizing and siting problem in distribution networks and three simple decision making strategies are carried out in this work, aiming at common good among perspectives of concern. The main features and contributions of this work are described as follows:

• Three objective functions are considered regarding the proposed multi-objective model: energy losses as a technical aspect; DG plant installation costs as an economic aspect; and equivalent CO₂ emission as an environmental concern of society. To the best of the authors knowledge these objective functions have not been simultaneously considered in the way they are approached in this paper.
• A new multi-objective solution methodology based on Genetic Algorithm combined with Maximin metric, named in this work as Multi-Objective Hybrid Genetic Algorithm (MOHGA), are implemented to obtain optimal Pareto sets of solution alternatives.
• Max-Min approximation as non-preference criterion and Minimal power losses and maximum net present value as preference criteria are applied as decision making strategies to select final solutions from obtained optimal Pareto sets.
• The approach robustness allows the application of proposed methodology in real-size distribution networks, as evidenced by the results with 918-bus Brazilian network.

To address the proposed modeling for DG sizing and siting problem and the adopted solution process, the following assumptions are made in this work:

• Only renewable energy sources are considered (hydraulic, wind, and photovoltaic).
• Network connection buses and maximum capacity (divided in modules) of generators are known data of the problem, in order to take into account proper conditions such as available source of energy, environmental restrictions, and occupation area.
• Maximum capacity for DG plants is set in 5 MW, since it covers common regulations (specifically, in Brazil, this value corresponds to the maximum allowed for DG’s).

This paper is organized as follows: the proposed multi-objective optimization model and solution method are addressed in Section 2; Section 3 presents the results and analysis performed in the two networks as case studies, whose main conclusions are drawn in Section 4.

2. Modeling and Solution Strategies

This section presents the modeling of the proposed hybrid genetic algorithm. The nomenclature can be consulted in Appendix A.

In general terms, a multi-objective optimization problem consists of solving two or more usually conflicting objective functions, in which the decision variables must satisfy a set of equality, inequality and border constraints, as summarized in (1):

$$\begin{gathered} \mathrm{Minimize} F\left(x\right),\mathrm{where} F=\left[f_1,f_2,\dots ,f_{n_f}\right] \mathrm{and} x=\left[x_1,x_2,\dots ,x_{n_x}\right] \\ \mathrm{subject} \mathrm{to}\left\{\begin{array}{c}{g}_g\left(x\right)=0,g=1,\dots ,n_g \\ h_h\left(x\right)\le 0,h=1,\dots ,n_h \\ x_{min}\le x\le x_{max} \end{array}\right\} \end{gathered}$$

(1)

where n_f-dimensional vector $F$ is the set of objective-functions, n_x-dimensional vector x corresponds to the decision variables of the optimization problem, $g_g$ and $h_h$ functions are the equality and inequality constraint functions, respectively; finally, $x_{min}$ and $x_{max}$ are related to lower and upper boundaries, respectively, of each decision variable.

2.1. Multi-Objective Optimization Model

The DG sizing and siting problem addressed in this work assumes that the locations of accessible primary energy sources and the maximum generation capacity available for DG projects are previously known. Each DG plant n for a total number of N plants can install $ND{G}_n$ modules for a total number of $ND{G}_n^{max}$ modules, each one with capacity $P_n^{DG}$, such that the power output of each DG plant n is given by $ND{G}_n.P_n^{DG}$. Therefore, decision variable vector x of the optimization problem is composed by network buses and number of modules of each DG plant n, with total number 2 · N (size and site) of variables.

The vector of multi-objective functions ($F$) of the proposed modeling is formed by three objective functions ($f_1,$ $f_{2,}$ $f_3$). The first objective-function ($f_1$) represents an economical viewpoint and corresponds to minimize the total installation cost of DG plants ($C_{instal}$), obtained by Equation (2), where $C{O}_{instal}^n$ is the investment cost of the n-th DG plant, $ND{G}_n$ is the quantity of generation modules of the n-th DG plant to be installed and N is the total number of DG plants to be connected in the network. In this paper, installation cost data are mean overnight cost: 1497 USD/kWe for onshore wind, 1210 USD/kWe for photovoltaic plants, and 1492 USD/kWe for hydro [25].

$$C_{instal}={\displaystyle \sum }_{n=1}^{N}C{O}_{instal}^n . ND{G}_n$$

(2)

The second objective function ($f_2$) corresponds to the minimization of daily active power losses ($LA{E}_{daily}$ in MWh), which is one of the objectives most commonly considered in DG sizing and siting planning [26]. The required data to calculate branch currents are obtained by a backward/forward sweep load flow known by Power Summation Method (PSM) and the daily energy losses are calculated by Equation (3), where $r_{k-m}$ and $I_{k-m}$ are the resistance and current of the k-m branch, respectively; $N_T$ is the number of time intervals considered in the daily analysis, ${\Omega }_L$ is the set of distribution network branches, and $T_p$ is the duration of the time interval. In this case, time intervals of one hour are considered, aiming at a better discretization of daily consumption, although other time intervals can be considered in the modeling without significant changes in results.

$$f_2=LA{E}_{daily}={\displaystyle \sum }_{p=1}^{N_T}{\displaystyle \sum }_{k-m}^{{\Omega }_L}{r}_{k-m} .I_{k-m}^2{T}_p$$

(3)

The third objective function ($f_3$) reflects environmental concerns and corresponds to the minimization of daily amount of equivalent CO₂ emission $EqC{O}_{2}E$, given by Equation (4). CO₂ emission factors $EqC{O}_{2}EF$ are based on [27,28,29,30]: 21 gCO₂eq/kWh for onshore wind, 17 gCO₂eq/kWh for photovoltaic and 105 gCO₂eq/kWh for hydro, while adopted capacity factors cf are [26]: 0.18 for photovoltaic, 0.34 for onshore wind and 0.47 for hydro. In this case, $c{f}_n$ is the capacity factor of the n-th DG plant and $P_n^{DG}$ is the active power capacity for each module of the n-th DG plant.

$$EqC{O}_{2}E={\displaystyle \sum }_{p=1}^{N_T}{\displaystyle \sum }_{n=1}^{N}c{f}_n.P_n^{DG}.ND{G}_n.EqC{O}_{2}E{F}_n{T}_p$$

(4)

It should be noted that a greater number of DG modules results in higher installation costs and CO₂ emissions; nonetheless, dispersed generation in distribution systems represents load reductions and, therefore, provides power loss reductions. Thus, minimization of installation costs and CO₂ emissions are conflicting with minimization of power losses.

Daily generation curves for each primary energy source (solar, hydro, and wind) and daily load curves for the three consumer classes (residential, commercial, and industrial) assumed in this work for power flow simulations are presented in Figure 1. These curves are based on Brazilian DG plants and load characteristics and can be changed according to local characteristics, although generation curves were based on the capacity factors.

Equality constraints (g) are referred to the power balance in system nodes, as shown in [27,29,31], and defined in this work as $PS{M}_{\mathrm{equations}}\left(x,p\right)$. Inequality constraints (h) usually represent inherent distribution systems characteristics or regulatory restrictions, such as voltage level constraints, cable capacity, and limits on long-time and short-time voltage variations. Due to the large number of constraints that can be modeled, three operational constraints were chosen: overvoltage, overcurrent, and penetration index.

Overvoltage and overcurrent constraints are considered in the proposed model as they represent network limitations, which are generally set by local regulations. Concerning these constraints, the maximum voltage level ($V_{\max }$) allowed is 1.05 p.u. and overcurrent is identified using the network section ampacity (A_k−m). Another constraint considered in the model is related to the fast voltage variation due to renewable DG intermittence, such that $\Delta V_k=V_k^{\mathrm{with} DG}-V_k^{\mathrm{without} DG}$ is calculated every hourly power flow simulation and then a $\Delta V_{\max }$ equal to 0.05 p.u. is defined to verify the compliance with referred constraint.

The penetration index (PI) represents a measure of impact (load relief) of DG plants on electrical systems. Various works found in the technical literature try to find or simply suggest a DG penetration value able to provide benefits to DisCo and DG owners without compromising the network operation. This index is calculated as shown in Equation (5) and a maximum penetration index is defined in each case study in this work.

$$PI=\left(\frac{{{\displaystyle \sum }}_{n=1}^{N}ND{G}_n .P_n^{DG}}{\underset{p=1,2,\dots ,N_T}{\max }\left({{\displaystyle \sum }}_{i\in {\mathsf{\Omega }}_B}{P}_i^p\right)}\right)$$

(5)

Therefore, the complete mathematical model is presented in Equation (6).

$$\begin{gathered} \mathrm{Minimize} \left\{\begin{array}{c}{f}_1=C_{instal}={\displaystyle {\displaystyle \sum }_{n=1}^N}C{O}_{instal}^n . ND{G}_n\\ f_2=LA{E}_{daily}={\displaystyle {\displaystyle \sum }_{p=1}^{N_T}}{\displaystyle {\displaystyle \sum }_{k-m}^{{\mathsf{\Omega }}_L}}{r}_{k-m} .I_{k-m}^2{T}_p\\ f_3=EqC{O}_{2}E={\displaystyle {\displaystyle \sum }_{p=1}^{N_T}}{\displaystyle {\displaystyle \sum }_{n=1}^N}c{f}_n.P_n^{DG}.ND{G}_n.EqC{O}_{2}E{F}_n{T}_p\end{array}\right\} \\ \mathrm{subject} \mathrm{to} \left\{\begin{array}{c}PS{M}_{\mathrm{equations}}\left(x,p\right)\\ PI\le P{I}_{\max } \\ I_{k-m}\le A_{k-m} \\ V_k\le V_{\max } \\ \Delta V_k\le \Delta V_{\max } \end{array}\right\} \end{gathered}$$

(6)

For each candidate solution, two types of penalization for constraint violations are adopted. When the PI is violated, the number of generation modules $NG{D}_n$ of an n-th DG randomly chosen is decreased until the PI is attended. When any of the other constraints are violated, the objective function corresponding to the total installation cost is increased by an additional connection cost $C_{con}$, aiming to simulate real situations where network reinforcements will be necessary. In this work, the connection cost is modeled as an exponential function multiplied by the installation cost, as given in Equation (7).

$$C_{\mathrm{con}}=\left\{\begin{array}{c}{C}_{instal}\left[e^{\frac{\max \left({{\displaystyle \sum }}^{}\frac{I_{k-m}\left(t\right)}{A_{km}}-1\right) }{N_B} }-1\right]+\\ +C_{instal}\left[e^{\max \left(\frac{\max \left({{\displaystyle \sum }}^{}{V}_k\left(t\right)-V_{\max }\right)}{N_B}, \frac{\max \left({{\displaystyle \sum }}^{}\mathsf{\Delta }{V}_k\left(t\right)-\mathsf{\Delta }{V}_{\max }\right)}{N_B}\right)}-1\right]\\ \forall V_k\left(t\right)>V_{\max } ; \mathrm{where} k\in {\mathsf{\Omega }}_B\\ \forall I_{k-m}\left(t\right)>A_{k-m} ; \mathrm{where} k-m \in {\mathsf{\Omega }}_L\\ \forall t\in {\mathsf{\Omega }}_T\end{array}\right.$$

(7)

2.2. Multi-Objective Solution Methodology

The proposed multi-objective solution methodology (MOHGA) consists of two steps: a Genetic Algorithm routine to perform the optimization process in searching of feasible solutions (population in GA terminology) and the Maximin metric routine for dominance measure and classification of the solutions in population to form the Pareto-set.

For each i-th iteration of the optimization process, a feasible solution $X_i$ represented by variable vector x (called individual in the GA terminology) is evaluated and a vector of objective-functions $F\left(X_i\right)$ is obtained. However, interpretations of the Maximin metric depends heavily on the values of the objective functions, which have different units and magnitudes. To mitigate this problem, a normalization of vector $F\left(X_i\right)$ shown in Equation (8) is proposed, where $F\left(X_0\right)$ corresponds to the vector of objective functions evaluated in the base-individual $X_0$ referring to the solution of mono-objective problem of the system loss minimization, so that no null value to any of the objectives can be obtained.

$$Y_i=\frac{F\left(X_i\right)}{F\left(X_0\right)}=\left[y_1^i,y_2^i,\dots ,y_{n_f}^i\right] \forall X_i\in Pop,i\in \left[1,Popsize\right]$$

(8)

Maximin metric provides two useful informations [27,32]: (1) negative value indicates a non-dominated solution; (2) the more negative is the value, the less crowded is the region of Pareto frontier the solution lies. Thus, Maximin metric can be used as an additional fitness criterion to evaluate a population of solutions in order to provide observation of Pareto dominance along with the degree of clustering aiming to obtain diversity of solutions in Pareto sets. Consequently, the Pareto set can be updated at each iteration with alternatives from the population of solutions with the most negative (non-dominated) Maximin metric values. Equation (9) presents the Maximin metric of a normalized vector of objective functions Y_i.

$$maxmi{n}_i=\max \left\{\underset{j=1,\dots ,Npop , j\ne i }{\min }\left\{y_1^i-y_1^j,\dots ,y_{n_f}^i-y_{n_f}^j\right\}\right\} ,i\in \left[1,Popsize\right]$$

(9)

GA solution process starts with a population and applies genetic operators to search new feasible alternatives of solution in each iteration. The new population is inserted in the last Pareto set, the resulting set is evaluated by Maximin metric as ranking criterion and only solutions with negative Maximin metric are chosen to update the Pareto set. The process is repeated until the adopted maximum number of iterations is reached.

Figure 2 exemplifies the adopted codification (chromosome) of alternative solutions (individuals) for four primary sources that can be inserted in two buses. In this example, the proposed solution suggests the installation of 4 DG units of type 1 at bus 13; for type 2, the installation of 5 DG units at bus 36 and 3 DG units at bus 58; for type 3, the installation of one DG unit at bus 3 and 2 DG units at bus 47; and, for type 4, the installation of 4 DG units at bus 62. The genetic operators applied in GA solution process are described as follow:

• Elitism: best individuals from the current Pareto set are used as individuals in the next iteration. In this work, the number of best individuals to be considered in the new population is equal to 5% of the current population size.
• Parental Selection: a tournament selection among three random individuals from the current iteration is applied. The individual with more negative Maximin metric wins the competition and becomes a father for the next generation.
• Mutation: a fixed mutation tax of 5% is adopted.
• Recombination: the process is always accomplished (recombination tax of 100%).

Three decision criteria considering the concept of preference were adopted to identify a final solution among Pareto frontier setpoints: minimum losses of active power point, maximum net present value (NPV) point, and Max-Min approximation point.

Minimum losses of active power criterion in this context represents the best solution for the DisCo viewpoint, since the utility usually seeks to improve the system efficiency.

Maximum net present value criterion represents the best solution for the DG owner viewpoint, since this one intends to sell the maximum energy with the lowest investment cost. Net present value for 10 years is calculated by Equation (10), where operation and maintenance costs are fixed as 14.5, USD/kWe.year for photovoltaic, 62.5 USD/kWe.year for onshore wind generation, and 44.76 USD/kWe.year for hydro generation [26].

$$NPV={\displaystyle \sum }_{t=1}^{10}\frac{{{\displaystyle \sum }}_{n=1}^N\left(SE.c{f}_n.P_n^{DG}.ND{G}_n-\left(C_{op}^n+C_m^n\right). P_n^{DG}.ND{G}_n\right)}{{(1+MAR)}^t}-C_{instal}$$

(10)

In this case, the minimum attractiveness rate (MAR) is adopted by the DG decision-maker.

Max-Min approximation (MMA) is a metric that calculates the gravity center of a set of points aiming the best compromise among all of the objective functions, being a benchmark for equilibrium among different criteria [27,29], since this metric is a non-preference criterion for not considering the values of the decision-maker to choose a final solution. Given a Pareto set with l non-dominated solutions, the MMA metric for the i-th alternative within the final Pareto optimal set is calculated according to Equation (11), where index j is related to the j-th objective function.

$$\begin{gathered} MM{A}_i=\left[\frac{y_1^{max}-y_1^i}{y_1^{max}-y_1^{min}}\cdots \frac{y_j^{max}-y_j^i}{y_j^{max}-y_j^{min}}\cdots \frac{y_{nf}^{max}-y_{nf}^i}{y_{nf}^{max}-y_{nf}^{min}}\right],i\in \left[1,l\right] \\ \mathrm{solution}=X_k ; \mathrm{where} k=index\left(max\left\{\underset{\begin{array}{c}i=1,\dots ,l\\ \end{array}}{min} \left\{MM{A}_i\right\}\right\}\right) \end{gathered}$$

(11)

Diversity of alternatives in Pareto sets can be evaluated according to the scattering of non-dominated solutions on the Pareto frontier. Spacing metric numerically evaluates how well the solutions in the Pareto frontier are distributed, so that value zero for this metric indicates that all the solutions are equidistantly spaced [33]. Given a Pareto set with l non-dominated solutions, the Spacing metric (S) of the set is determined by Equation (12).

$$\begin{gathered} S=\sqrt{\frac{1}{l-1} {\displaystyle \sum }_{i=1}^l\left(\overline{d}-d_i\right)} \\ {d}_i=\underset{\begin{array}{c}j=1,\dots ,l\\ j\ne i \end{array}}{min}\left\{\frac{\left|y_1^i-y_1^j\right|}{y_1^{max}-y_1^{min}}+\cdots +\frac{\left|y_{nf}^i-y_{nf}^j\right|}{y_{nf}^{max}-y_{nf}^{min}}\right\}, i\in \left[1,l\right] \end{gathered}$$

(12)

where d_i is the spacing factor of the i-th solution and $\overline{d}$ is the average value of all d_i.

3. Results and Analysis

The modeling for the DG sizing and siting problem and the multi-objective solution methodology (MOHGA) proposed in this work are applied in two case-studies and main results are analyzed in graphs and tables. Case-studies are carried out in medium voltage systems: 69-bus test system known from literature (Case Study I) and a 918-bus Brazilian distribution system (Case Study II). Simulations were performed on a 2.21 GHz Intel Core i7-8750H CPU using MATLAB 2018b (9.5.0.944444). The elapsed time for Case Study I was 500 s and 4490 s for Case Study II, both with $Popsize=100$ and 500 iterations.

3.1. Case Study I: 69-Bus Test System

First, the 69-bus and 12.66 kV distribution network [34] is simulated for a generalized analysis of the model and solution method.

Table 1. Case study I: insertion buses, maximum number of DG modules and unity capacity.

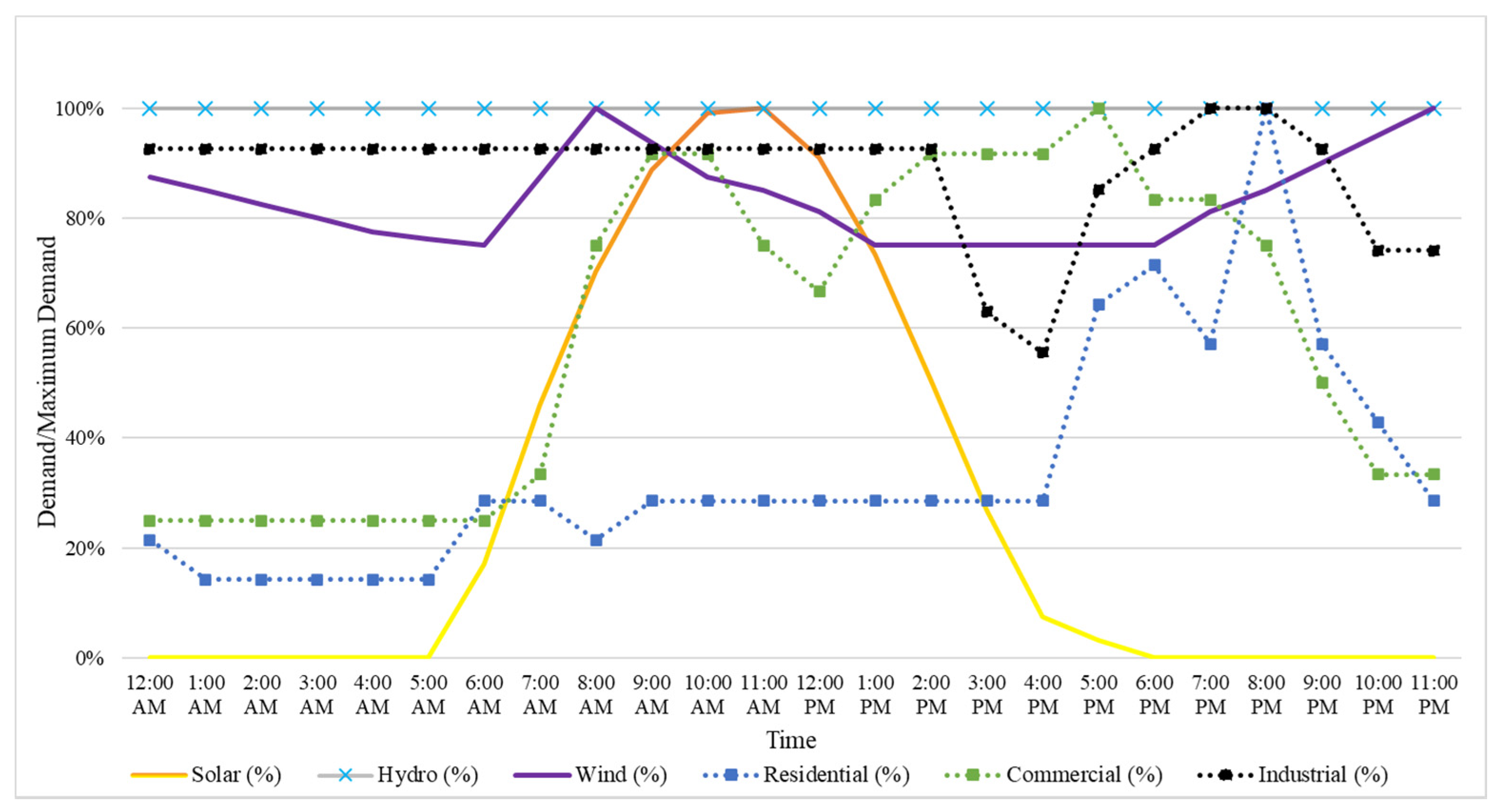
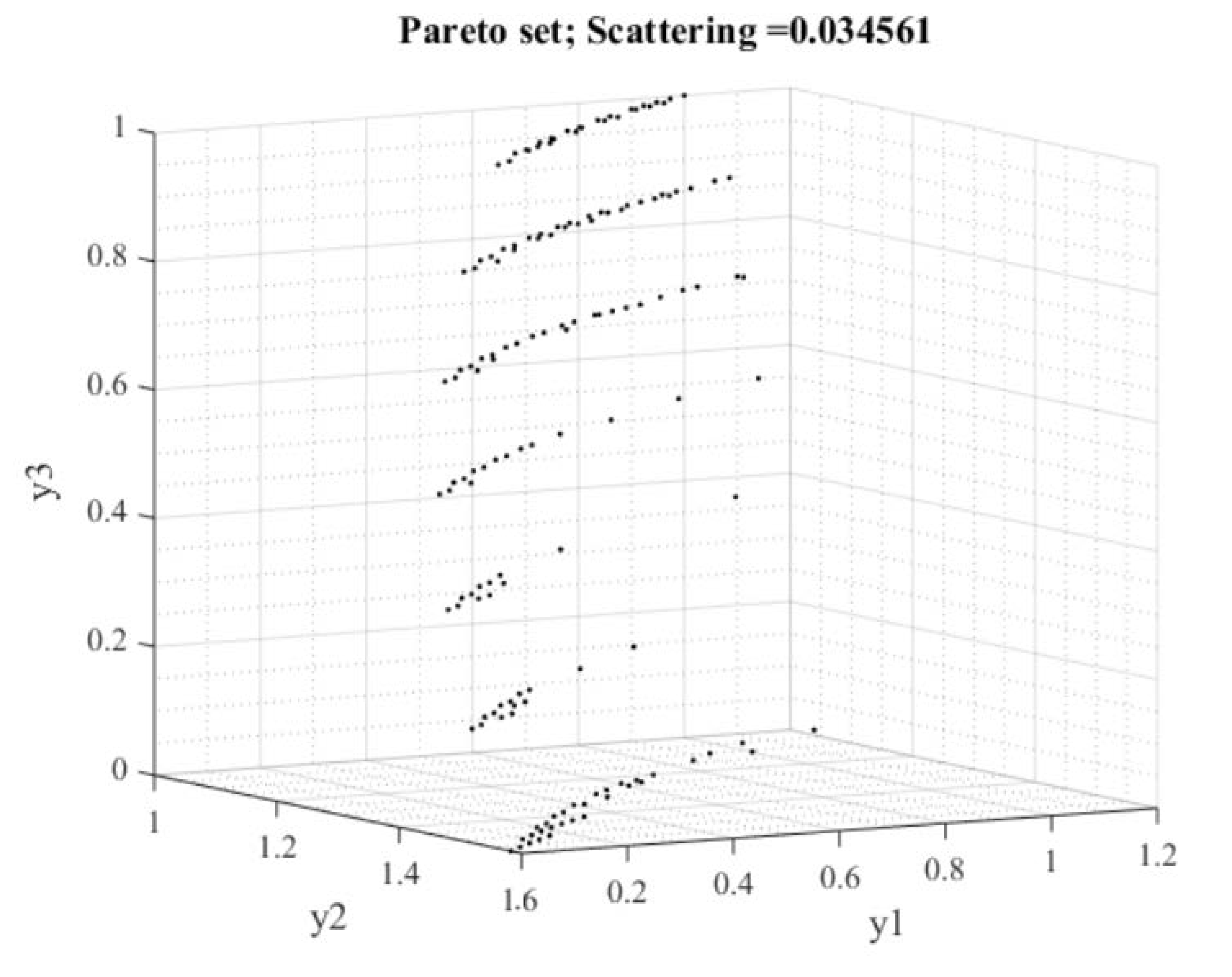
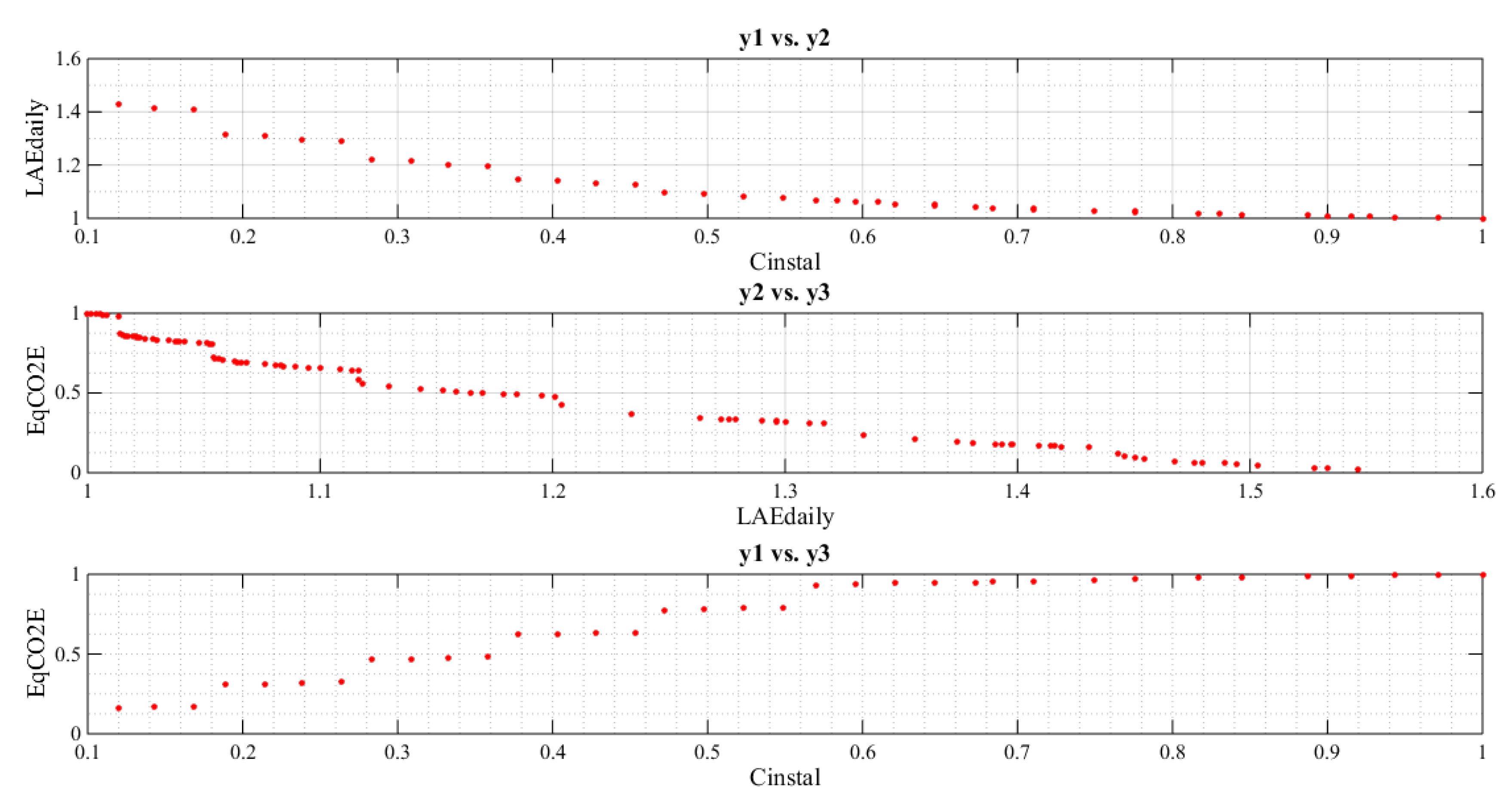
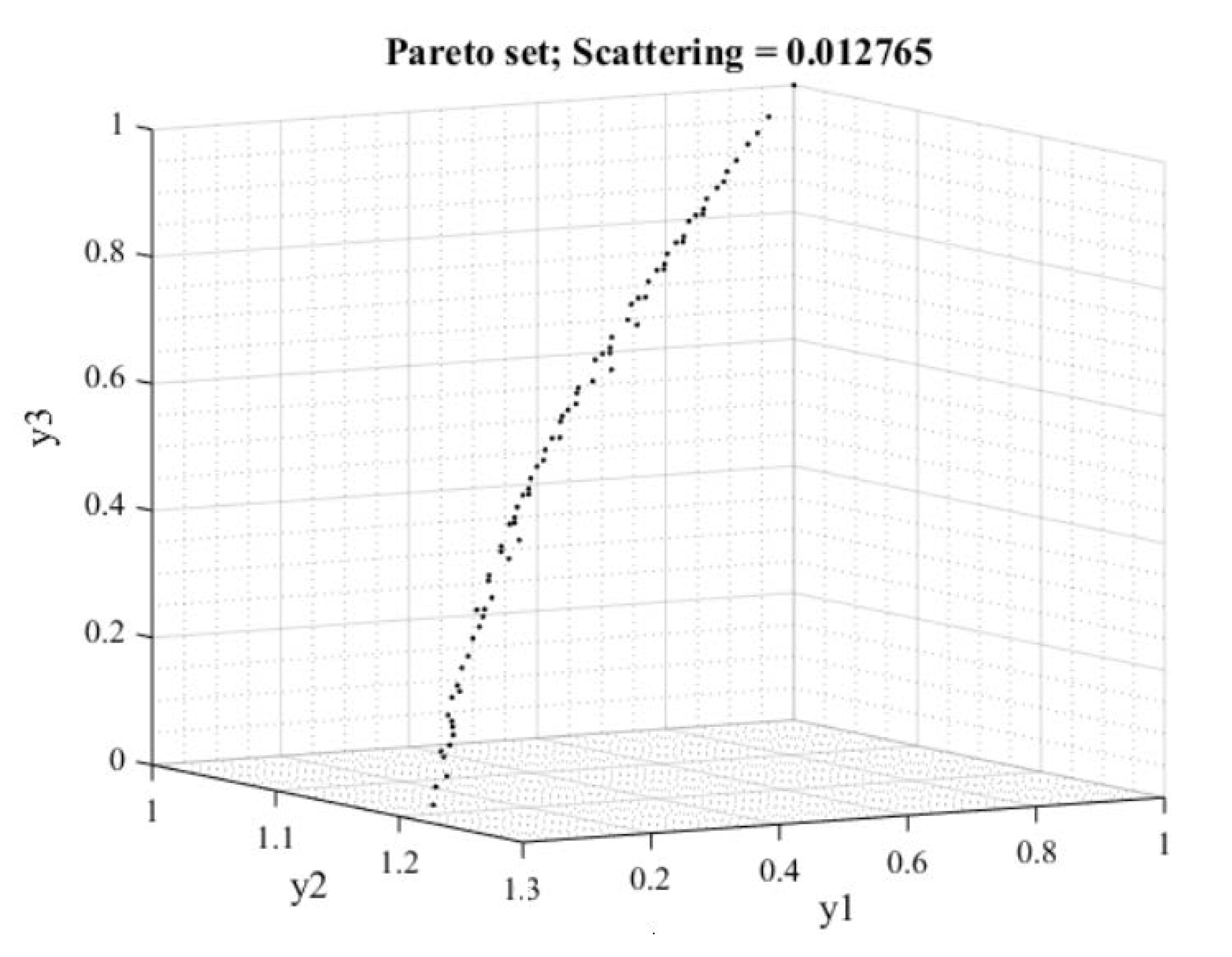
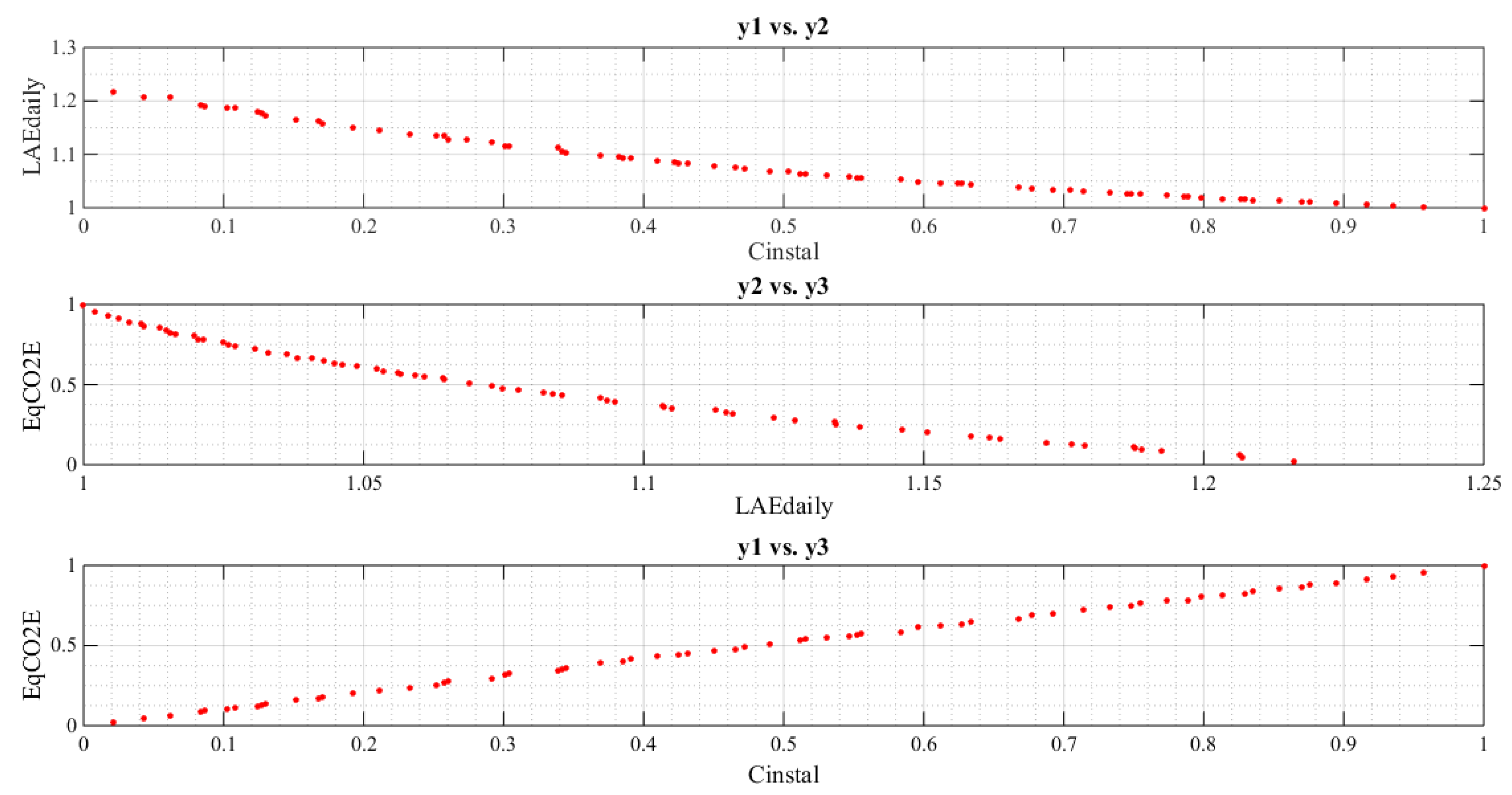
Type	DG Insertion Buses				$\mathit{N}\mathit{D}{\mathit{G}}_{\mathit{n}}^{\mathbf{max}}$	${\mathit{P}}_{\mathit{n}}^{\mathit{D}\mathit{G}}\hspace{0.17em}\hspace{0.17em}\left(\mathbf{kW}\right)$
Photovoltaic (PV)	13	29	32	-----	20	100
Wind Turbine (W)	3	38	47	68	10	150
Hydro (H)	24	36	58	62	8	300

presents the number of generation modules and power capacity of each DG plant, as well as the buses at which DG projects can be installed. Aiming to enlarge the search and solution spaces, a higher than usual 30~40% maximum penetration index $P{I}_{max}$= 70% is considered in this case-study.

The Pareto frontier obtained by the proposed multi-objective solution method based on Genetic Algorithm and Maximin metric (MOHGA) is presented in Figure 3, where y1, y2 and y3 are the normalized total installation cost of DG plants ($C_{instal}$), daily active power losses ($LA{E}_{daily}$), and daily amount of equivalent CO₂ emission ($EqC{O}_{2}E$), respectively. Good scattering of Pareto frontier points (3.4%) certify the Maximin metric efficiency to aid multi-objective solution methods in the searching of diversity of solution alternatives.

The scale of values for the axes in Figure 3 is related to the proposed normalization factors (value of objective functions referring to the solution obtained by miminization of daily active power losses considered as a mono-objective problem). Minimum power loss solution implies that normalized power losses of any alternative of solution achieve a range higher than 1.0, as observed in y2 axis. As minimization of daily active power losses seeks to maximum generation, the normalized values for the other two objective functions correspond to the maximum installation cost of DG plants and maximum daily amount of equivalent CO₂ emission, so that y1 and y3 axes attain values lower than 1.0.

Analysis of results identifies that the obtained Pareto-set presents 81% of individuals with photovoltaic in bus 13 with an average power of 272 kWe, 84% of individuals with wind source in bus 68 with an average power of 511 kWe, and 83% of its individuals with hydro source in bus 62 with an average power of 1.07 MWe. The Pareto-set also presents the set of buses 13 (PV)-68 (wind)-62 (hydro) in 60% of the individuals. Thus, analysis of Pareto-sets can also identify better locations for DG installations in distribution networks.

Figure 4 presents the normalized objective functions plotted two by two aiming to verify conflict among them. It can be observed that the curvature in y1-y2 and y2-y3 planes indicates that, as mentioned, minimization of installation costs and minimization of CO₂ emissions are conflicting with minimization of network power losses.

Table 2. Case study I: final solution phenotypes of minimum power losses, maximum NPV and MMA decision criteria.

Decision Criteria	(PV) Bus	(W) Bus	(H) Bus	(PV) NDG	(W) NDG	(H) NDG	Cinstal (106 USD)	LAEdayly (MWh)	EqCO2EF (ton/10 Years)	NPV (106 USD—10 Years)
Min. losses	13	68	62	4	5	6	4.74	1.93	2.28	1.742
Max. NPV	29	68	62	0	5	6	4.20	1.95	2.26	1.844
MMA	13	68	62	2	1	3	2.80	2.30	1.11	1.290

shows the phenotypes of solution alternatives chosen from Pareto-set, based on the three adopted decision criteria: minimum losses, maximum NPV and MMA point.

The solution based on the minimum losses of active power criterion attains comparatively larger quantities of DG generation modules, which reflects the DisCo viewpoint seeking to improve system efficiency by power loss reductions. Despite of higher installation costs of hydro and wind plants, the comparatively low capacity factor of photovoltaic plants may explain the absence of generation units from this primary energy source observed in the solution based on maximum net present value criterion, since the DG owner seeks to sell the highest amount of energy aiming a shorter payback time. Concerning the solution of the Max-Min approximation criterion, the comparatively lower number of generation modules reflects the needs for negotiations among conflicting goals to support a more efficient decision-making process.

The solution based on the criterion of minimum losses presents daily active power losses $LA{E}_{daily}$ = 1.93 MWh, which results a power loss reduction of 36.7% in comparison to the daily active power losses $LA{E}_{daily}$ = 3.05 MWh when no dispersed generation is allocated in the distribution network, although a installation cost of 4.74 × 10⁶ USD will be necessary.

Regarding the maximum NPV criterion, a minimum attractiveness rate MAR = 15% and energy price 0.15 $/kWh are adopted in this work, so that the chosen solution presents a net benefit of 1.844 × 10⁶ USD. If the DisCo will be the DG owner, $LA{E}_{dayly}$ = 1.95 MWh can be converted in USD using the same energy price and MAR as interest rate, which will result in savings of 7.4 × 10⁶ USD to the DisCo. In this case, both minimum losses and maximum NPV can be adopted as preference criteria to the DisCo.

MMA decision criterion presents daily active power losses $LA{E}_{daily}$ = 2.3 MWh, which results in a power loss reduction of 24.6% (DisCo savings: 4.95 × 10⁶ USD) compared to the case with no dispersed generation in the distribution network. MMA solution represents approximately 60% of installation cost and 50% of equivalent CO₂ emission compared to the minimum losses and maximum NPV criteria. Therefore, MMA can be adopted as a non-preference decision criterion aiming at common good among perspectives of concern.

3.2. Case Study II: 918-Bus Test System

The 918-bus/13.8 kV distribution network corresponds to a Brazilian urban feeder from Goiania, State of Goiás. The data for this system can be requested to the authors. Network buses on which DG projects can be inserted, as well as the number of generation modules and power capacity of each module are presented in

Table 3. Case study II: insertion buses, maximum number of DG modules and unity capacity.

Type	DG Insertion Buses					$\mathit{N}\mathit{D}{\mathit{G}}_{\mathit{n}}^{\mathbf{max}}$	${\mathit{P}}_{\mathit{n}}^{\mathit{D}\mathit{G}}\hspace{0.17em}(\mathbf{kW})$
PV-01	129	248	367	565	666	15	150
PV-02	138	301	468	737	811	20	100

. Only photovoltaic types were allowed since it is a downtown urban feeder. The maximum penetration index is fixed in $P{I}_{max}=120\%$, so that power flow from the substation to the grid is possible. In PV-02 was given a higher efficiency and higher cost in comparison to previous cases, simulating a technological advance: $cf$ = 20% and $C{O}_{instal}$ = 1500 USD/kWe, respectively.

Figure 5 shows the feeder picture (on Google Earth) and current during a typical day.

Figure 6 depicts the Pareto frontier obtained by the proposed approach. In this case, y1, y2, and y3 are the normalized total installation cost, daily power losses and amount of equivalent CO₂ emission, respectively. A well scattering of Pareto frontier points (1.3%) proves over again the efficiency of the Maximin metric to tackle multi-objective solution methods in searching diversity of solution alternatives.

The obtained Pareto-set presents two prevailing buses for installation of photovoltaic plants: for PV-01 type, 47% of the individuals propose bus 565 with 440 kWe of average power and 42% suggest bus 666 with 1440 kWe of average power; for PV-02 type, predominance is in bus 468 (95% of individuals) with an average power of 1265 kWe. Complementarily, the pair of buses 565–468 is in 47% of individuals and the pair 666–468 in 38%, totalizing 85% of solution alternatives from Pareto-set.

Normalized objective functions plotted two by two in Figure 7 and observation of curvature in y1-y2 and y2-y3 planes indicate over again that minimization of installation costs and of CO₂ emissions are conflicting with minimization of network power losses.

Phenotypes of solution alternatives based on decision criteria are shown in

Table 4. Case study II: final solution phenotypes of minimum power losses, maximum NPV and MMA decision criteria.

Decision Criteria	(PV-01) Bus	(PV-02) Bus	(PV-01) NDG	(PV-02) NDG	Cinstal (106 USD)	LAEdayly (MWh)	EqCO2EF (ton/10 Years)	NPV (106 USD— 10 Years)
Min. losses and Max. NPV	666	468	14	20	5.57	3.42	0.31	0.99
MMA	565	468	1	17	2.28	3.72	0.14	0.54

, where MAR = 15% and energy price 0.15 $/kWh are adopted in maximum NPV criterion.

The comparatively larger quantities of generation modules observed in the solution based on minimum losses and maximum net present value criteria reflects an agreement of goals to both DisCo and DG owner, since higher production of energy implies in lower losses to the DisCo seeking of efficiency while it results in higher sales and shorter payback time to the DG owner. The comparatively lower number of generation modules regarding the solution for the Max-Min approximation criterion reflects again the need for tradeoffs among conflicting goals in such a way as to ensure success in the decision-making process.

The solution based on both minimum losses and maximum NPV criteria presents daily active power losses $LA{E}_{daily}$ = 3.42 MWh at an installation cost of 5.57 × 10⁶ USD and net benefit of 0.99 × 10⁶ USD, resulting in a power loss reduction of 17.8% in comparison to the case with no dispersed generation ($LA{E}_{daily}$ = 4.16 MWh). When DG is owned by the DisCo, $LA{E}_{dayly}$ can also be converted in USD based on the same energy price and MAR as interest rate, which would result in savings of 4.88 × 10⁶ USD to the DisCo.

MMA decision criterion results in daily active power losses ($LA{E}_{daily}$) of 3.72 MWh, corresponding with 10.6% of power loss reduction. In this case, the DisCo savings are 2.9 × 10⁶ USD compared to the case with no dispersed generation. The solution obtained through MMA represents approximately 50% of equivalent CO₂ emission and 59% of installation cost compared to the minimum losses and maximum NPV criteria. It is important to mention that MMA criterion suggests installation of PV-02 type, since it is technologically superior, producing better results, even at a higher price. Thus, it can be concluded over again that MMA can be adopted as a non-preference decision criterion to satisfy varied perspectives of concern.

4. Conclusions

This paper presents a multi-objective modeling for the DG sizing and siting problem based on technical, economical and environmental aspects, where a multi-objective Genetic Algorithm and Maximin metric (MOHGA) were applied in the searching process to obtain Pareto sets with diversity of solutions. Locations (buses) for possible DG insertions and maximum capacity divided in generation modules were considered. Two case-studies were carried out to testify algorithm effectiveness and decision criteria considering the concept of preference were applied to choose a final solution from Pareto sets.

Management decisions typically involve considerations from a wide range of criteria and multi-objective modeling can be of interest to stakeholders, especially when tradeoffs among conflicting aspects are needed to support a more efficient decision-making.

Pareto frontier plots demonstrate that the applied methodology of solution process (MOHGA) obtained a satisfactory set of solution alternatives in terms of diversity, which can be understood as an acceptable sampling of the space of decision variables is achieved, thus providing an efficient option for solving multiobjective optimization problems.

The case-studies carried out demonstrate that several criteria (such as minimal losses solution, maximum NPV solution and MMA solution) allow decision makers (planners, DG owners, regulatory agencies, etc.) to develop strategies to meet their necessities (such as reduction of costs, CO₂ emissions and technical losses, etc.) at the same time, which is consistent with a more systematic strategy of generation expansion planning.

Intermittent sources with higher capacity factors also show a prevalence compared to the others, which can be noticed by the higher dimensions of wind and hydro DG’s in case study I. This result points out the continuous need for a technological advance in DG technologies, especially photovoltaic, to increase their capacity factors before other energy sources. Finally, this work also illustrates the high complexity of renewables integration in distribution networks and emphasizes the necessity of research in this field.