Two- and Three-Dimensional Numerical Investigation of the Influence of Holes on the Fatigue Crack Growth Path
Abstract
:1. Introduction
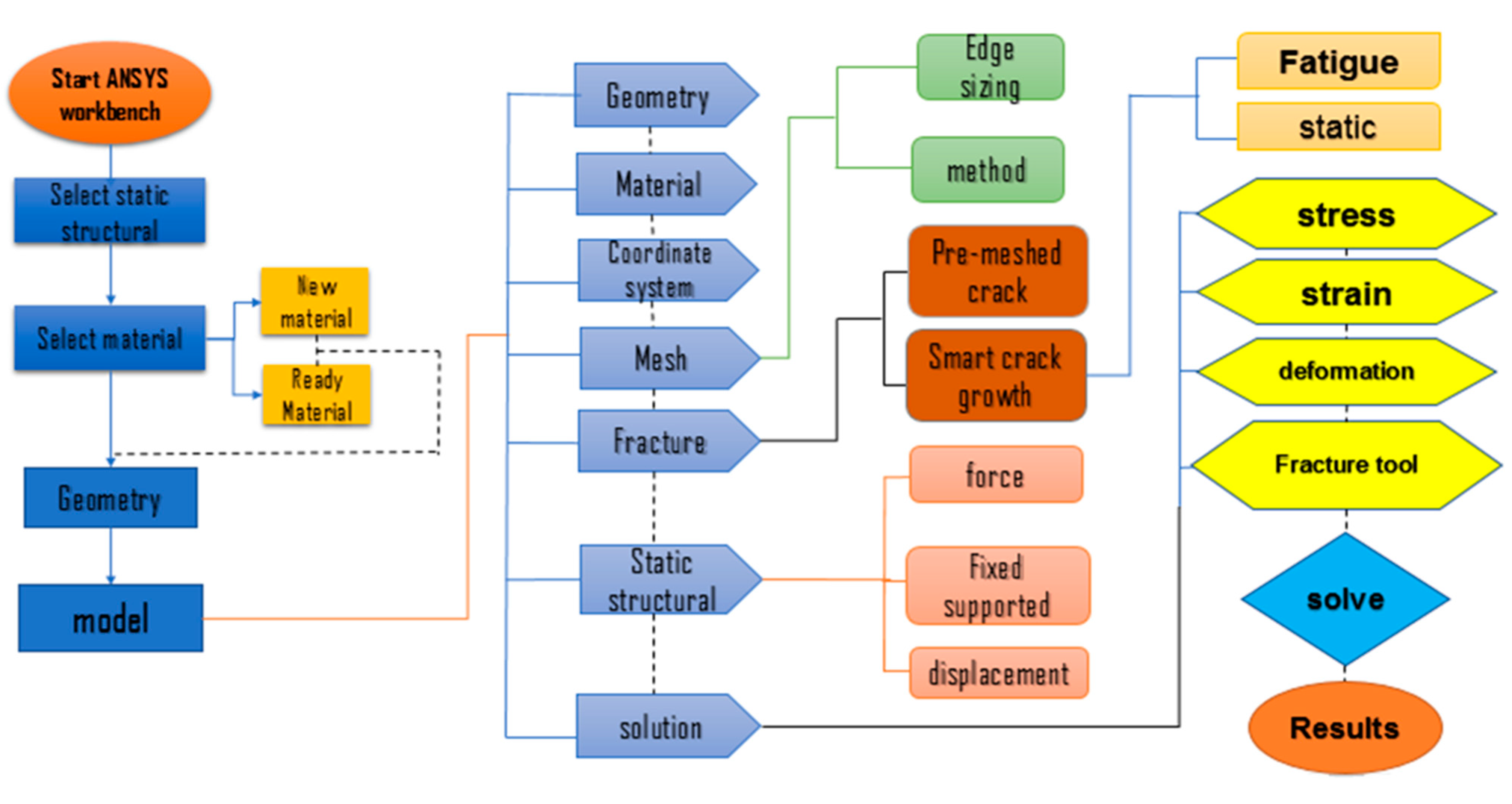
2. Mixed Mode Fatigue Life Evaluation Procedure Using ANSYS
3. FRANC2D/L Procedure
4. Results and Discussion
4.1. Modified Compact Tension Specimen (MCTS)
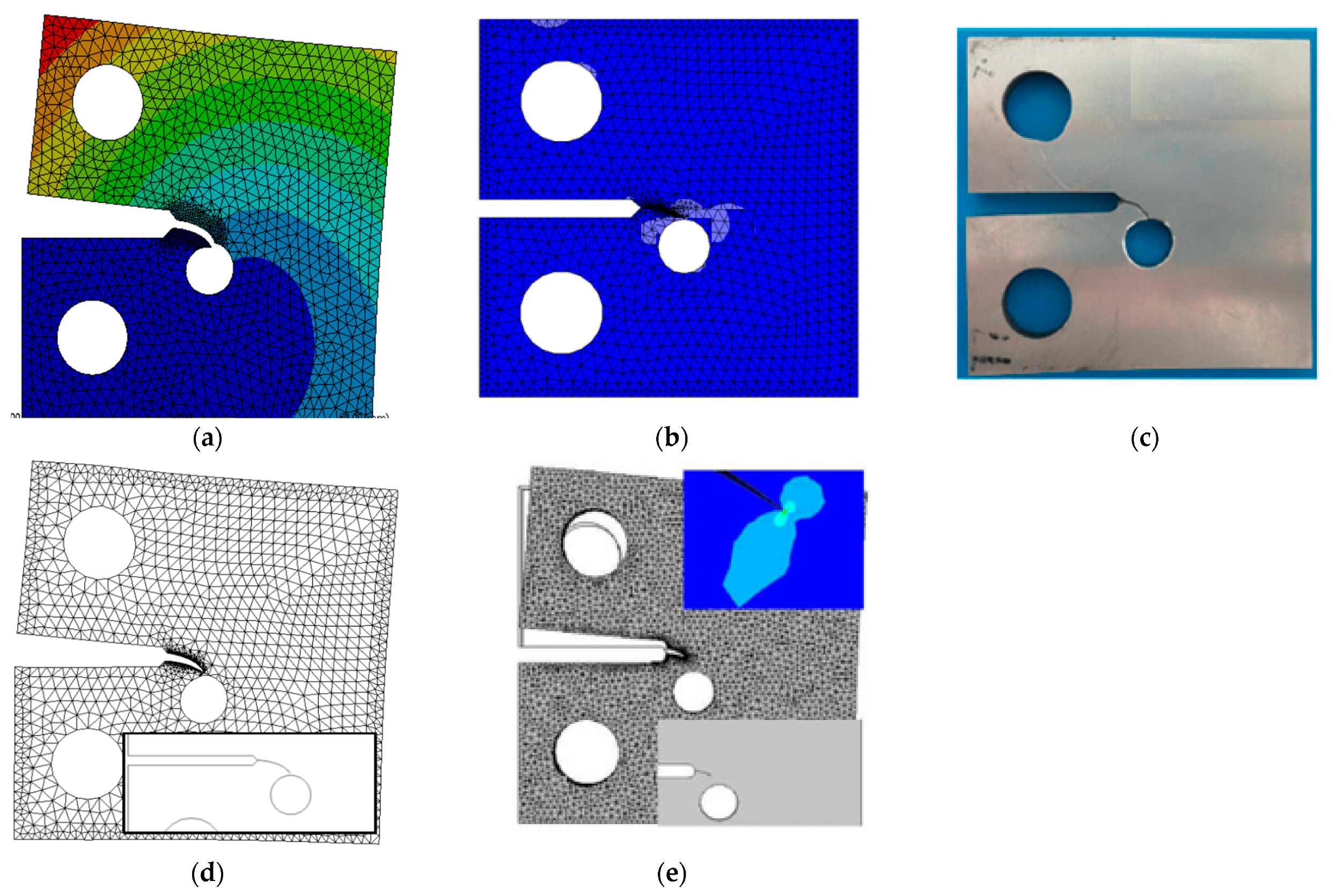
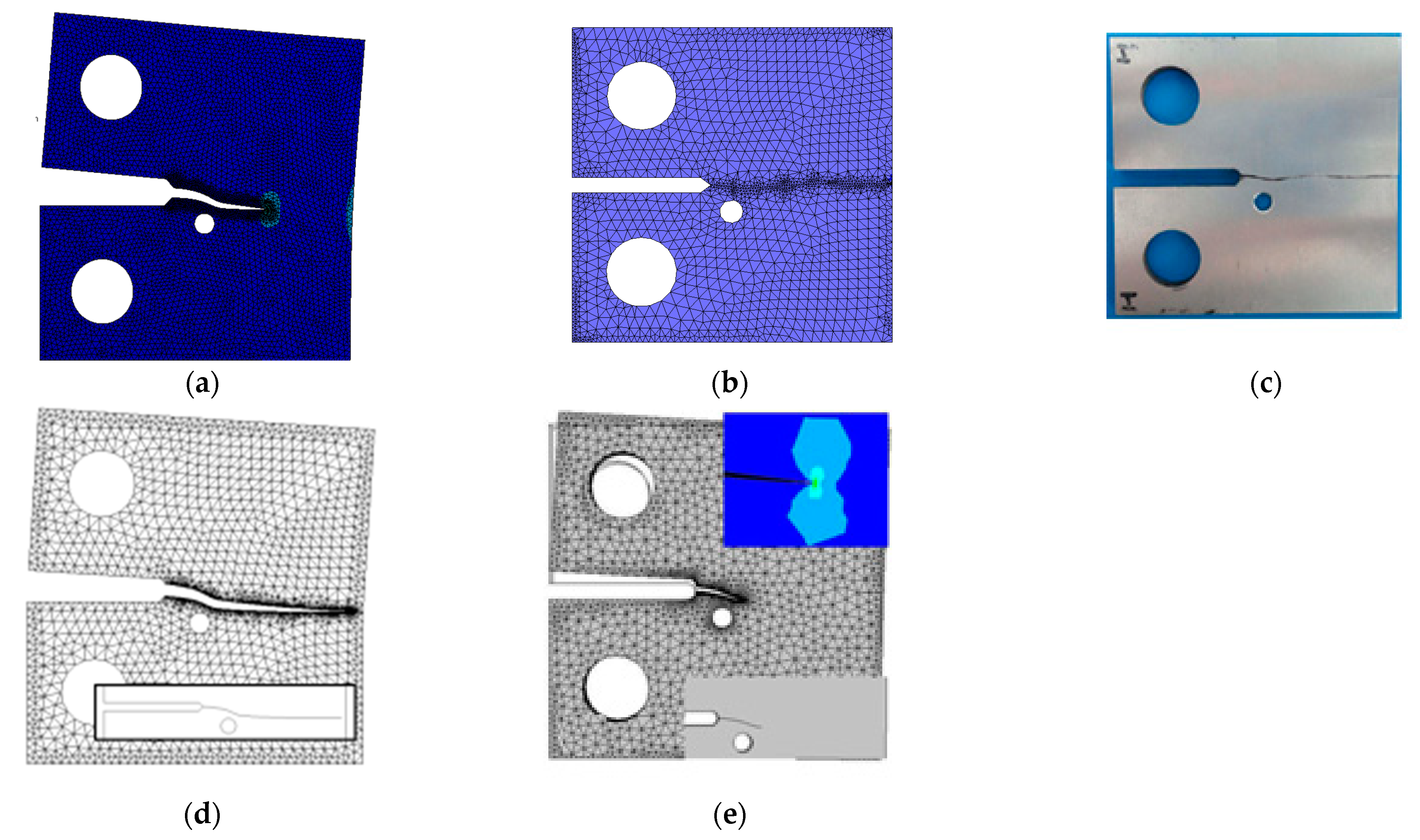
4.1.1. G1 and G2 Specimens
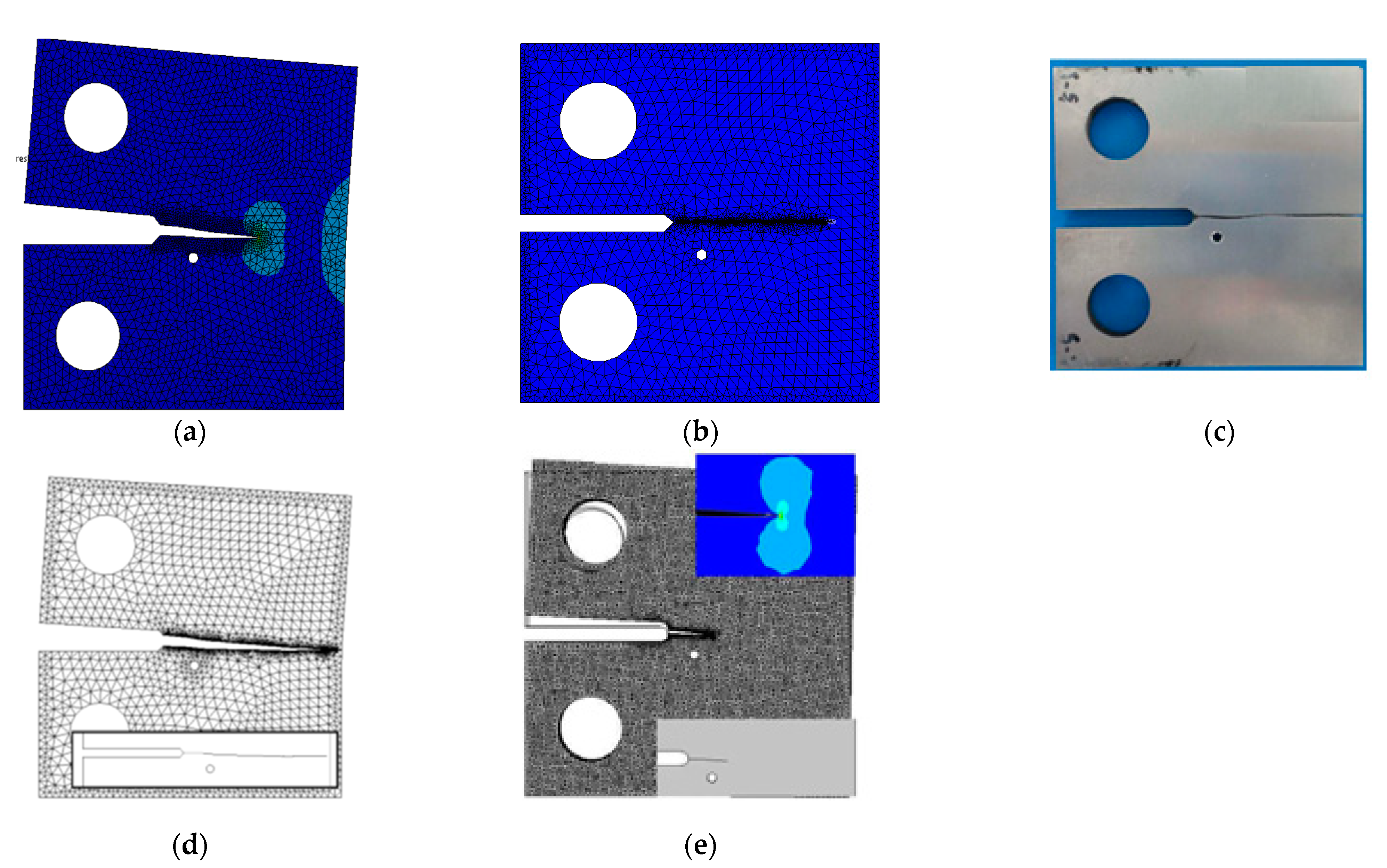
4.1.2. G3 Specimen
4.1.3. G4 Specimen
4.1.4. G5 Specimen
4.1.5. G6 Specimen
4.1.6. G7 Specimen
- 1
- For several geometries such as G1, G5, G6, and G7, the author of [29] did shown the completed crack growth path to be comparable to the experimental path in his computational results.
- 2
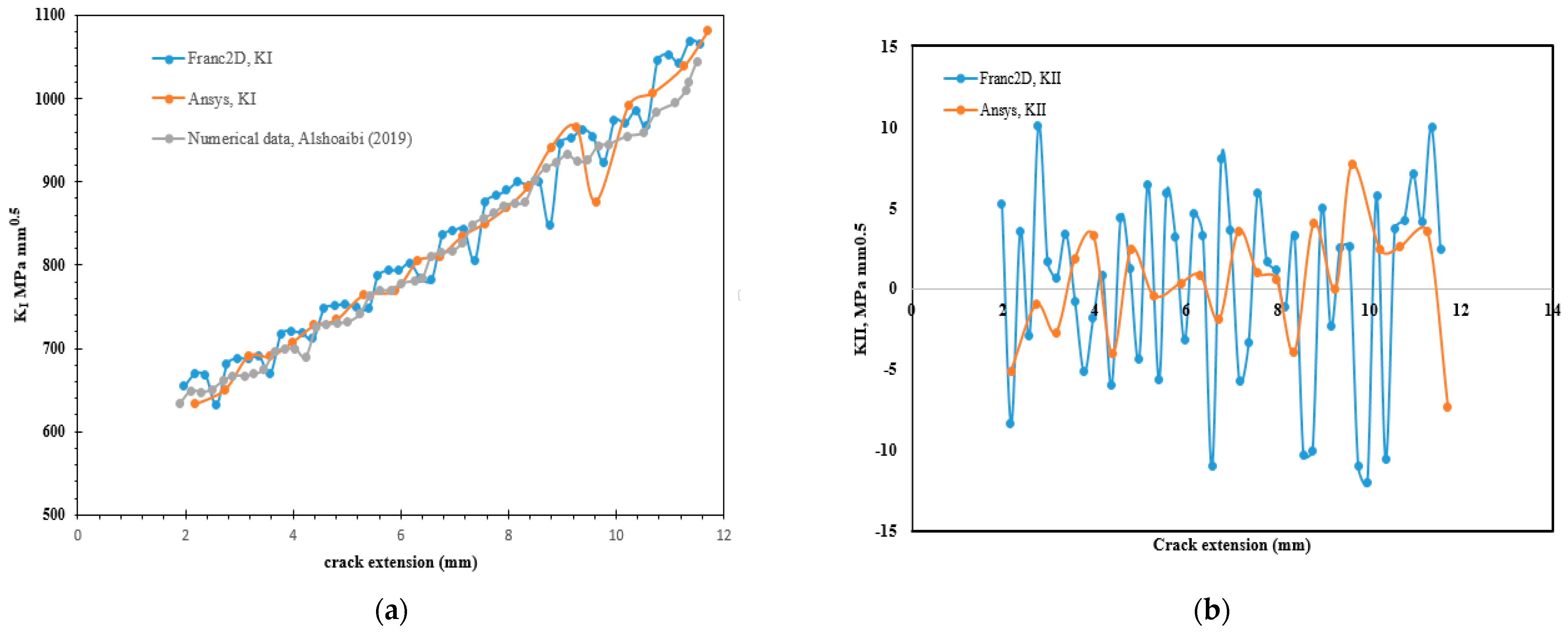
- The values of the second mode of stress intensity component, KII, which have a significant influence on the crack growth path according to Equation (1), have not been represented accurately by the author [29]. If the KII values were close to zero, the crack would propagate in a straight line, but as the values are increased, the crack began to grow in a curvature trajectory as many crack growth paths were achieved for the studied geometries.
- 3
- The author [29] used the J-integral method to evaluate the stress intensity factors, which were also used in the present study in both software, resulting in a comparable result for SIFs, whereas there were no comparable results for the fatigue life cycles number for the ANSYS results computed by [29] compared to the FRANC3D results [32], which were achieved in the present study with comparable results as shown in Table 3.
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kumar, S.; Singh, I.; Mishra, B.; Singh, A. New Enrichments in XFEM to Model Dynamic Crack Response of 2-D Elastic Solids. Int. J. Impact Eng. 2016, 87, 198–211. [Google Scholar] [CrossRef]
- Pandey, V.; Singh, I.; Mishra, B.; Ahmad, S.; Rao, A.V.; Kumar, V. A New Framework Based on Continuum Damage Mechanics and XFEM for High Cycle Fatigue Crack Growth Simulations. Eng. Fract. Mech. 2019, 206, 172–200. [Google Scholar] [CrossRef]
- Alshoaibi, A.M.; Fageehi, Y.A. 2D Finite Element Simulation of Mixed Mode Fatigue Crack Propagation for CTS Specimen. J. Mater. Res. Technol. 2020, 9, 7850–7861. [Google Scholar] [CrossRef]
- Dirik, H.; Yalçinkaya, T. Crack Path and Life Prediction under Mixed Mode Cyclic Variable Amplitude Loading through XFEM. Int. J. Fatigue 2018, 114, 34–50. [Google Scholar] [CrossRef]
- Demir, O.; Ayhan, A.O.; Iriç, S. A New Specimen for Mixed Mode-I/II Fracture Tests: Modeling, Experiments and Criteria Development. Eng. Fract. Mech. 2017, 178, 457–476. [Google Scholar] [CrossRef]
- Zhang, R.; Guo, R. Determination of Crack Tip Stress Intensity Factors by Singular Voronoi Cell Finite Element Model. Eng. Fract. Mech. 2018, 197, 206–216. [Google Scholar] [CrossRef]
- Sih, G.; Liebowitz, H. Mathematical Fundamentals. In Fracture; Academic Press: New York, NY, USA, 1968; Volume 2, pp. 67–190. [Google Scholar]
- Hellan, K. Introduction to Fracture Mechanics; McGraw-Hill: New York, NY, USA, 1985. [Google Scholar]
- Barsom, J.; Rolfe, S. Fracture and Fatigue in Structure: Application of Fracture Mechanics; American Society for Testing and Materials: Philadelphia, PA, USA, 1999. [Google Scholar]
- Broek, D. Elementary Engineering Fracture Mechanics; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Belytschko, T.; Black, T. Elastic Crack Growth in Finite Elements with Minimal Remeshing. Int. J. Numer. Method Eng. 1999, 45, 601–620. [Google Scholar] [CrossRef]
- Huynh, H.D.; Nguyen, M.N.; Cusatis, G.; Tanaka, S.; Bui, T.Q. A Polygonal XFEM with New Numerical Integration for Linear Elastic Fracture Mechanics. Eng. Fract. Mech. 2019, 213, 241–263. [Google Scholar] [CrossRef]
- Surendran, M.; Natarajan, S.; Palani, G.; Bordas, S.P. Linear Smoothed Extended Finite Element Method for Fatigue Crack Growth Simulations. Eng. Fract. Mech. 2019, 206, 551–564. [Google Scholar] [CrossRef]
- Rozumek, D.; Marciniak, Z.; Lesiuk, G.; Correia, J. Mixed Mode I/II/III Fatigue Crack Growth in S355 Steel. Procedia Struct. Integr. 2017, 5, 896–903. [Google Scholar] [CrossRef]
- Bergara, A.; Dorado, J.; Martin-Meizoso, A.; Martinez-Esnaola, J.M. Fatigue Crack Propagation in Complex Stress Fields: Experiments and Numerical Simulations Using the Extended Finite Element Method (XFEM). Int. J. Fatigue 2017, 103, 112–121. [Google Scholar] [CrossRef]
- Alshoaibi, A.M. Finite Element Procedures for the Numerical Simulation of Fatigue Crack Propagation Under Mixed Mode Loading. Struct. Eng. Mech. 2010, 35, 283–299. [Google Scholar] [CrossRef]
- Fageehi, Y.A.; Alshoaibi, A.M. Numerical Simulation of Mixed-Mode Fatigue Crack Growth for Compact Tension Shear Specimen. Adv. Mater. Sci. Eng. 2020, 2020, 5426831. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.; Wang, Q.; Zeng, W.; Liu, G.; Sun, J.; He, L.; Bui, T.Q. Dynamic Brittle Crack Propagation Modeling Using Singular Edge-Based Smoothed Finite Element Method with Local Mesh Rezoning. Eur. J. Mech. A Solids 2019, 76, 208–223. [Google Scholar] [CrossRef]
- Gomes, G.; Miranda, A.C. Analysis of Crack Growth Problems Using the Object-Oriented Program Bemcracker2D. Fratt. Ed Integr. Strutt. 2018, 12, 67–85. [Google Scholar] [CrossRef] [Green Version]
- Fageehi, Y.; Alshoaibi, A.M. Nonplanar Crack Growth Simulation of Multiple Cracks Using Finite Element Method. Adv. Mater. Sci. Eng. 2020, 2020, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Alshoaibi, A.M. Numerical Modeling of Crack Growth under Mixed-Mode Loading. Appl. Sci. 2021, 11, 2975. [Google Scholar] [CrossRef]
- Alshoaibi, A.M. Computational Simulation of 3D Fatigue Crack Growth under Mixed-Mode Loading. Appl. Sci. 2021, 11, 5953. [Google Scholar] [CrossRef]
- Alshoaibi, A.M.; Fageehi, Y.A. Numerical Analysis of Fatigue Crack Growth Path and Life Predictions for Linear Elastic Material. Materials 2020, 13, 3380. [Google Scholar] [CrossRef] [PubMed]
- Alshoaibi, A.M.; Fageehi, Y.A. Simulation of Quasi-Static Crack Propagation by Adaptive Finite Element Method. Metals 2021, 11, 98. [Google Scholar] [CrossRef]
- Paris, P.; Erdogan, F. A Critical Analysis of Crack Propagation Laws. J. Basic Eng. 1963, 85, 528–533. [Google Scholar] [CrossRef]
- Coffin, L. Cyclic Deformation and Fatigue of Metals. Fatigue and Endurance of Metals [Russian Translation]; USSR: Moscow, Russia, 1963; pp. 257–272. [Google Scholar]
- Wöhler, A. Versuche Zur Ermittlung Der Auf Die Eisenbahnwagenachsen Einwirkenden Kräfte Und Die Widerstandsfähigkeit der Wagen-Achsen. Z. Für Bauwes. 1860, 10, 583–614. [Google Scholar]
- Bjørheim, F. Practical Comparison of Crack Meshing in ANSYS Mechanical APDL 19.2; University of Stavanger: Stavanger, Norway, 2019. [Google Scholar]
- ANSYS. Academic Research Mechanical, Release 19.2, Help System. Coupled Field Analysis Guide 2020, ANSYS, Inc., (ONLINE). Available online: https://www.mdpi.com/2075-4701/11/3/397/htm (accessed on 26 May 2021).
- Kumar, P.; Makhatha, M.E.; Sengupta, S.; Dutt, A.K. Prediction of the Propagation of Fatigue Cracks in Part-Through Cracked Pipes with CASCA and FRANC2D. Trans. Indian Inst. Met. 2020, 73, 1417–1420. [Google Scholar] [CrossRef]
- Ahola, A.; Björk, T.; Barsoum, Z. Fatigue Strength Capacity of Load-Carrying Fillet Welds on Ultra-High-Strength Steel Plates Subjected To Out-Of-Plane Bending. Eng. Struct. 2019, 196, 109282. [Google Scholar] [CrossRef]
- Zhang, X.-Q.; Zhang, X.; Li, L.; Duan, S.-W.; Li, S.-Z.; Huang, Z.-L.; Zhang, Y.-W.; Feng, J.-Y. Investigation of the Influence of Small Hole on the Fatigue Crack Growth Path. J. Fail. Anal. Prev. 2016, 16, 391–399. [Google Scholar] [CrossRef]
- Alshoaibi, A.M. Comprehensive Comparisons of Two-and Three-Dimensional Numerical Estimation of Stress Intensity Factors and Crack Propagation in Linear Elastic Analysis. Int. J. Integr. Eng. 2019, 11, 45–52. [Google Scholar] [CrossRef] [Green Version]













| Specimen | Hole Parameters (mm) [32] | |||||
|---|---|---|---|---|---|---|
| d1 | h1 | v1 | d2 | h2 | v2 | |
| G1 | ||||||
| G2 | 8 | 6.5 | 3 | |||
| G3 | 8 | 10.5 | 3 | |||
| G4 | 8 | 14.5 | 3 | |||
| G5 | 2 | 6.5 | 3 | |||
| G6 | 4 | 6.5 | 3 | |||
| G7 | 5 | 6.5 | 3 | 5 | 6.5 | 3 |
| MCTS | FRANC2D/L | ANSYS Workbench | ||
|---|---|---|---|---|
| Nodes | Elements | Nodes | Elements | |
| G1 | 4722 | 2314 | 166835 | 121915 |
| G2 | 4576 | 2352 | 160678 | 112195 |
| G3 | 4684 | 2367 | 176831 | 121916 |
| G4 | 4687 | 2477 | 156815 | 107646 |
| G5 | 4635 | 2295 | 167885 | 114429 |
| G6 | 4647 | 2285 | 175459 | 121574 |
| G7 | 5129 | 2446 | 172245 | 116462 |
| Specimen | Number of Cycles (ANSYS) | Number of Cycles (FRANC2D) | Number of Cycles (FRANC3D) [32] | Number of Cycles [29] |
|---|---|---|---|---|
| G1 | 11923 | 11848 | 11765 | 44803 |
| G2 | 6243 | 6325 | 6018 | 52116 |
| G3 | 4021 | 4125 | 3818 | 70751 |
| G4 | 4685 | 4712 | 4716 | 46314 |
| G5 | 6219 | 6189 | 6018 | 52116 |
| G6 | 5618 | 5587 | 5519 | 44968 |
| G7 | 7425 | 7385 | 7211 | 57762 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fageehi, Y.A. Two- and Three-Dimensional Numerical Investigation of the Influence of Holes on the Fatigue Crack Growth Path. Appl. Sci. 2021, 11, 7480. https://doi.org/10.3390/app11167480
Fageehi YA. Two- and Three-Dimensional Numerical Investigation of the Influence of Holes on the Fatigue Crack Growth Path. Applied Sciences. 2021; 11(16):7480. https://doi.org/10.3390/app11167480
Chicago/Turabian StyleFageehi, Yahya Ali. 2021. "Two- and Three-Dimensional Numerical Investigation of the Influence of Holes on the Fatigue Crack Growth Path" Applied Sciences 11, no. 16: 7480. https://doi.org/10.3390/app11167480






