Modeling Activity-Time to Build Realistic Plannings in Population Synthesis in a Suburban Area
Abstract
:1. Introduction
2. Related Works
3. Problem Statement and Contributions
3.1. Temporal Aspects of Activities in a Daily Planning
3.2. Contributions and Limitations of the Work
- The proposed approach is based on public empirical data of distributions related to the temporal aspect of activities; it captures the temporal constraints based on the next activities to select time-choices (duration and end-time) of the current activity. A more classical approach would use socio-economic data to determine parameters of utility-based method: these socio-economic data are usually related to individuals and requires a complex and arbitrary population segmentation process. We believe our method is more simple and straightforward.
- Other approaches that use the process of serial insertion of activity often face scheduling conflicts between two activities with overlapping time distribution: they usually proceed by removing one activity or reducing its duration. Our method has the ability to avoid this kind of coarse approximation by taking into account the following activity hours when scheduling the preceding activity.
- On other approaches based on “time budget”, the duration and travel time values are independent of location: duration and travel time are computed first, then an activity-location is chosen to fit the remaining time of the “budget”. Our approach is more realistic with a process that starts with the choice of activities to conduct during the day, then the location-choice for these activities based on a gravitation model, then a transportation mode-choice based on travel distance, and only then is the activity-time estimated. In this approach, one adapts the hours instead of adapting the location of its activity.
- Over the region of interest, the greater Paris, the reference method Eqasim [11] is based on much finer data that are not publicly available: the precise schedule of activities of a subsample of the population. To generate a larger synthetic population from this subsample, the algorithm applies, for each activity, a random sampling of the departure time around the real departure time within a 30 min range. In our experience, this algorithm can lead to negative activity-duration for some agents, with a start-time higher than the end-time of the activity. In our approach, the trips departure time (activity end-time) are generated based on end-time distribution of each activity and satisfied following activities constraints.
- The proposed approach’s benefit for models that use MATSim is that it improves the quality of the initial plans (in terms of score), which allows MATSim to perform the plans with a better quality; moreover, it ensures, for each agent, the feasibility of its plan (i.e., that the agent participates in all of their activities) and keeps a realistic distributions of activities for the different attributes, namely end-time and duration.
- Our model is detailed and reproducible. It also uses only public data and can therefore be directly applied to any case study on any French territory. To the best of our knowledge, this is the first detailed proposal of this kind.
- The algorithm is a sequential approach that starts with generating the sequence of activities, then location-choice and mode-choice (detailed in [16]), and finally, the proposed time-choice process. At this level, the time-choice process cannot modify the activity-chain.
- The proposed model does not consider socio-economic variables (age, employee status, etc.) in the time-choice process. For example, the older (or retired) agents have a tendency to do the shopping activity early in the day. The time-choice process does not consider the traffic status, when it selects the activity-start/end-time or when it calculates the travel-time to the next activity.
- The model cannot infer activity patterns that are absent in the data, such as mobility of people who go back home for lunch or those going shopping during the lunch break for instance.
- The typical day modeled is a day of week in a pre-COVID-19 world, and the adaptation to a post-COVID-19 scenario requires time distributions that are still unknown at the time of publication. The ENTD is the only French census publicly available describing distributions of hours of activities. It is performed once every 10 years: the last one was started in 2018–2019 and is not published yet. We made the hypothesis that these data are still relevant in a pre-COVID-19 situation in terms of hours of activities, since modes of consumption and work have not changed significantly at the time of the model. In a post-COVID-19 situation times of activities, especially work hours, can be expected to change with the introduction of work-from-home and more agile model of office and therefore the time distribution of connected secondary activities.
4. Proposed Methodology to Set Time-Choices from Travel Survey
4.1. Constraints in a Chain of Activities
4.2. Survey Data Description
- distributions:
- -
- Duration-distribution: each activity has a duration-distribution, which represents the proportion of users who participate in this activity for a given duration.
- -
- End-time distribution: for each activity, the end-time distributions can be reconstructed from observations, regrouped, and based on a time-period.
- -
- Travel speed-distribution: in this approach, each transport mode has a travel-speed value (an approximate value), it was used to estimate the travel time from an activity to another one. Four transportation modes are considered: car, public transportation, bicycle, and walking; for each of these modes, a travel speed-distribution is extracted from the observations based on the travel distance and the travel time.
- Activity-chains (demand file): activity-sequence and transport-modes of agents is the main input of this approach, these plans are loaded without the temporal attributes (duration, start-time, or end-time).
- Optional parameters:
- -
- Activity gap: some activities require a gap-duration; we define the gap value as the minimum time between two activities of the same type. An example of such activity is : a parent has to drop off their child to the kindergarten; the child spends at least the there (at the kindergarten-place), which means that the parent cannot come back to pick him up (which means a second -activity) before this time () is over (Figure 4).
- -
- Activity-duration tolerance coefficient: the activity-duration tolerance (a tolerance refers to a positive or negative delay) represents the proportion of time that an agent can spend in an activity, more or less comparable to the typical (selected) duration. Two duration delay coefficients are defined: (1) static coefficient, which depends on the type of activity (independently from the selected duration of the activity); (2) dynamic coefficient depends on the selected duration, and is used if the duration distribution is available. These coefficients are used to control the duration delay value, with the aim to keep the duration within limits (minimum and maximum) values defined by the distribution.
- -
- Travel time delay coefficient: each trip (transfer from an activity to another) has a travel time. In real life, an agent can travel faster or slower than the estimate time; this difference of time is called a delay, and the delay coefficient is used to define the maximum delay of travel time using a travel-mode.
4.3. Time-Choice Setting: Overview
- Potential current activity latest time: this references the latest time possible to end (leave) the current activity. This parameter depends on three components:
- -
- Maximum time is the latest simulation time, defined by the user. For example, for the generation of plan for a period of full day (starting at 00:00:00), the maximum time is 24:00:00.
- -
- Activity latest end-time: this is the latest possible time for the current activity, namely the activity closing-time. This value is extracted from the activity end-time distribution.
- -
- Minimum latest remaining activities’ start-time with travel time and duration: this is the latest possible time for an agent to leave the current activity while being able to reach (and participate in) all the remaining activities (Figure 5).
- Earliest next possible visit time: this is defined for the activities with a gap value. It represents the earliest time that an individual can start (or end) the current activity; this parameter depends the last visit time (that activity) and the gap value.
- Potential activity end-time range: this range is calculated based on the current activity attributes, namely (1) start-time, (2) duration and delay duration, (3) earliest next possible visit time, and (4) the current activity latest time.
- Selected end-time value: once the end-time range is calculated, an end-time is selected from this range and the selection process is based on the activity-distribution. The process is as follows:
- -
- Select all possible end-time proportions from the activity-distribution which belong to the end-time range.
- -
- Calculate the selection (normalized) probability for each proportion.
- -
- Select an end-time proportion from the normalized distribution.
- -
- Randomly select an end-time value from the selected proportion.
- Generate the travel time to the next activity: this parameter is calculated based on three components, namely Euclidean distance between current and next activity, the used transport mode travel-speed, and the generated travel time delay.
5. Travel Demand Description
5.1. Trip Purpose and Transportation Mode
5.2. Travel Demand Distributions
5.2.1. Activity-Duration: Typical Value and Distribution
5.2.2. End-Time Distribution
5.2.3. Travel Speed Range by Mode
5.3. Travel Demand Parameters
5.3.1. Chains of Activity from the Demand File
5.3.2. Activity-Gap for Kindergarten
5.3.3. Tolerance on Activity-Duration and Travel Time
6. Algorithm for Time-Choices Setting
- : two activities from the activity-plan.
- A: current activity.
- B: next immediate activity to A in the activity-plan.
- : remaining activities (that follow A in the activity-plan).
- z: remaining activity .
- : earliest end-time of A.
- : latest end-time of A.
- : earliest (simulation) time (in this study, it is defined as 05:30).
- : typical duration of x.
- : gap value of x.
- : duration distribution of x.
- : end-time distribution of x.
- : end-time value from the distribution ().
- : latest end-time value from the distribution .
- : earliest end-time value from the distribution .
- : euclidean distance from x to y.
- : transport mode used to go from x to y.
- : travel speed of the transport mode m.
- : activity-set from x to y.
- : cardinal of C.
- : first element of C, .
- : last element of C, .
- : duration delay coefficient of x.
- : dynamic duration delay coefficient of x.
- : static duration delay coefficient of x.
- : travel time delay from activity x to activity y.
- : transport mode m travel time delay coefficient.
- P: proportion-time set.
- p: proportion-time, .
- : distribution rate of p.
- : selection probability of p.
6.1. End-Time Range Components
6.1.1. Local Latest Time ()
6.1.2. Start Time Minus Total Travel Time and Durations
6.1.3. Potential Activity End-Time Range
6.1.4. Earliest Next Visit Time
6.1.5. Update the End-Time Range
6.2. Activity-End-Time: A Final Value
6.2.1. Select an End-Time Value
6.2.2. Update the Activity-Attributes
6.3. Next Activity: Travel and Start-Time
6.3.1. Travel Time to the Next Activity
6.3.2. Start-Time of the Next Activity
6.4. Time-Choices Illustration
Activity-Plan and Trips Travel Time
- Travel time from an activity to its next activities, from the initial predicted travel time;
- Estimation of the first home departure time: H1 end-time;
- Calculation of latest possible time for H1 activity: local latest time ;
- An initial range for H1-end-time considered alone;
- Modification of H1-end-time range taking into account all the activities to be done during the day;
- Building H1 departure time distribution;
- Drawing final H1 departure time from distribution;
- Computing H1-K1 travel time and K1-start-time knowing H1-departure time;
- Estimating K1-end-time and travel time to work; no duration since it is kindergarten activity;
- Estimating work-related time-choices: duration, end-time, and travel time to next activity.
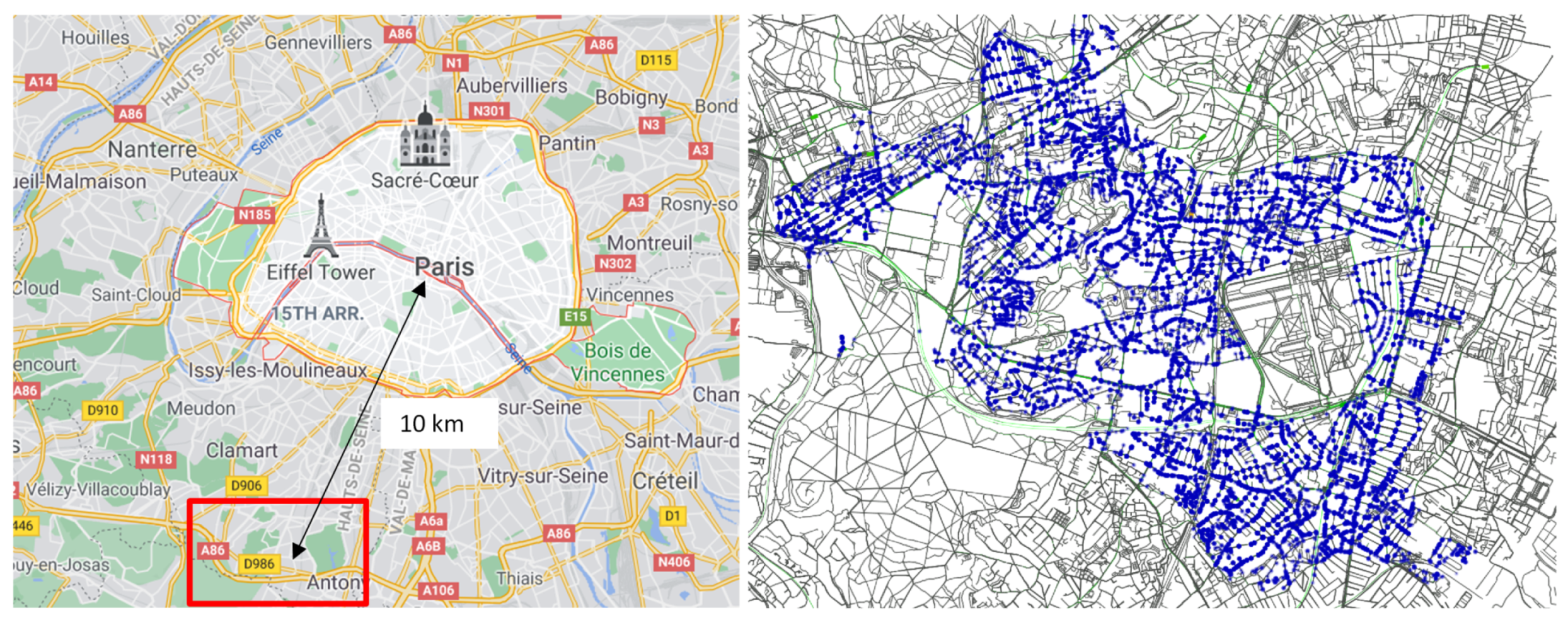
7. Urban Experiment
7.1. Model Validation
7.2. Model Simulation
7.3. Model Parameters Setting
7.4. Experimental Results
- Shopping distribution is underestimated in the morning and at lunch time (from 9 h to 12 h), mainly because shopping trips to the bakery or at lunchtime are not considered. In the evening, the shopping time distribution is over-estimated: first, the construction of the activity-plan (where shopping is a secondary activity) is mainly attached to agents who perform a primary activity (work or education), which restricts the horizon time for shopping to only the evening time. Secondly, shopping has a large distribution time from 7 h to 22 h, which will give more freedom for agents to perform shopping later in the day, while in France, the large shopping areas close between 19 h to 21 h, and only small areas are still open until 22 h. At the national scale, part of the population does shopping activity once per week and in large shopping areas, while in the catchment area, the people have tend to shop in the local small areas. Restricting the closing time of shopping places to 19 or 20 h can considerably reduce the number of observations from ENTD (the proposed approach’s training data), which will affect the performance of the proposed approach.
- Leisure distribution is overestimated at the end of the day due to the direct impact of performing the primary activities early in the day, which implies a delay in the start of leisure activity.
- Restaurant shows a major difference with the ENTD since the model dismisses of the lunch activity occurring at noon. The activity is shifted at the end of the day, and one can see the modeled ending time of dinner follows the same tendency as in ENTD but with more participation.
8. Discussion
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ABM | Activity-Based Modeling |
| ALBATROSS | A Learning BAsed TRansportation Oriented Simulation System |
| CEMDAP | Comprehensive Econometric Microsimulator for Daily Activity-travel Patterns |
| ENTD | Enquête Nationale Transports et Déplacements |
| DEPLOC | Déplacements locaux |
| MATSim | Multi-Agent Transport Simulation |
| MORPC | Mid-Ohio Regional Planning Commission |
| SCHEDULER | Computational-process modelling of household activity scheduling |
| TASHA | Travel Activity Scheduler for Household Agents |
Appendix A. Illustration Example
| A | B | A-End-Time | Mode | Speed (m/s) | Travel Time | B-Start-Time |
|---|---|---|---|---|---|---|
| H1 | K1 | 08:25:00 | car | 9.10 | 00:02:10 | 08:27:10 |
| K1 | work | 08:27:10 | car | 13.00 | 00:14:06 | 08:41:16 |
| work | K2 | 13:56:00 | car | 14.30 | 00:13:13 | 14:09:13 |
| K2 | home | 14:09:13 | car | 11.60 | 00:01:50 | 14:11:03 |
| H2 | leisure | 19:45:00 | pt | 4.30 | 00:09:00 | 19:54:00 |
| leisure | shopping | 21:18:15 | walk | 1.15 | 00:05:00 | 21:23:15 |
| shopping | H3 | 21:59:00 | pt | 6.50 | 00:12:12 | 22:11:12 |
References
- Bessghaier, N.; Zargayouna, M.; Balbo, F. Management of urban parking: An agent-based approach. In Artificial Intelligence: Methodology, Systems, and Applications; Springer: Berlin/Heidelberg, Germany, 2012; pp. 276–285. [Google Scholar]
- Bonabeau, E. Agent-based modeling: Methods and techniques for simulating human systems. Proc. Natl. Acad. Sci. USA 2002, 99 (Suppl. 3), 7280–7287. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Saadi, I.; Mustafa, A.; Teller, J.; Farooq, B.; Cools, M. Hidden markov model-based population synthesis. Transp. Res. Part B Methodol. 2016, 90, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Moeckel, R.; Spiekermann, K.; Wegener, M. Creating a synthetic population. In Proceedings of the 8th International Conference on Computers in Urban Planning and Urban Management (CUPUM), Sendai, Japan, 27–29 May 2003; pp. 1–18. [Google Scholar]
- Blom Västberg, O.; Karlström, A.; Jónsson, D.; Sundberg, M. Including Time in a Travel Demand Model Using Dynamic Discrete Choice. 2016. Available online: https://mpra.ub.uni-muenchen.de/75336/ (accessed on 18 August 2021).
- Bhat, C.; Guo, J.; Srinivasan, S.; Sivakumar, A. Comprehensive econometric microsimulator for daily activity-travel patterns. Transp. Res. Rec. 2004, 1894, 57–66. [Google Scholar] [CrossRef] [Green Version]
- Vovsha, P.; Petersen, E.; Donnelly, R. Model for allocation of maintenance activities to household members. Transp. Res. Rec. 2004, 1894, 170–179. [Google Scholar] [CrossRef]
- Gärling, T.; Kwan, M.; Golledge, R. Computational-process modelling of household activity scheduling. Transp. Res. Part B Methodol. 1994, 28, 355–364. [Google Scholar] [CrossRef] [Green Version]
- Arentze, T.; Timmermans, H. Albatross: A Learning Based Transportation Oriented Simulation System; Citeseer: Princeton, NJ, USA, 2000. [Google Scholar]
- Miller, E.; Roorda, M. Prototype model of household activity-travel scheduling. Transp. Res. Rec. 2003, 1831, 114–121. [Google Scholar] [CrossRef]
- Hörl, S.; Balac, M. Reproducible Scenarios for Agent-Based Transport Simulation: A Case Study for Paris and Île-de-France; IVT, ETH Zurich: Zurich, Switzerland, 2020. [Google Scholar]
- Roorda, M.; Miller, E.; Habib, K. Validation of TASHA: A 24-h activity scheduling microsimulation model. Transp. Res. Part A Policy Pract. 2008, 42, 360–375. [Google Scholar] [CrossRef] [Green Version]
- Zeid, M.; Rossi, T.; Gardner, B. Modeling time-of-day choice in context of tour-and activity-based models. Transp. Res. Rec. 2006, 1981, 42–49. [Google Scholar] [CrossRef]
- Ettema, D.; Bastin, F.; Polak, J.; Ashiru, O. Modelling the joint choice of activity timing and duration. Transp. Res. Part A Policy Pract. 2007, 41, 827–841. [Google Scholar] [CrossRef]
- Vovsha, P.; Bradley, M. Hybrid discrete choice departure-time and duration model for scheduling travel tours. Transp. Res. Rec. 2007, 1894, 46–56. [Google Scholar] [CrossRef]
- Delhoum, Y.; Belaroussi, R.; Dupin, F.; Zargayouna, M. Activity-based demand modeling for a future urban district. Sustainability 2020, 12, 5821. [Google Scholar] [CrossRef]
- Horni, A.; Nagel, K.; Axhausen, K.W. (Eds.) The Multi-Agent Transport Simulation MATSim; Ubiquity Press: London, UK, 2016; License: CC-BY 4.0. [Google Scholar]
- ENTD Census. Available online: https://www.statistiques.developpement-durable.gouv.fr/enquete-nationale-transports-et-deplacements-entd-2008 (accessed on 18 August 2021).




























| Conf | Static | Dynamic | Description |
|---|---|---|---|
| A | x | Standard static coefficients | |
| B | x | Double standard static coefficients | |
| C | x | Maximum dynamic coefficients | |
| D | Null static coefficients | ||
| E | x | Random dynamic coefficients | |
| F | x | x | Standard static coefficients |
| Random dynamic coefficients |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Delhoum, Y.; Belaroussi, R.; Dupin, F.; Zargayouna, M. Modeling Activity-Time to Build Realistic Plannings in Population Synthesis in a Suburban Area. Appl. Sci. 2021, 11, 7654. https://doi.org/10.3390/app11167654
Delhoum Y, Belaroussi R, Dupin F, Zargayouna M. Modeling Activity-Time to Build Realistic Plannings in Population Synthesis in a Suburban Area. Applied Sciences. 2021; 11(16):7654. https://doi.org/10.3390/app11167654
Chicago/Turabian StyleDelhoum, Younes, Rachid Belaroussi, Francis Dupin, and Mahdi Zargayouna. 2021. "Modeling Activity-Time to Build Realistic Plannings in Population Synthesis in a Suburban Area" Applied Sciences 11, no. 16: 7654. https://doi.org/10.3390/app11167654






