Experimental Investigation of the Reynolds Shear Stress Exceedance Rate for the Injury and Disorientation Biocriteria Boundary in the Pool-Orifice and Vertical Slot Type Fishways
Abstract
:1. Introduction
1.1. State-of-the-Art Review
1.2. Aim of the Paper
2. Methodology
- Injury boundary—medium turbulence condition (>50 N/m2) that can induce minor injury to some species, but does not incur significant mortality over 48 h post-exposure period;
- Disorientation boundary—low turbulence condition (>30 N/m2) that may cause a startle response that would likely put the fish at risk of predation or other hazards.
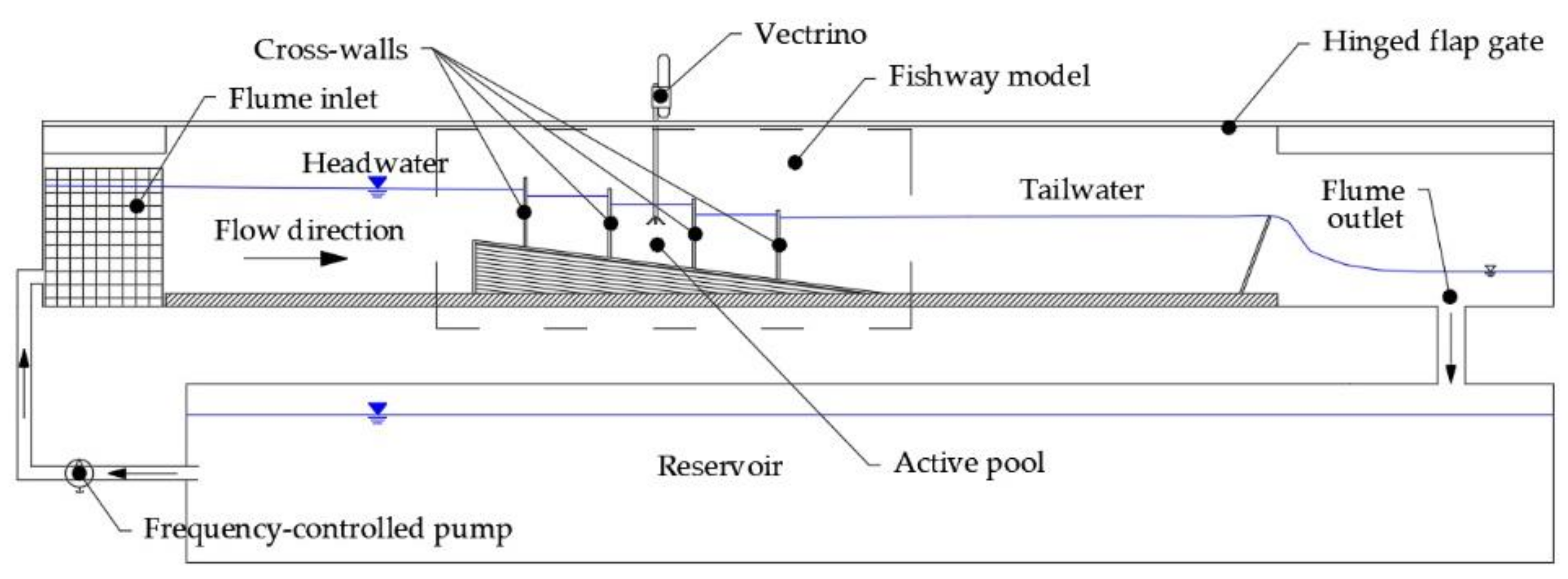
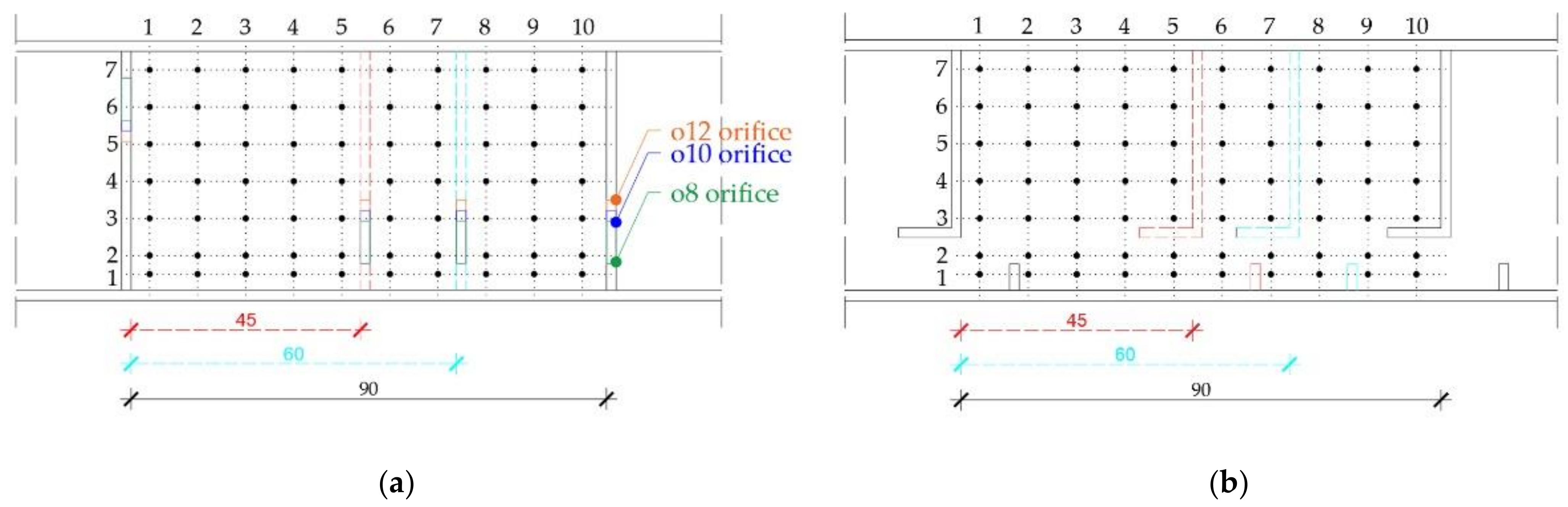
2.1. Experimental Setup
2.2. Flow Velocity Measurement Technique
3. Results
4. Discussion
5. Conclusions
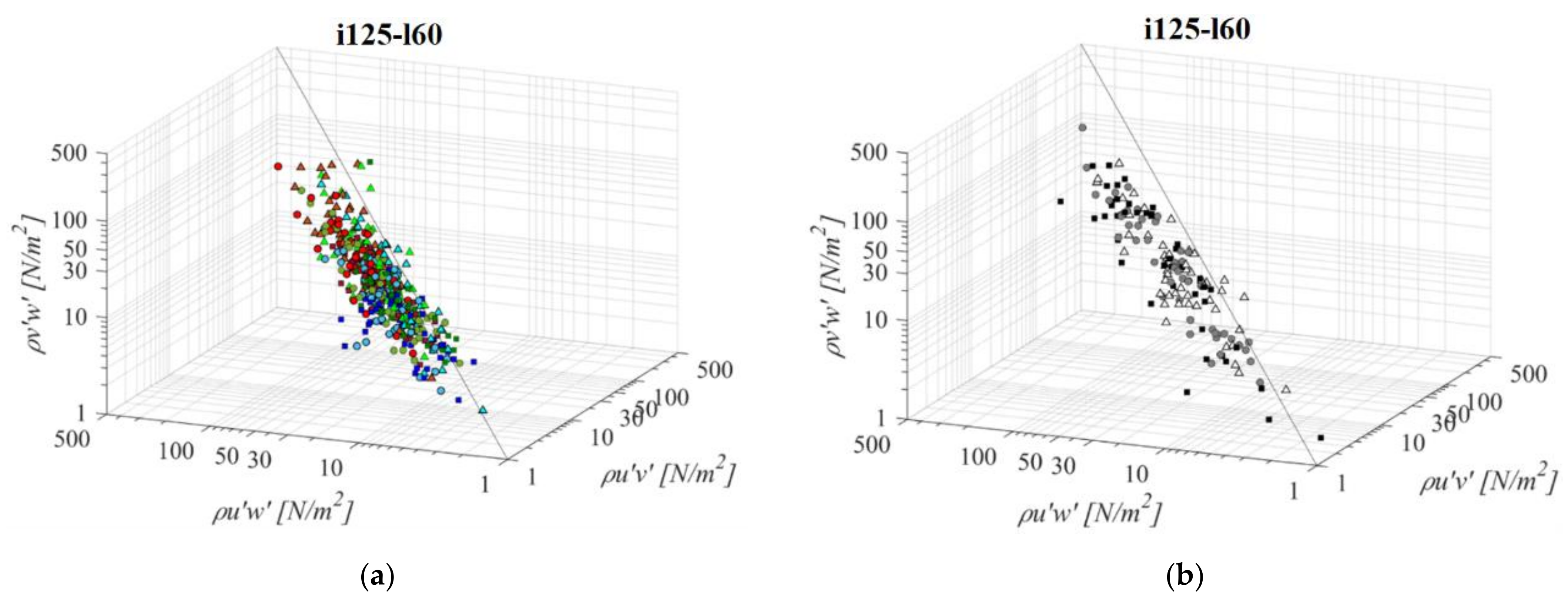
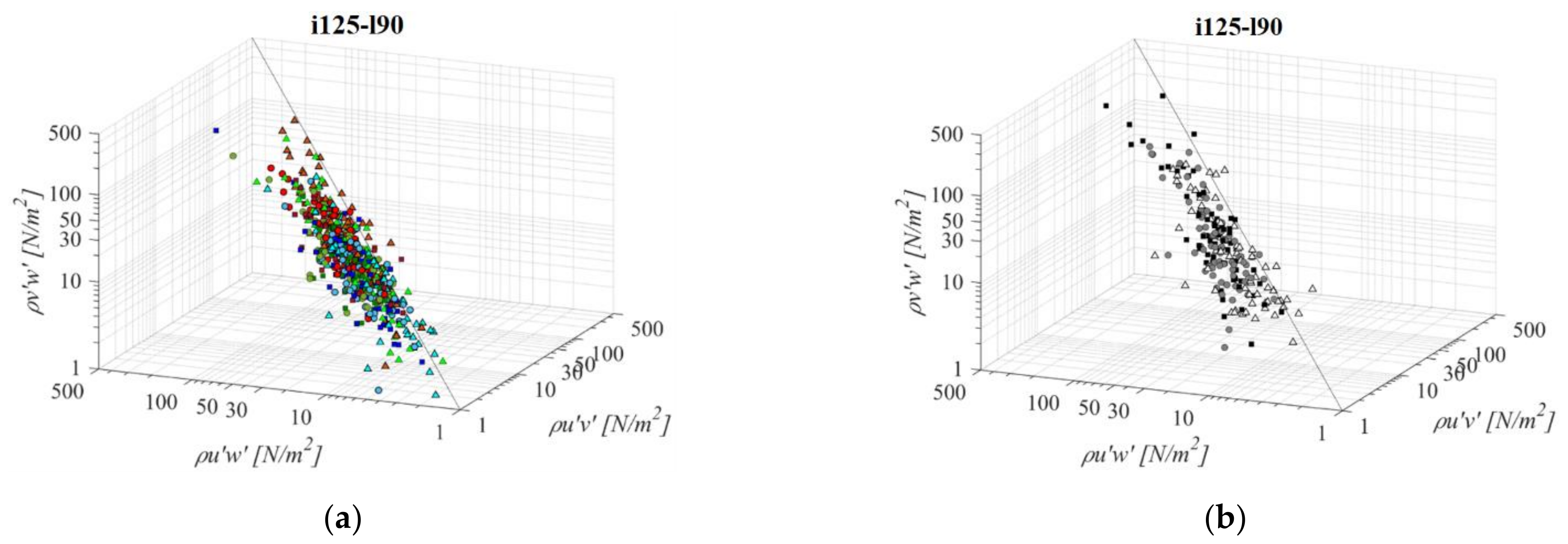
- RSS distribution across the 3 planes suggest that a streamwise RSS component is significantly larger than the horizontal and vertical component. In the PO fishway, τuw is higher than concurrent τuv and τvw by 67% and 61% on average, respectively. In the VS fishway, τuw is higher than concurrent τuv and τvw by 92% and 86% on average, respectively. Horizontal and vertical RSS components are similar, with average differences between them at 3% for all fishways and not exceeding 44% in the PO fishway and 14% in the VS fishway;
- A majority of all analyzed fishway configurations have been observed to have favorable conditions for fish passage, according to Odeh et al.’s biocriteria boundaries. All PO fishways have RSS values below the injury boundary across the entire pool, while the disorientation boundary is exceeded only for orifices o10 and o12. For all VS fishways, the disorientation boundary is exceeded by a streamwise RSS component, while the injury boundary is exceeded for l60 and all slopes. τuv and τvw do not exceed the disorientation boundary, but are close to it (>20 N/m2) for all VS fishway configurations;
- In the PO fishways RSS is inversely correlated with the orifice size and is correlated with its proximity to the main flow jet: all RSS components are observed to increase with the increase of the orifice size (while retaining the same bottom slope and pool length) and all RSS components are increasing from plane A towards plane C. A change in slope and pool length has no significant influence on the change in RSS values for PO fishways;
- In the VS fishways, RSS is inversely correlated with the bottom slope: all RSS components are observed to increase with the decrease in the bottom slope. All RSS components are decreasing from plane A towards plane C. A change in the pool length has no significant influence on the change in RSS values for VS fishways;
- A fraction of the RSS values below the biocriteria boundaries is reducing with the increase in the orifice size for PO fishways and with the increase of pool length in the VS fishways. A fraction of RSS values below the biocriteria boundaries in the VS fishway is significantly lower than in the counterpart PO fishway.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
List of Symbols and Abbreviations
| i075 | fishway configuration with bottom slope of 7.5% |
| i100 | fishway configuration with bottom slope of 10% |
| i125 | fishway configuration with bottom slope of 12.5% |
| l45 | fishway configuration with pool length of 45 cm |
| l60 | fishway configuration with pool length of 60 cm |
| l90 | fishway configuration with pool length of 90 cm |
| o8 | pool-orifice fishway configuration with orifice size of 8 cm × 8 cm |
| o10 | pool-orifice fishway configuration with orifice size of 10 cm × 10 cm |
| o12 | pool-orifice fishway configuration with orifice size of 12 cm × 12 cm |
| Plane A | plane parallel to the fishway bottom near the surface of the flow |
| Plane B | plane parallel to the fishway bottom in the middle of the flow |
| Plane C | plane parallel to the fishway bottom near the bottom of the pool |
| PO | pool-orifice fishway |
| RSS | Reynold’s shear stress |
| VS | vertical slot fishway |
| u | streamwise velocity component [m/s] |
| u′ | fluctuation of the streamwise velocity component u [m/s] |
| v | spanwise velocity component v [m/s] |
| v′ | fluctuation of the spanwise velocity component v [m/s] |
| w | vertical velocity component w [m/s] |
| w′ | fluctuation of the vertical velocity component w [m/s] |
| ρ | water density [kg/m3] |
| τuw | Reynold’s shear stress in the streamwise plane [N/m2] |
| τuv | Reynold’s shear stress in the horizontal plane [N/m2] |
| τvw | Reynold’s shear stress in the vertical plane [N/m2] |
References
- Fehér, J.; Gáspár, J.; Veres, K.S.; Kiss, A.; Kristensen, P.; Peterlin, M.; Globevnik, L.; Kirn, T.; Semerádová, S.; Künitzer, A.; et al. Hydromorphological Alterations and Pressures in European Rivers, Lakes, Transitional and Coastal Waters; European Topic Centre on Inland, Coastal and Marine Waters CENIA: Prague, Czech Republic, 2012; p. 76. [Google Scholar]
- Nilsson, C.; Reidy, C.A.; Dynesius, M.; Revenga, C. Fragmentation and flow regulation of the world’s large river systems. Science 2005, 5720, 405–408. [Google Scholar] [CrossRef] [Green Version]
- Tickner, D.; Opperman, J.J.; Abell, R.; Acreman, M.; Arthington, A.H.; Bunn, S.E.; Cooke, S.J.; Dalton, J.; Darwall, W.; Edwards, G.; et al. Bending the Curve of Global Freshwater Biodiversity Loss: An Emergency Recovery Plan. BioScience 2020, 70, 330–342. [Google Scholar] [CrossRef] [PubMed]
- Binder, T.R.; Cooke, S.J.; Hinch, S.G. The Biology of Fish Migration. In Encyclopedia of Fish Physiology: From Genome to Environment; Farrell, A.P., Ed.; Academic Press: San Diego, CA, USA, 2011; pp. 1921–1927. [Google Scholar]
- Grill, G.; Lehner, B.; Thieme, M.; Geenen, B.; Tickner, D.; Antonelli, F.; Babu, S.; Borrelli, P.; Cheng, L.; Crochetiere, H.; et al. Mapping the world’s free-flowing rivers. Nature 2019, 569, 215–221. [Google Scholar] [CrossRef] [PubMed]
- Dynesius, M.; Nilsson, C. Fragmentation and Flow Regulation of River Systems in the Northern Third of the World. Science 1994, 266, 753–762. [Google Scholar] [CrossRef] [PubMed]
- IPBES. Global Assessment Report on Biodiversity and Ecosystem Services; Intergovernmental Science-Policy Platform on Biodiversity and Ecosystem Services: Bonn, Germany, 2019; p. 56.
- EEA. WISE-WFD Database: European Waters—Assessment of Status and Pressures; European Environment Agency: Luxembourg, 2021. [Google Scholar]
- Freyhof, J.; Bergner, L.; Ford, M. Threatened Freshwater Fishes of the Mediterranean Basin Biodiversity Hotspot: Distribution, Extinction Risk and the Impact of Hydropower; EuroNatur and RiverWatch: Radolfzell, Germany; Vienna, Austria, 2020; p. 350. [Google Scholar]
- Kriechbaumer, T. Field-Based Measurement of Hydrodynamics Associated with Engineered in-Channel Structures: The Example of Fish Pass Assessment; Cranfield University: Bedford, UK, 2016. [Google Scholar]
- Franklin, A. Evaluation of Nature-Like and Technical Fish Passes for the Passage of Alewife (Alosa pseudoharengus) at Two Coastal Streams in New England; University of Massachusetts Amherst: Massachusetts, MA, USA, 2009. [Google Scholar]
- Fuentes-Pérez, J.F.; Silva, A.T.; Tuhtan, J.A.; García-Vega, A.; Carbonell-Baeza, R.; Musall, M.; Kruusmaa, M. 3D modelling of non-uniform and turbulent flow in vertical slot fishways. Environ. Model. Softw. 2018, 99, 156–169. [Google Scholar] [CrossRef]
- Katopodis, C. Introduction to Fishway Design; Freshwater Institute, Central and Arctic Region, Department of Fisheries and Oceans: Winnipeg, MB, Canada, 1992. [Google Scholar]
- Romão, F.; Quaresma, A.L.; Santos, J.M.; Amaral, S.D.; Branco, P.; Pinheiro, A.N. Multislot Fishway Improves Entrance Performance and Fish Transit Time over Vertical Slots. Water 2021, 13, 275. [Google Scholar] [CrossRef]
- Pena, L.; Puertas, J.; Bermúdez, M.; Cea, L.; Pena, E. Conversion of Vertical Slot Fishways to Deep Slot Fishways to Maintain Operation during Low Flows: Implications for Hydrodynamics. Sustainability 2018, 10, 2406. [Google Scholar] [CrossRef] [Green Version]
- Lupandin, A.I. Effect of Flow Turbulence on Swimming Speed of Fish. Biol. Bull. 2005, 32, 461–466. [Google Scholar] [CrossRef]
- Silva, A.T.; Katopodis, C.; Santos, J.M.; Ferreira, M.T.; Pinheiro, A.N. Cyprinid swimming behaviour in response to turbulent flow. Ecol. Eng. 2012, 44, 314–328. [Google Scholar] [CrossRef] [Green Version]
- Webb, P.W.; Weihs, D. Stability versus Maneuvering: Challenges for Stability during Swimming by Fishes. Integr. Comp. Biol. 2015, 55, 753–764. [Google Scholar] [CrossRef] [Green Version]
- Tritico, H.M.; Cotel, A.J. The effects of turbulent eddies on the stability and critical swimming speed of creek chub (Semotilus atromaculatus). J. Exp. Biol. 2010, 213, 2284–2293. [Google Scholar] [CrossRef] [Green Version]
- Bermúdez, M.; Puertas, J.; Cea, L.; Pena, L.; Balairón, L. Influence of pool geometry on the biological efficiency of vertical slot fishways. Ecol. Eng. 2010, 36, 1355–1364. [Google Scholar] [CrossRef]
- Hinch, S.G.; Rand, P.S. Optimal swimming speeds and forward-assisted propulsion: Energy-conserving behaviours of upriver-migrating adult salmon. Can. J. Fish. Aquat. Sci. 2000, 57, 2470–2478. [Google Scholar] [CrossRef]
- Liao, J.C.; Beal, D.N.; Lauder, G.V.; Triantafyllou, M.S. Fish Exploiting Vortices Decrease Muscle Activity. Science 2003, 302, 1566–1569. [Google Scholar] [CrossRef]
- Gao, Z.; Andersson, H.I.; Dai, H.; Jiang, F.; Zhao, L. A new Eulerian–Lagrangian agent method to model fish paths in a vertical slot fishway. Ecol. Eng. 2016, 88, 217–225. [Google Scholar] [CrossRef] [Green Version]
- Cotel, A.J.; Webb, P.W. Living in a Turbulent World—A New Conceptual Framework for the Interactions of Fish and Eddies. Integr. Comp. Biol. 2015, 55, 662–672. [Google Scholar] [CrossRef] [Green Version]
- Fuentes-Pérez, J.F.; Sanz-Ronda, F.J.; de Azagra, A.M.; García-Vega, A. Non-uniform hydraulic behavior of pool-weir fishways: A tool to optimize its design and performance. Ecol. Eng. 2016, 86, 5–12. [Google Scholar] [CrossRef]
- O’Connor, J.; Stuart, I.; Jones, M. Guidelines for the Design, Approval and Construction of Fishways; Arthur Rylah Institute for Environmental Research and Department of Environment, Land, Water and Planning: Melbourne, Australia, 2017; p. 60. [Google Scholar]
- Khodier, M.A.; Tullis, B.P. Fish Passage Behavior for Severe Hydraulic Conditions in Baffled Culverts. J. Hydraul. Eng. 2014, 140, 322–327. [Google Scholar] [CrossRef]
- Calluaud, D.; Pineau, G.; Texier, A.; David, L. Modification of vertical slot fishway flow with a supplementary cylinder. J. Hydraul. Res. 2014, 52, 614–629. [Google Scholar] [CrossRef]
- Plaut, I. Critical swimming speed: Its ecological relevance. Comp. Biochem. Physiol. Part A Mol. Integr. Physiol. 2001, 131, 41–50. [Google Scholar] [CrossRef]
- Marriner, B.A.; Baki, A.B.M.; Zhu, D.Z.; Thiem, J.D.; Cooke, S.J.; Katopodis, C. Field and numerical assessment of turning pool hydraulics in a vertical slot fishway. Ecol. Eng. 2014, 63, 88–101. [Google Scholar] [CrossRef]
- Branco, P.; Santos, J.M.; Katopodis, C.; Pinheiro, A.; Ferreira, M.T. Pool-type fishways: Two different morpho-ecological cyprinid species facing plunging and streaming flows. PLoS ONE 2013, 8, e65089. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Wang, X.; Xuan, G.; Liang, D. Effect of parameters of pool geometry on flow characteristics in low slope vertical slot fishways. J. Hydraul. Res. 2020, 58, 395–407. [Google Scholar] [CrossRef]
- An, R.; Li, J.; Liang, R.; Tuo, Y. Three-dimensional simulation and experimental study for optimising a vertical slot fishway. J. Hydro-Environ. Res. 2016, 12, 119–129. [Google Scholar] [CrossRef]
- Quaranta, E.; Katopodis, C.; Revelli, R.; Comoglio, C. Turbulent flow field comparison and related suitability for fish passage of a standard and a simplified low-gradient vertical slot fishway. River Res. Appl. 2017, 33, 1295–1305. [Google Scholar] [CrossRef]
- Bombač, M.; Novak, G.; Mlačnik, J.; Četina, M. Extensive field measurements of flow in vertical slot fishway as data for validation of numerical simulations. Ecol. Eng. 2015, 84, 476–484. [Google Scholar] [CrossRef]
- Guo, Z.; Sun, X.; Dong, Z. An Experimental Study of Turbulent Structures in a Flat-Crested Weir-Type Fishway. Appl. Sci. 2019, 9, 40. [Google Scholar] [CrossRef] [Green Version]
- Yagci, O. Hydraulic aspects of pool-weir fishways as ecologically friendly water structure. Ecol. Eng. 2010, 36, 36–46. [Google Scholar] [CrossRef]
- Duguay, J.M.; Lacey, R.W.J.; Gaucher, J. A case study of a pool and weir fishway modeled with OpenFOAM and FLOW-3D. Ecol. Eng. 2017, 103, 31–42. [Google Scholar] [CrossRef]
- Cotel, A.J.; Webb, P.W. The Challenge of Understanding and Quantifying Fish Responses to Turbulence-Dominated Physical Environments. In Proceedings of the Natural Locomotion in Fluids and on Surfaces, Minneapolis, MN, USA, 1–5 June 2010; Childress, S., Hosoi, A., Schultz, W.W., Wang, J., Eds.; Springer: New York, NY, USA, 2012; pp. 15–33. [Google Scholar]
- Noonan, M.J.; Grant, J.W.A.; Jackson, C.D. A quantitative assessment of fish passage efficiency. Fish Fish. 2012, 13, 450–464. [Google Scholar] [CrossRef]
- Hatry, C.; Binder, T.R.; Thiem, J.D.; Hasler, C.T.; Smokorowski, K.E.; Clarke, K.D.; Katopodis, C.; Cooke, S.J. The status of fishways in Canada: Trends identified using the national CanFishPass database. Rev. Fish Biol. Fish. 2013, 23, 271–281. [Google Scholar] [CrossRef]
- Maerten, E.; Eens, M.; Knaepkens, G. Performance of a pool-and-weir fish pass for small bottom-dwelling freshwater fish species in a regulated lowland river. Anim. Biol. 2007, 57, 423–432. [Google Scholar] [CrossRef]
- Rossi, J.B.; Sanagiotto, D.G. Pool-type Fishway with Orifices: 3D Numerical Simulation of the Flow. J. Multidiscip. Eng. Sci. Technol. 2020, 7, 12293–12300. [Google Scholar]
- Larinier, M. Pool fishways, pre-barrages and natural bypass channels. Bull. Français De La Pêche Et De La Piscic. 2002, 364, 54–82. [Google Scholar] [CrossRef] [Green Version]
- Wu, S.; Rajaratnam, N.; Katopodis, C. Structure of Flow in Vertical Slot Fishway. J. Hydraul. Eng. 1999, 125, 351–360. [Google Scholar] [CrossRef]
- Ordeix, M.; Pou-Rovira, Q.; Sellares, N.; Bardina, M.; Casamitjana, A.; Sola, C.; Munne, A. Fish pass assessment in the rivers of Catalonia (NE Iberian Peninsula). A case study of weirs associated with hydropower plants and gauging stations. Limnetica 2011, 30, 405–426. [Google Scholar] [CrossRef]
- Stephens, T.A.; Bledsoe, B.P.; Fox, B.D.; Kolden, E.; Kondratieff, M.C. Effects of whitewater parks on fish passage: A spatially explicit hydraulic analysis. Ecol. Eng. 2015, 83, 305–318. [Google Scholar] [CrossRef] [Green Version]
- Schilt, C.R. Developing fish passage and protection at hydropower dams. Appl. Anim. Behav. Sci. 2007, 104, 295–325. [Google Scholar] [CrossRef]
- Belletti, B.; Garcia de Leaniz, C.; Jones, J.; Bizzi, S.; Börger, L.; Segura, G.; Castelletti, A.; van de Bund, W.; Aarestrup, K.; Barry, J.; et al. More than one million barriers fragment Europe’s rivers. Nature 2020, 588, 436–441. [Google Scholar] [CrossRef]
- Szabo-Meszaros, M.; Navaratnam, C.U.; Aberle, J.; Silva, A.T.; Forseth, T.; Calles, O.; Fjeldstad, H.-P.; Alfredsen, K. Experimental hydraulics on fish-friendly trash-racks: An ecological approach. Ecol. Eng. 2018, 113, 11–20. [Google Scholar] [CrossRef]
- Odeh, M.; Noreika, J.F.; Haro, A.; Maynard, A.; Castro-Santos, T.; Cada, G.F. Evaluation of the Effects of Turbulence on the Behavior of Migratory Fish; U.S. Department of Energy: Portland, OR, USA, 2002; p. 46.
- Silva, A.T.; Santos, J.M.; Ferreira, M.T.; Pinheiro, A.N.; Katopodis, C. Effects of water velocity and turbulence on the behaviour of Iberian barbel (Luciobarbus bocagei, Steindachner 1864) in an experimental pool-type fishway. River Res. Appl. 2011, 27, 360–373. [Google Scholar] [CrossRef]
- Santos, J.M.; Silva, A.; Katopodis, C.; Pinheiro, P.; Pinheiro, A.; Bochechas, J.; Ferreira, M.T. Ecohydraulics of pool-type fishways: Getting past the barriers. Ecol. Eng. 2012, 48, 38–50. [Google Scholar] [CrossRef]
- FAO. Fish Passes–Design, Dimensions and Monitoring; Food and Agriculture Organization of the United Nations: Rome, Italy, 2002; p. 119. [Google Scholar]
- Armstrong, G.S.; Aprahamian, M.W.; Fewings, G.A.; Gough, P.J.; Reader, N.A.; Varallo, P.V. Environment Agency Fish Pass Manual: Guidance Notes on the Legislation, Selection and Approval of Fish Passes in England And Wales; GEHO 0910 BTBP-E-E; Almondsbury: Bristol, UK, 2010; p. 369. [Google Scholar]
- Mallen-Cooper, M. Taking the mystery out of migration. In Proceedings of the Workshop on Fish Movement and Migration, Bendigo, Australia, 28–29 September 1999; Hancock, D.A., Smith, D.C., Koehn, J.D., Eds.; Australian Society for Fish Biology: Bendigo, Australia, 2000; pp. 101–111. [Google Scholar]
- Tarrade, L.; Texier, A.; David, L.; Larinier, M. Topologies and measurements of turbulent flow in vertical slot fishways. Hydrobiologia 2008, 609, 177. [Google Scholar] [CrossRef] [Green Version]
- Kucukali, S. Flow and Turbulence Measurements in a Diagonal Brush Fish Pass: A Field Study. In Proceedings of the 7th IAHR International Symposium on Hydraulic Structures, Aachen, Germany, 15–18 May 2018. [Google Scholar]
- Hogan, Z. Review of Migratory Freshwater Fish. In Proceedings of the Convention on Migratory Species, Bergen, Norway, 20–25 November 2011; p. 37. [Google Scholar]
- Gilja, G.; Ocvirk, E.; Cikojević, A. Experimental investigation of flow field in a physical fishway model. In Proceedings of the 16th International Symposium Water Management & Hydraulic Engineering WMHE 2019, Skopje, North Macedonia, 5–7 September 2019; pp. 1–12. [Google Scholar]
- Ocvirk, E.; Gilja, G.; Bujak, D.; Cikojević, A.; Jelić, D. Nomogrami za proračun funkcionalnosti tehničkih ribljih staza na malim pragovima. Hrvat. Vode 2020, 28, 9–20. [Google Scholar]
- Baki Abul Basar, M.; Zhu David, Z.; Rajaratnam, N. Turbulence Characteristics in a Rock-Ramp-Type Fish Pass. J. Hydraul. Eng. 2015, 141, 04014075. [Google Scholar] [CrossRef]
- Wahl, T.L. Analyzing ADV Data Using WinADV. In Proceedings of the Joint Conference on Water Resources Engineering and Water Resources Planning & Management, Minneapolis, MN, USA, 30 July–2 August 2000; pp. 1–10. [Google Scholar]
- Martin, V.; Fisher, T.S.R.; Millar, R.G.; Quick, M.C. ADV Data Analysis for Turbulent Flows: Low Correlation Problem. In Proceedings of the Hydraulic Measurements and Experimental Methods Specialty Conference, Estes Park, CO, USA, 28 July–1 August 2002; pp. 1–10. [Google Scholar]
- Jesson, M.A.; Bridgeman, J.; Sterling, M. Novel software developments for the automated post-processing of high volumes of velocity time-series. Adv. Eng. Softw. 2015, 89, 36–42. [Google Scholar] [CrossRef] [Green Version]
- Goring, D.G.; Nikora, V.I. Despiking Acoustic Doppler Velocimeter Data. J. Hydraul. Eng. 2002, 128, 117–126. [Google Scholar] [CrossRef] [Green Version]
- Wahl, T.L. Discussion of ‘‘Despiking Acoustic Doppler Velocimeter Data’’ by Derek G. Goring and Vladimir I. Nikora. J. Hydraul. Eng. 2003, 129, 484–487. [Google Scholar] [CrossRef] [Green Version]



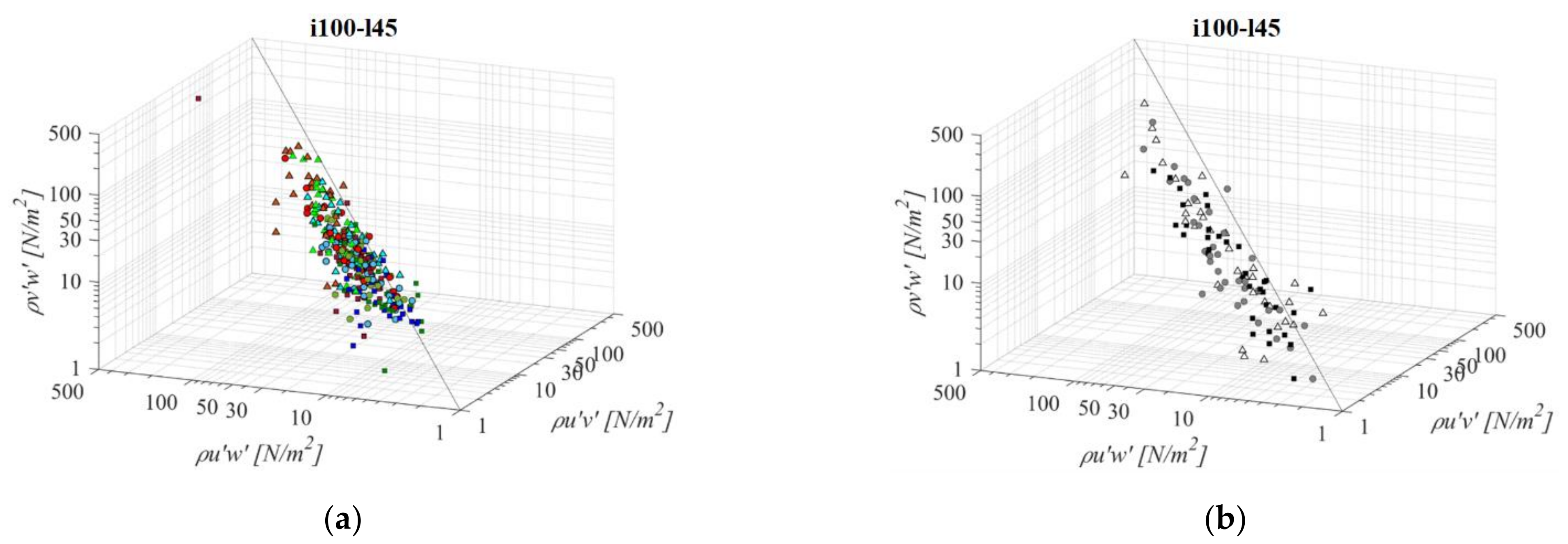

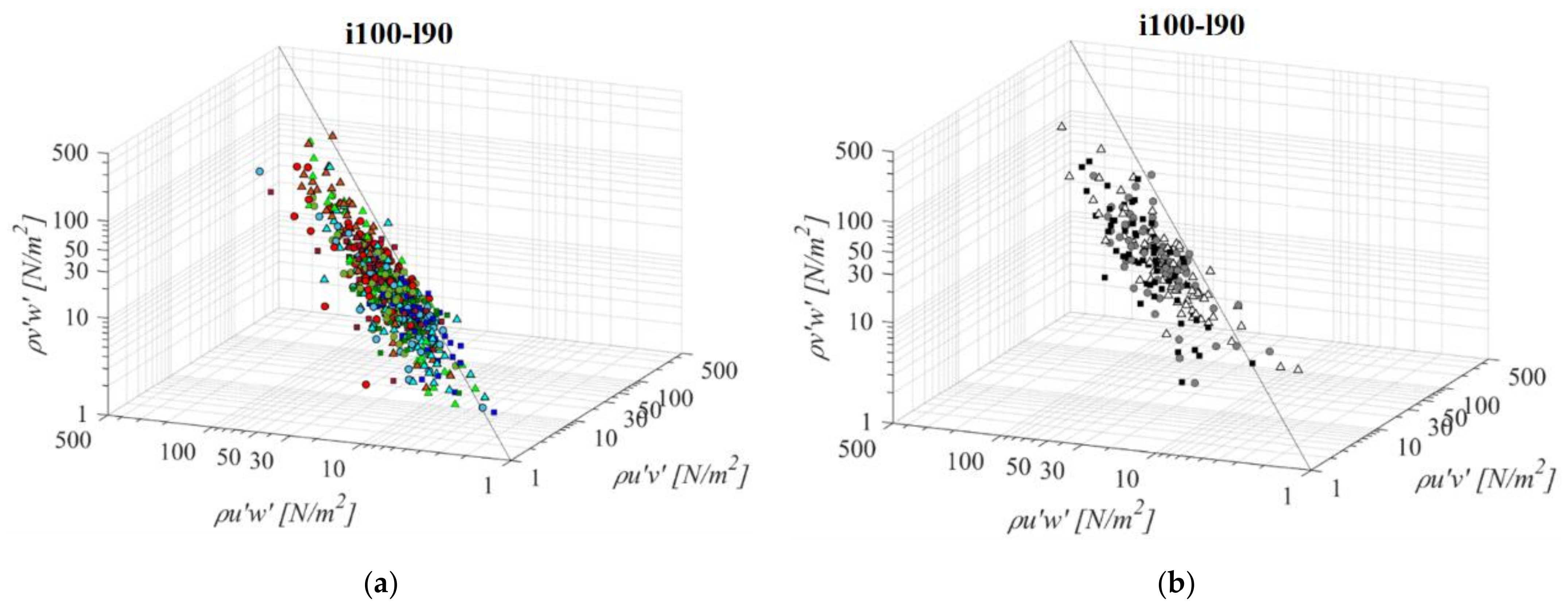
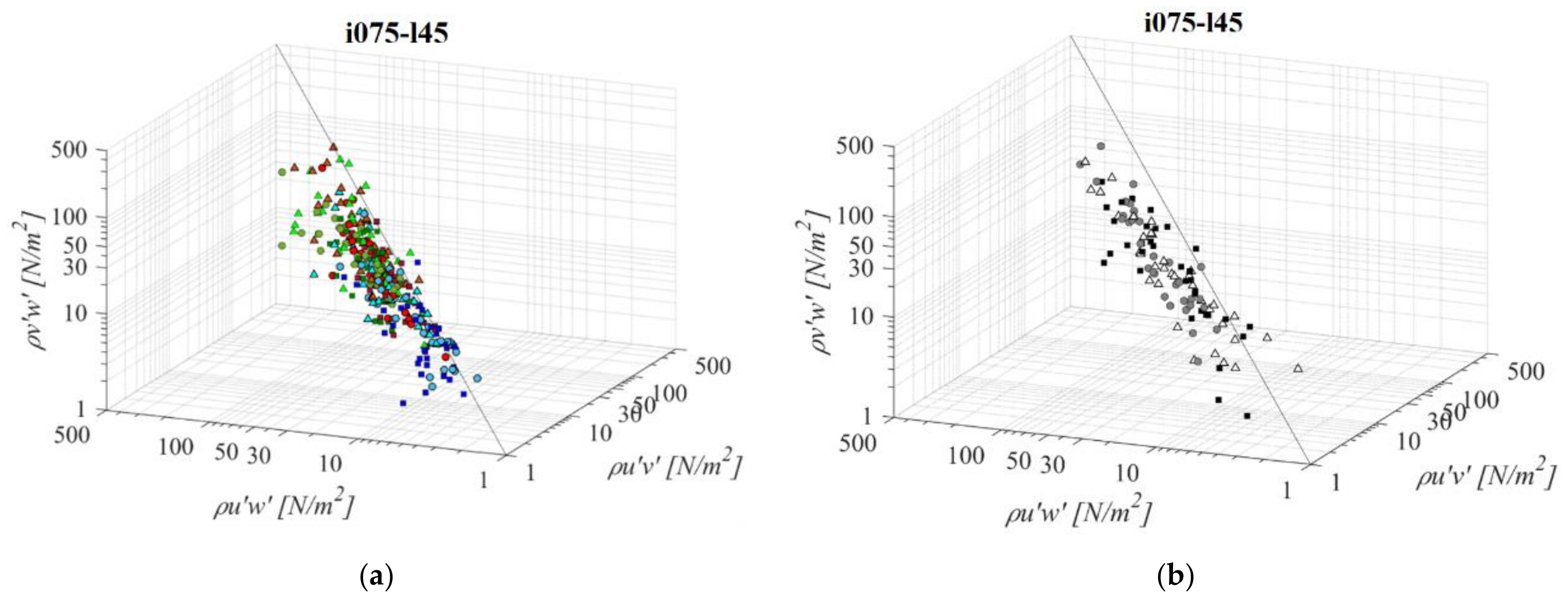
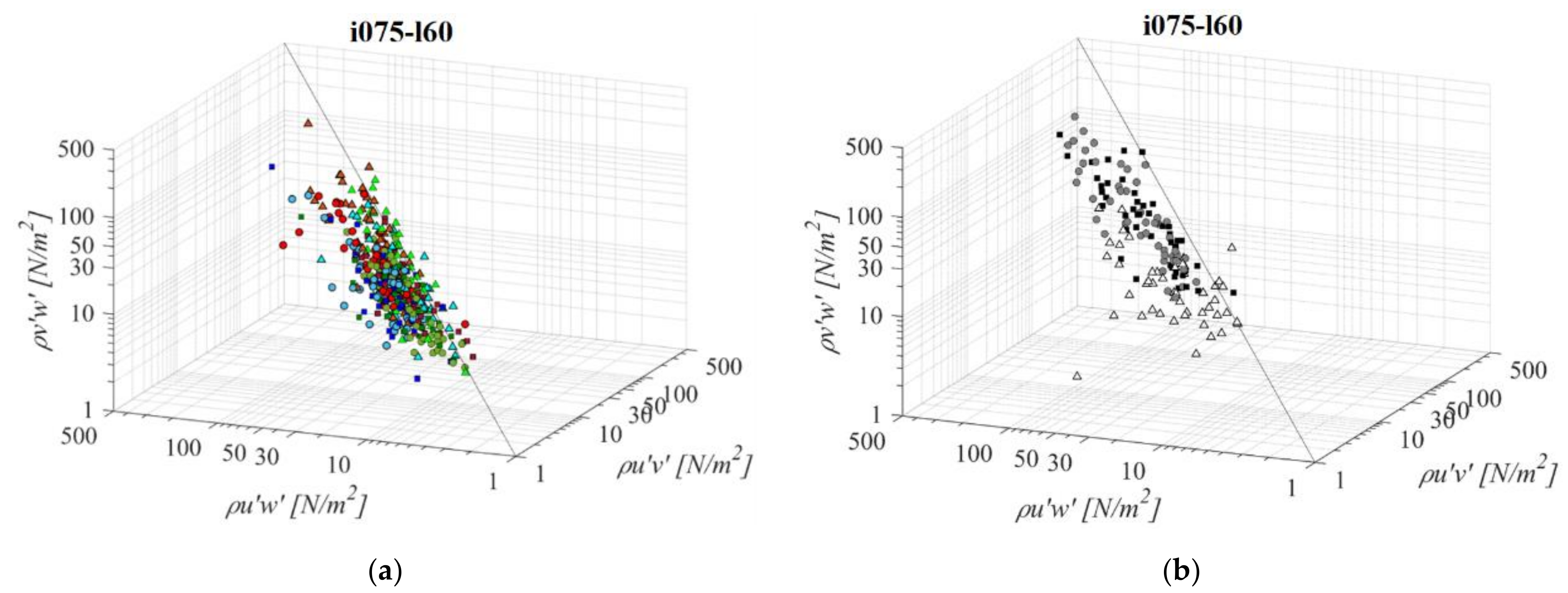

| Fishway | Orifice | Bottom Slope | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| i075 | i100 | i125 | ||||||||
| Pool Length | ||||||||||
| l45 | l60 | l90 | l45 | l60 | l90 | l45 | l60 | l90 | ||
| PO | o8 | 87/98 | 75/92 | 81/96 | 87/96 | 91/98 | 82/93 | 74/92 | 89/93 | 81/94 |
| o10 | 56/80 | 74/93 | 58/83 | 76/90 | 71/92 | 67/83 | 77/90 | 64/79 | 63/87 | |
| o12 | 63/84 | 53/79 | 45/70 | 65/82 | 55/79 | 58/76 | 64/84 | 52/75 | 51/76 | |
| VS | 18/59 | 27/46 | 57/82 | 23/56 | 17/42 | 62/79 | 40/62 | 32/62 | 78/94 | |
| Fishway | Orifice | Bottom Slope | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| i075 | i100 | i125 | ||||||||
| Pool Length | ||||||||||
| l45 | l60 | l90 | l45 | l60 | l90 | l45 | l60 | l90 | ||
| PO | o8 | 97/100 | 95/99 | 94/98 | 97/100 | 96/99 | 97/99 | 92/98 | 96/100 | 98/99 |
| o10 | 82/93 | 93/98 | 82/93 | 96/99 | 91/98 | 96/100 | 92/98 | 90/97 | 94/99 | |
| o12 | 87/98 | 82/95 | 76/91 | 88/97 | 83/95 | 80/94 | 89/97 | 79/92 | 86/96 | |
| VS | 86/96 | 66/85 | 69/89 | 93/98 | 71/85 | 69/89 | 90/97 | 77/90 | 72/84 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gilja, G.; Ocvirk, E.; Fliszar, R. Experimental Investigation of the Reynolds Shear Stress Exceedance Rate for the Injury and Disorientation Biocriteria Boundary in the Pool-Orifice and Vertical Slot Type Fishways. Appl. Sci. 2021, 11, 7708. https://doi.org/10.3390/app11167708
Gilja G, Ocvirk E, Fliszar R. Experimental Investigation of the Reynolds Shear Stress Exceedance Rate for the Injury and Disorientation Biocriteria Boundary in the Pool-Orifice and Vertical Slot Type Fishways. Applied Sciences. 2021; 11(16):7708. https://doi.org/10.3390/app11167708
Chicago/Turabian StyleGilja, Gordon, Eva Ocvirk, and Robert Fliszar. 2021. "Experimental Investigation of the Reynolds Shear Stress Exceedance Rate for the Injury and Disorientation Biocriteria Boundary in the Pool-Orifice and Vertical Slot Type Fishways" Applied Sciences 11, no. 16: 7708. https://doi.org/10.3390/app11167708
APA StyleGilja, G., Ocvirk, E., & Fliszar, R. (2021). Experimental Investigation of the Reynolds Shear Stress Exceedance Rate for the Injury and Disorientation Biocriteria Boundary in the Pool-Orifice and Vertical Slot Type Fishways. Applied Sciences, 11(16), 7708. https://doi.org/10.3390/app11167708








