Positioning Parameter Determination Based on Statistical Regression Applied to Autonomous Underwater Vehicle
Abstract
:1. Introduction
- (a)
- The average absolute error is used as the criterion discard or replacement, so the data is smoothed by the combination of mean filtering and linear smoothing;
- (b)
- The positioning accuracy is improved by SRAKF that can calculate the accurate solutions of the predicted error covariance matrix and measurement noise matrix;
- (c)
- The unscented transformation is used to calculate the nonlinear integral operation. This method is conductive to increasing the state estimation accuracy by suppressing the truncation error caused by numerical integration.
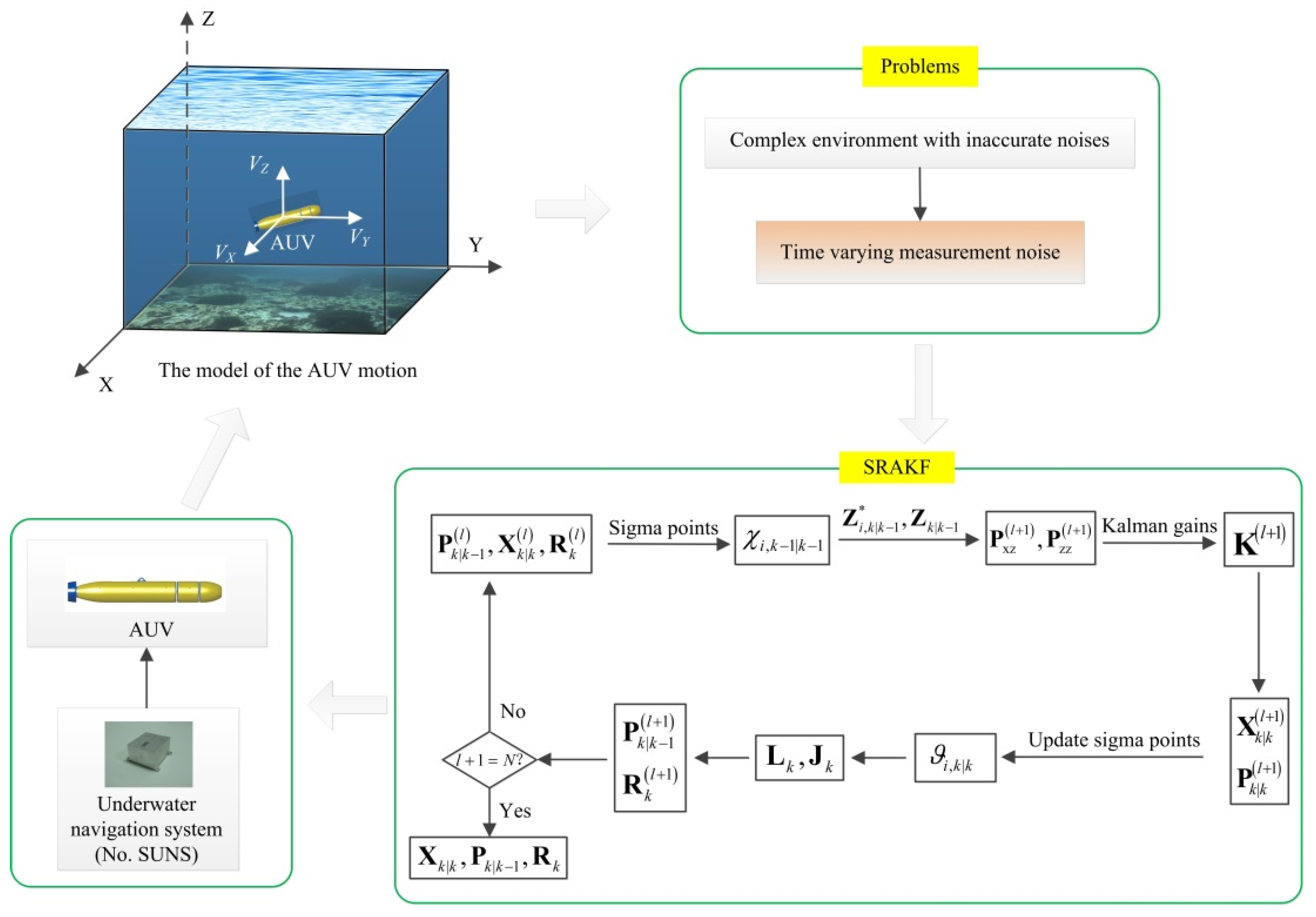
2. Problem Statement and Preliminaries
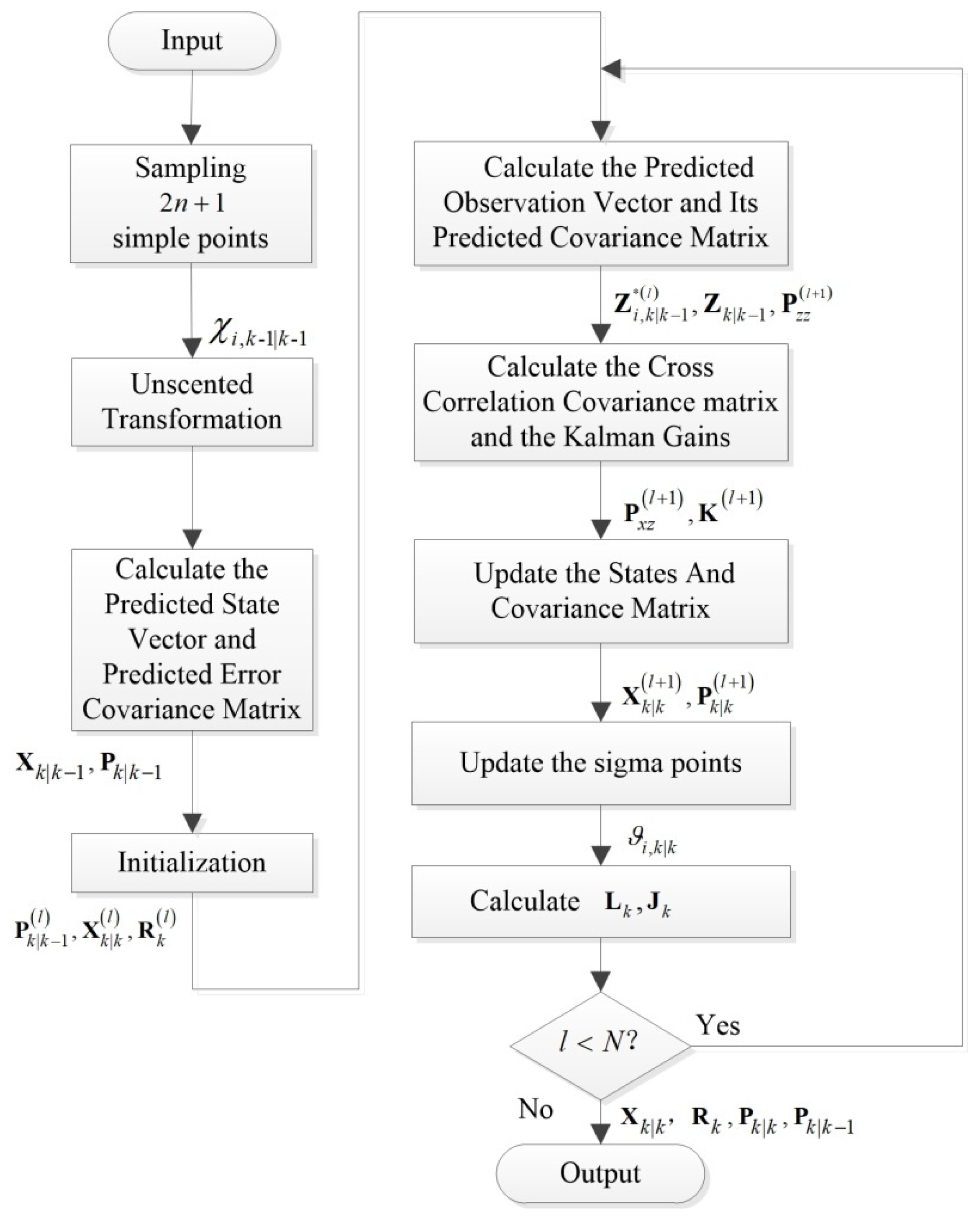
3. The Statistical Regression Adaptive Kalman Filtering Algorithm
3.1. The Expectation Approach
3.2. The Maximization Approach
3.3. The Analysis of the Convergence of the Proposed Algorithm
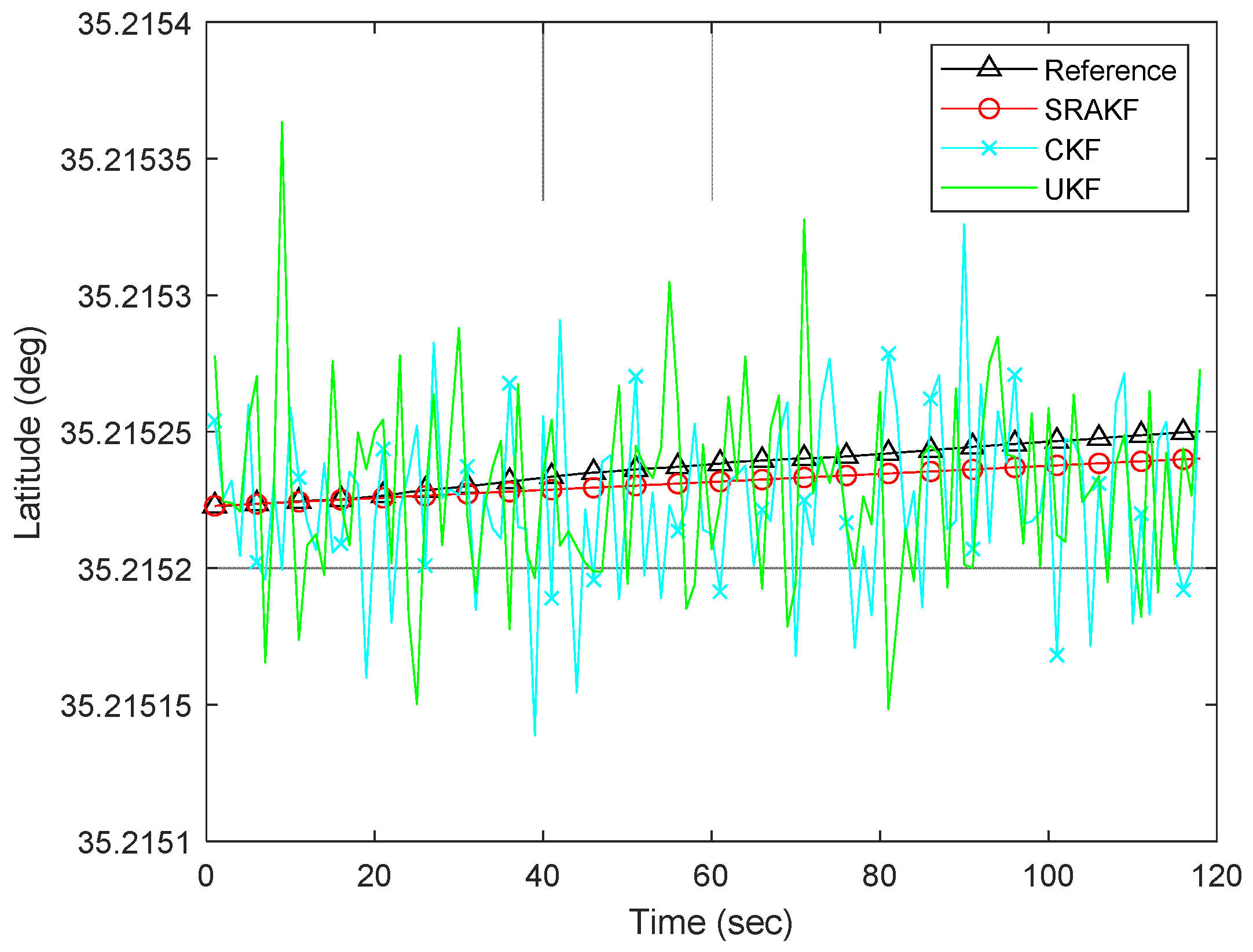
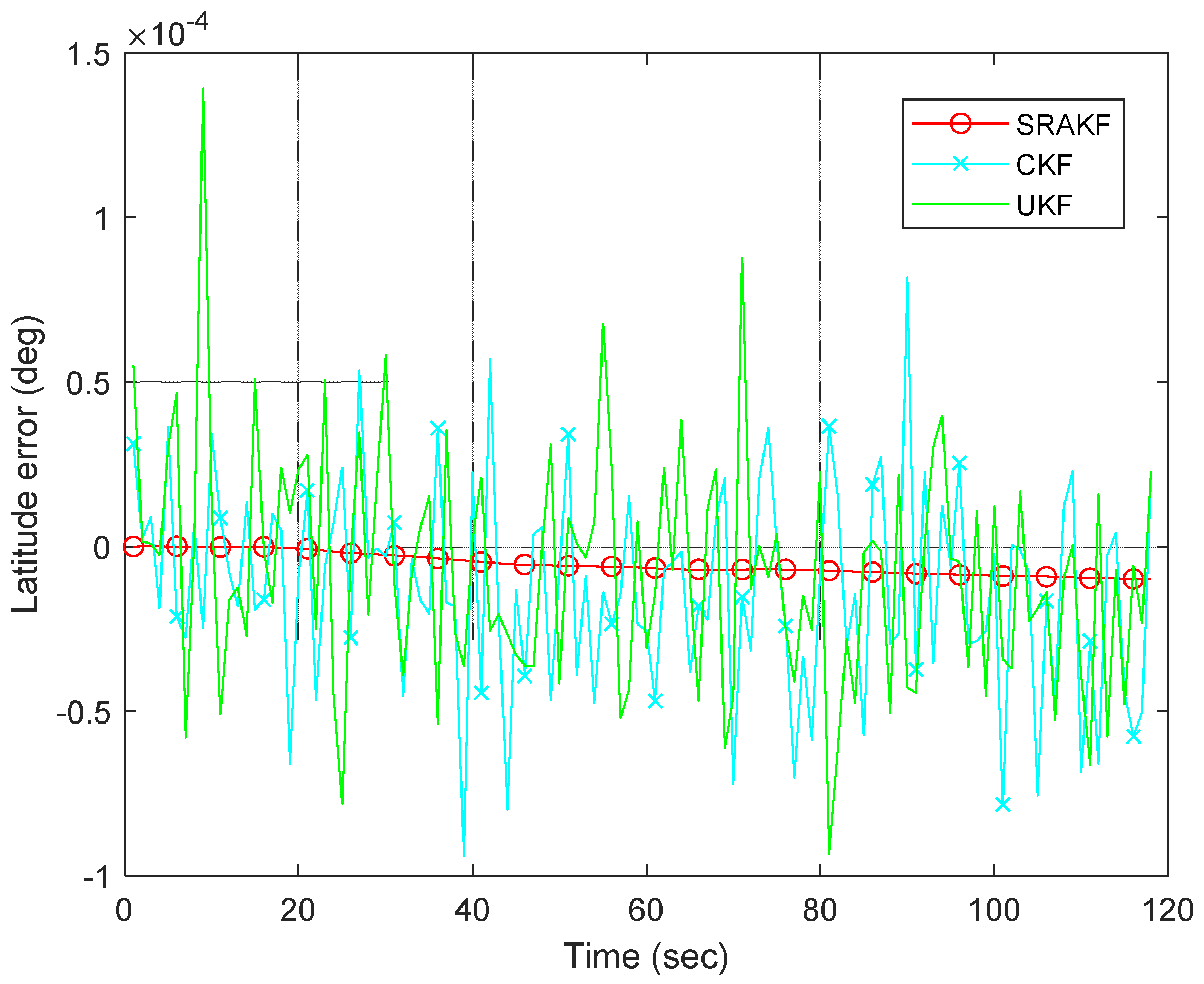
4. Lake Trial Experiments and Results
4.1. The Accuracy Verification of the SRAKF
4.1.1. Case 1: Surface Lake Trial
4.1.2. Case 2: Underwater Lake Trial
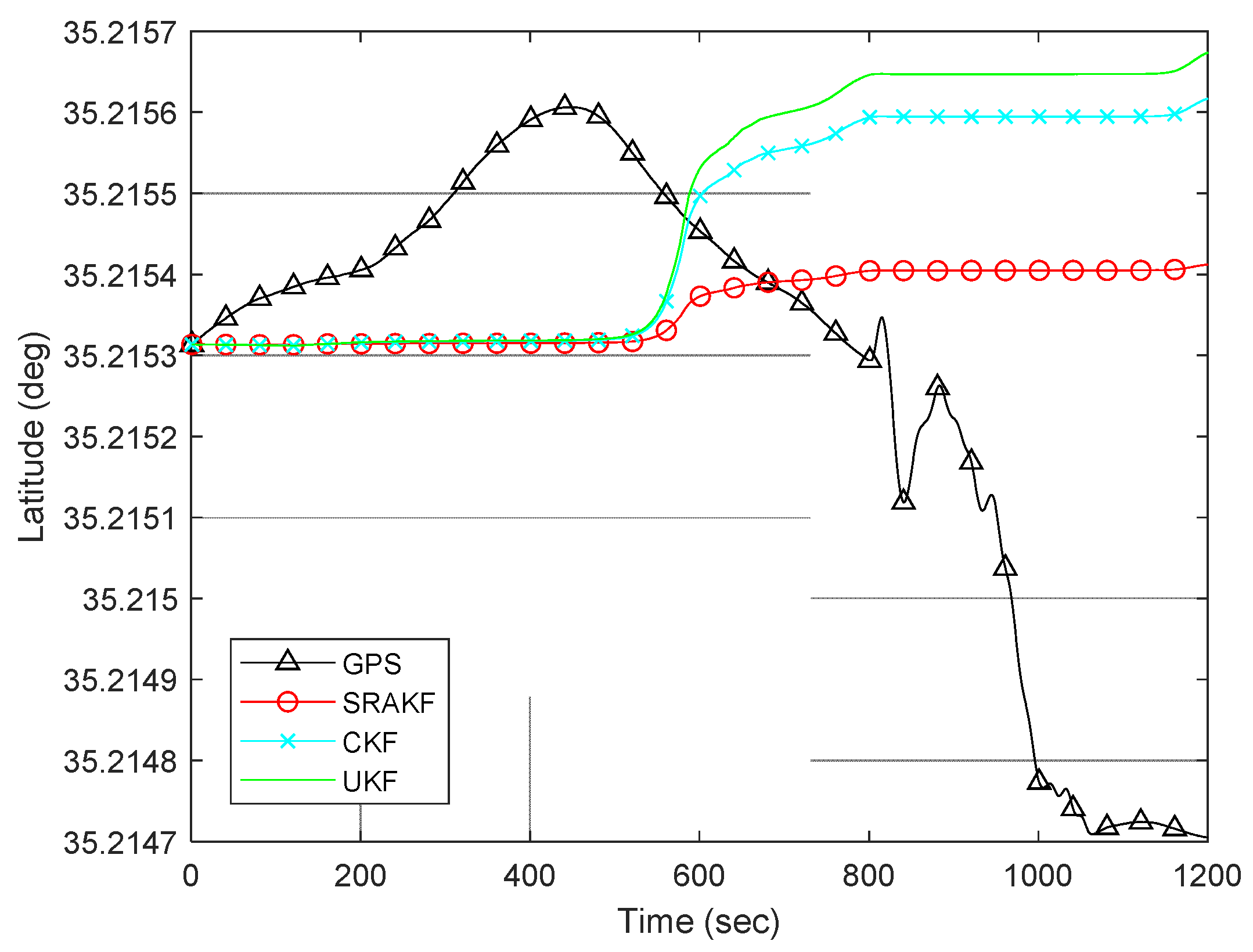
4.2. The Robustness Lake Trial
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Walker, C.R.; Stringfield, J.Q.; Wolbrecht, E.T.; Anderson, M.J.; Canning, J.R.; Bean, T.A.; Odell, D.L.; Frenzel, J.F.; Edwards, D.B. Measurement of the Magnetic Signature of a Moving Surface Vessel with Multiple Magnetometer-Equipped AUVs. Ocean Eng. 2013, 64, 80–87. [Google Scholar] [CrossRef]
- Eriksen, C.C.; Osse, T.J.; Light, R.D.; Wen, T.; Lehman, T.W.; Sabin, P.L.; Ballard, J.W.; Chiodi, A.M. Seaglider: A Long-Range Autonomous Underwater Vehicle for Oceanographic Research. IEEE J. Ocean. Eng. 2001, 26, 424–436. [Google Scholar] [CrossRef] [Green Version]
- Qin, J.H.; Wang, S.; Kang, Y.; Liu, Q.C. Circular Formation Algorithms for Multiple Nonholonomic Mobile Robots: An Optimization-based Approach. IEEE Trans. Ind. Electron. 2019, 66, 3693–3701. [Google Scholar] [CrossRef]
- Stutters, L.; Liu, H.H.; Tiltman, C.; Brown, D.J. Navigation Technologies for Autonomous Underwater Vehicles. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2008, 38, 581–589. [Google Scholar] [CrossRef]
- Grenon, G.; An, P.E.; Smith, S.M.; Healey, A.J. Enhancement of the Inertial Navigation System for the Morpheus Autonomous Underwater Vehicles. IEEE J. Ocean. Eng. 2001, 26, 548–560. [Google Scholar] [CrossRef]
- Morton, R.A.; Leach, M.P.; Paine, J.G.; Cardoza, M.A. Monitoring Beach Changes Using GPS Surveying Techniques. J. Coast. Res. 1993, 9, 702–720. [Google Scholar]
- Watson, C.; Coleman, R.; Handsworth, R. Coastal Tide Gauge Calibration: A Case Study at Macquarie Island Using GPS Buoy Techniques. J. Coast. Res. 2008, 24, 1071–1079. [Google Scholar] [CrossRef]
- Crassidis, J.L.; Lai, K.L.; Harman, R.R. Real-Time Attitude-Independent Three-Axis Magnetometer Calibration. J. Guid. Control Dyn. 2005, 28, 114–117. [Google Scholar] [CrossRef]
- Xiong, K.; Liu, L.; Liu, Y. Non-Linear Robust Filter Design for Satellite Attitude Determination. IET Control Theory Appl. 2010, 4, 1222–1234. [Google Scholar] [CrossRef]
- Nemra, A.; Aouf, N. Robust INS/GPS Sensor Fusion for UAV Localization Using SDRE Nonlinear Filtering. IEEE Sens. J. 2010, 10, 789–798. [Google Scholar] [CrossRef] [Green Version]
- Yao, Q.J. Adaptive Finite-Time Sliding Mode Control Design for Finite-Time Fault-Tolerant Trajectory Tracking of Marine Vehicles with Input Saturation. J. Frankl. Inst. Eng. Appl. Math. 2020, 357, 13593–13619. [Google Scholar] [CrossRef]
- Huang, H.Q.; Shi, R.D.; Zhou, J.; Yang, Y.; Song, R.; Chen, J.F.; Wu, G.Q.; Zhang, J.J. Attitude Determination Method Integrating Square-Root Cubature Kalman Filter with Expectation-Maximization for Inertial Navigation System Applied to Underwater Glider. Rev. Sci. Instrum. 2019, 90, 095001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Y.; Zhang, H.; Xu, L.W.; Cao, C.H.; Gulliver, T.A. Adoption of Hybrid Time Series Neural Network in the Underwater Acoustic Signal Modulation Identification. J. Frankl. Inst. Eng. Appl. Math. 2020, 357, 13906–13922. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Hu, J.B. Robust Control for a Quadrotor Aircraft with Small Overshoot and High-Precision Position Tracking Performance. J. Frankl. Inst. Eng. Appl. Math. 2020, 357, 13386–13409. [Google Scholar] [CrossRef]
- Loebis, D.; Sutton, R.; Chudley, J.; Naeem, W. Adaptive Tuning of a Kalman Filter via Fuzzy Logic for an Intelligent AUV Navigation System. Control Eng. Pract. 2004, 12, 1531–1539. [Google Scholar] [CrossRef]
- Dong, L.Y.; Xu, H.L.; Feng, X.S.; Han, X.J.; Yu, C. An Adaptive Target Tracking Algorithm Based on EKF for AUV with Unknown Non-Gaussian Process Noise. Appl. Sci. 2020, 10, 3413. [Google Scholar] [CrossRef]
- Noureldin, A.; Karamat, T.B.; Eberts, M.D.; El-Shafie, A. Performance Enhancement of MEMS-Based INS/GPS Integration for Low-Cost Navigation Applications. IEEE Trans. Veh. Technol. 2009, 58, 1077–1096. [Google Scholar] [CrossRef]
- Huang, H.Q.; Chen, X.Y.; Zhang, B.; Wang, J. High Accuracy Navigation Information Estimation for Inertial System Using the Multi-Model EKF Fusing Adams Explicit Formula Applied to Underwater Gliders. ISA Trans. 2017, 66, 414–424. [Google Scholar] [CrossRef]
- Li, W.L.; Wu, W.Q.; Wang, J.L.; Lu, L.Q. A Fast SINS Initial Alignment Scheme for Underwater Vehicle Applications. J. Navig. 2013, 66, 181–198. [Google Scholar] [CrossRef] [Green Version]
- Julier, S.; Uhlmann, J.; Durrant-Whyte, H.F. A New Method for the Nonlinear Transformation of Means and Covariances in Filters and Estimators. IEEE Trans. Autom. Control 2000, 45, 477–482. [Google Scholar] [CrossRef] [Green Version]
- Zhou, H.; Zhao, H.; Huang, H.Q.; Zhao, X. A Cubature-Principle-Assisted IMM-Adaptive UKF Algorithm for Maneuvering Target Tracking Caused by Sensor Faults. Appl. Sci. 2017, 7, 1003. [Google Scholar] [CrossRef] [Green Version]
- Huang, Y.L.; Zhang, Y.G.; Chambers, J.A. A Novel Kullback–Leibler Divergence Minimization-Based Adaptive Student’s t-Filter. IEEE Trans. Signal Process. 2019, 67, 5417–5432. [Google Scholar] [CrossRef]
- Tong, X.; Su, Y.; Li, Z.F.; Si, C.W.; Han, G.W.; Ning, J.; Yang, F.H. A Double-Step Unscented Kalman Filter and HMM-Based Zero-Velocity Update for Pedestrian Dead Reckoning Using MEMS Sensors. IEEE Trans. Ind. Electron. 2020, 67, 581–591. [Google Scholar] [CrossRef]
- Chen, Y.; Lee, M.K.; Birla, M.B.; Li, H.J.; Li, G.M.; Duan, X.Y.; Wang, T.D.; Oldham, K.R. Motion Estimation for a Compact Electrostatic Microscanner via Shared Driving and Sensing Electrodes in Endomicroscopy. IEEE/ASME Trans. Mechatron. 2020, 25, 661–672. [Google Scholar] [CrossRef]
- Huang, H.Q.; Tang, J.C.; Zhang, B.; Chen, J.F.; Zhang, J.J.; Song, X. A Novel Nonlinear Algorithm for Non-Gaussian Noises and Measurement Information Loss in Underwater Navigation. IEEE Access 2020, 8, 118472–118484. [Google Scholar] [CrossRef]
- Cao, H.L.; Zhang, Y.J.; Han, Z.Q.; Shao, X.L.; Gao, J.Y.; Huang, K.; Shi, Y.B.; Tang, J.; Shen, C.; Liu, J. Pole-Zero-Temperature Compensation Circuit Design and Experiment for Dual-Mass MEMS Gyroscope Bandwidth Expansion. IEEE/ASME Trans. Mechatron. 2019, 24, 677–688. [Google Scholar] [CrossRef]
- Zhu, Y.X.; Cheng, X.H.; Hu, J.; Zhou, L.; Fu, J.B. A Novel Hybrid Approach to Deal with DVL Malfunctions for Underwater Integrated Navigation Systems. Appl. Sci. 2017, 7, 759. [Google Scholar] [CrossRef] [Green Version]
- Moon, T.K. The Expectation-Maximization Algorithm. IEEE Signal Process. Mag. 1996, 13, 47–60. [Google Scholar] [CrossRef]
- Gu, Y.; Liu, J.C.; Li, X.L.; Chou, Y.X.; Ji, Y. State Space Model Identification of Multirate Processes with Time-Delay Using the Expectation Maximization. J. Frankl. Inst. Eng. Appl. Math. 2019, 356, 1623–1639. [Google Scholar] [CrossRef]
- Huang, H.Q.; Tang, J.C.; Liu, C.; Zhang, B.; Wang, B. Variational Bayesian-Based Filter for Inaccurate Input in Underwater Navigation. IEEE Trans. Veh. Technol. 2021. [Google Scholar] [CrossRef]
- Huang, H.Q.; Chen, X.Y.; Zhou, Z.K.; Liu, H.; Lv, C.P. Study on INS/DR Integration Navigation System Using EKF/RK4 Algorithm for Underwater Gliders. J. Mar. Sci. Technol. 2017, 25, 84–95. [Google Scholar]
- Huang, H.Q.; Zhou, J.; Zhang, J.; Yang, Y.; Song, R.; Chen, J.F.; Zhang, J.J. Attitude Estimation Fusing Quasi-Newton and Cubature Kalman Filtering for Inertial Navigation System Aided with Magnetic Sensors. IEEE Access 2018, 6, 28755–28767. [Google Scholar] [CrossRef]
- Ghahramani, Z. Learning Dynamic Bayesian Network, Adaptive Processing of Temporal Information, Lecture Notes in Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Bar-Shalom, Y.; Li, X.R.; Kirubarajan, T. Estimation with Applications to Tracking and Navigation; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Lefebvre, T.; Bruyninckx, H.; De Schutter, J. Comment on “A New Method for the Nonlinear Transformation of Means and Covariances in Filters and Estimators”. IEEE Trans. Autom. Control 2001, 47, 1406–1408. [Google Scholar] [CrossRef] [Green Version]
- Schön, T.B.; Wills, A.; Ninness, B. System Identification of Nonlinear State-Space Models. Automatica 2011, 47, 39–49. [Google Scholar] [CrossRef] [Green Version]
- Zhao, S.Y.; Liu, F. Bayesian Estimation for Jump Markov Linear Systems with Non-Homogeneous Transition Probabilities. J. Frankl. Inst. Eng. Appl. Math. 2013, 350, 3029–3044. [Google Scholar] [CrossRef]


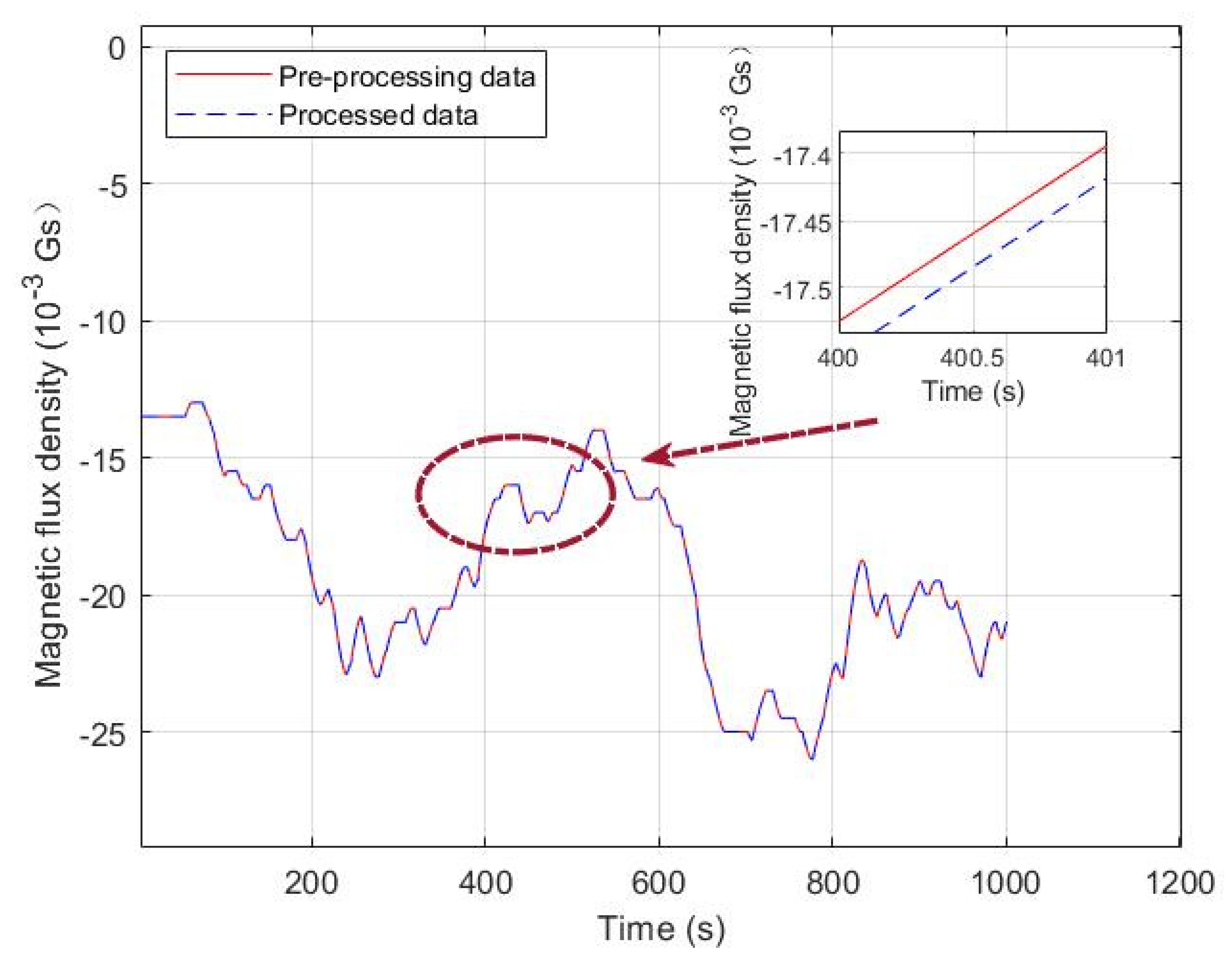

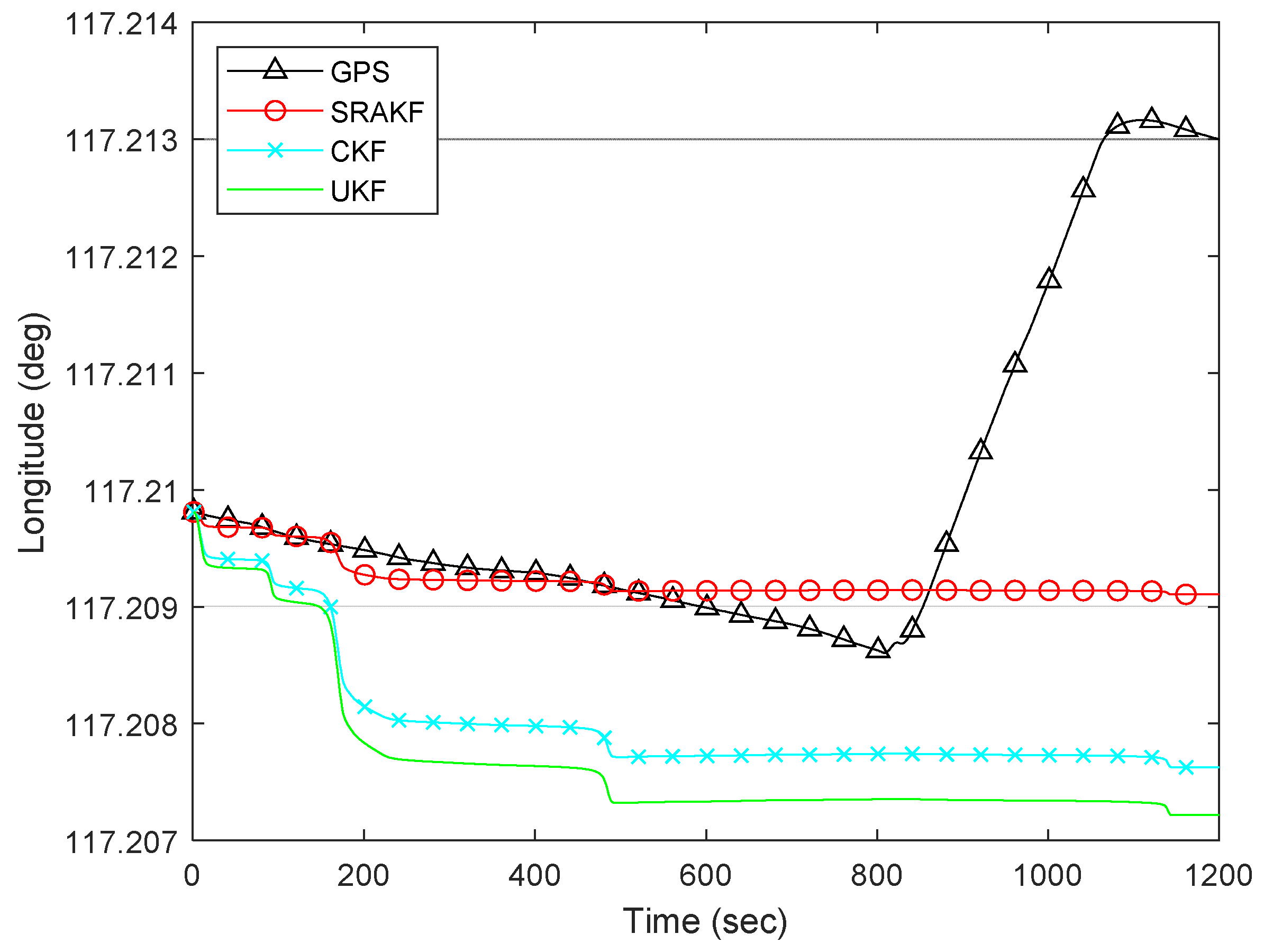
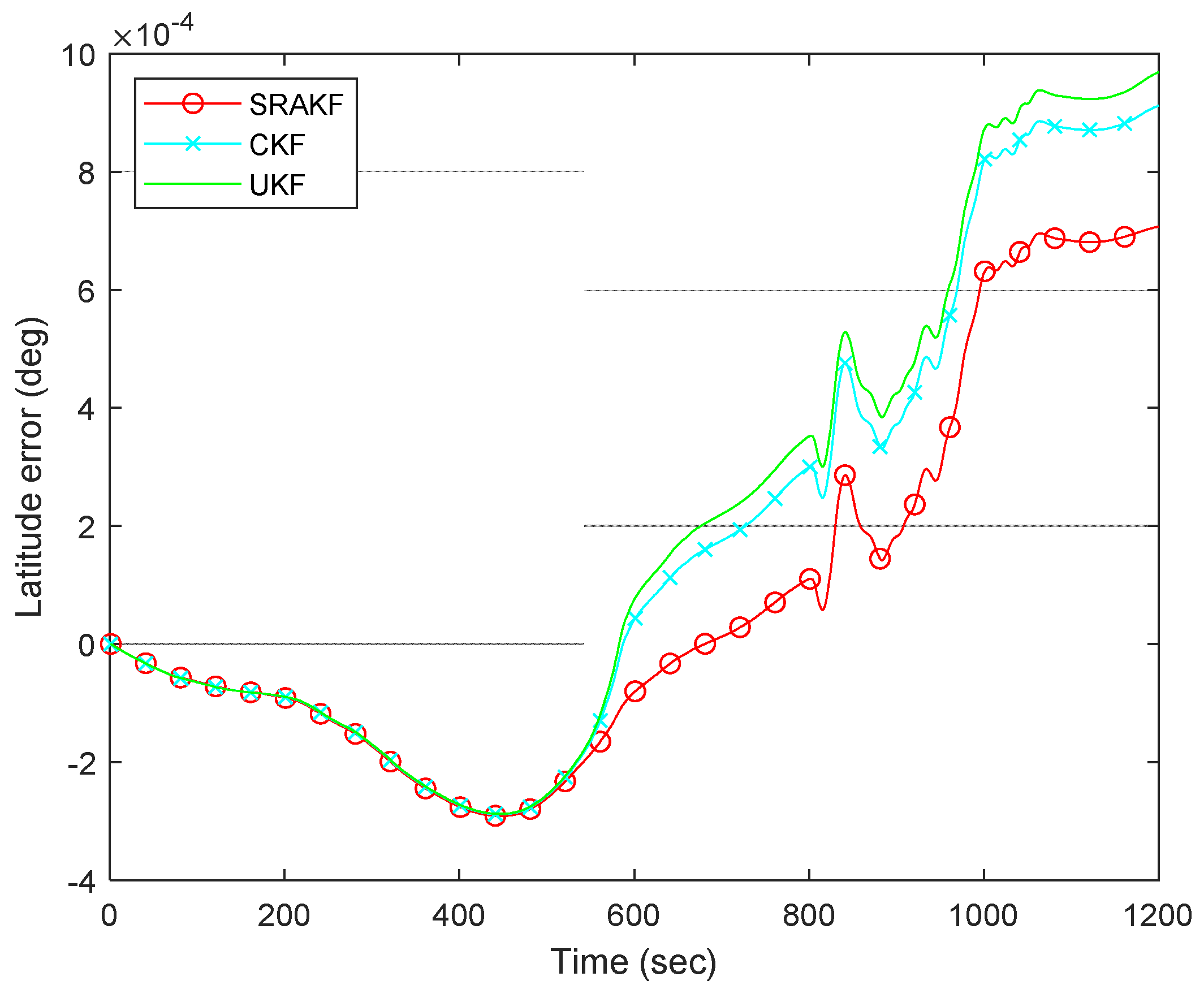
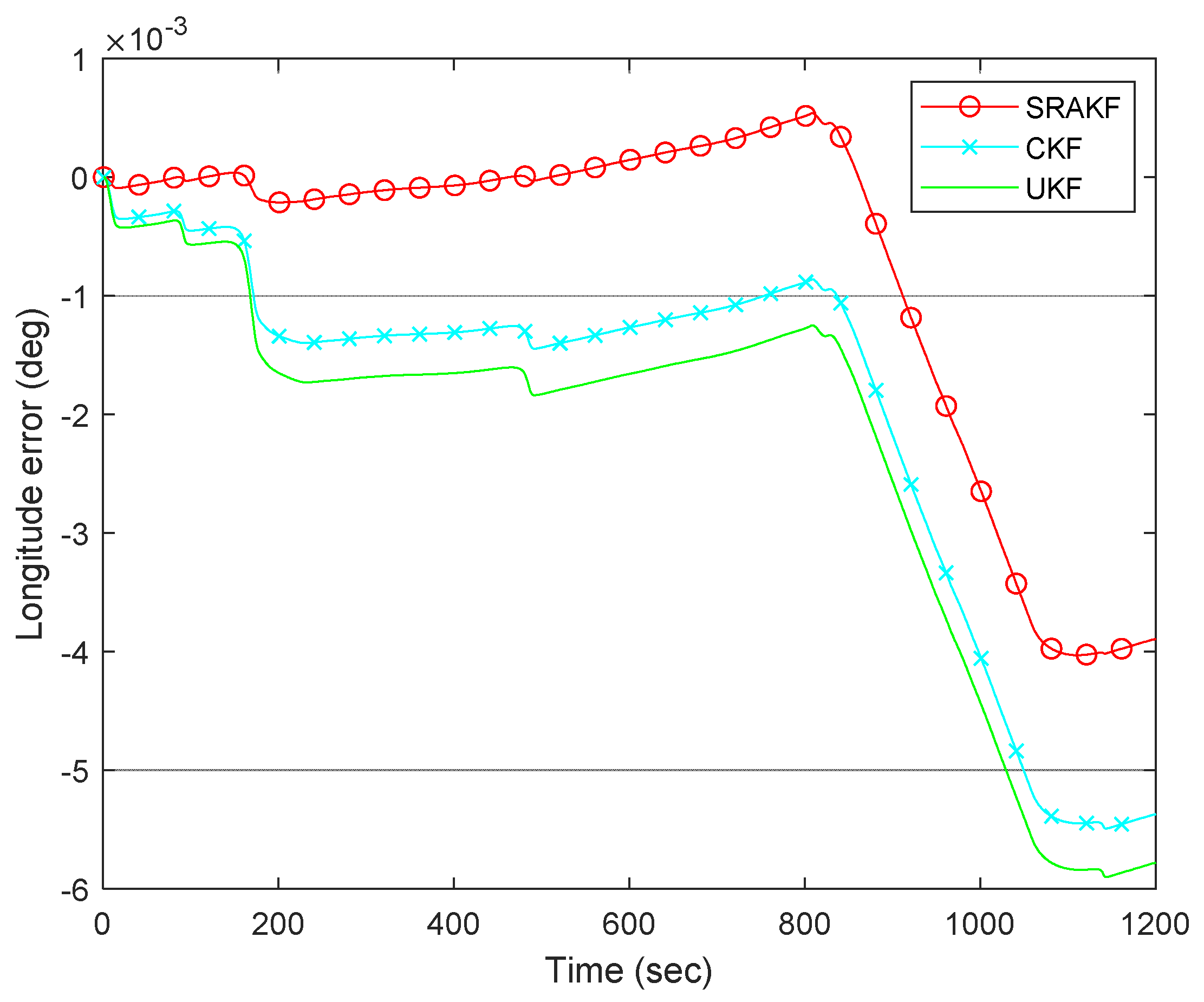



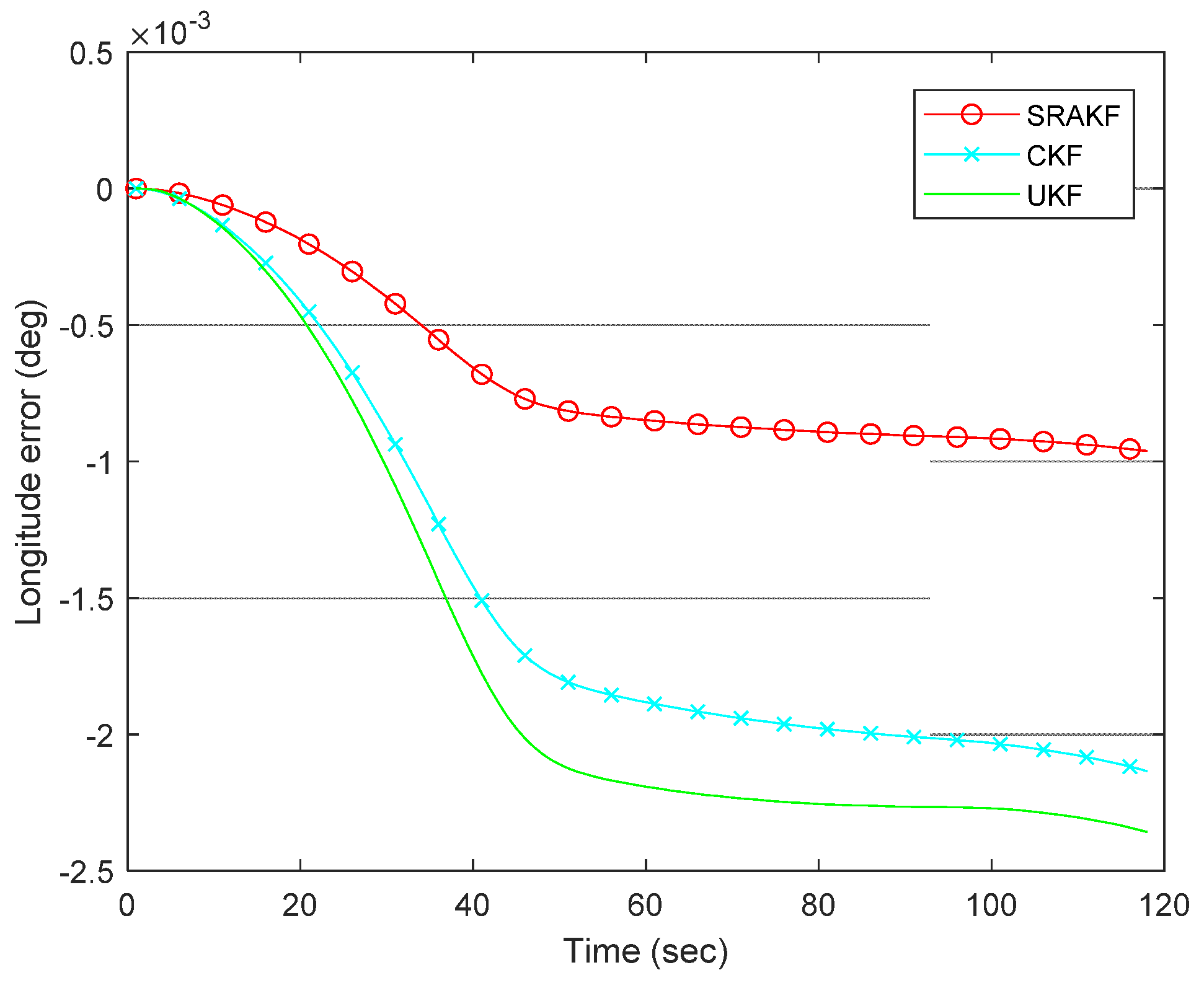


| Pre-Processing Data | Processed Data | |||||
|---|---|---|---|---|---|---|
| Sensors | Acce | Gyro | Mag | Acce | Gyro | Mag |
| RMSE | 0.1260 | 0.0035 | 0.0076 | 0.0886 | 0.0026 | 0.0051 |
| Accelerometers | Resolution | 0.1 mg(at ± 2 g range) |
| Bias in-run stability (RMS, Allan variance) | 50 μg | |
| SF accuracy | 0.1% | |
| Gyroscopes | Resolution | 0.01 deg/sec (at ± 250 deg/sec range) |
| Bias in-run stability (RMS, Allan variance) | 4 deg/hr | |
| SF accuracy | 0.01% | |
| Magnetometers | Resolution | 10 nT |
| Bias in-run stability (RMS, Allan variance) | 0.1 nT | |
| SF accuracy | 0.02% |
| Algorithms | UKF | CKF | SRAKF | |
|---|---|---|---|---|
| RMSE | ||||
| (deg) | 3.4998 × 10−4 | 3.2523 × 10−4 | 2.4298 × 10−4 | |
| (deg) | 2.2862 × 10−3 | 1.9509 × 10−3 | 8.9344 × 10−4 | |
| Algorithms | UKF | CKF | SRAKF | |
|---|---|---|---|---|
| RMSE | ||||
| (deg) | 1.1179 × 10−5 | 4.6089 × 10−6 | 2.0964 × 10−6 | |
| (deg) | 1.6797 × 10−3 | 1.4708 × 10−3 | 6.6276 × 10−4 | |
| Algorithms | UKF | CKF | SRAKF | |
|---|---|---|---|---|
| RMSE | ||||
| (deg) | 2.9388 × 10−5 | 2.9013 × 10−5 | 5.4470 × 10−6 | |
| (deg) | 2.3801 × 10−3 | 2.3713 × 10−3 | 1.4696 × 10−4 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, H.; Tang, J.; Zhang, B. Positioning Parameter Determination Based on Statistical Regression Applied to Autonomous Underwater Vehicle. Appl. Sci. 2021, 11, 7777. https://doi.org/10.3390/app11177777
Huang H, Tang J, Zhang B. Positioning Parameter Determination Based on Statistical Regression Applied to Autonomous Underwater Vehicle. Applied Sciences. 2021; 11(17):7777. https://doi.org/10.3390/app11177777
Chicago/Turabian StyleHuang, Haoqian, Jiacheng Tang, and Bo Zhang. 2021. "Positioning Parameter Determination Based on Statistical Regression Applied to Autonomous Underwater Vehicle" Applied Sciences 11, no. 17: 7777. https://doi.org/10.3390/app11177777
APA StyleHuang, H., Tang, J., & Zhang, B. (2021). Positioning Parameter Determination Based on Statistical Regression Applied to Autonomous Underwater Vehicle. Applied Sciences, 11(17), 7777. https://doi.org/10.3390/app11177777







